Nat. Commun. | 过冷冰核在异质环境中形成的微观路径：经典与非经典的竞争

香港科技大学黄旭辉教授（点击查看介绍）课题组首次通过基于分子动力学模拟构建的马尔科夫态模型来揭示了异质结冰的“非经典成核理论”机理，并且展示了“经典成核”与“非经典成核”的系综路径在过冷条件下的共存性。该研究成果近期发表于国际知名学术期刊《自然•通讯》（Nature Communications）。

水在低温条件结冰等相变现象十分普遍。此类相变不仅影响着大气气候、地质环境、生命生存等，而且是基础科学研究的关键问题。尤其在材料科学、低温生物学、物理学等领域有着重要意义及潜在应用价值。大约在百年前，吉布斯（Gibbs）等人基于热力学原理提出了“经典成核理论”。该理论认为相变需经过一个单步的成核过程，该过程对应于跨越一个自由能垒。例如，过冷水形成小冰核，仅当形成的拥有最终冰结构的冰核偶然超过临界尺寸，即当系统跨越临界冰核所对应的自由能垒，相变才能自发发生。但是，从动力学角度，由于系统倾向于沿着最低自由能的路径演化，在晶核形成的过程中极有可能形成不同于最终晶体结构的“中间过渡结构”，(如 Ostwald所述)。而这类成核理论被统称为“非经典成核理论”。实验中已经发现许多材料的结晶过程都不遵循“经典成核理论”，例如一些蛋白质及钙盐晶体的形成。但是，由于成核过程的偶然性、微观性以及快速性，微观观察挑战巨大。而探测该过程中是否存在过渡结构则更加困难。

自然界大部分的冰都是通过外界材料诱导成核，即“异质成核”，随后生长形成的。因此理解冰的异质成核机理，不仅能作为经典例子更深层次地理解相变成核机理，而且对潜在应用，如设计不结冰表面、防霜材料等，具有重要指导意义。利用大规模全原子分子动力学模拟，黄教授课题组研究了在异质条件下水变成冰核随时间演化的路径（Heterogeneous ice nucleation）。通过结合马尔可夫态模型（Markov State Models）和过渡路径理论(Transition path theory)，黄教授课题组揭示了“经典成核”和“非经典成核”的路径能够在过冷条件下（230开尔文）共存。其中，区别于经典成核路径中主要经历六角形冰（hexagonal ice，图1a左）直接形成这一步，在非经典成核路径中发现冰核混合着菱形（rhombic ice，图1a右）和六角形结构。而这混合冰核的形成只是成核过程的第一步，随着时间演化，这混合结构进一步转变成纯六角形冰。更有趣的是，通过定位和比较两类路径的临界冰核，该工作进一步发现沿着非经典路径的临界冰核主要得益于混合结构能够提高临界冰核位形熵，从而降低了沿着非经典路径需要跨越的自由能能垒；与之相比，经典路径所对应的临界冰核有着较低的作用势能。由此揭示了沿着截然两条不同成核路径能够在同一条件下共存。另外，通过建立及比较不同温度下冰核形成的马尔可夫态模型，黄教授课题组进一步发现了随着温度升高，成核路径逐渐趋向于走经典成核路径。

图1. 冰结构及选择代表性特征（反应坐标）。a、六角形和菱形冰结构。粉红色，青色，白色，和深灰色球分别代表六边形，菱形的氧原子，氢原子，和表面。紫色虚线代表氢键。b、冰（六角形和菱形）在不同的层。c、通过输入不同数量的特征, 重构系统动力学。当输入特征数为五时，其所构建的动力学在最慢的三个尺度已接近十八个输入特征全集所构建的动力学。

该工作开创性地运用马尔科夫态模型研究冰核形成的动力学。马尔科夫态模型已经被广泛运用于分析研究生物大分子构象变化的动力学，例如生物蛋白等的功能性构象变化 ^[1-2]。概括来说，马尔可夫态模型通过对系统轨迹所经历的相空间进行粗粒化分态处理，对时间进行离散化处理，从而在离散的时间序列上建立起离散态之间的动力学。当离散时间的间隔（lag time, τ）足够长，系统的运动仅由当前的状态决定而与之前的历史无关。这种情况被称为马尔科夫过程（Markovian）。在马尔科夫过程中，只要得到态与态之间的转移概率，就可以由主方程预测整个系统的长时间演化：P(t + nτ) = Tⁿ(τ)∙P(t)，其中P(t)为系统在t时刻处于某态的概率，T(τ)为时间间隔为τ 时态与态之间的转移概率。根据遍历性公设，一条在相空间中遍历的轨迹采样等同于按概率分布的多条轨迹的采样集合，因此实际体系中，转移概率矩阵可以通过大量的分子动力学模拟轨迹的数据合集来获取。当获得了实现马尔可夫过程的转移概率矩阵，研究离散态之间的动力学也就水到渠成了。

对于冰核形成的过程，为了建立马尔科夫模型，选择适当的特征（反应坐标）来代表系统在相空间所对应的态的转变是成功的关键。黄教授课题组利用Spectral-oASIS算法从初始的18个特征中选出5个代表特征。该算法能够选择一定数量的特征子集去最优化地重构特征全集的动力学。这五个特征分别为最大冰核中分子的个数，最大冰核中菱形冰的个数，最大冰核中六角形冰的个数，以及最大冰核中第二层，第三次，及三层以上六角形冰的个数（图1b）。通过这五个特征，其在最慢的三个动力学上能够达到18个特征的时间尺度（图1c）。因此我们可以认为冰核形成的动力学能够很好的被重构。拥有了合适的输入特征，接着就可以建立马尔可夫态模型。具体流程包括：（i）利用k-centers算法将相空间划分成1000个小态，通过Implied timescale analysis和Chapman-Kolmogorov test 验证建立的马尔可夫态模型在小态维度上实现马尔可夫过程；（ii）为了分析和展示方便，该工作利用PCCA+算法将小态合并成8个大态。具体详细步骤可参考原文及黄教授课题组的一些综述文章 ^[3-4]。

利用建立的马尔可夫态模型，黄教授课题组通过蒙特卡洛模拟在小态间的马尔可夫转变，产出足够数量的轨迹展示冰核形成过程，如图2a和2b所示。黄教授课题组发现生成的轨迹能够复现初始分子动力学模拟中就存在的经典和非经典成核过程。具体而言，在生成轨迹中有些轨迹包含一个激活过程（activation），而有些轨迹包含两个激活过程。沿着一个激活过程的轨迹，主要只有六角形冰形成，对应于经典成核路径（图2c，灰色路径）；而沿着两个激活过程的轨迹，在早期的形成的冰核中伴有大量的菱形结构，而这菱形冰后来又消失转化成了六角形冰（图2c，紫色，橙色，及红色路径）。这些路径对应于非经典的成核理论。通过结合过渡路径理论，黄教授课题组发现沿着不同路径成核的比例相近，由此论证了在温度为230开尔文条件下异质冰核形成经典和非经典路径的共存性。

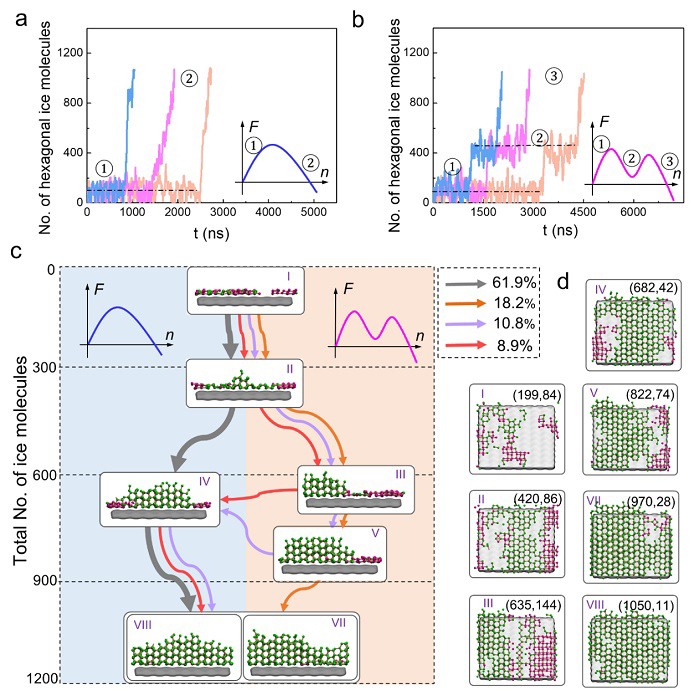
图2. 温度为230开尔文时的冰核形成路径。a、拥有单个激活过程的经典成核路径的马科夫链蒙特卡洛模拟生成轨迹。b、拥有两个激活过程的非经典成核路径的马科夫链蒙特卡洛模拟生成的轨迹。c、比较经典成核和非经典成核路径。灰色为经典路径，红色、紫色和橙色为非经典路径。其中每个构象图为每个大态的代表性构象（正向）。紫色球，绿色球，及灰色表面分别代表菱形、六角形冰以及表面。d、对应于c中每个大态沿[101]方向的构象图。

“有趣的是通过结合马尔可夫态模型和过渡路径理论，我们能够定位临界冰核，从而发现了沿着非经典路径的临界冰核主要得益于混合结构能够提高临界冰核位形熵，从而降低了该路径的自由能能垒。另外，通过比较不同温度下冰核形成路径，我们发现了随着温度升高，成核路径逐渐趋向于走经典成核路径，这可能对成核路径的调控具有指导意义。”黄教授说，“值得指出的是，该建模方法同样适用于研究其他相变成核过程，能够为类似研究提供一个强大的普适工具。”

该工作第一作者为香港科技大学博士后李楚，通讯作者为香港科技大学黄旭辉教授。

原文（扫描或长按二维码，识别后直达原文页面，或点此查看原文）：

Temperature-dependent kinetic pathways of heterogeneous ice nucleation competing between classical and non-classical nucleation

Chu Li, Zhuo Liu, Eshani C. Goonetilleke & Xuhui Huang

Nat. Commun., 2021, 12, 4954, DOI: 10.1038/s41467-021-25267-2

导师介绍

黄旭辉

https://www.x-mol.com/university/faculty/304555 

参考文献：

1. Unarta, I.S., Cao, S., Kubo, S., Wang, W., Cheung, P.P.H., Gao, X., Takada, S., Huang, X.* "Role of Bacterial RNA Polymerase Gate Opening Dynamics in DNA Loading and Antibiotics Inhibition Elucidated by quasi-Markov State Model", Proc. Nat. Acad. Sci. U.S.A., 118(17), e2024324118, (2021).

2. Peng, S., Wang, X., Zhang, L., He, S., Zhao, X. S.*, Huang, X.*, & Chen, C.*“Target search and recognition mechanisms of glycosylase AlkD revealed by scanning FRET-FCS and Markov state models.” Proc. Nat. Acad. Sci. U.S.A., 117(36), 21889-21895, (2020).

3. Wang, W., Cao, S., Zhu, L., Huang, X.*, “Constructing Markov State Models to Elucidate the Functional Conformational Changes of Complex Biomolecules”, WIREs Comput Mol Sci., 8:e1343, (2017).

4. Konovalov, K.A., Unarta, I.S., Cao, S., Goonetilleke1, E.C., Huang, X.*, “Markov state models to study the functional dynamics of proteins in the wake of machine learning”, J. Am. Chem. Soc. Au, Published On-line, (2021), DOI:10.1021/jacsau.1c00254.