Nature封面：“大道至简”的科学证据

首先，请诸君做个小测试。

下图是个乐高搭建的模型，一个“小人”站在尚未完工的屋檐下。糟糕的是，屋顶只有一个角有支柱支撑，稳定性很差，随时会掉下来砸到小人。现在要求您改进这个模型，保证小人的安全。需要注意的是，乐高积木并不免费，每增加一块需要花费10美分。您会怎么选择？

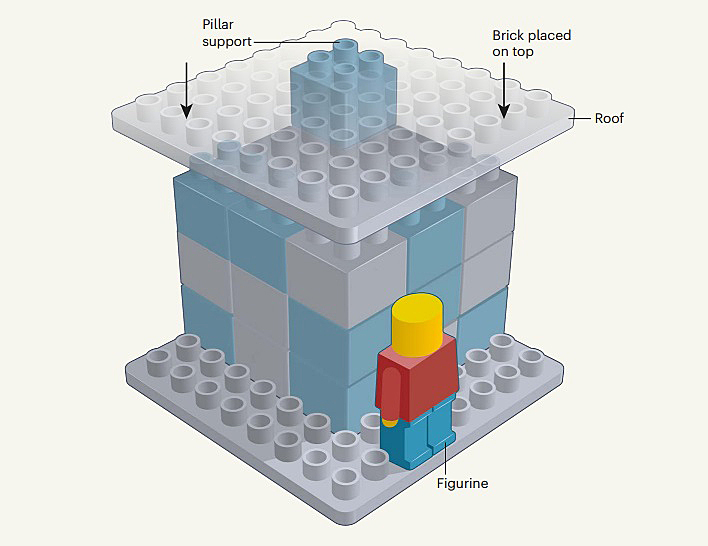
图1. 稳定性需改进的乐高模型。图片来源：Nature ^[1]

请您先记住您的这次选择。接下来，让我们把条件稍微改一下——每增加一块乐高积木需要花费10美分，但减少现有结构中的乐高积木却完全免费。您又会怎么选择？

不知道您的两次选择是否会有不同。笔者的第一次选择，是花费10美分在下图所示位置1处增加一个支柱，虽然不绝对稳定，但也足以支撑屋顶不掉落；而笔者的第二次选择，则是在“减少现有结构中的乐高积木却完全免费”的提示下，注意到可以去掉下图所示位置2处的支柱，让屋顶直接连在基座上，这样不但不用花钱，而且稳定性更好。

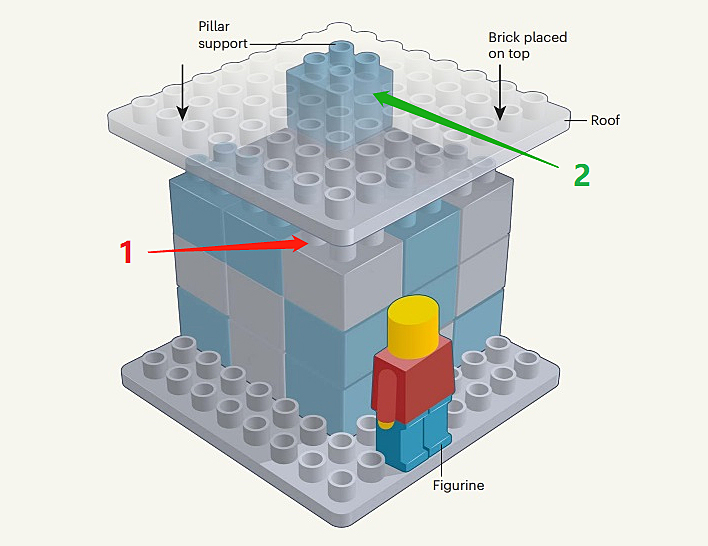
图2. 笔者的两次选择。

笔者的选择并非个例，而是与近期一篇Nature 杂志封面论文中的多数受试者选择相同。这个小小的测试在一定程度上支持了我们可能都曾有过的感受——在处理问题时，尤其在时间紧迫、领域陌生、存在决策压力的情况下，人们更倾向于加上一点什么（即增量方法），而不太容易想到要减去一点什么（即减量方法），即便后者可能更有优势。这也反应了我们日常挂在嘴边的一些道理，比如中国传统文化中的“大道至简”，以及现在非常流行的一句英语鸡汤“Less is more”。

图3. 当期封面。图片来源：Nature

回到来自美国弗吉尼亚大学的Gabrielle S. Adams和Benjamin A. Converse等人的这篇论文，他们研究的正是人们的这种思维模式。除了上面这个测试（实验1）之外，他们还设计了其他的多种测试，实验参与者总人数达到1585人。让我们来看看他们的其他测试项目。

一个测试项目是参与者需要为改进一个纸面上的微型高尔夫球场而献计献策。先来感受一下作者们简单粗暴的画风。

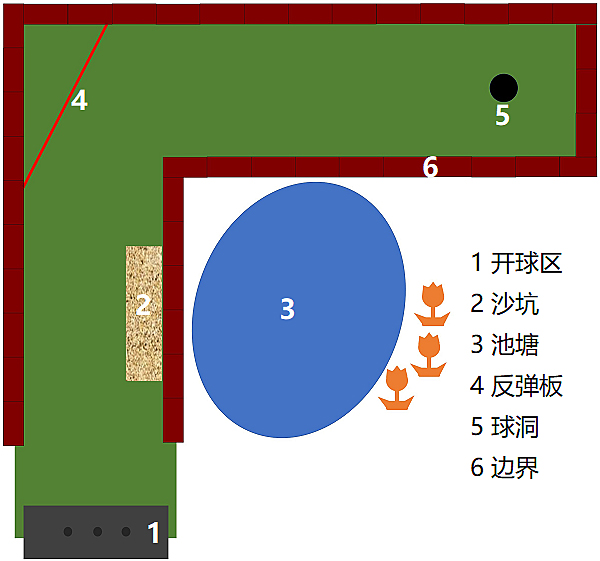
图4. 需改进的微型高尔夫球场（图中标注为笔者外加）。图片来源：Nature

不同的实验设定略有不同。比如，实验2中参与者要想象他们是这个高尔夫球场的助理经理，而老板给的工作就是“列出所有在不花费巨资的情况下改进这个球场的建议”。一组参与者获得了提示，“你既可以增加新设施，也可以去掉已有设施”，而另一组没有。这个实验与之前乐高模型实验最大的区别在于，乐高模型实验只需关注一点，而这个实验要求列出所有可能的改变，这样就可以在最大程度上减少评估在选择阶段的潜在作用。参与者的改进意见被归为三类：增量方案（例如为了提高难度而添加一个沙坑）、减量方案（例如为了减少难度而移除沙坑）或不增不减方案（例如调换开球区与球洞的位置）。结果也很有意思，给出的提示不会影响参与者提出一个增量方案的概率，却提高了参与者提出减量方案的概率。这意味着，对减量的提示似乎启发了参与者做出新的选择。

另一个项目类似于玩电脑游戏，参与者会看到一个10×10的网格（下图），每个格子要么绿色要么白色，鼠标点击会切换颜色。游戏的目标是用最少的点击次数使得网格左右上下都对称。一组参与者有三次练习的机会（下图a-c），然后面对最终任务（下图d），而另一组参与者没有练习机会，直接面对最终任务。练习的图案是专门设计的，可以让参与者有更多机会发现增量方案比减量方案要麻烦。比如下图a中的练习图案，增量方案需要点击9次增加9个绿色格子，而减量方案仅需点击3次去掉3个绿色格子。结果显示，有练习机会的参与者选择减量方案的比例要明显高于没有练习机会的参与者，这表明当参与者有更多的机会去思考特定任务中增量方案的缺点时，他们更有可能选择更优的减量方案。不过，在较高认知负荷（cognitive load）条件下，比如一边测试一边转动脑袋，或者一边测试一边分心从另外随机出现的数字中点出某一数字，参与者就不再倾向于选择更优的减量方案了。

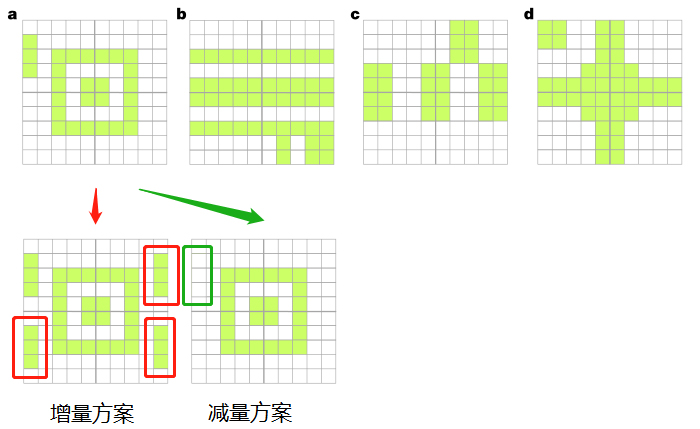
图5. 需改为对称的绿白网格（图中增量、减量方案为笔者外加）。图片来源：Nature

这些实验证明，在遇到问题时人们默认的解决方案更可能是增量方案，而非减量方案。要让人们意识到减量方案的优势，需要有额外的提示，或者有机会发现增量方法的缺点，或者能集中注意力以降低认知负荷。也就是说，做决策的过程，要有意识的避免“增量陷阱”，才有可能实现最优。这和“大道至简”的人生智慧不谋而合。

很久以前，曾有人问意大利美术家米开朗基罗“你是如何创作出著名雕塑大卫的？”他答道：“我只不过是从一块巨大的大理石上凿去多余的石头，留下来的就是大卫。”在我们的生活和工作中，做加法并不一定是最优方案，要经常提醒自己想想减法是否更优，断离舍，去糟粕留精华，或许更显智慧。

原文（扫描或长按二维码，识别后直达原文页面，或点此查看原文）：

People systematically overlook subtractive changes

Gabrielle S. Adams, Benjamin A. Converse, Andrew H. Hales, Leidy E. Klotz 

Nature, 2021, 592, 258–261, DOI: 10.1038/s41586-021-03380-y

参考文献：

1. Adding is favoured over subtracting in problem solving. Nature, 2021, 592, 189-190, DOI: 10.1038/d41586-021-00592-0

（本文由水村山郭供稿）