For fixed 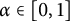$\alpha \in [0,1]$ , consider the set 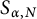$S_{\alpha ,N}$ of dilated squares 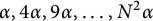$\alpha , 4\alpha , 9\alpha , \dots , N^2\alpha \, $ modulo 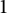$1$ . Rudnick and Sarnak conjectured that, for Lebesgue, almost all such 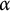$\alpha $ the gap-distribution of 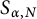$S_{\alpha ,N}$ is consistent with the Poisson model (in the limit as N tends to infinity). 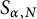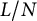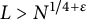In this paper, we prove a new estimate for the triple correlations associated with this problem, establishing an asymptotic expression for the third moment of the number of elements of $S_{\alpha ,N}$ in a random interval of length $L/N$ , provided that $L> N^{1/4+\varepsilon }$ . 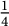The threshold of $\tfrac {1}{4}$ is substantially smaller than the threshold of 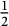$\tfrac {1}{2}$ (which is the threshold that would be given by a naïve discrepancy estimate).

Unlike the theory of pair correlations, rather little is known about triple correlations of the dilations 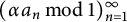$(\alpha a_n \, \text {mod } 1)_{n=1}^{\infty } $ for a nonlacunary sequence 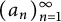$(a_n)_{n=1}^{\infty } $ of increasing integers. This is partially due to the fact that the second moment of the triple correlation function is difficult to control, and thus standard techniques involving variance bounds are not applicable. We circumvent this impasse by using an argument inspired by works of Rudnick, Sarnak, and Zaharescu, and Heath-Brown, which connects the triple correlation function to some modular counting problems.

In Appendix B, we comment on the relationship between discrepancy and correlation functions, answering a question of Steinerberger.

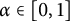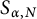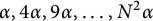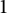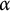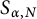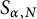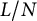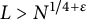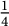对于固定 $\alpha \in [0,1]$ ，考虑扩张正方形 $\alpha , 4\alpha , 9\alpha , \dots , N^2\alpha \的集合 $S_{\alpha ,N}$ , $ 模 $1$ 。Rudnick 和 Sarnak 推测，对于 Lebesgue，几乎所有这样的 $\alpha $$ S_{\alpha,N}$ 的间隙分布都与泊松模型一致（在N趋于无穷大的极限内）。在本文中，我们证明了与该问题相关的三重相关的新估计，建立了在长度 为 $L/的随机区间内 $S_{\alpha ,N}$ 的元素个数的三阶矩的渐近表达式N$ , 前提是 $L> N^{1/4+\varepsilon }$ 。 $\tfrac {1}{4}$ 的阈值远小于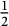 $\tfrac {1}{2}$ 的阈值（这是由天真的差异估计给出的阈值）。

与对相关理论不同，对于非空缺序列 $(a_n的膨胀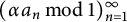 $(\alpha a_n \, \text {mod } 1)_{n=1}^{\infty } $ 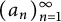)_{n=1}^{\infty } $ 个递增整数。这部分是由于三重相关函数的二阶矩难以控制，因此涉及方差界限的标准技术不适用。我们通过使用受 Rudnick、Sarnak 和 Zaharescu 以及 Heath-Brown 的作品启发的论点来绕过这一僵局，该论点将三重相关函数与一些模块化计数问题联系起来。

在附录 B 中，我们评论了差异和相关函数之间的关系，回答了 Steinerberger 的问题。