Canadian Journal of Mathematics ( IF 0.6 ) Pub Date : 2021-02-26 , DOI: 10.4153/s0008414x21000110 Feng Dai , Andriy Prymak
This paper studies a new Whitney type inequality on a compact domain
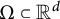 $\Omega \subset {\mathbb R}^d$
that takes the form
$$ \begin{align*} \inf_{Q\in \Pi_{r-1}^d(\mathcal{E})} \|f-Q\|_p \leq C(p,r,\Omega) \omega_{\mathcal{E}}^r(f,\mathrm{diam}(\Omega))_p,\ \ r\in {\mathbb N},\ \ 0<p\leq \infty, \end{align*} $$
$\Omega \subset {\mathbb R}^d$
that takes the form
$$ \begin{align*} \inf_{Q\in \Pi_{r-1}^d(\mathcal{E})} \|f-Q\|_p \leq C(p,r,\Omega) \omega_{\mathcal{E}}^r(f,\mathrm{diam}(\Omega))_p,\ \ r\in {\mathbb N},\ \ 0<p\leq \infty, \end{align*} $$
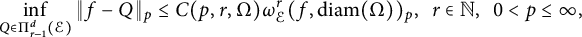 where
where
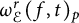 $\omega _{\mathcal {E}}^r(f, t)_p$
denotes the rth order directional modulus of smoothness of
$\omega _{\mathcal {E}}^r(f, t)_p$
denotes the rth order directional modulus of smoothness of
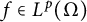 $f\in L^p(\Omega )$
along a finite set of directions
$f\in L^p(\Omega )$
along a finite set of directions
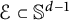 $\mathcal {E}\subset \mathbb {S}^{d-1}$
such that
$\mathcal {E}\subset \mathbb {S}^{d-1}$
such that
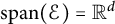 $\mathrm {span}(\mathcal {E})={\mathbb R}^d$
,
$\mathrm {span}(\mathcal {E})={\mathbb R}^d$
,
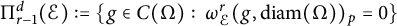 $\Pi _{r-1}^d(\mathcal {E}):=\{g\in C(\Omega ):\ \omega ^r_{\mathcal {E}} (g, \mathrm {diam} (\Omega ))_p=0\}$
. We prove that there does not exist a universal finite set of directions
$\Pi _{r-1}^d(\mathcal {E}):=\{g\in C(\Omega ):\ \omega ^r_{\mathcal {E}} (g, \mathrm {diam} (\Omega ))_p=0\}$
. We prove that there does not exist a universal finite set of directions
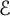 $\mathcal {E}$
for which this inequality holds on every convex body
$\mathcal {E}$
for which this inequality holds on every convex body
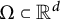 $\Omega \subset {\mathbb R}^d$
, but for every connected
$\Omega \subset {\mathbb R}^d$
, but for every connected
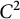 $C^2$
-domain
$C^2$
-domain
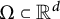 $\Omega \subset {\mathbb R}^d$
, one can choose
$\Omega \subset {\mathbb R}^d$
, one can choose
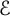 $\mathcal {E}$
to be an arbitrary set of d independent directions. We also study the smallest number
$\mathcal {E}$
to be an arbitrary set of d independent directions. We also study the smallest number
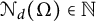 $\mathcal {N}_d(\Omega )\in {\mathbb N}$
for which there exists a set of
$\mathcal {N}_d(\Omega )\in {\mathbb N}$
for which there exists a set of
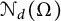 $\mathcal {N}_d(\Omega )$
directions
$\mathcal {N}_d(\Omega )$
directions
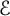 $\mathcal {E}$
such that
$\mathcal {E}$
such that
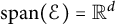 $\mathrm {span}(\mathcal {E})={\mathbb R}^d$
and the directional Whitney inequality holds on
$\mathrm {span}(\mathcal {E})={\mathbb R}^d$
and the directional Whitney inequality holds on
 $\Omega $
for all
$\Omega $
for all
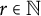 $r\in {\mathbb N}$
and
$r\in {\mathbb N}$
and
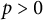 $p>0$
. It is proved that
$p>0$
. It is proved that
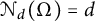 $\mathcal {N}_d(\Omega )=d$
for every connected
$\mathcal {N}_d(\Omega )=d$
for every connected
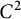 $C^2$
-domain
$C^2$
-domain
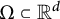 $\Omega \subset {\mathbb R}^d$
, for
$\Omega \subset {\mathbb R}^d$
, for
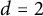 $d=2$
and every planar convex body
$d=2$
and every planar convex body
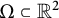 $\Omega \subset {\mathbb R}^2$
, and for
$\Omega \subset {\mathbb R}^2$
, and for
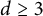 $d\ge 3$
and every almost smooth convex body
$d\ge 3$
and every almost smooth convex body
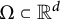 $\Omega \subset {\mathbb R}^d$
. For
$\Omega \subset {\mathbb R}^d$
. For
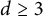 $d\ge 3$
and a more general convex body
$d\ge 3$
and a more general convex body
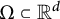 $\Omega \subset {\mathbb R}^d$
, we connect
$\Omega \subset {\mathbb R}^d$
, we connect
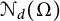 $\mathcal {N}_d(\Omega )$
with a problem in convex geometry on the X-ray number of
$\mathcal {N}_d(\Omega )$
with a problem in convex geometry on the X-ray number of
 $\Omega $
, proving that if
$\Omega $
, proving that if
 $\Omega $
is X-rayed by a finite set of directions
$\Omega $
is X-rayed by a finite set of directions
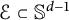 $\mathcal {E}\subset \mathbb {S}^{d-1}$
, then
$\mathcal {E}\subset \mathbb {S}^{d-1}$
, then
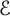 $\mathcal {E}$
admits the directional Whitney inequality on
$\mathcal {E}$
admits the directional Whitney inequality on
 $\Omega $
for all
$\Omega $
for all
 $r\in {\mathbb N}$
and
$r\in {\mathbb N}$
and
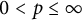 $0<p\leq \infty $
. Such a connection allows us to deduce certain quantitative estimate of
$0<p\leq \infty $
. Such a connection allows us to deduce certain quantitative estimate of
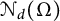 $\mathcal {N}_d(\Omega )$
for
$\mathcal {N}_d(\Omega )$
for
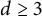 $d\ge 3$
.
$d\ge 3$
.
A slight modification of the proof of the usual Whitney inequality in literature also yields a directional Whitney inequality on each convex body
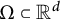 $\Omega \subset {\mathbb R}^d$
, but with the set
$\Omega \subset {\mathbb R}^d$
, but with the set
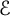 $\mathcal {E}$
containing more than
$\mathcal {E}$
containing more than
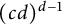 $(c d)^{d-1}$
directions. In this paper, we develop a new and simpler method to prove the directional Whitney inequality on more general, possibly nonconvex domains requiring significantly fewer directions in the directional moduli.
$(c d)^{d-1}$
directions. In this paper, we develop a new and simpler method to prove the directional Whitney inequality on more general, possibly nonconvex domains requiring significantly fewer directions in the directional moduli.
中文翻译:

关于定向惠特尼不等式
本文研究了紧凑域
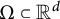 $\Omega \subset {\mathbb R}^d$
上的新 Whitney 类型不等式,其形式为
$$ \begin{align*} \inf_{Q\in \Pi_{r-1} ^d(\mathcal{E})} \|fQ\|_p \leq C(p,r,\Omega) \omega_{\mathcal{E}}^r(f,\mathrm{diam}(\Omega) )_p,\ \ r\in {\mathbb N},\ \ 0<p\leq \infty, \end{align*} $$
$\Omega \subset {\mathbb R}^d$
上的新 Whitney 类型不等式,其形式为
$$ \begin{align*} \inf_{Q\in \Pi_{r-1} ^d(\mathcal{E})} \|fQ\|_p \leq C(p,r,\Omega) \omega_{\mathcal{E}}^r(f,\mathrm{diam}(\Omega) )_p,\ \ r\in {\mathbb N},\ \ 0<p\leq \infty, \end{align*} $$
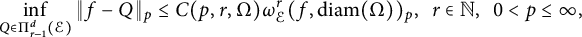 其中
其中
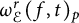 $\omega _{\mathcal {E}}^r(f, t )_p$
表示
$f\in L^p(\Omega )$
沿有限方向集
$\mathcal {E}\subset \mathbb {S}^{d-1}的第r阶方向模数
$
使得
$\mathrm {span}(\mathcal {E})={\mathbb R}^d$
,
$\omega _{\mathcal {E}}^r(f, t )_p$
表示
$f\in L^p(\Omega )$
沿有限方向集
$\mathcal {E}\subset \mathbb {S}^{d-1}的第r阶方向模数
$
使得
$\mathrm {span}(\mathcal {E})={\mathbb R}^d$
,
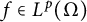
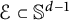
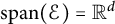
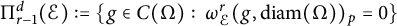 $\Pi _{r-1}^d(\mathcal {E}):=\{g\in C(\Omega ):\ \omega ^r_{\mathcal {E}} (g, \mathrm {diam } (\Omega ))_p=0\}$
。我们证明不存在
这个不等式在每个凸体
$\Omega \subset {\mathbb R}^d$
上都成立的通用有限方向集
$\Pi _{r-1}^d(\mathcal {E}):=\{g\in C(\Omega ):\ \omega ^r_{\mathcal {E}} (g, \mathrm {diam } (\Omega ))_p=0\}$
。我们证明不存在
这个不等式在每个凸体
$\Omega \subset {\mathbb R}^d$
上都成立的通用有限方向集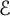 $\mathcal {E}$
,但是对于每个连接的
$C^ 2$
-domain
$\Omega \subset {\mathbb R}^d$
,可以选择
$\mathcal {E}$
作为任意d独立方向的集合。我们还研究了存在一组
$\mathcal {N}_d(\Omega )$
方向
$\mathcal {E的最小数
$\mathcal {N}_d(\Omega )\in {\mathbb N}$
}$
$\mathcal {E}$
,但是对于每个连接的
$C^ 2$
-domain
$\Omega \subset {\mathbb R}^d$
,可以选择
$\mathcal {E}$
作为任意d独立方向的集合。我们还研究了存在一组
$\mathcal {N}_d(\Omega )$
方向
$\mathcal {E的最小数
$\mathcal {N}_d(\Omega )\in {\mathbb N}$
}$
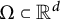
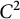
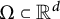
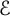
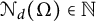
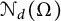
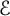 使得
使得
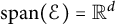 $\mathrm {span}(\mathcal {E})={\mathbb R}^d$
并且对于所有
$r\in {\mathbb N}$
和
$p,方向 Whitney 不等式在
$\mathrm {span}(\mathcal {E})={\mathbb R}^d$
并且对于所有
$r\in {\mathbb N}$
和
$p,方向 Whitney 不等式在
 $\Omega $
上成立>0 美元
。证明了
$\mathcal {N}_d(\Omega )=d$
对于每个连接的
$C^2$
-domain
$\Omega \subset {\mathbb R}^d$
,对于
$d=2$
和每个平面凸体
$\Omega \subset {\mathbb R}^2$
,对于
$d\ge 3$
和每个几乎光滑的凸体
$\Omega \subset {\mathbb R}^d$
。对于
$d\ge 3$
和更一般的凸体
$\Omega \subset {\mathbb R}^d$
$\Omega $
上成立>0 美元
。证明了
$\mathcal {N}_d(\Omega )=d$
对于每个连接的
$C^2$
-domain
$\Omega \subset {\mathbb R}^d$
,对于
$d=2$
和每个平面凸体
$\Omega \subset {\mathbb R}^2$
,对于
$d\ge 3$
和每个几乎光滑的凸体
$\Omega \subset {\mathbb R}^d$
。对于
$d\ge 3$
和更一般的凸体
$\Omega \subset {\mathbb R}^d$
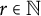
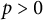
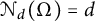
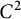
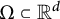
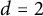
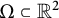
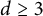
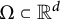
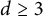
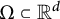 ,我们将
,我们将
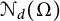 $\mathcal {N}_d(\Omega )$
与 X 射线数
$\mathcal {N}_d(\Omega )$
与 X 射线数
 $\Omega $
上的凸几何问题联系起来,证明如果
$\Omega $
上的凸几何问题联系起来,证明如果
 $\Omega $
是通过有限方向集进行 X 射线
$\Omega $
是通过有限方向集进行 X 射线
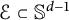 $\mathcal {E}\subset \mathbb {S}^{d-1}$
,则
$\mathcal {E}\subset \mathbb {S}^{d-1}$
,则
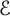 $\mathcal {E}$
承认所有
$r\in {\mathbb N}在
$\mathcal {E}$
承认所有
$r\in {\mathbb N}在 $\Omega $
上的方向惠特尼不等式
$\Omega $
上的方向惠特尼不等式
 $
和
$
和
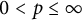 $0<p\leq \infty $
。这样的联系使我们能够推断出对
$d\ge 3$
的
$0<p\leq \infty $
。这样的联系使我们能够推断出对
$d\ge 3$
的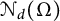 $\mathcal {N}_d(\Omega )$
的某些定量估计
。
$\mathcal {N}_d(\Omega )$
的某些定量估计
。
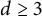
对文献中常见的 Whitney 不等式的证明稍作修改,也会在每个凸体
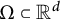 $\Omega \subset {\mathbb R}^d$
上产生一个定向 Whitney 不等式,但集合
$\Omega \subset {\mathbb R}^d$
上产生一个定向 Whitney 不等式,但集合
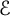 $\mathcal {E}$
包含更多比
$\mathcal {E}$
包含更多比
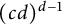 $(cd)^{d-1}$ 个
方向。在本文中,我们开发了一种新的更简单的方法来证明方向惠特尼不等式在更一般的、可能是非凸域上需要显着更少的方向模量。
$(cd)^{d-1}$ 个
方向。在本文中,我们开发了一种新的更简单的方法来证明方向惠特尼不等式在更一般的、可能是非凸域上需要显着更少的方向模量。











































 京公网安备 11010802027423号
京公网安备 11010802027423号