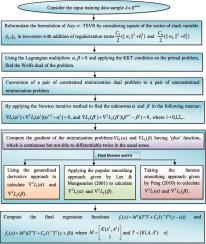
The main objective of twin support vector regression (TSVR) is to find the optimum regression function based on the $\epsilon$-insensitive up- and down-bound with equal influences on the regression function where all the data points have a different location above the up-bound points and below the down-bound points. However, the effects of all data points must be distinct based on their distribution in the regression function. Recently, asymmetric $\nu$-twin support vector regression (Asy-$\nu$-TSVR) is encouraged on the same subject but still, the present matrices in the mathematical formulation have faced the problem of semi-definite. In order to handle this problem effectively, a new regressor model named as robust asymmetric Lagrangian $\nu$-twin support vector regression using pinball loss function (URALTSVR) proposes as a pair of the unconstrained minimization problem to handle not only the noise sensitivity and instability of re-sampling but also consist positive definite matrices. Here, we suggest the proposed model URALTSVR in such a way where the pinball loss function is playing a vital role to control the fitting error inside the asymmetric tube. One of the advantages is that unlike TSVR and Asy-$\nu$-TSVR, it considers the concept of structural risk minimization principle through the inclusion of regularization term as well as change the one-norm of the vector of the slack variable by two-norm, which yields the dual problem to be strongly convex, stable and well-posed. Aforementioned, the proposed formulation has a continuous and piecewise quadratic problem that is solved by their gradients based iterative approaches. Specifically, we analyze the three implementations of URALTSVR with the baselines approaches support vector regression (SVR), TSVR and Asy-$\nu$-TSVR, which discard the dependencies to solve a pair of quadratic programming problem (QPP) for obtaining the unique global solution. Overall, SRALTSVR1 based on smooth approximation function performs outstanding for artificial and real-world datasets.

双支持向量回归（TSVR）的主要目标是基于 $\epsilon$不敏感的上下限，对回归函数具有相同的影响，在该函数中，所有数据点在上界点上方和下界点下方均具有不同的位置。但是，所有数据点的影响必须基于它们在回归函数中的分布而不同。最近不对称$\nu$-双支持向量回归（Asy-$\nu$（TSVR）鼓励在同一主题上使用，但仍然，目前数学公式中的矩阵面临半定性问题。为了有效处理此问题，新的回归模型称为鲁棒非对称拉格朗日模型$\nu$使用弹球损失函数（URALTSVR）的双胞胎支持向量回归建议作为一对无约束最小化问题，以解决噪声敏感性和重采样的不稳定性，并且还包括正定矩阵。在这里，我们建议所提出的模型URALTSVR，其中弹球损失功能对于控制非对称管内的装配误差起着至关重要的作用。优点之一是，与TSVR和Asy-$\nu$-TSVR，它通过包含正则项来考虑结构风险最小化原理的概念，并将松弛变量的矢量的一个范数更改为两个范数，从而产生对偶问题：强凸，稳定和身体状况良好。如上所述，所提出的公式具有连续和分段的二次问题，该问题通过基于梯度的迭代方法得以解决。具体来说，我们使用支持向量回归（SVR），TSVR和Asy-$\nu$-TSVR，它丢弃依赖关系以解决一对二次编程问题（QPP），以获得唯一的全局解决方案。总体而言，基于平滑逼近函数的SRALTSVR1在人工和真实数据集方面均表现出色。