Canadian Mathematical Bulletin ( IF 0.5 ) Pub Date : 2020-08-20 , DOI: 10.4153/s0008439520000661 William Chan
A set
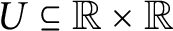 $U \subseteq {\mathbb {R}} \times {\mathbb {R}}$
is universal for countable subsets of
$U \subseteq {\mathbb {R}} \times {\mathbb {R}}$
is universal for countable subsets of
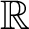 ${\mathbb {R}}$
if and only if for all
${\mathbb {R}}$
if and only if for all
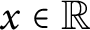 $x \in {\mathbb {R}}$
, the section
$x \in {\mathbb {R}}$
, the section
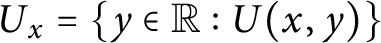 $U_x = \{y \in {\mathbb {R}} : U(x,y)\}$
is countable and for all countable sets
$U_x = \{y \in {\mathbb {R}} : U(x,y)\}$
is countable and for all countable sets
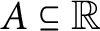 $A \subseteq {\mathbb {R}}$
, there is an
$A \subseteq {\mathbb {R}}$
, there is an
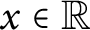 $x \in {\mathbb {R}}$
so that
$x \in {\mathbb {R}}$
so that
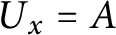 $U_x = A$
. Define the equivalence relation
$U_x = A$
. Define the equivalence relation
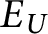 $E_U$
on
$E_U$
on
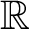 ${\mathbb {R}}$
by
${\mathbb {R}}$
by
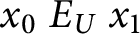 $x_0 \ E_U \ x_1$
if and only if
$x_0 \ E_U \ x_1$
if and only if
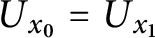 $U_{x_0} = U_{x_1}$
, which is the equivalence of codes for countable sets of reals according to U. The Friedman–Stanley jump,
$U_{x_0} = U_{x_1}$
, which is the equivalence of codes for countable sets of reals according to U. The Friedman–Stanley jump,
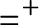 $=^+$
, of the equality relation takes the form
$=^+$
, of the equality relation takes the form
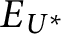 $E_{U^*}$
where
$E_{U^*}$
where
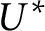 $U^*$
is the most natural Borel set that is universal for countable sets. The main result is that
$U^*$
is the most natural Borel set that is universal for countable sets. The main result is that
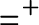 $=^+$
and
$=^+$
and
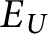 $E_U$
for any U that is Borel and universal for countable sets are equivalent up to Borel bireducibility. For all U that are Borel and universal for countable sets,
$E_U$
for any U that is Borel and universal for countable sets are equivalent up to Borel bireducibility. For all U that are Borel and universal for countable sets,
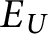 $E_U$
is Borel bireducible to
$E_U$
is Borel bireducible to
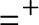 $=^+$
. If one assumes a particular instance of
$=^+$
. If one assumes a particular instance of
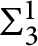 $\mathbf {\Sigma }_3^1$
-generic absoluteness, then for all
$\mathbf {\Sigma }_3^1$
-generic absoluteness, then for all
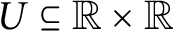 $U \subseteq {\mathbb {R}} \times {\mathbb {R}}$
that are
$U \subseteq {\mathbb {R}} \times {\mathbb {R}}$
that are
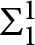 $\mathbf {\Sigma }_1^1$
(continuous images of Borel sets) and universal for countable sets, there is a Borel reduction of
$\mathbf {\Sigma }_1^1$
(continuous images of Borel sets) and universal for countable sets, there is a Borel reduction of
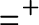 $=^+$
into
$=^+$
into
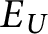 $E_U$
.
$E_U$
.
中文翻译:

可数实数集的代码等价
集合
$U \subseteq {\mathbb {R}} \times {\mathbb {R}}$
对于
${\mathbb {R}}$ 的
可数子集是通用的
当且仅当对于所有
$x \in {\ mathbb {R}}$
,部分
$U_x = \{y \in {\mathbb {R}} : U(x,y)\}$
是可数的并且对于所有可数集
$A \subseteq {\mathbb {R }}$
,有一个
$x \in {\mathbb {R}}$
这样
$U_x = A$
。通过
$x_0 \ E_U \ x_1$
定义
${\mathbb {R}}
$上
的等价关系
$E_U$
当且仅当
$U_{x_0} = U_{x_1}$
,这是可数集的代码等价根据U的实数
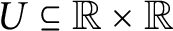
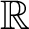
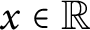
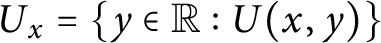
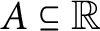
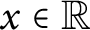
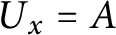
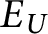
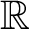
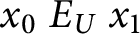
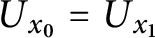 . 等式关系的 Friedman–Stanley 跳跃
$=^+$
的形式
为 $E_{U^*}$
,其中
$U^*$
是最自然的 Borel 集,对于可数集是通用的。主要结果是
$=^+$
和
$E_U$
对于任何是 Borel 和可数集通用的U都等价于 Borel 双可约性。对于所有对可数集来说是 Borel 和通用的U,
$E_U$
是 Borel 可双约到
$=^+$ 的
。如果假设
$\mathbf {\Sigma }_3^1$ -
泛型绝对性的特定实例
,那么对于所有
$U \subseteq {\mathbb {R}} \times {\mathbb {R}}$
. 等式关系的 Friedman–Stanley 跳跃
$=^+$
的形式
为 $E_{U^*}$
,其中
$U^*$
是最自然的 Borel 集,对于可数集是通用的。主要结果是
$=^+$
和
$E_U$
对于任何是 Borel 和可数集通用的U都等价于 Borel 双可约性。对于所有对可数集来说是 Borel 和通用的U,
$E_U$
是 Borel 可双约到
$=^+$ 的
。如果假设
$\mathbf {\Sigma }_3^1$ -
泛型绝对性的特定实例
,那么对于所有
$U \subseteq {\mathbb {R}} \times {\mathbb {R}}$
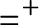
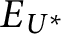
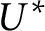
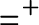
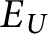
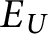
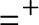
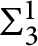
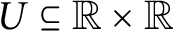 这是
$\mathbf {\Sigma }_1^1$
(Borel 集的连续图像)和可数集的通用,有
$=^+$
的 Borel 减少
到
$E_U$
。
这是
$\mathbf {\Sigma }_1^1$
(Borel 集的连续图像)和可数集的通用,有
$=^+$
的 Borel 减少
到
$E_U$
。
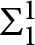
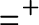
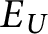











































 京公网安备 11010802027423号
京公网安备 11010802027423号