Introduction

Using graphs for smart city network applications has a long history for improving our lives, as reviewed in Helbing et al. (2014), where the authors discussed different models of crowd disasters, and different useful approached to system behaviour that help handling those cases. Another aspect of improving human lives is also by devising smart cooperation strategies, as reviewed in Perc et al. (2017), where the authors review the advances in the understanding of human cooperation, focusing on spatial pattern formation and on the spatio-temporal dynamics of observed solutions. A key aspect of these applications are also the information cascades, as reviewed in Jalili and Perc (2017), where the authors review models that describe information cascades, that are dynamical processes in complex networks. These describe the spreading dynamics of campaigns, diseases, rumors, etc., which initially start from a node or a set of nodes in the network. A special emphasis is given to the role and consequences of node centrality. Different smart city applications, with the combination of social benefits are a topic of contemporary research in many papers over the last couple of years such as (Barzilai et al. 2018), that handles social priorities in a smart junction with an algorithm that takes into consideration these priorities. In the last decade the topic of large dynamic graphs became popular since it lies at the core of many modern smart city network applications. Managing these graphs in a distributed manner is an efficient heuristic dealt with in many papers such as the ones of (Mondal and Deshpande 2012; Yang et al. 2012; Wang et al. 2014; Gao et al. 2014; Gonzalez et al. 2014). Large distributed dynamic (LDD) graphs creates a problem known as the distributed monitoring problem, presented by Cormode et al. (2006), and dealt with by Babcock and Olston (2003), in which we wish to find if an LDD graph holds a certain global property, while its distributed sub-graphs are constantly changing, and might or might not hold this property locally. We denote a certain graph by G=(V,E), for which v∈V and e∈E are the graphs’ vertices (having different entities), and graph connections respectively. We denote a global graph property by T, which can set as a certain threshold. We denote the local graph properties (thresholds) by Ti where i≤k and k is the number of sub-graphs G is distributed to. These sub-graphs are denoted by data-sets D1,D2,.....Dk.

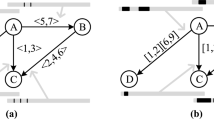
An example (described in Fig. 1), shows an attribute which can be handled in a certain graph G which is \(\overline {deg}(G(V))\)– the vertices average degree (number of edges incident to a vertex). At some starting point t=0 Fig. 1 panel (a) \(\overline {deg}(D_{1}(V))|_{t=0}=2.5, \overline {deg}(D_{2}(V))|_{t=0}=2.4\) and \(\overline {deg}(D_{3}(V))|_{t=0}=2.67\), giving \(\overline {deg}(G(V))|_{t=0}=2.52\), which is greater than some global threshold T arbitrary set to be ≥ 1.6.

Fig. 1
figure 1

A schematic global smart city graph breaching caused by a local breach. The attribute which is handled in a graph G is \(\overline {deg}(G(V))\)– the vertices average degree (number of edges incident to a vertex). a At some starting point \(t=0 \overline {deg}(D_{1}(V))|_{t=0}=2.5, \overline {deg}(D_{2}(V))|_{t=0}=2.4\) and \(\overline {deg}(D_{3}(V))|_{t=0}=2.67\), giving \(\overline {deg}(G(V))|_{t=0}=2.52\), which is greater than the global graph threshold T preliminary set to be ≥ 1.6. b A change occurs locally at t= 1min for which \(\overline {deg}(D_{1}(V))|_{t=1}=1\), meaning several edges in D1 (B, C) were removed and the local threshold T1 was breached, however not the global T, since still \(\overline {deg}(G(V))|_{t=1}=1.97>1.6\). c A breach of T3 occurred at t=2, in which \(\overline {deg}(D_{3}(V))|_{t=2}=1.33\), i.e., several edges (J, K, L) in D3 were removed. In this case the global T breaches since \(\overline {deg}(G(V))|_{t=2}=1.57<1.6\)

Full size image

If a change occurs locally at t= 1min Fig. 1 panel (b) for which \(\overline {deg}(D_{1}(V))|_{t=1}=1\), meaning several edges in D1 (B, C) were removed, and the local threshold T1 was breached, but not the global T, since still \(\overline {deg}(G(V))|_{t=1}=1.97>1.6\). If a breach of T3 could have also occurred at t=2, for which \(\overline {deg}(D_{3}(V))|_{t=2}=1.33\), meaning several edges (J, K, L) in D3 were removed. Now, the global T would breach since \(\overline {deg}(G(V))|_{t=2}=1.57<1.6\).

A recent progress in the area of distributed monitoring problem (Yehuda et al. 2017) deals with classification between local sub-graphs breaches, trying to identify the ones that eventually lead to a global breach of the graph threshold T. This works established conventional graph analysis tools (e.g. non-linear properties of the regular LDD graphs, the number of triangles and the spectral gap) for detecting when T breaches. Moreover, several ways to handle non-trivial graphs have been suggested such as directed graphs, These non-trivial graphs include weighted graphs, graphs with nodes that contain different attributes, and combinations of these aspects (Lovász 1993; Hoory et al. 2006; Pavan et al. 2013).

Here, we suggest that the aforementioned tools should be combined in managing traffic and on-line social smart city network (OSN) applications. We demonstrate: a) Finding when T breaches is actually a new way do detect the fastest route from a source vertex to a target vertex in a geographic dynamic graph, b) Finding when T breaches is a way to define communities in smart city OSN’s. The details, description, examples and solving algorithms of these applications are presented in the following parts of this paper.

Related work

The problem of finding the fastest, time-dependent path in a real-time traffic application has become increasingly important. Kenneth and Cooke (1966) presented a pioneering work in this subject. Ziliaskopoulos and Mahmassani (1993) turned the problem to a discrete one and suggested using dynamic programming to fit the problem to a real-time environment. Lauther (2004) introduced a distributed geometrical geographic graph for his problem and a most accurate algorithm to solve it, but the handled graph was a static one. Describing OSNs (e.g. Facebook, Twitter, etc.) as a graph or more accurately as a network, has been the main topic of many recent studies among them (de Nooy 2012) and (Kadry and Al-Taie MZ 2014). In their analysis, the different users have been represented as vertices and their relationships are the edges that connect them. The edges could also be different user interactions (such as “like”, “follow”, etc.). One interesting aspect of these graphs is the vertices attributes. Every user may be characterized by different types of attributes, some numerical (such as, number of followers) and some textual (residence, school, etc.). The smart cities OSN graphs are inherently LDD graphs as the edges and vertices attributes are constantly changing (friendships end, work placed are changed, etc.). These graphs are very large at scale. An interesting question arises when we try to define concepts within the smart cities OSN. One of these concepts is a community. The descriptive graph structure of a community in an smart cities OSN was dealt with by Traud et al. (2011); Fortunato (2009); Newman and Park (2003) and more specifically on Facebook in the research of (Ugander et al. 2011).

Using LDD graphs for detecting the fastest path in a dynamic traffic graph

Applying the fastest path problem to a traffic real-time application (such as Waze), involves configuring a much more diversified graph than the trivial one that has just vertices and edges. First of all, the graph has to be a directed one (traffic lane direction), and a weighted one, as the weight itself can be observed in two different aspects: physical distance or travel time. The vertices are different interest points- such as a gas station, a street, or any other place that has geographic coordinates.

The main problem with this graph is that it is highly dynamic, i.e., its edges are constantly changing in time. The edges weights (considered as travel time) can increase (traffic load, accident) or decrease (traffic unload, road clearance). This creates a huge overhead for the calculations of the optimal real-time travel path. Distributing these graphs to LDD graphs is shown in Fig. 2a, b, c. Each of these graphs include three sub-graph datasets (denoted by D1,D2 and D3) which are the parts of a road map. The graph is directed (i.e the edges are all north-to-south), and the threshold T is defined as to fastest route from source (vertex A) to target (vertex L). The fastest path is denoted by the path between the filled blue circles. The green paths indicate a change in the local fastest path. Notice here that T can be also dynamic, and T can change as time goes by, and so does the source vertex (the car is constantly moving) although we ignore this in our analysis. The local Ti’s are also the fastest routes. At some starting point t=0, the global attribute, i.e., the fastest path is T=29 min (the blue route), were the local thresholds are T1=9 min,T2=11 min,T3=9 min.

Fig. 2
figure 2

A local breach affect in a real-time traffic application. When a global graph property is breached, the fastest path changes correspondingly. The fastest path is emphasized by the solid blue line. a At t=0 the global attribute, i.e. the fastest path is T=29 min and the local thresholds are T1=9 min,T2=11 min,T3=9 min. b At (t=3 min) a local breach occurs and the edge E−H reduces its weight from 6 min to 2 min changing the local threshold T2 from 11 min to 10 min (denoted by the green path). This local breach did not affect the global graph T, since the total path time from A to L trough E (A-C-D-E-H-I-L) 31 min is still slower than the original path time 29 min. c A local breach leading to a global graph breach and a path change. At t=9 min the edge H-I reduces its weight from 8 min to 3 min, changing the local threshold T3 from 9 min to 7 min. This breach broke the global T since the total path time is now faster, (26 min is faster than 29 min) and global path is updated from (A-C-D-F-G-I-L) to (A-C-D-E-H-I-L) noted by the dashed blue line

Full size image

The change in the graph after some time (at t=3 min) is depicted in Fig. 2b. A local change occurs, and the edge E−H reduces its weight from 6 min to 2 min, changing the local threshold T2 from 11 min to 10 min (denoted by the green path). This local breach didn’t break the global graph T, since the path time from A to L trough E (A-C-D-E-H-I-L) will take 31 min which is still slower than the original path time 29 min. So when does a local change, Ti changes the global T? Let’s examine an additional change described in Fig. 2c, that describes Di at t=9 min. A change occurred at t=9 min and the edge H-I reduces its weight from 8 min to 3 min, changing the local threshold T3 from 9 min to 7 min (green path). This breach also broke the global T since the total path time is now faster, (26 min is faster than 29 min), thus the local path changes to the green one and global path is also updated from (A-C-D-E-H-I-L) to (A-C-D-F-G-I-L). It is important to state here that the distribution of the internal graphs (Gm’s) is done beforehand and is not part of the optimization process. The division must be equal in size for the generality of use-case and for no computational overheads of prediction evaluations of the networks big-data, keeping the algorithm complexity viable. This important feature of complexity simplicity also justifies the choice of linear dependency between local and global property. In cases of complex dynamic networks, some properties may be not linear, thus more complex to manifest in distributed algorithms such as the ones described above.

Algorithm for finding the fastest route in LDD graphs

Finding the fastest path in an LDD graph is quite complex since at each point we must consider all possible paths between the source and target vertice for each Di(t). Based on a known fastest path algorithm (Pettie 2004) denoted by PTT(G), we present an algorithm for finding the fastest path in LDD graphs. The main idea of the algorithm is to find if a global threshold T was breached, meaning if there is a faster path from a current source to a target point. It is important to state here that the PTT algorithm is used for finding all-pairs shortest path, while the better-known Dijkstra algorithm (Dijkstra 1959), finds the shortest path from source to target (Dijkstra algorithm is used inside PTT).

The algorithm efficiency is with agreement to PTT(G) algorithm which is O(EV+V2log2V). It is important to notice in the algorithm that the important variable of currentPath holds the most efficient path in every time point, changing it according to the new paths iterated by the algorithm and compared to the current efficient one that it contains.

Algorithm explanation and complexity analysis

In stage 1 we find a new optional path time, by adding the time of the path from the current source to the source point of Dm, where the local Tm was breached, to Tm and to the time of the path from the target point of Dm to the target point of G. In this stage we run PTT twice, achieving a running time of O(EV+V2log2V). In stage 2 we create this new path described in stage 1, and in stage 3 we check if the new path is actually faster, meaning we check if the global T was breached. If so, we update both the current path and the global T. In stages 2 and 3 we have an O(1) complexity since the path is already set in stage 1. At the 4th and last stage we return the current path, whether it was changed or not, this stage is also of O(1) complexity, setting the algorithm’s total time at O(EV+V2log2V). This performance is a good improvement to current algorithm for finding fastest path with these dynamic conditions. Table 1 shows a benchmark comparison of state-of-the-art current algorithm that handle the similar problem, we can see that our algorithm holds a better complexity from the existing ones, and resembles (Pettie 2004), but ours gives the advantage of a dynamic one while the Pettie algorithm refers to static ones.

Table 1 A benchmark comparison for the algorithms’ performance
Full size table

Algorithm completeness and correctness-Initialization

For i=1, the invariant is respected: in the first iteration we check local Tm since it is the only one that could have changed.

Maintenance For i=m, given 1≤m≤n−1, without the loss of generality we take Dm as the dataset currently handled. There are two possible cases for this mth iteration:

  • newPathTime <f(D(k)), meaning T was breached and the current path is no longer the shortest one, but in that case we perform stages 1 and 2 in the algorithm and update the current path and T.

  • newPathTime >f(D(k)), meaning T was not breached and the current path is still the shortest one, thus the invariant is preserved.

Algorithm completeness and correctness-Termination

At the last iteration, given i=n, the two options mentioned above are similar for Dn, and respectively t(n), meaning in each of the options we get the minimal time for the current path, thus T remains the fastest path. Hence, the algorithm gives us the fastest route from the source point to the target.

More results of the algorithm

More results are shown in Table 2, in which we see the better performance time of the algorithm in juxtaposition to the singular fastest path calculation (the beginning T). The results are organized by different time-stamps, and are a continuance of the case-study shown in Fig. 2.

Table 2 Dynamic community definition for an LDD graph, a better performance time of the algorithm in juxtaposition to the singular fastest path calculation (the beginning T)
Full size table

Implementation of LDD graphs to the problem of defining communities in smart cities online social networks

Monitoring the changes in a community graph Fig. 3 can be both private (for each user), and both global (for all users). Local changes can be the number of followers, work place, the number of friends. The global changes, can be the average number of relationships or other graph attributes. Distributing the community graph can help us monitoring threshold demand we wish to define on the graph. For example we can see in Fig. 4 “The influential rock-stars city events”, where we have three graph datasets (denoted by D1,D2 and D3) which are the parts of the community. The graphs edges are mutual city events participators (enhanced by geographical proximity), we focus on the numeric attribute of average number of followers for every user, as well as the users average number of inner-community friendships (the vertices degrees). We define entry-level conditions of 1000 followers per user, and at least 2 inner-community friendships. The global threshold T is defined as an average of 1300 followers per user and an average of 2.5 inner-community friendships. The change in the graph after time goes by can be seen in Fig. 5, That describes D at t=3 min. A change occurred in this time space (0−3), and Bob participators un-friended Chuck participators, changing the local average degree in D1 from 2.5 to 2 which broke the local threshold of 2.5.

Fig. 3
figure 3

A local breach affect in a real-time smart city OSN application. The graph reviews real- time influential rock-stars events, distributed to three graph datasets (geographic regions) denoted by D1,D2 and D3. The graphs edges are friendships among events participators, and we focus on the numeric attribute of average number of participators of each event, as well as the users average number of inner-community friendships (the vertices degrees). a We define entry-level conditions of 1000 followers per user, and at least 2 inner-community friendships. The global threshold T is defined by the average of 1300 followers per user and an average of 2.5 inner-community friendships. The change in the graph after time goes by as can be seen in (b,c). b describes D at t=1 min. A change occurred in this time space (0−1), and Bob un-friended Chuck, changing the local average degree in D1 from 2.5 to 2 which broke the local threshold of 2.5. This change did not break T since the total average degree is still bigger than 2.5 (it changed from 3.5 to 3.33), thus the global community-defining conditions remained valid. c describes D at t=2 min. Several changes occurred in this time space (1-2), and the number of followers of the rock stars in D3 was reduces by 4900, changing the local average of followers from 1943.8 to 1127.2. This change broke T since the total average of followers is less than 1300 (1297.8), thus the community broke its defining conditions

Full size image
Fig. 4
figure 4

Community graph dataset D at t(0)

Full size image
Fig. 5
figure 5

Community graph dataset D at t(3)

Full size image

This change did not break T since the total average degree is still bigger than 2.5 (it changed from 3.5 to 3.33), thus the global community-defining conditions remains valid. When does a local change changes T? That we can see in Fig. 6, that describes D at t=9 min. Several changes occurred in this time space (3-9), and the number of avant participators of the Rock Stars in D3 was reduces by 4900, changing the local average of followers from 1943.8 to 1127.2. This change broke T since the total average of followers is now smaller than 1300 (it is 1297.8), thus the community broke its defining conditions.

Fig. 6
figure 6

Community graph dataset D at t(9)

Full size image

Algorithm and results for the problem of defining communities in an Online Social Network in LDD graphs

The main idea of the algorithm is to find if the global threshold T was breached. In this case we have two aspects of breaching: average number of followers, and average vertex degree, denoted before as f(D(k)) and d(D(k)) respectively. Notice that the i presented in the algorithm is that of the time-stamp iterations, and m is the dataset in which there is a local breach of Tm. The algorithm is as follows:

It is important to state here that the data portrayed in this section is extracted of real datasets that we used for the experimental evaluation. These adhered with our model and provided the results presents in this section.

Algorithm explanation and complexity analysis

We can see that in stage 1, we update the global f(D(i+1)) with the local breach of Dm by subtracting the change in f(Dm(i+1)), where the local Tm was breached. In stage 2 we do the exact same thing, only with d(D(i+1)). Both of these stages have an O(V) complexity since every vertex is being checked. In stage 3 we check both of the aspects f(D(i+1)) and d(D(i+1)) and compare them to the global T(f(D)) and T(d(f(D))), to see if they were breached. If so, we return false, since the definition of community was breached. If not we return true in stage 4, meaning the community definition remains. Both of these stages are of O(1) complexity (an atomic action of comparison), setting the algorithm’s total time at O(V).

Algorithm explanation and complexity analysis

Initialization

For i=1, the invariant is respected: in the first iteration, we check the f(D(i)) and d(D(i)). Since we assume that in t(0) the community definition holds, we can move on to the other iterations.

Maintenance

For i=k, given 1≤k≤n−1, without the loss of generality we take Dm as the dataset currently handled. There are four possible cases for this kth iteration that we can generalize into two cases:

  • f(D(k))−(f(Dm(k))−f(Dm(k+1)))<T(f(D)) or d(D(k))−(d(Dm(k))−d(Dm(k+1)))<T(d(D)) meaning T was breached and the definition of a community no longer holds, which cause in returning false.

  • f(D(k))−(f(Dm(k))−f(Dm(k+1)))≥T(f(D)) and d(D(k))−(d(Dm(k))−d(Dm(k+1)))≥T(d(D)) meaning T was not breached and the definition of a community holds, which cause in returning true. Thus the invariant is preserved.

Termination

At the last iteration, given i=n, the two options above are the same for Dn, meaning in each of the two options we get the answer whether T was breached or not, giving us a definitive result about the definition of a community.

More results of the algorithm

More results are shown in Table 3, in which we see see at every point the change effecting or not effecting T. The results are organized by different time-stamps, and are a continuance of the case-study shown in Figs. 4, 5 and 6.

Table 3 Dynamic community definition for an LDD graph
Full size table

Conclusions and future work

In this paper we presented a new approach for managing real-life applications using the methods presented in monitoring LDD graphs problems. The first one is the geographic applications, for which the problem being monitored is the fastest path from a source vertex to a target vertex. The second application is the smart city OSNs, in which the problem being monitored is the definition of a community established by a certain criteria of graph attributes. The different meanings of the threshold T for the aforementioned application were studied, and their interesting experimental results were shown, along with efficient monitoring algorithms that can handle them. The algorithms correctness and completeness were proven, and their complexities were analyzed. An interesting juxtaposition can be done with our model and a proposed approach applied to a real-case big network of Wang et al. (2018), that applies a deep learning perspective to a connected traffic flow prediction. While the traffic flow prediction smartly intertwines efficient learning algorithms, the un-distributed network still has a high latency and overhead in comparison with our distributed network model, that needs less data to discover important features and breaches of them in the network. Delving more into the problem of Monitoring Large Dynamic graphs can yield even more interesting results, or even more possible applications especially the ones that involve handling non-trivial graphs such as directed graphs, weighted graphs, graphs with nodes that contain different attributes, and combinations of these aspects. A particularly interesting geographic application that we are currently developing is an algorithm for finding the fastest path in a distributed graph, that takes into consideration the future locations of traffic in the path, by using the graph multi-coloring method for scheduled connections shown in Bampas et al. (2015). OSN’s have even much more possible applications required in this field, such as security and access issues, communal popularity assessments, and fluid user networks. In this smart city OSN field we are currently developing access-control and information flow-control models, that use the distributed graph application presented in this paper. All of these subjects are currently being progressed.