Introduction and literature review

Liquid Composite Moulding (LCM) processes are widely used to manufacture complex 3D composite components. Controlling the forming of engineering fabrics, like Non-Crimp Fabrics (NCFs), is crucial to produce high-performance composites. To characterize the in-plane shear deformation, which is the dominant forming mechanism [1], the Uniaxial Bias Extension test (UBE) is commonly used [1, 2] (see Fig. 1). This shear test has the advantage of being quite simple from an experimental point of view. The UBE test consists in applying a tensile test on a rectangular specimen such that the warp and weft directions are orientated initially at 45° with respect to the pulling direction. The specimen must have a length twice longer than the width at least. During the test, the sample is deformed and three zones are theoretically identifiable, as shown in Fig. 1. The zone “A” corresponds to in-plane pure shear, the zones “B” are half-sheared, and the zones “C” are not deformed.

Fig. 1
figure 1

Bias extension test with a length L0 twice longer than width l0

Full size image

According to balanced woven fabrics mechanics, the hypotheses of this test are [2,3,4]:

  • Shear is defined by the rotation of fiber

  • No intra-ply fiber slippage occurs

From a macroscopic point of view, the rotation of fibers is modeled by pure shear kinematic. The shear deformation is defined by the shear angle (γ), which is expressed as a function of the angle (θ) between both fiber directions (equation (1)).

$$ \gamma =\frac{\pi }{2}-\theta $$
(1)

Geometrically, the shear angle (for pure shear) can be directly related to the displacement of the crosshead (D), the initial length (L0) and the initial width (l0) (equation (2)) [2,3,4,5].

$$ {\gamma}_{ps}(D)=\frac{\pi }{2}-2\bullet {\cos}^{-1}\left(\frac{\sqrt{2}}{2}\bullet \left(1+\frac{D}{\left({L}_0-{l}_0\right)}\right)\right) $$
(2)

Ferretti et al. [6] and Harrison et al. [7] have proposed new theories taking into account other mesoscopic deformation modes, in particular, the in-plane bending of fibers. Harrison et al. [8,9,10] have proposed some improvements concerning experimental methods for the UBE test applied to woven fabrics. These works aimed to limit deformation on the zone “C”, to reduce the fiber slippage between zones “B” and “C” and to avoid out-of-plane deformations. Moreover, Harrison et al. [11] proposed a kinematic analysis describing the fiber slippage during UBE test applied to woven fabric. Hartel et al. [12] have developed a test rig to characterized fabric at the mesoscopic scale, regarding several deformation mode.

For their high formability and their high performance, Non-Crimp Fabrics (NCF) are often chosen for high-performance composites manufacturing [13]. Unlike woven fabrics, where the weaving of orthogonal tows generates fibers undulation, NCFs are considered to have ideal unidirectional fiber paths. A stitch yarn maintains and ensures the integrity of the structures. However, its presence creates distortions of the fibrous tows and can induce deformation mechanisms, which are unique to NCFs. These mechanisms were also described with the presence of some defects on NCF reinforcements during forming processes [12, 14,15,16,17,18,19,20,21]. Chen et al. [22] and Deghboudj and Satha [23] showed experimentally the influence on shear stiffness when the stitching yarns are removed; and concluded that the stitches have a significant impact on the shear behavior. Colin et al. [24] quantified recently the occurrence of inter-stitch sliding depending on the shear deformation. Due to the stitch contribution, the asymmetry of the in-plane shear behavior of the NCF was studied [25,26,27]. Krieger et al. [16] proposed a geometrical approach to link the deformability to the stitching parameter. Then, they designed a tailored NCF based on stitching geometry to optimize both draping and handling [17]. Several works [28,29,30,31,32] have shown that intra-ply slippages are much more important for dry NCF compared to balanced woven fabrics during the UBE test (Fig. 2). The main consequence is an offset between the shear angle computed by the geometrical analysis (equation 2) and the measured shear angle [4, 28, 31,32,33]. In their review paper, Boisse et al. [2] preconized to measure experimentally the shear angle independently of the imposed displacement.

Fig. 2
figure 2

Review of literature about the measurement displacement / shear angle on NCF, a Bel et al. [18], b Bel [4], c Krieger et al. [16], d Härtel and Harrison [31], e Creech [28]

Full size image

In Bel et al. [32], the offset between theoretical and measured shear angles becomes significant from approximatively 10°. In his thesis work [4], two curves of the shear angle as a function of the elongation were presented for two different NCF structures. Differences with the analytical curve appear respectively at 20° and 30°. Creech et al. [28] have studied the influence of the load direction on the same NCF, perpendicularly and along the stitching direction. A good correlation until a shear angle of 10° and 30° respectively was shown. Divergence appeared at approximatively 25° in Krieger and al. [16] paper. Härtel and Harrison [31] evaluated the UBE test with several textile structures. They have shown that biaxial NCF material can experimentally fit the theory until a shear angle of 45° while a unidirectional NCF (sewed UD) correlates until a shear angle of 10° only.

Differences between theoretical and experimental shear angle are caused by the presence of intra-ply slippage. Some macroscopic and mesoscopic models have been proposed to include intra-ply slippage as a deformation mode [4, 18, 20, 28, 34, 35]. All these investigations lead to a better mechanical description of NCF materials. The variability of the divergence point between theoretical and measured shear angles is commonly explained by the diversity of material architectures. However, this variability is rarely associated to the lack of standardized experimental method of UBE test for NCF materials.

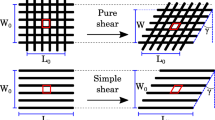
From a macroscopic point of view, two elementary shear kinematics are distinguished: pure shear and simple shear (Fig. 3). Usually, pure shear is used for describing bi-axial fabrics while simple shear is used for describing UD textiles. The assumptions behind are that bi-axial fabrics have two rigid directions (fibers directions) which can rotate. UD textiles have one rigid direction corresponding to the fibers while the second rigid direction is perpendicular to the first one [19, 35]. The simple shear represents the slippage of fibers along themselves. These definitions are implemented in the commercial FEM code PAM-FORM® (ESI Group).

Fig. 3
figure 3

Both pure shear behaviors, fabric and UD

Full size image

The present work brings an approach to evaluate and to increase reliability of UBE test for bi-axial NCF material. First, a new kinematic description of the UBE test is proposed based on the simple shear definition (following the previous work of Pourtier et al. [33]). The deformation mode represented by this kinematic is slippage without extension in the transverse direction. This new kinematic is compared to the classic one which is based on pure shear. Based on this comparison, a criterion is defined to detect slippages. This test is considered reliable if the pure shear kinematic is respected. The criterion makes it possible to estimate the reliability more precisely. The second part of this work applies this criterion on experimental UBE tests. The aim of this part is to show that increasing the sample width reduces slippage and ensures the accuracy of UBE test for bi-axial NCF. The mechanical shear behavior is also studied for each sample size. For different sample widths, the mechanical in-plane shear behavior is not identical. However, it is shown that the bigger the sample width is, the smaller the difference is. This convergence is essential to ensure the reliability of the UBE test.

Comparison between the pure shear and simple shear regarding the UBE test kinematic

Geometric configuration

The deformation of zone “A” has theoretically been studied as a function of both pure shear and simple shear kinematics [36] (Fig. 3). The kinematic study is based on the parallelogram OPQR which is considered as an elementary cell that includes the zone “A” (Fig. 4). Points O and Q belong both to the zones “C”. The point O is considered fixed during the test. Consequently, the point Q moves along the axis (OQ) with the imposed displacement D during the test.

Fig. 4
figure 4

Geometrical configuration of the zone A for investigated both simple and pure shear kinematics

Full size image

Both theories will be studied as a function of the fiber orientation, parallel to (OP). This orientation is characterized by the angle (w), angle between the axes (OQ) and (OP). From an experimental point of view, this angle can be measured directly on a visible face of the NCF. From this point, the distance d(Q, (OP)) between both parallel edges [QR] and [OP] is obtained by equation (3).

$$ d\left(Q,(OP)\right)=\left({L}_0-{l}_0+D\right)\bullet \sin (w) $$
(3)

This distance will be used for comparing both kinematics and for establishing the evaluation criterion of the UBE test reliability.

Pure shear kinematic

The pure shear kinematic corresponds to the classic UBE test theory. In this case, the angle θ between both fiber directions is directly linked to the angle (w) considering the symmetry of the test (equation (4)).

$$ \theta =2w $$
(4)

Therefore, the distance d(Q, (OP)) is rewritten (equation (6)) as a function of the imposed displacement (D) or as a function of the angle (w) using equations (1), (2), (3), (4) and the trigonometric relation bellow (equation (5)).

$$ \sin \left({\cos}^{-1}(x)\right)=\sqrt{1-{x}^2}\kern1.25em \forall x\in \left]-1,1\right[ $$
(5)
$$ d{\left(Q,(OP)\right)}_{ps}=\left({L}_0-{l}_o+D\right)\bullet \sqrt{1-\frac{1}{2}\bullet {\left(1+\frac{D}{L_0-{l}_0}\right)}^2}={L}_c\bullet \sin (2w) $$
(6)

Simple shear kinematic

NCF material is often described as a superposition of UD fiber layers. The shear mechanism of UD textile is modeled by simple shear kinematic. The objective of this section is to apply the simple shear kinematic to the zone “A” during UBE test in order to compare it with the pure shear classical one. The theoretical development presented connects the shear angle γ to the imposed displacement D and to the angle (w).

By definition, a simple shear kinematic implies the distance d(Q, (OP)) remains constant during the test (equation (7)) [36, 37].

$$ d{\left(Q,(OP)\right)}_{ss}={\left\Vert \overrightarrow{QP}\right\Vert}_{D=0}=\kern0.75em \frac{\sqrt{2}}{2}\bullet \left({L}_0-{l}_0\right)={L}_c $$
(7)

By combining the equations (3) and (7), the angle (w) is expressed as a function of the imposed displacement D by the equation (8).

$$ w={\sin}^{-1}(A)\kern0.5em with\kern0.5em A=\frac{\sqrt{2}}{2}\bullet \frac{1}{1+\frac{D}{L_0-{l}_0}} $$
(8)

The angles θ and w are related by the equation (9) inferred from the geometry of the zone “A” (Fig. 4).

$$ \sin \left(\theta -w\right)=\frac{L_c\bullet \sin (w)}{L_c+\Delta d} $$
(9)

Based on the definition of the shear angle (1), and using the equation (9), we get the equation (10).

$$ {\gamma}_{ss}(D)=\frac{\pi }{2}-\theta =\frac{\pi }{2}-\left(w+{\sin}^{-1}\left(\frac{L_c\bullet \sin (w)}{L_c+\Delta d}\right)\right) $$
(10)

Due to the distance d(Q, (OP)) which remains constant, the segments [QP] and [RO] are elongated by Δd during the test. This length can be calculated from the angle (w) and the displacement D by the equation (11).

$$ \Delta d+{L}_c=\sqrt{{L_c}^2\bullet {\sin}^2(w)+{\left(D+\sqrt{2}\bullet {L}_c-{L}_c\bullet \cos (w)\right)}^2} $$
(11)

Finally, by combining the equations (8), (10) and (11) we obtain the relation between the shear angle γUD, the sample size and the imposed displacement D (equation (12)). This equation is equivalent to equation (2) describing pure shear theory.

$$ {\gamma}_{ss}(D)=\frac{\pi }{2}-{\sin}^{-1}(A)-{\sin}^{-1}\left(\frac{L_c\bullet A}{\sqrt{{L_c}^2\bullet {A}^2+{\left(D+\sqrt{2}\bullet {L}_c-{L}_c\bullet \sqrt{1-{A}^2}\right)}^2}}\right) $$
(12)

Similarly, from equations (8), (10) and (11), we obtain the relation between the shear angle γUD and the angle (w) (equation (13)).

$$ {\gamma}_{ss}(D)=\frac{\pi }{2}-\theta =\frac{\pi }{2}-w-{\sin}^{-1}\left(\frac{\sin (w)}{\sqrt{1+\frac{1}{\sin^2(w)}-\frac{2}{\tan (w)}}}\right) $$
(13)

This equation has to be used for processing experimental measurement data for a simple shear analysis.

Comparison between pure shear and simple shear kinematics

This last theoretical section aims to compare both kinematics regarding the shear angle as a function of the imposed displacement and regarding the distance d(Q, (OP)) as a function of the shear angle.

Hartel and Harrison [31] have measured the shear angle during a UBE test on a sewed unidirectional (UD NCF). Their sample dimensions were 50 × 100 mm2. Using equation (2) and (13), both theories and their experimental measurements are compared (Fig. 5). In their tests, slippage was the main deformation mode. As shown in Fig. 5, the simple shear theory and the experimental results from Hartel et al. [31] fit well, which validates the strategy of using the simple shear kinematic to detect slippage. In addition, it is noticed that both theories are very close for small shear deformation but diverge for large deformation. The reason is that the pure shear theory has a maximum imposed displacement (equation (14)) whereas the simple shear theory has a horizontal asymptote (equation (15)).

$$ {D}_{ps}^{max}=\left(\sqrt{2}-1\right)\left({L}_0-{l}_0\right) $$
(14)
$$ \underset{D\to \infty }{\lim }{\gamma}_{ss}(D)=\frac{\pi }{2} $$
(15)
Fig. 5
figure 5

Comparison between the kinematic of the pure shear kinematic, the simple shear kinematic and an experimental measurement on sewed UD made by Hartel et al. in [31]

Full size image

As usually observed in literature, the pure shear theory is never respected for large shear deformation. Other deformation modes corresponding to other kinematics can occur, as presented in [11]. Consequently, the established simple shear kinematic is valid only if slippage is the unique deformation mode from a macroscopic point of view.

Finally, we can theoretically study the relative difference “dif” (equation (16)) between both simple and pure shear theories regarding the distance d(Q, (OP)) using the equations (6) and (7).

$$ dif=\frac{d{\left(Q,(OP)\right)}_{UD}-d{\left(Q,(OP)\right)}_{fab}}{d{\left(Q,(OP)\right)}_{UD}}=1-\sin (2w)=1-\cos \left(\gamma \right) $$
(16)

For a simple shear kinematic, this distance is independent of the angle (w) because it remains constant. Therefore, the relative difference can be expressed directly as a function of the shear angle (Fig. 6). This shows that for small deformation (until 10°), both theories are very close. For a shear angle of 10°, the difference is only 1.5% whereas it increases to 3% for a shear angle of 14°. This comparison explains why all the experimental results from the literature, cited in the introduction, correlate with the pure shear kinematic up to a shear angle of 10° at least.

Fig. 6
figure 6

Relative difference between the distances d(Q, (OP)) computed with simple shear and pure shear theory as a function of shear angles (equation (16))

Full size image

In the next section, experimental results will be compared to both kinematics, through the analysis of the shear angle as well as the distance d(Q, (OP)) along the test. By these comparisons, the main deformation mode (slippage or rotation) is identified on the visible face of the NCF. Thanks to this approach, it is clearly shown that the sample size influences on the deformation modes, and therefore on the in-plane shear behavior.

Materials and experimental procedure

The purpose of these experimental tests is to show that the sample size has an influence on the deformation mechanisms during UBE test for a bi-axial NCF, regardless of the ratio (length per width). A similar experimental study was already done for woven fabric by Harrison et al. [7].

The textile used is a 600 g.m−2 biaxial glass fiber NCF. This NCF is made of 600 tex glass fibers maintained by tricot stitches (76 dtex of PES). The stitching length is 3.3 mm and the gauge is 10 stitches per inch. Fiber directions are ±45° in regard to the stitching direction. The thickness (macroscopic definition) is 0.6 mm according to the standard ISO 5084.

All the samples verify an aspect ratio of 2.5. A regular pattern is drawn along the fibers to follow their orientation during the test. The stitching direction is always perpendicular to the loading direction. Specific grips have been developed in order to clamp specimens horizontally before placing them in a vertical tensile machine (MTS Criterion with a sensor of 1kN). This precaution ensures reducing undesirable deformations caused by the handling. The tensile speed is 50 mm/min. Each test is filmed in order to measure the fiber orientations. The image processing is done by an automated algorithm.

Three configurations are studied, corresponding to three sample widths (aspect ratio: 2.5):

  • 80 mm, which is recurring in the literature

  • 150 mm which is among the largest sizes frequently found in the literature

  • 200 mm which is unusual in the literature (present in [7] for woven fabric)

Kinematic analyses of experimental UBE tests for different sample size

Figure 7 presents UBE test pictures for each configuration at several shear angles (0°, 15°, 30°, 40°) in the zone “A”. These pictures were analyzed by an automated algorithm which measures the angle (w) along the drawing lines. At first, this section presents observed particularities concerning the zones “B”. Then, the zone “A” is studied using the kinematical analyses presented above for the different sample sizes.

Fig. 7
figure 7

Left: Pictures of the UBE tests at different shear angles. Right: Analysis of the fiber orientation for a shear angle of 40°

Full size image

Specificities observed on the zone “B”

For all the tests, the zones “A” and “C” are clearly identified through the fiber orientation. In contrast, the zones “B” are not identifiable in regard to the fiber orientation (angle (w)). In these zones, which should be half-sheared according to the pure shear theory, the angle (w) is half of the angle (w) in the zone “A”. However, on the observed face of the NCF, fibers in a zone “B” passing through a zone “C” remain parallel to the fibers in the zone “A”. Thus, the measured angle (w) is the same in this zone “B” and in the zone “A” (case 1). Also, fibers in a zone “B” passing through the zone “A” remain parallel to fibers in the zones “C”. Thus, the measured angle (w) is constant during the test (case 2).

Macroscopically, each zone “B” is a superposition of both cases. Therefore, the shear angle (γ) between both fiber directions in zone “B” is the half of the angle (θ) in the zone “A”, which is in accordance with the pure shear theory. However, the symmetry with respect to the vertical axis is not fulfilled regarding the fiber orientations. Thus, the equation (4) is not valid unlike the pure shear theory predicts it. By conclusion, zones “B” are half-sheared but the fiber orientations are not in line with the pure shear theory [3, 31].

Using a simple shear kinematic to describe the deformation mechanisms, it can be assumed that a zone “B” is composed of two UDs (one for each face of the NCF). For each side, there are two types of zone “B”: zone “B1” corresponding to case 1 and zone “B2” corresponding to case 2 (Fig. 8). These distinct deformation modes could be explained by boundary conditions and material orientation which are different. In the zone “B1”, fibers are clamped at the limit with the zone “C”, and subjected to an in-plane moment coming from the zone “A”. Therefore, the main deformation mode of these fibers is in-plane bending at the border shared with the zone “C”, similarly as in [7]. The in-plane bending combined to a simple shear (fiber slip) could then justify the observed kinematic.

Fig. 8
figure 8

Analysis of the B zone deformation mode assuming a simple shear kinematic

Full size image

In zone “B2”, fibers are initially parallel to fibers in the zone “C”, and then ‘pulled’ by the zone “A”. Therefore, the corresponding deformation mechanisms is most probably slippage (simple shear) combined with in-plane bending localized at the border shared with the zone “A”.

The presence of in-plane bending at the interface between the zones “C” and “B1” and the zones “A” and “B2” is not considered in the classic kinematic approaches used in this work. However, theories like the second gradient theory of Ferretti and al. [6], or mesoscopic approaches should be able to model this phenomenon.

It can be concluded from these observations that the mechanical behavior of the zones “B” for an NCF material is complex and not elementary. Furthermore, for the examined configurations, the deformation mechanisms in zones “B” do not depend on the sample size.

Experimental analysis of the zone “a” kinematic

From this point, the discussion is focused on the study of the zone “A” as a function of the sample size. The measurements of the angle ‘w’ in zone “A” are processed by two different ways. The first one is to compute the shear angle according to both simple (equation (13)) and pure (equations (1) and (4)) shear kinematics. The second one is to compute the distance d(Q, (OP)) from the measurements (equation (3)) and to compare it to both kinematics as a function of the shear angle. These analyses allow main deformation mode identification (slippage or rotation).

Regarding the shear angle theories applied in the zone “A”, two cases are investigated. First, considering that the kinematic corresponds to pure shear, the shear angle is computed as a function of the measured angle (w) by equation (1) and (4). As shown in the literature review, the experimental shear angle is then compared to the theoretical kinematic (Fig. 9). The second case is to consider that the kinematic corresponds to simple shear, assuming slippage is the main deformation mode. So, equation (13) is used for deducing the shear angle from the measured angle (w). This result is compared to the simple shear theory (Fig. 10).

Fig. 9
figure 9

Pure shear kinematic: comparison between the experimental shear angles and the theoretical kinematic

Full size image
Fig. 10
figure 10

Simple shear kinematic: comparison between the experimental shear angles and the theoretical kinematic

Full size image

In order to compare the results of samples with different dimensions, the theoretical shear angle of each theory is chosen as x-axis. Indeed, each theory gives an equivalent imposed displacement as a function of the sample size and the shear angle (equation (2) for pure shear and equation (12) for simple shear). This imposed displacement is considered to select experimental data. Hence, a 45° straight line corresponds to a perfect fit between the considered theory and the experimental data.

Until a shear angle of 10°, there is no significant difference between the theories and the experimental data (Figs. 9 and 10). After 10°, the experimental data present a better fit with the simple shear theory than with the pure shear theory until a shear angle of 15° for the 200 × 500 mm2 sample, until 20° for the 150 × 375 mm2 and until 26° for the 80 × 200 mm2 sample. After these angles, both 150 mm width and 200 mm width curves are almost parallel to the pure shear theory until 40°.

Two conclusions can be established:

  • A change of kinematic appears with the shear. Before this change, slippage seems to be the main deformation mode. After that, rotation is the main deformation mechanism

  • The sample size has a significant influence on this behavior change. The bigger the sample size is, the earlier the deformation mode occurs

In order to have a better understanding of the kinematic, a comparison of the distances d(Q, (OP)) between the pure shear kinematic (equation (6)), the simple shear kinematic (equation (7)) and the experimental measurement is shown in (Fig. 11). For simple shear, this distance is independent of the shear angle, thus the latter is taken as a homogenous input. To compute the shear angle from experimental measurements, two equations are available: the equation (4) (according to the pure shear theory) and the equation (13) (according to the simple shear theory). Both are used, which gives two experimental curves for each sample size. Concerning the distance d(Q, (OP)), the equation (3) is used whatever the chosen kinematic is.

Fig. 11
figure 11

Distance d (Q, (OP)) as a function of the shear angle, the kinematic (simple or pure shear) and the sample size

Full size image

As shown previously in Fig. 6, theoretical distances d(Q, (OP)) computed for both kinematics are close until a shear angle of 10°. After 10°, both theories diverge regarding the relative difference (equation (16)). For a shear angle of 10°, the relative difference is 1.5%; while for a shear angle of 14°, the relative difference rises up to 3%.

Hence, the relative difference of distances d(Q, (OP)) between experimental data and simple shear theory is computed. As done for the comparison between theoretical kinematics, if the relative difference exceeds 1.5%, divergence is assumed.

By analyzing the Fig. 11, all of the three sample sizes curves are close to both theories until a shear angle of 10°. After 10° and until a divergence point (given by the 1.5% threshold), all the experimental measurements fit with the simple shear theory independently of the sample width. Table 1 summarizes the divergence points for each experimental configuration according to the threshold defined before. After the divergence point, the experimental kinematics become closer to the pure shear theory. We can also notice the divergence points are not exactly the same for both computation methods. This deviation is explained by the plotting variable choice (shear angle) on the x-axis. Indeed, the distance d(Q, (OP)) is computed with the same equation for both theories. However, the shear angle (x-axis) does depend on the used theory, which involve a dilatation along the x-axis between simple shear and pure shear experimental curves.

Table 1 Divergence point as a function of the sample size and the theory used for computing the experimental shear angle
Full size table

The main outcomes of these kinematic studies are:

  • Before 10°: the main deformation mode (rotation or slippage) cannot be identified. Both kinematics are too close.

  • Between 10° and the divergence point: slippage is the main deformation mode. The simple shear theory is the most representative.

  • After the divergence point: rotation of fibers is the main deformation mode. The pure shear theory is the most representative. However, the deviation induced by the slippage remains. Therefore, having a divergence point as close as possible to 10° (for a 1.5% threshold) is suitable.

  • Increasing the sample size brings the divergence point closer to 10°. Thus, a sample is large enough if the pure shear theory, and so the classic kinematic of the UBE test, is respected.

Two analyses have been presented. The first one is based on the comparison between the measured shear angle during the test and both theorical kinematics. This analysis permits to estimate the main deformation mode, and to find approximatively the divergence point. The second one, which is based on the distance d(Q, (OP)), allows to compare directly both kinematics with the experimental results. A threshold is defined to find the divergence point. It is noticed that there is a strong correlation between both analyses.

Influence of deformation mode and specimen size on the in-plane shear stress-strain behavior

The previous part has shown a change of deformation modes during a UBE test for the studied NCF. It has also shown the sample size impacts directly this change of deformation modes. In this current section, the influence of deformation modes and sample size on the resultant in-plane shear stress-strain behavior is investigated. The measured shear angles are used to normalize the shear strain. The measured load is also normalized by the engineering stress, as proposed by Cao et al. [38] (equation 17).

$$ {\sigma}_y=\frac{\sqrt{2}}{2}\bullet \frac{F}{t_0\bullet {l}_0\bullet \sin (w)} $$
(17)

This normalization method considers the macroscopic axial stress (σy) as a function of the applied load (F), the initial thickness (t0), the initial width (l0), and the fibers orientation (w). The engineering stress is plotted as a function of the shear angle and of the sample size in Fig. 12.

Fig. 12
figure 12

Influence of the sample size on the behavior using a UBE test

Full size image

The behaviors gotten from the three sample sizes can each be broken down into three parts. The first part is located between a shear angle of 0° and 6°. Behaviors present a linear increase of the engineering axial stress. In the second part, behaviors decrease significantly. The ending of this second part depends on the sample size. The decrease is until 23° for the 80 × 200 mm2 specimens; until 17° for the 150 × 375 mm2 specimens and until 14° for the 200 × 500 mm2 specimens. It is noted that the end of the second part correlates with the divergence points obtained with the kinematic analyses (see Table 1). During these two first parts of the stress-strain behaviors, the standard deviation is important and reduces at the end of the second part. In the third and last part, the behaviors increase again and the standard deviation remains quite low.

From these observations, it is assumed both first and second parts together are linked to slippage mechanisms. Also, this particular type of in-plane shear behavior has already been observed experimentally in literature. De Luycker [3] linked it to specific fiber sizing on 3D-woven. Zhao et al. [39] and Pourtier et al. [40] have observed a similar behavior after adding chemical agents (epoxy resin tackifier or binder systems) on respectively woven fabrics and NCF. As for this study, no chemical agent had been added. Hence, fiber sizing is probably responsible for the mechanical behavior observed. In fact, the weak chemical interactions may resist against small deformation. Passing 6°, slippages occur until the change of deformation mode, which depends of the sample size.

For the third part of the shear stress-strain behaviors, we assume that the mechanical response is mainly structural, corresponding to a classic woven fabric pure shear behavior.

It also observed that both largest sample behaviors (200 × 500 mm2 and 150 × 375 mm2) are close, especially compared to the behavior of the smaller sample (80 × 200 mm2). Consequently, it is supposed that increasing the sample size converges the in-plane shear stress-strain behavior. This point is crucial since it shows that UBE test can be independent of sample size (if large enough), which is required to guarantee characterization reliability.

Conclusion and perspectives

The UBE test is commonly used to characterize in-plane shear behavior of NCF. A specific kinematic is associated to this test, which is determinant for shear stress and shear strain normalizations. The literature review shows this kinematic is always respected for small shear deformation (approximatively until 10°). After 10°, several kinematics are observed for NCF material. Some of them fit the theory until 50° whereas others diverge at 10°. It is assumed this divergence point between the theoretical kinematic and the measured one depends mostly on the NCF structure. This kinematical divergence is linked to the fiber slippage, which normally should not be present during UBE test. This calls the reliability of UBE test into question regarding NCF characterization.

The present investigation aims firstly to propose a theoretical method which permits to identify more precisely the main deformation mode during an experimental UBE test. Secondly, an experimental work highlights the influence of sample size on the deformation mode, and consequently on the UBE test reliability.

In the first section, a two-way kinematic approach has been proposed. At first, the kinematic of the test is detailed assuming pure shear classical theory. It describes the deformation we should observe during a UBE test. Secondly, the kinematic of the test is established assuming simple shear theory, which is a macroscopic description of slippage for UD material. As the hypotheses behind these kinematics are different, the measurement treatments differ. Thus, it is not obvious to compare them together and directly with experimental data in respect to the shear angle. Consequently, kinematics are compared through the distance d(Q, (OP)). Indeed, this distance is independent of shear deformation for the simple shear kinematic. Therefore, it is possible to compare all the kinematics (experimental and theoretical) directly.

This theoretical two-way approach shows the proximity of both theories for small deformation. So, it is not possible to determine the main deformation mode bellow a shear angle of 10°, as it is usually done in literature.

In the second section, an experimental study presents the influence of the sample size on the deformation mode during a UBE test. The deformation modes were studied following the fiber orientation and using the previous kinematical analyses. The study of the zone “A” has shown that slippage is the main deformation mode at the beginning of the test for the used NCF. Then a change of behavior is observed: rotation of fibers becomes the main deformation mode. Hence, the larger the sample is, the earlier the change of behavior appears. The 200 mm width specimens have a kinematic which is close to the theoretical pure shear one. In conclusion, increasing the sample width leads to improve the UBE test reliability for NCF material.

The experimental part has also highlighted a specific behavior in the zones “B”. Indeed, these zones are half-sheared during the test from a macroscopic point of view. However, the fiber orientations do not correspond to the pure shear kinematic whatever the sample width is. A reflection based on simple shear assumption is proposed. Further works are required to investigate the deformation mechanism more deeply. It may also imply some specific changes concerning the force normalization methods for NCF material.

In the third and final section, the in-plane shear stress-strain behavior is analyzed and connected to the deformation modes as a function of the shear angle and the sample size. The outcomes are that behaviors of both largest samples are close to each other compared to the behavior of the smallest sample. As for the kinematic analyses, this convergence is relevant to ensure the reliability of the UBE test.

This work illustrates the importance of the sample width for UBE test. Then, another experimental study has to be done to understand the impact of the aspect ratio. It will give a complete overview of the sample size influence on the UBE test reliability for NCF material.

As bi-axial NCF materials present a large architecture diversity, similar studies have to be done on other NCF. A benchmark of these results should help to standardize the UBE test for NCF material, or at least, to propose some common good practices.