The Hall–Petch and inverse Hall–Petch relations and the hardness of nanocrystalline metals

Abstract

We review some of the factors that influence the hardness of polycrystalline materials with grain sizes less than 1 µm. The fundamental physical mechanisms that govern the hardness of nanocrystalline materials are discussed. The recently proposed dislocation curvature model for grain size-dependent strengthening and the 60-year-old Hall–Petch relationship are compared. For grains less than 30 nm in size, there is evidence for a transition from dislocation-based plasticity to grain boundary sliding, rotation, or diffusion as the main mechanism responsible for hardness. The evidence surrounding the inverse Hall–Petch phenomenon is found to be inconclusive due to processing artefacts, grain growth effects, and errors associated with the conversion of hardness to yield strength in nanocrystalline materials.

Introduction

In this review, we focus on how the hardness of metals is affected by the interaction between dislocations and grain boundaries, particularly as the grain size is reduced to the nanometre scale. Hardness (H) has been related to the compressive flow stress of a material by the following relation:

$$ H = 3\sigma_{0.08} , $$

(1)

where $\sigma_{0.08}$ is the compressive flow stress of the tested material at a strain of 8% [1]. Equation (1) and variants of it [2, 3] have been in use for about a century [4,5,6,7,8]. Hardness is most commonly measured through indentation testing [9, 10], which involves pressing a piece of hard material (the indenter) into a test specimen under a known force and measuring the resulting imprint area. The indentation process has been found to depend strongly on indenter geometry, depth of indentation, and specimen size [1].

In the 1950s, Hall and Petch demonstrated that the yield stress $\sigma$ (Fig. 1 ) [11, 12] (and hence the hardness) scales with the inverse square root of grain size, d, in polycrystalline materials according to the following relation:

$$ \sigma = \sigma_{0 } + k d^{ - 1/2} , $$

(2)

where k is a measure of the local stress needed to initiate plastic flow at a grain boundary and σ₀ is the resistance to dislocation motion in the grain interior [13]. This relationship has been explained by a dislocation pile-up model for the stress concentration at the tip of a slip band [13, 14], but recently, the validity of this relationship has been debated [15].

Figure 1

The relationship between lower yield point (σ_LYP) and grain size, d, in mild steel. The yield stress of the single crystal was obtained from Ref. [16]. From [11]

In the 1980s, Gleiter et al. [17] pioneered research into polycrystalline materials whose grains are of nanometre size. It was thought then that these materials would exhibit superior hardness as well as superior wear resistance and fracture strength compared with their coarse-grained counterparts due to the large volume fraction of grain boundaries they contain as grain boundaries were known to govern the response of metals to deformation [18, 19]. Since that time, ultrafine-grained materials have been defined as having grain sizes in the range 100 nm < d < 500 nm, and nanocrystalline materials as having grain sizes less than 100 nm. There have been reports of nanocomposite coatings with Vickers microhardness (Hv) of up to ~ 40 GPa [20], which is of the same order of magnitude as diamond (Hv~ 70–90 GPa) [21]. This ‘super-hardness’ of nanocrystalline materials is of interest to the biomedical [22], military and electronics industries [23, 24].

Although hardness measurements of some nanocrystalline samples have been reported to be consistent with the behaviour expected by the Hall–Petch law, grain boundary weakening has also been reported for nanocrystalline materials having typical grain sizes less than 30 nm: the so-called inverse Hall–Petch effect [25, 26]. The inverse Hall–Petch effect has been observed both experimentally [25] as well as in molecular dynamics (MD) simulations [27,28,29,30]. The weakening has been attributed to (1) processing artefacts [18, 26], (2) disordered grain boundaries [31], and (3) the higher percentage of material in grain boundaries for nano- as opposed to micro-grained materials [32, 33] coupled with the intrinsic relative softness of material in grain boundaries (Fig. 2) [30]. Other studies, such as the one reported by Conrad [34], considered a possible explanation for the effect as being the transition from dislocation controlled to grain boundary and diffusion-dominated deformation [19].

Figure 2

Molecular dynamics simulations of hardness-depth relations for a on a grain boundary and b near a grain boundary for nanocrystalline pure iron. From [30]

One important problem at present with MD simulations is that since the cost of computation time needed to track the motion of atoms in a solid is very high [35], the timescale that can be investigated is very short. The consequence of this is that the strain rate in the simulations is many orders of magnitude higher than the experiment [29] lying high up in the shock-loading regime (10¹⁰ s⁻¹) whereas the strain rate for normal indentation experiments is quasistatic (typically 10⁻³ s⁻¹). Recent studies by Gurrutxaga-Lerma and colleagues have shown that the quasistatic theory of dislocations is not valid for shock plasticity [36, 37]. This is because a quasistatic analysis ‘ignores the finite time for elastic signals to travel in the medium’ so that the ‘stresses created by dislocations behind the shock front are felt instantaneously by [dislocation] sources ahead of the shock front’ [36]. The practical outcome of applying a quasistatic analysis is that ‘dislocation sources [are] activated ahead of the shock front’ (Fig. 3), which does not happen.

Figure 3

Quasistatic analysis showing unphysical dislocation nucleation ahead of a shock front at a 0.9 ns and b 2 ns. From [36]

In “The role of dislocations in the deformation of nanocrystalline materials” section of this review, the evidence for and against key theories that have been developed to explain the deformation mechanisms operating in nanocrystalline materials are discussed along with recent reports claiming the absence of the Hall–Petch effect in grain size strengthening. In “The inverse Hall–Petch phenomenon” section, the inverse Hall–Petch phenomenon is discussed and the mechanisms postulated to explain grain size weakening are summarised. In “Synthesis of ‘super-hard’ nanocrystalline materials” section, the main methods used to synthesise nanocrystalline materials are summarised and the importance of grain boundary structure on the hardness of metals is discussed. “Summary and conclusions” section presents the overall conclusions reached.

The role of dislocations in the deformation of nanocrystalline materials

Extending the classic dislocation pile-up mechanism

Under an applied stress, many dislocation loops are generated in the same glide plane by Frank–Read sources [38]. These dislocation loops then accumulate against grain boundaries. The shear stress at the head of these pile-ups increases with their length until the stress exceeds a threshold value, at which point dislocation sources are activated in the adjacent grains, initiating plastic flow. The deformation is described by Eq. (2), the Hall–Petch relation. Figure 4 shows that the hardness of nanometre-sized nickel follows a Hall–Petch dependence as the grain size is reduced, supporting the dislocation pile-up theory.

Figure 4

Plot of hardness against reciprocal square root of grain size for nickel electroplated material with coarse and nano-sized grains. Note that in this paper Hughes et al. [39] and Torrents et al. [40]. From [13]

However, there exists a large body of evidence suggesting that the Hall–Petch relation is not universally valid for nanocrystalline materials. Pande et al. [41] argued that Eq. (2) is only valid if there are a large number of dislocations in a pile-up (Fig. 5) and that, as grain size decreases, the pile-up mechanism saturates when the number of dislocations in the pile-up tends to 1 [42, 43]. This limit is discussed further in “Expansion of a single dislocation loop against the grain boundary resistance” section. Additionally, there is a lack of evidence that directly connects the pile-up length to grain size [14, 43]. A Bayesian analysis of aggregated Hall–Petch data, presented by Li et al. [15] and discussed in “The size effect” section, indicates that the pile-up mechanism does not account for the wide scatter in the data.

Figure 5

Graph showing that the linear Hall–Petch relationship is valid for a number of dislocations, n, which is larger than 20. The discrete nature of the dislocations in the pile-up is apparent for smaller n, leading to a breakdown in the Hall–Petch model for small pile-up lengths and hence small grain sizes. From [41]

Expansion of a single dislocation loop against the grain boundary resistance

As the number of dislocations in a pile-up decreases, their discreteness becomes apparent [15, 31] (see also Fig. 5). The limiting case of a single dislocation loop expanding against a grain boundary is described by Eq. (3):

$$ \sigma = \sigma_{0} + m\left[ {\tau_{0} + \left( {3Gb/4\pi l} \right)\left\{ {\left( {5/6} \right)\left( {{ \ln }\left[ {4l/b} \right] - 1} \right) - 1/16} \right\} + \tau_{c} } \right], $$

(3)

where l is the loop diameter (taken to be equal to the grain diameter), τ₀ is the multislip shear stress for deformation within grain volumes, b is the Burgers vector, G the shear modulus, and m is the Taylor orientation factor. In constructing this equation, a term τ_c (the shear stress required to penetrate through the grain boundary) was added to the equation of expansion of a circular dislocation loop [15, 44]. This theory has been supported by several experimental studies [45, 46], as shown in Fig. 6.

Figure 6

Data for electrodeposited nickel, exhibiting stress values greater than those estimated from the Hall–Petch relation. The two curved lines show the values of stress σ calculated using Eq. (2). The transition between them is marked at n = 1, where n is the number of dislocations in a pile-up. From [46]

More commonly as the grain size decreases, a lower strength is observed than the Hall–Petch relation predicts. In Fig. 7, data reanalysed by Hansen and Ralph can be seen to be in agreement with Eq. (2) for coarse grains. At n = 1 (where n is the number of dislocation loops), the pile-up model predicts a transition to a higher stress than Hall–Petch [46, 47]. The discontinuity in the prediction stems from the transition from the Hall–Petch equation (which assumes n is large) to Eq. (3), when n is small [46]. Lu et al. [48] tested nano-twinned copper, taking the twin thickness as the effective grain size. Their data can be seen in Fig. 7 to initially follow the Hall–Petch relation but with a lower gradient due to the properties of coherent twin boundaries. A reversal of the Hall–Petch relation can be seen in their data at smaller grain sizes, which they ascribed to grain boundary weakening. Armstrong suggested, however, that this may be an artefact of the preparation of the nano-twinned material [44]. This matter is discussed further in “The inverse Hall–Petch phenomenon” section. In conclusion, the data presented in Fig. 7 are not in agreement with the single dislocation loop model.

Figure 7

Log/log stress-grain size graph for copper. The black line shows the theoretical values calculated using Eq. (2) for larger grain sizes and Eq. (3) for smaller grain sizes. Note that in this paper Lu et al. [48], Li and Liu [47], Armstrong and Smith [49], and Hansen and Ralph [50]. From [46]

Work-hardening models

In these models, dislocations are produced from ledge sources (Fig. 8) [51]. The stress required to move a dislocation through a forest array of extrinsic dislocations is of a form similar to that of the Taylor equation which describes work hardening [52],

$$ \sigma = \sigma_{0} + \alpha Gb\sqrt \rho , $$

(4)

where ρ is the average dislocation density, α is a property of the material, and σ₀ is defined in Eq. (2).

Figure 8

Schematic diagram of the grain boundary ledge model. From [15]

Li et al [15]. proposed that the density of ledges scales with grain boundary area per unit volume of material. Their idea implies that fine-grained materials have a greater dislocation density and longer dislocation lines when they yield. Ledges have been imaged using transmission electron microscopy (TEM), e.g. Fig. 9 [52]. In this micrograph, the dislocation density was measured at distances of ~ 10 µm and ~  1 µm from the grain boundary in a coarse-grained polycrystal. The dislocation density was found to be roughly three times greater near the boundary than in the grain interior for engineering strains of up to 1% in 304 stainless steel [52], aligned with the schematic dislocation distribution shown in Fig. 10.

Figure 9

Bright-field TEM image of 304 stainless steel at a strain of 0.8%. Grain boundary ledges are visible. From [52]

Figure 10

Schematic diagram of the distribution of dislocations produced by ledge sources in fine-grained polycrystalline materials. From [52]

Yang and Vehoff [53] studied the influence of grain size on hardness using nano-indentation and a high-resolution atomic force microscope. For an indent depth of 28 nm in ultrafine-grained nickel, they found a d^−0.5 relation between the applied force and the individual grain size (Fig. 11). Since the strain is proportional to the dislocation density [54], the increase in flow stress is proportional to $\sqrt \rho .$ The authors argued that the increase in hardness was due to an increase in the dislocation density rather than a decrease in the pile-up length. This observation supports the work-hardening model. Evidence of the activation of dislocation sources in adjacent grains was gathered from the analysis of grain size-dependent ‘pop-ins’ (discontinuities in the force–displacement curve) [55].

Figure 11

Nano-indentation of ultrafine-grained nickel. a A force–displacement curve with increasing indentation depth. The pop-in indicates the activation of dislocation sources in adjacent grains. b Variation in applied force with grain size for an indentation depth of 28 nm. An inverse square root relationship is observed. From [53]

In Fig. 12, the first pop-in corresponds to the initial yield point of nickel. The later pop-ins were taken by Yang and Yehoff as evidence for the activation of sources in grains adjacent to the indented grains. The figure also shows the following: (a) the first pop-ins (at the initial yield point) occurred at forces and displacements that were independent of the grain size; (b) for later pop-ins, the force increased and the displacement decreased with decreasing grain size. Since the pile-up length L is related to the number of dislocations n by

$$ L = D/2 = 2nA/\tau , $$

(5)

where D is the grain size, $\tau$ is the external stress, and A is a constant. If the stress for activation of sources in adjacent grains is constant (as assumed by Hall–Petch theory), the pop-in load must be higher for smaller grains. This is supported by the experimental data shown in Fig. 12.

Figure 12

Graphs showing the forces and displacements at which pop-ins occur for nano-indentation on nano-nickel. From [53]

The authors conclude that in ultrafine-grained nickel, hardness scales with dislocation density (rather than pile-up length) where the pile-up length is within the grain size (supporting the Orowan model). However, they also found clear evidence for dislocation source activation in adjacent grains, and hence, a higher external load is needed to nucleate dislocation sources in adjacent grains for smaller grain sizes.

Meyers et al. [18] argued against this idea, pointing out that when the spacing of ledges is in the nanometre range, there would be a grain size below which this deformation mechanism is no longer operational. We would postulate that for grains a few nanometres in diameter, the grain boundaries may no longer be sharp and therefore point defects could be seen rather than the ledges that can be seen in Fig. 9.

Cordero et al. [14] also claimed in their study that there was no direct evidence that links the density of grain boundary ledges (which are affected by grain size) to the density of the dislocations produced.

The core and mantle model

According to several other models, including those due to Meyers and Ashworth [56] and Raj and Ashby [57], a grain can be treated as a composite, which is an improvement on ‘rule of mixtures’ models [58]. The composite model consists of the grain interior (the ‘core’), which is under homogeneous stress, and a work-hardened layer (the ‘mantle’) in which impurity segregation may occur adjacent to grain boundaries (Fig. 13).

Figure 13

Simplified schematic of the Meyers–Ashworth model. From [56, 59]

The predicted stress–grain size relationship for the model shown schematically in Fig. 13 is given by the following equation [18]:

$$ \sigma_{y} = \sigma_{fG} + 8k_{MA} \left( {\sigma_{fgb} - \sigma_{fG} } \right)d^{ - 0.5} - 16k_{MA}^{2} \left( {\sigma_{fgb} - \sigma_{fG} } \right)d^{ - 1} , $$

(6)

where $\sigma_{fG}$ is the flow stress of the dislocation-free interior, $\sigma_{fgb}$ is the flow stress of the grain boundary region, and k_MA is a fitted parameter. Equation (6) is in agreement with the Hall–Petch dependence for micron-sized grains, but it predicts a reduction in slope for smaller grain sizes. Figure 14 appears to show an agreement between experimental data and the Meyers–Ashworth model. However, Li et al. [15] recently concluded after analysis of a larger body of data that there is little correlation between experimental data and elastic anisotropy models such as those discussed above.

Figure 14

Plot of yield stress, σ_y, against the inverse root of the grain size (D^−0.5) for iron. The dotted line shows the σ_y values estimated using Eq. (5). For details of the papers from which the data in this plot were obtained, consult Ref. [59]

In the Ashby plastic anisotropy model [57], deformation takes place in two stages [14, 60]. Firstly, grain boundary shearing occurs along glide planes. This leads to voids and overlaps between grains (Fig. 15). Then, to restore compatibility at grain boundaries, arrays of ‘geometrically necessary’ dislocations (GNDs) are generated from the grain boundaries. The deformation is described by

$$ \sigma = \sigma_{0} + \alpha Gb\sqrt {\rho_{\text{GN}} + \rho_{\text{SS}} } \approx \sigma_{0} + \alpha Gb\sqrt {\frac{b\varepsilon }{4D}} , $$

(7)

where ρ_SS refers to ‘statistically stored’ dislocations (as would build up in a uniformly strained single crystal) and ρ_GN refers to GNDs. The approximation shown in Eq. (7) is valid in the limit of small strains where ρ_GN ≫ ρ_SS. The model predicts the following relationship between the Hall–Petch coefficient k and the plastic strain ε namely $k \propto \sqrt \varepsilon$ in the limit of small plastic strains [14].

Figure 15

Schematic diagram for elastic and plastic accommodation models, such as the Meyers–Ashworth and Ashby models. From [15]

Figure 16, taken from Cordero et al. [14], is a summary of six decades of investigations of the Hall–Petch effect in which k was measured as a function of plastic strain. Cordero et al. note that a parabolic strain dependence was not found experimentally. Rather in the majority of cases, although k increases with strain, it did so according to a number of other relations. They attributed the lack of a clear parabolic dependence to their invalid assumption of small strain in the historic studies they examined. Cordero et al. ascribed the small number of cases where k did not increase either to sample processing effects or to the effects of twinning (as opposed to glide) as a deformation mechanism. Despite this, Cordero et al. [14] argued that Ashby’s model is the most consistent overall with their examination of the literature on the strain dependence of the Hall–Petch coefficient and with experimental observations of dislocation substructure. However, against this Li et al. [15] argued that the Ashby model is not consistent with the experimental data they obtained.

Figure 16

The strain dependence of the Hall–Petch coefficient for several fcc, bcc, and hcp metals. In the majority of cases, k can be seen to increase with strain. From [14]

The size effect

Recently Li et al. [15] conducted a Bayesian meta-analysis on the body of available Hall–Petch data. They concluded that there was no experimental evidence for the 60-year-old Hall–Petch effect (Fig. 17). The authors made use of Matthews critical thickness theory [61] for thin metallic multilayers (Fig. 18a), to derive a relation by which the grain diameter is inversely proportional to dislocation curvature and hence to stress (Fig. 18b). This dictates the minimum strength for dislocation plasticity. For nano-grained materials, other mechanisms (discussed in Table 1) can result in data points that lie in the ‘no data’ region of the log(strength) − log(size) region of Fig. 17. These data points fall below the minimum strength predicted by the size effect equation (which is based on a dislocation curvature model). This is due to the onset of grain boundary sliding in some nano-grained materials and the transition away from dislocation-based plasticity. Li et al. concluded that

$$ \varepsilon \left( d \right) = \varepsilon_{0} + \frac{{k{ \ln }d}}{d}, $$

(8)

where k~  1 and a variable $\varepsilon_{0}$ best described the data and where ε = σ/Y is the stress normalised by the elastic modulus. They also postulated that a random error in grain size determination explains the apparent agreement with Eq. (2).

Figure 17

Graphical representation of the distribution of expected data if Eq. (8) holds. The absence of experimental data below the minimum strength strongly suggests that grain boundary effects are an extension of the ‘smaller is stronger’ size effect seen in micromechanical testing. If the values of k and σ₀ are uniform in log σ −  log d space, there is a relative probability density of 2 above the line and 0 below. Figure from the graphical abstract of [62]

Figure 18

Schematic diagrams of the size effect. a An illustration of Matthews critical thickness concept [61] for a spiral and Frank–Read dislocation source [38] in a strained epitaxial layer on a substrate. b A Frank–Read source operating inside a grain. A smaller grain diameter requires greater dislocation curvature. From [15]

Table 1 Summary of proposed mechanisms responsible for the grain size weakening effect

Li et al. [15] claimed that their data were not subject to any sampling bias, as all available data from the published studies were considered. However, the published data are subject to publication bias, defined as the tendency on the part of researchers to publish articles based on the perceived strength of the findings of a particular study [63]. So for the phenomenon under review in the present article, sampling is skewed towards results that are in agreement with the long-standing Hall–Petch relationship. Additionally, Li et al. assumed that since there was no underlying physics governing the distribution of k and σ₀, their values were uniformly distributed in log σ−  log d space (Fig. 17), in agreement with Benford’s Law [64, 65]. Benford’s law is applicable to large data sets where the data points come from many different distributions that span several orders of magnitude [66, 67]. The law states that the probability that the first digit of a number is p is given by

$$ Pben\left( p \right) = \log \left( {1 + \frac{1}{p}} \right)\quad p \, = \, 1,2 \ldots ,9, $$

(9)

although its physical significance is not well understood [68]. The validity of this assumption requires further investigation in light of the behaviour of k in Fig. 16 and the higher k values reported for fcc metals as compared to bcc metals [69].

Bayesian updating resulted in O_n = 2ⁿP₀, where O_n are the odds that Eq. (8) is true and n are the number of datasets that fall above the 1/d line (Fig. 19). Therefore, even with a low prior probability P₀ that such a well-established equation is incorrect, the odds were found to be overwhelmingly in favour of Eq. (8). Hence, Li et al. [15] argued that the grain size strengthening of metals is driven by constraints on the dislocation curvature and therefore that the pile-up, grain boundary ledges, and core and mantle models make a much weaker contribution to grain size strengthening than the dislocation curvature.

Figure 19

Comparison of the pile-up and grain boundary ledge model with aggregated Hall–Petch data. The heavy black line shows the predictions of the pile-up model calculated using Eq. (2). The dark blue dashed lines show the range of theoretical values calculated on the basis of the grain boundary ledge model described by Eq. (4). The red chain dotted lines show the range of predictions of the slip-distance model, which is not evaluated in this review paper. The intensity of the shading corresponds to the probability of finding data in each region according to the models discussed where white represents a probability close to zero. From [15]

The inverse Hall–Petch phenomenon

Since Chokshi et al. first reported a negative slope in a Hall–Petch plot for nanocrystalline copper and palladium in 1989 (Fig. 20) [25], there have been several reports of grain size softening and hardening in the grain size range below 100 nm (Fig. 21). One of the first models to capture the Hall–Petch transition theoretically for grain sizes less than 100 nm was published by Konstantinidis and Aifantis [70].

Figure 20

The first experimental results indicating a negative Hall–Petch slope for nanocrystalline copper and palladium at room temperature. From [25]

Figure 21

Plot of data from a number of publications showing the range of grain size strengthening and weakening behaviour for nanocrystalline copper. For details of the papers from which the data in this plot were obtained, consult Ref. [18]

Although Chokshi et al. attributed the softening effect to the onset of Coble creep [71], researchers have since suggested several other theories to explain it including flaws in the synthesis of the nanocrystallites [26], the presence of disordered grain boundaries [31], or a transition to and from dislocation-based deformation to grain boundary sliding or rotation [72,73,74].

Koch et al. argued [26] that incomplete densification during synthesis of nanocrystallites via inert gas condensation (as employed by Chokshi et al. [25]) and ball milling methods [75] can lead to residual porosity in nano-grained materials and consequently to poor bonding between particles, resulting in a decrease in the strength of these materials [26]. Armstrong argued that a reduction in Hall–Petch slope could be caused by the presence of disordered grain boundaries in nanocrystalline materials, which would allow plastic flow to be transmitted more easily between grains [31].

Mechanisms governing grain size weakening

Several theoretical models that have been proposed over the years to explain grain size softening are summarised in Table 1. The articles referred to in that table should be consulted for more information on the derivation of and evidence that supports each theory (Figs. 22, 23, 24).

Figure 22

Computed stress against plastic strain for nano-grained copper with a grain size of 20 nm. The solid line shows perfect grain boundary bonding. The dashed line is computed assuming that the boundaries have η_gb = 0, so that free slip can occur. The strength for free slip is two-thirds that of the equivalent material with perfect grain boundaries, therefore showing that grain boundary sliding accounts for one-third of the resulting stress whereas plastic deformation within grains accounts for the remaining two-thirds. From [59]

Figure 23

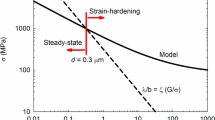
Model for grain size dependence of shear stress (τ). At large grain sizes, the Hall–Petch relationship holds. At d^*, a transition occurs at maximum strength. For d < d^*, Coble creep diffusion dominates. In reality, there is competition between the two mechanisms due to the grain size distribution in nanocrystalline materials. From [19]

Figure 24

Rotational deformation via the motion of disclinations. a Drawing showing the distortion of {110} planes seen in a high-resolution TEM image of mechanically milled, nano-grained iron powder. It shows direct observation of partial disclination dipoles. The set of terminating planes making up an individual partial disclination is labelled I. The planes located between two partial disclinations (labelled II) are rotated relative to those outside the disclination dipole (labelled III). From [72]. b A schematic of a nanocrystalline solid under mechanical tension. Motion of disclination dipoles (triangles) results in rotational deformation. The non-parallel lines in the inset represent the disclinations. From [73]

Zhang and Aifantis [79] built on the individual mechanisms shown in Table 1. They examined the mechanical grain boundary energy in order to explain both the conventional and inverse Hall–Petch relation for numerous experimental investigations. They also provided a theoretical expression to predict the grain size at which the transition occurs from strengthening to weakening with decreasing grain size. They used a gradient plasticity framework to capture the softening behaviour by treating the grain boundaries as a separate phase with a finite thickness rather than as a surface as is normally done for larger grain sizes. The grain structure assumed is shown in Fig. 25 where it can be seen that they identified a ‘grain interior’ (GI) phase (which is purely elastic), a ‘grain boundary’ (GB) phase of thickness L_gb (which is assumed to be soft and prone to deformation through rotation and sliding), and a plastic ‘GI–GB’ phase of thickness L_g adjacent to the grain boundary which accounts for the transition from the ductile GB to the rigid GI phase due to the limited diffusion into the grain interior of dislocations and disclination dipoles generated at the grain boundary.

Figure 25

Unit cell model with grain boundary (GB) phase, grain interior (GI) phase comprised of GI-GB layers, and elastic GI cores. From [79]

Zhang and Aifantis’ [79] gradient plasticity model includes an interface energy term $\gamma_{\text{gb}}$ which allows the interface itself to follow its own yield behaviour. $\gamma_{\text{gb}}$ is positive for microscopic grains as grain boundaries inhibit plastic flow (the yield stress of the GB phase is greater than the yield stress of the GI phase), whereas for nanometre-sized grains, $\gamma_{\text{gb}}$ is negative because the grain boundaries behave plastically and are softer than the grain interior (the yield stress of the GB phase is less than the yield stress of the GI phase).

The stress of the unit cell shown in Fig. 25 upon yielding of the grain boundary and adjacent grain boundary layers is given by

$$ \overline{\overline{\sigma }} = \sigma_{0} + \frac{k}{\sqrt d } + \frac{{\gamma_{\text{gb}} }}{2ad}, $$

(10)

where the grain boundary thickness is some fraction of the grain size (i.e. L_g = ad, where d is the grain size and a is a constant with a value lying between 0 and 1) and $\sigma_{0}$ is defined in Eq. (2). Equation (10) was used by Zhang and Aifantis to analyse the data published by a number of authors (see Fig. 26). As the figure shows, it provides a good fit for seven different nanocrystalline metals and alloys.

Figure 26

Plots that fit Eq. (13) to experimental data for nanocrystalline metals and alloys published by a number of different authors. For details of the papers from which this data came from, consult [79]

However, it was pointed out by Zhang and Aifantis that the processing methods were not the same for the various experimental data sets they compared in Fig. 26 (see “Synthesis of ‘super-hard’ nanocrystalline materials” section of our review for a discussion about synthesis methods). We also note that they used Tabor’s hardness-yield stress relation to compare experimental data which could potentially introduce errors for nano-grained materials (this matter is discussed further in the “Discussion of the evidence” section).

The critical grain size at which material behaviour transitions from the ‘normal’ Hall–Petch to the inverse Hall–Petch relation can be calculated using Eq. 11 which gives the grain size d_c at which peak material strength occurs. This critical size can be directly computed if the GB energy $\gamma_{\text{gb}}$, the fraction a of the GB thickness that yields and the Hall–Petch coefficient k are known for the material.

$$ d_{\text{c}} = \left( {\gamma_{\text{gb}} /\left( {ak} \right)} \right)^{2} . $$

(11)

There is currently no general consensus on the mechanism that gives rise to the inverse Hall–Petch behaviour exhibited by some nano-grained materials as a number of different theories including Coble creep, grain rotation, and gradient plasticity have some experimental support. The experimental evidence used to support the theories discussed in this section is considered in “Discussion of the evidence” section.

Discussion of the evidence

Due to the difficulty in obtaining bulk defect-free nanocrystalline specimens for testing, there is a dearth of reliable strength and hardness measurements for materials with nano-sized grains [14]. Stress-induced coarsening, due to either grain boundary migration or grain rotation, can occur during indentation testing of nanocrystalline materials (Fig. 27), which can introduce errors into the experimental estimation of hardness.

Figure 27

Plot of hardness (calculated using Tabor’s formula H = 3σ_Y) against the dwell time of an indenter in the sample. The grain growth zone is assumed to spread from beneath the indenter and eventually occupy the whole plastic zone. t_f is the time taken for the volume fraction of the grain growth zone to increase linearly from 0 to 100% relative to the plastic zone. The graph shows that the calculated hardness decreases with time, which is consistent with the experimental data. The decrease in hardness with dwell time is monotonic and does not saturate as time is increased. The paper referred to in this figure as Zhang et al. is Ref. [80]. From [81]

Brooks et al. [2] argued that Eq. (1) (Tabor’s classic hardness-yield stress formula) overestimates the yield stress in electrodeposited nanocrystalline materials. They reported that the ratio of hardness to yield stress lay between 4 and 8.6 for the materials they studied rather than 3 (see Fig. 28a). However, Zhang et al. [3] estimated, more conservatively, that the ratio of hardness to yield stress was between 2.3 and 3.7 for a number of nanocrystalline copper and copper-zinc alloys (Fig. 28b).

Figure 28

Plots showing the results of an investigation of the relationship between hardness and yield strength in nanocrystalline materials. a Graph showing the overestimation of the yield strength predicted using Eq. (1) compared to experimental data for nanocrystalline materials from Cahoon et al. [82] and Gao [83]. Figure from [2]. b Graph showing the ratio of hardness to yield strength for copper and copper-zinc alloys with grain sizes in the range 34 < d < 200 nm, subjected to different pre-treatments such as equal channel angular pressing (ECAP), high-pressure torsion (HPT) and annealing. Figure from [3]

The Tabor relation is widely used in papers that argue for and against the inverse Hall–Petch effect in nanocrystalline materials (e.g. [14, 79]). For example, Cordero et al. used Eq. (1) to convert nano-indentation hardness measurements into yield strengths (Fig. 29). They then plotted this data alongside yield strengths measured using compression or tension tests. Given the results of Brooks et al. [2] and Zhang and Aifantis [79], this methodology should be used with caution since as just discussed the classic Tabor relation appears not to hold for all nanocrystalline materials.

Figure 29

Aggregated Hall–Petch data for body centred cubic (bcc) metals. The red dashed lines are best fits to the data using Eq. (2). The closed points are Vickers or nano-indentation hardness measurements converted using Eq. (1). The open points correspond to yield strengths measured by compression or tensile testing. Cordero et al. ascribed the scatter seen to differences in sample preparation and testing, rather than an indication that Eq. (2) may not be valid. From [14]

Molecular dynamics (MD) simulations [27, 84, 85] have predicted a peak in hardness for copper with grain sizes in the range 10 nm < d < 15 nm. The simulations also support the existence of the inverse Hall–Petch slope and deformation via grain boundary slip. Although MD simulations allow researchers to directly model atoms and investigate grain boundary structure for grains less than 10 nm in size [86], the simulated strain rates are so high as to be inaccessible experimentally [87] (see the discussion of Fig. 3 in “Introduction” section). Also due to computational limitations, simulations cannot handle samples larger than a few hundreds of nanometres in size and therefore cannot be related simply to macroscopic experiments [84].

For all the reasons mentioned above, the experimental evidence currently available for the inverse Hall–Petch relationship is inconclusive. So in order to prove the existence of the inverse Hall–Petch effect, and the mechanisms behind it, many more experimental studies need to be performed in which (1) consistent material processing methods are used, (2) direct yield stress measurements are made (rather than assuming the Tabor hardness-yield stress relation), and (3) attention is given to grain size coarsening effects during testing. If these investigations are carried out, the uncontrollable factors in the experiments performed so far will be minimised and reliable data will be generated for materials with typical grain sizes in the nanometre range.

Synthesis of ‘super-hard’ nanocrystalline materials

The nature of the grain boundaries within nanocrystalline materials is influenced by the synthesis method used (a summary may be found in Table 2) and can be modified to cause ‘super’-hardness. Severe plastic deformation (SPD) has produced materials which have a hardness greater than the extrapolated Hall–Petch relationship [22]. Balasubramanian and Langdon [22] attributed this to three main effects:

Table 2 Summary of common synthesis methods for nanocrystalline materials

A larger fraction of high-angled grain boundaries (HAGBs)

HAGBs are more effective in impeding dislocation slip as there is greater crystallographic misalignment across the grain boundary. The fraction of HAGBs can be increased from 55 to 80% by increasing the number of high-pressure torsion (HPT) turns from one half to ten [88].

Segregation of impurity and alloying elements at grain boundaries

Precipitation of alloying elements in grain boundary regions suppresses the emission of dislocations from grain boundaries. Additionally, the precipitates cause drag on GNDs [22, 89].

Non-equilibrium grain boundaries (NGBs)

SPD produces more dislocations than geometrically necessary to accommodate plastic deformation at grain boundaries, causing an increase in grain boundary energy [22, 89].

Hu et al. [88] recently showed that careful use of annealing can result in the doubling of hardness of nano-grained nickel and nickel-molybdenum without altering the grain size (Fig. 28a). They found that the indentation produced little coarsening for their annealed samples. They thus concluded that structural relaxation and segregation of the molybdenum in the alloy causes relaxation of local stress levels at grain boundaries, which then become more stable to straining. This could reduce the threat of grain coarsening to the refinement process.

They also argued that grain boundary mediated deformation (which can cause softening) is replaced by deformation by the generation of extended partial dislocations at grain boundaries. The emission of partials is suppressed due to impurity segregation, similar to the suggestions by Valiev mentioned above [89], enhancing the formation of extended stacking faults. The large stresses required for nucleation of dislocations from stable grain boundaries results in a high hardness and a (1/d) grain size dependence. Hu et al. [88] argued that differences in grain boundary structure can explain the controversy over hardening and softening behaviour reported with decreasing grain size in previous studies. Their results could lead to the synthesis of further ‘super’-hard materials.

They showed that the inverse Hall–Petch effect was eliminated by annealing their samples. If this result was only due to structural grain boundary relaxation, then this could imply that the inverse Hall–Petch effect is simply a result of processing defects. However, if impurity segregation after annealing was the dominant mechanism for the hardening behaviour they saw, then the inverse Hall–Petch relation (governed by the mechanisms discussed in “The inverse Hall–Petch phenomenon” section) would still be valid for a pure single-phase nanocrystalline material. Figure 28b, c could suggest that while a combination of relaxation and segregation at grain boundaries plays a role in the reversal of the inverse Hall–Petch behaviour seen upon annealing, the dominant mechanism is in fact molybdenum segregation since they reported a much greater increase in peak hardness for their nickel-molybdenum samples compared to the pure nano-grained nickel they tested (Fig. 30).

Figure 30

a Increased hardness for annealed nickel and nickel-molybdenum nanocrystalline samples. The open symbols show as-deposited samples, and the closed symbols are samples that have been annealed. The blue solid line follows the relation $H_{v} \sim1/\sqrt d$ and the red line follows Hv ~ 1/d. b Plot of the variation in microhardness as a function of annealing temperature for nano-grained nickel and nickel-molybdenum with varying concentrations of molybdenum. c Plot of the variation in maximum microhardness increment produced by annealing as function of initial grain size. Open symbols represent data for other types of nano-grained materials. From [88]

Summary and conclusions

This article has reviewed the hardness of nanocrystalline metals, focusing on the theories describing dislocation plasticity, grain size weakening, and super-hardness effects. The main conclusions reached are outlined below.

Deformation mechanisms

100 nm < d < 1 µm: Core and mantle type models best describe the deformation behaviour.

30 nm < d < 100 nm: Dislocation ledge spacing becomes large compared to the grain size; therefore, there is a transition from a dislocation-based plasticity to grain boundary sliding as the main mechanism responsible for hardness. There is a dearth of reliable hardness measurements in this grain size range, and therefore, the main accommodation mechanism cannot be distinguished.

d < 30 nm: Transition from nanocrystalline to amorphous behaviour.

The relationship between hardness and grain size

Although Li et al.’s [15] arguments for a (log d)/d relationship are compelling, they require further statistical analysis and corroboration in order to overturn the large body of evidence that supports the $d^{ - 0.5}$ relationship, which has been added to recently by Armstrong [13] and Cordero et al. [14].

The inverse Hall–Petch effect

A transition from dislocation-based plasticity to a grain boundary sliding mechanism could explain the reversal in Hall–Petch slope. This transition has been seen to occur at grain sizes from around 100 nm [18] down to 10 nm [27, 84, 85, 88]. An analytical expression to predict the theoretical critical grain size was devised by Zhang and Aifantis on the basis of the grain boundary plasticity theory [79]. However, the inverse Hall–Petch effect could also result from processing artefacts or stress-induced grain growth during testing. Based on the available experimental evidence, the existence of the inverse Hall–Petch effect cannot be confirmed.

Processing methods

Inert gas condensation and mechanical alloying can result in grain size weakening due to incomplete densification resulting in porosity. Severe plastic deformation can result in HAGBs, segregation of alloying elements, and NGBs which produce ‘super-hardness.’ Short annealing treatments have recently been used to increase the hardness of nickel-molybdenum alloys by up to 120% [88] by reducing the local stress levels at grain boundaries.