Introduction

Topological insulators (TIs)1,2 and semimetals3,4,5,6,7 have received a tremendous amount of attention in the last decade due to the appearance of exotic properties, such as spin-momentum locked gapless surface state in TIs8,9, Fermi-arc states10,11,12 and negative magnetoresistance in Weyl semimetals (WSMs)7,13,14. These insulators can be characterized by topological invariants/indices, like Fu-Kane \({{\mathbb{Z}}}_{2}\) indices15 and mirror Chern numbers16,17 for TIs and topological crystalline insulators (TCIs), respectively. However, WSMs are topological metallic states with discrete accidental twofold degenerate points, described by the three-dimensional (3D) Weyl equation. Due to the lack of strict Lorentz invariance, the type-II Weyl points can be strongly tilted18, which have no analogy in high-energy physics. In contrast to the point-like bulk Fermi surfaces of the type-I WSMs7,19,20,21,22,23,24,25, these type-II WSMs26,27,28,29,30 have both electron pockets and hole pockets touching at the Weyl points, resulting in various novel physical properties31,32.

Topological materials that host superconductivity are ideal systems to detect topological superconductivity (TSC) and Majorana fermions33,34,35,36,37,38,39. The topological surface Dirac-cone states can be used to generate two-dimensional (2D) TSC induced by the intrinsic bulk superconductivity40,41,42,43. Very recently, the superconducting gap of the predicted topological surface Dirac-cone states in FeTe1-xSex44,45 has been detected in recent angle-resolved photoemission spectroscopy (ARPES)46 and scanning tunneling microscope experiments47. In noncentrosymmetric WSMs, 3D time-reversal symmetric TSC can arise from sign-changing superconductivity in Fermi surfaces with different Chern numbers48,49. However, to the best of our knowledge, almost all noncentrosymmetric WSMs need external pressure or doping to induce or enhance superconductivity50,51,52,53,54,55. Due to the lack of suitable candidates, 3D TSC is studied very little experimentally. Therefore, the material proposal of a WSM with high-quality single crystals and relatively higher superconducting transition temperature (\({T}_{\mathrm{C}}\)) is of great interest.

Ternary transition metal pnictides TT’X (T=Zr, Hf; T’=Ru; X=P, As) are a series of well-known superconductors56,57. As we know, there are three different types of crystal structures for these compounds57,58, i.e. the Fe\({}_{2}\)P-type hexagonal structure (h-phase), the TiNiSi-type orthorhombic structure (o-phase), and the TiFeSi-type orthorhombic structure (o\(^{\prime}\)-phase). Superconductivity is found in both h- and o-phases, and the superconducting transition temperature \({T}_{\mathrm{C}}\) is generally higher for h-phase than that for o-phase. In this work, we only focus on the h-phase of TT’X, exhibiting relatively high \({T}_{\mathrm{C}}\) (such as 12.7 K for HfRuP56, 13.3 K for ZrRuP and 12 K for ZrRuAs57). Based on the first-principles calculations, the nontrivial topological properties of these materials in the normal state (above \({T}_{\mathrm{C}}\)) are revealed. When spin-orbit coupling (SOC) is ignored, they possess two nodal rings slightly above the Fermi energy (\({E}_{\mathrm{F}}\)) in the \({k}_{z}=0\) plane, with each surrounding a K point in the hexagonal Brillouin zone (BZ). After the consideration of SOC, they enter either a WSM phase (e.g., HfRuP) with 12 pairs of type-II Weyl points (WPs) due to the lack of inversion symmetry, or a topological crystalline insulating (TCI) phase (e.g., ZrRuAs) with trivial Fu-Kane \({{\mathbb{Z}}}_{2}\) indices59 but nontrival mirror Chern numbers. The nontrivial electronic topology in these materials could intrigue tremendous experimental study of the interplay between topological electronic states and superconductivity.

Results and discussion

Crystal structure and electronic band structures

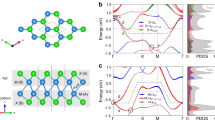
The h-phase of TT’X is of space group \(P\bar{6}2m\) (#189) with a layered structure. Each layer in the hexagonal lattice is occupied by either T and X atoms or T’ and X atoms. All atoms have positions in the layers parallel to the crystallographic ab-plane and separated by a half of the lattice constant c. The triangular clusters of three T’ atoms (T’\({}_{3}\)) are formed in the ab-plane. In the crystal structure of the TT’X shown in Fig. 1a, b, the T’\({}_{3}\) clusters and the planer structure are clearly shown. The high-symmetry k-points and surface projections are shown in Fig. 1c. The structure has two kinds of mirror symmetries, \({m}_{z}\;{\mathrm{and}}\;{m}_{x}\), which are vital to define the mirror Chern numbers as will be shown below. Meantime, we have successfully grown the single crystals of ZrRuAs and HfRuP, as shown in Fig. 1d, e, respectively. The hexagonal structure and superconductivity are confirmed by the x-ray diffraction (XRD) and resistivity measurements, respectively. More details and data (i.e., magnetic susceptibility) can be found in the Supplementary Material.

Fig. 1: The crystal structure, BZs, XRD spectra and transport properties of TT’X.
figure 1

a The top view of the crystal, with brown, gray and green balls representing T, T’ and X atoms, respectively. b The perspective view of the crystal. c The bulk BZ, (001)-surface BZ and (100)-surface BZ. Hereafter, (001) [(100) or (010)] refers to the surface normal vector in terms of the Cartesian coordinates. d and e Indexed powder XRD spectra of ZrRuAs and HfRuP, respectively. Red stars are small amount of impurities. The left insets of (d) and (e) are photographs of ZrRuAs and HfRuP single crystals, respectively. The right insets of them are temperature dependent longitudinal resistivity of ZrRuAs and HfRuP at various magnetic fields. The magnetic fields are perpendicular to c axis and electronic current direction.

Full size image

We first checked the electronic band structure without SOC. Among these compounds, we mainly investigated HfRuP and ZrRuAs for details in the following, as typical examples of the type-II WSM phase and TCI phase, respectively. More results on other compounds are presented in the Supplementary Material. From the band dispersion of HfRuP in Fig. 2a, one can notice there is a direct energy gap shadowed in light blue near \({E}_{\mathrm{F}}\), except the band crossings along both \(M-K\,{\mathrm{and}}\,K-\Gamma\) lines. These two lines are actually in the \({k}_{z}=0\) plane, where the \({m}_{z}\) symmetry is present. The \({m}_{z}\) eigenvalues of the two crossing bands are computed to be \(\pm \!1\), respectively. Thus, the two crossing points are parts of the \({m}_{z}\)-protected nodal rings, each of which surrounds a K point in the \({k}_{z}=0\) plane, as depicted in Fig. 2c. This situation is different from that in CaAgAs60, where there is only one nodal ring surrounding the \(\Gamma\) point. The two nodal rings circled around two K points are also found for all other compounds (see electronic band structures of ZrRuAs, HfRuAs and ZrRuP in Supplementary Section A). We conclude that the band inversion happens at the K point, which is supported by the theory of topological quantum chemistry61,62. By exchanging the highest valence band (\({\Gamma }_{4}\)) and the lowest conduction band (\({\Gamma }_{1}\)) at the K point (with little group \({D}_{3h}\)) only, the occupied bands become trivial, being a linear combination of elemental band representations61.

Fig. 2: The electronic band structures of HfRuP without (a) and with (b) SOC.
figure 2

The irreducible representations of selected bands at K point are indicated. (c) The nodal lines are presented in the \({k}_{z}=0\) plane without SOC. With SOC, the WPs above the \({k}_{z}=0\) plane are labeled as “+”(+1) and “o”(−1) in the first BZ. Here, a*, b*, and c* are the reciprocal primitive vectors. d The \({k}_{z}\) dispersion of the electronic bands through the WP W1 shown in (c). e The dispersion of the WP W1 along the line P-Q shown in (c). The fractional coordinates of W1, P and Q are (0.2761, −0.4654, 0.02439), (0.2603, −0.4603, 0.02439), and (0.2919, −0.4705, 0.02439). Hereafter, the positions of k-points are given in units of (a*, b*, c*). ARPES spectrum (f) and curvature intensity (g) plots of ZrRuAs, showing band structure along H-K-H. For comparison, the calculated band structure along H-K-H is superposed on the experimental data in (g). h–i are the same as (f–g), but along L-M-L.

Full size image

After including SOC, the band structure doesn’t change too much, but the bands do split due to the lack of inversion symmetry. To confirm the reliability of the density functional theory (DFT) band structures, we have performed ARPES measurement for ZrRuAs, shown in Fig. 2f–i. The observed spectra along H-K-H and L-M-L lines match very well with the DFT calculations (red lines in Fig. 2g, i), especially for the low-energy bands. We clearly see that the energy bands at K point are much lower than that at M point. In addition, the degeneracy of the two nodal rings is lifted by SOC. The 2D time-reversal invariant (TRI) planes (e.g., \({k}_{y}=0\,{\mathrm{and}}\,{k}_{z}=0\) etc.) become fully gapped, making the \({{\mathbb{Z}}}_{2}\) invariants well-defined. In CaAgAs, the single nodal line enclosing \(\Gamma\) point guarantees that the \({k}_{y}=0\) (or \({k}_{z}=0\)) plane is \({{\mathbb{Z}}}_{2}\) nontrivial with an infinitesimal SOC gap. But, it’s not the case with two nodal rings around two K points. The \({{\mathbb{Z}}}_{2}\) invariants for both \({k}_{y}=0\,{\mathrm{and}}\,{k}_{z}=0\) planes remain trivial in the series of these compounds. Note that the \({k}_{y}=0\) plane is gapped even without SOC, and no gapless point is found in all TRI planes. To confirm triviality of \({{\mathbb{Z}}}_{2}\) invariants, we have calculated the Wannier charge centers (WCCs) of the \({k}_{z}\)-directed (\({k}_{y}\)-directed) Wilson loops as a function of \({k}_{x}\) (called Wilson-loop bands) for the \({k}_{y}=0\) (\({k}_{z}=0\)) plane. The results of ZrRuAs are shown in Fig. 3a, b, suggesting a trivial \({{\mathbb{Z}}}_{2}\) invariant in the \({k}_{y}=0\) plane and \({k}_{z}=0\) plane. Accordingly, the Fu-Kane \({{\mathbb{Z}}}_{2}\) indices59 for the 3D bulk are computed to be (0;000) for all the compounds. The detailed calculations for the \({{\mathbb{Z}}}_{2}\) invariants in all six TRI planes (only four of them are distinct due to the symmetry) are presented in Supplementary Section B63. Furthermore, the symmetry indicators64,65,66,67 for these compounds are computed to be \({{\mathbb{Z}}}_{3m,0}=1\;{\mathrm{and}}\;{{\mathbb{Z}}}_{3m,\pi }=0\), revealing the topological nature of the SOC gap (shadowed in light blue) in Fig. 2b.

Fig. 3: The WCCs of TRI planes.
figure 3

a and b The WCCs of the \({k}_{z}\)-directed and \({k}_{y}\)-directed Wilson loops as a function of \({k}_{x}\) for the \({k}_{y}=0\;{\rm{and}}\;{k}_{z}=0\) planes, respectively. c and d The WCCs of the \({k}_{z}\)-directed Wilson loops as a function of \({k}_{y}\) in the \({k}_{x}=0\) plane of HfRuP and ZrRuAs, respectively. Red and blue circles represent the flow of the WCCs for the bands with mirror \(+i\,{\rm{and}}-\!i\) eigenvalues, respectively. The horizontal dashed lines are reference lines.

Full size image

Mirror Chern numbers and WPs

Due to the presence of mirror symmetry, the mirror Chern number is well defined as long as the mirror plane is fully gapped. Because time-reversal symmetry commutes with the mirror symmetries, the Chern numbers satisfy \({C}_{i}=-{C}_{-i}\), with the subscript \(\pm i\) representing the mirror eigenvalues in the presence of SOC. With time-reversal symmetry, the mirror Chern number is defined as \({C}_{m}=({C}_{+i}-{C}_{-i})/2\). As we know, it can be further reduced to \({\chi }_{+i}-{\chi }_{-i}\) in half of the mirror plane, where \({\chi }_{+i(-i)}\) is easily obtained in the plot of Wilson-loop bands, by counting the number of the positively-sloped bands crossing a horizontal reference line (the dashed line in Fig. 3c, d) and subtracting from it the number of the negatively-sloped crossing ones in the mirror eigenvalue \(+i\,(-i)\) subspace. The results of ZrRuAs for the \({k}_{z}=0\) plane are shown in Fig. 3b. The mirror Chern number \({C}_{{m}_{z}}\) in ZrRuAs is computed to be \(-2\) for the \({k}_{z}\) = 0 plane, while it’s zero for the \({k}_{z}=\pi\) plane. That’s the case for all the compounds (see more in Supplementary Section C).

The lack of inversion symmetry allows the appearance of WPs in the systems. The nonzero mirror Chern number \({C}_{{m}_{z}}=-2\) suggests there are some strings of gauge singularities (i.e., the Dirac string) going through the \({k}_{z}=0\) plane68, which have to either terminate at WPs in the 3D BZ, or thread some other nontrivial planes. Our systematic calculations show that these compounds can be classified into two classes: (i) one has zero Chern number \({C}_{{m}_{x}}=0\) with 12 pairs of type-II WPs, termed a WSM phase; (ii) the other one has nonzero mirror Chern number \({C}_{{m}_{x}}=2\) with no WPs, termed a TCI phase. In the WCCs of HfRuP for the \({k}_{x}=0\) plane in Fig. 3c, \({C}_{{m}_{x}}\) is obtained to be 0. WPs are found in this compound, which is consistent with the topological WSM phase. However, for ZrRuAs, HfRuAs and ZrRuP, \({C}_{{m}_{x}}\) turns out to be 2, as shown in Fig. 3d and in Supplementary Section C. Accordingly, no WP is found in these three materials. The detailed calculations of mirror Chern numbers are presented in Supplementary Section C.

By checking the energy gap and the associated topological monopole charge, we find that six pairs of WPs emerge from each nodal ring. Thus, there are 12 pairs of WPs in total (as shown in the first BZ in Fig. 2c). They reside at the same energy, because they are all related by either time-reversal symmetry or the crystalline symmetry \({D}_{3h}\) (including 12 symmetry operators). The coordinate of the WP W1 enclosed by a dashed circle in Fig. 2c is [0.2761\({\bf{a}}\)*, \(-0.4654{\bf{b}}\)*, 0.02439\({\bf{c}}\)*]. From the band dispersion of the WP W1 along the \({k}_{z}\)-direction (Fig. 2d) and the P-Q direction (Fig. 2e), we conclude that it belongs to a type-II WP69, and its energy level (\({E}_{\mathrm{W}}\)) is about 28 meV above \({E}_{\mathrm{F}}\) (i.e., \({E}_{\mathrm{W}}\) − \({E}_{\mathrm{F}}=28\) meV), very close to the Fermi energy. The topological monopole charge is computed with the Wilson-loop method applied on an enclosed manifold surrounding a single WP. The monopole charge of the WP W1 is +1. The distribution of all the WPs above the \({k}_{z}=0\) plane is illustrated in Fig. 2c, with the “+(o)” symbol representing the topological monopole charge of \(+1(-1)\), while these below the \({k}_{z}=0\) plane possess the opposite monopole charge shown in Fig. 2c because of the \({m}_{z}\) symmetry.

Fermi arcs on surfaces

Surface Fermi arcs connecting the projections of two WPs with opposite chirality are expected in a WSM. For this purpose, the surface spectrum is computed based on the surface Green’s function method70 in the maximally localized Wannier function (MLWF) Hamiltonian of a half-infinite structure. First, the (001)-surface energy contour of HfRuP is obtained in Fig. 4a with \(E-{E}_{\mathrm{W}}=0\) meV. Since the two WPs with opposite chirality project onto the same point on the (001)-surface, no topological arc states are guaranteed to come out from the projections. However, we find that there are two trivial arc states (following the two dashed guiding lines) coming out of each WP projection: one is crossing the \({k}_{x}=0\) line; the other one is crossing the BZ boundary, (i.e., the \(\bar{K}-\bar{M}\) line. Second, the computed (100)-surface energy contour is presented in Fig. 4b. Since they are type-II WPs, the WPs should be located at the touching points between the electron pocket and the hole pocket. We do see that the projected points A and B are the touching points of two pockets. The constant energy contour with energy slightly below (or above) \({E}_{\mathrm{W}}\) is presented in Supplementary Section D. We find that two surface Fermi arc states (indicated by dashed lines) are connected to the projected points (i.e., A and B). For the projected point C, it’s hard to see any surface state from it, because it is not projected onto a proper surface. At last, the computed (010)-surface energy contour is obtained and shown in Fig. 4c, where the WPs with the same chirality project onto each other. As long as the projected electron/hole pockets (enclosing the projections of the WPs) are separated from each other, two topological Fermi arc states can be expected. Unfortunately, the metallic bulk states are projected into a big continuum, which makes the Fermi arc states invisible. Our ARPES experiment to search for the arc states on the (100)-surface is still in process.

Fig. 4: The surface spectra of HfRuP.
figure 4

The (001)-surface (a), (100)-surface (b) and (010)-surface (c) energy contours with \(E-{E}_{\mathrm{W}}=0\) meV. The projections of the WPs are indicated by diamonds or “x” symbols.

Full size image

Exotic TSC

With intrinsic superconductivity, topological materials are promising platforms to realize TSCs owing to the nontrivial topology of the wave function in normal states. For example, surface Dirac fermions can realize a 2D TSC even for an s-wave pairing state40,44. Also, the FS topology in the normal state directly affects the TSC. In 3D, the integer topological quantum number in a TRI superconductor is determined by the sign of the pairing order parameter and the first Chern number of the Berry phase gauge field on the FSs2. A WSM phase of a superconductor hosts the nontrivial FSs originating from WPs. Providing the two key ingredients: the nontrivial FSs and superconductivity, the WSM phase of HfRuP can be served as a good platform to realize the TRI TSC in 3D. Besides, the previous works71,72 report that the nontrivial mirror Chern number can generate multiple Majorana fermions in Cd\({}_{3}{\mathrm{As}}_{2}\) and SrRuO\({}_{4}\). These compounds in the TCI phase are very promising candidates to search for the topological crystalline superconductors too.

Discussion

Based on the DFT calculations, we find that there are two nodal rings in the band structure without SOC for the h-phase of TT’X, which is different from the situation in CaAgAs. After including SOC, they enter either a WSM phase with 12 pairs of type-II WPs, or a TCI phase with non-zero mirror Chern numbers. The single crystals for the two distinct topological phases are grown successfully. Their superconductivity and electronic band structures are verified by our resistivity, magnetic susceptibility and ARPES measurements, respectively. The series of Ru-based compounds are the desired single-crystal materials, which host both superconductivity below \({T}_{\mathrm{C}}\) and topological states above \({T}_{\mathrm{C}}\). The experimental study of the interplay between superconductivity and Weyl or nontrivial mirror Chern states would be stimulated after this work.

At the stage of finalizing the present paper, we are aware of the mention of Weyl nodes in similar materials in the ref. 73. Our result of WPs in HfRuP is consistent with it, while the result for ZrRuP is different. That is because the topology (the annihilation of Weyl points) in ZrRuP may be sensitive to the parameters of the structure.

Methods

The first-principles calculations were performed based on the DFT with the projector augmented wave (PAW) method74,75 as implemented in VASP package76,77. The generalized gradient approximation (GGA) of Perdew-Burke-Ernzerhof (PBE) type was adopted for the exchange-correlation functional78. The kinetic energy cutoff of the plane wave basis was set to 400 eV. A 10 × 10 × 16 k-point mesh for BZ sampling was adopted. The experimental lattice parameters were employed79,80. The internal atomic positions were fully relaxed until the forces on all atoms were smaller than 0.01 eV/Å (the relaxed atomic positions are shown in Supplementary Section A). The electronic structures were carried out both with and without SOC. The topological invariants and chiral charge were computed through the Wilson-loop technique. The MLWF method was used to calculate the surface states81.