Introduction

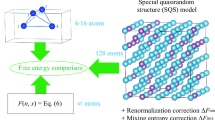
Prediction of stable phases of multicomponent systems is a crucial step in understanding thermodynamics of alloys. The increasing availability of density functional theory (DFT) based methods, and systematic approaches for phase prediction such as the cluster-expansion method1 have made inroads in modeling few-component systems. However, obtaining phase diagrams for ternary compositions and beyond has remained a challenging and often unfeasible task due to the complexity of the problem. In addition to predicting potential stable phases, an extra challenge is the coexistence of phases and prediction of phase fractions. To overcome these restrictions, we present a Multi-Cell Monte Carlo, or (MC)\({}^{2}\) algorithm, that is capable of predicting for a chemically complex crystalline system both the coexistence of multiple phases and the composition and structure of the different phases in a single run. To the best of our knowledge, this is the first and only method that can capture the phase boundary from only one initial composition, without the need to interpolate intermediate compositions.

Coexisting supercells in Monte Carlo simulations have previously been used within the Gibbs ensemble method2 for the simulation of vapor/liquid equilibrium, where atoms are constantly deleted/inserted in the cells. In crystalline solids, deleting/inserting atoms in each cell creates point defects. Therefore, the Gibbs ensemble MC has not been applied to phase predictions in solids. Recently, we have introduced the first multi-cell MC ‘relaxation’ method for solids, which required a fixed number of atoms in each cell.3 However, the fixed cell sizes restricted the compositional variations and did not allow for prediction of phase fractions.

Here, we introduce a new algorithm that eliminates the fixed size restriction while profiting from the concept of multi-cell MC. Each cell is assigned a molar ratio which controls its percentage in the total system. The molar ratios are determined by the ‘lever rule’ so that the total composition of the system is constant. In contrast to the atom-transfer idea in a Gibbs ensemble MC simulation, the transfer of random atoms is achieved here by changing the species of an atom in one or more cells, which we call a ‘flip’ move. A flip move changes the composition in each cell and thus the overall set of molar ratios, equivalent to the transfer of a group of random atoms among the cells. Flip moves were first introduced by Kofke and Glandt to establish the semigrand canonical ensemble4 and can happen locally (one random atom in one random supercell) or globally (one or more random atoms in all cells simultaneously). While local flips are sufficient, occasional global flips accelerate convergence without any loss of generality. In the current work, the total energy of each cell is computed with DFT at 0 K, and no vibrational entropy is considered. The relaxation is allowed in all lattice and basis degrees of freedom at zero pressure. Note that in general, the energy can also be evaluated under a constant, nonzero pressure. We specifically choose zero pressure in this work to apply \({({\rm{MC}})}^{2}\) to the prediction of equilibrium phase diagrams.

The lever rule is a tool to determine the equilibrium phase fractions in binary systems.5 Applied to two cells, representing two phases of a binary system with overall concentration \({c}^{j}\) of component j, the lever rule determines the molar fraction \({f}_{i}\) of phase i to conserve the initial stoichiometry:

$$\begin{array}{ccc}{x}_{1}^{1}{f}_{1}+{x}_{2}^{1}{f}_{2}&=&{c}^{1},\\ {x}_{1}^{2}{f}_{1}+{x}_{2}^{2}{f}_{2}&=&{c}^{2},\end{array}$$
(1)

where \({x}_{i}^{j}\) is the concentration of component j in phase i. In matrix form, Eq. (1) becomes \({\bf{XF}}={\bf{C}}\) with matrix \({\bf{X}}=\{{x}_{i}^{j}\}\) and vectors \({\bf{F}}\,=\,\{{f}_{i}\}\,and\,{\bf{C}}\,=\,\{{c}^{j}\}\). The molar ratios (\({f}_{1}\,{\rm{and}}\,{f}_{2}\)) are obtained from \({\bf{F}}={{\bf{X}}}^{-1}{\bf{C}}\). While \({\bf{C}}\) is constant, \({\bf{X}}=\{{n}_{i}^{j}/{N}_{i}\}\) is updated after each MC step, where \({n}_{i}^{j}\) is the number of atoms of species j in cell i containing \({N}_{i}\) total atoms. Note that equation \({\bf{F}}={{\bf{X}}}^{-1}{\bf{C}}\) is not restricted to binary systems but equally applies to any system with an arbitrary number of components m.

In order to keep the matrix \({\bf{X}}\) square and thus invertible, we always use m cells, representing m phases, for an m-component system. This is sensible since the Gibbs phase rule states that under constant pressure—and excluding special points such as eutectic points—at most, m phases can coexist in equilibrium for an m-component system.5 If the actual number of phases is fewer than m, then the corresponding molar fraction of the additional cells will become zero, as demonstrated in the examples below.

The particle flip moves, combined with the lever rule applied to multiple cells, mimics the effect of varying cell size and composition, without the need for particle insertion/deletion in the cells (see (MC)\({}^{2}\) flowchart in Supplementary Fig. 1).

In \({({\rm{MC}})}^{2}\), two levels of simulation can be envisioned: within individual cells and considering all cells combined. Within each cell i, and ignoring all other cells, the total number of atoms \({N}_{i}\) is fixed, but the ratio of the different species can change. This corresponds to the semigrand canonical ensemble. However, globally the total number of atoms \({\sum }_{i=1}^{m}{N}_{i}\) as well as total numbers of each species in the entire simulation is fixed by assigning the appropriate molar fraction to each cell via the lever rule. Because temperature and pressure are additionally fixed across all cells, the entire simulation represents an isothermal-isobaric ensemble with acceptance criterion for a move from step k to step \(k+1\)6

$${P}^{{\rm{acc}}}=\min \left[1,\exp \left(-\beta \Delta H+N\sum _{i=1}^{m}\mathrm{ln}\frac{{V}_{i}(k+1)}{{V}_{i}(k)}\right)\right],$$
(2)

with \(\beta =1/{k}_{B}T\,{\rm{where}}\,{k}_{B}\) denotes the Boltzmann constant, T is the temperature, and \({V}_{i}\) is the volume of cell i. Note that in Eq. 2\({V}_{i}\) is used rather than \({V}_{i}{f}_{i}\). The reason for this choice is that the virtual cells, mimicking a different volume of \({V}_{i}(k){f}_{i}(k)\), do not contribute new configurations to sample and consequently do not change the probability density. The number of atoms in each cell \({N}_{i}\) is assumed to be equal to N for simplicity. The term \(\Delta H\) is the enthalpy change of all cells combined

$$\Delta H= \sum_{i=1}^{m}m[{U}_{i}(k+1)+p{V}_{i}(k+1)]{f}_{i}(k+1)-\sum_{i=1}^{m}m[{U}_{i}(k)+p{V}_{i}(k)]{f}_{i}(k)$$
(3)

where \({U}_{i}\) is the internal energy of cell i. Note that in the most general case, \({({\rm{MC}})}^{2}\) can be performed on a system under constant but nonzero pressure and/or temperature, for instance combined with molecular dynamics (MD) simulations instead of energy minimization for evaluation of the energy. However, here we focus on the case of \(p=0\) and use energy minimizations that are carried out at \(T=0\) K. As such, contribution of the vibrational entropy is neglected, but can be included if finite-temperature MD is used instead. In addition, in the case of crystalline solids, with sufficiently large simulation cells, studied in this paper, the volume change after flipping one atom in the cell is negligible. Therefore, the term \({V}_{i}(k+1)/{V}_{i}(k)\approx 1\). Considering this ratio and the fact that pressure is set to zero here to obtain equilibrium phase diagrams, the acceptance criterion can be simplified to

$${P}^{{\rm{acc}}}=\min \left\{1,\exp \left[-m\left(\sum _{i=1}^{m}{U}_{i}(k+1){f}_{i}(k+1)-\sum_{i=1}^{m}{U}_{i}(k){f}_{i}(k)\right)/{k}_{B}T\right]\right\}.$$
(4)

The factor m appears in the exponent since \({\sum }_{i}{f}_{i}=1\) and we need the weighted sum and not the average energy of the cells in the exponent.

Results and discussion

Au–Pt binary alloy

An equiatomic Au–Pt alloy is chosen as our first benchmark. This simulation starts with two fcc cells, since both Au and Pt have the fcc structure. Each cell contains 32 atoms with special quasirandom structure (SQS).7 Note that a SQS cell is chosen to optimally define a random alloy as the initial phase, but is not necessary for \({({\rm{MC}})}^{2}\) in general. See Supplementary Section 6 for examples starting with different initial configurations. Since the Au–Pt phase diagram has a miscibility gap at low temperatures,8 this alloy is expected to decompose into Pt- and Au-rich phases.

Figure 1 shows the evolution of (a) composition, (b) molar fraction, and (c) total energy of each cell at 600 K. While both cells start with equal numbers of Au and Pt atoms, after \(\sim\)500 steps, Cell 1 contains mostly Pt atoms, while Cell 2 has an Au-rich composition (Fig. 1a). At this point, energy and molar fractions start to equilibrate as well. At equilibrium, the all-Pt phase 1 forms 40% of the solid, leaving \(\sim 60\)% of phase 2 with \(\sim 82\)% Au. Therefore, \({({\rm{MC}})}^{2}\) not only predicts the separation into a Pt- and Au-rich phases correctly, but also yields the relative amounts and composition of each phase. This is the major new finding of this paper, and when performed at various temperature/composition combinations,\({({\rm{MC}})}^{2}\)can directly predict the phase diagram of alloys. The rapid energy drop at the beginning of the simulation in Fig. 1c, is an early indication that phase separation is favorable. After the \(\sim\)500-step point, the energy stabilizes at a certain value, indicative of convergence, and an energy or concentration convergence check, which can easily be implemented, would have terminated the simulation already at that point. Energy calculations for a series of snapshots with the ‘accurate’ settings (see Methods Section), shown in Fig. 1 c validate our ‘fast’ DFT setup. Figure 2 shows the excellent agreement between our \({({\rm{MC}})}^{2}\) predictions of Au–Pt phase boundaries at 600, 800, and 1000 K and experiment.9 The points at the different temperatures are the ensemble average compositions in the plateau-regime after the “burn-in” phase of the Monte Carlo runs, e.g. last 60\(\%\) of steps for the 600 K (327 \({}^{\circ }\)C) run. The error bars represent the systematic error that arises from the finite size of the simulation cells, which is \(1/N\approx 3 \%\) in this case. The statistical error, i.e. the standard error of mean, is shown in Table 1. The statistical error is small compared to the systematic error and thus is omitted in the phase diagram. The small statistical error also confirms that our simulations are reasonably converged.

Fig. 1
figure 1

\({({\rm{MC}})}^{2}\)predictions for energy and composition of AuPt at 600 K vs. MC steps with (a) cell compositions (yellow represents gold, blue platinum); (b) molar fractions for both cells and (c) change of energy relative to the initial step (dots are energies recalculated with ‘accurate’ DFT settings).

Full size image
Fig. 2: \({({\rm{MC}})}^{2}\) prediction for the Au–Pt phase boundary at 600, 800, and 1000 K vs. experimental phase diagram, redrawn from Grolier et al.9.
figure 2

The error bars represent the systematic error that arises from the finite size of the simulation cells, which is \(1/N\approx 3 \%\) in this case.

Full size image
Table 1 Standard error of the calculated equilibrium Pt concentration in Fig. 2.
Full size table

Hf–Zr binary alloy

Next, we test (MC)2 for a Hf–Zr binary alloy. The initial structures for this simulation are 2 hcp cells with 24 atoms randomly assigned with Hf or Zr. More details can be found in the supplementary materials. We successfully predict the complete solubility at 400, 700, and 1000 K. Figure 3 shows, as an example, the results for an equiatomic Hf–Zr alloy at \(T=400\) K, where the system fluctuates around the initial equiatomic composition during the entire run (Fig. 3a) without any significant change in energy (Fig. 3c). The negligible energy change also suggests that the system is completely soluble and can assume any composition in the whole concentration range, which in turn comfirms the fluctuation throughout the simulation observed in Fig. 3a, b. Unlike the case of Au–Pt where the molar fractions converge to a constant value, the molar fractions for Hf–Zr fluctuate from zero to 100%, indicating that \({({\rm{MC}})}^{2}\) maintains a single phase around the initial concentration, since no other composition could result in 0% vs. 100% fraction (Fig. 3c). Again, the energies from the ‘fast’ setting are confirmed by the ‘accurate’ setting results, as shown in (Fig. 3c).

Fig. 3
figure 3

\({({\rm{MC}})}^{2}\)predictions for energy and composition of Hf–Zr at 400 K vs. MC steps with (a) cell compositions (yellow represents hafnium, blue zirconium); (b) molar fractions for both cells and (c) change of energy relative to the initial step (dots are energies recalculated with ‘accurate’ DFT settings. Molar fractions fluctuate between 0 and 1, indicating a single phase alloy without change in initial composition.

Full size image

HfZrTaNb quaternary alloy

The unique predictive power of \({({\rm{MC}})}^{2}\) becomes evident when applied to multicomponent systems, particularly beyond ternary alloys where phase diagrams do not exist and cluster-expansion calculations start to falter. As an example, we study the quaternary, equiatomic, HfNbTaZr high-entropy alloy, known to form a body-centered cubic (bcc) single-phase random solid solution after casting.10 Figure 4 summarizes the results of a (MC)\({}^{2}\) run at 300 K, starting with four equiatomic random bcc SQS cells with 36 atoms each (9 of each species). Cells 3 and 4 are gradually enriched by Nb/Ta and Hf/Zr respectively, while the other two cells maintain more or less equiatomic composition (Fig. 4a). However, since the molar fractions of Cells 1 and 2 are zero, they do not represent phases after the phase separation has taken place and thus are discarded by (MC)\({}^{2}\). Therefore, the only remaining phases are Nb/Ta and Hf/Zr formed in Cells 3 and 4, respectively. Since the bcc structure, at low temperature, is unstable for Hf and Zr11 and cell volume and shape are optimized by VASP along with atomic positions, the Hf/Zr-rich Cell 4 manages to transform into a hexagonal close packed (hcp) lattice from the initial bcc lattice, as shown in the structures accompanying Fig. 4a. Therefore, \({({\rm{MC}})}^{2}\) predicts the phase separation of the bcc HfZrTaNb HEA into two phases of Nb/Ta (bcc) and Hf/Zr (hcp). These predictions are consistent with recent atom probe tomography results, which found a secondary phase enriched in Hf and Zr after sufficient annealing.12 Despite this successful prediction, there is no guarantee that such transformations would be observed for an arbitrary system, where the system can get stuck in a metastable configuration. We recommend trying different initial structures, especially when no previous knowledge about the system is available.

Fig. 4: Predicted stable phases of the quaternary HfZrTaNb high entropy alloy using 4 cells.
figure 4

(a) shows the change in composition in each cell, starting from the same equiatomic random composition with bcc structure. Initial and final atomic structures are shown on the left and right side of the plot (a). (b) shows the associated energy change as a function of Monte Carlo steps and (c) shows the distribution of each element in each cell, (.i.e composition of each cell multiplied by the corresponding molar ratio) at the final step. Cells 1 and 2 have zero molar fractions, implying phase separation into two phases: a Nb-Ta BCC phase in Cell 3 and a Hf–Zr hcp phase in Cell 4.

Full size image

Ni–Sn system and formation of intermetallics

Besides random alloys, \({({\rm{MC}})}^{2}\) also gives sensible results for systems forming ordered intermetallics, as we show for the Ni–Sn binary system (details in Supplementary Section 5.) Here, a (MC)\({}^{2}\) run for a Ni–12.5 at\(\%\)Sn alloy at 400 K correctly predicts formation of pure Ni with fcc structure and the ordered \({\text{D0}}_{\text{19}}\) (underlying hcp stacking) \({\text{Ni}}_{3}\text{Sn}\,\) phase, in agreement with experiments from13 (Fig. 5). Note that the solubility ranges, shaded in gray, are below the resolution of this simulation which is \(\approx 4\,\text{at.} \%\) due to the cell size.

Fig. 5: \({({\rm{MC}})}^{2}\) prediction at 400 K for Ni–Sn superimposed on the Ni-rich part of the experimental phase diagram from ref. 13
figure 5

The initial (Ni–12.5 at \(\%\) Sn fcc solid solution) and final (fcc Ni+ordered \({\text{D0}}_{\text{19}}{\text{Ni}}_{3}\text{Sn}\,\)) compositions are marked with empty and full circles on the phase diagram respectively. The atomic arrangements are shown with periodic images in viewing directions \(a=[1\bar{1}0]\), \(b=[\bar{1}\bar{1}2]\), and \(c=[111]\).

Full size image

As a final note, we reiterate that the current implementation of (MC)\({}^{2}\) takes into account the configurational entropy contribution to the free energy, while vibrational entropy is not included. Inclusion of the latter can be achieved for example by combining \({({\rm{MC}})}^{2}\) with molecular dynamics at finite temperature, which would extend the sensible applicability range of (MC)\({}^{2}\) to considerably higher temperatures. We suggest to restrict the application of \({({\rm{MC}})}^{2}\), without vibrational entropy, to temperatures sufficiently below the solidus curve.

In summary, we have introduced the \({({\rm{MC}})}^{2}\) method to predict both stable phases and phase fractions in multicomponent alloys. As we have demonstrated, each converged \({({\rm{MC}})}^{2}\) run identifies either a region of miscibility, or the relevant phase boundaries for the simulated temperature and composition. The algorithm in \({({\rm{MC}})}^{2}\) takes advantage of parallel computations of multiple cells and provides the unique capability to identify relevant phases and phase boundaries without any prior knowledge of possible phases.

Methods

Computational methods

DFT calculations are performed with the plane-wave package VASP,14,15 where the choices for settings and SQS,7 generated with the Alloy Theoretic Automated Toolkit (ATAT),16 are described in Supplement Sections 2–4 in detail. Two settings for the DFT calculations are used, ‘accurate’ and ‘fast’. The ‘accurate’ setting ensures a total energy convergence of 0.2 meV/atom, while the ‘fast’ settings with reduced k-point meshes and cutoff energies are used during the MC simulations. Upon completion of a (MC)\({}^{2}\) run with ‘fast’ settings, 9 intermediate configurations are recalculated with ‘accurate’ parameters. The energy differences between the two settings quantify the error from the ‘fast’ settings and verify that general trends and results remain unchanged.