Large-signal model of 2DFETs: compact modeling of terminal charges and intrinsic capacitances

Abstract

We present a physics-based circuit-compatible model for double-gated two-dimensional semiconductor-based field-effect transistors, which provides explicit expressions for the drain current, terminal charges, and intrinsic capacitances. The drain current model is based on the drift-diffusion mechanism for the carrier transport and considers Fermi–Dirac statistics coupled with an appropriate field-effect approach. The terminal charge and intrinsic capacitance models are calculated adopting a Ward–Dutton linear charge partition scheme that guarantees charge conservation. It has been implemented in Verilog-A to make it compatible with standard circuit simulators. In order to benchmark the proposed modeling framework we also present experimental DC and high-frequency measurements of a purposely fabricated monolayer MoS₂-FET showing excellent agreement between the model and the experiment and thus demonstrating the capabilities of the combined approach to predict the performance of 2DFETs.

Introduction

Since the emergence of graphene, over a surprisingly short period of time, an entire new family of two-dimensional materials (2DMs) has been discovered.¹ Some of them are already used as channel materials in FETs, being promising candidates to augment silicon and III–V compound semiconductors via heterogeneous integration for advanced applications. In this context, the development of electrical models for 2D semiconductor-based FETs (2DFETs) is essential to: (1) interpret experimental results; (2) evaluate their expected digital/RF performance; (3) benchmark against existing technologies; and (4) eventually provide guidance for circuit design and circuit-level simulations.

Several compact models for three-terminal FETs based on graphene and related 2D materials (GRMs) have been recently published encompassing both static and dynamic regimes.^{2,3,4,5,6,7,8,9,10} In particular, Suryavanshi et al.² proposed a semi-classical transport approach for the drain current combining the intrinsic FET behavior with models of the contact resistance, traps and impurities, quantum capacitance, fringing fields, high-field velocity saturation and self-heating. However, the dynamic regime is described using a charge model derived for bulk MOSFETs¹¹ that fails to capture the specific physics of the 2D channel, since it considers that the channel is always in a weak-inversion regime and therefore the channel charge can be assumed to be linearly distributed along the device. Wang et al.³ reported on a compact model restricted to the static regime of graphene FETs and based on the “virtual-source” approach, valid for both the saturation and linear regions of device operation. Also based on the “virtual-source” approach, Rakheja et al.⁴ studied quasi-ballistic graphene FETs. Nevertheless, they also employed the approximation derived for bulk MOSFETs¹¹ for the dynamic regime description even though the channel material considered is graphene. Jiménez early developed a model describing the drain current for single layer transition metal dichalcogenide (TMD) FETs based on surface potential and drift-diffusion approaches but the dynamic behavior of the TMD-FETs was not treated.⁵ Also based on surface potential and drift-diffusion arguments, Parrish et al.⁶ presented a compact model for graphene-based FETs for linear and non-linear circuits, but the dynamic regime description was roughly estimated by equally splitting the total gate capacitance between gate-drain and gate-source capacitances. A charge-based compact model for TMD-based FETs only valid for the static regime but simultaneously including interface traps, ambipolar current behavior, and negative capacitance was proposed by Yadav et al.⁷ Taur et al.⁸ presented an analytic drain current model for short-channel 2DFETs combining a subthreshold current model based on the solution to 2D Poisson’s equation and a drift-diffusion approach to get an all-region static description. Rahman et al.⁹ discussed a physics-based compact drain current model for monolayer TMD-FETs considering drift-diffusion transport description and the gradual channel approximation to analytically solve the Poisson’s equation. Unfortunately, none of them faced the dynamic regime operation. Finally, Gholipour et al.¹⁰ proposed a compact model that combines both the drift-diffusion and the Landauer–Buttiker approaches to properly describe the long- and short-channel FETs in flexible electronics, respectively. As a key feature, the mechanical bending is considered by linearly decreasing the channel material bandgap with respect to the applied strain. However, the capacitance model was roughly approximated by considering that the top (back) gate-drain and top (back) gate-source capacitances are just the geometrical top (back) gate capacitance. In summary, up to date the dynamic description of 2DFETs has been either roughly approximated or not specifically addressed for such devices. Our aim is to develop an accurate and physics-based compact model of the terminal charges and corresponding intrinsic capacitances of four-terminal (4T) 2DFETs valid for all operation regimes. In doing so, we present such a model together with the drain current equation, developed by some of us,¹² based on drift-diffusion theory where the surface potential is the key magnitude of the model. So that, the combination of both approaches gives rise to a compact large-signal model suitable for commercial TCAD tools employed in the simulation of circuits based on 2DFETs. The model has been shown to reproduce with good agreement DC and high-frequency measurements of a fabricated n-type MoS₂-based FET, and has been used to predict the output transient of a three-stage ring oscillator.

Results

Large-signal model of four-terminal 2DFETs

We first deal with the development of the large-signal model of 4T 2DFETs by the sequential formulation of the electrostatics, the drain current equation, the terminal charge model, and the corresponding intrinsic capacitance description.

The cross-section of the considered dual-gated 2DFET is depicted in Fig. 1a. For the sake of brevity, we derive here the expressions for an n-type device (the extension to a p-type transistor can be obtained straightforwardly). Provided that the semiconductor bandgap is not too small, we can assume that p(x) ≪ n(x) in all regimes of operation, where p(x) and n(x) are the hole and electron carrier densities, respectively. Upon application of 1D Gauss’ law to the double-gate stack shown in Fig. 1b, the electrostatics can be described using the equivalent circuit depicted in Fig. 1c:

$$Q_{\mathrm {net}}(x) + Q_{\mathrm {it}}(x) = - C_{\mathrm {t}}\left( {V_{\mathrm {g}} - V_{{\mathrm {g}}0} - V(x) + V_{\mathrm {c}}(x)} \right) - C_{\mathrm {b}}\left( {V_{\mathrm {b}} - V_{{\mathrm {b}}0} - V(x) + V_{\mathrm {c}}(x)} \right),$$

(1)

where Q_net(x) = q(p(x) – n(x)) is the overall net mobile sheet charge density and q is the elementary charge. C_t = ε₀ε_t/t_t (C_b = ε₀ε_b/t_b) is the top (back) oxide capacitance per unit area where ε_t (ε_b) and t_t (t_b) are the top (back) gate oxide relative permittivity and thickness, respectively; and V_g – V_g0 (V_b – V_b0) is the overdrive top (back) gate voltage. These latter quantities comprise work-function differences between the gates and the 2D channel and any possible additional charges due to impurities or doping. The energy qV_c(x) = E_C(x) − E_F(x) represents the shift of the quasi-Fermi level with respect to the conduction band edge and –qV(x) = E_F(x) is the quasi-Fermi level along the channel. This latter quantity must fulfill the boundary conditions: (1) V(x = 0) = V_s (source voltage) at the source end; (2) V(x = L) = V_d (drain voltage) at the drain end.

Fig. 1

a Cross-section of the 2DFET considered in the modeling framework. A 2DM plays the role of the active channel. b Scheme of the 2DM-based capacitor showing the relevant physical and electrical parameters. c Equivalent capacitive circuit of the 2DFET.

2D crystals are far from perfect and suffer from diverse non-idealities. In particular, interface traps are unavoidable in FETs, even for those processed by state-of-the-art CMOS technology,¹³ impacting negatively the performance of 2DFETs.¹⁴ Therefore, it is mandatory to include them in order to achieve an accurate predictive TCAD tool. For n-type devices, acceptor-like traps (which are negatively charged when occupied by electrons and are energetically located in the upper half of the bandgap¹⁵) contribute the most to the device electrical characteristics.¹⁶ Assuming the traps are situated at an effective energy E_it = – qV_it below the conduction band, the occupied trap density can be written as n_it = N_it/(1 + exp(V_c − V_it/V_th)), where N_it is the effective trap density considered to be a delta function in energy. The trap charge density is then Q_it = –qn_it and the interface trap capacitance C_it at the oxide–semiconductor interface (taken as a combination from both interfaces of the ultra-thin 2D channel) can be computed as:

$$C_{\mathrm {it}} = \frac{{{\mathrm d}Q_{{\mathrm {it}}}}}{{{\mathrm d}V_{\mathrm c}}} = \frac{{qN_{{\mathrm {it}}}}}{{2V_{{\mathrm {th}}}}}\frac{1}{{1 + \cosh \left( {\frac{{V_{\mathrm c} \,-\, V_{{\mathrm {it}}}}}{{V_{{\mathrm {th}}}}}} \right)}},$$

(2)

where V_th = k_BT/q is the thermal voltage, k_B is the Boltzmann constant, and T is the temperature. The term C_it adds to the quantum capacitance C_q, as shown in Fig. 1c.

We can, thus, find an expression to calculate the overall net mobile sheet density assuming a parabolic dispersion relationship modeled in the effective mass approximation and using Fermi–Dirac statistics¹²:

$$Q_{{\mathrm {net}}}(x) = - qn(x) = - C_{{\mathrm {dq}}}V_{{\mathrm {th}}}u\left( {V_{\mathrm c}} \right);\quad u\left( {V_{\mathrm c}} \right) = \,\ln \left( {1 + e^{ - \frac{{V_c}}{{V_{{\mathrm {th}}}}}}} \right),$$

(3)

where C_dq = q²D₀ is defined as the degenerated-quantum capacitance, which corresponds to the upper-limit achievable when the 2D carrier density becomes heavily degenerated.¹⁷ D₀ = g_K(m^K/2πħ²) + g_Q(m^Q/2πħ²)exp[−ΔE₂/k_BT] is the 2D density of states, with ħ being the reduced Planck’s constant, g_K (g_Q) the degeneracy factor and m^K (m^Q) the conduction band effective mass at the K (Q) band valley. In most TMDs, the second conduction valley, labeled as Q valley, is non-negligible since the energy separation between the K and Q conduction valleys, ΔE₂, is only around 2k_BT.^18,19 Thus, two conduction band valleys may participate in the transport process. The rest of valleys are, on the contrary, far away in energy to contribute to the electrical conduction,²⁰ and hence can be neglected for practical purposes.

The quantum capacitance of the 2DM can be computed by evaluating C_q = dQ_net/dV_c resulting in:

$$C_q = C_{{\mathrm {dq}}}\left( {1 - e^{ - u}} \right).$$

(4)

Due to the complexity of Eq. (1) and considering the relation between Q_net and V_c given by Eq. (3), it is not possible to get an explicit expression for V_c as a function of the applied bias. However, an iterative Verilog-A algorithm can be implemented to evaluate the chemical potential at the source and drain edges, which are the relevant quantities determining the drain current. In doing so, V_cs = V_c|_V=Vs and V_cd = V_c|_V=Vd are obtained, respectively, from Eqs. (1) and (3) by a construct^21,22 which lets the circuit simulator to iteratively solve both equations during run-time.

In the diffusive regime, the drain current of a 2DFET can be accurately computed by the following compact expression¹²:

$$I_{{\mathrm {ds}}} = \mu \frac{W}{L}C_{{\mathrm {dq}}}V_{{\mathrm {th}}}^2\left[ {\left( {1 + \frac{{C_{{\mathrm {dq}}}}}{{C_{{\mathrm {tb}}}}}} \right)\left( {\frac{{u_{\mathrm s}^2 - u_{\mathrm d}^2}}{2}} \right) + \left( {e^{ - u_{\mathrm d}} - e^{ - u_{\mathrm s}}} \right)} \right],$$

(5)

where u_s = u(V_cs) and u_d = u(V_cd); C_tb = C_t + C_b; W and L are the device width and length, respectively; and µ is the carrier mobility which has been assumed to be dependent of the applied electric field, carrier density, and temperature as in ref. ² Once we have a suitable expression for describing the static behavior of the device, the dynamic response must be analyzed to build a large-signal model. In doing so, the terminal currents in the time domain can be computed as:

$$i_{ k}(t) = \frac{{{\mathrm d}Q_{k}}}{{{\mathrm d}t}} = C_{{k \mathrm {g}}}\frac{{{\mathrm d}v_{\mathrm g}}}{{{\mathrm d}t}} + C_{{k\mathrm {d}}}\frac{{{\mathrm d}v_{\mathrm d}}}{{{\mathrm d}t}} + C_{{k\mathrm {s}}}\frac{{{\mathrm d}v_{\mathrm s}}}{{{\mathrm d}t}} + C_{{k\mathrm {b}}}\frac{{{\mathrm d}v_{\mathrm b}}}{{{\mathrm d}t}},$$

(6)

where k stands for g, d, s, and b, i.e. top gate, drain, source and back-gate, respectively. The terminal currents, thus, can be obtained by either computing the time derivative of the corresponding terminal charge or by the weighted sum of the time derivative of the terminal voltages, where the weights are given by the intrinsic capacitances.

The intrinsic capacitances of FETs are modeled in terms of the terminal charges. Specifically, from the electrostatics given in Eq. (1) the following relations are derived²³:

$$Q_{{\mathrm {gb}}} = Q_{\mathrm g} + Q_{\mathrm b} = - W{\int_0^L} {Q_{{\mathrm {net}}}(x){\mathrm d}x},$$

(7)

$$Q_{\mathrm g} = Q_0 - \frac{{WC_{\mathrm t}}}{{C_{{\mathrm {tb}}}}}{\int_0^L} {Q_{{\mathrm {net}}}(x){\mathrm d}x},$$

(8)

$$Q_{\mathrm b} = - Q_0 - \frac{{WC_{\mathrm b}}}{{C_{{\mathrm {tb}}}}}{\int_0^L} {Q_{{\mathrm {net}}}(x){\mathrm d}x},$$

(9)

where Q₀ = WLC_tC_b(V_g − V_g0 − V_b + V_b0)/C_tb. The charge controlled by both the drain and source terminals is computed based on the Ward–Dutton’s linear charge partition scheme,²⁴ which guarantees charge conservation:

$$Q_{\mathrm d} = W{\int_0^L} {\frac{x}{L}Q_{{\mathrm {net}}}(x){\mathrm d}x},$$

(10)

$$Q_{\mathrm s} = - \left( {Q_{\mathrm g} + Q_{\mathrm b} + Q_{\mathrm d}} \right) = W{\int_0^L} {\left( {1 - \frac{x}{L}} \right)Q_{{\mathrm {net}}}(x){\mathrm d}x}.$$

(11)

The above expressions can be conveniently written using u as the integration variable, as it was done to model the drain current in Eq. (5). Based on the fact that the drain current is the same at any point x along the channel (i.e. we are under the quasi-static approximation framework), we get from the transport model the following equations needed to evaluate the charges in Eqs. (7)–(11):

$$\begin{array}{l}{\mathrm d}x = \frac{{\mu W}}{{I_{{\mathrm {ds}}}}}Q_{{\mathrm {tot}}}\left( u \right)\frac{{{\mathrm d}V}}{{{\mathrm d}V_{\mathrm c}}}\frac{{{\mathrm d}V_{\mathrm c}}}{{{\mathrm d}u}}{\mathrm d}u\\ x = \frac{{\mu W}}{{I_{{\mathrm {ds}}}}}\left[ {{\int_{u_{\mathrm s}}^u} {Q_{{\mathrm {tot}}}\left( u \right)\frac{{{\mathrm d}V}}{{{\mathrm d}V_{\mathrm c}}}\frac{{{\mathrm d}V_{\mathrm c}}}{{{\mathrm d}u}}{\mathrm d}u} } \right]\end{array}.$$

(12)

Replacing Eq. (12) in Eqs. (7) and (10), the following compact expressions are obtained for the terminal charges Q_gb and Q_d:

$$\begin{array}{l}Q_{{\mathrm {gb}}} = Q_{{\mathrm {2D}}}\frac{{2\left( {3C_{{\mathrm {tb}}}\left( {e^{u_{\mathrm d}}\left( {1 \,+\, u_{\mathrm s}} \right) - e^{u_{\mathrm s}}\left( {1 \,+\, u_{\mathrm d}} \right)} \right) \,+\, e^{u_{\mathrm s}}e^{u_{\mathrm d}}\left( {C_{{\mathrm {dq}}} \,+\, C_{{\mathrm {tb}}}} \right)\left( {u_{\mathrm d}^3 \,-\, u_{\mathrm s}^3} \right)} \right)}}{{6C_{{\mathrm {tb}}}\left( {e^{u_{\mathrm d}} \,-\, e^{u_{\mathrm s}}} \right) \,+\, 3e^{u_{\mathrm s}}e^{u_{\mathrm d}}\left( {C_{{\mathrm {dq}}} \,+\, C_{{\mathrm {tb}}}} \right)\left( {u_{\mathrm d}^2 \,-\, u_{\mathrm s}^2} \right)}}\\ Q_{\mathrm d} \approx - Q_{{\mathrm {2D}}}\frac{2}{{15}}\frac{{3u_{\mathrm d}^5 \,-\, 5u_{\mathrm d}^3u_{\mathrm s}^2 \,+\, 2u_{\mathrm s}^5}}{{\left( {u_{\mathrm d}^2 \,-\, u_{\mathrm s}^2} \right)^2}}\end{array},$$

(13)

where Q_2D = WLC_dqV_th. Equation (13) can be replaced in Eqs. (8), (9) and (11) to get the terminal charges Q_g, Q_b, and Q_s, respectively. Q_d in Eq. (13) has been simplified by assuming that the term e^(2ud+2us) is prevalent over other low-order terms, e.g., e^ud and e^us.

Once the terminal charges are evaluated, a four-terminal FET can be modeled with 4 self-capacitances and 12 intrinsic transcapacitances given by:

$$C_{ij} = - \frac{{\partial Q_i}}{{\partial V_j}}\quad i \,\ne\, j\quad \quad \quad C_{ij} = \frac{{\partial Q_i}}{{\partial V_j}}\quad i = j\quad \quad \quad i,j = g,d,s,b,$$

(14)

where C_ij describes the dependence of the charge at terminal i with respect to a varying voltage applied to terminal j assuming that the voltage at any other terminal remains constant. Due to charge conservation and considering a reference-independent model, only nine independent capacitances are needed to describe the 4T device. In addition, taking advantage of the relations between the top- and back-gate capacitances,²⁵ the computation of only four capacitances is enough; for instance, C_gg, C_gd, C_dg, and C_dd can be chosen as the independent set.

Model validation

In order to validate the presented model, we perform the DC and RF measurements of an experimental monolayer MoS₂-FET. The fabricated device consists of an n-type channel of a chemical vapor deposited (CVD) MoS₂ monolayer transferred onto 285 nm intrinsic Si/SiO₂ wafer. The 150-nm-long MoS₂ channel is contacted with a stack of 2/70 nm Cr/Au and electrostatically controlled by an embedded gate formed by a 10-nm barrier of atomic layer deposited Al₂O₃ and a gate metal stack consisting of 2/23 nm Ti/Au. More details on the fabrication and characterization process can be found in the Methods section. Table 1 summarizes the input parameters used for simulating the device under test. The extracted 2D semiconductor–metal contact resistance for the device is 3.5 kΩ µm and has been included in the simulation by connecting lumped resistors to the source and drain terminals.

Table 1 Input parameters of the 2DFET under test.

We first test our model by comparing the DC transfer characteristics (TCs) obtained at two different drain voltages. A good agreement between both, measurements and simulations, has been achieved as shown in Fig. 2. The model predicts the DC behavior accurately in all regimes of operation with current values ranging between 10⁻³ up to 10² µA/µm. However, the experimental device departs from the exponential trend for values in the limit of the IRDS specification for low-power applications, being the OFF current actually limited by the onset of hole current at negative V_gs (see Supplementary Notes and Supplementary Fig. S1 for a detailed discussion). This small mismatch, however, does not impact the dynamic operation prediction. Indeed, we have assessed the expected RF performance of such device in Fig. 3 by benchmarking the simulated small-signal current gain (h21) and unilateral power gain (U) against the results extracted from the experimental S-parameters (after de-embedding) measured in the range 0.1–15 GHz. Both, simulated h21 and U, are predicted with excellent agreement to the experimental measurements. In order to evaluate the RF performance, we calculate the intrinsic capacitances, plotted in Fig. 4 (solid lines). The relative error between the numerical solution of Eq. (14) by using the expressions in Eqs. (8)–(11) and the analytical computation of Eq. (14) by using the compact expressions in Eq. (13) is less than 2% for the bias window considered in Fig. 4. The results are presented together with the intrinsic capacitances relying on the well-known conventional charge model developed for bulk MOSFETs¹¹ and elsewhere used to model 2DFETs². As can be seen, the latter is accurate only either when a low drain bias is applied or if the device is operated in the subthreshold regime (see Supplementary Notes and Supplementary Fig. S2 for more details).

Fig. 2

Transfer characteristics for different drain voltages in a linear and b logarithmic scales. Simulations are plotted with solid lines, and experimental measured data with symbols. Dashed lines in b highlight both the IRDS high-performance and low-power I_OFF current limits.

Fig. 3

Simulated (solid line) and measured (symbols) RF performance of the MoS₂-based FET described in Table 1 (V_gs = 4.4 V; V_ds = 3.5 V). The device shows a cut-off frequency f_T = 20.2 GHz and a maximum oscillation frequency f_max = 11.3 GHz.

Fig. 4

Intrinsic capacitances versus a overdrive gate bias (at V_ds = 1 V) and b drain bias (at V_gs – V_g0 = 3.4 V). Solid lines represent our model outcome and dashed lines show the data calculated using the model adopted in ref. ²

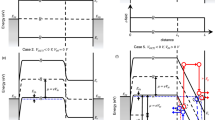
The trends in the intrinsic capacitances can be better understood looking at the overdrive gate and drain bias dependences of both gate (Q_g) and drain (Q_d) charges, which are depicted in Fig. 5a, b, respectively. Figure 5c, d shows the same bias dependence of a set of four independent intrinsic capacitances of the 4T 2DFET under test. As the device is an n-type transistor, we have also plotted the shift of the quasi-Fermi level with respect to the conduction band edge at both the drain/source sides (corresponding to the chemical potentials V_cd and V_cs) in Fig. 5e, f. For the sake of clarity, we provide a separate discussion of the intrinsic capacitances according to the transistor operation regime.

Fig. 5

Gate and drain charges versus a overdrive gate bias (at V_ds = 1 V) and b drain bias (at V_gs – V_g0 = 3.4 V). Intrinsic capacitances versus c overdrive gate bias (at V_ds = 1 V) and d drain bias (at V_gs – V_g0 = 3.4 V). Shift of the Fermi level with respect to the conduction band edge, namely, the chemical potential at the drain (V_cd) and source (V_cs) sides versus e overdrive gate bias (at V_ds = 1 V) and f drain bias (at V_gs – V_g0 = 3.4 V).

Subthreshold regime (OFF operation): If both V_cd and V_cs > 10V_th, then Q_g, Q_d ∼ 0 (see Fig. 5a). Therefore the channel is empty of carriers and the device operates in the OFF state. This situation happens for overdrive gate biases lower than the threshold voltage, V_A, according to Fig. 5e. Given the aforementioned conditions then C_gg ≈ C_tC_bWL/C_tb and C_gd ≈ C_dg ≈ C_dd ≈ 0, see to the left of A1 point in Fig. 5c.

Saturation regime (ON operation): On the other hand, when V_cd > 10V_th while V_cs < 10V_th, the pinch-off is originated at the drain side. This situation is produced for overdrive gate biases between V_A and V_B in Fig. 5e (“A–B” section). Both C_gg (“A1–B3” section) and C_dg (“A1–B2” section) jump because the channel charge at the source side becomes very sensitive to the Fermi level location when it is close to the conduction band edge. However, C_gd and C_dd are negligible (“A1–B1” section) because the depletion region close to the drain prevents this terminal to control the channel charge. The saturation regime is also observed at the right column of Fig. 5 for drain biases higher than V_C (drain saturation voltage) in Fig. 5f (right of C point). The intrinsic capacitances C_gg (right of C3 point) and C_dg (right of C2 point), shown in Fig. 5d, decrease with respect to the linear regime (left of C point, explained below) because the channel is depleted at the drain side, so both Q_g and Q_d become less sensitive to V_gs as compared to the linear regime. On the other hand, C_gd and C_dd are negligible (right of C1 point), as Q_g and Q_d cannot be controlled anymore by the drain terminal after the depletion of the channel drain side, which is confirmed in Fig. 5b.

Linear (ohmic) regime (ON operation): This regime takes place when both V_cd and V_cs < 10V_th. This situation is produced for gate overdrive voltages higher than V_B in Fig. 5e (right of B point), where the channel starts to leave the depletion scenario at the drain side. Then a jump is observed in C_gg (right of B3 point), C_dg (right of B2 point), C_gd and C_dd (right of B1 point) as a consequence of the recovered electrical connection between the channel and the drain terminal (see Fig. 5a, c). The linear regime can be also observed at the right column of Fig. 5 for drain biases lower than V_C (see Fig. 5f). The negative value of V_cs means that the channel is degenerated at the source side for the specific bias considered in this study. In Fig. 5d, it can be seen that C_gg (left of C3 point), C_dg (left of C2 point), C_gd and C_dd (left of C1 point) decrease with V_ds as the channel get closer to the drain depletion condition reached at V_ds = V_C.

Finally, with the aim of showing the potential of the developed TCAD tool, a relevant circuit commonly used to evaluate the performance of a digital technology, namely, a ring oscillator (RO) is simulated. The design of a three-stage based RO encompasses both DC and transient simulations. Each device has been described by the parameters shown in Table 1 that have been demonstrated to accurately reproduce the fabricated MoS₂-based FET in Figs. 2 and 3. Specifically, we have designed the three-stage RO to oscillate at a specific frequency f_osc = 3^1/2/(2πR_ddC) ≈ 1 GHz by using a resistor connected to each drain of R_dd = 20.4 kΩ and capacitors connected to the output of each stage with C = 13.5 fF. In doing so, each single stage has been designed to show a voltage gain of 3.7 at f_osc, upon biasing it at V_gs = 1.25 V and V_ds = 3.5 V. Figure 6 shows how the technology assessed in this work provides a suitable switching characteristic around 1 GHz. The simulation predicts a distorted sinusoidal as the AC component goes over a large range of bias with imperfect linearity. It is worth noticing that a small-signal model (in contrast with a large-signal model) could not predict that feature. Supplementary Fig. S3 provides a comparison of the compact model outcome against experimental measurements of bilayer MoS₂ FETs²⁶ comprising the assessment of transfer characteristics, output characteristics, the performance of an inverter, and a five-stage ring oscillator based on such devices, the latter validating the large-signal prediction capability of the model.

Fig. 6

Three-stage ring oscillator switching at a frequency around 1 GHz based on the 2DFETs described in Table 1. The supply bias is 3.5 V.

Discussion

A physics-based large-signal compact model of four-terminal 2D semiconductor-based FETs, implemented in Verilog-A, has been presented. The model captures the terminal charges and capacitances covering all the operation regimes, so accurate time domain simulations and frequency response studies at the circuit level are feasible within the validity of the quasi-static approximation. The model can be incorporated to existing commercial circuit simulators enabling the simulation of digital and RF applications based on emerging 2D technologies. We have checked that the model outcome is consistent with our experimental measurements of MoS₂-FET devices targeting RF applications. Finally, a design of a three-stage ring oscillator has been carried out to exhibit the potential of the TCAD tool presented and showing the feasibility of using this technology in switching applications in the gigahertz range.

Methods

Fabrication

The MoS₂ FET reported in this paper belongs to the same batch as the devices published in ref. ²⁷ by some of the authors. The fabrication process begins with patterning two embedded gate fingers on intrinsic Si/SiO₂ (>20 kΩ cm). Then, the embedded 150-nm gate metal stack consisting of 2/23 nm Ti/Au was defined and deposited by using electron beam lithography (EBL) and e-beam evaporation. Large area atomic single layer CVD MoS₂, grown by a standard vapor transfer process as described in ref. ,²⁷ was then transferred by poly(methyl methacrylate)-assisted wet transfer. Phosphoric acid etching was used to connect the embedded gate fingers and the gate pad. The active MoS₂ channel was etched using Cl₂/O₂ plasma. Finally, source and drain (S/D) contacts consisting of 2/70 nm Cr/Au were patterned through a final EBL step.

Electrical measurements

The electrical DC characterization was done on a Cascade Microtech Summit 11000B-AP probe-station using an Agilent B1500A parameter analyzer. Microwave performance was characterized using an Agilent two-port vector network analyzer (VNA-E8361C). All measurements were taken at room temperature, in ambient atmosphere, and in the dark. The intrinsic microwave performance is obtained after de-embedding the measured data using OPEN and SHORT structures. The OPEN de-embedding was performed on the as-measured device-under-test by etching away the MoS₂ in the active regions. The SHORT de-embedding is subsequently carried out by depositing a strip of metal across the channel region, shorting out all pads.

Circuit simulations

The developed large-signal model of 4T 2DFETs is implemented in Verilog-A and included as a separate module in Keysight© Advanced Design System (ADS), a popular electronic design automation software for RF and microwave applications. It calculates the electrostatics by iteratively solving Eqs. (1) and (3) during run-time using a construct,^21,22 and computes the static and dynamic response of the device by evaluating Eqs. (5) and (6), respectively, using the compact expressions derived in this work.