Introduction

The global quantum network1 is believed to be the next-generation information-processing platform and promises an exponential increase in computation speed, a secure means of communication,2,3 and an exponential saving in transmitted information.4 The efficient distribution of quantum state and entanglement is a key ingredient for such a global platform. Entanglement distribution5 and quantum teleportation6 can be employed to transmit quantum states over long distances. By exploiting entanglement swapping5 and quantum purification, the transmission distance could be extended significantly, and the fidelities of transmitted states can be enhanced up to unity, which is known as quantum repeaters.7 However, with the increased of complexity of quantum networks, especially when many parties require simultaneous communication and communication rates exceed the capacity of quantum channels, low transmission rates, or long delays, known as bottleneck problems, are expected to occur. Thus, it is important to resolve the bottleneck problem and achieve high-speed quantum communication. This question is in the line with issues related to quantum communication complexity, which attempts to reduce the amount of information to be transmitted in solving distributed computational tasks.8

The bottleneck problem is common in classical networks. A landmark solution is the network coding concept,9 where the key idea is to allow coding and replication of information locally at any intermediate node in the network. The metadata arriving from two or more sources at intermediate nodes can be combined into a single packet, and this distribution method can increase the effective capacity of a network by minimizing the number and severity of bottlenecks. The improvement is most pronounced when the network traffic volume is near the maximum capacity obtainable via traditional routing. As a result, network coding has realized a new communication-efficient method to send information through networks.10

A primary question relative to quantum networks is whether network coding is possible for quantum-state transmission, which is referred as quantum network coding (QNC). Classical network coding cannot be applied directly in a quantum case due to the no-cloning theorem.11 However, remarkable theoretical effort has been directed at this important question. For example, Hayashi et al.12 were the first to study QNC, and they proved that perfect quantum state cross-transmission is impossible in the butterfly network, i.e., the fidelity of crossly transmitted quantum states cannot reach one. However, if two senders have shared entanglements priorly, the perfect QNC is possible by exploiting quantum teleportation.13,14,15 Thus, various studies have focused on network coding for quantum networks, such as the multicast problem,16,17 QNC based on quantum repeaters,18 QNC-based quantum computation,19 and other efficient quantum-communication protocols with entanglement.20,21,22,23 Despite these theoretical advances, to the best of our knowledge, an experimental demonstration of QNC has not been realized in a laboratory, even for the simplest of cases.

In this study, we provide the first experimental demonstration of a perfect QNC protocol on the butterfly network. This experiment adopted the protocol proposed by Hayashi,14 who proved that perfect QNC is achievable if the two senders have two prior maximally entangled pairs, while it is impossible without prior entanglement. We demonstrate this protocol by employing eight photons generated via spontaneous parametric downconversion (SPDC). We observed a cross-transmission of single-photon states with an average fidelity of 0.9685 ± 0.0013, as well as cross-transmission of two-photon entanglement with an average fidelity of 0.9611 ± 0.0061, both of which are greater than the theoretical upper bounds without prior entanglement.

Results

QNC on butterfly network

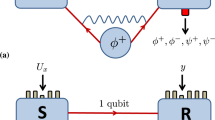
Network coding refers to coding at a node in a network.9 The most famous example of network coding is the butterfly network, which is illustrated in Fig. 1a. While network coding has been generally considered for multicast in a network, its throughput advantages are not limited to multicast. We focus on a simple modification of the butterfly network that facilitates an example involving two simultaneous unicast connections. This is also known as 2-pairs problem,24,25 which seeks to answer the following: for two sender–receiver pairs (S1–R1 and S2–R2), is there a way to send two messages between the two pairs simultaneously? In the network shown in Fig. 1a, each arc represents a directed link that can carry a single packet reliably. Here, is a single packet b1 presents at sender S1 that we want to transmit to receiver R1, and a single packet b2 presents at sender S2 that we want to transmit to receiver R2 simultaneously. The intermediate node C1 breaks from the traditional routing paradigm of packet networks, where intermediate nodes are only permitted to make copies of received packets for output. Intermediate node C1 performs a coding operation that takes two received packets, forms a new packet by taking the bitwise sum or XOR), of the two packets, and outputs the resulting packet b1 ⊕ b2. Ultimately, R1 recovers b2 by taking the XOR of b1 and b1 ⊕ b2, and similarly R2 recovers b1 by taking the XOR of b2 and b1 ⊕ b2. Therefore, two unicast connections can be established with coding and cannot without coding.

Fig. 1
figure 1

Classical network coding and quantum network coding on a butterfly network. a Classical network coding on a butterfly network. Dash line with arrow represents information flow with a capacity of a single packet. In the two simultaneous unicast connections problem, one packet b1 presented at source node S1 is required to transmit to node R1, and the other packet b2 presented at source node S2 is required to transmit to node R2 simultaneously. The intermediate node C1 performs a coding operation XOR ⊕ on b1 and b2. C2 makes copies of b1 ⊕ b2 and sends them to R1 and R2, respectively. R1 and R2 decode by performing further XOR operations on the packets that they each receive. b Quantum network coding on butterfly network. The red line with arrow represents quantum information flow with a capacity of a single qubit, and the dash line with arrow represents classical information flow with a capacity of a two bits. See main text for more details

Full size image

In the case of quantum 2-pairs problem, the model is the same butterfly network (Fig. 1a) with unit-capacity quantum channels and the goal is to send two unknown qubits crossly, i.e., to send ρ1 from S1 to R1 and ρ2 from S2 to R2 simultaneously. However, two rules prevent applying classical network coding directly in the quantum case: (i) an XOR operation for two quantum states is not possible; (ii) an unknown quantum state cannot be cloned exactly. Therefore, it has been proven that the quantum 2-pairs problem is impossible.12

Hayashi proposed a protocol that addresses the quantum 2-pairs problem by exploition prior entanglements between two senders.14 As shown in Fig. 1b, the scheme is a resource-efficient protocol that only requires two pre-shared pairs of maximally entangled state |Φ+〉 between the two senders. Notice that if the sender (S1, S2) nodes and receiver (R1, R2) nodes allow to share prior entanglements, then transmitting classical information with classical network coding can complete the task only by using quantum teleportation.13 If free classical between all nodes is not limited, perfect 2-pair communication over the butterfly network is possible.26 However, we consider a more practical situation that the sender and receiver nodes do not share any prior entanglements. Also, the channel capacity is limited to transmit either one qubit or two classical bits. Hayashi proved that the average fidelity of quantum state transmitted is upper bounded by 0.9504 for single-qubit state, and 0.9256 for entanglement without prior entanglement.14 However, with prior entanglement between senders, the average fidelity can reach 1. The protocol is summarized as follows (see Fig. 1b).

  1. 1.

    S1 (S2) applies the Bell-state measurement (BSM) between the transmitted state ρ1 (ρ2) and one qubit of |Φ+〉. According to the result of BSM m1n1 (m2n2), S1 (S2) perform the unitary operation \(X^{m_1}Z^{n_1}\) (\(X^{m_2}Z^{n_2}\)) on the other qubit of |Φ+〉.

  2. 2.

    S1 (S2) sends the quantum state (after the unitary operation) to R2 (R1), and sends the classical bits m1n1 (m2n2) to C1. C1 performs the XOR on m1 and m2, n1 and n2, respectively, then sends m3 = m1 ⊕ m2 and n3 = n1 ⊕ n2 to C2. C2 makes copies of m3n3 and sends them to R1 and R2, respectively.

  3. 3.

    R1 and R2 recover the quantum states ρ1 and ρ2 by applying the unitary operation \(X^{m_3}Z^{n_3}\) on their received quantum states.

Experimental realization

We demonstrate the perfect QNC protocol by employing the polarization degree of freedom of photons generated via SPDC. As shown in Fig. 2a, an ultraviolet pulse (with a central wavelength of 390 nm, power of 100 mW, pulse duration of 130 fs, and repetition of 80 MHz) passes through four 2-mm-long BBO crystals successively, and generates four maximally entangled photon pairs via SPDC in the form of \(\left| {{\mathrm{\Psi }}^ + } \right\rangle _{ij} = 1\sqrt 2 \left( {\left| {HV} \right\rangle + \left| {VH} \right\rangle } \right)_{ij}\). Here, H (V) denotes the horizontal (vertical) polarization and i, j denote the path modes. Then, we use a Bell-state synthesizer to reduce the frequency correlation between two photons27,28 (as shown in Fig. 2b). After the Bell-state synthesizer, |Ψ+〉ij is converted to \(\left| {{\mathrm{\Phi }}^ + } \right\rangle _{ij} = 1\sqrt 2 \left( {\left| {HH} \right\rangle + \left| {VV} \right\rangle } \right)_{ij}\). We set narrow-band filters with full-width at half-maximum (λFWHM) of 2.8 and 3.6 nm for the e- and o-ray, respectively, and, with this filter setting, we observe an average two-photon coincidence count rate of 21,000 per second with a visibility of 99.6% in the |H(V)〉 basis and visibility of 99.0% in the |+ (−)〉 basis, from which we calculate the fidelity of prepared entangled photons with an ideal |Φ+〉 of 99.3%. We estimate a single-pair generation rate of p ≈ 0.0036, and overall collection efficiency of 28%.

Fig. 2
figure 2

Schematic drawing of the experimental setup. a An ultraviolet pulse successively pass through four BBO crystals, and generate four pairs of maximally entangled photons. We use four Bell-state synthesizer (shown in Fig. 2b) to improve the counter rate of entangled photon pair. To avoiding a mess of illustration, we separated propagation of ultraviolet pulse. In our experiment, the ultraviolet pulse is guided by mirrors to shine on four BBO one by one. All the photons are collected by single-mode fiber and detected by single-photon detecters (SPD). The coincidence is recored by several home-made field-programmable gate arrays (FPGA). See main text for more details. b Bell-state synthesizer. The generated photons are compensated by a HWP at 45° and 1-mm-long BBO crystal. Then, one photon is rotated by a HWP at 45°, and finally two photons are recombined on a PBS. With Bell-state synthesizer makes ordinary ray(o-ray) exiting from one port of PBS and extraordinary ray(e-ray) exiting the other port of PBS. c The unitary operation \(U_i = X^{m_i}Z^{n_i}\) is realized by HWPs. We post-selectively apply Ui according to mini. c Symbols used in a–c. BBO beta barium borate crystal, PBS polarizing beam splitter, HWP Half-wave plate, QWP quarter-wave plate, SPD single-photon detector

Full size image

|Φ+〉12 and |Φ+〉34 are the two entangled pairs priorly shared between S1 and S2, i.e., S1 holds photons 1 and 3 and S2 holds photons 2 and 4. |Φ+〉56 and |Φ+〉78 are held by S1 and S2, respectively. Photon 5 is projected on \(\alpha _1^ \ast \left| H \right\rangle + \beta _1^ \ast \left| V \right\rangle\) to prepare ρ1 with ideal form in α1|H〉 + β1|V〉. Similarly, photon 7 is projected on \(\alpha _2^ \ast \left| H \right\rangle + \beta _2^ \ast \left| V \right\rangle\) to prepare ρ2 with ideal form α2|H〉 + β2|V〉.

On S1’s side, by finely adjusting the position of the prism on the path of photon 1, we interfere with photons 1 and photon 6 on a polarizing beam splitter (PBS) to realize a Bell-state measurement (BSM). The BSM projects photons 1 and 6 to |ψ〉 ∈ {|Ψ+〉, |Ψ−〉, |Φ+〉, |Φ−〉}. As the complete BSM is impossible with linear optics, we perform the complete measurements with two setup settings by rotating the angle of the half-wave plate (HWP) on path 6 or 1 before they interfere from 0° to 45°. Note that in each setup, the success probability to identify two of the Bell states is 50%. So, the total success probability is 25% in our experiment. The BSM results (different responses on the four detectors after the interference) are related to two classical bits denoted as m1n1 ∈ {00, 01, 10, 11}. According to the BSM results, S1 applies the unitary operation U1 = \(X^{m_1}Z^{n_1}\) on photon 3, and then sends m1n1 to node C1 and photon 3 to the receiver node R2. Here, we use X, Y, Z to represent the Pauli-X, Pauli-Y, and Pauli-Z matrix. Similarly, on the S2 side, we interfere with photons 4 and 8 on a PBS to realize a BSM with result of m2n2, according to which S2 applies the unitary operation U2 = \(X^{m_2}Z^{n_2}\) on photon 2. Then, S2 sends m2n2 to node C1 and sends photon 2 to the receiver node R1.

On node C1, we perform the XOR operation on m1 and m2 and n1 and n2, and send the results m3 = m1 ⊕ m2, n3 = n1 ⊕ n2 to node C2, where we make two copies of m3n3 and send these copies to R1 and R2. Finally, according to m3n3, we apply the unitary operation U3 = \(X^{m_3}Z^{n_3}\) on photons 3 and photon 2 to recover ρ2 and ρ1.

In our experiment, the unitary operation is realized by HWPs with transformation matrix \(U(\theta ) = \left( {\begin{array}{*{20}{c}} {{\mathrm{cos2}}\theta } & {{\mathrm{sin2}}\theta } \\ {{\mathrm{sin2}}\theta } & { - {\mathrm{cos2}}\theta } \end{array}} \right)\), where θ is the angle fast axis relative to the vertical axis. X0Z0 = I means no operation on the photon. Here, X0Z1 = Z is realized by setting an HWP at 0°. X1Z0 = X is realized by setting an HWP at 45°, and X1Z1 = XZ is realized by setting two HWPs (one at 45° and the other at 0° (shown in Fig. 2c)).

Experimental results

We first show that two single-photon states can be crossly delivered from S1 to R2 and from S2 to R1 simultaneously in the butterfly network. S1 and S2 can prepare six individual quantum states ρ1 and ρ2 with an average fidelity of 99.3%. ρ1 and ρ2 have an ideal form of ρ1 = |ϕ1〉〈ϕ1| and ρ2 = |ϕ2〉〈ϕ2|, where \(\left| {\phi _1} \right\rangle ,\left| {\phi _2} \right\rangle\) ∈ \(\left\{ {\left| H \right\rangle ,\left| V \right\rangle ,\left| \pm \right\rangle = \frac{1}{{\sqrt 2 }}\left( {\left| H \right\rangle \pm \left| V \right\rangle } \right),\left| {L(R)} \right\rangle = \frac{1}{{\sqrt 2 }}\left( {\left| H \right\rangle \pm i\left| V \right\rangle } \right)} \right\}\). In our experiment, both S1 and S2 irrelatively select ρ1 and ρ2 from six states for transmission, thereby resulting in a total of 36 combinations. After recover of R1 and R2, we measure the fidelities between the recovered state \(\rho _1^\prime\) (\(\rho _2^\prime\)) and the ideal input state ρ1 = |ϕ1〉〈ϕ1| (ρ2 = |ϕ2〉〈ϕ2|), i.e., \(F_{S_1 \to R_2} = Tr\left( {\left| {\phi _1} \right\rangle \left\langle {\phi _1} \right|\rho _1^\prime } \right)\) and \(F_{S_2 \to R_1} = Tr\left( {\left| {\phi _2} \right\rangle \left\langle {\phi _2} \right|\rho _2^\prime } \right)\). We project the photon on the |ϕ〉(|ϕ⊥〉) basis and record the counts N+ and N−, where |ϕ⊥〉 is the orthogonal state of |ϕ〉. Thus, the fidelity of the transferred single-photon state can be calculated by \(F = \frac{{N_ + }}{{N_ + + N_ - }}\). The average fidelities over all possible BSM outcomes are shown in Fig. 3a. Note that each BSM has four possible outcomes, thus there are 16 combinations of outcomes for the two BSMs. For each combination, we apply the unitary operations and record the measured fidelities. In Fig. 3a, the red line represents the theoretical upper bound of the average fidelity without prior entanglement, i.e., Fth = 0.9503. Specifically, Fig. 3b shows the histogram of all measured fidelities of the 576 situations, and the average fidelity is quantified as \(\bar F = \mathop {\sum}\nolimits_i {p_i} F_i = 0.9685 \pm 0.0013\), where pi and Fi are the probability and fidelity shown in Fig. 3b. The average fidelity beyonds Fth = 0.9503 with 14 standard deviations.

Fig. 3
figure 3

Fidelities of crossly transmitted quantum states. a The green bar represents \(F_{S_1 \to R_2}\), and the yellow bars represent \(F_{S_2 \to R_1}\). The pair-appeared bars represent fidelities measured simultaneously at R1 and R2. For example, HR means that S1 delivers |H〉 and S2 delivers |R〉. The red line represents the threshold of Fth = 0.9503. The fourfold coincidence is ~1.5 counts per second. We accumulate coincidences for 240 s, and a total of 720 counts for each two-state transition. The error bars are calculated assuming a Poisson statistics for the coincidence counts and Gaussian error propagation. b Histogram of state fidelities

Full size image

We also show that two-photon entanglement can be established crossly with this setup, i.e., two-photon entanglement can be established between S1 and R2 and S2 and R1, simultaneously. Here, the experimental setup is the same, S1(S2) does not project photon 5(7) on α*|H〉 + β*|V〉, and photon 5(7) is retained to perform the joint measurements with photon 2(3). To quantify the cross-entanglement between photons 5 and 2 and 7 and 3, we measure the entanglement witness on rho52 and ρ73, respectively. In particular, we measure the entanglement witness 〈W〉 = I/2 − |Φ+〉〈Φ+|, which can also be related to the entanglement fidelity 〈W〉 = 1/2 − Fent. Here, Fent is defined as the entanglement fidelity between the entanglement state ρij and the maximal entanglement state |Φ+〉, i.e., Fent = Tr(ρij|Φ+〉〈Φ+|). |Φ+〉〈Φ+| can be decomposed to local observables as \(\left| {{\mathrm{\Phi }}^ + } \right\rangle \left\langle {{\mathrm{\Phi }}^ + } \right| = \frac{{II + XX - YY + ZZ}}{4}\). By measuring the expected values of local observables, we can calculate the entanglement fidelity. The local observable \({\cal{O}}\) can be expressed as \({\cal{O}} = \left| \phi \right\rangle \left\langle \phi \right| - \left| {\phi _ \bot } \right\rangle \left\langle {\phi _ \bot } \right|\), where |ϕ〉(|ϕ⊥〉) is the eigenstate of \({\cal{O}}\) with eigenvalue of 1(−1). The expected value of \({\cal{O}}\) can be calculated by the counts \(\langle {\cal{O}}\rangle = \frac{{N_ + - N_ - }}{{N_ + + N_ - }}\). The experimental results of the fidelities of cross-entanglement are shown in Fig. 4. We calculate that the average fidelity of two crossly established entanglement is 0.9611 ± 0.0061, which beyonds 0.9256 with 5.8 standard deviations.

Fig. 4
figure 4

Fidelities of crossly established entanglement. The green bar represents entanglement established between S1 to R2, and the yellow bars represents S2 to R1. The pair-appeared bars represent the fidelities measured simultaneously. For each BSM, there are four possible outcomes, thus there are 16 situations. The red line represents the threshold of Fth = 0.9256. The fourfold coincidence is about three counts per second. We accumulate coincidences for 120 s, and total 720 counts for each two-state transition. The error bars are calculated assuming a Poisson statistics for the coincidence counts and Gaussian error propagation

Full size image

Discussion

QNC provides an alternative solution for the transition of quantum states in quantum networks. Compared to entanglement swapping, QNC demonstrates superiority especially when quantum resources are limited or a high communication rate is required.29 In addition, large-scale QNC demonstrates superiority relative to fidelity performance as well.30 In this paper, We have demonstrated the first perfect QNC on a butterfly network. The average fidelities of cross-state transmission and cross-entanglement distribution achieved in our experiment exceed the theoretical upper bounds permitted without prior entanglement. We expect that our results will pave the way to experimentally explore the advanced features of prior entanglement in quantum communication. In addition, we expect that our results will realize opportunities for various studies of efficient quantum communication protocols in quantum networks with complex topologies.