Introduction

Metrology, which studies high precision measurement and estimation, has been one of the main driving forces in science and technology. Recently, quantum metrology, which uses quantum mechanical effects to improve the precision, has gained increasing attention for its potential applications in imaging and spectroscopy.1,2,3,4,5,6

One of the main quests in quantum metrology is to identify the highest precision that can be achieved with given resources. Typically the desired parameter, ω, is encoded in a dynamics Λω. After an initial probe state ρ0 is prepared, the parameter is encoded in the output state as ρω = Λω(ρ0). Proper measurements on the output state then reveals the value of the parameter. To achieve the highest precision, one needs to optimize the probe states, the controls during the dynamics and the measurements on the output states. Previous studies have been mostly focused on the optimization of the probe states and measurements.6 The control only starts to gain attention recently.7,8,9,10,11,12,13,14,15,16,17,18 It has now been realized that properly designed controls can significantly improve the precision limits. The identification of optimal controls, however, is often highly complicated and time-consuming. This issue is particularly severe in quantum parameter estimation, as typically optimal controls depend on the value of the parameter, which can only be estimated from the measurement data. When more data are collected, the optimal controls also need to be updated, which is conventionally achieved by another run of the optimization algorithm. This creates a high demand for the identification of efficient algorithms to find the optimal controls in quantum parameter estimation.

Over the past few years, machine learning has demonstrated astonishing achievements in certain high-dimensional input-output problems, such as playing video games19 and mastering the game of Go.20 Reinforcement Learning (RL)21 is one of the most basic yet powerful paradigms of machine learning. In RL, an agent interacts with an environment with certain rules and goals set forth by the problem desired. By trial and error, the agent optimizes its strategy to achieve the goals, which is then translated to a solution to the problem. RL has been shown to provide improved solutions to many problems related to quantum information science, including quantum state transfer,22 quantum error correction,23 quantum communication,24 quantum control25,26,27, and experiment design.28

Here we show that RL serves as an efficient alternative to identify controls that are helpful in quantum parameter estimation. A main advantage of RL is that it is highly generalizable, i.e., the agent trained through RL under one value of the parameter works for a broad range of the values. There is then no need for re-training after the update of the estimated value of the parameter from the accumulated measurement data, which makes the procedure less resource-consuming under certain situations.

Results

We consider a generic control problem described by the Hamiltonian:29

$$\hat H(t) = \hat H_0(\omega ) + \mathop {\sum}\limits_{k = 1}^p {u_k} (t)\hat H_k,$$
(1)

where \(\hat H_0\) is the time-independent free evolution of the quantum state, ω the parameter to be estimated, uk(t) the kth time-dependent control field, p the dimensionality of the control field, and \(\hat H_k\) couples the control field to the state.

The density operator of a quantum state (pure or mixed) evolves according to the master equation,30

$$\partial _t\hat \rho (t) = - i\left[ {\hat H(t),\hat \rho (t)} \right] + \Gamma \left[ {\hat \rho (t)} \right],$$
(2)

where \(\Gamma [\hat \rho (t)]\) indicates a noisy process, the detailed form of which depends on the specific noise mechanism and will be detailed later.

The key quantity in quantum parameter estimation is the QFI,31,32,33,34 defined by

$$F(t) = {\mathrm{Tr}}\left[ {\hat \rho (t)\hat L_s^2(t)} \right],$$
(3)

where \(\hat L_s(t)\) is the so-called symmetric logarithmic derivative that can be obtained by solving the equation \(\partial _\omega \hat \rho (t) = \frac{1}{2}[ {\hat \rho (t)\hat L_s(t) + \hat L_s(t)\hat \rho (t)} ]\).31,32,35 According to the Cramér-Rao bound, the QFI provides a saturable lower bound on the estimation as \(\delta \hat \omega \ge \frac{1}{{\sqrt {nF(t)} }}\), where \(\delta \hat \omega = \sqrt {E[(\hat \omega - \omega )^2]}\) is the standard deviation of an unbiased estimator ω̂, and n is the number of times the procedure is repeated. Our goal is therefore to search for optimal control sequences uk(t) that maximize the QFI at time t = T (typically the conclusion of the control), F(T), respecting all constraints possibly imposed in specific problems. Practically, we consider piecewise constant controls so the total evolution time T is discretized into N steps with equal length ΔT labeled by j, and we use \(u_k^{(j)}\) to denote the strength of the control field uk on the jth time step. Researches of such problem are frequently tackled by the Gradient Ascent Pulse Engineering (GRAPE) method,29 which searches for an optimal set of control fields by updating their values according to the gradient of a cost function encapsulating the goal of the optimal control. It has been found that GRAPE is successful in preparing optimal control pulse sequences that improve the precision limit of quantum parameter estimation in noisy processes.11,12 Many alternative algorithms can tackle this optimization problem such as the stochastic gradient ascent(descent) method and microbial genetic algorithm,36 but the convergence to the optimal control fields becomes much slower when the dimensionality (p) of the control field or the discretization steps (N) increases. Other optimal quantum control algorithms, such as Krotov’s method37,38,39,40,41 and CRAB algorithm,42 typically depend on the value of the parameter, thus need to be run repeatedly along the update of the estimation, which is highly time-consuming. More efficient algorithms are thus highly desired.

In this work, we employ RL to solve the problem and compare the results to GRAPE. Our implementation of GRAPE follows ref. 11 Figure 1 shows schematics of the RL procedure and the Actor-Critic algorithm21 used in this work. In order to improve the efficiency of computation, we used a parallel version of the Actor-Critic algorithm called Asynchronous Advantage Actor-Critic (A3C) algorithm.43 For more extensive reviews of RL, Actor-Critic algorithm and A3C, see Methods and the Supplementary Methods.

Fig. 1
figure 1

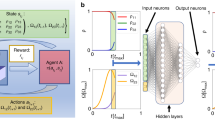
Schematics of the reinforcement learning procedure. a the RL agent-environment interaction as a Markovian decision process. The RL agent who first takes an action is prescribed by a neural network. The action is essentially the control field which steers the qubit. Then, depending on the consequence of the action, the agent receives a reward. b Schematic flow chart of one training step of the Actor-Critic algorithm. The hollow arrows show the data flow of the algorithm, and the dotted arrows show updates of the states and the neural network. In each time step, the state evolves according to the action chosen by the neural network, generating a new state which is used as the input to the network in the next time step. The loss function (detailed in Methods and the Supplementary Methods) is used to update the parameters of the neural network so as to optimize its choice of actions. The procedure is repeated until actions in all time steps are generated, forming the full evolution of the state and concluding one training episode

Full size image

Next we apply the algorithm to two commonly considered noisy processes: dephasing and spontaneous emission, to demonstrate the effect of the algorithm.

Dephasing dynamics

Under dephasing dynamics, the master equation, Eq. (2), takes the following form:11

$$\partial _t\hat \rho (t) = - i\left[ {\hat H(t),\hat \rho (t)} \right] + \frac{\gamma }{2}\left[ {\hat \sigma _{\mathbf{n}}\hat \rho (t)\hat \sigma _{\mathbf{n}} - \hat \rho (t)} \right],$$
(4)

where

$$\hat H(t) = \frac{1}{2}\omega _0\hat \sigma _3 + {\mathbf{u}}(t) \cdot {\boldsymbol{\sigma }},$$
(5)

the control field u(t) = (u1, u2, u3) is a magnetic field that couples to σ = (σ̂1, σ̂2, σ̂3), and γ is the dephasing rate which is taken as 0.1 throughout the paper. We consider a dephasing along a general direction given by \({\mathbf{n}} = ({\mathrm{sin}}\vartheta {\mathrm{cos}}\phi ,{\mathrm{sin}}\vartheta {\mathrm{sin}}\phi ,{\mathrm{cos}}\vartheta )\), \(\hat \sigma _{\mathbf{n}} = {\mathbf{n}} \cdot {\boldsymbol{\sigma }}\). The parameter to be estimated is ω0 in Eq. (5), the true value of which is assumed to be 1, and we take ω0−1 = 1 as our time unit. We choose the probe state, i.e. the initial state of the evolution, as \((|0\rangle + |1\rangle )/\sqrt 2\) in all subsequent calculations, where |0〉, |1〉 are the eigenstates of \(\hat \sigma _3\).

In Fig. 2 we present our numerical results on QFI under dephasing dynamics with ϑ = π/4, ϕ = 0 using square pulses. Figure 2a–c show the results for ΔT = 0.1. Figure 2a shows the training process in terms of F(T)/T as functions of the number of training epochs. The blue line shows results from the training using A3C algorithm. The value of F(T)/T corresponding to results from GRAPE and the case with no control are shown as the orange dotted line and gray dashed line, respectively. The red line shows results from “A3C + PPO”, an enhanced version of A3C which converges faster.44 The details of this algorithm is explained in the Supplementary Methods. We can see that after sufficient training epochs, results from A3C exceed that for the case with no control, and approaches the optimal results found by GRAPE. On the other hand, “A3C + PPO” converges more quickly to essentially the same result of A3C.

Fig. 2
figure 2

Quantum parameter estimation under dephasing dynamics with ϑ = π/4, ϕ = 0 using square pulses. a–c results for ΔT = 0.1, T = 5. d–f results for ΔT = 1, T = 10. a, d show the learning procedure, namely F(T)/T as functions of training epochs. b, e show F(t)/t for one of the best training results selected from a and d respectively. c and f show the pulse profiles corresponding to b and e

Full size image

We select one training outcome from those with best performances in Fig. 2a and show F(t)/t and the pulse profiles in Fig. 2b, c respectively. As can be seen from Fig. 2b, both GRAPE and A3C outperform the case with no control, while the results of A3C are comparable to those from GRAPE.

Figure 2d–f show results with a larger time step, ΔT = 1. From the training results shown in Fig. 2d, we see that results from A3C occasionally exceed those from GRAPE, for example at training epoch ~1600 and 3000. F(t)/t and the pulse profile of one of the best-performing results is again shown in Fig. 2e, f, and we see from Fig. 2e that A3C indeed outperforms GRAPE in this case.

We have discussed dephasing dynamics along a particular axis pertaining to Fig. 2, and the results for several other dephasing axes are shown in the Supplementary Discussion. We conclude from these results that in most cases, the A3C algorithm is capable to produce results comparable to those from GRAPE, while in selected situations (e.g. larger ΔT) A3C may outperform GRAPE.

We now discuss the generalizability of the control sequences for quantum parameter estimation, a key result of this paper. As the true value of ω0 is not known a priori, the control sequence has to be found optimal for a chosen ω0. When such sequence is applied in situations under other ω0 values, the true value is still measured, but the resulting QFI is lower than when the optimal control for true ω0 is used. In order to raise the QFI, one must then perform a second measurement using control sequences optimized for the estimated true value of ω0. The entire procedure therefore involves two steps, using different pulse sequences. This is fundamentally different than other typical measurements in quantum control, e.g. evaluation of fidelities of quantum gates,45 for which there is no need for a second pulse sequence or a second measurement.

The dotted lines in the left column of Fig. 3 show the QFI resulting from measurements with the optimal control found for ω0 = 1 with GRAPE. Results without control are shown as gray dashed lines for comparison. The range of ω0 covers a period of 2π/T. As expected, the QFI is largest at ω0 = 1, but reduces as ω0 deviates from 1. As ω0 further varies, the QFI increases at some values of ω0 which may be due to the geometric relationship of the phase that corresponding to those ω0 values and the phase at ω0 = 1. In any case, these QFI values are consistently lower than the value at ω0 = 1. An obvious way to improve the QFI is to generate new optimal control sequences for each value of ω0 from GRAPE, but this is costly as the computational complexity scales as \({\cal{O}}(N^{3})\). A detailed discussion on the computational complexity can be found in Supplementary Discussion.

Fig. 3
figure 3

Generalizability of the control under dephasing dynamics. a, c F(T)/T vs ω0 for three different methods. Note that the results from the GRAPE method are obtained using the pulses generated for ω0 = 1 only, while those from A3C are obtained using a neural network trained at ω0 = 1. b, d average F(T)/T in a range [1 − Δω, 1 + Δω] corresponding to the results of a and c respectively. a, b ΔT = 0.1, T = 5; c, d ΔT = 1, T = 10

Full size image

With A3C we have an efficient solution to this problem. We can train the neural network at ω0 = 1, and use this particular network to generate control sequences for different ω0 values. The neural network is only trained at ω0 = 1. However, the trained neural network works for a broad range of parameter values. There is no need to re-train the neural network with the updated estimation of the parameter. The computational cost is thus simply \({\cal{O}}\left(N\right)\) so it is much more efficient than generating new sequences with GRAPE. These results from A3C are shown in the left column of Fig. 3 as blue solid lines which represents the best-performing sequence from 100 trials generated from the trained neural network. For ΔT = 0.1 (Fig. 3a), although the QFI in the training ω0 = 1 is slightly lower for A3C than that of GRAPE, A3C demonstrates higher generalizability as the QFI deceases slowly when ω0 deviates from 1. For ΔT = 1 (Fig. 3c), the QFI of A3C is consistently higher than GRAPE except a narrow range of ω0 around 0.65.

To further reveal the generalizability of different methods, we consider the measurement in an ensemble with ω0 uniformly distributed in [1 − Δω, 1 + Δω]. The performance of the quantum parameter estimation is therefore given by the average F(T)/T,

$$\langle F(T)/T\rangle = \frac{1}{{2\Delta \omega }}{\int_{1 - \Delta \omega }^{1 + \Delta \omega }} F (T)/T d\omega .$$
(6)

These results are shown in the right column of Fig. 3, which are averages of the data in the corresponding panels in the left column. As seen from Fig. 3b (ΔT = 0.1), 〈F(T)/T〉 for GRAPE is high at small Δω but drops quickly as Δω is increased. On the contrary, 〈F(T)/T〉 for A3C is lower than that for GRAPE at small Δω, but decays much more slowly. As a consequence, 〈F(T)/T〉 for A3C exceeds that for GRAPE beyond Δω ≳ 0.22. This result indicates that for measurements involving a reasonably varying parameter, A3C demonstrates higher generalizability. For ΔT = 1, the results of A3C always exceed GRAPE as seen from Fig. 3d. The result for A3C decays much more slowly than that for GRAPE, in consistency with the ΔT = 0.1 case.

Intuitively without control and noise, the optimal strategy is preparing the initial probe state as \((|0\rangle + |1\rangle )/\sqrt 2\), since this state has the fastest rate of rotations under the Hamiltonian. Since the evolution of the state is also affected by dephasing, competitions exist between the parametrization and the effect of noise. When the evolution time is short, the parametrization dominates, in which case the control does not help much. However, in experimentally relevant situations the evolution time is typically long enough for noises to dominate. The controls are therefore useful as they can steer the states to regions where those states are less affected by the noise, even if such states may have a slower speed of parametrization. GRAPE and RL-based methods are both systematical ways to find controls, however, as we have demonstrated, A3C is more generalizable.

Spontaneous emission

A process involving the spontaneous emission is described by the Lindblad master equation:11

$$\begin{array}{*{20}{l}} {\partial _t\hat \rho (t)} \hfill & = \hfill & { - i\left[ {\hat H(t),\hat \rho (t)} \right] + \gamma _ + \left[ {\hat \sigma _ + \hat \rho (t)\hat \sigma _ - - \frac{1}{2}\left\{ {\hat \sigma _ - \hat \sigma _ + ,\hat \rho (t)} \right\}} \right]} \hfill \\ {} \hfill & {} \hfill & { + \gamma _ - \left[ {\hat \sigma _ - \hat \rho (t)\hat \sigma _ + - \frac{1}{2}\left\{ {\hat \sigma _ + \hat \sigma _ - ,\hat \rho (t)} \right\}} \right],} \hfill \end{array}$$
(7)

where \(\hat \sigma _ \pm = (\hat \sigma _1 \pm i\hat \sigma _2)/2\) and \(\hat H\) is defined as Eq. (5). The relaxation rates are taken as γ+ = 0.1, γ− = 0 throughout our discussion.

Figure 4 shows numerical results on QFI with spontaneous emission. Figure 4a–c are for ΔT = 0.1, T = 10, and Fig. 4d–f show calculations with a larger time step ΔT = 1, T = 20. Figure 4a, d [left column] show the A3C training processes, in which the results from GRAPE are indicated as orange dotted line for reference. We see that “A3C + PPO” converges faster, and both A3C and “A3C + PPO” saturate to values slightly lower than GRAPE. Again, one of the best-performing control is picked out and the corresponding F(t)/t and pulse profiles are shown in the middle and right column respectively. From Fig. 4b, e we see that for the best result from A3C, the QFI is lower than, but comparable to results from GRAPE.

Fig. 4
figure 4

Quantum parameter estimation under spontaneous emission using square pulses. a–c results for ΔT = 0.1, T = 10. d–f results for ΔT = 1, T = 20. a, d show the learning procedure. b and e show F(t)/t for one of the best training results selected from a and d respectively. c and f show the pulse profiles corresponding to b and e

Full size image

As in the case of dephasing dynamics, we consider the generalizability of different methods in a situation involving ω0 that distributes uniformly in a range. Again, we use GRAPE to obtain optimal control sequences for ω0 = 1 and apply that to other values. For A3C, we trained the neural network at ω0 = 1; the resulting sequence is then used to obtain an estimate of the true ω0 value. A new sequence is then generated using the neural network already trained at ω0 = 1 with the estimated ω0. The best-performing results out of 100 A3C outputs are shown as the blue solid lines in Fig. 5, while the results from GRAPE are shown as the orange dotted lines. The left column of Fig. 5 shows F(T)/T as functions of ω0 for two ΔT values. In both cases, the GRAPE method outperforms A3C in a narrow neighborhood around ω0 = 1, but its QFI decreases substantially as ω0 further deviates. On the other hand, A3C exhibits great generalizability: for ΔT = 0.1 the QFI does not decrease until ω0 is reduced to ω0 ≲ 0.6, while for ΔT = 1 the QFI remains approximately the same for the entire range of ω0 considered. The average F(T)/T in the range [1 − Δω, 1 + Δω] are shown in the right column of Fig. 5. In Fig. 5b, A3C outperforms GRAPE when Δω ≳ 0.22, while in Fig. 5d, A3C outperforms GRAPE in an even larger range Δω ≳ 0.07.

Fig. 5
figure 5

Generalizability of the control under spontaneous emission. a, c F(T)/T vs ω0 for three different methods. Note that the results from the GRAPE method are obtained using the pulses generated for ω0 = 1 only, while those from A3C are obtained using a neural network trained at ω0 = 1. b, d average F(T)/T in a range [1 − Δω, 1 + Δω] corresponding to the results of a and c respectively. a, b ΔT = 0.1, T = 10; c, d ΔT = 1, T = 20

Full size image

Overall we conclude that in the case of spontaneous emission, the A3C algorithm provides comparable results to GRAPE, although it cannot give higher QFIs. Nevertheless, A3C has much greater generalizability, as is consistent with the case concerning the dephasing dynamics.

Sequences with Gaussian pulses

For all results shown above, the control sequences involve square pulses only. In practical experiments, shaped pulses are sometimes used. Therefore in this section we consider Gaussian pulses as an example. The total time T is still divided into smaller pieces with ΔT. However, at the jth piece the piecewise constant pulse is replaced by a Gaussian centering on that piece and truncated on the ends:

$$u^{(j)}(t) = A^{(j)}{\mathrm{exp}}\left\{ { - \left[ {\left( {t - t^{(j)}} \right)/\sigma ^{{\mathrm{g}},(j)}} \right]^2} \right\},$$
(8)

where A(j) indicates the amplitude and σg,(j) the flatness of the pulse. We demonstrate here that with A3C method it is natural to accommodate non-boxcar pulses.

In Fig. 6 we show A3C results using Gaussian pulses and compare them to GRAPE results using square pulses. Figure 6a–c show results under dephasing dynamics with ϑ = π/4, and Fig. 6d–f show results under the spontaneous emission. In both cases ΔT = 1, T = 10. For dephasing dynamics, our best results from A3C outperform GRAPE, as is also the case for square pulses generated by A3C. For spontaneous emission, our best-performing result has a QFI value slightly lower than those from GRAPE with square pulses, but their values are very close. These results indicate that A3C method can naturally accommodate pulses other than square shape. We note that our use of Gaussian pulses is theoretical, and in practical situations, experimentally more relevant ones such as the Blackman pulses45 should be used. These shaped pulses are implemented by introducing constraints to the gradient in GRAPE46 or by modifying the action from the RL agent directly.

Fig. 6
figure 6

Quantum parameter estimation using Gaussian pulses as building blocks for A3C. a–c dephasing dynamics with ϑ = π/4. d–f spontaneous emission. a, d show the learning procedures. b, e show F(t)/t for the best training results selected from each case. c, f show the Gaussian pulse profiles, respectively. Note that the GRAPE results shown here use square pulses. Parameters: ΔT = 1, T = 10

Full size image

Discussion

The generalizability of RL, or sometimes called “generalization” in the literature, is an actively studied topic in computer science, for example on problems related to game playing where the RL agent trained under one level of the game can be used to clear other levels.47,48,49,50 While the reason why RL is generalizable is not completely clear, one suggestion has it that it likely arises from the underfitting by the neural network to the training data,51 which is supported by studies showing that reducing overfitting improves generalizability.50

The generalizability in fact has a much wider scope than what has been studied here. In the so-called “transfer learning”,52 experiences gained from one training of the RL agent can be used to improve its performance on different but related tasks by, for example, minimal updates of the network parameters. In contrast, our method does not alter network parameters while only generalizes the neural network in new RL environments with different parameters to estimate. We therefore believe that RL can be made even more generalizable by further studies involving more sophisticated algorithms.

To summarize, RL, in particular the A3C algorithm, is capable of finding the control protocol that enhances QFI in a way comparable to the traditionally used GRAPE method, and is in certain situations superior than GRAPE, e.g. for pulse sequences with larger time steps. Moreover, RL can naturally accommodate non-boxcar pulse shapes. Nevertheless, the key advantage afforded by RL is the generalizability, namely the neural network trained for one estimated parameter value can efficiently generate pulse sequences that provide reasonably enhanced QFI for a broad range of parameter values, while in order to achieve the same level of QFI the GRAPE algorithm has to be applied in full each time with a new parameter estimation. Our results therefore suggest that RL-based methods can be powerful alternatives to commonly used gradient-based ones, capable to find control protocols that could be more efficient in practical quantum parameter estimation.

Methods

In this section we describe the RL framework shown in Fig. 1. We also provide an expansive review of the RL methods and the detail on implementation in the Supplementary Methods.

Figure 1a shows the RL agent who takes an action as prescribed by a neural network. In our problem, the action is essentially the control field which steers the qubit according to the master equation, Eq. (2), and the resulting state of the evolution determines the reward the agent receives. In practice, the reward encodes the QFI, i.e. higher reward will be obtained when greater QFI is given by the control.

The action taken by the agent implies a time evolution of the quantum state according to Eq. (2) with the control field, uk(t). All possible actions therefore form a continuous set. We solve this problem using the Actor-Critic algorithm,21 as shown in Fig. 1b. Such algorithm is particularly suitable to our problem as it can treat continuous actions. The key of the algorithm is that the neural network is not only updated using the reward, but also a state value, the latter of which greatly improves the efficiency of the training procedure. At certain time step, the neural network takes the density matrix of the quantum state as an input, and outputs both an action, and a state value which assesses how likely the state will lead to a larger QFI. The state is then evolved using the output action, obtaining the new state and QFI, which is then implemented into the reward. The reward and state value combines into a so-called “loss function” that provides feedback, by updating the neural network, for the RL agent to make better decisions. The RL agent takes the new quantum state to repeat the above step until time T is reached, concluding one “episode” of training. After that, the quantum state is reset for the next episode to begin with. A completed episode outputs a pulse profile by sequencing the actions taken in each time step.

In order to improve the efficiency of computation, we used a parallel version of the Actor-Critic algorithm called Asynchronous Advantage Actor-Critic (A3C) algorithm.43 In this case, several copies of the agent and environment (called local agents and environments) run in parallel, and as each of them finishes one episode, the solution is delivered to a global agent for further optimization. The optimal policy among these results is then regarded as the output from one “epoch” of training, i.e. one epoch involves several episodes of training from different local agents. Since different local agents deliver their results at different times, the procedure is asynchronous. The details of both the Actor-Critic and the A3C algorithm are described in the Supplementary Methods, as well as the pseudo-code describing the implementation of the algorithm.