Introduction

Water intake structures play a critical role in river-to-hydropower systems, which are essential for harnessing water resources to meet the increasing global demand for clean and renewable energy sources. Bottom rack intakes are vital part of small hydropower plants in mountainous rivers with coarse bed load. Since the first hydraulic description of the bottom rack intake is presented by Orth et al. (1954), numerous studies have focused on estimating the diverted discharge coefficient (DDC) of bottom racks, which is a fundamental design parameter of these structures. The orifice equation (Eq. 1) can be solved to obtain the amount of discharge diverted across the bottom intake (Henderson 1966):

$$- \frac{{{\text{d}}Q}}{{{\text{d}}x}} = C_{{\text{d}}} \cdot \varepsilon \cdot B \cdot \sqrt {2gY}$$
(1)

where Y is the suitable value of hydraulic head, g is the gravitational constant; B is the rack width, Cd is the diverted discharge coefficient (DDC) and ε is the rack void ratio. The orifice equation as a function of the total energy has been considered by several authors, but there are different evaluations of DDC and Y (Righetti and Lanzoni 2008; Razaz and Faghfour Maghrebi 2008a, b; Kamanbedsat and Shafaie Bajestani 2008; Bina 2011; Shafaie Bajestani and Shakourirad 1997; Bina and Saghi 2017; Subramanya 1994; Kumar et al. 2010; Brunella et al. 2003; Castillo et al. 2013, 2016a, b, 2017; Bina 2018; García et al. 2019; Carrillo et al. 2018; Calderón et al. 2021; Chan et al. 2018; Chang et al. 2018; Zamanieh Shahri et al. 2019; Mirnourollahi et al. 2020) in this regards. By relating the DDC and Y to the available and easy to capture characteristics of approaching flow, dQ/dxwould be constant and Eq. 1 can be written in the form of Eq. 2 to estimate diverted discharge by the bottom rack, where Qd is the diverted discharge by rack and E0 is the specific flow head of approaching flow.

$$Q_{{\text{d}}} = C_{{\text{d}}} \cdot \varepsilon \cdot B \cdot L\sqrt {2gE_{0} }$$
(2)

A plethora of research has investigated the hydraulic performance of the rack using experimental or numerical modeling, and various factors influencing the DDC. Geometric parameters, such as the arrangement and position of bars relative to the main flow, different geometric shapes of bars, rack length, void ratio, and sediment parameters, have all been found to affect the DDC (Subramanya 1994; Kumar et al. 2010; Brunella et al. 2003; Castillo et al. 2013, 2016a). Additionally, hydraulic parameters of the approaching flow, including flow rate, depth, specific energy, Froude number, and Reynolds number, play a crucial role in determining the DDC (Kamanbedsat and Shafaie Bajestani 2008; Bina 2011; Razaz and Faghfour Maghrebi 2008b; Bina 2018).

While extensive experimental research has been conducted to understand the hydraulic behavior of bottom racks (Righetti and Lanzoni 2008; Razaz and Faghfour Maghrebi 2008a, b; Kamanbedsat and Shafaie Bajestani 2008; Bina 2011; Shafaie Bajestani and Shakourirad 1997; Bina and Saghi 2017; Subramanya 1994; Kumar et al. 2010; Brunella et al. 2003; Castillo et al. 2013, 2016a; Bina 2018), with the development of powerful computational fluid dynamics (CFD) software, numerical models have attracted more attention because they allow the simulation of various conditions that cannot be investigated in physical models due to laboratory limitations. In addition, numerical modeling saves the time and cost of designing these structures. Castillo et al. (2017) numerically analyzed a bottom racks with longitudinal bars using ANSYS CFX code and proposed an exponential adjustment to calculate DDC. García et al. (2019) presented a multi-parametrical tool (DIMARCK) for design of required bottom racks length based on experimental works. DIMRACK serves as a computational tool for bottom racks design with the possibility of taking into account multiple different parameters such as different void ratios, bar types, longitudinal slope, and flowrates. Carrillo et al. (2018) used ANSY CFD to numerically model the free water surface, wetted rack length, and DDC. They found that, regarding DDC, circular bars show bigger maximum values than T-shape bars with the same void ratio. Calderón et al. (2021) used OpenFOAM code to investigate flow field over bottom rack and inside collection chamber. Chan et al. (2018) built a numerical model of bottom rack in ANSYS FLUENT to assess air concentration of air–water flow. Chang et al. (2018) investigated the hydraulic performance of the intake structure via three-dimensional CFD modeling, using the volume-of-fluid (VOF) method. Zamanieh Shahri et al. (2019) numerically studied sediment flow over bottom intake racks with Flow3D code. Castillo et al. (2016b) studied bottom rack occlusion by flow with gravel-sized sediment, using ANSYS CFX. Mirnourollahi et al. (2020) both experimentally and numerically investigated a square orifice bottom intake in subcritical condition with FLUENT code.

While many research on bottom racks has traditionally focused on racks with circular bars, there is a growing interest in exploring non-circular racks, making the investigation of non-circular longitudinal bars an important area of study. In this regard, the current research studied the flow filed over bottom rack intake with non-circular longitudinal bars (rhombus bars and rounded-edge rectangle bars) in super critical flow condition using a numerical model developed by Flow3D software and the DCC was estimated based on numerical results. Also, the results of non-circular model were compared with circular bar model to find the best bar geometry for maximum amount of flow diversion. The findings presented in this paper contribute to the development of sustainable river-to-hydropower systems and offer practical insights for the design and operation of efficient water intake structures.

Materials and methods

Governing equations

The governing equations for open channel flow are the continuity and momentum equations, which is described by the differential Navier–Stokes equations. For incompressible flow, these equations can be written as Hosseini et al. (2015):

$$\frac{{\partial u_{i} }}{{\partial x_{i} }} = 0$$
(3)
$$\frac{\partial }{{\partial x_{i} }}\left( {u_{i} u_{j} } \right) = - \frac{\partial p}{{\partial x_{i} }} + \frac{{\partial \tau_{ij} }}{{\partial x_{j} }}g$$
(4)

where i and j are standard tensor notations, ui is the time averaged velocity component in the x direction, p is pressure, g is gravity acceleration, ρ is density, and τij is a stress tensor, which can be written as Eq. (5):

$$\tau_{ij} = \left[ {\rho \left( {\nu + \nu_{t} } \right)\left[ {\frac{{\partial u_{i} }}{{\partial x_{j} }} + \frac{{\partial u_{j} }}{{\partial x_{i} }}} \right]} \right] - \left[ {\frac{2}{3}\rho \left( {k_{{\text{T}}} + \vartheta_{t} } \right)\frac{{\partial u_{i} }}{{\partial x_{i} }}\delta_{ij} } \right]$$
(5)

where ν and νt represent the kinematic viscosity of the fluid and the viscosity of turbulence, respectively, kT is the turbulence kinetic energy, and δij is the Kronecker delta. Different turbulence models are used in this study.

Experimental model

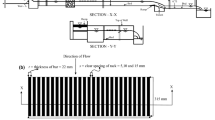
In the current study, a physical model developed by Righetti and Lanzoni (2008) was used to investigate the flow field over a non-circular bottom rack intake and estimate the DDC. The model consisted of a laboratory flume that was 12 m long and 0.25 m wide, with a bottom rack containing longitudinal bars, as depicted in Fig. 1. The experiments were conducted under clear water conditions (i.e., no sedimentation) and supercritical flow state at the upstream of the rack. The researchers measured and recorded the velocity vectors at different points over the rack, including between the bars, using a backscatter laser Doppler anemometer (LDA). Based on dimensional analysis and laboratory data, they proposed the following regression relation for DDC:

$$Q_{{\text{d}}} = C_{{{\text{d0}}}} \varepsilon BL\sqrt {2gE_{0} } \left( {\frac{a}{2}\frac{L}{{E_{0} }}{\text{Fr}}_{{\text{H}}} + 1} \right)\tanh \left[ {b_{0} \left( {\sqrt 2 - {\text{Fr}}_{{\text{H}}} } \right)^{{b_{1} }} } \right]$$
(6)

where a, b0, and b1 are constant laboratory coefficients, which in the experiments performed, these values are: b1 = 0.6093, b0 = 1.5, a =  − 0.1056. Also L is the rack length, B is the rack width, ε is the rack void ratio, E0 is the specific energy of the approaching flow, Cd0 is the DDC in static conditions (the DDC value when FrH tends to zero), and FrH is the modified Froude number for approaching flow.

Fig. 1
figure 1

Sketch of the experimental apparatus (Righetti and Lanzoni 2008)

Full size image

Numerical model

Model geometry

The numerical model developed in this study was constructed based on the geometry and boundary conditions of the physical model introduced by Righetti and Lanzoni (2008) utilizing Flow3D software. The numerical model consisted of three distinct blocks, representing the upstream channel, the bottom rack intake, and the downstream channel, which effectively emulated the laboratory model (Fig. 2). To ensure a three-dimensional fully developed flow conditions before bottom rack (Razaz and Faghfour Maghrebi 2008a, b), an additional 6 m of the upstream channel was appended to the model, even though the length of the bottom rack channel in the physical model was initially set to 45 cm (see Fig. 2).

Fig. 2
figure 2

Plan, longitudinal and cross section used in numerical modeling

Full size image

Indeed, in open channels, the velocity gradients in the entrance and near the channel bed are high due to the growing boundary layer (see Fig. 3). The boundary layer thickness (δ) increases with distance from the entrance of the channel. After a certain distance (establishment length, Le), the boundary layer reaches the free surface where after the velocity profile remains invariant. Information about this establishment length is required for any experimental study and numerical modeling of free surface flows. Beyond this distance (Le), the flow is fully developed. This condition is essential for accurately simulating the hydraulic behavior of the water passing through the bottom rack intake. Neglecting this aspect could lead to inaccurate predictions and biased results, as the flow behavior near the inlet may not represent the actual flow characteristics in real-world scenarios. Bonakdari et al. (2014) proposed a dimensionless relation to calculate the necessary establishment length in a linear relationship between the dimensionless length of the flow developing zone and the Reynolds number which is as follows. This equation is in good agreement with Kirkgoz and Ardichoglu (1997) work, for smooth channels:

$$\frac{{L_{{\text{e}}} }}{h} = a\left( {\frac{{{\text{Re}}}}{{{\text{Fr}}}}} \right) + b$$
(7)

where Le is establishment length, h is water depth, Re is Reynolds number, Fr is Froude number, and a, b are constant (Orth et al. 1954).

Fig. 3
figure 3

Boundary layer and fully developed open channel flow (Bonakdari et al. 2014)

Full size image

In the current research, not only Le calculated based on Eq. (7), but also estimated according to the experimental setup of the first author (Razaz and Faghfour Maghrebi 2008b; Chan et al. 2018). For this, one-dimensional velocity profiles (along the channel) were measured and drawn in different cross sections upstream the rack using calibrated miniature propeller (with ± 1% precision) and compared to each other. The full development of boundary layer for the approaching flow was concluded from similarity of velocity profiles upstream of rack, and, due to the symmetry of the velocity distribution in each cross section. In sum up, to ensure the accuracy and validity of the results, 6 m of the upstream channel before the lower rack was added to the model.

To establish the numerical model of the bottom rack and its components (Fig. 2), multi-block meshing technique was employed. This approach allowed for the utilization of varying mesh sizes in different regions of the model, optimizing computational efficiency while maintaining precision. In the upstream channel block, a mesh size of 8 mm was adopted along 5.75 m upstream of the bottom rack, while it was reduced to 4 mm near the upstream end of the bottom rack. For the bottom rack block, which spanned a length of 0.45 m, a mesh size of 2 mm was chosen to ensure accurate representation of the geometric features, including the bars and bar clearance. Additionally, the downstream channel, with a length of 0.2 m, was modeled with a mesh size of 4 mm (Fig. 2). To minimize any numerical errors and improve precision at the boundaries between the blocks, gradual changes in mesh size were implemented. For instance, at the boundary between the 8 mm and 4 mm grids within the upstream channel block, the mesh size was gradually reduced by half, effectively equalizing the mesh size at the boundary between the two regions. This mesh size optimization strategy facilitated a smooth transition between different mesh sizes and helped to mitigate instability at the interfaces, resulting in more reliable and accurate numerical simulations. The combination of realistic boundary conditions and mesh size adjustments allowed for the accurate simulation of the fluid dynamics and provided valuable insights into the behavior of the flow around the bottom rack structure.

The rack length

Righetti and Lanzoni employed a fixed length of 0.45 m for their laboratory model of the bottom rack. However, in an effort to enhance the accuracy of the DDC estimation, this study incorporated three different rack lengths, namely, 0.3 m, 0.45 m, and 0.6 m, in the numerical models of the bottom rack. The selection of these rack lengths was intended to encompass values both greater and less than the length used in the experimental model of Righetti and Lanzoni.

The rack slope

The water depth and flow rates of the approaching flow were meticulously chosen to ensure that the upstream flow Froude number fell within the range of 1.05 to 2.05. This range was selected to replicate rivers with supercritical flow conditions. The specific values of water depth and flow rate used in the simulations are presented in Table 1.

Table 1 Water depth and flow rate for upstream approaching flow in the current model
Full size table

The rack cross section shape

In the numerical model, the study considered three different cross sections of rack bars to investigate the effect of bar shape on the bottom rack performance. The rack cross section shapes included a rhombus (with equal diameters of 2 cm), a circular shape (with a diameter of 2 cm), and a rounded-edge rectangle (a 2 × 2 cm rectangle with both upper edges rounded by 1 cm radius quarter circles, similar to the laboratory model used by Righetti and Lanzoni in (2008). Figure 4 illustrates the bottom rack cross sections used in the current numerical models, all of which have equal thickness and width for each individual bar.

Fig. 4
figure 4

Bottom rack cross sections used in the current numerical models

Full size image

Turbulence model

Flow3D software offers five different turbulence models: Prandtl mixing length model, single equation model, standard k-ε model, RNG k-ε model, and large eddy simulation (LES) model (Flow Science 2007). In this study, a comparative analysis of the turbulence models was performed to identify the best model that best fit the experimental data. The calculated discharge diverted by the bottom racks (Qd) was compared to the experimental results in all 16 series for each turbulence model. Three error criteria were employed to assess the performance of the turbulence models in the numerical simulations, and the results are presented in Table 2. The criteria included R2, MAE, and RMSE values, with a unit value for R2 and lower MAE and RMSE values indicating a better fit to the experimental data. As indicated in Table 3, the RNG k–ε model demonstrated the closest agreement with the experimental results and was deemed most suitable for the current study. This finding aligns with previous research conducted by other researchers (Hosseini et al. 2015; Ghasemzadeh 2013)).

Table 2 Error criteria used for evaluation of turbulence models in this study (Hosseini et al. 2015)
Full size table
Table 3 Evaluation of turbulence models in the current study
Full size table

In the given formula, "O" represents the real value of the dependent variable, "P" denotes the predicted value of the variable, and "N" stands for the number of variables involved in the analysis.

Boundary and initial conditions

Boundary conditions play a critical role in hydraulic simulations, defining the behavior of the fluid at the domain boundaries. The boundary conditions in current study encompassed flow inlet, outlet, rigid boundary, and the boundary of the water surface based on the defined library in Flow3D code. The volume flow rate is defined for inlet boundary condition with a defined water surface elevation and discharge. An outflow boundary is used at the outlets because the details of the flow velocity and pressure are not known prior to solving the flow problem (Flow Science 2007; Ghasemzadeh 2013). A rigid boundary is defined using a standard wall function. A symmetrical boundary condition is used for the middle block and water surface. This condition reduces computational overhead while preserving the overall flow symmetry. Figure 5 illustrates the arrangement of boundary conditions for all mesh blocks, providing a visual representation of how each boundary is treated in the simulation. Additionally, Table 4 offers a detailed account of the specific boundary conditions applied to each mesh block in all directions within the current study.

Fig. 5
figure 5

Boundary conditions for the numerical model, including the wall condition (W), the symmetry condition (S), volume flow rate (Q), and the outflow condition (O)

Full size image
Table 4 Boundary conditions for all mesh blocks
Full size table

The initial conditions define conditions at the beginning of the simulation (usually denoted by time 0). Initial values of flow are required at every node before commencing an unsteady or steady time stepping simulation. In the case of current model, all the simulations begin at time zero with specified flow discharge and relevant flow depth at the beginning of channel (flow inlet boundary condition) and dry bed over the rack, downstream of the rack and at the diverted channel. The initial velocity at the inlet boundary estimated based on the specified flow discharge and relevant flow depth, and is set to be zero at the regions.

Time step

The time step in the simulation is a crucial parameter that affects numerical stability and accuracy. The time step can be automatically calculated by Flow3D or set manually by the user. To prevent potential instability, the software automatically adjusted the time step as needed to achieve stable conditions within an acceptable range while solving the equations. Initially, in the current simulation, the time step was set at 1% of the total simulation time. If this value led to an unstable solution, the time step was reduced by 50%, and the simulation parameters were recalculated until stability was achieved. Conversely, if a stable solution was attained at 1%, the time step increases by 50% to expedite the simulation, while maintaining stability (Zamanieh Shahri et al. 2019; Hosseini et al. 2015).

The total simulation time for each run averaged 80 s, resulting in an automatically adjusted time step of 0.6 s. This approach ensures both numerical stability and computational efficiency during the simulations.

Fluid properties

The fluid considered in this study was water, and its properties were specified to facilitate accurate simulations. The fluid had a viscosity of 0.001 Pa s, a density of 1000 kg/m3, a surface tension of 0.072 N/m, gravity acceleration of 9.81 m/s2, atmospheric pressure of 101.3 MPa, and a room temperature of 20 °C (Hosseini et al. 2015; Flow Science 2007). These properties are essential for correctly modeling the behavior of water within the hydraulic system.

Number of Runs: To comprehensively explore the effects of different geometric and hydraulic variables on the hydraulic system's behavior, a total of 81 model executions were required. These included variations in three parameters: rack lengths, rack slopes, rack shapes, and flow rates. The combinations of these variables led to 81 unique simulation scenarios (N = 3 × 3 × 3 × 3 = 81). The numerical model parameters for each run are provided in Appendix.

Results and discussion

Model assessment

The validity of the simulation model relies on its ability to accurately represent the actual system. In this study, validation was performed to quantitatively assess the agreement between the model's predictions and the observations from the experiments. The comparison was based on the discharge diverted by the bottom intake (Qd) and the discharge passed over the bottom intake (Qr) for 16 models (T1 to T16 runs) that were constructed exactly according to the experimental tests conducted by Righetti and Lanzoni (2008). The results of this comparison are presented in Table 5 and Fig. 6. In Fig. 6, the calculated Qd and Qr for the 16 models were plotted against their experimental values, showing agreement along the line of agreement. Additionally, the relative error (ER) in estimating Qd and Qr was computed using the following equation:

$$E_{{\text{R}}} \left( \% \right) = \frac{{(Q_{{\text{d}}} \quad {\text{or}}\quad Q_{{\text{r}}} )_{{\text{a}}} - (Q_{{\text{d}}} \quad {\text{or}}\quad Q_{{\text{r}}} )_{{\text{c}}} }}{{(Q_{{\text{d}}} \quad {\text{or}}\quad Q_{{\text{r}}} )_{{\text{a}}} }} \times 100$$
(8)

In the equation, (Qd or Qr)a represents the experimental values of Qd or Qr obtained from the work of Righetti and Lanzoni (2008), while (Qd or Qr)c denotes the numerical values of Qd or Qr obtained from the Flow3D model used in the current study. The average relative error for estimating Qd and Qr was found to be 0.7525% and 0.165%, respectively. These values indicate a high level of agreement between the experimental and model results, demonstrating the appropriateness and accuracy of the numerical model in simulating the system.

Fig. 6
figure 6

Comparison of numerical and experimental results of flow discharges over bottom intake for Qr and Qd in all 16 tests

Full size image
Table 5 Experimantal and numerical results comparison for rounded bars
Full size table

Mesh analysis

Using multi-block meshing technique and adjusting mesh sizes in different regions improved the accuracy of simulations and provided more reliable results. This focus on mesh sizes offers optimized and trustworthy representations of flow behavior around the bottom intake structure. To reach the optimum mesh size and demonstrate the independence of simulation results from mesh sizes, five tests were conducted for model T6 with different mesh sizes, as shown in Table 6. Comparing the numerical simulation results with the physical model for discharge diverted by the bottom intake (Qd) and the discharge passed over the bottom intake (Qr) revealed significant errors for MITN1 and MITN 2. This suggests that these mesh sizes were unable to adequately model the void space between the bottom intake bars, resulting in a reduced diversion flow and less pronounced Coanda Effect, leading to less accurate results. On the other hand, MITN 4 and MITN 5 results were very close to MITN 3, indicating that reducing the mesh size had minimal impact on the results. Therefore, by adopting the optimal mesh dimensions according to MITN 3, the desired results can be reliably obtained through numerical simulation, while avoiding the additional costs and time required for modeling with smaller mesh sizes (Table 6).

Table 6 Mesh independence test results
Full size table

Diverted discharge ratio

The diverted discharge ratio (DDR) is defined as the fraction of the total upstream flow diverted by the bottom intake to the downstream collection channel, represented by Qd/Qt. The DDR serves as a reasonable dimensionless performance parameter for the bottom rack, reflecting its ability and efficiency to divert the main stream of the river. In this study, the DDR for racks with different hydraulic and geometric conditions was extracted from the numerical results after conducting 81 series of runs. The effect of different parameters on DDR was investigated. To achieve this, the DDR, obtained by dividing the diverted flow (Qd) by the bottom intake, was plotted against the total upstream flow rate (Qt) for all three bar cross sections of the bottom rack intakes used in this study and showed in Fig. 7. Each diagram in Fig. 7 represents an investigation of the independent effect of a specific geometric parameter (rack slope and length) on the magnitude and intensity of change in the DDR values, while keeping the other parameters constant. Based on Fig. 7, the following observations can be made:

  • In all types of bottom racks, as the upstream flow rate increases, the diverted discharge ratio (DDR) decreases. This is attributed to the increase in specific energy, leading to a larger portion of the flow passing over the rack rather than being diverted. It is worth noting that this finding aligns with the results obtained by other researchers (Razaz and Faghfour Maghrebi 2008a; Kamanbedsat and Shafaie Bajestani 2008; Bina 2011; Shafaie Bajestani and Shakourirad 1997; Bina and Saghi 2017; Bina 2018; Zamanieh Shahri et al. 2019).

  • As the rack slope increases, the diverted discharge ratio (DDR) decreases due to flow separation around the rack bars. Steeper rack slopes lead to flow separation occurring at a greater distance from the upstream edge of the rack. This results in a more significant reduction in DDR for longer length bottom intakes, and the greatest DDR is observed in racks with a rhombus bar cross section. Moreover, it is noted that the magnitude of DDR changes for rack slopes ranging from 0.1% to 2.5% is greater than those with slopes between 2.5% to 4.0%. These observations highlight the influence of rack slope on DDR and provide valuable insights into the performance characteristics of the bottom intake system (see Table 7 for details).

  • As the rack length decreases, the diverted discharge ratio (DDR) also decreases. This reduction is more pronounced in the bottom intakes with rhombus bars compared to those with circular and rounded bars. Additionally, the DDR decrease for rack lengths between 0.30m to 0.45m is greater than the reduction observed for racks with lengths ranging from 0.45m to 0.60m. These findings highlight the impact of rack length on DDR and underscore the significance of the bar cross-sectional shape in determining the diversion efficiency of the bottom intake system (see Table 8 for details).

  • Overall, the results indicate that bottom racks with rhombus bars exhibit the highest diverted discharge coefficient (DDC), diverting approximately 95% of the total flow rate at 2.22 L per second. This phenomenon occurs because the bottom rack with rhombus bars creates negative pressures with higher magnitudes around the bars, leading to increased water draw-in. These negative pressures around the bars, known as the “Coanda effect”, cause the water flow to be redirected toward the bottom rack bars instead of following the mainstream flow.

The tendency of a fluid to adhere to a curved surface (Fig. 8) is called as the coanda effect. This phenomenon occurs because of the reduction in pressure caused by the high velocities of the jet (Bharathwaj et al. 2016). The balance of forces on the fluid causes the adhesion of the jet fluid on the curved surface (Newman 1961). These forces which cause this adhesion are the radial pressure and the centrifugal forces. The contact pressure of the fluid jet with the wall is lower than the ambient pressure when the jet comes in contact with the wall. It is lower because of the viscous drag phenomena created by the interaction of the fluid with the wall surface (Michele et al. 2013). The difference in pressure observed here is the primary cause for the fluid’s attachment to the curved wall surface. The graph in Fig. 9, illustrating the pressure values around the bottom rack bars, visually represents the negative pressure effect induced by the Coanda effect. Additionally, the plot in Fig. 10 depicts the pressure contours along the bottom rack with rhombus bars, showing a reduction in pressure along the intake length due to the Coanda effect and the attraction of flow toward the bottom rack bars.

Table 7 DDR decrease rate in different rack slopes during test discharge rates, in percent
Full size table
Table 8 DDR decrease rate in different rack lrngthes during test discharge rates, in percent
Full size table
Fig. 7
figure 7

The DDR changes versus different rack slope, length, and approaching flow rate

Full size image
Fig. 8
figure 8

The Coanda effect: attraction of a jet to a solid body of round shape (Michele et al. 2013)

Full size image
Fig. 9
figure 9

Pressure distribution around different type bottom racks bars along the rack length

Full size image
Fig. 10
figure 10

Pressure contours along bottom racks with rhombus bars, test run T46

Full size image

Table 9 presents the calculated diverted discharge ratios (DDR) derived from the 81 series of tests conducted for bottom racks equipped with circular, rhombus, and rounded rectangle bars in the current study. Since the highest DDR values were observed in the rack with rhombus bars, Table 9 provides a comparison and calculation of the DDR differences between rhombus bars and the other two rack types. The results clearly indicate that averagely, the rack with rhombus bars can divert upstream flow 23.35% and 35.92% more than the circular and rounded bars, respectively, within the range of parameter variations considered in this research. These findings underscore the superior diversion performance of the rhombus bar configuration and provide valuable insights for optimizing bottom intake designs.

Table 9 DDR differences in bottom racks with different bar cross section in this study
Full size table

The DDC estimation

Indeed, the diverted discharge ratio (DDR) is a significant function parameter for bottom rack intakes. However, another crucial and widely used function parameter in bottom rack intake studies is the diverted discharge coefficient (DDC). The DDC plays a key role in Eq. 2, and many experimental and numerical studies on bottom racks have aimed to estimate this parameter. In the present study, the DDC was estimated based on the numerical results of the model and dimensional analysis. Generally, the DDC, represented by Cd, can be expressed using the following relationship, which is dependent on the parameters that influence it.

$$C_{{\text{d}}} = f_{1} \left( {\rho ,\mu ,g,\varepsilon ,S_{1} ,L,y_{0} ,V_{0} ,{\text{S}}{\text{.F}}{.}} \right)$$
(9)

By estimating the DDC, this study aims to enhance the understanding of bottom rack intake performance and provide valuable insights for future design and optimization efforts.

In Eq. (9), ρ and μ represent the density and dynamic viscosity of the fluid, respectively. The acceleration due to gravity is denoted by “g”. Parameters ε and L stand for the void ratio and rack length, respectively, while y0 and V0 represent the depth and velocity of the approaching flow, respectively. The last factor influencing the diverted discharge coefficient (DDC) is the geometric shape of the bar cross section, which is presented as the shape factor (S.F.) in this relation. According to the Buckingham Π theorem, considering ρ, V0, and y0 as the repeating parameters, the DDC (Cd) is a function of non-dimensional parameters as described below (Bina 2011; Bina and Saghi 2017):

$$C_{{\text{d}}} = f\left( {{\text{Re}} ,{\text{Fr}}_{0} ,\varepsilon ,S_{1} ,\frac{L}{{y_{0} }},{\text{S}}{\text{.F}}{.}} \right)$$
(10)

where Re and Fr0 are the Reynolds number and the Froude number of the upstream approaching flow, respectively. It is worth noting that most researchers have ignored the effect of the Reynolds number due to turbulence, but some others have considered it (Razaz and Faghfour Maghrebi 2008a; Kamanbedsat and Shafaie Bajestani 2008; Bina 2011; Shafaie Bajestani and Shakourirad 1997; Bina and Saghi 2017; Bina 2018; Castillo et al. 2017; García et al. 2019; Carrillo et al. 2018; Calderón et al. 2021; Chan et al. 2018; Chang et al. 2018; Zamanieh Shahri et al. 2019). Based on the experimental research experience of the first author of this research, the Reynolds number values of the flow in the laboratory channel with the same dimension, slope, and flow discharge of the current model are more than 30,000, but are much less than the values in natural rivers (Bina 2011; Bina and Saghi 2017; Hosseini et al. 2015). Therefore, if we want to generalize the fit equations extracted from such laboratory or numerical model to real problems at the scale of natural rivers, and be able to use it for design of real bottom intake structures, it is necessary to ignore Reynolds number in DDC estimation, such as many researchers performed (Razaz and Faghfour Maghrebi 2008a; Bina 2011; Bina 2018; Castillo et al. 2017; García et al. 2019; Carrillo et al. 2018; Calderón et al. 2021; Chan et al. 2018; Chang et al. 2018; Zamanieh Shahri et al. 2019).

All parameters in Eq. 10 (except Re) were used to extract regression equations for estimating DDC, based on their values in Appendix 1. Before that, correlation analysis was done to see how independent variables (Fr0, ε, S1, L/y0, S.F.) effect on DDC (as dependent variable), using SPSS software. Correlation analysis, also known as bivariate, is primarily concerned with finding out whether a relationship exists between variables and then determining the magnitude and action of that relationship. The results of the Pearson correlation analysis using SPSS software for different types of bottom racks are shown in Table 10. The Pearson correlation measures the strength of the linear relationship between two variables. It has a value between − 1 and 1, with a value of − 1 meaning a total negative linear correlation, 0 being no correlation, and + 1 meaning a total positive correlation (Landau and Everitt 2004). These analyses provide valuable insights into the significance of various parameters affecting the DDC of bottom rack intakes and contribute to the understanding of their hydraulic performance under different flow conditions.

Table 10 Independent parameters which has the most correlation with DDC
Full size table

In the above table, Au and Ad are the upper and the lower area of the cross sections, respectively.

To explore the combined influence of factors affecting the diverted discharge coefficient (Cd), a multiple regression analysis, involving both linear and non-linear models, was conducted using SPSS software. Equations 11 through 13 depict the best-fitted relations obtained from the numerical data for different types of rack intakes. Through these regression analyses, the relationships between the influencing dimensionless parameters were quantified, providing a comprehensive understanding of their collective impact on Cd. The derived equations offer valuable predictive models for estimating Cd under various configurations of bottom rack intakes, assisting in optimizing the design and performance assessment of such systems in practical applications.

  • Rounded Rectangle Bars:

    $$\begin{aligned} & C_{{\text{d}}} = 0.859 - 0.292\left( {S_{1} } \right) - 0.103\left( {{\text{Fr}}_{0} } \right) - 0.013\left( {\frac{L}{{y_{0} }}} \right) - 0.037\left( {\frac{{A_{{\text{u}}} }}{{A_{{\text{d}}} }}} \right) \\ & {\text{RMSE}} = 0.312,\quad {\text{MAE}} = 0.778,\quad R^{2} = 93\% \\ \end{aligned}$$
    (11)

  • Rhombus Bars:

    $$\begin{aligned} & C_{{\text{d}}} = 1.094 - 0.046{\text{Log}}\left( {S_{1} } \right) - 0.017{\text{Exp}}\left( {Fr_{0} } \right) - 0.45{\text{Log}}\left( {\frac{L}{{y_{0} }}} \right) \\ & {\text{RMSE}} = 0.741\quad {\text{MAE}} = 0.583\quad R^{2} = 88\% \\ \end{aligned}$$
    (12)

  • Circular Bars:

    $$\begin{aligned} & C_{{\text{d}}} = 0.885 - 0.016{\text{Log}}\left( {S_{1} } \right) - 0.022{\text{Exp}}\left( {{\text{Fr}}_{0} } \right) - 0.253{\text{Log}}\left( {\frac{L}{{y_{0} }}} \right) \\ & {\text{RMSE}} = 0.297\quad {\text{MAE}} = 0.237\quad R^{2} = 97\% \\ \end{aligned}$$
    (13)

To ensure the accuracy, validity, and applicability of the proposed equations, a comprehensive error analysis and comparison with the equations of other researchers were conducted. The relative error of estimation for Eqs. 10–12 was calculated using the following formula:

$$E_{{\text{R}}} \left( \% \right) = \frac{{(C_{{\text{d}}} )_{{\text{c}}} - (C_{{\text{d}}} )_{{\text{m}}} }}{{(C_{{\text{d}}} )_{{\text{m}}} }} \times 100$$
(14)

where ER represents the relative error of Cd estimation, (Cd)c is the calculated DDC using the proposed Eqs. (11–13), and (Cd)m is the DDC obtained from the numerical analysis.

Where ER is relative error of Cd estimation, (Cd)c is the calculated DDC by the proposed Eqs. (11–13) and (Cd)m is the DDC obtained from numerical analysis. Subsequently, standard deviation and mean relative error were estimated to assess the accuracy and reliability of the proposed equations. The results are then summarized in Table 11, providing a comprehensive overview of the performance of the proposed equations in predicting the diverted discharge coefficient under different scenarios. By quantifying the standard deviation and mean relative error, the robustness and precision of the proposed equations were evaluated, confirming their capability to provide accurate estimations of Cd for a wide range of hydraulic and geometric conditions. Through the comprehensive error analysis and comparison, the proposed equations demonstrated high accuracy and reliability, showcasing their potential as valuable tools for predicting the diverted discharge coefficient in practical applications involving various bottom rack intake configurations. The summarized results in Table 11 further support the validity and practicality of the proposed equations in the field of bottom rack intake studies.

Table 11 Standard deviation and mean relative error for Eqs. 11–13
Full size table

In Fig. 11, a comparison is made between the calculated diverted discharge coefficient (Cd)c obtained from the proposed Eqs. (11–13) and diverted discharge coefficient (Cd)m obtained from the numerical analysis. The figure also includes the corresponding confident range of relative errors.

Fig. 11
figure 11

Comparison of the calculated DDC by the proposed equations, (Cd)c versus DDC obtained from numerical analysis, (Cd)m and the confident range for relative errors

Full size image

To assess the accuracy and reliability of the proposed equations, the average values of relative errors, standard deviation of mean relative errors, and a confidence level of 95% were considered. Based on these analyses, the confident range for the relative error of Eqs. 11, 12, and 13 were found to be ± 4.7%, ± 8.1%, and ± 5.5%, respectively. This implies that with a 95% probability, the relative errors for the estimation of Cd would fall within the above-specified ranges (Bina 2011; Razaz and Faghfour Maghrebi 2008b).

The confident range provides an important measure of the precision and consistency of the proposed equations in predicting the diverted discharge coefficient under different conditions. The narrow and relatively small confident ranges for Eqs. 11, 12, and 13 indicate that the proposed equations offer reliable and accurate estimations of Cd, enhancing the confidence in their practical application for various bottom rack intake configurations.

These findings validate the efficacy of the proposed equations and reinforce their potential as valuable tools for predicting the diverted discharge coefficient with a high level of certainty, providing researchers and engineers with a robust method for analyzing and designing bottom rack intake systems.

Result comparison using current research data

To assess the efficiency and accuracy of the proposed relations in this study, the diverted discharge coefficient (DDC) of longitudinal bars bottom racks with circular cross section (Eq. 1) was compared with relations proposed by other researchers using current data obtained from the numerical model. For this comparison, data from 27 series of runs were utilized.

To begin, Eq. 13 was employed to calculate the DDC for the circular bottom racks, and subsequently, the diverted discharge (Qd) was calculated using Eq. 2. Simultaneously, the DDC for the 27 series of numerical data for circular bottom racks was calculated using relations proposed by Subramanya (1994), Shafaie Bajestani and Shokoohirad (1997), Kamanbedsat and Shafaie Bajestani 2008, Righetti and Lanzoni (2008), Kumar et al. (2010), and Bina (2011), followed by the calculation of the corresponding diverted discharge for each case.

Finally, the errors of estimation for the diverted discharge, such as root mean square error (RMSE) and mean absolute error (MAE), were compared and summarized in Table 12. The results in Table 12 demonstrate that the proposed relation in this study exhibits the best fit to the available data and has the minimum errors in comparison with the relations proposed by Bina and Righetti.

Table 12 Comparison the valid equations for Cd by former researchers in circular cross section longitudinal bars bottom rack
Full size table

This comparison validates the superior performance and accuracy of the proposed relation in predicting the diverted discharge and demonstrates its efficiency compared to other existing relations proposed by different researchers. The findings further confirm the practicality and applicability of the proposed relation for estimating the diverted discharge in longitudinal bars bottom racks with circular cross section under various flow conditions, contributing to the advancement of research in this field.

Conclusions

The current research aimed to investigate the performance of bottom racks, especially those with non-circular cross section bars, using numerical models prepared with Flow3D. The selection of hydraulic and geometric conditions for the models was based on a comprehensive literature review and practical considerations relevant to bottom racks. These structures are commonly used in mountainous rivers with steep slopes and supercritical flow conditions, employing longitudinal bars to divert a significant portion of the river flow.

In the present study, three types of bottom racks with different cross sections (rhombus bars, rounded-edge rectangle bars, and circular bars) were numerically modeled under supercritical flow conditions. Various discharges, rack lengths, and rack slopes were simulated in the numerical models, and the diverted and remained discharges were calculated to extract the following key results:

  • The RNG k–ε turbulence model was found to be the most suitable turbulence modeling approach for accurately capturing the flow field around bottom rack intakes.

  • An inverse relationship was observed between the approach flow rate and the diverted discharge by the bottom rack, indicating that an increase in the approach flow rate leads to a decrease in the diverted discharge.

  • The longitudinal slope of the rack was inversely related to the diverted discharge, meaning that an increase in the rack slope resulted in a decrease in the diverted discharge.

  • On the other hand, an increase in the rack length was directly related to an increase in the diverted discharge, suggesting that longer racks have the potential to divert more flow.

Subsequently, convenient relations for the diverted discharge coefficient (DDC) were derived for bottom racks with rhombus bars, rounded-edge rectangle bars, and circular bars using dimensional analysis. Based on the 81 series of runs on the numerical models, it was found that racks with rhombus bars averagely could divert 23.35% and 35.92% more flow compared to circular and rounded bars, respectively, within the range of changes considered in this research. This significant advantage is attributed to the formation of more negative pressures around rhombus bars, resulting in enhanced flow diversion, known as the "Coanda effect." Consequently, bottom racks with rhombus bars are deemed the most efficient type for diverting river flow under similar conditions.

To validate the accuracy, validity, and applicability of the proposed equations, extensive error analysis and comparisons with other existing equations were conducted. The results of these analyses demonstrate the reliability and precision of the proposed equations in predicting the diverted discharge coefficient under various geometries and conditions, further supporting their practical utility in the field of bottom rack intake studies.