Abstract
Investigating rotation curves and the Tully–Fisher ratio within galaxies represents a central theme of extensive research and scientific interest. Despite several theoretical models, a comprehensive explanation of the observed correlation between galaxy types and their rotation curves remains elusive. This study endeavors to bridge this knowledge gap by delving into the discernible connection between the presence of dark matter and galaxy classification. By meticulously examining the gravitational field's dependency on its source's point symmetry, we introduce a novel theoretical framework that offers a coherent rationale for these empirical findings. Our proposed model explains the appearance of dark matter as a direct consequence of the reduction of point symmetry in gravitational systems. Neither arbitrary systems with a high mass density nor a perfectly spherically symmetric mass distribution give the observable effects of dark matter. Special attention was paid to the axial symmetry scenario as a reasonable approach for modeling the mass distribution in most galaxies. We thoroughly analyzed, showing strong agreement with experimental observations for dwarf, Sb, and Scd galaxies. Thus, our study provides a compelling theoretical foundation for elucidating the intricate interplay between galaxy types, rotation curves, and the presence of dark matter, shedding new light on the dynamics of the cosmos.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 4.0 license. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
Although Einstein's theory of general relativity is recognized as one of the most successful theories, several remarkable experimental observations during the past century have outlined a new revolution in cosmology. Universe expansion and galaxy rotational curves, Tully–Fisher relations, black hole paradoxes, and others have uncovered the incompleteness of the classical theory of general relativity. The competing paradigms of dark matter and modified gravity are still fighting for supremacy, even though they have undergone significant transformations, and the many shortcomings of both theories have been eliminated.
Since the pioneering work of Mordehai Milgrom in 1983, numerous theoretical models have been proposed to explain the phenomenon of Modified Newtonian Dynamics (MOND) [1, 2]. Most previous MOND models had similar advantages and disadvantages. On the positive side, they successfully predicted flat rotation curves (mass-asymptotic speed relation) and the baryonic Tully–Fisher relation. However, they also suffer from limitations, such as inconsistency with short-distance observations or the introduction of additional fitting parameters unrelated to classical General Relativity or other fundamental constants [3]. These parameters can potentially lead to instability of solar structures [4, 5].
An attempt to extend MOND to the relativistic case was partially successful using the TeVeS model proposed by Bekenstein [6]. This model was derived from first principles using the Lagrange approach and scalar field potential. However, it fails to account for gravitational lensing because of the tracelessness of the electrodynamic part of the stress-energy tensor. Additionally, a problem related to superluminal modes in the field was identified by authors in [7, 8].
A more self-consistent theory was proposed by Verlinde and further developed by Hossenfelder. This model aims to mimic dark energy or matter behavior, depending on the conditions. The corresponding Lagrangian is constructed using a vector field with a term proportional to the inverse volume, representing the dark matter component. To resolve the problem of MOND-like behavior at short distances (e.g. the Solar System), it is argued that the Nernst Theorem (3rd law of thermodynamics) requires non-negative entropy, causing the terms to vanish near massive objects [9]. Thus, the field avoids interaction with light and massive objects. To the best of our knowledge, no quantitative evaluations or comparisons with experimental results have been performed for this model. Nevertheless, one notable advantage of this model is that it is parameter-free [10].
It should be noted that, to the best of our knowledge, none of the existing theories explain the observed differences in the Tully–Fisher relations for different types of galaxies, as clearly indicated by experimental results. The study of rotation curves and the Tully–Fisher ratio has garnered significant attention in understanding the dynamics of galaxies. Numerous models have been proposed to comprehend these phenomena [11]; however, no study has yet explained the observed correlation between galaxy types and rotation curves. This correlation suggests that the 'dark matter effect' is more prominent in spiral galaxies while comparatively weaker in lenticular galaxies [12, 13]. Notably, dispersion was observed within each group of galaxies based on their type. The recent investigation of galaxy clusters, on the other, shows that they less prominently demonstrate the effect of 'dark matter' [14]. At the same time, another investigation [15] showed that their shape is closer to a sphere than previously mentioned.
Over the past decades, numerous scientific groups have compared a huge number of experimental results, demonstrating a reliable correlation between galaxy morphology and rotation curves. In particular, paper [16] showed that taking into account the ellipticity of a galaxy when classifying it into fast and slow rotators significantly improves the result. The investigation, carried out by D. Obreschkow and K. Glazebrook, clearly demonstrates a tendency to decrease the angular momentum with an increase in the bulge mass fraction in spiral galaxies [17]. A similar study was also carried out for barred galaxies. This study demonstrated that the angular momentum tends to increase with increasing bar fraction for galaxies containing short bars. While long-bar galaxies show more complex behavior: the maximum bar fraction is reached for an intermediate angular momentum observed [18]. In light of these observations, we believe that the dependence of the gravitational field on the point symmetry of the source offers the most logical and compelling explanation.
In this paper, we propose a modified theory of general relativity. Our model preserves the key idea that the curvature of space-time causes gravitational pulling. Additional types of curvatures were also considered. Adding torsion to the theory of relativity was first proposed by Eli Cartan. After that, this theory was supplemented and developed by many authors [19–23]. Generally, this problem is related to the space of the affine connection [24]. Usually, a condition similar to the Cartan spin coupling equation is imposed on the torsion. This theory is used to eliminate singularities arising in the classical theory of relativity. This article proposes another approach to define torsion. In our approach, it is related to the point symmetry of the system. The proposed approach, as shown, can be used to explain the effects of dark matter.
Briefly, the theoretical idea can be described in three stages: In the first step, torsion is added while using covariant differentials to extend possible cases of space-time curvature. The torsion effect arises when the Christoffel symbols are not symmetric relative to the bottom indexes permutation. The second step is to modify the equation for the stress-energy tensor. This is achieved by rotating the material part relative to the field. Rotation is considered to be a new missing type of variation. Generally, the new form of the equation for the stress-energy tensor is not symmetric and breaks the law of conservation of angular momentum. Therefore, in the third step, we obligate the new terms in the equation to cancel each other. As a result, the equation for stress-energy tensor preserves its classical form. However, new terms arise in the space-time curvature owing to non-zero torsion. As shown below, modification is essential only for systems with anisotropic mass distributions.
2. Modified gravity equations
In this section, we perform the described above procedure. The first step is to define the covariant derivative with torsion for an arbitrary contravariant vector, Aγ :

where the operator in the second term  is the symmetric part of the Christoffel symbols,
is the symmetric part of the Christoffel symbols,
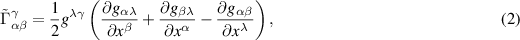
where  denotes the asymmetric part. Geometrically, it can be treated as the origin of torsion. The equation for the asymmetric part is obtained below. The definition of the covariant derivative with equations (1) and (2) preserve metric tensors gαβ
as covariant constants, that is, covariant derivatives from gαβ
are always equal to zero. The second step can now be performed. The equation for the stress-energy tensor can be obtained by varying the action integral (see, for example, section 94 in [25]). The metric tensor components are the variational variables. Variation of the metric tensor:
denotes the asymmetric part. Geometrically, it can be treated as the origin of torsion. The equation for the asymmetric part is obtained below. The definition of the covariant derivative with equations (1) and (2) preserve metric tensors gαβ
as covariant constants, that is, covariant derivatives from gαβ
are always equal to zero. The second step can now be performed. The equation for the stress-energy tensor can be obtained by varying the action integral (see, for example, section 94 in [25]). The metric tensor components are the variational variables. Variation of the metric tensor:

where both terms on the right-hand side can be expressed through their coordinates variation  . The first is associated with coordinate skewing and has the following form:
. The first is associated with coordinate skewing and has the following form:

The second is added to describe the rotation of the system as a whole:

where  and
and  is the fully antisymmetric tensor. The factor
is the fully antisymmetric tensor. The factor  is the variations of the rotational angles. Performing the variation of the action integral and using the metric variation in the form (3)–(5), one can obtain the new equation for the stress-energy tensor Tαβ
:
is the variations of the rotational angles. Performing the variation of the action integral and using the metric variation in the form (3)–(5), one can obtain the new equation for the stress-energy tensor Tαβ
:

where

and the covariant derivatives are defined by equation (1). As mentioned in the Introduction, equation (6) with  and zero torsion
and zero torsion  correctly describes the conservation laws for energy and momentum:
correctly describes the conservation laws for energy and momentum:

In summary, our statement is that equation (8) is correct, however, the case when  and
and  is not unique. There are other cases in which equation (8) is realized. Thus, equations. (6)–(8) can be used to determine the asymmetric part of the Christoffel symbol. The system of equations can be rewritten as:
is not unique. There are other cases in which equation (8) is realized. Thus, equations. (6)–(8) can be used to determine the asymmetric part of the Christoffel symbol. The system of equations can be rewritten as:
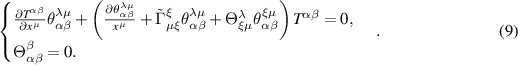
Each line in (9) is a set of four equations, whereas the number of independent components for the asymmetric part of the Christoffel symbol is 24. The Ricci tensor is modified as follows:

where  is the Ricci tensor without torsion and
is the Ricci tensor without torsion and  is the part with torsion. To obtain this formula, we used (1) and the bottom set of equations from (9). The space-time could be deformed in both ways, with and without torsion. Therefore, we should introduce a dimensionless parameter ε to write the gravitational field action in the most general way:
is the part with torsion. To obtain this formula, we used (1) and the bottom set of equations from (9). The space-time could be deformed in both ways, with and without torsion. Therefore, we should introduce a dimensionless parameter ε to write the gravitational field action in the most general way:
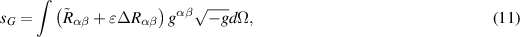
where  . The equations for the gravitational field are modified as next:
. The equations for the gravitational field are modified as next:

where κ is the gravitational constant and c is the speed of light. Parameter ε should be connected to the cosmological constant. However, the problem of expanding our Universe goes beyond the scope of the investigation.
3. Non-relativistic limit
In this section, we consider the classical limit of the equations from the previous section. It is assumed that the Newtonian gravitational potential is significantly smaller than the square of the speed of light. For convenience, we adopted a unit system in which the speed of light is equal to one. In this limit, we assume that  and
and  , where µ represents the mass density and ϕ represents the gravitational potential. The diagonal components of the metric tensor, other than g00, were set to −1, while the non-diagonal components were set to zero. In Addition, all other components of the stress-energy tensor were assumed to be zero. Further simplification can be achieved by considering a stationary scenario with time-independent gravitational potential. The simplest intuitive solutions can be obtained when the non-zero components of
, where µ represents the mass density and ϕ represents the gravitational potential. The diagonal components of the metric tensor, other than g00, were set to −1, while the non-diagonal components were set to zero. In Addition, all other components of the stress-energy tensor were assumed to be zero. Further simplification can be achieved by considering a stationary scenario with time-independent gravitational potential. The simplest intuitive solutions can be obtained when the non-zero components of  are
are  ,
,  ,
,  (plus three asymmetric components obtained via bottom index permutation). The Poisson equation for the gravitational potential ϕ was transformed into the following partial differential equation:
(plus three asymmetric components obtained via bottom index permutation). The Poisson equation for the gravitational potential ϕ was transformed into the following partial differential equation:

where  can be represented by the formulas:
can be represented by the formulas:

where l, m and n can be any permutation of 1, 2, 3, and summation performed over spatial indices. We have added a small parameter, o → 0 to equation (14) to resolve uncertainties (factor i is the imaginary unit and  means real part of the term). A small parameter o can be interpreted as a fluctuation in the gravitational potential arising from the imperfection of a certain symmetry (axial or spherical). The parameter can be excluded if there is no rotational symmetry. The explicit form of the
means real part of the term). A small parameter o can be interpreted as a fluctuation in the gravitational potential arising from the imperfection of a certain symmetry (axial or spherical). The parameter can be excluded if there is no rotational symmetry. The explicit form of the  in Cartesian coordinates is as follows:
in Cartesian coordinates is as follows:

where m and n can be any two of 1, 2, 3. Equations (7) and (15) shows that the gravitational potential with high rotational symmetry zeroes out of the corresponding components of  . To analyze, we suppose that the mass distribution function has ellipsoidal symmetry
. To analyze, we suppose that the mass distribution function has ellipsoidal symmetry  . We can also assume the same symmetry for the potential. The highest symmetry case, when
. We can also assume the same symmetry for the potential. The highest symmetry case, when  (spherical symmetry), gives us only
(spherical symmetry), gives us only  which equals zero identically. From the obtained equation, we can conclude that the correct solution corresponds to the case when all
which equals zero identically. From the obtained equation, we can conclude that the correct solution corresponds to the case when all  . Thus, we will get the classical Newtonian potential
. Thus, we will get the classical Newtonian potential  (as observed in our Solar System). In the case of the spheroid,
(as observed in our Solar System). In the case of the spheroid,  , there is no stationary solution for infinitely small o. In the lowest symmetry case,
, there is no stationary solution for infinitely small o. In the lowest symmetry case,  , no components
, no components  equal zero identically. It should be noted that axial symmetry is not impossible but implies additional restrictions on the mass distribution. Because of the importance of axial symmetry in our Universe, particularly for galaxies, we perform a more detailed investigation in the next section [26].
equal zero identically. It should be noted that axial symmetry is not impossible but implies additional restrictions on the mass distribution. Because of the importance of axial symmetry in our Universe, particularly for galaxies, we perform a more detailed investigation in the next section [26].
4. Axial symmetry
The approximation of the mass distribution model with axial symmetry is a reasonable approach for many objects in our Universe. As in the previous section, we used units c = 1. In the following, we use spherical coordinates, and only  and
and  are essential. All dependencies on the azimuthal angle φ should be excluded. As far as we suppose o → 0 we have to impose additional restrictions on the mass distribution function µ. Thus, we avoid infinitely large terms
are essential. All dependencies on the azimuthal angle φ should be excluded. As far as we suppose o → 0 we have to impose additional restrictions on the mass distribution function µ. Thus, we avoid infinitely large terms  , because for axial symmetry
, because for axial symmetry  . This restriction has the following form:
. This restriction has the following form:

where  is an arbitrary, continuous function. The effect of 'dark matter' depends on this function. We use the following form of the function:
is an arbitrary, continuous function. The effect of 'dark matter' depends on this function. We use the following form of the function:

where a and zd are the constants. The latter parameter can be threaded as the exponential width of the galaxy disc. Substituting (17) into (16), then the result into (13) and (14), one will get:
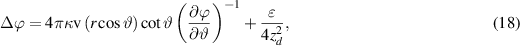
where the last term on the right-hand side appears owing to the torsion, the corresponding value  may be threaded as the density of 'dark matter.'
may be threaded as the density of 'dark matter.'
Clearly, the solution satisfies the conditions  for r → 0 and for
for r → 0 and for  . The latter means that the effect of 'dark matter' is negligible near the center of the galaxy and far away from it. It should be noted that the very slight decrease of the mass density with distance for this model is generally unrealistic and can describe only a certain part of the real galaxy. A more realistic model is discussed in the next section. The velocity defining the rotational curve can be obtained from the third Newtonian law for a non-inertial system that is fixed to orbit:
. The latter means that the effect of 'dark matter' is negligible near the center of the galaxy and far away from it. It should be noted that the very slight decrease of the mass density with distance for this model is generally unrealistic and can describe only a certain part of the real galaxy. A more realistic model is discussed in the next section. The velocity defining the rotational curve can be obtained from the third Newtonian law for a non-inertial system that is fixed to orbit:

In other words, the centrifugal force is equal to the gravitational force. The real measurements were assumed to be the average over the angles of (19),
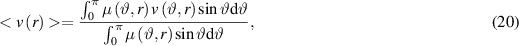
where  and
and  are defined by equations (16)–(18). The normalization condition for the mass density
are defined by equations (16)–(18). The normalization condition for the mass density  is:
is:
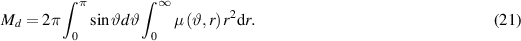
The calculation results are shown in (figure 1.) All calculations used the same  . The other parameters are listed in table 1. Dwarf galaxies NGC7537 and IC1029 are well described without a bulge (frames (b) and (c), solid lines). However, galaxies M31 and M101 should have an essential part of the mass distributed as a bulge. According to our model, the mass distribution should satisfy equation (16). To preserve the consistency of the theory, we can add only point mass Mb
at r = 0 (dashed line in figure 1(c)). The experimental data were obtained from [26, 27]. The dash-dotted lines correspond to the classical Newtonian potential. As noted, a more accurate theory must consider some mechanism of the breakdown of perfect symmetry. This is roughly equivalent to replacing o with some finite value. Thus, there will not be any restriction (16). This idea developed in a more detailed theory that considers disorder inside the system.
. The other parameters are listed in table 1. Dwarf galaxies NGC7537 and IC1029 are well described without a bulge (frames (b) and (c), solid lines). However, galaxies M31 and M101 should have an essential part of the mass distributed as a bulge. According to our model, the mass distribution should satisfy equation (16). To preserve the consistency of the theory, we can add only point mass Mb
at r = 0 (dashed line in figure 1(c)). The experimental data were obtained from [26, 27]. The dash-dotted lines correspond to the classical Newtonian potential. As noted, a more accurate theory must consider some mechanism of the breakdown of perfect symmetry. This is roughly equivalent to replacing o with some finite value. Thus, there will not be any restriction (16). This idea developed in a more detailed theory that considers disorder inside the system.
Figure 1. Rotational curves: theory vs experiment. Frames a, b, and c correspond to the galaxies NGC7537, IC1029, M31, and M101. The filled circles are the experimental data. The solid lines describe the theoretical results averaged over polar angle (see equations (19) and (20)). The dotted lines are theoretical results for certain polar angles (450, 600, 750, 900). The dash-dotted lines describe averaged rotational curves or the Newtonian classical potential.
Download figure:
Standard image High-resolution imageTable 1. The parameters used for the calculation.
| param. |

|

|

|
 (dis.) (dis.) |
 (s.) (s.) |
|---|---|---|---|---|---|

|

|

|

|

|

|

| 0 | 0 |

|

|

|

| 2.4 | 2 | 6 | 5.4 | 4.5 |

| — | — | — | 7.5 | 9 |

| — | — | — | 3 | 5.4 |

| — | — | — | 28.5 | 28.5 |
5. Disorder effect
In the previous section, we considered a classical system with ideal axial symmetry. Generally, this idealization is more appropriate for young galaxies because they have a large mass distributed more homogeneously as a gas. Young galaxies are flat, but old galaxies are more bulge-like. Thus, in old galaxies, we have two attributes compared to younger ones: (i) they are less homogeneous (considering mass distribution), and (ii) they are more bulge-like. These two attributes are interrelated. Inhomogeneity, which harms the axial symmetry, can lead to random moments of force. The average values of these moments are zero, but they change the behavior of the system owing to autocorrelation. This random moment of force can be described by the following equities [28]:
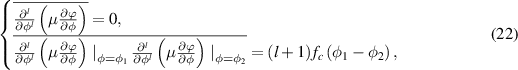
where  , the overline means averaging over the interstellar scale and fc
is the correlation function. The correlated orbital phase differences are summarized below. To ensure accuracy, we must omit terms where
, the overline means averaging over the interstellar scale and fc
is the correlation function. The correlated orbital phase differences are summarized below. To ensure accuracy, we must omit terms where  because they primarily correspond to stable structures, such as star systems or clusters. The remaining terms yield negative values in the correlation sum. This negative correlation can be explained by examining the orbit of a stable structure encountering excess mass. Prior to the closest approach, there was an increase in the moment of force, followed by a subsequent decrease. This leads to a negative correlation between the two orbit segments [29]:
because they primarily correspond to stable structures, such as star systems or clusters. The remaining terms yield negative values in the correlation sum. This negative correlation can be explained by examining the orbit of a stable structure encountering excess mass. Prior to the closest approach, there was an increase in the moment of force, followed by a subsequent decrease. This leads to a negative correlation between the two orbit segments [29]:

where parameter w can be interpreted as the characteristic energy of the interaction between inhomogeneities per unit volume. We perform the following steps to obtain the correct equation for the averaged gravitational potential over the interstellar scale: (i) consider the non-relativistic limit of equation (9), (ii) use the hypothesis about the random moment of force (22)–(23), (iii) compose the products of the left-hand and right-hand sides that give  , (iv) perform averaging over orbit phases and φ for the obtained equation, and finally (v) find
, (iv) perform averaging over orbit phases and φ for the obtained equation, and finally (v) find  from the averaged equation. The resulting equation for the averaged gravitational potential can be rewritten as (see appendix
from the averaged equation. The resulting equation for the averaged gravitational potential can be rewritten as (see appendix

where

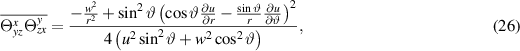
and

Restriction (16) to the mass distribution does not play any role. Therefore, the mass distribution can be an arbitrary function of r and ϑ. Similar to the previous section, the value  can be interpreted as the density of 'dark matter.' It is mostly positive (considering that
can be interpreted as the density of 'dark matter.' It is mostly positive (considering that  and
and  is small). To obtain (22)–(27) we neglected derivatives from
is small). To obtain (22)–(27) we neglected derivatives from  . However, based on its physical meaning, we conclude that
. However, based on its physical meaning, we conclude that  . Considering equation (26) for the surface
. Considering equation (26) for the surface  , we conclude that:
, we conclude that:

The last equality holds only for the surface, but we assume that it is performed in the entire space. From the sequence of equation (28), we will obtain (see appendix
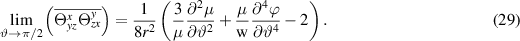
The equation (29) shows that 'dark matter' density could be positive on surface  only if the baryonic mass density has local minima on the surface. In the rest of the entire space, as in the previous section, the value of the 'dark matter' term mostly depends on the disc width of the galaxy. We use a simplified model for the galaxy's mass distribution with a bulge and disc. We minimize the intersection of bulge and disc and describe their cutoffs using the sigmoid function:
only if the baryonic mass density has local minima on the surface. In the rest of the entire space, as in the previous section, the value of the 'dark matter' term mostly depends on the disc width of the galaxy. We use a simplified model for the galaxy's mass distribution with a bulge and disc. We minimize the intersection of bulge and disc and describe their cutoffs using the sigmoid function:
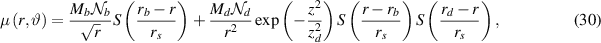
where  ,
,  are normalization constants,
are normalization constants,  are the radii of the bulge and disc,
are the radii of the bulge and disc,  are the corresponding masses and
are the corresponding masses and  is the sigmoid function with the smoothing parameter rs
. The results of the rotational curve calculations for galaxies M31 and M101 are shown in figures 1(c) and(d). The parameters for the calculation are listed in table 1, (columns 'M31(dis.)' and 'M101(dis.)'). A comparison of the 'dark matter' effect versus the baryonic mass effect can be made with the analysis of figures 2(a) and (b). As expected, the presence of dark matter inside the bulge is low. The negative values of the 'dark matter' density near the surface
is the sigmoid function with the smoothing parameter rs
. The results of the rotational curve calculations for galaxies M31 and M101 are shown in figures 1(c) and(d). The parameters for the calculation are listed in table 1, (columns 'M31(dis.)' and 'M101(dis.)'). A comparison of the 'dark matter' effect versus the baryonic mass effect can be made with the analysis of figures 2(a) and (b). As expected, the presence of dark matter inside the bulge is low. The negative values of the 'dark matter' density near the surface  are caused by the maximum values of the baryonic mass density here. Whereas 'dark matter' is substantial in regions of space where the baryonic mass intensively decreases along the galaxy's axis.
are caused by the maximum values of the baryonic mass density here. Whereas 'dark matter' is substantial in regions of space where the baryonic mass intensively decreases along the galaxy's axis.
Figure 2. The contour plots of the normalized 'dark matter' density: (a) for the galaxy M31, (b) for the galaxy M101 (see equations (24)–(29)). Normalization is performed on the baryonic total mass.
Download figure:
Standard image High-resolution image6. Conclusion
This study presents a modified theory of gravity within the framework of general relativity. Including torsion in the Minkowski space, which arises from an anisotropic mass distribution, offers a novel approach to address several cosmological puzzles. By extending the classical equations of general relativity by introducing torsion and modifying the stress-energy tensor equation, the model demonstrates promise in explaining phenomena such as the rotation curves of galaxies. The proposed model avoids the introduction of new fields and empirical constants and relies instead on fundamental principles. It provides a parameter-free framework that aligns with observational data and is consistent with the cosmological observations. The model's success in predicting the flat rotation curves and the baryonic Tully–Fisher relation represents significant progress in addressing the limitations of classical general relativity. Moreover, the ability of the model to account for the differences in the Tully–Fisher relations among various types of galaxies sets it apart from previous theories. This observation supports the idea that anisotropic mass distributions are crucial for understanding the galactic dynamics.
In particular, the theory describes well the experimental observations of rotation curves for dwarf, Sb, and Scd galaxies. It also correctly describes most of the observations on the correlation between the morphology and rotation curves. It should also be noted that the results described for long-barred galaxies do not fit into the overall picture [18], but could be explained by the competing influence of disorder. After all, as noted, the model described in section V is very simplified. The actual model should depend on the morphology of the particular galaxy.
Additional theoretical and experimental studies are required to validate the proposed model. Simulations based on hydrodynamic and thermodynamic equations are necessary to explore the model's behavior in various scenarios. On the other hand, some essential results of the classical general relativity such as gravitational lensing remain correct by default because the torsion effect is negligible for the mass high-density regime and chancels totally when a mass distribution is isotropic.
In summary, this study's modified theory of gravity offers a promising framework to address long-standing cosmological puzzles. The inclusion of torsion in the Minkowski space and modifications to the stress-energy tensor equation provide new avenues for understanding the behavior of galaxies. Further theoretical development, computational simulations, and experimental tests are crucial for evaluating the model's full potential and implications for understanding the Universe.
We formulated the main conclusions that can be relied upon when assessing the correctness of the model. The effect of dark matter should not appear in spherically symmetric systems with isotropic mass distribution. There are significant restrictions on the mass distribution in space for axially symmetric systems, which can be eliminated only by considering internal disorder. In axially symmetric systems, the role of dark matter is greater, the flatter the disk. The effect of the disorder can cause a negative value of 'dark matter' density near the regions where the baryonic mass density is maximal. The latter result can be a key to the solution of the 'dark energy' problem and Universe expansion.
Data availability statement
All data that support the findings of this study are included within the article (and any supplementary files).
Appendix A:
Below, we use indexes x, y, and z instead of 1, 2 and 3 which is more intuitive in the non-relativistic limit. The classical form for the equations (9) can be written as follows:

where  . Making products for each two equations from (A.1) and perform averaging one obtains:
. Making products for each two equations from (A.1) and perform averaging one obtains:
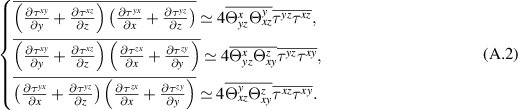
Next, we move to spherical coordinates and assume that all terms containing derivatives with respect to azimuthal angle disappear during averaging. We leave only terms  and
and  . The results of the calculations, taking into account these assumptions, look like this:
. The results of the calculations, taking into account these assumptions, look like this:
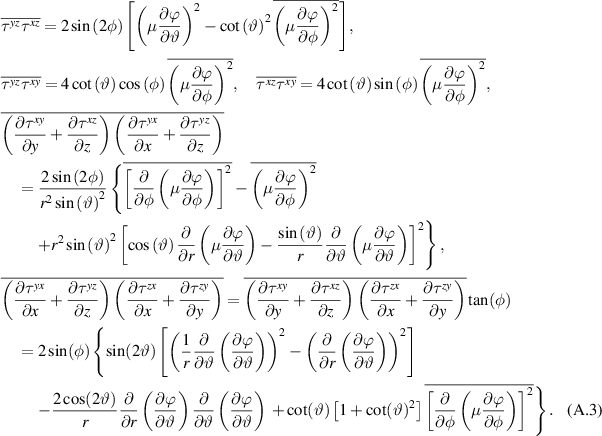
Taking into account (22) and (23) and the property  one can obtain (25)–(27).
one can obtain (25)–(27).
Appendix B:
If we assume that the potential is mirror symmetric with respect to the yx-plane, then this means that it has an extremum on this plane. This causes the denominator of (26) to be zero on this plane. To eliminate the singularity, we suppose:
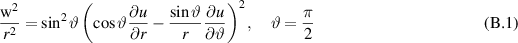
taking into account that  on the xy-plane we arrive to the equality (28). Another consequence of the mirror symmetry of the problem is the absence of odd powers in the expansion of the mass and potential into the Taylor series:
on the xy-plane we arrive to the equality (28). Another consequence of the mirror symmetry of the problem is the absence of odd powers in the expansion of the mass and potential into the Taylor series:
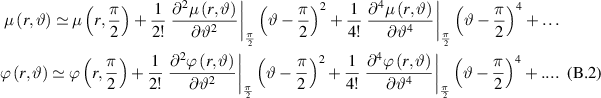
Next, using (B.2), (28) and twice applying the L'Hopital's rule:
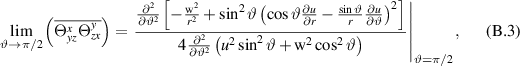
one can obtain the equality (29).


