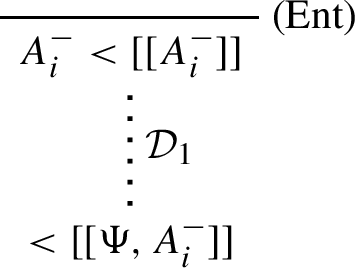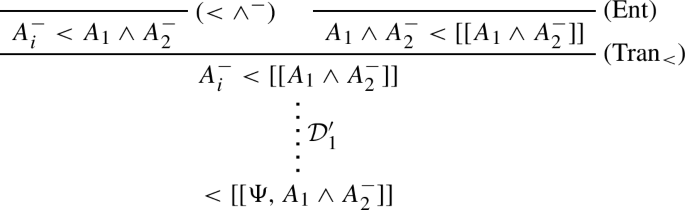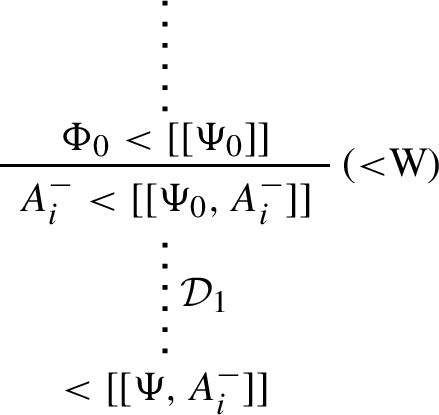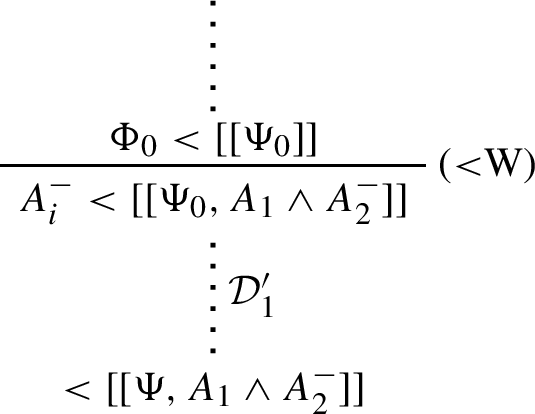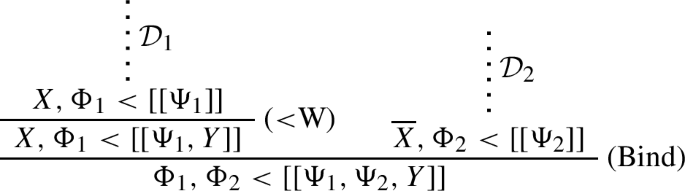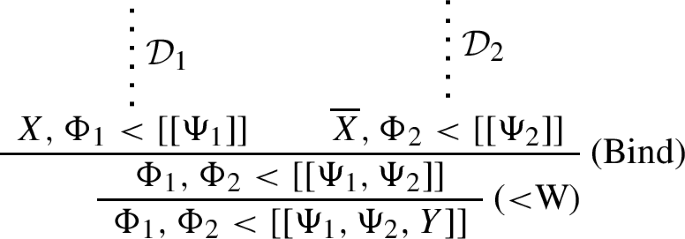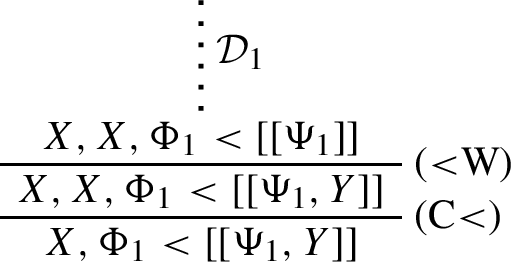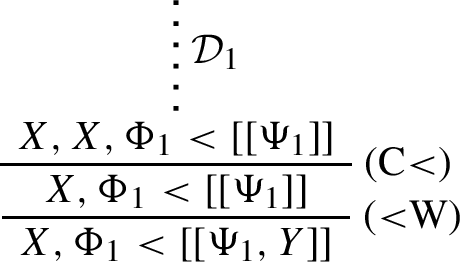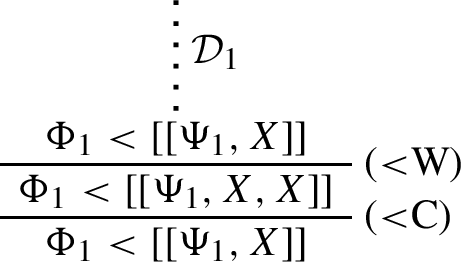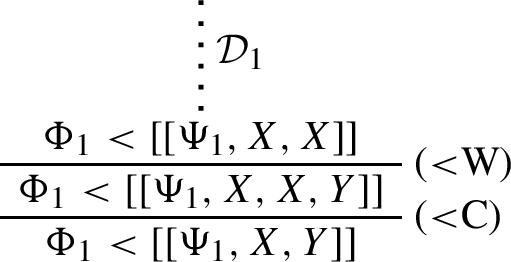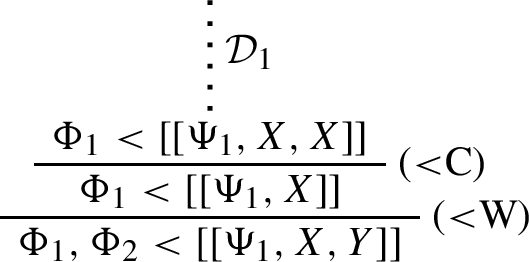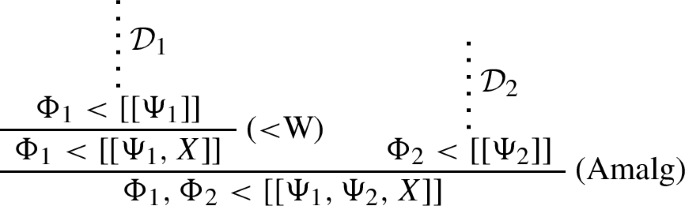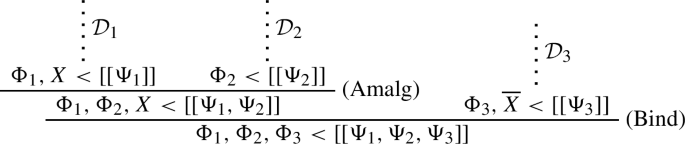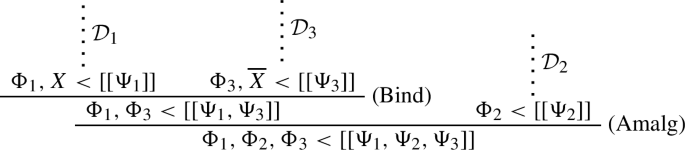Abstract
According to an intuitive picture of relevant entailment, an entailment is relevant if all the formulas it contains contribute to its validity. In this paper, we provide a ground-theoretic analysis of this notion of contribution, and as a result of relevant entailment. We build a system of bilateral logical grounding within which we can derive classical entailment and analyze the contribution of premises and conclusions, in terms of a certain type of connection between their respective logical grounds. The resulting framework is shown to have a strong unifying and explanatory power by bringing together the notions of grounding and relevance and explaining the commonalities and differences between alternative contribution-based accounts of relevance.
Similar content being viewed by others
Notes
The first one is vacuously truth-preserving because the two premises cannot be true together. But it is truth-preserving nonetheless.
See for example Poggiolesi (2020) for a recent attempt to account for the logical grounding of relevant implication.
Sequent elements are individuated by their specific role of premise or conclusion within a sequent. If we say that A and B are the same sequent element, we mean that A and B are the same formula occurring as a premise or the same formula occurring as a conclusion. If the same formula occurs both as a premise and as a conclusion, its premise-occurrence does not count as the same sequent element as its conclusion-occurrence.
The notation for the various sequent formats is borrowed from (Humberstone, 2011, Sect. 1.21).
Informally speaking, a multiset is just like a set except that the same element may occur in it several times. A formal definition of multisets, relations and operations on multisets is given in Sect. A.1 of the technical appendix
By the monotonicity of truth-preservation, we refer to the well-known property that if
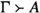 preserves truth, then
preserves truth, then
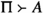 also preserves truth for all
\(\Pi \supseteq \Gamma \).
also preserves truth for all
\(\Pi \supseteq \Gamma \).This point has been made by Brauer (2020, p. 342).
This notion of difference-making is structurally similar to a notion of difference-making for grounding defined by Krämer and Roski (2017).
The definition of perfect validity was first introduced by Tennant (1984) in the context of Set–Set sequents.
What we introduce below as a definition of relevanceB is presented by Brauer only as a property that is provably equivalent to “relevance” as he defines it (Brauer, 2020, p. 445). That property being somewhat simpler to state, we decided to adopt it as our official definition.
By substitution here we understand homomorphic substitution, i.e. the substitution of formulas for propositional variables. Insofar as classical validity is closed under homomorphic substitution, it is reasonable to assume the division of the logical labor directed towards validity to be so closed. We do not commit here to the debated view whether logical form in general is closed under homomorphic substitution (see Schurz (2001) for a discussion). In logics such as Carnap’s modal logic where validity is closed under isomorphic substitution only (i.e., of propositional variables for propositional variables), the division of logical labor should be similarly closed under isomorphic substitution only. If one wishes to identify the class of relevant modal entailments, taking Carnap’s modal logic as the standard, this would indeed be the right thing to do. We thank an anonymous reviewer for pressing this point.
Those relevance theorists who deny that relevant entailment in general is closed under homomorphic substitution will leave the boat here and say that this notion of relevance overgenerates (Brauer, 2020; Schurz, 1991, 1999). Note however that our goal here is not to identify the one true notion of relevance, but to draw a coherent map of the space of possible contribution-based accounts.
For the skeptical or curious reader, we can give the following example due to Tony Dale. The sequent
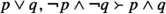 is neither perfectly valid nor a substitution instance of a perfectly valid sequent in Mset–Mset format. But it is, after contraction, a substitution instance of
is neither perfectly valid nor a substitution instance of a perfectly valid sequent in Mset–Mset format. But it is, after contraction, a substitution instance of
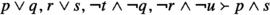 which is perfectly valid. See Tennant (1984, p. 199) for a discussion of this example.
which is perfectly valid. See Tennant (1984, p. 199) for a discussion of this example.It is briefly considered, and rejected, by Brauer (2020, p. 450). Brauer does not see why the class of relevant entailments in general should be closed under substitution, hence his coherent rejection of both relevanceT and relevanceBT.
In a different context, Nils Kurbis has explored and defended a form of bilateralism in proof-theoretic semantics that also takes falsity as primitive, on a par with truth. See Kürbis (2019).
The adoption of a non-factive notion of ground for technical reasons has become standard in the literature. See e.g. Correia (2013, p.36).
This informal characterization is to be taken with a grain of salt. It holds strictly speaking only for “gaunt” derivable grounding sequents, (i.e. grounding sequents that cannot be obtained by uniform substitution from other \(\textsf{GK}\)-derivable grounding sequents, except by substituting propositional variables for propositional variables). For example, fixing the truth of both p and q is sufficient, and required, to fix the truth of \(p \wedge q\). But such a simple characterization fails for other instances of ( \(<\wedge ^+\)) such as \(p^+, \lnot p^+ < p \wedge \lnot p\) or \(p \vee \lnot p^+, q \vee \lnot q^+ < (p \vee \lnot p) \wedge (q \vee \lnot q\)). Furthermore, this minimal determination semantics would work primarily for non-strict grounding, for, trivially, the truth-value of p minimally determines the truth-value of p. Then the strict notion would have to be defined in terms of the non-strict notion. For these reasons, a minimal truth-functional determination semantics for \(\textsf{GK}\) along the lines given above needs to be carefully worked out to take such complications into account. In the interest of space, we leave that work for another occasion.
For the classicists with inferentialist proclivities, we provide an alternative inferentialist interpretation of both logical ground an entailment in Sect. E of the Appendix.
We however thank an anonymous reviewer for raising this issue in these terms.
This might seem like a wrong result from the standpoint of Relevance Logicians who abhor Disjunctive Syllogism. However, the simple instance of Disjunctive Syllogism given as an example is a perfect entailment and will be relevant according to all the accounts considered in Sect. 2. So far, so good.
We use the derivable rule (EntR)—instead of the (Ent) axiom followed by an application of (Tran<) —in order to shorten the derivation. The resulting derivation is strictly speaking not analytic but may be understood as an abbreviation of the longer analytic derivation using (Ent) and (Tran<). The criterion of contribution spelled out in Definition 11 is meant to apply to the latter.
Schurz (1999, p. 15) introduced a similar distinction between weakly proof-based and strongly proof-based relevance in his insightful study of proof-theoretic criteria of relevance.
See, e.g., Negri et al. (2001, p. 58).
See Tennant (1984) for an earlier Set–Set sequent calculus that is proved adequate for perfectible validity.
We use “explanatory reasoning” here as an umbrella term covering both Litland’s explanatory arguments and explanatory rejections. From our standpoint, Litland’s explanatory arguments are explanatory reasonings from acceptances to acceptances, and explanatory rejections are explanatory reasonings from acceptances to rejections.
Funding for this research was provided by an FNRS Belgium WIP grant with identifier PGY F.4540.20. All authors contributed equally to the ideas expressed in the paper. The order of the authors reflects their involvement in the writing process. We thank João Daniel Dantas who greatly contributed to many brainstorming sessions about these ideas. We are also indebted to the audiences of many workshops and conferences in Hamburg, Louvain-la-Neuve, Berlin, Campinas, Leuven, Pamplona, Salamanca, Bochum, and Paris, where we presented preliminary versions of the results in this paper. Our final words are for the two anonymous reviewers who had the patience to carefully examine previous versions of this paper and provided many insightful comments that lead to enormous improvements
References
Anderson, A. R., & Belnap, N. D. (1975). Entailment: The logic of relevance and neccessity (Vol. I). Princeton University Press.
Brauer, E. (2020). Relevance for the classical logician. Review of Symbolic Logic, 13(2), 436–457. https://doi.org/10.1017/s1755020318000382
Burgess, J. P. (2009). Philosophical logic. Princeton University Press.
Correia, F. (2013). Logical grounds. Review of Symbolic Logic, 7(1), 1–29. https://doi.org/10.1017/s1755020313000300
Fine, K. (2012). Guide to ground. In Correia, F., & Schnieder, B. (Eds.) Metaphysical grounding (pp. 37–80). Cambridge University Press.
Gärdenfors, P. (1976). Relevance and redundancy in deductive explanations. Philosophy of Science, 43(3), 420–431. https://doi.org/10.1086/288697
Gentzen, G. (1969). Investigations into logical deduction. In M. E. Szabo (Ed.), The collected papers of Gerhard Gentzen (pp. 68–131). Amsterdam: North-Holland Pub. Co.
Humberstone, L. (2011). The Connectives. MIT Press.
Krämer, S., & Roski, S. (2017). Difference-making grounds. Philosophical Studies, 174(5), 1191–1215. https://doi.org/10.1007/s11098-016-0749-5
Kürbis, N. (2019). Proof and falsity: A logical investigation. Cambridge University Press.
Litland, J. E. (2023). Ground first: Against the proof-theoretic definition of ground. Synthese, 201(1), 1–26. https://doi.org/10.1007/s11229-022-04028-8
Moore, G. E. (1920). Iii.—External and internal relations. Proceedings of the Aristotelian Society, 20(1), 40–62. https://doi.org/10.1093/aristotelian/20.1.40
Negri, S., von Plato, J., & Ranta, A. (2001). Structural Proof Theory. Cambridge University Press.
Poggiolesi, F. (2020). Grounding principles for (relevant) implication. Synthese, 198(8), 7351–7376. https://doi.org/10.1007/s11229-019-02523-z
Read, S. (1988). Relevant logic: A philosophical examination of inference. Wiley-Blackwell.
Restall, G. (2005). Multiple conclusions. In Hájek, P., Valdés-Villanueva, L., Westerståhl, D. (Eds.) Logic, methodology and philosophy of science. College Publications.
Ripley, D. (2017). Bilateralism, coherence, warrant. In F. Moltmann & M. Textor (Eds.), Act-based conceptions of propositional content (pp. 307–324). Oxford University Press.
Schnieder, B. (2011). A logic for ‘because’. Review of Symbolic Logic, 4(3), 445–465. https://doi.org/10.1017/s1755020311000104
Schnieder, B. (2018). On ground and consequence. Synthese, 198(Suppl 6), 1335–1363. https://doi.org/10.1007/s11229-018-02012-9
Schurz, G. (1991). Relevant deduction. Erkenntnis, 35(1–3), 391–437. https://doi.org/10.1007/BF00388295
Schurz, G. (1999). Relevance in deductive reasoning: A critical overview. In G. Schurz & M. Ursic (Eds.), Beyond Classical Logic (pp. 9–56). Academia Verlag.
Schurz, G. (2001). Carnap’s modal logic. In W. Stelzner & M. Stockler (Eds.), Zwischen traditioneller und moderner Logik (pp. 365–380). Brill.
Smiley, T. J. (1959). Entailment and deducibility. Proceedings of the Aristotelian Society, 59, 233–254. https://doi.org/10.1093/aristotelian/59.1.233
Tennant, N. (1979). Xi-entailment and proofs. Proceedings of the Aristotelian Society, 79(1), 167–190. https://doi.org/10.1093/aristotelian/79.1.167
Tennant, N. (1984). Perfect validity, entailment and paraconsistency. Studia Logica, 43(1–2), 181–200. https://doi.org/10.1007/BF00935749
Verdée, P., Bal, I.D., & Samonek, A. (2019). A non-transitive relevant implication corresponding to classical logic consequence. Australasian Journal of Logic, 16(2), 10–40.https://doi.org/10.26686/ajl.v16i2.5273
Weingartner, P. (1985). A simple relevance-criterion for natural language and its semantics, In Dorn, G., Weingarten, P. (Eds.) Foundations of Logic and Linguistics. Problems and Solutions (pp. 563–575). Plenum.
Weingartner, P., & Schurz, G. (1986). Paradoxes solved by simple relevance criteria. Logique Et Analyse, 29(113), 3–40.
Yablo, S. (2014). Aboutness. Oxford: Princeton University Press.
Yablo, S. (2020). Relevance without minimality. https://www.syablo.com/uploads/1/0/1/0/101008698/relevance_without_minimality__rev_3-20_.docx.pdf.pdf.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix
We provide in this appendix the proofs for all the Propositions and Theorems announced in the main text. When necessary, we include Definitions and prove Lemmas not mentioned in the text.
Preliminaries
1.1 Multisets
Multisets are collections of objects in which repetitions matter, even though order does not.
Definition 15
(Multiset) A multiset over a set X is a pair \(\langle X, \lambda \rangle \), where \(\lambda : X \mapsto \mathbb {N}\) assigns a number of copies to each member of X.
We shall use double braces to describe multisets extensionally. The string “ \(\{\hspace{-2.77771pt}\{a,a,b \}\hspace{-2.77771pt}\}\)” describes the multiset \({\textbf {X}}=\langle X,\lambda _X\rangle \) such that \(\lambda _X(a)=2\), \(\lambda _X(b)=1\), and \(\lambda (x)=0\) for all member x of X distinct both from a and b.
We shall use a number of relations and operations on multisets.
Definition 16
(Multiset membership, inclusion, addition, difference)
When \({\textbf {X}}=\langle X,\lambda _X \rangle \) and \({\textbf {Y}}=\langle Y, \lambda _Y \rangle \):
-
\(x \in {\textbf {X}}\) if \(\lambda _X(x) \ge 1\) (membership)
-
\({\textbf {X}} \subseteq {\textbf {Y}}\) if \(X \subseteq Y\) and for all \(x \in X\), \(\lambda _X(x) \le \lambda _Y(x)\) (inclusion)
-
\({\textbf {X}} + {\textbf {Y}}=\langle X \cup Y, \lambda _{X+Y} \rangle \), where for all \(x \in X \cup Y\), \(\lambda _{X+Y}(x)=\lambda _X(x)+\lambda _Y(x)\) (addition)
-
\({\textbf {X}} - {\textbf {Y}}=\langle X \cup Y, \lambda _{X-Y} \rangle \), where for all \(x \in X \cup Y\), \(\lambda _{X-Y}(x)=\lambda _X(x)-\lambda _Y(x)\) if \(\lambda _X(x) \ge \lambda _Y(x)\), otherwise \(\lambda _{X-Y}(x)=0\) (difference)
1.2 Syntax
Definition 17
( \(\mathcal {L}\)-formula) Given a set of propositional variables \(\mathcal {V}\), the set \(\mathcal {L}\) of \(\mathcal {L}\)-formulas is defined by the following grammar:
Since we shall not work with any other language, \(\mathcal {L}\)-formulas will simply be called “formulas” hereafter.
We shall use the usual conventions for removing parentheses when no ambiguity results. For instance, we shall write “ \(\lnot \lnot p \supset p\)” instead of “ \(((\lnot (\lnot p)) \supset p)\)”.
We shall use upper Greek letters, e.g., \(\Gamma , \Delta , \Pi , \Sigma , \dots \) as meta-variables for multisets of formulas and upper case Roman letters, e.g., \(A, B, C, \dots \), as metavariables for formulas.
Definition 18
(Sequent) When
\(\Gamma \) and
\(\Delta \) are multisets of formulas, the string “
 ” is called a sequent.
” is called a sequent.
We shall use commas for multiset-theoretic addition and have formulas stand for their own singleton multisets. Thus, “
 ” stands for “
” stands for “
 ”.
”.
Definition 19
(Substitution map) A substitution map on \(\mathcal {L}\) is a map \(\sigma : \mathcal {V} \mapsto \mathcal {L}\) that assigns formulas to propositional variables.
Definition 20
( \(\sigma \)-instance) Given a formula A, and an substitution map \(\sigma \), the \(\sigma \)-substitution \(A^\sigma \) is defined recursively as follows:
-
1.
if \(A \in \mathcal {V}\), then \(A^\sigma =\sigma (A)\),
-
2.
if \(A=\lnot B\), then \(A^\sigma =\lnot B^\sigma \),
-
3.
if \(A= B \circ C\), then \(A^\sigma =B^\sigma \circ C^\sigma \), for all \(\circ \in \{ \wedge , \vee , \supset \}\).
We shall also use the following handy abbreviation, when \(\Gamma =\{\hspace{-2.77771pt}\{A_1, \dots , A_n \}\hspace{-2.77771pt}\}\):
Definition 21
(Substitution instance)
-
A sequent
 is a
\(\sigma \)-substitution instance of
is a
\(\sigma \)-substitution instance of
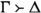 if
\(\Pi =\Gamma ^\sigma \) and
\(\Sigma =\Delta ^\sigma \).
if
\(\Pi =\Gamma ^\sigma \) and
\(\Sigma =\Delta ^\sigma \). -
A sequent
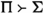 is a substitution instance of
is a substitution instance of
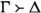 if it is a
\(\sigma \)-substitution instance of
if it is a
\(\sigma \)-substitution instance of
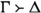 , for some substitution map
\(\sigma \).
, for some substitution map
\(\sigma \).
Classical relevance
We shall not rehearse here the standard definition of classical validity for classical propositional logic.Footnote 28
1.1 Classical logic
We shall take the Mset–Mset sequent calculus \(\textsf{LK}\) (see Table 4) as our official proof-theoretic presentation of Classical Propositional Logic.
1.2 Perfect validity
Proposition B.1
A sequent
 is perfectly valid iff it is valid and all its premises and conclusions make a difference to the validity of
is perfectly valid iff it is valid and all its premises and conclusions make a difference to the validity of
 .
.
Proof
(left-to-right) Immediate. (right-to-left) Let
 be any proper subsequent of
be any proper subsequent of
 and let A be some sequent element in
\(\Gamma + \Delta \) but not in
\(\Pi + \Sigma \). We only deal with the case where A is a premise, the case where A is a conclusion being symmetrical. By assumption,
and let A be some sequent element in
\(\Gamma + \Delta \) but not in
\(\Pi + \Sigma \). We only deal with the case where A is a premise, the case where A is a conclusion being symmetrical. By assumption,
 is invalid. By the monotonicity of classical validity,
is invalid. By the monotonicity of classical validity,
 is also invalid. We conclude that every proper subsequent of
is also invalid. We conclude that every proper subsequent of
 is invalid and thus that
is invalid and thus that
 is perfectly valid.
\(\square \)
is perfectly valid.
\(\square \)
1.3 Perfectible validity
We shall make use of the system \(\textsf{LK}^\text {r}\) as our official proof-theoretic presentation of the notion of perfectible validity in Mset–Mset format (see Table 5). This system is taken from Verdée et al. (2019) where it is named NTR.Footnote 29
Theorem B.1
 is
\(\textsf{LK}^\text {r}\)-derivable iff it is perfectibly valid.
is
\(\textsf{LK}^\text {r}\)-derivable iff it is perfectibly valid.
Proof
See Theorems 1 and 2 of Verdée et al. (2019).
There is a close connection between
\(\textsf{LK}^\text {r}\) and
\(\textsf{LK}\). It can be shown that one recovers the full power of
\(\textsf{LK}\) simply by adding the structural rules of Weakening (W
 ) and (
) and (
 W) to
\(\textsf{LK}^\text {r}\). Let us call
\(\textsf{LK}^*\) the resulting sequent calculus.
W) to
\(\textsf{LK}^\text {r}\). Let us call
\(\textsf{LK}^*\) the resulting sequent calculus.
Proposition B.2
 is
\(\textsf{LK}^*\)-derivable iff it is
\(\textsf{LK}\)-derivable.
is
\(\textsf{LK}^*\)-derivable iff it is
\(\textsf{LK}\)-derivable.
Proof
(left-to-right) It is enough to show that (
 ), (
), (
 ), (
), (
 ) and (
) and (
 ) are derivable in
\(\textsf{LK}\). In all cases, the derivability is easily obtained by appropriately weakening the input sequents in order to apply the corresponding unstarred rule. We illustrate the procedure with (
) are derivable in
\(\textsf{LK}\). In all cases, the derivability is easily obtained by appropriately weakening the input sequents in order to apply the corresponding unstarred rule. We illustrate the procedure with (
 ), leaving the three remaining cases to the reader:
), leaving the three remaining cases to the reader:

(right-to-left) In light of the well-known eliminability of (Cut) in
\(\textsf{LK}\) (Gentzen, 1969), it is enough to show that (
 ), (
), (
 ), and (
), and (
 ) are derivable in
\(\textsf{LK}^*\). In the first two cases, the rule is easily derived by applying the corresponding starred rule, followed by appropriate contraction steps, as illustrated by the (
) are derivable in
\(\textsf{LK}^*\). In the first two cases, the rule is easily derived by applying the corresponding starred rule, followed by appropriate contraction steps, as illustrated by the (
 ) case, leaving the symmetrical derivation of (
) case, leaving the symmetrical derivation of (
 ) to the reader:
) to the reader:

The derivability of (
 ) is only slightly more complex:
) is only slightly more complex:

\(\square \)
1.4 RelevanceB
Proposition B.3
If
 is relevantB and
is relevantB and
 is relevantB, then
is relevantB, then
 is relevantB.
is relevantB.
Proof
See Proposition 3.2 in (Brauer, 2020, p.446). \(\square \)
Proposition B.4
The set of relevantB sequents is the smallest set comprising the set of relevantDM sequents and closed under (Amalgamation), (C
 ) and (
) and (
 C).
C).
Proof
(
\(\subseteq \)) That all relevantDM sequents are relevantB is immediate from the definitions. The closure of relevanceB under (Amalgamation) follows from Proposition B.3. Contracting a relevantB
 sequent preserves, for all
\(A \in \Gamma + \Delta \), the existence of a perfect subsequent
\(\Pi \Rightarrow \Sigma \) of
\(\Gamma + \Delta \) such that
\(A \in \Pi + \Delta \). (
\(\supseteq \)) Suppose that
sequent preserves, for all
\(A \in \Gamma + \Delta \), the existence of a perfect subsequent
\(\Pi \Rightarrow \Sigma \) of
\(\Gamma + \Delta \) such that
\(A \in \Pi + \Delta \). (
\(\supseteq \)) Suppose that
 is relevantB. For all
\(A \in \Gamma + \Delta \), let
is relevantB. For all
\(A \in \Gamma + \Delta \), let
 be a perfectly valid subsequent of
be a perfectly valid subsequent of
 such that
\(A \in \Pi _A + \Sigma _A\). Let
\(\Phi \) be the set of all sequents
such that
\(A \in \Pi _A + \Sigma _A\). Let
\(\Phi \) be the set of all sequents
 such that
\(A \in \Gamma + \Delta \). One then recovers
such that
\(A \in \Gamma + \Delta \). One then recovers
 by Amalgamating two by two the members of
\(\Phi \) and contracting the supernumerary copies of formulas. So
by Amalgamating two by two the members of
\(\Phi \) and contracting the supernumerary copies of formulas. So
 is part of the smallest set comprising the set of relevantDM sequents and closed under (Amalgamation), (C
is part of the smallest set comprising the set of relevantDM sequents and closed under (Amalgamation), (C
 ) and (
) and (
 C).
\(\square \)
C).
\(\square \)
1.5 RelevanceBT
Proposition B.5
 is relevantBT iff for all
\(A \in \Gamma + \Delta \), there is a perfectibly valid subsequent
is relevantBT iff for all
\(A \in \Gamma + \Delta \), there is a perfectibly valid subsequent
 of
of
 such that
\(A \in \Pi + \Sigma \).
such that
\(A \in \Pi + \Sigma \).
Proof
(left-to-right) By assumption,
 is relevantBT. Then
is relevantBT. Then
 has a relevantB abstraction
has a relevantB abstraction
 . Let
\(\sigma \) be the corresponding substitution map, and let
\(A \in \Gamma + \Delta \). Then
\(A=\sigma (B)\) for some
\(B \in \Pi + \Sigma \). By the definition of relevanceB, there is a perfectly valid subsequent
. Let
\(\sigma \) be the corresponding substitution map, and let
\(A \in \Gamma + \Delta \). Then
\(A=\sigma (B)\) for some
\(B \in \Pi + \Sigma \). By the definition of relevanceB, there is a perfectly valid subsequent
 of
of
 such that
\(B \in \Pi ' + \Sigma '\). Then from
such that
\(B \in \Pi ' + \Sigma '\). Then from
 , after appropriate Contraction steps, one gets a perfectibly valid subsequent of
, after appropriate Contraction steps, one gets a perfectibly valid subsequent of
 and
\(\sigma (B)=A \in \Pi + \Sigma \). (right-to-left) For each
\(A \in \Gamma +\Delta \), let
and
\(\sigma (B)=A \in \Pi + \Sigma \). (right-to-left) For each
\(A \in \Gamma +\Delta \), let
 be any perfectibly valid subsequent of
be any perfectibly valid subsequent of
 . By the definition of perfectibility, there is a perfectly valid sequent
. By the definition of perfectibility, there is a perfectly valid sequent
 such that
such that
 can be obtained from
can be obtained from
 , possibly after some Contraction steps, for some substitution map
\(\sigma _{A}\). Let
, possibly after some Contraction steps, for some substitution map
\(\sigma _{A}\). Let
 . We will use these perfectly valid sequents to construct a relevantB abstraction of
. We will use these perfectly valid sequents to construct a relevantB abstraction of
 . To do so, we reletter the members of
\(\Phi \) in such a way that distinct propositional variables are replaced with distinct propositional variables, and no two members of the resulting set of perfect sequents
\(\Psi \) share a propositional variable. By so doing, we have defined for each
\(A \in \Gamma + \Delta \) an injective substitution map
\(\tau _{A}\) from
\(\mathcal {V}\) to
\(\mathcal {V}\), such that
. To do so, we reletter the members of
\(\Phi \) in such a way that distinct propositional variables are replaced with distinct propositional variables, and no two members of the resulting set of perfect sequents
\(\Psi \) share a propositional variable. By so doing, we have defined for each
\(A \in \Gamma + \Delta \) an injective substitution map
\(\tau _{A}\) from
\(\mathcal {V}\) to
\(\mathcal {V}\), such that
 . Thus the inverse map
\(\tau _{A}^{-1}\) exists and is also a substitution map, for all A. We define the substitution map
\(\sigma \) as follows:
. Thus the inverse map
\(\tau _{A}^{-1}\) exists and is also a substitution map, for all A. We define the substitution map
\(\sigma \) as follows:

Let
\(\Theta _{A}=\Pi ^{\tau _{A}}_{A}\) and
\(\Omega _{A}=\Sigma ^{\tau _{A}}_{A}\). Now, for all A,
 is obtained by the uniform substitution of variables to variables from the perfectly valid
is obtained by the uniform substitution of variables to variables from the perfectly valid
 . Therefore,
. Therefore,
 is also perfectly valid. Let
is also perfectly valid. Let
 be the result of Amalgamating all the
be the result of Amalgamating all the
 such that
\(A \in \Gamma + \Delta \). By Proposition B.3,
such that
\(A \in \Gamma + \Delta \). By Proposition B.3,
 is relevantB. By the construction of
\(\sigma \), suitable contractions of
is relevantB. By the construction of
\(\sigma \), suitable contractions of
 give us back
give us back
 . Thus
. Thus
 is a relevantB abstraction of
is a relevantB abstraction of
 , which makes the latter relevantBT.
\(\square \)
, which makes the latter relevantBT.
\(\square \)
Ground and entailment
In this section, we prove the results connecting the notions of logical grounding with the notion of entailment. We adopt a synthetic approach here and prove the strongest and most general results available. As a result, the results announced in the body of the paper often come out as corollaries of the stronger results we prove here.
We have in total five systems for reasoning about non-strict mediate full logical ground, represented by order of strength in Fig. 1:
The system \(\textsf{GK}\), described in Table 2, contains the grounding axioms for the connectives and the principles of Reflexivity (Irr \(_<\)) and Transitivity (Tran \(_<\)). The other systems can be obtained as follows:
-
\(\textsf{GLK}^\text {r}\)= \(\textsf{GK}\) + (Bind) + (C<) + (<C)
-
\(\textsf{GLK}\)= \(\textsf{GLK}^\text {r}\) + (<W)
-
\(\textsf{GLK}^\text {ra}\)= \(\textsf{GLK}^\text {r}\) + (Amalg)
-
\(\textsf{GLK}^\text {a}\)= \(\textsf{GLK}\) + (Amalg)
Proposition C.1
\(\Phi < X\) is \(\textsf{GLK}\)-derivable iff it is \(\textsf{GLK}^\text {a}\)-derivable.
Proof
(left-to-right) Immediate. (right-to-left) The Amalgamation rule is derivable in \(\textsf{GLK}\) by (<W). \(\square \)
Definition 22
\(X=A^x\) is an absolute subformula of \(Y=B^y\) if A is a subformula of B.
Definition 23
A \(\textsf{GLK}^\text {a}\)-derivation has the absolute-subformula property if each formula occurring in the derivation is an absolute subformula of some signed formula occurring as a groundee at the root of the derivation tree.
Proposition C.2
All \(\textsf{GLK}^\text {ra}\)-derivations have the absolute-subformula property.
Proof
An easy induction on the length of \(\textsf{GLK}^\text {ra}\)-derivations. \(\square \)
The following abbreviations will prove handy. If \(\Gamma = \{\hspace{-2.77771pt}\{A_1, \dots , A_n \}\hspace{-2.77771pt}\}\), then:
-
\(\Gamma ^+ = \{\hspace{-2.77771pt}\{A_1^+, \dots , A_n^+ \}\hspace{-2.77771pt}\}\)
-
\(\Gamma ^- = \{\hspace{-2.77771pt}\{A_1^-, \dots , A_n^- \}\hspace{-2.77771pt}\}\).
We define the translation function \(\tau \) taking a grounding sequent into an ordinary sequent as follows:
-
1.
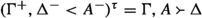 .
. -
2.
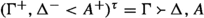 .
. -
3.
\({(\Gamma ^+, \Delta ^- < [[\Pi ^-, \Sigma ^+]])^\tau =}\)
 .
.
Lemma C.1
If \(\Psi < X\) is derivable in \(\textsf{GLK}\), then \((\Psi < X)^\tau \) is valid.
Proof
By induction on the length of a \(\textsf{GLK}\)-derivation of \(\Psi < X\). (Ent)-instances translate into (Id) instances. It is easily seen that translations of impure grounding axioms are derivable by applying the corresponding operational rule of \(\textsf{LK}^*\) to appropriate instances of the (Id) axiom. We only give the derivation for the conjunction axioms as an illustration and leave the remaining cases to the reader. For axiom ( \(< \wedge ^-_{i}\)), i.e., \(A_i^- < A_1 \wedge A_2^-\), with \(i \in \{1,2\}\), the corresponding \(\textsf{LK}^*\)-derivation is:

For axiom ( \(<\wedge ^+)\), i.e. \(A^+, B^+ < A \wedge B^+\), the corresponding \(\textsf{LK}^*\)-derivation is:

The next step is to show that the property is preserved by all rules of \(\textsf{GLK}\). It is obviously the case for the (<W), (C<), (<C) rules, in virtue of the corresponding structural rules of \(\textsf{LK}^*\). The property is similarly preserved by (Tran<) in virtue of the admissibility of the (Cut) rule in \(\textsf{LK}^*\). (Bind) preserves the property also in virtue of the admissibility of (Cut) in \(\textsf{LK}^*\). Finally, (Amalg) preserves the property in virtue of the structural rules of Weakening in \(\textsf{LK}^*\). \(\square \)
The proof also establishes the following:
Corollary C.1
If \(\Phi < X\) is derivable in \(\textsf{GLK}^\text {r}\), then \((\Phi < X)^\tau \) is derivable in \(\textsf{LK}^\text {r}\).
Lemma C.2
If
 is derivable in
\(\textsf{LK}^*\), then
\({< [[\Gamma ^-, \Delta ^+]]}\) is derivable in
\(\textsf{GLK}\).
is derivable in
\(\textsf{LK}^*\), then
\({< [[\Gamma ^-, \Delta ^+]]}\) is derivable in
\(\textsf{GLK}\).
Proof
By induction on the length of a derivation
\(\mathcal {D}\) of
 in
\(\textsf{LK}^*\). The property holds if
\(\mathcal {D}\) reduces to an instance of the (Id) axiom:
in
\(\textsf{LK}^*\). The property holds if
\(\mathcal {D}\) reduces to an instance of the (Id) axiom:

To show that each rule of
\(\textsf{LK}^*\) preserves the property, it suffices to show how to simulate within
\(\textsf{GLK}\) each rule of
\(\textsf{LK}^*\). This is trivial for the structural rules of Weakening and Contraction. To simulate the operational rules, we need to insert the corresponding grounding axiom and an application of (Tran
\(_<\)) when the e-term corresponding to the active formula is first introduced by the (Ent) axiom or an application of (<W). We give a detailed treatment of the introduction of conjunction to the left (
 ), and leave the rest as exercises to the reader. Suppose we have a derivation
\(\mathcal {D}_0\) of
\(< [[ \Psi , A_i^- ]]\), from which we want to obtain a derivation
\(\mathcal {D}\) of
\(< [[ \Psi , A_1 \wedge A_2^- ]]\). There are two possibilities:
), and leave the rest as exercises to the reader. Suppose we have a derivation
\(\mathcal {D}_0\) of
\(< [[ \Psi , A_i^- ]]\), from which we want to obtain a derivation
\(\mathcal {D}\) of
\(< [[ \Psi , A_1 \wedge A_2^- ]]\). There are two possibilities:
-
1.
\(\mathcal {D}_0\) is of the form:
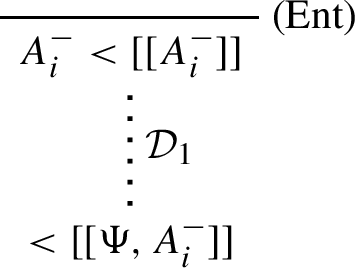
then \(\mathcal {D}\) is:
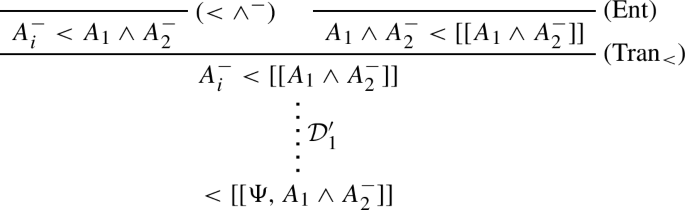
where \(\mathcal {D}'_1\) is obtained by substituting \(A_1 \wedge A_2^-\) to all descendents of the occurrence of \(A_i^+\) in the instance of (Ent) in \(\mathcal {D}_0\) above.
-
2.
\(\mathcal {D}_0\) is of the form:
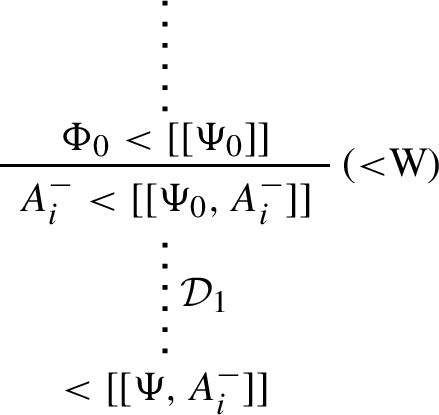
then \(\mathcal {D}\) is:
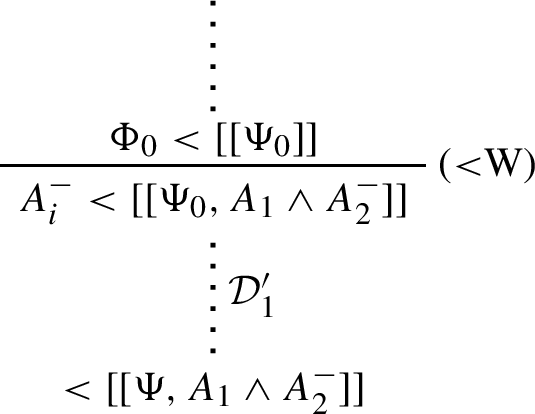
where \(\mathcal {D}'_1\) is obtained by substituting \(A_1 \wedge A_2^-\) to all descendents of the occurrence of \(A^+_i\) in the output of (<W) in \(\mathcal {D}_0\) above.
The proof also establishes the following:
Corollary C.2
If
 is derivable in
\(\textsf{LK}^\text {r}\), then
\({< [[ \Gamma ^-, \Delta ^+ ]]}\) is derivable in
\(\textsf{GLK}^\text {r}\).
is derivable in
\(\textsf{LK}^\text {r}\), then
\({< [[ \Gamma ^-, \Delta ^+ ]]}\) is derivable in
\(\textsf{GLK}^\text {r}\).
Theorem C.1
\(< [[\Gamma ^-, \Delta ^+]]\) is derivable in
\(\textsf{GLK}\) iff
 is valid.
is valid.
Proof
By Lemmas C.1 and C.2, Proposition B.2, and the adequacy of \(\textsf{LK}\) for classical validity.
Theorem C.2
\(< [[\Gamma -, \Delta ^+]]\) is derivable in
\(\textsf{GLK}^\text {r}\) iff
 is perfectibly valid.
is perfectibly valid.
Proof
By Corollaries C.1 and C.2, and Theorem B.1.
Analytic derivations
In this section, we prove the results concerning analytic derivations.
We shall approach the problem of finding an analytic derivation for every \(\textsf{GLK}^\text {a}\)-derivable grounding sequent in a constructive way, by providing an effective method for transforming any given \(\textsf{GLK}^\text {a}\)-derivation into an analytic \(\textsf{GLK}^\text {a}\)-derivation of the same grounding sequent. The main steps of the transformation are broken down into the following Lemmas.
Lemma D.1
If \(\Phi < X\) is derivable in \(\textsf{GLK}^\text {a}\), it has a derivation where no application of (<W) is followed by the application of any other rule.
Proof
We consider any derivation \(\mathcal {D}\) of \(\Phi < X\) where (<W) is applied exactly once in last position. We consider all possible rule applications for the continuation of \(\mathcal {D}\) and show how to construct a derivation \(\mathcal {D}^\dagger \) of the same sequent where no application of (<W) is followed by the application of any other rule.
-
\(\mathcal {D}\) cannot continue with (Tran<).
-
\(\mathcal {D}\) continues with (Bind). Then \(\mathcal {D}\) is of the form:
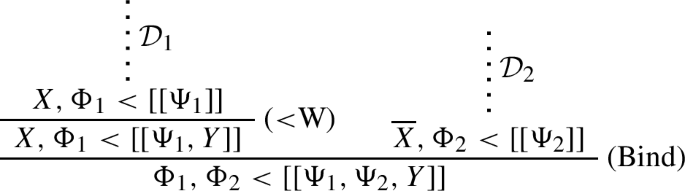
and \(\mathcal {D}^\dagger \) is:
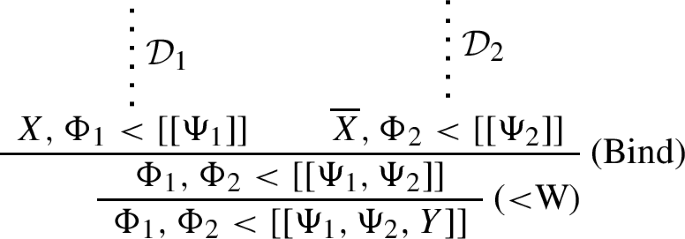
-
\(\mathcal {D}\) continues with (<W). Then \(\mathcal {D}^\dagger =\mathcal {D}\).
-
\(\mathcal {D}\) continues with (C<). Then \(\mathcal {D}\) is of the form:
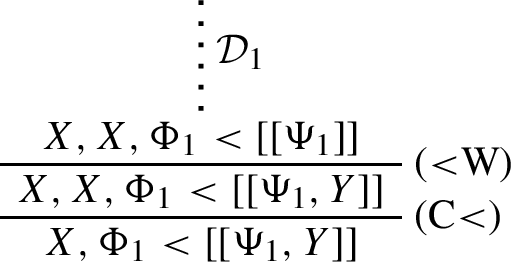
and \(\mathcal {D}^\dagger \) is:
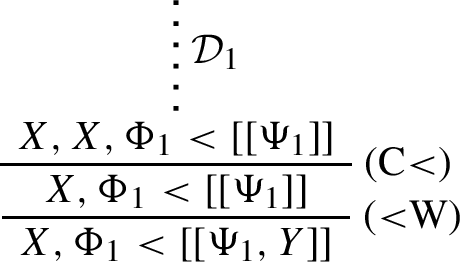
-
\(\mathcal {D}\) continues with (<C). There are two possibilities:
-
1.
if \(\mathcal {D}\) is of the form:
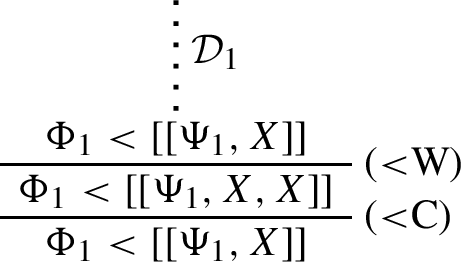
then \(\mathcal {D}^\dagger \) is:
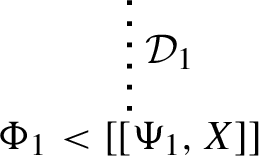
-
2.
if \(\mathcal {D}\) is of the form:
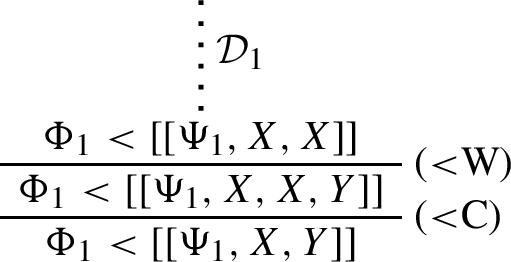
then \(\mathcal {D}^\dagger \) is:
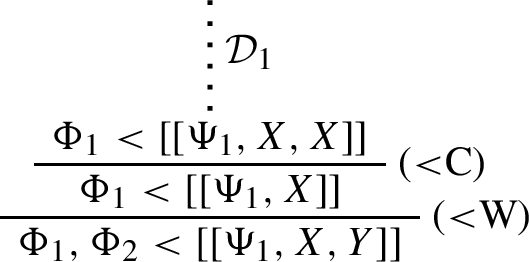
-
1.
-
\(\mathcal {D}\) continues with (Amalg). Then \(\mathcal {D}\) is of the form:
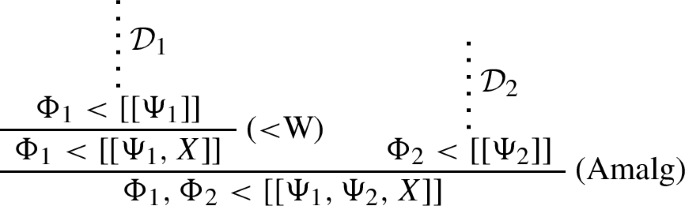
and \(\mathcal {D}^\dagger \) is:

By successively replacing, within a derivation, each initial segment \(\mathcal {D}_0\) containing exactly one application of (<W) in penultimate position, by \(\mathcal {D}_0^\dagger \), one eventually obtains a derivation of the same sequent where no application of (<W) is followed by an application of any other rule. \(\square \)
Lemma D.2
If \(\Phi < X\) is derivable in \(\textsf{GLK}^\text {ra}\), it has a derivation where no application of (Tran \(_<\)) or (Bind \(_<\)) follows an application of (Amalg).
Proof
We consider any \(\textsf{GLK}^\text {ra}\)-derivation \(\mathcal {D}\) where (Amalg) is applied exactly once in last position. We consider all possible rule applications for the continuation \(\mathcal {D}_0\) of \(\mathcal {D}\) and show how to construct of derivation of the same sequent where no application of (Tran \(_<\)) or (Bind) follows an application of (Amalg).
-
\(\mathcal {D}\) cannot continue with (Tran \(_<\)).
-
\(\mathcal {D}\) continues with (Bind). \(\mathcal {D}_0\) is of the form:
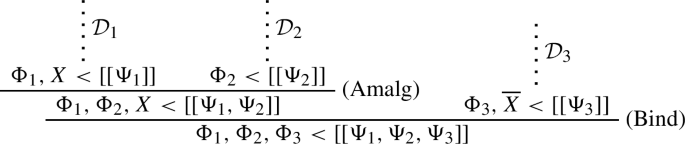
and \(\mathcal {D}_0^\dagger \) is:
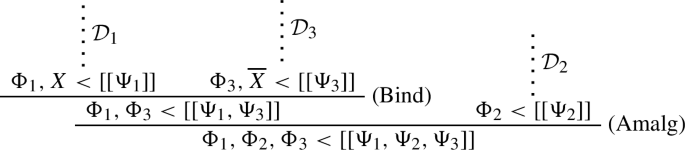
-
\(\mathcal {D}\) continues with (C<), (<C) or (Amalg). Then \(\mathcal {D}_0^\dagger =\mathcal {D}_0\).
By successively replacing, within a derivation \(\mathcal {D}\) of \(\Phi < X\), each initial segment \(\mathcal {D}_0\) containing exactly one application of (Amalg) in penultimate position, by \(\mathcal {D}_0^\dagger \), one eventually obtains a derivation of \(\Phi < X\) where no application of (Tran<) or (Bind) follows an application of (Amalg). \(\square \)
Theorem D.1
If \(\Phi < X\) is derivable in \(\textsf{GLK}^\text {a}\), it has an analytic \(\textsf{GLK}^\text {a}\)-derivation.
Proof
Let \(\mathcal {D}_0\) be any \(\textsf{GLK}^\text {a}\)-derivation of \(\Phi < X\). By Lemma D.1, \(\Phi < X\) has a derivation \(\mathcal {D}_1\) where no application of (<W) is followed by an application of any other rule. In other words, \(\mathcal {D}_1\) has a largest (<W)-free initial segment \(\mathcal {D}_2\), which is a \(\textsf{GLK}^\text {ra}\)-derivation of the sequent \(\Phi _1 < X_1\). By Lemma D.2, \(\Phi _1 < X_1\) has a derivation \(\mathcal {D}_3\) where no application of (Tran \(_<\)) or (Bind) follows an application of (Amalg). So \(\mathcal {D}_3\) has a largest (Amalg)-free initial segment \(\mathcal {D}_4\) that is a \(\textsf{GLK}^\text {r}\)-derivation of the sequent \(\Phi _2 < X_2\). Now, let \(\mathcal {D}_5\) be the result of replacing, within \(\mathcal {D}_1\), the initial segment \(\mathcal {D}_2\) with \(\mathcal {D}_3\). Then \(\mathcal {D}_5\) is an analytic \(\textsf{GLK}^\text {a}\)-derivation of \(\Phi < X \). \(\square \)
Corollary D.1
-
If \(\Phi < [[\Psi ]]\) is derivable in \(\textsf{GLK}\), it has an analytic \(\textsf{GLK}\)-derivation.
-
If \(\Phi < [[\Psi ]]\) is derivable in \(\textsf{GLK}^\text {r}\), it has an analytic \(\textsf{GLK}^\text {r}\)-derivation.
-
If \(\Phi < [[\Psi ]]\) is derivable in \(\textsf{GLK}^\text {ra}\), it has an analytic \(\textsf{GLK}^\text {ra}\)-derivation.
Proposition D.1
If \(< [[ \Psi ]]\) has an analytic \(\textsf{GLK}^\text {ra}\)-derivation \(\mathcal {D}\), all members of \(\Psi \) are contributors in \(\mathcal {D}\).
Proof
By definition, all analytic \(\textsf{GLK}^\text {ra}\)-derivations of \(< [[ \Psi ]]\) have an empty Weakening Phase. Therefore, all members of \(\Psi \) are contributors there. \(\square \)
Lemma D.3
If \(X_1\) and \(X_2\) are two contributors in an analytic \(\textsf{GLK}^\text {r}\)-derivation, they are co-contributors.
Proof
By induction on the length of the Binding Phase of an analytic \(\textsf{GLK}^\text {r}\)-derivation \(\mathcal {D}\). By assumption, there are at least two contributors, so in the base case the Binding Phase is of the form:

Then \(X_1\) and \(X_2\) are immediate co-contributors and a fortiori co-contributors. The induction step is trivial in cases where the Binding Phase ends with (<C) or with (C<). Suppose \(\mathcal {D}\) ends with an application of (Bind). It has the form:

If \(X_1,X_2 \in \Psi _i\) with \(i \in \{ 1,2 \}\), they are co-contributors by the induction hypothesis. If \(X_1 \in \Psi _1\) and \(X_2 \in \Psi _2\), then we focus on the closest ancestor of Y that occurs in the Grounding Phase of \(\mathcal {D}_1\). By construction, this ancestor occurs in a grounding sequent with an s-term on the right containing exactly one signed formula, call it \(X_3\). Let \(X_4\) be the unique signed formula in the s-term of the grounding sequent of the Grounding Phase of \(\mathcal {D}_2\) where \(\overline{Y}\) has its closest ancestor. By construction, \(X_3\) and \(X_4\) are immediate co-contributors, and hence co-contributors. By the induction hypothesis, \(X_1\) and \(X_3\) are co-contributors, and \(X_2\) and \(X_4\) are co-contributors. By transitivity, \(X_1\) and \(X_2\) are co-contributors. \(\square \)
Theorem D.2
For all analytic \(\textsf{GLK}\)-derivation \(\mathcal {D}\) of \(< [[ \Phi ]]\), all the contributors in \(\mathcal {D}\) are joint contributors.
Proof
Let \(X_1\) and \(X_2\) be any two contributors in an analytic \(\textsf{GLK}\)-derivation \(\mathcal {D}\). They are a fortiori two contributors in the \(\textsf{GLK}^\text {r}\)-derivation \(\mathcal {D}'\) obtained by removing the Weakening Phase of \(\mathcal {D}\). By Lemma D.3, they are co-contributors. Since the Weakening Phase of \(\mathcal {D}\) adds no further contributors, we conclude that the contributors of \(\mathcal {D}\) are joint contributors. \(\square \)
Corollary D.2
For all analytic \(\textsf{GLK}^\text {r}\)-derivation \(\mathcal {D}\) of \(< [[ \Phi ]]\), all members of \(\Phi \) are joint contributors in \(\mathcal {D}\).
Lemma D.4
If \(< [[ \Phi ]]\) has an analytic \(\textsf{GLK}^\text {a}\)-derivation where the members of \(\Phi \) are joint contributors, \(< [[ \Phi ]]\) has a \(\textsf{GLK}^\text {r}\)-derivation.
Proof
Let \(\mathcal {D}\) be an analytic \(\textsf{GLK}^\text {a}\)-derivation of \(< [[ \Phi ]]\) where the members of \(\Phi \) are joint contributors. Then its Weakening Phase is empty (otherwise, some member of \(\Phi \) would not be a contributor). If its Amalgamation Phase is empty, \(\mathcal {D}\) is a \(\textsf{GLK}^\text {r}\)-derivation. If its Amalgamation Phase is not empty, let \(< [[ \Psi _1 ]]\) and \(< [[ \Psi _2 ]]\) be any two inputs to the Amalgamation Phase inherited from the Binding Phase, and let \(X_1 \in \Psi _1\) and \(X_2 \in \Psi _2\). By construction \(X_1\) and \(X_2\) are not co-contributors. The only way for the members of \(\Phi \) to be joint contributors is for a descendent of \(X_1\) or of \(X_2\) to be contracted out by (<C). It follows that all the inputs to the Amalgamation Phase share the same signed formulas. Then \(< [[ \Phi ]]\) is derivable from some such input by (<C) alone, and thus has a \(\textsf{GLK}^\text {r}\)-derivation. \(\square \)
Theorem D.3
 is relevantT iff for some analytic
\(\textsf{GLK}^\text {a}\)-derivation
\(\mathcal {D}\) of
\({< [[ \Gamma ^-, \Delta ^+ ]]}\), all sequent elements are joint contributors in
\(\mathcal {D}\).
is relevantT iff for some analytic
\(\textsf{GLK}^\text {a}\)-derivation
\(\mathcal {D}\) of
\({< [[ \Gamma ^-, \Delta ^+ ]]}\), all sequent elements are joint contributors in
\(\mathcal {D}\).
Proof
(left-to-right) By Theorem C.2, Corollaries D.1, and D.2. (right-to-left) Let
\(\mathcal {D}\) be an analytic
\(\textsf{GLK}^\text {a}\)-derivation of
\(< [[ \Gamma ^-, \Delta ^+ ]]\) where all sequent elements are joint contributors. By Lemma D.4 and Theorem C.2,
 is relevantT.
\(\square \)
is relevantT.
\(\square \)
Theorem D.4
 is relevantDM iff for all analytic
\(\textsf{GLK}^\text {a}\)-derivations of
\({< [[ \Gamma ^-, \Delta ^+ ]]}\), all sequent elements are joint contributors.
is relevantDM iff for all analytic
\(\textsf{GLK}^\text {a}\)-derivations of
\({< [[ \Gamma ^-, \Delta ^+ ]]}\), all sequent elements are joint contributors.
Proof
(left-to-right) Suppose that
 is relevantDM and let
\(\mathcal {D}\) be an analytic
\(\textsf{GLK}^\text {a}\)-derivation
\(\mathcal {D}\) of
\(< [[ \Gamma ^-, \Delta ^+ ]]\). Its Weakening Phase is empty, otherwise, some proper subsequent of
is relevantDM and let
\(\mathcal {D}\) be an analytic
\(\textsf{GLK}^\text {a}\)-derivation
\(\mathcal {D}\) of
\(< [[ \Gamma ^-, \Delta ^+ ]]\). Its Weakening Phase is empty, otherwise, some proper subsequent of
 would be valid, by Proposition C.1 and Theorem C.1. If its Amalgamation Phase is empty,
\(\mathcal {D}\) is an analytic
\(\textsf{GLK}^\text {r}\)-derivation. By Corollary D.2, all sequent elements are joint contributors in
\(\mathcal {D}\). If its Amalgamation Phase is non-empty, let
\(< [[ \Pi ^-, \Sigma ^+ ]]\) be some input to the Amalgamation Phase inherited from the Binding Phase. Because
would be valid, by Proposition C.1 and Theorem C.1. If its Amalgamation Phase is empty,
\(\mathcal {D}\) is an analytic
\(\textsf{GLK}^\text {r}\)-derivation. By Corollary D.2, all sequent elements are joint contributors in
\(\mathcal {D}\). If its Amalgamation Phase is non-empty, let
\(< [[ \Pi ^-, \Sigma ^+ ]]\) be some input to the Amalgamation Phase inherited from the Binding Phase. Because
 is relevantDM,
is relevantDM,
 cannot be a subsequent of
cannot be a subsequent of
 . Since
\(< [[ \Pi ^-, \Sigma ^+ ]]\) is an input to the Amalgamation Phase, for all X, if
\( X\in \Pi ^- + \Sigma ^+\), then
\(X \in \Gamma ^- + \Delta ^+\). It follows that
\(< [[ \Gamma ^-, \Delta ^+ ]]\) is obtainable from
\(<[[\Pi ^-, \Sigma ^+ ]]\) by applications of (<C) only and thus has an analytic
\(\textsf{GLK}^\text {r}\)-derivation, which is a fortiori an analytic
\(\textsf{GLK}^\text {a}\)-derivation where all sequent elements are joint contributors, by Corollary D.2. (right-to-left) By contraposition. Suppose that
. Since
\(< [[ \Pi ^-, \Sigma ^+ ]]\) is an input to the Amalgamation Phase, for all X, if
\( X\in \Pi ^- + \Sigma ^+\), then
\(X \in \Gamma ^- + \Delta ^+\). It follows that
\(< [[ \Gamma ^-, \Delta ^+ ]]\) is obtainable from
\(<[[\Pi ^-, \Sigma ^+ ]]\) by applications of (<C) only and thus has an analytic
\(\textsf{GLK}^\text {r}\)-derivation, which is a fortiori an analytic
\(\textsf{GLK}^\text {a}\)-derivation where all sequent elements are joint contributors, by Corollary D.2. (right-to-left) By contraposition. Suppose that
 has a valid proper subsequent
has a valid proper subsequent
 . By Theorems C.1 and D.1,
\(< [[ \Pi ^-, \Sigma ^+ ]]\) has an analytic
\(\textsf{GLK}\)-derivation. It is easy to continue that derivation by enough applications of (<W) as necessary to reach
\(< [[\Gamma ^+, \Delta ^-]]\). That derivation is an analytic
\(\textsf{GLK}^\text {a}\)-derivation relative to which some sequent elements are not contributors. A fortiori, it is not the case that all sequent elements are joint contributors.
\(\square \)
. By Theorems C.1 and D.1,
\(< [[ \Pi ^-, \Sigma ^+ ]]\) has an analytic
\(\textsf{GLK}\)-derivation. It is easy to continue that derivation by enough applications of (<W) as necessary to reach
\(< [[\Gamma ^+, \Delta ^-]]\). That derivation is an analytic
\(\textsf{GLK}^\text {a}\)-derivation relative to which some sequent elements are not contributors. A fortiori, it is not the case that all sequent elements are joint contributors.
\(\square \)
Theorem D.5
 is relevantB iff for all analytic
\(\textsf{GLK}^\text {a}\)-derivation of
\({< [[ \Gamma ^-, \Delta ^+ ]]}\) all sequent elements are contributors.
is relevantB iff for all analytic
\(\textsf{GLK}^\text {a}\)-derivation of
\({< [[ \Gamma ^-, \Delta ^+ ]]}\) all sequent elements are contributors.
Proof
(left-to-right) Suppose that
 is relevantB. By Definition of relevanceB, for all
\(A \in \Gamma + \Delta \), there is a perfectly valid subsequent
is relevantB. By Definition of relevanceB, for all
\(A \in \Gamma + \Delta \), there is a perfectly valid subsequent
 of
of
 . By Theorem D.4, for all
\(A \in \Gamma + \Delta \), and all analytic
\(\textsf{GLK}^\text {a}\)-derivation of
\(< [[\Pi _A^-, \Sigma _A^+]]\), all sequent elements are joint contributors. By Lemma D.4 and Corollary D.1,
\([[\Pi _A^-, \Sigma _A^+]]\) has an analytic
\(\textsf{GLK}^\text {r}\)-derivations, for all
\(A \in \Gamma + \Delta \). Then by means of (Amalg) and (<C), one obtains an analytic
\(\textsf{GLK}^\text {ra}\)-derivation of
\(< [[\Gamma ^-, \Delta ^+]]\) where all sequent elements are contributors, by Proposition D.1. (right-to-left) We prove the contrapositive. Suppose that for some
\(A \in \Gamma + \Delta \) all subsequent
. By Theorem D.4, for all
\(A \in \Gamma + \Delta \), and all analytic
\(\textsf{GLK}^\text {a}\)-derivation of
\(< [[\Pi _A^-, \Sigma _A^+]]\), all sequent elements are joint contributors. By Lemma D.4 and Corollary D.1,
\([[\Pi _A^-, \Sigma _A^+]]\) has an analytic
\(\textsf{GLK}^\text {r}\)-derivations, for all
\(A \in \Gamma + \Delta \). Then by means of (Amalg) and (<C), one obtains an analytic
\(\textsf{GLK}^\text {ra}\)-derivation of
\(< [[\Gamma ^-, \Delta ^+]]\) where all sequent elements are contributors, by Proposition D.1. (right-to-left) We prove the contrapositive. Suppose that for some
\(A \in \Gamma + \Delta \) all subsequent
 such that
\(A \in \Pi + \Sigma \) is either invalid or imperfectly valid. If at least one such subsequent
such that
\(A \in \Pi + \Sigma \) is either invalid or imperfectly valid. If at least one such subsequent
 is imperfectly valid, it has a valid proper subsequent. By Theorem D.1, one has an analytic
\(\textsf{GLK}^\text {a}\)-derivation of
\(<[[\Pi ^-, \Sigma ^+]]\) which, by appropriate Weakening steps, is easily extended to a
\(\textsf{GLK}^\text {a}\)-derivation of
\([[\Gamma ^-, \Delta ^+]]\) where the sequent elements introduced by Weakening are not contributors. If all subsequents
is imperfectly valid, it has a valid proper subsequent. By Theorem D.1, one has an analytic
\(\textsf{GLK}^\text {a}\)-derivation of
\(<[[\Pi ^-, \Sigma ^+]]\) which, by appropriate Weakening steps, is easily extended to a
\(\textsf{GLK}^\text {a}\)-derivation of
\([[\Gamma ^-, \Delta ^+]]\) where the sequent elements introduced by Weakening are not contributors. If all subsequents
 of
of
 such that
\(A \in \Pi + \Sigma \) are invalid, then
such that
\(A \in \Pi + \Sigma \) are invalid, then
 is invalid, and by Theorem C.1, not derivable in
\(\textsf{GLK}\), nor in
\(\textsf{GLK}^\text {a}\), by Proposition C.1. A fortiori, it has no analytic
\(\textsf{GLK}^\text {a}\)-derivation of
\(< [[ \Gamma ^-, \Delta ^+ ]]\) where all sequent elements are contributors.
\(\square \)
is invalid, and by Theorem C.1, not derivable in
\(\textsf{GLK}\), nor in
\(\textsf{GLK}^\text {a}\), by Proposition C.1. A fortiori, it has no analytic
\(\textsf{GLK}^\text {a}\)-derivation of
\(< [[ \Gamma ^-, \Delta ^+ ]]\) where all sequent elements are contributors.
\(\square \)
Theorem D.6
 is relevantBT iff for some analytic
\(\textsf{GLK}^\text {a}\)-derivation of
\(< [[ \Gamma ^-, \Delta ^+ ]]\) all sequent elements are contributors.
is relevantBT iff for some analytic
\(\textsf{GLK}^\text {a}\)-derivation of
\(< [[ \Gamma ^-, \Delta ^+ ]]\) all sequent elements are contributors.
Proof
(left-to-right) Suppose that
 is relevantBT. By Proposition B.5, for all
\(A \in \Gamma + \Delta \), there is a perfectibly valid subsequent
is relevantBT. By Proposition B.5, for all
\(A \in \Gamma + \Delta \), there is a perfectibly valid subsequent
 of
of
 . By Theorem C.2 and Corollary D.1,
\(<[[\Pi _A^-, \Sigma _A^+]]\) has an analytic
\(\textsf{GLK}^\text {r}\)-derivation for all such A. By means of (Amalg) and (<C) one constructs a analytic
\(\textsf{GLK}^\text {ra}\)-derivation of
\(< [[ \Gamma ^-, \Delta ^+ ]]\), where all sequent elements are contributors, by Proposition D.1. (right-to-left) Suppose we have an analytic
\(\textsf{GLK}^\text {a}\)-derivation
\(\mathcal {D}\) of
\(< [[ \Gamma ^-, \Delta ^+ ]]\) where all sequent elements are contributors. Then
\(\mathcal {D}\) can be decomposed into a number of
\(\textsf{GLK}^\text {r}\)-derivations
\(< [[ \Gamma _1^-, \Delta _1^+ ]]\), ...,
\(< [[ \Gamma _n^-, \Delta _n^+ ]]\) which branch together by a series of applications of (Amalg), (C<) and (<C). By Theorem C.2,
. By Theorem C.2 and Corollary D.1,
\(<[[\Pi _A^-, \Sigma _A^+]]\) has an analytic
\(\textsf{GLK}^\text {r}\)-derivation for all such A. By means of (Amalg) and (<C) one constructs a analytic
\(\textsf{GLK}^\text {ra}\)-derivation of
\(< [[ \Gamma ^-, \Delta ^+ ]]\), where all sequent elements are contributors, by Proposition D.1. (right-to-left) Suppose we have an analytic
\(\textsf{GLK}^\text {a}\)-derivation
\(\mathcal {D}\) of
\(< [[ \Gamma ^-, \Delta ^+ ]]\) where all sequent elements are contributors. Then
\(\mathcal {D}\) can be decomposed into a number of
\(\textsf{GLK}^\text {r}\)-derivations
\(< [[ \Gamma _1^-, \Delta _1^+ ]]\), ...,
\(< [[ \Gamma _n^-, \Delta _n^+ ]]\) which branch together by a series of applications of (Amalg), (C<) and (<C). By Theorem C.2,
 , ...,
, ...,
 are perfectibly valid subsequents of
are perfectibly valid subsequents of
 . Then, for all
\(A \in \Gamma + \Delta \), there is a perfectibly valid subsequent
. Then, for all
\(A \in \Gamma + \Delta \), there is a perfectibly valid subsequent
 of
of
 such that
\(A \in \Pi + \Sigma \). By Proposition B.5,
such that
\(A \in \Pi + \Sigma \). By Proposition B.5,
 is relevantBT.
\(\square \)
is relevantBT.
\(\square \)
Corollary D.3
 is relevantBT iff
\({< [[\Gamma ^-, \Delta ^+]]}\) is derivable in
\(\textsf{GLK}^\text {ra}\).
is relevantBT iff
\({< [[\Gamma ^-, \Delta ^+]]}\) is derivable in
\(\textsf{GLK}^\text {ra}\).
Inferentialism
Our integrated account of logical ground and entailment has shown a bias toward semantic Bolzano-Tarski-style accounts of entailment. It would be interesting if our account could also be given an inferentialist interpretation.
Now, bilateralism is so central to our approach, that it will need to be preserved in any inferentialist interpretation. Fortunately, there is a brand of inferentialist bilateralism that takes acceptance and rejection as primitive attitudes in terms of which the meaning of connectives and the notion of entailment can be defined (Restall, 2005; Ripley, 2017). This is the route we will follow here.
As a matter of fact, Litland (2023) has proposed a bilateralist inferentialist account of logical grounding, formally very similar to ours, where a notion of rejection is introduced. According to Litland’s inferentialism about ground, grounding claims express explanatory arguments. In the bilateral version of this inferentialism, one considers in addition antigrounding claims, which express explanatory rejections. While an explanatory argument is an answer to the question: “why p ?”, an explanatory rejection is an answer to the question: “why not p ?” In other words, Litland’s bilateral move consists in introducing an attitude of rejection (rather than falsity as a semantical primitive notion), on par with acceptance when it comes to the outputs of explanatory reasoning.
It is natural for us to propose a similar understanding of the system \(\textsf{GK}\), except that we do not limit the attitude of rejection to the output of explanatory reasoning, but also allow for premises to be rejected, as well as accepted.Footnote 30
In general terms, a grounding sequent of the form
says that the acceptance of \(A_1, \dots , A_n\) and the rejection of \(B_1, \dots , B_m\) together ground the acceptance of C. Symmetrically, a grounding sequent of the form
says that the acceptance of \(A_1, \dots , A_n\) and the rejection of \(B_1, \dots , B_m\) together ground the rejection of C. The calculus \(\textsf{GK}\) is easily seen to be sound for such an interpretation.
When it comes to entailment, an influential proposal of Restall (2005) defines multiple-conclusion entailments in terms of acceptance and rejection as follows:
Definition 24
 is valid if it is incoherent to accept all the premises and reject all the conclusions.
is valid if it is incoherent to accept all the premises and reject all the conclusions.
Now, our calculi \(\textsf{GLK}\) and \(\textsf{GLK}^\text {r}\) do not straightforwardly fit this interpretation, but a simple modification enables them to accommodate it. Instead of representing sequents by terms of the form \([[ A^-_1, \dots , A^-_n, B^+_1, \dots , B^+_m ]]\) where the comma is read disjunctively, we could represent them by terms of the form:

In the general case, grounding sequents of the form:

mean that the acceptance of \(A_1, \dots , A_n\) and the rejection of \(B_1, \dots , B_m\) together ground the incoherence of simultaneously accepting \(C_1, \dots , C_l\) and rejecting \(D_1, \dots , D_k\).
It is not difficult to adapt \(\textsf{GLK}\) to this new syntax, as the definition of \(\textsf{GLK}\)’ shows (see Table 6). It is not difficult either to check that the results about \(\textsf{GLK}\) carry over to \(\textsf{GLK}\)’ – one only needs to add a modality in front of sequent terms and invert the signs within them. So our ground-theoretic analysis of relevant entailment can also be adopted from such a bilateralist inferentialist point of view.Footnote 31
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Saint-Germier, P., Verdée, P. & Villalonga, P.T. Relevant entailment and logical ground. Philos Stud (2024). https://doi.org/10.1007/s11098-024-02101-1
Accepted:
Published:
DOI: https://doi.org/10.1007/s11098-024-02101-1




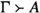 preserves truth, then
preserves truth, then
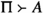 also preserves truth for all
also preserves truth for all
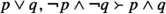 is neither perfectly valid nor a substitution instance of a perfectly valid sequent in
is neither perfectly valid nor a substitution instance of a perfectly valid sequent in 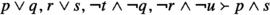 which is perfectly valid. See Tennant (
which is perfectly valid. See Tennant ( is a
is a
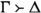 if
if
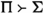 is a substitution instance of
is a substitution instance of
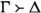 if it is a
if it is a
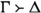 , for some substitution map
, for some substitution map

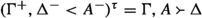 .
.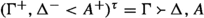 .
.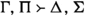 .
.