Contingentism and paraphrase

Abstract

One important challenge for contingentists is that they seem to be unable to account for the meaning of some apparently meaningful modal discourse that is perfectly intelligible for necessitists. This worry is particularly pressing for higher-order contingentists, contingentists who hold that it is not only contingent which objects there are, but also contingent which semantic values there are for higher-order variables to quantify over. Objections against higher-order contingentism along these lines have been presented in Williamson (Mind 119(475):657–748, 2010; Modal logic as metaphysics, Oxford University Press, 2013, ch. 7), and Fritz and Goodman (Mind 126(504):1063–1108, 2017). This paper presents a way for contingentists to respond to these challenges. The upshot is that the contingentist can account for the meaningfulness of the problematic modal claims by pretending necessitism to be true, but in some cases it turns out to be indeterminate whether they are true. I defend this strategy against the objections against pretence-strategies presented in Fritz and Goodman (Mind 126(504):1063–1108, 2017, §4). Furthermore, I defend the plausibility of the resulting indeterminacy from the contingentist’s perspective.

1 The trouble cases

Necessitism consists in the thesis that necessarily everything necessarily exists. Contingentism is the denial of necessitism. I will focus on a challenge for contingentism as it is presented by Fritz and Goodman (2017). They illustrate the challenge with the following quote from Richard Dawkins:

‘Most people are never going to die because they are never going to be born. The potential people who could have been here in my place but who will in fact never see the light of day outnumber the sand grains of Arabia.’ (Dawkins, 1998, p. 1)

It seems clear that Dawkins makes a meaningful and not obviously false statement. It also seems clear that most contingentists take a literal reading to be obviously false: People who will never be born, or non-concretized individuals, are precisely the sort of entities contingentists wish to get rid of. This poses a paraphrase challenge to contingentists: How can they systematically account for the kind of modal discourse the above Dawkin quote exemplifies? To put it with Fritz and Goodman, the challenge is to

‘[p]rovide a systematic strategy that, for any sentence involving modalized quantification, produces a new sentence, not involving modalized quantification, that expresses the proposition conveyed by the original sentence.’ (Fritz & Goodman, 2017, p. 1067)

Necessitists have no problem with talk that, on the surface level, seems to be about mere possibilia, i.e. talk that involves modalized quantification (quantification of the sort we find in the Dawkins quote). They can just interpret sentences involving modalized quantification literary. Necessitists hold that there are entities that are possibly concretized and born persons, but that actually are never going to be born. They can count them (or measure their cardinality) and straightforwardly interpret claims about what most of them are like. Contingentists are in trouble when it comes to certain cases of modalized quantification. They can express the claim that there possibly are uncountably many stars (or more people than actual grains of sand). However, they cannot straightforwardly account for the claim that there are uncountably many merely possible stars that are pairwise incompossible (i.e cannot exist in the same possible world). Picturesquely put, the contingentist would have to move across possible worlds to collect these stars and the contingentist arguably has no vantage point from which this can be done. One available option for contingentists to avoid this shortcoming is to maintain that necessarily all properties necessarily exist and to embrace haecceitism.¹ Haecceitists (in the relevant sense) say that necessarily there is a haecceity for every object x, i.e. a property F such that necessarily, an entitiy has F just in case it is identical to x. If this assumption is combined with necessitism for properties, we get the result that necessarily, every object has a haecceity that necessarily exists (a view prominently endorsed by Plantinga 1983). We can now let the haecceities stand in for objects and take recourse to them when interpreting modalized quantification. Fritz and Goodman show that there is a further way to meet the paraphrase challenge, namely by subscribing to the following package: ‘Necessarily coextensive properties are identical, properties of individuals can apply to merely possible individuals, and properties of properties can apply to properties which there could not even possibly be’ (Fritz & Goodman, 2017, p. 1093). Independently of whether this combination of committments can be defended, it is clear that many higher-order contingentists will wish to hold that properties can only apply to existent individuals. This claim (which is also known as the being constraint) seems to be an integral part of a sparse and arguably commonsensical view according to which all there is to say about a world from its own perspective is which objects there are and what they are like. For this reasons, it is a worthwhile task to investigate whether the higher-order contingentist who embraces the being constraint, henceforth called the strict contingentist,² can meet the given paraphrase challenge.

In this paper I defend a way for the strict contingentist to meet the paraphrase challenge that can roughly be described as a pretence-strategy. I will make the involved pretence precise by providing a function that assigns contingentist models their necessitist counterparts. My proposal takes sentences involving modalized quantifiers (like those from the Dawkins quote) to be meaningful and not obviously false. At the same time, it takes many sentences involving modalized quantification to be indeterminate. This indeterminacy will be achieved by supervaluating over a class of admissible necessitist models.

Before I turn to formally spelling out my proposed solution, I will situate it in the dialectical landscape of contigentist responses. Contingentists have a variety of options to deal with statements involving modalized quantification. For example, the sentence

• (People) Most possible people never have been and never will be born.

Can be paraphrased as saying that most possible human DNA chains (understood as types of biologically possible chains of nucleotides) are such that there never has been and never will be a human with this DNA chain. Fritz and Goodman discuss a number of available strategies (Fritz & Goodman, 2017, §§2–3) and show that some sentences involving modalized quantification cannot be paraphrased given standard first-order and higher-order resources. An example of a sentence that is troubling in this way (and that will be reviewed below after I presented my solution) is

• (Particles) There are uncountably many possibly concrete elementary particles of which necessarily at most finitely many are concretized.

This suggests that from the perspective of the contingentist, there is a distinction between those sentences involving modalized quantification that are troubling and those that are not. With this distinction in place, the paraphrase challenge can be elucidated by means of the following argument to the conclusion that strict contingentism is false:

• (1) (People) is a meaningful sentence.

• (2) If (People) is a meaningful sentence, then (Particles) is a meaningful sentence.

• (3) No systematic strategy that produces a meaningful paraphrase of (Particles) is available to the strict contingentist.

• (4) If (Particles) is a meaningful sentence and (3), then strict contingentism is false.

I agree with (1). It seems clear to me that it would speak against the contingentist’s position if they would have to pretend to not understand (People) or its likes. They could be stubborn, for, as Williamson puts it, ‘[i]t is hard to argue with a claim not to understand’ (Williamson, 2010, p. 711), but many (including me) will also hold that it is for good reason that these days ‘claiming not to understand (...) is rather less popular’ (Williamson, 2010, p. 711). In any case, it is worthwhile to have an option on the table that allows the strict contingentist to accept (1). The strict contingentist should plausibly also accept (2). Once they in principle accept that modalized sentences are meaningful, it seems unmotivated to deny that sentences like (Particles) are unintelligible. It seems also clearly desirable to not have to paraphrase modalized sentences in a piecemeal fashion, which makes reliance on the falsity of (4) unattractive for the strict contingentist. My aim in this paper is to give the strict contingentist resources to deny (3).

However, things look different if we replace ‘meaningful’ with ‘determinately true or determinately false’ in the premises (1)–(4). Call the premises resulting from this substitution (1$^{\prime }$)–(4$^{\prime }$). The solution proposed in this paper does not allow to deny (3$^{\prime }$), for my proposal has it that sentences like (Particle) will be indeterminate and hence neither determinately true nor determinately false. Consequently, my proposal holds water only if the strict contingentist can deny one of (1$^{\prime }$), (2$^{\prime }$), (4$^{\prime }$). The view that I will advertise consists in denying (2$^{\prime }$) and accepting (3$^{\prime }$) whilst accepting (2) and denying (3).

The tenability of a position with these commitments will be defended at the end of Sect. 3. The next section will spell out how the function that assigns contingentist models their necessitist counterparts works and how it can be used to pretend necessitism. The third section will develop the way the mentioned indeterminacy arises and defend the claim that many sentences involving modalized quantification are indeterminate.

It will become clear that my proposal is similar to the proposals called hyper-possibility paraphrases in Fritz and Goodman (2017). The fourth section will defend my proposal against the objections Fritz and Goodman put forward against such paraphrases.

2 How to pretend Necessitism

In a nutshell, my proposal can be summarized as follows: I accept (as it is mandated by a result developed in Fritz 2018 and reported in Fritz and Goodman 2017) that there are numerous different semantic models that yield the same truth-values for all sentences not involving modalized quantification that the strict contingentist can express. Fixing a particular interpretation for the non-logical constants, there is a class of models that gets the non-modalized facts right in the following sense: Exactly those sentences not involving modalized quantification that are in fact true are true in these models. Call the contingentist models in this class $\mathbb {M}_c$ ‘admissible’. I spell out a function $\mathcal {F}$ that maps each contingentist model to a corresponding necessitist model. The class of admissible necessitist models is $\mathcal {F}(\mathbb {M}_c)$, the image of $\mathbb {M}_c$ under the function $\mathcal {F}$. It is unproblematic to understand modalized quantification in necessitist models. For this reason, if one holds a particular admissible contingentist model $M_c$ fixed, then one can provide a non-trivial meaning for a sentence involving modalized quantification by evaluating this sentence in the necessitist model $\mathcal {F}(M_c)$. Given that there is no unique true model for the contingentist, but a proper class of admissible models $\mathbb {M}_c$, they will arrive at a proper class of admissible necessitist models $\mathcal {F}(\mathbb {M}_c)$. My proposal is to treat these models as precisifications and to supervaluate on the models in $\mathcal {F}(\mathbb {M}_c)$. The determinate sentences will be those the models in $\mathcal {F}(\mathbb {M}_c)$ agree on and the indeterminate ones will be those the models are divided on.

An informal way to elucidate the idea uses the notion of pretence. We input a contingentist model (or a class of contingentist models) as its argument and the function delivers the model (class of models) that we should use in pretending that necessitism is true.

In this section I will start with a single contingentist model and develop the way this model gets assigned its necessitist counterpart. The result that there are multiple admissible models and the indeterminacy that hence arises will be discussed in the next section. Furthermore I will, for the sake of presentation, start by focusing on contingentism with respect to which individuals there are and, in the beginning, ignore questions concerning higher-order contingentism.

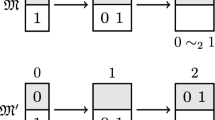
In the frame of a variable domain model $\langle W,@,\mathcal {D},R\rangle$, W is a set of worlds, $@\in W$ is a distinguished world (the actual world), and $\mathcal {D}$ is a function from W to sets of individuals that assigns each world its domain $\mathcal {D}(w)$.³$R\subseteq W\times W$ is an accessibility relation. For simplicity it will be assumed in what follows that $R=W\times W$, which guarantees that the logic of metaphysical modality is S5. Variable domain models lend themselves to modelling contingentist positions, for these models allow that worlds have different domains. In a variable domain model $\langle W,@,\mathcal {D},R, V\rangle$, the being constraint can be secured by imposing the following constraint concerning the valuation V: If V(F, w) is the extension V assigns to the n-adic predicate F at world w and $\langle x_1,\ldots , x_n\rangle \in V(F,w)$, then $\lbrace x_1,\ldots ,x_n\rbrace \subseteq \mathcal {D}(w)$.

Let $M_c=\langle W,@,\mathcal {D},R, V\rangle$ be such a variable domain model for a standard first-order modal language $\mathcal {L}$ and assume that V respects the being constraint. I will assume the standard semantic clauses for the usual truth-functional connectives, the necessity operator $\Box$, and its dual $\Diamond$. This will guarantee that M validates all theorems and rules of standard first-order predicate logic.

We first enrich $\mathcal {L}$ with a monadic predicate C (for chunkiness in the sense of Williamson 2010, see below) and the pretend-necessitism-operator $\odot$. Informally, formulas embedded under this operator are evaluated under the pretence of necessitism. For example, ‘$\odot \Box \forall x\Box \exists y(x=y)$’ is the claim that necessitism holds under the pretence of necessitism and ‘$\forall x\odot \Box \exists y (x=y)$’ says that everything is such that, under the pretence of necessitism, necessarily something is identical to it. Obviously, both claims should come out as true.

We stipulate that at every world w, the extension of C is identical to the domain of w ($V(C,w) =D(w)$). Williamson glosses chunkiness as ‘grounded in the concrete’ (Williamson, 2010, p. 673f). The rough idea is that the chunky objects are all and only those the contingentist takes to exist. In our context, C has the function to store the information that gets lost when a model gets mapped on its necessitist counterpart. Now we can define the function $\mathcal {F}$ that maps every model M to its necessitist counterpart. If $M_c$ is such that all worlds have the same domain (i.e. if $\forall w,v\in W(\mathcal {D}(w)=\mathcal {D}(v)$), then let $\mathcal {F}(M_c)=M_c$. (This condition guarantees that the function does not change anything if we input a necessitist model.) If some worlds have non-identical domains, then the necessitist model that $M_c=\langle W,@,\mathcal {D},R, V\rangle$ gets mapped onto, is $\langle W,@,\mathcal {D}^*,R, V^*\rangle$, with $\mathcal {D}^*$ and $V^*$ working as follows: The function $\mathcal {D}^*$ assigns each $v\in W$ the same domain $\mathcal {D}^*(v)=\bigcup \lbrace \mathcal {D}(w)\mid w\in W\rbrace$, the union of the domains of all worlds in W. The valuation $V^*$ does only differ from V when logical predicates are concerned: For every non-logical predicate, the intension (extension across all worlds) assigned by $V^*$ is identical to the intension assigned by V. In contrast to V, $V^*$ allows logical predicates to apply to all individuals in $\bigcup \lbrace \mathcal {D}(w)\mid w\in W\rbrace$. For example, even if x is not chunky in w, $\langle x,x\rangle$ will be in the extension $V^*$ assigns to the 2-adic identity-predicate at w. We get the result that necessitist models not only accept the being-constraint, but also the further constraint that non-logical predicates necessarily do not apply to non-chunky individuals.⁴

The definition of $\mathcal {F}$ guarantees that, for arbitrary M, $\mathcal {F}(M)$ is such that all worlds have the same domain. This and the above assumptions about the valuation V guarantee that $\mathcal {F}(M_c)$ validates the Simplest Quantified Modal Logic (${\textit{SQML}}$), as it is called in e.g. Linsky and Edward (1994), which includes the Barcan formula and its converse as theorems. The assumption that $R=W\times W$ furthermore guarantees that $\mathcal {F}(M)$ validates ${\textit{SQML}}+S5$.

The necessitist models we arrive at belong to a class of necessitist models that validate the theory ${\textit{Aux}}[{\textit{Nec}}]$ specified in Williamson (2010). Williamson specifies a necessitist theory that consists of (i) the claim of necessitism ($\Box \forall x\Box \exists y\;x=y$), (ii) the claim that everything is possibly chunky ($\forall x\Diamond Cx$), and the claim that for each non-logical predicate F, necessarily, F does not apply to non-chunky individuals ($\Box \forall x_1\ldots \forall x_n (F x_1\ldots x_n\rightarrow (Cx_1\wedge \ldots \wedge Cx_n))$) (see Williamson, 2010, p. 688). That (i) holds is guaranteed by $\mathcal {F}(M_c)$ being a constant domain model. That (ii) holds is guaranteed by the stipulation that for every $w\in W$, $V(C,w) =\mathcal {D}(w)$ and that the constant domain of $\mathcal {F}(M_c)$ is the union of all domains of $M_c$. That (iii) holds is guaranteed by the assumption that V respects the being constraint, by the assumption that $V^*$ aligns with V as far as non-logical predicates are concerned, and by the way the intension of C is stipulated.⁵

The generation of counterpart-models has some similarities to the suppositional approach proposed by Fine (2016, §4). He glosses the strategy underlying this approach as follows:

‘We might imagine that each possible world within the possibilist’s pluriverse contains a barrier between what is actual and what is possible—with all the actual objects of the world lying to the right of the barrier and all the merely possible objects of the world lying to its left. The actualist first slides the barrier all the way to the left so that all possible objects lie to its right and he then introduces a dummy barrier to mark where the actual barrier once lay (under the N/C construal of the debate, the new dummy barrier will mark the distinction between what is and is not ‘chunky’).’ (Fine, 2016, p. 558)

The construction of the new domains of the worlds in $\mathcal {F}(M_c)$ by fusing the domains of all worlds in $M_c$ corresponds to the sliding of the barrier and the introduction of the chunkiness-predicate corresponds to the introduction of a dummy mark. The most important difference between my proposal and Fine’s approach is that Fine argues on behalf of a possibilist who has an entire pluriverse including merely possible objects at their disposal (although these merely possible objects are not real, only the actual objects are real).⁶ My aim in this paper is to propose a solution that can be accepted by the strict contingentist who does not have a possibilits pluriverse at their disposal. If the contingentist settled on a single contingentist model, then they would commit to there being a metaphysically distinguished possibilist pluriverse. The strict contingentist should not do so, however, for reasons discussed in the next section. There I will revisit the suppositional approach and show how my proposal evades the objections mounted against Fine’s approach in Williamson (2016).

After the construction of counterpart models has been introduced, the next step is to show how we can use them to pretend necessitism. Here the pretend-necessitism-operator $\odot$ comes into play. It allows us to express sentences under the pretence of necessitism. Let A be a formula that is evaluated at the actual world according to $M_c$. Now the result of prefixing A with the pretend-necessitism-operator will be evaluated at the actual world according to $\mathcal {F}(M_c)$.⁷

Formally, one can give the following semantic clause for the $\odot$-operator:

$$\begin{aligned} M, w\models \odot A \quad \text {iff}\quad \mathcal {F}(M), w\models A \end{aligned}$$

The switching of models for the evaluation of formulas embedded under an operator might be a bit unorthodox, but it affords a natural way to model the pretence of necessitism. Philosophers who are appalled by the idea of model-switching will find a way to evaluate all formulas within one overarching semantic model presented in the appendix.

That the given semantic clause leads to the pretence of necessitism, formalized as $\odot \Box \forall x\Box \exists y\;x=y$, is guaranteed by the construction of $\mathcal {F}$. Every individual (or higher-order entity) that is in the domain of some world in $M_c$ is in the domain of every world in $\mathcal {F}(M_c)$. This also gives us the result that $\forall x\odot \Box \exists y (x=y)$. The informal idea is that when the contingentist pretends necessitism, they take the same things to be around in space and time and they take these to be exactly as they actually are. Only the quantifiers are taken to have more to range over, namely the possible entities of other possible worlds.

We can now make sense of the claim that most possible people will never be born as follows. Let ‘P’ say of individuals that they are persons, let ‘B’ say of individuals that they will be born, let $\mathcal {M}$ be the most-quantifier and let ‘$\mathcal {M} xy (A[x],B[y])$’ say that most individuals of which A holds are such that B holds of them (see Fritz & Goodman, 2017, fn. 43). Now ‘$\odot \mathcal {M} xy (\Diamond Px, \lnot By)$’ can be taken to express that most possible persons will never be born. The $\odot$-operator leads to evaluating the formula in a necessitist model. The quantifier ranges over all objects in the constant domain of this model (chunky or not), and the quantified sentence as a whole says that most of these objects that are persons in some world will never be born in the actual world.

As will be shown in an appendix, the $\odot$-operator obeys the following principles:

$$\begin{aligned} K_{\odot }&: \odot (A\rightarrow B)\rightarrow (\odot A\rightarrow \odot B)\\ D_{\odot }&: \odot A\rightarrow \lnot \odot \lnot A\\ CD_\odot&: \lnot \odot \lnot A\rightarrow \odot A\\ 4_{\odot }&: \odot A\rightarrow \odot \odot A\\ 5_{\odot }&:\lnot \odot \lnot A\rightarrow \odot \lnot \odot \lnot A \end{aligned}$$

Notably, the axiom

$$\begin{aligned} T_{\odot }: \odot A\rightarrow A \end{aligned}$$

is not valid (and will plausibly fail in many models). According to the contingentist $\Diamond \exists x A(x)\wedge \lnot \exists x \Diamond A(x)$ is plausibly true for some instances of A (for the contingentist will likely allow failures of the Barcan formula), but $\Diamond \exists x A(x)\rightarrow \exists x \Diamond A(x)$ will, for arbitrary M, be true at every world of $\mathcal {F}(M)$ (by the design of $\mathcal {F}$).

Concerning quantificational principles, it should be noted that while

$$\begin{aligned} BF_{\odot }:\forall x\odot A(x)\rightarrow \odot \forall x A(x) \end{aligned}$$

is not a theorem, its converse

$$\begin{aligned} CBF_{\odot }: \odot \forall x A(x)\rightarrow \forall x\odot A(x) \end{aligned}$$

is.⁸

I will proof these claims by means of a semantic argument in the appendix. This will be done by providing a semantic model for the $\odot$-operator that does without mapping models onto further models, but internalises the mapping to one overarching model. In this model the $\odot$-operator works as a usual necessity-operator.

Once the domains of individuals of the necessitist models are constructed (by taking the union of the domains of individuals of the corresponding contingentist models), the higher-order domains of the necessitist models can be generated from them. This can be done straightforwardly if intensionalism is assumed. Taking properties of individuals as an example, the intensionalist takes every subset of the necessitist domain of individuals to model the semantic value of a monadic first-order predicate.⁹

Up to now I have focused on individual models and their counterparts. However, for reasons that will become clear in the next section, the strict higher-order contingentist cannot non-arbitrarily settle on one particular model. This will force the strict contingentist to accept indeterminacy, a feature that will be discussed in the next section.

3 Modalized quantification and indeterminacy

Can there be two models that agree on all sentences that the strict contingentist accepts without paraphrase¹⁰ and at the same time disagree on which sentences are true under the pretence of necessitism? As it is shown in Fritz (2018) and Fritz and Goodman (2017), the answer is: Yes. The example-sentence (Particles) is such a sentence. One can construct two models that Fritz and Goodman describe as follows:

‘In one model the domain of all possible individuals is countable, while in the other model the domain of all possible individuals is uncountable. In both models, every finite subset of possible individuals is the domain of some world, all worlds have finite domains, and no two worlds have the same domain; the actual worlds of both models have the same domain. We generate higher-order domains from the first-order domains in accordance with the idea that the distinctions that there are at a world are exactly those that can be drawn using the materials that there are at that world. (...) [W]e can prove that the two models validate exactly the same formulae of our infinitary higher-order modal language.’ (Fritz & Goodman, 2017, p. 1083)¹¹

By assuming that the individuals are particles, we arrive at a pair of models that differ with respect to whether (Particles) should be interpreted as true at them. After all, the union of the domains of one of the models is countable, the union of the domains of the other model is uncountable. This shows that there are facts about models that seem to be inexpressible from the perspective of any particular world in the model. For the strict contingentist, there seems to be no way to non-arbitrarily decide between models that are different but accord insofar as they model all the truths that can be stated from the perspective of the actual world. Given that the strict contingentist should avoid arbitrary decisions, they should accept all such models as admissible.

At this point I assume that the strict contingentist should accept that a description of modal space stated without employing the pretend-necessity operator is all they are entitled to. We can call all true modal statements not involving the pretend-necessity operator the contingentist’s modal theory. According to my assumption, the contingentist should accept that this modal theory fixes all determinate truths about modal space (understood as truths about all possible worlds and their inhabitants). As a result, some aspects of modal space will be left underdetermined (e.g. the question how many non-actual objects there are). Given that determinacy is understood as a modality (as it is suggested by the supervaluationist treatment), there are various ways modal space could be like and actuality is unsettled between these ways for modal space to be. In making this assumption, I deny the contingentist any ideology that the necessitist might find objectionable. In particular, I deny any reference to merely possible objects or truths about what modal space would look like if necessitism were true that are not mandated by the contingentist’s modal theory. This makes my proposal acceptable for the strict contingentist and forestalls the objection that the contingentist uses expressive means that are undermining their view.¹²

If we stick to the assumption that the strict contingentist’s modal theory gives us all the determinate facts about modal space, one might wonder how many models agree on all these facts. How many admissible models are there? Fritz proves the claim that (given one focuses on closed models, a certain class of models that are argued to be suitable for modelling higher-order contingentism in Fritz and Goodman 2016) ‘there are at least $\kappa$ many possible individuals, for a given uncountable cardinality $\kappa$, is inexpressible’ (Fritz, 2018, p. 652). There are proper class many uncountable cardinalities, which leads to the result that the strict contingentist should be prepared to accept that there are proper class many admissible models.

How can the strict contingentist interpret modal discourse, given this plethora of admissible models? The straightforward option I will defend is to supervaluate on these models. According to this procedure, a formula A is determinately true (or supertrue) iff it is true in all admissible models, determinately false (or superfalse) iff true in no model, and indeterminate otherwise. More precisely:

• A is determinately true iff every $M\in \mathbb {M}_C$ is such that $M,@\models A$.

• A is determinately false iff every $M\in \mathbb {M}_C$ is such that $M,@\models \lnot A$.

• A is indeterminate iff (i) some $M\in \mathbb {M}_C$ is such that $M,@\models A$ and (ii) some $M\in \mathbb {M}_C$ is such that $M,@\models \lnot A$.

Note that these clauses only use the distinguished actual world. For a modal statement to be true is for it to be true at the actual world. For this reason there is no need to assume that the admissible models agree on which and how many worlds there are. The non-actual worlds only serve the purpose of semantic modelling. Also note that I only talk about indeterminacy in the metalanguage, not in the object-language. This avoids questions concerning the behaviour of an indeterminacy-operator in the object-language, in particular how it behaves in embedded contexts, that are only tangential to the current project.

The admissible models were accepted as admissible on the basis of agreeing on all sentences that the strict contingentist accepts without paraphrase. For this reason all these sentences are either determinately true or determinately false. The option of indeterminacy only kicks in when the troublesome talk that seems to be about mere possibilia comes into play. Given the framework constructed in the last section, only sentences involving the $\odot$-operator are candidates for indeterminacy.

The strict contingentist should be prepared that some sentences involving modalized quantification will be indeterminate. Above I assumed that there are predicates in our language that allow to say of a collection of things how many they are. This allows to say of domains of individuals whether they have uncountably many members. If we are in a situation as described above, then some members of $\mathcal {F}(\mathbb {M}_c)$ will be such that there are uncountably many members in the domains of the worlds, whereas others will be such that the domains are countable. Hence the models will disagree on the truth our paraphrase of (Particles).¹³

At this point it should be clear how my proposal differs from Fine’s suppositional approach. By not presupposing a particular distinguished model that yields the contingentist’s modal formula, I, unlike Fine, do not make use of a distinguished possibilist modal pluriverse. Fine’s proposal can be read as the instruction to ‘suppose, of each possible object, that necessarily there is some actual thing that it is’ (Fine, 2016, p. 564). Williamson objects that ‘to suppose something about a non-actual object is to go beyond actualist terms’ and that, for this reason, ‘we have not been given a reduction of possibilist to actualist discourse in any useful sense’ (Williamson, 2016, p. 583).

I do not propose to pretend for any (actual or non-actual object) that it necessarily actual, but to pretend the truth of necessitism. That I do not pretend something of any objects makes my proposal immune to Williamson’s worry. This and the fact that my proposal incurs indeterminacy are related. If we (assuming that there are possible objects to suppose something for them) first take every possible object and then suppose for each of them that it is necessarily actual, then we arrive at a single necessitist model that gives the way modal would determinately be like if every entity was actual. If we suppose necessitism without supposing anything of any object, we might not get a determinate way modal space would be like if everything was actual. Here is an independent case to make the point that the procedures crucially differ: If we suppose of every one of the 36.465 boats that exist that it is made of wood, then we arrive at a supposition according to which there are 36.465 boats that are made of wood. If we suppose that every boat is made of wood (without supposing anything of a particular boat), then we do not make a supposition that gives us a determinate number of boats.¹⁴

At this point some readers might wonder whether I did in fact help myself not to one distinguished possibilitst pluriverse (like Fine does), but to a plethora of candidate-pluriverses, each of which is given by one of the admissible models. My response is that my use of model-theoretic resources does not commit me to there being any (candidate) modal spaces or possibilist pluriverses. I do not claim that any of the models exhaustively describes some reality, only that they can be used to understand how the $\odot$-operator works. My stance towards both the contingentist and the necessitist models is instrumentalist. The models are not assumed to be isomorphic to reality, for there might well be proper class many objects (e.g. pure sets) while every model has a set-sized domain.

What kind of indeterminacy is the contingentist committed to? Is it semantic indeterminacy or metaphysical determinacy? The solution could be developed in either way, so we can allow for disagreement among contingentists. In fact, I think, different stripes of contingentists can be distinguished based on how they interpret the resulting indeterminacy.

Following Barnes and Williams (2011), we can characterize metaphysical indeterminacy as indeterminacy that persists even if all semantic indeterminacy is resolved. A position that plausibly takes the vocabulary involved in the supposition of necessitism to be semantically indeterminatey is modal logicism as described in Rayo (2020). Rayo identifies Williamson’s necessitist doctrine with the conjunction of the claim that necessarily everything necessarily exists and the claim that it is possible to quantify over absolutely everything (which Rayo calls ‘Absolutism’). Rayo observes that ‘[b]y Absolutism, there is a definite answer to the question of how many individuals there are’ (Rayo, 2020, p. 3). By the assumption that necessarily everything necessarily exists, it follows that there could not be more individuals than there actually are. This contradicts the conviction of the proponent of an infinitely extensible ontology who claims that for every collection of objects xx, there could be all objects among xx and then some. Rayo proposes (on behalf of the modal logicist) that an answer to the question how many objects there are is always dependent on a what he calls a ‘partition of logical space’. Such a partition exhaustively divides the space of ways the world can be into mutually exclusive maximal possibilities (or possible worlds, if you will). Each partition has its own necessity-operator, which can identified with a candidate precisification of ‘it is necessary that’. This would allow the contingentist to characterize the indeterminacy of sentences involving the $\odot$-operator as semantic indeterminacy. Each model in $\mathbb {M}_C$ corresponds to a way to carve modal space and models a distinct maximally precise notion of necessity.¹⁵

Philosophers who have sympathies for the claim that ‘it is necessary that’ and the other locutions involved are not semantically indeterminate will hold that questions like the one whether (Particles) holds are maximally precise questions that receive indeterminate answers because the world does not decide on their truth. There is one maximally precise notion of metaphysical necessity, but it is worldly indeterminate which propositions are necessary. The availability of this option shows that the present strategy is compatible with a view on which modal notions are joint carving (in the sense of Sider 2011 and contrary to what Sider himself argues in Sider 2011, §12), as long as it is accepted that the answers to questions formulated in joint-carving notions can be metaphysically indeterminate.¹⁶

There is no need to decide in the context of this paper. In any case, sentences involving modalized quantification will be interpreted as meaningful. This allows to deny premise (3) of the anti-contingentist argument presented in the first section. However, many of these meaningful sentence will be indeterminate. For this reason my proposal demands accepting (3$^{\prime }$) of the modification of the above argument. The contingentist hence has to deny (2$^{\prime }$). Is this a tenable position?

There seem to be two main objections against this view of modal space. The first one (directed at those who take the indeterminacy to be metaphysical) concerns the general question whether indeterminacy in the world should be accepted. This question cannot be properly addressed in the scope of this paper. It should be mentioned, however, that numerous recent contributions to the metaphysical literature defend the theoretical viability of metaphysical indeterminacy and offer ways for it to be understood.¹⁷ This suggests that proposals that make use of metaphysical indeterminacy deserve being taken seriously.

The second, more specific objection, targets the proposed denial of (2$^{\prime }$). For reasons given in the first section, I agree with those who press the paraphrase challenge that it would be unmotivated for the contingentist to deny (2) and to hold that some (well-formed) sentences involving modalized quantifications are intelligible and others are not. At the same time I maintain that holding that some of these sentences have determinate truth-values whereas others are indeterminate is tenable. One might worry that considerations parallel to those that support (2) also support (2$^{\prime }$).

The contingentist can respond by clarifying what their metaphysical commitments allow them to state. i.e. to give a principled account of the limits of their modal theory (as this locution has been introduced above). According to the paraphrase challenge no modal theory that is metaphysically acceptable for the contingentist allows them to make sense of discourse involving modalized quantification. The proposal made in this paper responds to this challenge by showing that the contingentist can make sense of discourse involving modalized quantification even if the truth-values of some parts of this discourse are not settled by their modal theory. It is an entirely different challenge for the contingentist to give a principled account of which parts of this discourse remains indeterminate. Speaking in terms of truthmakers, the paraphrase-challenge is based on the worry that the contingentist does not have enough truthmakers at their disposal. The new challenge is based on the worry that the contingentist has no principled way to decide which truthmakers they have at their disposal. This new challenge has to be met, preferably by developing a principled modal theory for higher-order contingentists. It is, however, largely independent from the paraphrase-challenge and requires its own discussion.

Understanding the necessitist claims but refusing to accept that they have a determinate answer is a compromise between pretending to not understand and providing determinate answers. This gives us at least a prima facie case for indeterminacy.

4 Pretence and hyper-possibility

Fritz and Goodman discuss and object to a strategy they call hyper-possibility paraphrases. They explicitly take proposals based on fictions (or pretence) and those based on counterfactually supposing necessitism to be instances of this strategy (see Fritz & Goodman, 2017, p. 1089). They take the unifying idea behind these strategies as follows: ‘The most promising versions of these proposals are all instances of a more general paraphrase strategy, appealing to some notion of possibility distinct from metaphysical possibility (fictional possibility, counterfactual possibility, etc.) according to which it is possible for there to be all actually metaphysically possible individuals’ (Fritz & Goodman, 2017, p. 1090). The way my operator works allows quantifying into its scope.¹⁸ If one uses methods like Vlach-operators, there would also be no problem about scoping out of the $\odot$-operator. For this reasons I assume that my proposal meets the success condition specified in Fritz and Goodman (2017, §4.2) and I will focus on how my proposal handles the revenge problem layed out in Fritz and Goodman (2017, §4.3). Here is how they spell out the revenge problem:

‘The same considerations that lead us to think that all metaphysically possible elementary particles are metaphysically incompossible should lead us to think that all metaphysically possible elementary particles are hyper-incompossible, namely, that it is hyper-necessary that whatever actually metaphysically possible elementary particles there are, it is hyper-possible that there be all of them and one more actually metaphysically possible elementary particle.’ (Fritz & Goodman, 2017, p. 1092)

The $\odot$-operator is its own dual (as it is witnessed by $D_{\odot }$ and $CD_{\odot }$), so if it is interpreted as a hyperpossibility-operator, then hyperpossibility and hypernecessity turn out to be identical. This makes it hard to see how the revenge-worry could be formulated as a worry that tells against my strategy.

In any case, I agree (at least for the sake of argument) that contingentists are committed to the claim that all metaphysically possible particles are metaphysically incompossible. Under the pretence of necessitism, things are less clear. The necessitist cannot accommodate that necessarily, whichever objects there are, there could be one more metaphysically possible elementary particle. The reason is that necessitists believe that every metaphysically possible elementary particle exists at every world. How does the necessitist evade the worry that some objects are incompossible and hence cannot exist at the same world? The necessitist can easily accommodate that whichever individuals are chunky, possibly all of them and one more are chunky. The necessitist will argue that the cases that lead the contingentist to accepting incompossibility turn out to be cases of impossible joint chunkiness (rather than impossible joint existence).¹⁹ If this way to evade the worry is successful for the necessitist, it seems unclear to me why the pretender of necessitism cannot simply insist that under the pretence of necessitism, there is no possibility for the existence of any objects, but those that necessarily exist. If the necessitist can solve the problem, then this solution also works under the pretence of necessitism.

However, one might worry that the necessitist is not successful in avoiding a worry very close to the above revenge worry. It has been argued (by e.g. Sider 2009, Rayo 2020; Roberts 2019) that modal space is infinitely extensible in the sense that there is no plurality of objects xx such that it is absolutely impossible that there are all among xx and then some. If the arguments for infinite extensibility are successful, then the necessitist seems to be in trouble, for they arguably are committed to there being plurality of objects xx such that necessarily all and only the xx exist. I cannot discuss whether this objection against necessitism is successful in the context of this paper. For my present purposes it is sufficient to note that if the objection is fatal for necessitism, then it cannot be used by the necessitist to argue against a contingentist proposal on how to interpret necessitist discourse for dialectical reasons.

The proponent of the revenge worry hence faces a dilemma: Either the defender of the pretence strategy can make use of the necessitist’s solution to the worry, or the necessitist is in no position to use the worry against the contingentist. However, the proponent of the pretence strategy can say more about the second horn than diagnosing that the situation is dialectically unstable for the necessitist. They can accommodate the extensibility worry. My proposal is compatible with the claim that it is indeterminate how many entities there would be if necessitism was true. It allows that (i) for every admissible model M, there is another admissible model $M^{\prime }$ such that the fusion of the domains of all worlds in $M^{\prime }$ is a proper superset of the fusion of the domains of all worlds in M and that (ii) there is no upper bound on the cardinality of the domains of the models. I contend that this does justice to the spirit of the revenge worry to the extent to which its spirit should be done justice to and that it also gives us a relevant sense of infinite extensibility.

Appendix: An alternative semantics for the pretence-operator

The idea of a model-switching semantic clause for the $\odot$-operator might raise some eyebrows (although it is technically unproblematic and, as a reviewer pointed out, model changes are extensively studied in dynamic epistemic logic). One way to avoid changing models (suggested by a referee) would be to semantically define what it is for a sentence to be suppositionally true in a contingentist model (by using quantifiers that range over the union of all objectual domains) and to then say that $\odot A$ is true in a model just in case it is suppositionally true in the model. The aim of this appendix is to present a further way to model the $\odot$-operator using a binary accessibility-relation.

We, again, start with a contingentist model $M_c=\langle W,@,\mathcal {D},R, V\rangle$. From this model the pretence-allowing model $M_{\odot }=\langle W_{\odot },@,\mathcal {D}_{\odot },R_{\Diamond },R_{\odot }, V_{\odot }\rangle$ will be generated as follows: $W_{\odot }= W\times \lbrace 1,2\rbrace$. World-number-pairs whose second place is occupied by the number 1 will play the role of contingentist worlds and those whose second place is occupied by the number 2 play the role of necessitist worlds. $\mathcal {D}_{\odot }$ is a function such that for every $w\in W$, $\mathcal {D}_{\odot }(\langle w,1\rangle )=\mathcal {D}(w)$ and $\mathcal {D}_{\odot }(\langle w,2\rangle )= \bigcup \lbrace \mathcal {D}(v)\mid v\in W\rbrace$ (the union of the domains of all worlds in W). For every predicate P (logical or non-logical) and $w \in W$, $V_{\odot }(P, \langle w,1\rangle )=V(P,w)$ and for every non-logical predicate F furthermore $V_{\odot }(F, \langle w,2\rangle )=V(F,w)$. Logical predicates are allowed to apply to all objects in the domain of the necessitist worlds $\langle w,2\rangle$. It is easy to check that this semantics is set up such that (i) $M_c, w\models A$ iff $M_\odot , \langle w,1\rangle \models A$ and (i) $\mathcal {F}(M_c), w\models A$ iff $M_\odot , \langle w,2\rangle \models A$. This feature allows to semantically interpret formulas involving the $\odot$-operator without a change in models.

$R_{\Diamond }$ is the accessibilty-relation used to model the usual modal operators $\Box$ and $\Diamond$. For every $w,v\in W$, $\langle \langle w,1\rangle ,\langle v,1\rangle \rangle \in R_{\Diamond }$ iff $\langle \langle w,2\rangle ,\langle v,2\rangle \rangle \in R_{\Diamond }$ iff $\langle w,v\rangle \in R$. For no $w,v\in W$ we have $\langle \langle w,1\rangle ,\langle v,2\rangle \rangle \in R_{\Diamond }$ or $\langle \langle w,2\rangle ,\langle v,1\rangle \rangle \in R_{\Diamond }$ (if necessitism is true/false, then it is necessarily true/false). This yields the result that if R is an equivalence-relation then so is $R_{\Diamond }$. If R partitions the worlds into one equivalence class, then $R_{\Diamond }$ partitions it into two equivalence classes. This guarantees an S5-modal logic for necessity. $R_{\odot }$ will be used to model the $\odot$-operator. For every $w\in W$, the pair $\langle \langle w,1\rangle ,\langle w,2\rangle \rangle$ is in $R_{\odot }$. Additionally, for every $w\in W$, the pair $\langle \langle w,2\rangle ,\langle w,2\rangle \rangle$ is in $R_{\odot }$. No further elements are in $R_{\odot }$. Every world sees exactly one world, namely its necessitist counterpart-world (which might be itself, if it is a necessitist world).

The semantic clause for the $\odot$-operator reads:

$$\begin{aligned} M_{\odot },w_\odot \models \odot A\;\text {iff for every}\;v_\odot \in W_\odot \;\text {such that}\;\langle w_\odot , v_\odot \rangle \in R_{\odot }: M_{\odot },v_\odot \models A \end{aligned}$$

According to this semantic clause the $\odot$-operator works like a usual necessity-operator. It is easy to check that $R_{\odot }$ is serial, transitive, euclidean, and functional. These conditions yield the modal theorems $D_\odot$, $4_\odot$, $5_\odot$ and $CD_{\odot }$, respectively. $R_{\odot }$ is not reflexive, which allows for failures of $T_\odot$. To see that this model validates $CBF_\odot$ and does not validate $BF_\odot$, it is crucial to see that if $\langle w_\odot , v_\odot \rangle \in R_{\odot }$, then it is guaranteed that $\mathcal {D}(w_\odot )\subseteq \mathcal {D}(v_\odot )$, but not that $\mathcal {D}(v_\odot )\subseteq \mathcal {D}(w_\odot )$.