Introduction

In the pursuit of materials development for extreme environments, 3D microstructural information is essential input for structure-property models1. Many engineering materials are polycrystalline, meaning they are composed of many smaller crystals called grains, and the arrangement of these grains impacts their thermomechanical properties. To collect crystallographic microstructure information, 3D microscopy techniques have been developed that span lengthscales from nanoscale to mesoscale2. These experiments require costly or challenging to access equipment, like synchrotron light sources for high X-ray fluxes3,4,5, precise automated robotic mechanical polishing and imaging6,7, or high-energy ion beams and/or short pulse lasers coupled to electron microscopes8,9. Recent advances in 3D characterization have reduced the time required for data collection, but serial sectioning methods (where material is progressively removed from the sample between images) are still slow processes that require expensive microscopes10,11. During serial sectioning for microstructural information, typical experimental steps might include material removal and cleanup (mechanical polishing, laser ablation, focused ion beam milling) and imaging for orientation or chemical information. As such, any efforts that reduce the total number of required serial sections in a 3D experiment will ultimately lead to substantive time and cost savings.

One such 3D material characterization technique is 3D electron backscatter diffraction, or EBSD. EBSD is a scanning electron microscope (SEM) imaging modality that maps crystal lattice orientation by analyzing Kikuchi diffraction patterns that are formed when a focused electron beam is scattered by the atomic crystal structure of a material according to Bragg’s law. A grid of Kikuchi patterns is collected by scanning the electron beam across the sample surface. These patterns are then indexed to form a grid of orientations, which are commonly represented as images in RGB color space using inverse pole figure (IPF) projections. EBSD maps are used to determine the microstructural properties such as texture, orientation gradients, phase distributions, and point-to-point orientation correlations, all of which are critical for understanding material performance12. When scaling to 3D, these EBSD scans must be done sequentially with serial sectioning, which is a time-consuming and energy-intensive process, often requiring hundreds of millions of EBSD patterns to be collected per sample. This cost motivates methods to reduce the number of required points, such as smart or sparse sampling13,14,15, or machine learning super-resolution16. In these methods, missing information can be inferred using interpolation-based algorithms (bicubic, bilinear, or nearest neighbor) or data-based learning. Recent progress in computer vision16,17,18 has shown that the generation of missing samples/data with data-based learning outperforms traditional interpolation algorithms for RGB images. However, unlike RGB images, EBSD maps carry embedded crystallography, so existing learning-based methods are not well suited to generate missing EBSD data.

In our previous work19, we developed a deep learning framework for 2D super-resolution that utilized an orientationally-aware, physics-based loss function to generate high-resolution (HR) EBSD maps from experimentally gathered low-resolution (LR) maps. This approach allowed for significant gains in 2D resolution, but expansion to 3D remained difficult due to data availability limitations (3D EBSD is expensive and time consuming to gather). To address this, here we have designed a 3D deep learning framework based on quaternion convolution neural networks (QCNN) with self-attention alongside physics-based loss to super-resolve high resolution 3D maps using as little data as possible. Using real-valued convolution for quaternion-based data has been shown to be inefficient and has loss in the inter-channel relationship that arise from quaternion vector interdependencies20; which leads to longer training times and larger data burdens. We demonstrate that a quaternion-valued neural network is more efficient and produces better results than real-valued convolution neural networks such as those used in previous work19.

The crystallographic information contained in EBSD maps is generally expressed in the form of crystal orientations spatially resolved at each pixel or voxel. These orientations, like other rotational data, can be expressed unambiguously using quaternions. They therefore can be incorporated into network architecture as prior information by using quaternion-valued convolution for local-level correlation, rather than real-valued or complex-valued convolution. The basic component in traditional CNN-based architectures is real-valued convolutional layers, which extract high-dimensional structural information using a set of convolution kernels. This approach is well-suited for unconstrained image data like RGB, but when convolution kernels fail to account for strict inter-channel dependencies where present, the result is greater learning complexity. Some successful efforts have been made to design lower-complexity architectures by extending real-valued convolution to complex-valued convolution21,22 and quaternion-valued convolution23,24,25 in the field of robotics26, speech and text processing20, computer graphics27,28, and computer vision25,29. Although these convolution layers are useful to learn local correlations, they struggle to learn long-range correlations, whereas transformer-based architectures have recently shown significant success in learning long-range correlations in natural language30 and vision tasks18,31. However, the computational complexity of transformer-based architectures grows quadratically with the spatial resolution of input images due to self-attention layers, so transformers alone are not well-suited for restoration tasks. However, recent work by Zamir18 proposed self-attention across channel dimensions to reduce complexity from quadratic to linear with progressive learning for image restorations and showed superior results to convolution-based architecture alone.

Inspired by this idea, we propose the use of quaternion self-attention for EBSD super-resolution, using physics-aware quaternion convolution for orientation recognition, a physics-based loss function that is sensitive to material crystal symmetry, and progressive learning to incorporate long-range material relationships. Physics-aware quaternion convolution follows the approach of20,21,32, where convolution is depth-wise and uses a reduced number of interdependent weights whose connectivity is based on the Hamiltonian. We use a loss function that accurately measures the crystal orientations in EBSD maps and also accounts for the hexagonal close-packed symmetry present in α-phase Ti-6Al-4V and Ti-7Al, the two alloys investigated here. Finally, progressive learning refers to having variable patch sizes instead of fixed patch sizes during training, which is relevant for most engineered material microstructures, where important features can span across length scales (and patch sizes). The titanium alloys studied herein are well-known to have many different microstructural variants accessible via processing, resulting in varying grain size and morphology. For the datasets that we consider specifically, the Ti-6Al-4V variant has smaller equiaxed grains, while the Ti-7Al alloy has much larger grain size, so applying a fixed patch size across these two materials would be sub-optimal. To enforce long-range learning among these grain features, we used progressive patch sizes starting from 16 to 100 during the training of the network. Training behaves in a similar fashion to curriculum learning processes where the network starts with a simpler task and gradually moves to learning more complex ones.

Results

Deep learning framework

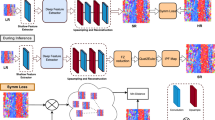
The objective of our framework is to generate missing sample planes from experimental 3D EBSD data that is sparse along the z-axis. In this approach, material researchers collect sparsely sectioned 3D EBSD data (blue planes) as shown in Fig. 1a, due to the high cost associated with serial sectioning and collecting 3D EBSD data at higher resolution. Ideally, a 3D deep learning framework would be designed to generate the missing planes (gray planes), but experimental EBSD data is costly to gather, so available 3D data is extremely limited. Additionally, 3D neural networks require more learned parameters, which, with limited available data, increases the likelihood of overfitting. Instead of a full 3D architecture, a deep learning network is implemented on 2D EBSD maps orthogonal to the sectioned planes, shown as the xz or yz planes in Fig. 1c. Our network takes sparsely sectioned xz or yz EBSD maps as input to generate the missing rows normal to the z-axis. The generated 2D EBSD maps are then combined into a 3D volume. EBSD collection is a point-based scanning method that is directionally independent; therefore missing z rows can be generated from xz or yz EBSD maps, and two 3D volumes can be formed from each sparsely sectioned dataset.

Fig. 1: Q-RBSA EBSD Resolution Enhancement Framework.
figure 1

In the experimental pipeline shown in (a), material researchers collect EBSD orientation information for each (x,y) coordinate in a given sectioning plane, and then remove material using laser ablation or robotic polishing to reach the next plane in the z direction to build a 3D volume. In our framework (b), researchers collect EBSD information from a reduced set of points (blue planes), omitting some planes that would normally be gathered (gray planes). The missing information (green planes) are then generated in 2D as a series of (x,z) or (y,z) planes by our quaternion-based, physics-informed deep learning framework, shown in (c). Here, the network takes advantage of orthogonal independence to efficiently generate 3D volumes using less data, as large amounts of EBSD are costly and the choice of serial sectioning direction has minimal impact on the resultant final volume.

Full size image

Network architecture

Although EBSD maps are visualized similarly to RGB images, they are multidimensional maps with inter-channel relationships, where crystal orientation is described using Euler angles, quaternions, matrices, or axis-angle pairs. Our previous work19 demonstrated that quaternion EBSD representation is well-suited to orientation expression for loss function design, due to its efficient rotation simplification and avoidance of ambiguous representation. However, we previously used real-valued convolution layers to learn features, which is sub-optimal for EBSD orientation maps where orientations are represented as unit-vector quaternion rotations. Generally speaking, convolution networks provide local connectivity and translation equivariance, which are desirable properties for images, but if additional feature correlations are going to be learned efficiently, it is critical to encode relevant structural modalities into the network architecture and loss function. Real-valued convolution can still learn unit quaternion inter-channel information, but it requires extra network complexity, and by consequence, additional data to inform that complexity. Here, the use of quaternion convolution efficiently encodes prior orientation information into kernels, and also has the advantage of reducing the number of trainable parameters by 4, as explained supplementary.

QCNN33 use basic quaternion convolution operation which computes the Hamilton product between the input feature maps and kernel filters rather than just computing correlations between them, as is done in real-valued convolution34. For instance, if we consider Pinput as an input feature map of size (4K2 × H × W), and F as a quaternion kernel filter of size (4K2 × f × f), where K2 is the number of kernel filters in the previous layer, H and W are the height and width of the input feature map (Pinput), and f is the spatial size of the quaternion kernel filter (F), then we can split the input feature map (Pinput) into four components (PR, PX, PY, PZ) along the channel dimension, where each component has a dimension of (K2 × H × W). Similarly, the kernel filter (F) can be divided into four components (FR, FX, FY, FZ) along the channel dimension, where each component has a dimension of (K2 × f × f). The quaternion convolution (QConv) of input feature maps (Pinput) with a single kernel filter (F) is defined as follows

$${P}_{quaternion}^{{\prime} }=F\otimes {P}_{input}$$
(1)
$$\left[\begin{array}{c}{P}_{R}^{{\prime} }\\ {P}_{X}^{{\prime} }\\ {P}_{Y}^{{\prime} }\\ {P}_{Z}^{{\prime} }\end{array}\right]=\left[\begin{array}{c}{F}_{R}* {P}_{R}-{F}_{X}* {P}_{X}-{F}_{Y}* {P}_{Y}-{F}_{Z}* {P}_{Z}\\ {F}_{X}* {P}_{R}+{F}_{R}* {P}_{X}-{F}_{Z}* {P}_{Y}+{F}_{Y}* {P}_{Z}\\ {F}_{Y}* {P}_{R}+{F}_{Z}* {P}_{X}+{F}_{R}* {P}_{Y}-{F}_{X}* {P}_{Z}\\ {F}_{Z}* {P}_{R}-{F}_{Y}* {P}_{X}+{F}_{X}* {P}_{Y}+{F}_{R}* {P}_{Z}\end{array}\right]$$
(2)

Here, ⊗ is the Hamilton product, and * represents real-valued convolution operation34. The output quaternion feature map (\({P}_{quaternion}^{{\prime} }\)) has a dimension of (4 × H × W) for a single kernel filter, where each component (\({P}_{R}^{{\prime} },{P}_{X}^{{\prime} },{P}_{Y}^{{\prime} },{P}_{Z}^{{\prime} }\)) has a dimension of (1 × H × W). H and W are the height and width of the output feature maps. For a better understanding of quaternion convolution, please refer to the Supplementary Figs. 1, 2, 3 as provided in the supplementary section.

Introducing non-linearity through an activation function is not straightforward for quaternions, as the only functions that satisfy the Cauchy-Riemann-Fueter equations in the quaternion domain are linear or constant32. However, locally analytic quaternion activation functions have been adapted for use in QNNs with standard backpropagation algorithms35,36. There are two classes of these quaternion-valued activation functions: fully quaternion-valued functions and split functions. Fully quaternion-valued activation functions are an extension to the hypercomplex domain of real-valued functions, such as sigmoid or hyperbolic tangent functions. Despite their better performance37, careful training is needed due to the occurrence of singularities that can affect performance. To avoid this, split activation functions37,38 have been presented as a simpler solution for QNNs. In split activation functions, a conventional real-valued function is applied component-wise to a quaternion, alleviating singularities while holding true the universal approximation theorem as demonstrated in38. We have used the split ReLU function which is defined as follows:

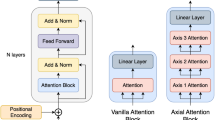
$$ReLU({P}_{quaternion}^{{\prime} })=\left[\begin{array}{c}ReLU({P}_{R}^{{\prime} })\\ ReLU({P}_{X}^{{\prime} })\\ ReLU({P}_{Y}^{{\prime} })\\ ReLU({P}_{Z}^{{\prime} })\end{array}\right]$$
(3)

Our network architecture shown in Fig. 2 consists of three parts: a shallow feature extraction module, a deep feature extraction module, and an upsampling and reconstruction module.

Fig. 2: Quaternion Residual Block Self-attention (QRBSA) network.
figure 2

A sparsely sectioned 2D EBSD map is given to the QRBSA network (a) to generate a high-resolution 2D EBSD map. QRBSA consists of three parts: a Shallow feature extractor, a Deep feature extractor, and Upsampling and Reconstruction. The deep feature extractor uses a residual architecture (b) where residual self-attention blocks (c) are modified with quaternion convolution layers and transformer blocks (d) to efficiently handle orientation data. Quaternion convolution is used to learn local-level relationships, while quaternion transformer blocks learn the global statistics of feature maps. Pixelshuffle layer, modified for 1-dimensional upsampling, is used in the upsampling and reconstruction block to upsample feature maps.

Full size image

Shallow Feature Extractor module uses a single quaternion convolution layer (QConv), explained in Eq. (2), to reduce the spatial size of sparsely sectioned EBSD maps, while extracting shallow features.

$$\begin{array}{r}{F}_{0}={H}_{SF}({I}_{LR})\end{array}$$
(4)

Here, ILR is a sparsely sectioned 2D EBSD map and HSF(. ) is a single quaternion convolution layer of kernel filter size 3 × 3, which has 4 input channels and 128 output channels. The generated shallow features (F0) are given to the deep feature extractor module (HDF).

To learn from sparsely sectioned EBSD maps, our deep feature extractor module uses stacked quaternion residual self-attention (QRSA) blocks to extract high-frequency information and long skip connection to bypass low-frequency information. Residual blocks allow for a deeper network architecture, which provides a larger receptive field and better training stability. In our QRSA module, we use both CNN and transformer ideas to combine the effectiveness of the locality of CNNs with the expressivity of transformers that enables them to synthesize high-resolution EBSD maps. The CNN structure offers local connectivity and translation equivariance, allowing transformer components to freely learn complex and long-range relationships. Each quaternion residual self-attention (QRSA) block consists of two quaternion convolution layers and a piece-wise ReLU activation, explained in Eq. (3), between them, and a quaternion transformer block. The quaternion convolution layers with piece-wise ReLU activation help in learning the local structure of extracted shallow features, while the quaternion transformer block captures long-range correlations among features. The short-skip connection is useful to bypass low-frequency information during training.

$${F}_{DF}={H}_{DF}({F}_{0})$$
(5)
$${H}_{DF}=QRS{A}_{1}\circ QRS{A}_{2}\circ ...QRS{A}_{i}...\circ QRS{A}_{10}\circ QConv+I$$
(6)

where, HDF(. ) is a deep feature extractor module, and FDF is a 128 channels feature map which goes to the upscale and reconstruction module. QConv is a quaternion convolution layer as explained in Eq. (2), QRSAi is a ith quaternion residual self-attention (QRSA) block, and I is an identity feature maps.

The standard transformer architecture30 consists of self-attention layers, feedforward networks, and layer normalization. The original transformer architectures30,39 are not suitable for restoration tasks due to the requirement of quadratic complexity of spatial size \({{{\mathcal{O}}}}({W}^{2}{H}^{2})\), where W, H is the spatial size of images or EBSD maps. Similar to the approach of18 and as shown schematically in Fig. 3, we compute attention maps across the features dimension, which reduces the problem to linear complexity. However instead of depthwise convolution, we use quaternion convolution as explained in Eq. (2), which can be considered as a combination of depthwise convolution and group convolution, but with four-dimensional quaternion constraints. We have also incorporated an equivalent quaternion-based gating mechanism into the feedforward network within the transformer, and the traditional convolution used in18 has been replaced with quaternion convolution layers as explained in Eq. (2) to account for EBSD data modalities. Layer normalization plays a crucial role in the stability of training in transformer architectures. The quaternion layer-normalization is equivalent to the real-valued one by computing normalized features across each component of the quaternion separately, and allows the building of deeper architectures by normalizing the output at each layer. From the normalized features, the quaternion self-attention layer first generates query (Q), key (K) and value (V) projections enriched with the local context. After reshaping query and key projection to reshaped query (Qr) and reshaped key (Kr), a transposed attention map (A) is generated. The refined feature map, which has global statistical information, is calculated from the dot product of the value projection (Vr) and the attention map (A).

$$\,{{\mbox{Transposed Attention Map (A)}}}={{\mbox{Softmax}}}\,\left({K}_{r}.\frac{{Q}_{r}}{\alpha }\right)$$
(7)
$$\,{{\mbox{Quat-SelfAttention}}}({Q}_{r},{K}_{r},{V}_{r})={V}_{r}.{{\mbox{A}}}\,$$
(8)
$$\,{{\mbox{Gating}}}({X}_{2})={{\mbox{GeLU}}}\,({W}_{1}({X}_{2}))\odot {W}_{2}({X}_{2})$$
(9)

Where ⨀ represents elementwise multiplication, α is a learnable scaling parameter to control the magnitude of the dot product of Kr and Qr before applying softmax function and GeLU is Gaussian Error Linear Units activation function40, and Wi (i = 1,2) is a combination of quaternion convolution layers with kernel size 1 and 3, respectively.

Fig. 3: Quaternion Self Attention.
figure 3

Self-Attention in (a) is computed using quaternion convolution across feature dimension instead of spatial dimension to reduce computational complexity to linear. A transposed attention map (A) is calculated from reshaped query (Qr) and reshaped key (Kr). A quaternion self-attention is computed from the transposed attention map (A) and reshaped value (Vr). QUATERNION FEED FORWARD NETWORK: Shown in (b), performs controlled feature transformation to allow useful information to propagate further using gated quaternion convolution.

Full size image

The upsampling and reconstruction module has 1D pixelshuffle layers and quaternion convolution layers of kernel size 3. The original pixelshuffle layer41 is designed for 2D upsampling, but we have modified it for 1D upsampling in our framework that generates information in z dimension. Each block of the upsampling and reconstruction module upsamples deep features by a factor of 2, with the number of blocks depending on the scaling factors.

$${F}_{\uparrow }={H}_{\uparrow }({F}_{DF})$$
(10)
$${I}_{SR}={H}_{R}({F}_{\uparrow })$$
(11)

Where, each upsampling block (H↑) of the module has a quaternion convolution layer of kernel size (3 × 3) as explained in Eq. (2), and a 1D pixel-shuffle layer. The reconstruction block (HR) is a quaternion convolution layer of kernel size (3 × 3).

2D to 3D

The output of the QRBSA network is a 2D high-resolution EBSD map from a sparsely sectioned 2D EBSD map in the z direction. The 2D high-resolution EBSD maps are then combined to make a 3D volume. The missing z rows, as in Fig. 1c, can be generated either from xz plane (ynormal) or yz plane (xnormal). Therefore, there are two ways to form the 3D volume. In this work, we generated both 3D volumes separately, but we plan to design an algorithm in the future to combine the xz plane and yz plane information to make a single 3D volume.

Qualitative output comparison

The sparsely sectioned 3D EBSD data is downsampled by scale factors of 2, 4 in the z dimension by removing the xy planes (znormal) to reflect how EBSD resolution would be reduced in a serial sectioning experiment. Our network QRBSA is trained on 2D orthogonal planes (xnormal and ynormal) of paired sparsely sectioned EBSD maps and high-resolution EBSD maps, generating the high-resolution 2D maps in z dimension shown in Fig. 4. The most noticeable visual defects in 2D appear as pixel noise or short vertical lines, particularly around small grain features and high-aspect-ratio grains whose shortest axis is aligned with the z-direction. In addition to planar output analysis, we can also create 3D volumes from the sparsely sectioned xz planar (ynormal) or yz planar (xnormal) EBSD maps, and then sample the xy planes (znormal) from these volumes, as represented by the black arrows in Fig. 5, to evaluate how well the QRBSA is inferring missing z-sample planes. Note that the planes visualized in Fig. 5 are not immediately adjacent to any ground truth planes. We can observe that our deep learning framework is able to completely predict omitted xy planes, comparably to the ground truth xy plane, with the exception of some shape variations around grain boundaries, particularly in Ti-6Al-4V. We capture these errors in Fig. 5 in the column labeled misorientation angle map, which is contrast scaled such that all misorientation errors greater than 3∘ appear as white. Looking at this map, most of the high misorientation errors are at grain boundaries with the exception of some specific small grains in Ti-6Al-4V. Observations of this difference map indicate that if the xy plane in Fig. 5 had been omitted during experimental data collection, our framework would have estimated it with reasonable accuracy.

Fig. 4: Visual comparison of network output for example 2D EBSD maps with a scale factor of 4.
figure 4

The predicted EBSD maps (Network Output) from the QRBSA network are similar to the ground truth EBSD maps in for both the Ti-6Al-4V dataset (a) and both Ti-7Al datasets (b) and (c). The black rows correspond to the missing data in the sparsely sectioned input EBSD maps. In this case, one row of EBSD data is used for every three rows of missing EBSD data.

Full size image
Fig. 5: Neural network output vs. ground truth with difference map.
figure 5

The deep learning framework is able to estimate the missing xy planes due to sparse z-sampling (gray) with data that looks similar to the ground truth for Ti-6Al-4V in (a) and Ti-7Al in (b) and (c). The misorientation angle map column shows the minimum possible misorientation between ground truth and estimated EBSD maps with 3∘ thresholded maximum to better show low magnitude errors. This map indicates that learning grain shapes for Ti-6Al-4V is more difficult than for Ti-7Al, likely due to smaller grain size and more grain boundary regions.

Full size image

Quantitative output comparison

The pixel-wise distribution of minimum misorientations between network output and ground truth, referred to as misorientation error, is shown in Fig. 6. The x-axes of the histograms are thresholded and separated at 3∘, such that misorientation error of magnitude less than 3∘ is shown in Fig. 6a, and error greater than 3∘ is shown in Fig. 6b, c. These histograms show that the majority of network error is relatively unimodal and smaller in magnitude than about 0.4∘, meaning that it will fall primarily within the dark regions of the grains in the difference maps in Fig. 5, which correspond to small intragranular misorientation errors. On the other hand, most of the high misorientation errors in Fig. 5 are much larger than 3∘, which mostly correspond to errors in predicted grain boundary location, or small grains that were ill-defined in the low resolution input. While these errors are much larger in magnitude, Fig. 6b shows that these represent a very small fraction of network error. A more detailed inspection of this error in Fig. 6c shows that this larger error is relatively random and uniform, with the exception of a spike around 30∘, which can be seen in all three datasets. This spike in error around 30∘ may be related to the hexagonal symmetry of the titanium materials, as 30∘ is a high symmetry rotation within the 6/mmm point group, but even so, these errors represent less than 2% of the total.

Fig. 6: Histogram of Misorientation Angle for Ti-6Al-4V, Ti-7Al 1%, and Ti-7Al 3%.
figure 6

In (a), histograms of misorientation differences between predicted and ground truth are shown, where all values greater than 3∘ are clamped to 3∘. For all materials, most network error in predicted misorientation is lower than 0.5∘ in magnitude. In (b), the same error histograms are displayed, but now misorientation values less than 3∘ are clamped to 3∘. Because larger magnitude errors occur far less frequently than smaller errors, (c) contains a zoomed inset of misorientation angles greater than 3∘ to better show their distribution.

Full size image

The peak signal to noise ratio (PSNR) of misorientation angle between ground truth and experimental EBSD data is shown in Table 1 to quantitatively evaluate the performance of the QRBSA network for scale factors 2 and 4 for all three materials. Higher PSNR values represent more similarity with the ground truth. The PSNR of Ti-6Al-4V is lower compared to Ti-7Al datasets due to its higher texture variability, wider range of orientations, and generally smaller grain features. We performed this same analysis on four different network architectures with different computational complexity, as shown in Table 1.

Table 1 PSNR: comparison of PSNR of misorientation angle and complexity for different networks for scale factors 2 and 4.
Full size table

When considering the relationship between network complexity and performance for this use-case, a simpler deep residual architecture (EDSR)42, outperforms a more complex holistic attention network (HAN)43 on EBSD data despite having significantly lower computational complexity. The amount of available EBSD data in this case is significantly lower than open-source RGB image datasets, so simply increasing network complexity does not improve performance, as this added complexity demands additional training information and does not meaningfully consider relevant data modalities. QEDSR incorporates quaternion considerations in a similar architecture to EDSR, which greatly reduces in the number of network parameters, but also causes a slight drop in performance due to overall lack of complexity. We take advantage of this reduction in complexity to add in additional self-attention for better recognition of long-range patterns and global statistics. This QRBSA network demonstrates the best performance on EBSD map restoration, while still maintaining lower complexity than state-of-the-art residual architectures for single-image super-resolution tasks.

Discussion

Both quantitative and qualitative results demonstrate that this physics-based deep learning framework can accurately estimate the missing xy planes (znormal) of 3D EBSD data for multiple variants of titanium alloys, both with a coarser polycrystalline structure (Ti-7Al) and finer structure with stronger texture (Ti-6Al-4V). In 2D inferred EBSD planes show noise around small features, mostly in the form of point and line defects in the z-direction associated with grains whose overall shape information was lost due to omission of sample planes in low resolution. It is possible that a downsampling approach incorporating anti-aliasing could prevent this shape information loss44, but this approach would not be reflective of actual experimental downsampling in 3D EBSD. This general shape loss effect, along with a larger number of small grains, varying local crystallographic texture, and a wide range of represented crystal orientations, made the Ti-6Al-4V the most difficult dataset for inference. This is further evidenced by a larger number of grain boundary differences for Ti-6Al-4V in Fig. 5, as well as a lower PSNR score in Table 1. Additional noise analysis for generated xy planes is shown in the supplement, and there is ongoing work to improve performance using 3D architectures and grain shape information45 with adaptive multi-scale imaging in z dimension as more of this type of data becomes available.

The limiting factor when using the network approach presented here on serial-sectioned 3D microstructures is the ratio of serial sectioning spacing in the low-resolution input relative to the size of the microstructural features being imaged. For example, if the serial section spacing is large enough to skip entire grains or microstructural features in a material, those features will never be resolvable with super-resolution. Therefore, an informed super-resolution scaling factor choice must be made prior to any experiment to ensure that the low resolution input contains enough information for meaningful inference. Beyond this section depth limitation, the approach shown here is directly applicable to any serial sectioning technique for gathering 3D EBSD information, including FIB sectioning, laser ablation, and robotic serial sectioning6,7. Further, data from other 3D grain mapping techniques that rely on synchrotron X-ray sources such as diffraction contrast tomography (DCT)5 or high energy diffraction microscopy3,4 may also be applicable for the infrastructure presented here. Similar approaches to this may be particularly useful in lab source DCT experiments46,47, where the X-ray source constraints limit grain mapping resolution in comparison to synchrotron sources. For example, one could use difficult to acquire synchrotron X-ray mapping experiments as HR data to train a network to inform LR X-ray mapping experiments collected more routinely at the laboratory.

In summary, we have designed a quaternion-convolution-based deep learning framework with crystallography physics-based loss to generate costly high-resolution 3D EBSD data from sparsely sectioned 3D EBSD data while accounting for the physical constraints of crystal orientation and symmetry. Alongside this, an efficient quaternion-based transformer block was developed to learn long-range trends and global statistics from EBSD maps. Using quaternion convolution instead of regular convolution is critical for crystallographic data, both in terms of output quality and neural network complexity, as reducing the number of trainable parameters enables transformer addition without major complexity burden (see Table 1). This framework can be directly applied to any experimental 3D EBSD approaches that rely on serial sectioning techniques to collect orientation information.

Methods

EBSD datasets

EBSD maps represent crystal orientations collected at each physical pixel location in crystalline materials, which are fundamentally anisotropic and atomically periodic. Orientations for each pixel within the network learning environment are expressed in terms of quaternions of the form \(q={q}_{0}+\hat{i}{q}_{1}+\hat{j}{q}_{2}+\hat{k}{q}_{3}\). The quaternions are suitable to design a physics-based loss function for deep learning framework19. To avoid redundancy in quaternion space (between q and − q), all orientations are expressed with their scalar q0 as positive. For visualization according to established conventions, quaternions are reduced to the Rodrigues space fundamental zone based on space group symmetry, converted into Euler angles, and projected using IPF projection using the open-source Dream3D software48, as shown in our previous work19. Ground truth 3D EBSD datasets were experimentally collected from titanium alloy samples: Ti-6Al-4V and Ti-7Al (one Ti-7Al sample deformed in tension to 1%, and one to 3%), using a commercially-available rapid-serial-sectioning electron microscope referred to as the TriBeam8,10. More details of these datasets and their reconstruction are located in the supplemental material. Sparsely sectioned EBSD datasets are created by removing xy (znormal) planes from the high-resolution ground truth with a downscale factor of 2 and 4 (LR = \(\frac{1}{4}\)HR or LR = \(\frac{1}{2}\)HR). This is done to imitate the skipping of collection planes that would occur in a 3D experiment with more sparsely sectioned EBSD data (i.e., thicker section depth), which would not influence the electron beam-material interaction volume associated with the EBSD mapping process. More information about dataset pre-processing are given in the supplementary material.

Network implementation and output evaluation

We use a learning rate of 0.0002, an Adam optimizer with β1 = 0.9, β2= 0.99, ReLU activation, batch size of 4 and downscaling factor of 2 and 4. The patch size of HR EBSD maps is selected from {16, 32, 64, 100} during training of the network. The framework is implemented in PyTorch and trained on NVIDIA Tesla V100 GPU for 2000 epochs, which took approximately 100 h. Once training is completed, inference time for a given 2D LR EBSD map is on the order of less than one second for an imaging area that would normally take about 10 min to gather manually.

Loss

The QRBSA network is trained using a physics based loss function19, which uses rotational distance approximation loss with enforced hexagonal crystal symmetry. Rotational distance loss computes the misorientation angles between the predicted and ground truth EBSD map in the same manner that they would be measured during crystallographic analysis, with approximations to avoid discontinuities at the edge of the fundamental zone. The rotational distance θ between two unit quaternions can be computed as the following:

$$\begin{array}{l}q1\cdot q2=\cos (\theta )\,\,\longrightarrow \,\,\theta \,=\,4{\sin }^{-1}\left(\frac{{d}_{{{\mbox{euclid}}}}}{2}\right)\end{array}$$
(12)

where, deuclid = ∥q1 − q2∥2. While deuclid is Lipschitz, the gradient of θ goes to ∞ as deuclid → 2. To address this issue during neural network training, a linear approximation was computed at deuclid = 1.9, and utilized for points > 1.9.

Progressive Learning

In our previous work19, we used a fixed patch size of dimension 64 × 64 for training the CNN based architectures which help in learning local correlations. However, self-attention is required to have larger patch sizes, which aids in learning global correlations. Inspired from the work of Zamir18, we use progressive patch samples from sizes of {16, 32, 64, 100} in the training process to learn global statistics. We start from a smaller patch size in early epochs and increase to a larger patch sizes in the later epochs. The progressive learning acts like the curriculum learning process where a network starts with a simple tasks and gradually moves to learning a more complex one.