High harmonic generation in solids: particle and wave perspectives

We start with a theoretical derivation of the HHG in solids. Although these descriptions have been discussed in recent reviews [116, 117], we still present the relevant results for completeness and for the convenience of further discussion. Note that the aim of this review is to elucidate one of the numerous aspects of HHG in solid, namely the recollision picture. Some phenomena, such as multi-electron effects and propagation effects, are out of the scope of this paper. Therefore, here we show only the derivation of HHG from a single-electron Hamiltonian.

The HHG process in solids is modeled by a nonrelativistic electron in a periodic potential interacting with an external electromagnetic field, which is described by a minimal-coupling Hamiltonian [125] (atomic units (a.u.) are applied in this work unless stated)

$$\begin{align} \hat{H}(t) = \frac{[\hat{\textbf{p}}+\textbf{A(r,t)}]^2}{2}-U(\textbf{r},t)+V(\textbf{r}), \end{align} \tag{ 1 }$$

where $\textbf{A}(\textbf{r},t)$ and $U(\textbf{r},t)$ are the vector and scalar potentials of the external field, respectively, and $V(\textbf{r})$ is the crystal periodic potential. There is a gauge freedom in choosing $\textbf{A}(\textbf{r},t)$ and $U(\textbf{r},t)$,

$$\begin{align} \textbf{A}(\textbf{r},t) \rightarrow \textbf{A}(\textbf{r},t)+\nabla\chi(\textbf{r},t) \nonumber\\ U(\textbf{r},t) \rightarrow U(\textbf{r},t)-\partial_{t}\chi(\textbf{r},t), \end{align} \tag{ 2 }$$

with $\chi(\textbf{r},t)$ a differentiable real function. The gauge-independent quantities are the electric and magnetic fields

$$\begin{align} \textbf{F} & = -\nabla U-\partial_{t}\textbf{A}, \end{align} \tag{ 3 }$$

$$\begin{align} \textbf{B} & = \nabla \times \textbf{A}. \end{align} \tag{ 4 }$$

The minimal-coupling Hamiltonian (1) can be reduced to a simple form by using the dipole approximation, considering that the wavelengths of driving fields used for HHG are much larger than the dimension of the unit cell. In this case, the vector potential can be written in dipole approximation, $\textbf{k}\cdot\textbf{r}\ll1$, as $\textbf{A}(t) \equiv \textbf{A}(\textbf{r},t)$. The TDSE for this problem (in the dipole approximation) is given by

$$\begin{align} \mathrm i\partial_{t}\lvert\Psi(t)\rangle = H_{\textrm{VG}}(t)\lvert\Psi(t)\rangle = \left[\frac{[\hat{\textbf{p}}+\textbf{A}(t)]^2}{2}+V(\textbf{r})\right]\lvert\Psi(t)\rangle. \end{align} \tag{ 5 }$$

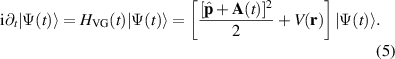
Here, we are applying the velocity gauge, in which $U(\textbf{r},t) = 0$ and $\textbf{A}(t) = -\int_{-\infty}^{t}\textbf{F}(\tau)\mathrm{d}\tau$.

We first consider the field-free states before the laser field is turned on. The eigenvalue equation can be written as

$$\begin{align} \left[\frac{\hat{\textbf{p}^{2}}}{2}+V(\textbf{r})\right]\psi_{i,\textbf{k}}(\textbf{r}) = E_{i}(\textbf{k})\psi_{i,\textbf{k}}(\textbf{r}). \end{align} \tag{ 6 }$$

In this equation, $\psi_{i,\textbf{k}}(\textbf{r})$ and $E_{i}(\textbf{k})$ are the Bloch functions and the energy band of the field-free crystal with a band index i and a crystal momentum k. In the coordinate representation, $\psi_{i,\textbf{k}}(\textbf{r})$ is a product of a plane wave and a periodic envelope function

$$\begin{align} \psi_{i,\textbf{k}}(\textbf{r}) = \mathrm e^{\mathrm i\textbf{k}\cdot\textbf{r}}u_{i,\textbf{k}}(\textbf{r}), \end{align} \tag{ 7 }$$

where $u_{i,\textbf{k}}(\textbf{r+R}) = u_{i,\textbf{k}}(\textbf{r})$ for all R from the Bravais lattice.

Let us now consider the instantaneous eigenstates of $H_{\textrm{VG}}(t)$ in the presence of a homogeneous external field, which satisfies

$$\begin{align} \left(\frac{[\hat{\textbf{p}}+\textbf{A}(t)]^2}{2}+V(\textbf{r})\right)|\varphi_{i,\textbf{k}_{0}}(t)\rangle = \widetilde{E}_{i,\textbf{k}_{0}}(t)|\varphi_{i,\textbf{k}_{0}}(t)\rangle. \end{align} \tag{ 8 }$$

Since the Hamiltonian is periodic in space, the Bloch theorem is applicable. The solution of equation (8) satisfying the Born–von Kármán boundary condition yields [126]

$$\begin{align} \langle r\lvert\varphi_{i,\textbf{k}_{0}}(t)\rangle & = \mathrm e^{-\mathrm i\textbf{A}(t)\cdot\textbf{r}}\psi_{i,\textbf{k}(t)}(\textbf{r}), \end{align} \tag{ 9 }$$

$$\begin{align} \widetilde{E}_{i,\textbf{k}_{0}}(t) & = E_{i}\textbf{(}\textbf{k}(t)\textbf{)}. \end{align} \tag{ 10 }$$

The states $\lvert\varphi_{i,\textbf{k}_{0}}(t)\rangle$ are called accelerated Bloch states or Houston functions [126, 127], and the time-dependent crystal momentum $\textbf{k}(t) = \textbf{k}_{0}+\textbf{A}(t)$ satisfies the acceleration theorem: $\frac{\mathrm{d}\textbf{k}}{\mathrm{d}t} = -\textbf{F}(t)$.

Then, we use the Houston functions as a basis for solving the TDSE with the ansatz

$$\begin{align} \lvert\Psi_{\textbf{k}_{0}}(t)\rangle & = \sum_{m}\alpha_{m,\textbf{k}_{0}}(t)\lvert\varphi_{m,\textbf{k}_{0}}(t)\rangle. \end{align} \tag{ 11 }$$

By inserting this ansatz into TDSE and projecting it onto $\langle\varphi_{n,\textbf{k}_{0}}(t)|$, one gets

$$\begin{align} &\mathrm i\partial_{t}\alpha_{n,\textbf{k}_{0}}(t)+\sum_{m}\alpha_{m,\textbf{k}_{0}}(t)\langle\varphi_{n,\textbf{k}_{0}}(t)|\mathrm i\partial_{t}\lvert\varphi_{m,\textbf{k}_{0}}(t)\rangle \nonumber\\ &\quad = \langle\varphi_{n,\textbf{k}_{0}}(t)|H_\textrm{VG}(t)\left[\sum_{m}\alpha_{m,\textbf{k}_{0}}(t)\lvert\varphi_{m,\textbf{k}_{0}}(t)\rangle\right]\nonumber\\ &\quad = E_{n}\textbf{(}\textbf{k}(t)\textbf{)}\alpha_{n,\textbf{k}_{0}}(t). \end{align} \tag{ 12 }$$

Note that $\langle \textbf{r}\lvert\varphi_{m,\textbf{k}_{0}}(t)\rangle = \mathrm e^{-\mathrm i\textbf{A}(t)\cdot\textbf{r}}\psi_{m,\textbf{k}(t)}(\textbf{r}) = \mathrm e^{\mathrm i\textbf{k}_{0}\cdot\textbf{r}}u_{m,\textbf{k}(t)}(\textbf{r})$ and the nonadiabatic couplings are $\langle\varphi_{n,\textbf{k}_{0}}(t)|\mathrm i\partial_{t}\lvert\varphi_{m,\textbf{k}_{0}}(t)\rangle = -\textbf{F}(t)\cdot\langle u_{n,\textbf{k}(t)}|\mathrm i\nabla_{\textbf{k}}|u_{m,\textbf{k}(t)}\rangle = -\textbf{F}(t)\cdot\textbf{d}_{nm}\textbf{(}\textbf{k}(t)\textbf{)}$. Then, one can obtain the following system of differential equations

$$\begin{align} \mathrm i\partial_{t}\alpha_{n,\textbf{k}_{0}}(t) = E_{n}\textbf{(}\textbf{k}(t)\textbf{)}\alpha_{n,\textbf{k}_{0}}(t)+\textbf{F}(t)\cdot\sum_{l}\textbf{d}_{ml}\textbf{(}\textbf{k}(t)\textbf{)}\alpha_{l,\textbf{k}_{0}}(t).\end{align} \tag{ 13 }$$

The connection between the TDSE and SBEs can be established by introducing the density matrix elements $\rho_{mn}^{\textbf{k}_{0}} = \alpha_{m,\textbf{k}_{0}}\alpha_{n,\textbf{k}_{0}}^{*}$. Multiplying equation (13) by $\alpha_{n,\textbf{k}_{0}}^{*}$ and summing by complex conjugate of the resulting equations, equation (13) can be rewritten into differential equations

$$\begin{align} \mathrm i\partial_{t}\rho_{mn}^{\textbf{k}_{0}}(t)& = [E_{m}\textbf{(}\textbf{k}(t)\textbf{)}-E_{n}\textbf{(}\textbf{k}(t)\textbf{)}]\rho_{mn}^{\textbf{k}_{0}}(t)+\textbf{F}(t)\nonumber\\ &\quad\cdot\sum_{l}\left[\textbf{d}_{ml}\textbf{(}\textbf{k}(t)\textbf{)}\rho_{ln}^{\textbf{k}_{0}}(t)-\rho_{ml}^{\textbf{k}_{0}}(t)\textbf{d}_{ln}\textbf{(}\textbf{k}(t)\textbf{)}\right]. \end{align} \tag{ 14 }$$

A dephasing term $-i(1-\delta_{mn})\rho_{mn}^{\textbf{k}_{0}(t)}/T_{2}$ can be introduced on the right-hand side of equation (14), which phenomenologically describes the many-body couplings such as electron–electron and electron–phonon scattering. Typical dephasing times in semiconductors were found to be a few to tens of femtoseconds [128, 129]. A shorter dephasing time suppresses the contribution of multiple recombination quantum paths and is always chosen to obtain agreement with the clean harmonic structure observed in experiments [49]. Although the phenomenological dephasing is computationally convenient, it can only give qualitative results, and the discussions on dephasing are still an active research topic [103, 130, 131].

For simplicity, we only consider an initially fully filled VB ('m = v') and an empty CB ('m = c') in our following discussions. In this case, equation (14) evolves as the two-band SBEs

$$\begin{align} \mathrm i\partial_{t}\rho_{cv}^{\textbf{k}_{0}}(t) & = \left\{\omega_{g}^{\textbf{k}(t)}+\textbf{F}(t)\cdot\left[\boldsymbol{\Lambda}_{c}^{\textbf{k}(t)}-\boldsymbol{\Lambda}_{v}^{\textbf{k}(t)}\right]\right\}\rho_{cv}^{\textbf{k}_{0}}(t) \nonumber\\ &\ \ \ \ +\textbf{F}(t)\cdot\textbf{d}^{\textbf{k}(t)}\left[\rho_{vv}^{\textbf{k}_{0}}(t)-\rho_{cc}^{\textbf{k}_{0}}(t)\right], \end{align} \tag{ 15 }$$

$$\begin{align} \mathrm i\partial_{t}\rho_{cc}^{\textbf{k}_{0}}(t) & = \textbf{F}(t)\cdot\left\{\textbf{d}^{\textbf{k}(t)}\left[\rho_{cv}^{\textbf{k}_{0}}(t)\right]^{*}-\left[\textbf{d}^{\textbf{k}(t)}\right]^{*}\rho_{cv}^{\textbf{k}_{0}}(t)\right\}, \end{align} \tag{ 16 }$$

$$\begin{align} \mathrm i\partial_{t}\rho_{vv}^{\textbf{k}_{0}}(t) & = -\textbf{F}(t)\cdot\left\{\textbf{d}^{\textbf{k}(t)}\left[\rho_{cv}^{\textbf{k}_{0}}(t)\right]^{*}-\left[\textbf{d}^{\textbf{k}(t)}\right]^{*}\rho_{cv}^{\textbf{k}_{0}}(t)\right\}. \end{align} \tag{ 17 }$$

$\omega_{g}^{\textbf{k}} = E_{c}(\textbf{k}) - E_{v}(\textbf{k})$, $\boldsymbol{\Lambda}_{m}^{\textbf{k}} = \textbf{d}_{mm}(\textbf{k})$ and $\textbf{d}^{\textbf{k}} = \textbf{d}_{cv}(\textbf{k})$ denote the band gap, Berry connection and transition dipole momentum, respectively. The SBEs can be further simplified by a transformation using an integrating factor

$$\begin{align} \alpha_{m,\textbf{k}_{0}}(t) = \tilde{\alpha}_{m,\textbf{k}_{0}}(t)\mathrm e^{\mathrm i\phi_{m}^{\textrm{D}}\textbf{(}\textbf{k}(t)\textbf{)}+\mathrm i\phi_{m}^{\textrm{B}}\textbf{(}\textbf{k}(t)\textbf{)}}, \end{align} \tag{ 18 }$$

where the dynamic phase $\phi_{m}^{\textrm{D}}\textbf{(}\textbf{k}(t)\textbf{)}$ and the Berry phase $\phi_{m}^{\textrm{B}}\textbf{(}\textbf{k}(t)\textbf{)}$ are defined by the following expressions

$$\begin{align} \phi_{m}^{\textrm{D}}\textbf{(}\textbf{k}(t)\textbf{)} & = -\int_{-\infty}^{t}E_{m}\textbf{(}\textbf{k}(\tau)\textbf{)}\mathrm{d}\tau, \end{align} \tag{ 19 }$$

$$\begin{align} \phi_{m}^{\textrm{B}}\textbf{(}\textbf{k}(t)\textbf{)} & = -\int_{-\infty}^{t}\textbf{F}(\tau)\cdot\boldsymbol{\Lambda}_{m}^{\textbf{k}(\tau)}\mathrm{d}\tau. \end{align} \tag{ 20 }$$

Using the notations $\Pi^{\textbf{k}_{0}}\,\,(t)\,\, =\,\, \tilde{\alpha}_{c,\textbf{k}_{0}}\,\,\tilde{\alpha}_{v,\textbf{k}_{0}}^{*}\,\, =$ $\rho_{cv}^{\textbf{k}_{0}}(t)\mathrm e^{-\mathrm i\left[\phi_{cv}^{\textrm{D}}\textbf{(}\textbf{k}(t)\textbf{)}+\phi_{cv}^{\textrm{B}}\textbf{(}\textbf{k}(t)\textbf{)}\right]}$, $N_{m}^{\textbf{k}_{0}}(t) = \tilde{\alpha}_{m,\textbf{k}_{0}}\tilde{\alpha}_{m,\textbf{k}_{0}}^{*} = \rho_{mm}^{\textbf{k}_{0}}(t)$ ($m = c,v$) and rearranging equations (15)–(17), one gets

$$\begin{align} \partial_{t}\Pi^{\textbf{k}_{0}}(t) & = -\mathrm i\textbf{F}(t)\cdot\textbf{d}^{\textbf{k}(t)}\left[N_{v}^{\textbf{k}_{0}}(t)-N\,{_{c}^{\textbf{k}_{0}}}(t)\right]\mathrm e^{-\mathrm i\left[\phi_{cv}^{\textrm{D}}\textbf{(}\textbf{k}(t)\textbf{)}+\phi_{cv}^{\textrm{B}}\textbf{(}\textbf{k}(t)\textbf{)}\right]}, \end{align} \tag{ 21 }$$

$$\begin{align} \partial_{t}N\,{_{c}^{\textbf{k}_{0}}}(t) & = 2\textrm{Re}\left\{\mathrm i\textbf{F}(t)\cdot\left[\textbf{d}^{\textbf{k}(t)}\right]^{*}\Pi^{\textbf{k}_{0}}(t)\mathrm e^{\mathrm i\left[\phi_{cv}^{\textrm{D}}\textbf{(}\textbf{k}(t)\textbf{)}+\phi_{cv}^{\textrm{B}}\textbf{(}\textbf{k}(t)\textbf{)}\right]}\right\}, \end{align} \tag{ 22 }$$

$$\begin{align} \partial_{t}N_{v}^{\textbf{k}_{0}}(t) & = - 2\textrm{Re}\left\{\mathrm i\textbf{F}(t)\cdot\left[\textbf{d}^{\textbf{k}(t)}\right]^{*}\Pi^{\textbf{k}_{0}}(t)\mathrm e^{\mathrm i\left[\phi_{cv}^{\textrm{D}}\textbf{(}\textbf{k}(t)\textbf{)}+\phi_{cv}^{\textrm{B}}\textbf{(}\textbf{k}(t)\textbf{)}\right]}\right\}, \end{align} \tag{ 23 }$$

where $\phi_{cv}^{D}\textbf{(}\textbf{k}(t)\textbf{)} = \phi_{c}^{D}\textbf{(}\textbf{k}(t)\textbf{)}-\phi_{v}^{D}\textbf{(}\textbf{k}(t)\textbf{)}$ and $\phi_{cv}^{B}\textbf{(}\textbf{k}(t)\textbf{)} = \phi_{c}^{B}\textbf{(}\textbf{k}(t)\textbf{)}-\phi_{v}^{B}\textbf{(}\textbf{k}(t)\textbf{)}$ are the transitional dynamic phase and Berry phase, respectively. Note that for HHG in semiconductors and insulators, the electrons are initially in the VB before the external field is turned on (i.e. $N_{v}^{\textbf{k}_{0}}(t_{0}) = 1$) and the population transfer to the CB is small. Thus, it is reasonable to explore equation (21) by using the Keldysh approximation $N_{v}^{\textbf{k}_{0}}(t)-N\,{_{c}^{\textbf{k}_{0}}}(t) \approx 1$. This decouples equations (21)–(23) so that they can be formally integrated,

$$\begin{align} \Pi^{\textbf{k}_{0}}(t)& = -\mathrm i\int_{t_{0}}^{t}\textbf{F}(t^{\prime})\cdot\textbf{d}^{\textbf{k}(t^{\prime})}\mathrm e^{-\mathrm i\left[\phi_{cv}^{\textrm{D}}\textbf{(}\textbf{k}(t^{\prime})\textbf{)}+\phi_{cv}^{\textrm{B}}\textbf{(}\textbf{k}(t^{\prime})\textbf{)}\right]}\mathrm{d}t^{\prime}, \end{align} \tag{ 24 }$$

$$\begin{align} N\,{_{c}^{\textbf{k}_{0}}}(t) & = \mathrm i\int_{t_{0}}^{t}\textbf{F}(t^{\prime})\cdot\left[\textbf{d}^{\textbf{k}(t^{\prime})}\right]^{*}\Pi^{\textbf{k}_{0}}(t^{\prime})\mathrm e^{\mathrm i\left[\phi_{cv}^{\textrm{D}}\textbf{(}\textbf{k}(t^{\prime})\textbf{)}+\phi_{cv}^{\textrm{B}}\textbf{(}\textbf{k}(t^{\prime})\textbf{)}\right]}\mathrm{d}t^{\prime}+\textrm{c.c.}, \end{align} \tag{ 25 }$$

$$\begin{align} N\,{_{v}^{\textbf{k}_{0}}}(t) & = N\,{_{v}^{\textbf{k}_{0}}}(t_{0})-N\,{_{c}^{\textbf{k}_{0}}}(t).\end{align} \tag{ 26 }$$

Finally, HHG in solids is determined by the microscopic current $\textbf{J}(t) = \sum_{\textbf{k}_0}\textbf{j}_{\textbf{k}_0}(t)$, where the contribution from an electron with an initial crystal momentum k₀ is evaluated as

$$\begin{align} \textbf{j}_{\textbf{k}_0}(t) & = -\langle\Psi_{\textbf{k}_0}(t)|\left[\hat{\textbf{p}}+\textbf{A}(t)\right]|\Psi_{\textbf{k}_0}(t)\rangle \nonumber\\ & = -\sum_{m,n}\langle\Psi_{\textbf{k}_0}(t)|\varphi_{m,\textbf{k}_{0}}(t)\rangle\langle\varphi_{m,\textbf{k}_{0}}(t)|\left[\hat{\textbf{p}}+\textbf{A}(t)\right]|\varphi_{n,\textbf{k}_{0}}(t)\rangle \nonumber\\ & \quad \times\langle\varphi_{n,\textbf{k}_{0}}(t)|\Psi_{\textbf{k}_0}(t)\rangle \nonumber\\ & = -\sum_{m,n}\langle\varphi_{m,\textbf{k}_{0}}(t)|\left[\hat{\textbf{p}}+\textbf{A}(t)\right]|\varphi_{n,\textbf{k}_{0}}(t)\rangle\rho^{\textbf{k}_{0}}_{nm}(t) \nonumber\\ & = -\sum_{m,n}\textbf{p}_{mn}^{\textbf{k}_{0}+\textbf{A}(t)}\rho^{\textbf{k}_{0}}_{nm}(t). \end{align} \tag{ 27 }$$

The momentum matrix elements can be determined by using the relation $\left[\hat{\textbf{p}}+\textbf{A}(t)\right] = -\mathrm i\left[\hat{\textbf{r}},\hat{H}_{VG}(t)\right]$, that is

$$\begin{align} \textbf{p}_{mn}^{\textbf{k}_{0}+\textbf{A}(t)} & = \langle\varphi_{m,\textbf{k}_{0}}(t)|\left[\hat{\textbf{p}}+\textbf{A}(t)\right]|\varphi_{n,\textbf{k}_{0}}(t)\rangle \nonumber\\ & = -\mathrm i\left\langle\varphi_{m,\textbf{k}_{0}}(t)\left|\left[\hat{\textbf{r}},\hat{H}_\textrm{VG}(t)\right]\right|\varphi_{n,\textbf{k}_{0}}(t)\right\rangle. \end{align} \tag{ 28 }$$

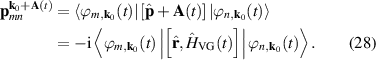
It is convenient to split the position operator into an intraband part $\hat{\textbf{r}}_{i}$ and an interband part $\hat{\textbf{r}}_{e}$ [132], where $\hat{\textbf{r}} = \hat{\textbf{r}}_{i}+\hat{\textbf{r}}_{e}$ and

$$\begin{align} \langle\psi_{m,\textbf{k}}|\hat{\textbf{r}}_{i}|\psi_{n,\textbf{k}^{\prime}}\rangle & = \delta_{mn}\left[\delta(\textbf{k}-\textbf{k}^{\prime})\textbf{d}_{mm}({\textbf{k}})+\mathrm i\nabla_{\textbf{k}}\delta(\textbf{k}-\textbf{k}^{\prime})\right], \end{align} \tag{ 29 }$$

$$\begin{align} \langle\psi_{m,\textbf{k}}|\hat{\textbf{r}}_{e}|\psi_{n,\textbf{k}^{\prime}}\rangle & = \left(1-\delta_{mn}\right)\delta(\textbf{k}-\textbf{k}^{\prime})\textbf{d}_{mn}({\textbf{k}}). \end{align} \tag{ 30 }$$

The relation between $\textbf{d}_{mn}({\textbf{k}})$ and the momentum matrix elements is given by

$$\begin{align} &\textbf{p}_{mn}^{\textbf{k}_{0}+\textbf{A}(t)} \nonumber\\& \quad = -\mathrm i\left\langle\varphi_{m,\textbf{k}_{0}}(t)\left|\left[\hat{\textbf{r}}\hat{H}_\textrm{VG}(t)-\hat{H}_\textrm{VG}(t)\hat{\textbf{r}}\right]\right|\varphi_{n,\textbf{k}_{0}}(t)\right\rangle \nonumber\\ & \quad = \sum_{l,\textbf{k}^{\prime}}[-\mathrm i\langle\varphi_{m,\textbf{k}_{0}}(t)|\hat{\textbf{r}}|\varphi_{l,\textbf{k}^{\prime}}(t)\rangle \langle\varphi_{l,\textbf{k}^{\prime}}(t)|\hat{H}_\textrm{VG}(t)|\varphi_{n,\textbf{k}_{0}}(t)\rangle \nonumber\\ &\qquad +\mathrm i\langle\varphi_{m,\textbf{k}_{0}}(t)|\hat{H}_\textrm{VG}(t)|\varphi_{l,\textbf{k}^{\prime}}(t)\rangle \langle\varphi_{l,\textbf{k}^{\prime}}(t)|\hat{\textbf{r}}|\varphi_{n,\textbf{k}_{0}}(t)\rangle] \nonumber\\ & \quad = \sum_{l,\textbf{k}^{\prime}}[-\mathrm i\langle\psi_{m,\textbf{k}_{0}+\textbf{A}(t)}|\hat{\textbf{r}}|\psi_{l,\textbf{k}^{\prime}+\textbf{A}(t)}\rangle E_{n}\textbf{(}\textbf{k}_{0}+\textbf{A}(t)\textbf{)}\delta_{ln}\delta(\textbf{k}_{0}-\textbf{k}^{\prime})\nonumber\\ &\qquad +\mathrm iE_{l}\textbf{(}\textbf{k}^{\prime}+\textbf{A}(t)\textbf{)}\delta_{ml}\delta(\textbf{k}_{0}-\textbf{k}^{\prime}) \langle\psi_{l,\textbf{k}^{\prime}+\textbf{A}(t)}|\hat{\textbf{r}}|\psi_{n,\textbf{k}_{0}+\textbf{A}(t)}\rangle] \nonumber\\ & \quad = \delta_{mn}\left[\nabla_{\textbf{k}}E_{n}\textbf{(}\textbf{k}(t)\textbf{)}\right]+\mathrm i(1-\delta_{mn})\left[E_{m}\textbf{(}\textbf{k}(t)\textbf{)}-E_{n}\textbf{(}\textbf{k}(t)\textbf{)}\right]\textbf{d}_{mn}\textbf{(}\textbf{k}(t)\textbf{)}. \end{align} \tag{ 31 }$$

Using the above relations, the microscopic current can be reorganized as an intraband and an interband contribution, i.e. $\textbf{J}(t) = \textbf{J}_{\textrm{er}}(t)+\textbf{J}_{\textrm{ra}}(t)$:

$$\begin{align} \textbf{J}_{\textrm{ra}}(t)& = -\sum_{m,\textbf{k}_{0}}\nabla_{\textbf{k}}E_{m}\textbf{(}\textbf{k}(t)\textbf{)}\rho^{\textbf{k}_{0}}_{mm}(t), \end{align} \tag{ 32 }$$

$$\begin{align} \textbf{J}_{\textrm{er}}(t)& = -\mathrm i\sum_{m\neq n,\textbf{k}_{0}}\left[E_{m}\textbf{(}\textbf{k}(t)\textbf{)}-E_{n}\textbf{(}\textbf{k}(t)\textbf{)}\right]\textbf{d}_{mn}\textbf{(}\textbf{k}(t)\textbf{)}\rho^{\textbf{k}_{0}}_{nm}(t). \end{align} \tag{ 33 }$$

In this form, the intraband and interband currents are divided by selecting the contribution from different band indices, where the prefix 'intra' and 'inter' comes from the selection of m = n and m ≠ n. The intraband term deals with the electrons in each individual band (select m = n), and it necessarily takes into account all bands. The interband term arises from the polarization oscillation between electrons in different bands (select m ≠ n). Inserting the equations (24)–(26) into equations (32) and (33), we find

$$\begin{align} \textbf{J}_{\textrm{ra}}(t) & = -\sum_{\textbf{k}_0}\nabla_{\textbf{k}}\omega_{g}^{\textbf{k}(t)}\int_{t_{0}}^{t}\mathrm{d}t^{\prime}\textbf{F}(t^{\prime})\cdot\left[\textbf{d}^{\textbf{k}(t^{\prime})}\right]^{*}\mathrm e^{\mathrm i\left[\phi_{cv}^{\textrm{D}}\textbf{(}\textbf{k}(t^{\prime})\textbf{)}+\phi_{cv}^{\textrm{B}}\textbf{(}\textbf{k}(t^{\prime})\textbf{)}\right]} \nonumber\\ &\ \ \ \ \times \int_{t_{0}}^{t^{\prime}}\textbf{F}(t^{^{\prime\prime}})\cdot\textbf{d}^{\textbf{k}(t^{^{\prime\prime}})}\mathrm e^{-\mathrm i\left[\phi_{cv}^{\textrm{D}}\textbf{(}\textbf{k}(t^{^{\prime\prime}})\textbf{)}+\phi_{cv}^{\textrm{B}}\textbf{(}\textbf{k}(t^{^{\prime\prime}})\textbf{)}\right]}\mathrm{d}t^{^{\prime\prime}}+\textrm{c.c.}, \end{align} \tag{ 34 }$$

$$\begin{align} \textbf{J}_{\textrm{er}}(t)& = \sum_{\textbf{k}_0}\omega_{g}^{\textbf{k}(t)}\left[\textbf{d}^{\textbf{k}(t)}\right]^{*}\mathrm e^{\mathrm i\left[\phi_{cv}^{\textrm{D}}\textbf{(}\textbf{k}(t)\textbf{)}+\phi_{cv}^{\textrm{B}}\textbf{(}\textbf{k}(t)\textbf{)}\right]}\int_{t_{0}}^{t}\textbf{F}(t^{\prime})\nonumber\\ & \quad \cdot\textbf{d}^{\textbf{k}(t^{\prime})}\mathrm e^{-\mathrm i\left[\phi_{cv}^{\textrm{D}}\textbf{(}\textbf{k}(t^{\prime})\textbf{)}+\phi_{cv}^{\textrm{B}}\textbf{(}\textbf{k}(t^{\prime})\textbf{)}\right]}\mathrm{d}t^{\prime}+\textrm{c.c.} \end{align} \tag{ 35 }$$

The HHG spectrum can be obtained by Fourier transforming the currents. In figure 1, we plot a typical high harmonic spectrum using the same parameters as in [82, 133]. It can be seen that the interband harmonics are dominant above the band gap (marked as a dashed vertical line), while the intraband harmonics contribute mainly to the lower order harmonics. This is a fairly common result [82, 133], so one tends to consider only the interband contributions in the plateau region.

The SBEs could be improved from a two-band to a multiband model by using the accurate energy bands and transition dipole moments from first-principle calculations. The multiband effects have also attracted a lot of attention in recent studies [96–98, 110, 134–136], where the electron is excited to higher CB or the quantum interference of different excitation paths among different pair of bands becomes important.

According to the above discussion, the relevant observables, i.e. the induced currents, are expressed as an integral form in the multi-dimensional space by using the Keldysh approximation. These integrals are often solved by using the stationary phase approximation, which leads to a series of equations identifying the points in the multi-dimensional space having the most significant contributions in their evaluation. These points are usually indicated as saddle points. Such an approach enables an approximate intuitive physical picture with classical perceptions of the quantum mechanical processes under investigation. Thus, the saddle-point methods are very powerful and valuable general theoretical tools to obtain asymptotic expressions of mathematical solutions and also help to gain physical insights into the underlying phenomena. Such techniques have been adapted to study the attosecond science in gaseous systems in the past [22, 34–39, 45–48] and have been extended to condensed-matter phase in recent years [82, 106–109].

The first step to solving the TDSE is to choose a laser gauge and a basis. The exact solution does not depend on this choice, but the chosen gauge and basis dictate approximations that one may wish to make, and they influence the physical interpretation of results [106, 107, 109, 137, 138]. Besides, the choice of gauge and basis may play an important role in the numerical description. The exact form of the Hamiltonian matrix and the truncation of states will strongly influence the solution of the electron dynamics [136, 139, 140]. Here, we focus on the recollision models with interband currents, where the prefix 'inter' highlight the transition between the CB and VB in the recombination step. We briefly summarize several typical analytical forms of interband current and the corresponding recollision models for HHG in solids based on saddle-point methods (see figure 2). Note that the integral form for the currents, the derivation of the SBEs and the corresponding physical pictures are similar for different specific basis, e.g. employing the Bloch states or the Houston states. Thus, we will only in detail introduce some typical models classified based on the choice of delocalized or localized basis for the CB and VB, respectively, and focus on the discussions of saddle-point equations and the corresponding recollision models.

• Simple recollision model (SRM)

Zoom In Zoom Out Reset image size

The original SRM deals with a direct band-gap centrosymmetric material, and the k-dependence of the transition dipole moment is neglected, i.e. $\textbf{d}^{\textbf{k}}\equiv\textbf{d}$ [106]. In this case, the berry phase is not included and only the dynamic phase is preserved in equation (35). Then, by transforming into the frame $\textbf{k} = \textbf{k}_{0}+\textbf{A}(t)$, one can obtain the interband current in frequency domain as

$$\begin{align} J_{\mu}^{\mathrm{SRM}}(\omega)& = \int_{-\infty}^{\infty}\mathrm{d}t \mathrm e^{\mathrm i \omega t} \mathrm{J}_{\mu}^{\mathrm{SRM}}(t) = \int_{-\infty}^{\infty}\mathrm{d}t\sum_{\mathbf{k}}\omega_{g}^{\textbf{k}}\textbf{d}_{\mu}^{*}\int^{t}_{t_{0}}\textbf{F}(s)\nonumber\\& \quad \cdot\textbf{d}\mathrm e^{-\mathrm i\left[S^{\textrm{SRM}}(\mathbf{k}, t, s)-\omega t\right]} \mathrm{d} s+\textrm{c.c.}. \end{align} \tag{ 36 }$$

Here $\mu = \{x, y, z\}$ is the Cartesian indices that denotes the µ component of a vector, and

$$\begin{align} S^{\textrm{SRM}}(\mathbf{k}, t, s) = \int_{s}^{t}\omega_{g}^{\kappa\left(\textbf{k},t, t^{\prime} \right)}\mathrm{d}t^{\prime} \end{align} \tag{ 37 }$$

is the accumulated phase with the time-dependent crystal momentum $\kappa\left(\textbf{k},t, t^{^{\prime}}\right) = \mathbf{k}-\mathbf{A}(t)+\mathbf{A}\left(t^{^{\prime}}\right)$. The phase of the exponential $S^{\textrm{SRM}}(\mathbf{k}, t, s)-\omega t$ in this integrand can vary wildly, introducing extreme cancellations that require increased precision in the numerical integration.

To overcome this problem, one can employ the method of steepest descents for the relevant oscillatory integrals, where only the phase stationary (saddle) point contributes to the integrand while highly oscillatory terms are neglected. Thus, the integrals can be approximated using the values of the integrand at stationary points of the action, reminiscent of the emergence of classical trajectories as the stationary-action points of the Feynman path integral. From this framework, the major contribution for equation (36) comes from the stationary (saddle) points and the corresponding saddle-point equations can be derived from the derivatives of the phase term

$$\begin{align} &\nabla_{\textbf{k}}\left[S^{\textrm{SRM}}(\mathbf{k}, t, s)-\omega t\right]\! =\! \Delta\textbf{r}(\textbf{k},t,s)\! =\! \int_{s}^{t}\nabla_{\textbf{k}}\omega_{g}^{\kappa(\textbf{k},t,t^{^{\prime}})}\mathrm dt^{^{\prime}}\! =\! 0, \end{align} \tag{ 38 }$$

$$\begin{align} &\nabla_{s}\left[S^{\textrm{SRM}}(\mathbf{k}, t, s)-\omega t\right] = \omega_{g}^{\kappa(\textbf{k},t,s)} = 0, \end{align} \tag{ 39 }$$

$$\begin{align} &\nabla_{t}\left[S^{\textrm{SRM}}(\mathbf{k}, t, s)-\omega t\right] = \omega_{g}^{\textbf{k}}+\textbf{F}(t)\cdot\Delta\textbf{r}(\textbf{k},t,s)-\omega = 0. \end{align} \tag{ 40 }$$

These results are also proposed by Vampa et al [106] using the length gauge SBEs with a Bloch basis. Note that the term $\textbf{F}(t)\cdot\Delta\textbf{r}(\textbf{k},t,s)$ in equation (40) is omitted in Vampa's work [106] considering the recollision condition equation (38). Neglecting the imaginary parts of the saddle point, the saddle-point conditions give the SRM similar to the three-step model of atomic HHG [4, 106]: (i) an electron–hole pair is created with zero crystal momentum at time s (at the Γ point); (ii) the electron and hole are separated by the laser field with the instantaneous velocity $\nabla_{\textbf{k}}\omega_{g}^{A(t)-A(t^{^{\prime}})}$; (iii) the electron and hole re-encounter to each other at time t and release a harmonic photon with energy $\omega = \omega_{g}^{\textbf{k}}$. In figure 3, we plot a sketch of the three-step dynamics within the SRM. In this model, both the electron and the hole are seen as classical particles and their motion follows the group velocity on the band structure. Then, the HHG is determined by the event of electron–hole coinciding at birth and recolliding at emission times. This analysis reveals that the trajectory picture of atomic HHG is applicable to solids with some modifications. It establishes a bridge between the microscopic electron–hole dynamics and the HHG emissions, and therewith opens the possibility to apply atomic HHS to the condensed matter phase. In addition, this model yields a simple approximate cutoff law for HHG in solids, which lies a little lower than the numerical results but gives an identical slope (see figure 4 in [106]).

• Extended recollision model (ERM)

Zoom In Zoom Out Reset image size

The ERM [108] is derived in a more general case where the transition dipole phase and berry phase are involved. Thus, we come back to the general form of interband current in equation (35)

$$\begin{align} J_{\mu}^{\mathrm{ERM}}(\omega)& = \int_{-\infty}^{\infty}\mathrm{d}t \mathrm e^{\mathrm i \omega t} \mathrm{J}_{\mu}^{\mathrm{ERM}}(t) \nonumber\\& = \int_{-\infty}^{\infty}\mathrm{d}t\sum_{\mathbf{k}} R_{\mu}^{\mathbf{k}} \int^{t}_{t_{0}} T^{\kappa(\textbf{k},t, s)} \mathrm e^{-\mathrm i\left[S^{\textrm{ERM}}(\mathbf{k}, t, s)-\omega t\right]} \mathrm{d} s+\textrm{c.c.} \end{align} \tag{ 41 }$$

For the sake of clarity, we rearrange the form of interband current using notations as those in [108]. $T^{\kappa(\textbf{k},t, s)} = \textrm{F}(s)|\mathbf{d}_{\|}^{\kappa(\textbf{k},t, s)}|$ is the Rabi frequency (mathematically, it is the amplitude of the term $\textbf{F}(s)\cdot\mathbf{d}^{\kappa(\textbf{k},t, s)}$) with $\mathbf{d}_{\|}^{\kappa(\textbf{k},t, s)}$ representing the component parallel to the electric field at ionization time, $R_{\mu}^{\mathbf{k}} = \omega_{g}^{\mathbf{k}}\left|d_{\mu}^{\mathbf{k}}\right|$ is the recombination dipole, and

$$\begin{align} S^{\textrm{ERM}}(\mathbf{k}, t, s)& = \int_{s}^{t}\left[\omega_{g}^{\kappa\left(\textbf{k},t, t^{^{\prime}}\right)}+\mathbf{F}\left(t^{^{\prime}}\right)\cdot\boldsymbol{\Lambda}_{cv}^{\kappa\left(\textbf{k},t, t^{^{\prime}}\right)}\right] \mathrm{d} t^{^{\prime}}\nonumber\\& \quad +\beta_{\mu}^{\mathbf{k}}-\beta_{\|}^{\kappa(\textbf{k},t, s)}. \end{align} \tag{ 42 }$$

is the accumulated phase with $\boldsymbol{\Lambda}_{cv}^{\textbf{k}} = \boldsymbol{\Lambda}_{c}^{\mathbf{k}}-\boldsymbol{\Lambda}_{v}^{\mathbf{k}}$ the Berry connection difference and $\beta_{\mu}^{\mathbf{k}} \equiv \arg \left(d_{\mu}^{\mathbf{k}}\right)$ the transition-dipole phases.

In the framework of saddle-point method, the major contribution to the integral over k come from the stationary points determined by taking the partial derivatives with respect to k

$$\begin{align} &\nabla_{\textbf{k}}\left[S^{\textrm{ERM}}(\mathbf{k}, t, s)-\omega t\right] \nonumber\\&\quad = \nabla_{\textbf{k}}\left\{\int_{s}^{t}\left[\omega_{g}^{\kappa\left(\textbf{k},t, t^{^{\prime}}\right)}+\mathbf{F}\left(t^{^{\prime}}\right) \cdot \boldsymbol{\Lambda}_{cv}^{\kappa\left(\textbf{k},t, t^{^{\prime}}\right)}\right] \mathrm{d} t^{^{\prime}}+\beta_{\mu}^{\mathbf{k}}-\beta_{\|}^{\kappa(\textbf{k},t, s)}\right\} \nonumber\\ &\quad = \int_{s}^{t}\nabla_{\textbf{k}}\omega_{g}^{\kappa\left(\textbf{k},t, t^{^{\prime}}\right)}\mathrm{d} t^{^{\prime}}+\int_{s}^{t}\nabla_{\textbf{k}}\left[\mathbf{F}\left(t^{^{\prime}}\right)\cdot\boldsymbol{\Lambda}_{cv}^{\kappa\left(\textbf{k},t, t^{^{\prime}}\right)}\right] \mathrm{d} t^{^{\prime}}\nonumber\\&\qquad +\nabla_{\textbf{k}}\beta_{\mu}^{\mathbf{k}}-\nabla_{\textbf{k}}\beta_{\|}^{\kappa(\textbf{k},t, s)}. \end{align} \tag{ 43 }$$

Using the relation $\nabla(\textbf{f}\cdot\textbf{g}) = \textbf{f}\times(\nabla\times\textbf{g})+(\textbf{f}\cdot\nabla)\textbf{g}+\textbf{g}\times(\nabla\times\textbf{f})+(\textbf{g}\cdot\nabla)\textbf{f}$ in the second term, one gets

$$\begin{align} &\int_{s}^{t}\nabla_{\textbf{k}}\left[\mathbf{F}\left(t^{^{\prime}}\right)\cdot\boldsymbol{\Lambda}_{cv}^{\kappa\left(\textbf{k},t, t^{^{\prime}}\right)}\right] \mathrm{d} t^{^{\prime}} \nonumber\\& \quad = \int_{s}^{t}\textbf{F}(t^{^{\prime}})\times\left(\nabla_{\textbf{k}}\times\boldsymbol{\Lambda}_{cv}^{\kappa\left(\textbf{k},t, t^{^{\prime}}\right)}\right)\mathrm{d} t^{^{\prime}} +\int_{s}^{t}\left(\textbf{F}(t^{^{\prime}})\cdot\nabla_{\textbf{k}}\right)\boldsymbol{\Lambda}_{cv}^{\kappa\left(\textbf{k},t, t^{^{\prime}}\right)}\mathrm{d} t^{^{\prime}} \nonumber\\ &\quad = \int_{s}^{t}\textbf{F}(t^{^{\prime}})\times\left(\boldsymbol{\Omega}_{c}^{\kappa(\textbf{k},t,t^{^{\prime}})}-\boldsymbol{\Omega}_{v}^{\kappa(\textbf{k},t,t^{^{\prime}})}\right)\mathrm{d} t^{^{\prime}}-\boldsymbol{\Lambda}_{cv}^{\kappa(\textbf{k},t,t^{^{\prime}})}\bigg|_{t^{^{\prime}} = s}^{t^{^{\prime}}t}, \end{align} \tag{ 44 }$$

with the Berry curvature $\boldsymbol{\Omega}_{m}^{\textbf{k}} = \nabla_{\textbf{k}}\times\boldsymbol{\Lambda}_{m}^{\textbf{k}}$. Substituting equation (44) into (43) and reorganizing the formula, the saddle-point condition with respect to the integration variable k is

$$\begin{align} \nabla_{\textbf{k}}\left[S^{\textrm{ERM}}(\mathbf{k}, t, s)-\omega t\right] = \Delta\textbf{r}(\textbf{k},t,s)-\Delta\textbf{D}(\textbf{k},t,s) = \textbf{0}, \end{align} \tag{ 45 }$$

with the electron–hole separation vector and group velocities

$$\begin{align} \Delta\textbf{r}(\textbf{k},t,s) = & \int_{s}^{t}\left[\textbf{v}_{c}^{\kappa(\textbf{k},t,t^{^{\prime}})}-\textbf{v}_{v}^{\kappa(\textbf{k},t,t^{^{\prime}})}\right]\mathrm{d}t^{^{\prime}} \end{align} \tag{ 46 }$$

$$\begin{align} \textbf{v}_{m}^{\kappa(\textbf{k},t,t^{^{\prime}})} = & \nabla_{\textbf{k}}E_{m}\textbf{(}\kappa(\textbf{k},t,t^{^{\prime}})\textbf{)}+\textbf{F}(t^{^{\prime}})\times\boldsymbol{\Omega}_{m}^{\kappa(\textbf{k},t,t^{^{\prime}})}, \end{align} \tag{ 47 }$$

and the structure-gauge invariant displacement

$$\begin{align} \Delta\textbf{D}(\textbf{k},t,s) = & \textbf{D}_{\mu}^{\textbf{k}}-\textbf{D}_{\|}^{\kappa(\textbf{k},t,s)} \end{align} \tag{ 48 }$$

$$\begin{align} \textbf{D}_{\mu}^{\textbf{k}} = & \boldsymbol{\Lambda}_{cv}^{\textbf{k}}-\nabla_{\textbf{k}}\beta_{\mu}^{\textbf{k}}.\end{align} \tag{ 49 }$$

Following the same procedure, the major contribution to the integral over s and t come from the stationary points determined by taking the partial derivatives with respect to s and t,

$$\begin{align} &\partial_{s}\left[S^{\textrm{ERM}}(\mathbf{k}, t, s)-\omega t\right] = 0 \nonumber\\&\quad \Leftrightarrow\ \partial_{s}\left\{\int_{s}^{t}\left[\omega_{g}^{\kappa\left(\textbf{k},t, t^{^{\prime}}\right)}+\mathbf{F}\left(t^{^{\prime}}\right)\cdot\boldsymbol{\Lambda}_{cv}^{\kappa\left(\textbf{k},t, t^{^{\prime}}\right)}\right] \mathrm{d} t^{^{\prime}}-\beta_{\|}^{\kappa(\textbf{k},t, s)}\right\} = 0 \nonumber\\ &\quad \Leftrightarrow\ -\omega_{g}^{\kappa\left(\textbf{k},t, s\right)}-\mathbf{F}\left(s\right)\cdot\boldsymbol{\Lambda}_{cv}^{\kappa\left(\textbf{k},t, s\right)}-\nabla_{\textbf{k}}\beta_{\|}^{\kappa(\textbf{k},t, s)}\partial_{s}\kappa(\textbf{k},t,s) = 0 \nonumber\\ & \quad \Leftrightarrow\ \left[\omega_{g}^{\kappa\left(\textbf{k},t, s\right)}+\mathbf{F}(s)\cdot\textbf{D}_{\|}^{\kappa(\textbf{k},t,s)}\right] = 0, \end{align} \tag{ 50 }$$

$$\begin{align} &\partial_{t}\left[S^{\textrm{ERM}}(\mathbf{k}, t, s)-\omega t\right] = 0 \nonumber\\ &\quad \Leftrightarrow\ \partial_{t}\left\{\int_{s}^{t}\left[\omega_{g}^{\kappa\left(\textbf{k},t, t^{^{\prime}}\right)}+\mathbf{F}\left(t^{^{\prime}}\right)\cdot\boldsymbol{\Lambda}_{cv}^{\kappa\left(\textbf{k},t, t^{^{\prime}}\right)}\right] \mathrm{d} t^{^{\prime}}-\beta_{\|}^{\kappa(\textbf{k},t, s)}\right\}-\omega = 0 \nonumber\\ &\quad \Leftrightarrow\ \omega_{g}^{\textbf{k}}+\mathbf{F}\left(t\right)\cdot\boldsymbol{\Lambda}_{cv}^{\textbf{k}}+\int_{s}^{t}\partial_{t}\left[\omega_{g}^{\kappa\left(\textbf{k},t, t^{^{\prime}}\right)}+\mathbf{F}\left(t^{^{\prime}}\right)\cdot\boldsymbol{\Lambda}_{cv}^{\kappa\left(\textbf{k},t, t^{^{\prime}}\right)}\right] \mathrm{d} t^{^{\prime}} \nonumber\\ &\qquad -\textbf{F}(t)\cdot\nabla_{\textbf{k}}\beta_{\|}^{\kappa(\textbf{k},t, s)}-\omega = 0 \nonumber\\ &\quad \Leftrightarrow\ \omega_{g}^{\textbf{k}}+\mathbf{F}\left(t\right)\cdot\left\{\boldsymbol{\Lambda}_{cv}^{\textbf{k}}-\nabla_{\textbf{k}}\beta_{\|}^{\kappa(\textbf{k},t, s)}+\int_{s}^{t}\nabla_{\textbf{k}}\left[\omega_{g}^{\kappa\left(\textbf{k},t, t^{^{\prime}}\right)}+\mathbf{F}\left(t^{^{\prime}}\right)\right.\right.\nonumber\\ & \left.\left.\qquad \qquad \qquad\,\, \cdot\boldsymbol{\Lambda}_{cv}^{\kappa\left(\textbf{k},t, t^{^{\prime}}\right)}\right] \mathrm{d} t^{^{\prime}}\right\}-\omega = 0 \nonumber\\ &\quad \Leftrightarrow\ \omega_{g}^{\textbf{k}}+\mathbf{F}\left(t\right)\cdot\left\{\boldsymbol{\Lambda}_{cv}^{\textbf{k}}-\nabla_{\textbf{k}}\beta_{\|}^{\kappa(\textbf{k},t, s)}+\Delta\textbf{r}(\textbf{k},t,s)-\boldsymbol{\Lambda}_{cv}^{\kappa(\textbf{k},t,t^{^{\prime}})}\bigg|_{t^{^{\prime}} = s}^{t^{^{\prime}}t}\right\}\nonumber\\ &\qquad-\omega = 0 \nonumber\\ &\quad \Leftrightarrow\ \omega_{g}^{\textbf{k}}+\mathbf{F}\left(t\right)\cdot\left[\Delta\textbf{r}(\textbf{k},t,s)+\textbf{D}_{\|}^{\kappa(\textbf{k},t,s)}\right] = \omega. \end{align} \tag{ 51 }$$

In the fifth line of equation (51), we use the results in equation (44). The saddle points $(\textbf{k}_{\textrm{sp}},t_{\textrm{sp}},s_{\textrm{sp}})$ can be obtained by solving the equations (45), (50), and (51), which are termed the tunneling, recollision, and emission equations, respectively.

One can see that the saddle points correspond to those crystal momenta $\textbf{k}_{\textrm{st}}$ for which the electron and hole are born at time s and recombine at time t with the electron–hole separation $\Delta\textbf{r}$ is equal to $\Delta\textbf{D}$. According to the saddle-point equations, the interband HHG can be interpreted in terms of the following three steps: i) the equation (50) gives the tunneling conditions $\textbf{k}^{^{\prime}} = \textbf{k}_{\textrm{sp}}+\textbf{A}(t_{\textrm{sp}})-\textbf{A}(s_{\textrm{sp}})$, that is, an electron–hole pair is created by tunneling from VB to CB at time s_sp and with an initial momentum $\textbf{k}^{^{\prime}}$; ii) the electron and hole are accelerated by the laser and the equation (45) constrains the relation between ionization time t_sp and emission time s_sp, i.e. the instant the electron–hole separation $\Delta\textbf{r}(\textbf{k}_{\textrm{sp}},t_{\textrm{sp}},s_{\textrm{sp}})$ is equal to $\Delta\textbf{D}(\textbf{k}_{\textrm{sp}},t_{\textrm{sp}},s_{\textrm{sp}})$; iii) the emission frequency ω due to the electron–hole pair recombination at time t_sp with crystal momentum $\textbf{k}_{\textrm{sp}}$ and relative separation $\Delta\textbf{r}$ is determined by equation (51), which is the energy conservation law. This three-step model is referred to as an extended recollision model (ERM) by relaxing the recollision condition by a preset recollision threshold R₀, which is introduced by Yue and Gaarde [108, 117]. As sketched in figure 4, the ERM allows such imperfect recollision that $\Delta\textrm{R}^{\mu} = \left|\Delta\textbf{r}(\textbf{k},t,s)-\Delta\textbf{D}(\textbf{k},t,s)\right|$ reaches its minimum within the region $\Delta\textrm{R}^{\mu}\lt\textrm{R}_{0}$. In other words, the recombination is also possible upon an imperfect overlap of the electron's and hole's wave packet, i.e. their centers do not overlap exactly. The spatial separation of the electron and hole upon recombination constitutes the formation of a dipole, which has a polarization energy $\mathbf{F}\left(t\right)\cdot\Delta\textbf{r}(\textbf{k},t,s)$. This affects the energy released as photons in the recombination process. Different from SRM, ERM introduces a recollision threshold that involves the delocalized feature of the electrons in solids. Moreover, the important role of Berry curvature and transition dipole phase has been pointed out by considering the nonzero displacement $\Delta\textbf{D}$ and energy shift $\mathbf{F}\left(t\right)\cdot\textbf{D}_{\|}^{\kappa(\textbf{k},t,s)}$.

• Wannier recollision model (WRM)

Zoom In Zoom Out Reset image size

By transforming the Bloch dipole moment $\textbf{d}^{\textbf{k}} = \textbf{d}_{cv}(\textbf{k})$ to Wannier dipole moment $\textbf{d}_{l} = \int_{V_{\textrm{crystal}}} w_{c}^{*}\left(\mathbf{r}-\mathbf{r}_{l}\right) \mathbf{r} w_{v}(\mathbf{r}) \mathrm{d} \mathbf{r}$, Parks et al develop a generalized quasi-classical approach accounting for the lattice structure [109]. There, they assume a centrosymmetric system for which the diagonal elements $\textbf{d}_{mm}(\textbf{k})$ can be set to zero. The connection between the Bloch and Wannier basis functions is given by a Fourier transform according to

$$\begin{align} u_{m, \mathbf{k}}(\mathbf{r}) = \sum_{j} w_{m}\left(\mathbf{r}-\mathbf{r}_{j}\right) \mathrm e^{-\mathrm i \mathbf{k} \cdot\left(\mathbf{r}-\mathbf{r}_{j}\right)}, \end{align} \tag{ 52 }$$

$$\begin{align} w_{m}\left(\mathbf{r}-\mathbf{r}_{j}\right) = \frac{1}{V_{\textrm{cell}}} \int_{\mathrm{BZ}} u_{m, \mathbf{k}}(\mathbf{r}) \mathrm e^{\mathrm i \mathbf{k} \cdot\left(\mathbf{r}-\mathbf{r}_{j}\right)} \mathrm{d} \mathbf{k}. \end{align} \tag{ 53 }$$

Here, $w_{m}\left(\mathbf{r}-\mathbf{r}_{j}\right)$ is the Wannier function of band m corresponding to the primitive unit cell at position r_j . V_cell is the volume of a unit cell, and the integration is performed over the first Brillouin zone (BZ). Then, the Bloch functions in transition dipole moment are replaced by Wannier functions with the help of relation (52), which leads to

$$\begin{align} \mathbf{d}^{\mathbf{k}} & = \sum_{j, k} \int_{V_{\textrm{cell}}} w_{c}^{*}\left(\mathbf{r}-\mathbf{r}_{k}\right)\left[\mathbf{r}-\mathbf{r}_{j}\right] w_{v}\left(\mathbf{r}-\mathbf{r}_{j}\right) \mathrm e^{\mathrm i \mathbf{k} \cdot\left(\mathbf{r}_{j}-\mathbf{r}_{k}\right)} \mathrm{d} \mathbf{r} \nonumber\\ & = \sum_{j, l} \int_{V_{\textrm{cell}}} w_{c}^{*}\left(\mathbf{r}-\left(\mathbf{r}_{j}+\mathbf{r}_{l}\right)\right)\left[\mathbf{r}-\mathbf{r}_{j}\right] w_{v}\left(\mathbf{r}-\mathbf{r}_{j}\right) \mathrm e^{-\mathrm i \mathbf{k} \cdot \mathbf{r}_{l}} \mathrm{d} \mathbf{r} \nonumber\\ & = \sum_{l} \mathrm e^{-\mathrm i \mathbf{k} \cdot \mathbf{r}_{l}} \int_{V_{\textrm{crystal}}} w_{c}^{*}\left(\mathbf{r}-\mathbf{r}_{l}\right) \mathbf{r} w_{v}(\mathbf{r}) \mathrm{d} \mathbf{r} = \sum_{l} \mathbf{d}_{l} \mathrm e^{-\mathrm i \mathbf{k} \cdot \mathbf{r}_{l}}. \end{align} \tag{ 54 }$$

In the above derivation, a transform $\mathbf{r}_{k} = \mathbf{r}_{j}+\mathbf{r}_{l}$ changes the summation index k with l in the second line, and performing $\sum_{j}$ changes the integration volume from a unit cell to the whole crystal in the second line. The Wannier dipole moment d_l are in form of the Fourier series expansion coefficients of the Bloch dipole moment, which describes a transition where an electron is born l lattice away from the hole. Inserting equation (54) into equation (36), one can obtain the real-space interband current,

$$\begin{align} J_{\mu}^{\mathrm{WRM}}(\omega) & = \sum_{j, l}\left\{\mathbf{d}_{j}^{*}\left[\mathbf{d}_{l} \cdot \mathbf{T}_{j l}(\omega)\right]-\mathbf{d}_{j}\left[\mathbf{d}_{l}^{*} \cdot \mathbf{T}_{j l}^{*}(-\omega)\right]\right\} \nonumber\\ & = \sum_{j, l}\left[\mathbf{P}_{j l}(\omega)-\mathbf{P}_{j l}^{*}(-\omega)\right], \end{align} \tag{ 55 }$$

$$\begin{align} \mathbf{T}_{j l}(\omega) & = \omega\sum_{\mathbf{k}}\int_{-\infty}^{\infty} \mathrm{d} t \int_{-\infty}^{t} \mathrm{d}s \mathbf{F}\left(s\right) \mathrm e^{\mathrm i \varphi\left(\mathbf{k},t,s,\mathbf{r}_{j},\mathbf{r}_{l}\right)} \end{align} \tag{ 56 }$$

where $\varphi\,\, \,\,= \,\,\,\,-\,\,\,\,\int_{s}^{t}\,\,\,\,\omega_{g}^{\kappa(k,t,t^{^{\prime}})}\,\,\,\,\mathrm{d}\,\,\,\,t^{^{\prime}}\,\,\,\,+\omega t+\mathbf{k} \cdot\left(\mathbf{r}_{j}-\mathbf{r}_{l}\right)+$ $\left[\mathbf{A}(t)-\mathbf{A}\left(s\right)\right] \cdot \mathbf{r}_{l}$. These integrals are solved by saddle-point integration with saddle-point conditions

$$\begin{align} \omega_{g}^{\kappa(\textbf{k},t,s)}+\textbf{F}(s)\cdot\textbf{r}_{l} = 0, \end{align} \tag{ 57 }$$

$$\begin{align} \Delta\textbf{r}(\textbf{k},t,s) = \textbf{r}_{j}-\textbf{r}_{l}, \end{align} \tag{ 58 }$$

$$\begin{align} \omega_{g}^{\textbf{k}}+\textbf{F}(t)\cdot\textbf{r}_{j} = \omega, \end{align} \tag{ 59 }$$

resulting from the partial derivatives with ϕ respect to s, k, and t. This Wannier quasi-classical description transforms the three-step model from reciprocal space to real space [109], and we call it Wannier recollision model (WRM). In figure 5, we show a sketch for the three steps in WRM: (i) an electron is transitioned from x₀ to $\textbf{x}_0 + \textbf{x}_l$ at birth time s; (ii) the electron–hole pair is separated by the laser field following the classical trajectory $\Delta\textbf{r}(\textbf{k},t,s)$; (iii) the electron and hole recombine at time t with probability amplitude $\mathbf{d}_{j} \mathrm e^{-\mathrm i \mathbf{k}_{s}\left(t_{b}, t_{r}\right) \cdot \mathbf{x}_{j}}$ and release a harmonic photon of frequency $\omega = \omega_{g}^{\textbf{k}}+\textbf{F}(t)\cdot\textbf{x}_{j}$ when the separation $\Delta\textbf{r}(\textbf{k},t,s)$ is equal to $\textbf{x}_{j}-\textbf{x}_{l}$. While Bloch analysis describes an electron–hole pair by a single trajectory, WRM describes it by a swarm of weighted trajectories that generate and recombine at different sites in the crystal. This enables to evaluate the contributions of individual lattice sites to the HHG process and hence addresses the question of localization of harmonic emission in solids.

• Wannier–Bloch recollision model

Zoom In Zoom Out Reset image size

A Wannier–Bloch approach was also developed by Osika et al [107]. Compared to WBR, they use a mixed representation, where Wannier wavefunctions and Bloch wavefunctions are used for characterizing the VB and CB, respectively. Therefore, this model provides an atomistic-like description of HHG in solid-state systems, where we have a k-dependence on the CB and localized recombination in the VB. In the Wannier–Bloch approach [107], it focuses on the 1D lattice and the TDSE is solved with the ansatz

$$\begin{align} |\Psi(t)\rangle = \sum_{j}\left|w_{v, j}\right\rangle a_{j}(t)+\int_{\mathrm{BZ}} a_{c}(k, t)\left|\psi_{c, k}\right\rangle\mathrm{d}k, \end{align} \tag{ 60 }$$

where the wave function of a single electron is expressed as a superposition of the localized Wannier wave states $\left|w_{v, j}\right\rangle$ in the VB and delocalized Bloch state $\left|\psi_{c, k}\right\rangle$ in the CB. Here, j runs over all atomic sites in the crystal. The Wannier functions of the mth band can be represented by a set of Bloch functions

$$\begin{align} \left|w_{m, j}\right\rangle = w_{m, j}(x) = \int_{\mathrm{BZ}}\psi_{m,k}\left(x-x_{j}\right) \tilde{w}_{m}(k)\mathrm{d}k. \end{align} \tag{ 61 }$$

In this form, $\tilde{w}_{m}(k)$ is a product of a normalization constant and a phase depending on crystal momentum k. For 1D lattice, the $\tilde{w}_{m}(\textbf{k})$ are independent of k provided the Wannier functions are real and symmetric under appropriate reflection, and they fall off exponentially with distance [140, 141]. Note that the Wannier functions form a completely orthogonal set in the VB but are not eigenfunctions of the Hamiltonian, the electron wave function may spread in the lattice because of the interatomic hopping and the acceleration driven by the laser field. Thus, the coefficient $a_{j}(t)$ acquires nonzero values during the laser pulse, and the harmonic emission is obtained by summing up the contribution of each Wannier state

$$\begin{align} J^{\mathrm{WBRM}}(\omega) & = \omega\int_{-\infty}^{+\infty}\mathrm{d}t\mathrm e^{\mathrm i\omega t}\sum_{k}\sum_{j}a_{j}^{*}(t)d_{jc}(k)a_{c}(k,t)+c.c., \nonumber\\ & = \omega\left|\tilde{w}_{v}\right|^{2}\int_{-\infty}^{+\infty}\mathrm{d}t\mathrm e^{\mathrm i\omega t}\sum_{\mathbf{k}}\sum_{j}\left[a_{j}(t)d^{k}\right]^{*}\mathrm e^{\mathrm ik x_{j}} \nonumber\\ &\quad \times\sum_{j^{^{\prime}}}\int_{t_{0}}^{t}\mathrm{d}s F(s)d^{\kappa(k,t,s)}\mathrm e^{-\mathrm i\kappa(k,t,s) x_{j^{^{\prime}}}}\mathrm e^{-\mathrm i\int_{s}^{t}E_{c}\textbf{(}\kappa(k,t,t^{^{\prime}})\textbf{)}\mathrm{d}t^{^{\prime}}}. \end{align} \tag{ 62 }$$

The transition dipole moment from the CB to the VB is $d_{jc}(k) = \left[\tilde{w}_{v}d^{k}\right]^{*}\mathrm e^{\mathrm ik x_{j}}$. Then, one can reorganize this current as a product of a global amplitude and phase

$$\begin{align} J^{\mathrm{WBRM}}(\omega) & = \sum_{j,j^{^{\prime}}}\sum_{k}\int_{-\infty}^{+\infty}\mathrm{d}t\int_{t_{0}}^{t}\mathrm{d}sf_{j,j^{^{\prime}}}(k,t,s)\mathrm e^{-\mathrm i\Phi_{j,j^{^{\prime}}}(k,t,s)+i\omega t}, \end{align} \tag{ 63 }$$

$$\begin{align} f_{j,j^{^{\prime}}}(k,t,s) & = \omega\left|\tilde{w}_{v}\right|^{2}\left|a_{j}(t)\right|\left[d^{k}\right]^{*}\left|a_{j^{^{\prime}}}(s)\right|F(s)d^{\kappa(k,t,s)}, \end{align} \tag{ 64 }$$

$$\begin{align} \Phi_{j,j^{^{\prime}}}(k,t,s) & = \int_{s}^{t}E_{c}\textbf{(}\kappa(k,t,t^{^{\prime}})\textbf{)}\mathrm{d}t^{^{\prime}}+\varphi_{a_{j}}(t)-k x_{j}-\varphi_{a_{j^{^{\prime}}}}(s)\nonumber\\& \quad +\kappa(k,t,s)x_{j^{^{\prime}}}. \end{align} \tag{ 65 }$$

Note that $\varphi_{a_{j}} \equiv \arg(a_{j})$ is the phase associated with the population coefficient a_j . The physical information about the radiation by means of the Wannier–Bloch approach is extracted from the saddle-point conditions

$$\begin{align} E_{c}\textbf{(}\kappa(k,t,s)\textbf{)}+\partial_{s}\varphi_{a_{j^{^{\prime}}}}(s)+F(s)x_{j^{^{\prime}}} = 0, \end{align} \tag{ 66 }$$

$$\begin{align} \int_{s}^{t}\nabla_{k}E_{c}\textbf{(}\kappa(k,t,t^{^{\prime}})\textbf{)}\mathrm{d}t^{^{\prime}}+x_{j^{^{\prime}}}-x_{j} = 0, \end{align} \tag{ 67 }$$

$$\begin{align} E_{c}(k)+\partial_{t}\varphi_{a_{j}}(t)+F(t)x_{j} = \omega, \end{align} \tag{ 68 }$$

which gives a recollision model [107] involving the delocalization of the electrons as shown in figure 6: (i) an electron located at the atomic site $\textbf{x}_{j^{^{\prime}}}$ is excited from the valence to the CB at time s; (ii) this electron is accelerated in the CB while the electron wave function spreads along the periodic lattice structure; (iii) at time t, the electron recombines at the site x_j , and the excess electron energy is emitted in the form of a high-harmonic photon. Then, the delocalization occurs because the electron can recombine with different Wannier sites from the one it has initially been excited from, considering the spreading of the electron wavefunctions. By analyzing the spatial-resolved HHG process, one can determine the degree of localization of the HHG process as a function of experimental parameters, with implications for HHG efficiency and for the emerging area of atto-nanoscience [142].

Zoom In Zoom Out Reset image size

Since all of the above models are rooted in the saddle-point approximation, it is valuable to revisit the validity of the saddle-point approximation in order to discuss the scope of the model and the corresponding recollision picture. Thus, we first recall a general form of saddle-point integration theorem. We quote only some of the derivations and conclusions that will be called upon in this review. More complete and rigorous discussions of the saddle-point method can be found in [23, 143]. The saddle-point approximation is a powerful method for analyzing the asymptotic behavior of a complex integration

$$\begin{align} I(\sigma) = \int_{C}f(z)\mathrm e^{\sigma g(z)}\mathrm{d}z, \end{align} \tag{ 69 }$$

with parameter $\sigma\gg1$. Both f(z) and g(z) are smooth complex analytical functions of z and C is the integral path. We consider non-degenerate multiple isolated stationary phase points $z = z_{s}$ (index s) where $g^{^{\prime}}(z) = \nabla_{z}g(z)|_{z = z_{s}} = 0$ and $g^{^{\prime\prime}}(z_{s})\neq0$. The integration path C can be deformed to follow an appropriate path through the critical points of the integrand utilizing the Cauchy–Goursat theorem [144] without changing the value of the integral. This allows one to make a very useful simplification in calculating the interested integral. By expanding the exponential in the integrand along the steepest descent into a truncated Taylor series around the stationary phase point, one can obtain

$$\begin{align} I(\sigma) & = \int_{C}f(z)\mathrm e^{\sigma g(z_{s})+\frac{1}{2}\sigma g^{^{\prime\prime}}(z_{s})(z-z_{s})^{2}+\cdots}\mathrm{d}z, \nonumber\\ &\approx \mathrm e^{\sigma g(z_{s})}\int_{C}f(z)\mathrm e^{\frac{1}{2}\sigma g^{^{\prime\prime}}(z_{s})(z-z_{s})^{2}}\mathrm{d}z. \end{align} \tag{ 70 }$$

Retaining to the second order, one gets a Gaussian function with width $O(\sqrt{1/\sigma})$. Using the generalized Riemann–Lebesgue lemma, the contributions for this type of integral come predominantly from the stationary phase points z_s , while the oscillatory parts of the integrand cancel out for large σ. Then, the integration in equation (69) can be asymptotically approximated as a sum of stationary phase point contributions

$$\begin{align} I(\sigma) & = \sum_{s}\left(\frac{2\pi}{\sigma}\right)^{\frac{1}{2}}\frac{f(z_{s})}{\sqrt{\det(-g^{^{\prime\prime}}(z_{s}))}}\mathrm e^{\sigma g(z_{s})}. \end{align} \tag{ 71 }$$

Equation (71) is called the saddle-point approximation and the expression $\nabla_{z}g(z)|_{z = z_{s}} = 0$ is referred to as the saddle-point equation (correspondingly, z_s is called the saddle point).

From the above discussion, the saddle-point approximation is valid only when σ is large enough. To give an intuitive illustration, we take a typical form of integral $I(\sigma,\sigma_{g}) = \int_{-\infty}^{+\infty}\mathrm e^{-\sigma_{g}\sigma x^{2}}\mathrm e^{\mathrm i\sigma x^{2}}\mathrm{d}x$ as an example, where $\mathrm e^{-\sigma_{g}\sigma x^{2}}$ and $\mathrm e^{\mathrm i\sigma x^{2}}$ corresponds to amplitude term f(z) and phase term $\mathrm e^{\sigma g(z)}$ in equation (69) respectively. Utilizing Cauchy–Goursat theorem [144], one can deform the integration path to follow the steepest descent, i.e. $z = (x+\mathrm iy) |_{x = y}$. In this form, for a fixed σ, a smaller σ_g describes a relatively slowly varying amplitude compared with the phase in the integrand around the saddle point x = 0. Figure 7 shows the behavior of $\mathrm e^{-\sigma_{g}\sigma x^{2}}\mathrm e^{\mathrm i\sigma x^{2}}$ along the steepest descent, where the parameter σ is set to 1 without loss of generality. Comparing the results for three different values of σ_g , it is shown that with decreasing σ_g the evaluation of the oscillatory integral converges to a Gaussian form contributed by the phase term, i.e. $I(\sigma,\sigma_{g}) = \int_{-\infty}^{+\infty}\mathrm e^{-\sigma_{g}\sigma x^{2}}\mathrm e^{\mathrm i\sigma x^{2}}\mathrm{d}x \approx \int_{-\infty}^{+\infty}\mathrm e^{\mathrm i\sigma x^{2}}\mathrm{d}x = \sqrt{\frac{2\pi}{-\mathrm i\sigma}}$. Namely, the saddle-point approximation (equation (71)) works well. However, for cases the oscillation of the amplitude term is comparable to ($\sigma_{g} = 1$) or even faster than ($\sigma_{g} = 10$) the phase term, the integration deviates from the result of saddle-point approximation. This conclusion can be also obtained with an analytical form $I(\sigma,\sigma_{g}) = \int_{-\infty}^{+\infty}\mathrm e^{-(\sigma_{g}-\mathrm i)\sigma x^{2}}\mathrm{d}x = \sqrt{\frac{2\pi}{(\sigma_{g}-\mathrm i)\sigma}}\xrightarrow{\lim{\sigma_{g}\rightarrow0}}\sqrt{\frac{2\pi}{-\mathrm i\sigma}}$. For the physical problems we are interested in, the coefficient in the phase term σ is related to the electron energy. Thus, one can expect that the saddle-point integral gives a reasonable approximation when the accumulated electron energy is large enough and the phase term of the integrand varies much faster than the other factors with respect to the integration variables.

Zoom In Zoom Out Reset image size

Combing back to equation (41), the HHG contributed by the interband current is expressed as an integral with amplitude and propagation phase terms. Within the saddle-point approximation, the interband current in equation (41) is given by a sum over all the relevant stationary values $\{\textbf{k}_{\textrm{sp}},t_{\textrm{sp}},s_{\textrm{sp}}\}$

$$\begin{align} J_{\mu}^{\mathrm{ter}}(\omega)&\approx\sum_{\textbf{k}_{\textrm{sp}},t_{\textrm{sp}},s_{\textrm{sp}}}H(\textbf{k}_{\textrm{sp}},t_{\textrm{sp}},s_{\textrm{sp}})\nonumber\\& \quad \times R_{\mu}^{\mathbf{k}_{\textrm{st}}}T^{\textbf{k}_{\textrm{sp}}-\textbf{A}(t_{\textrm{sp}}) +\textbf{A}(s_{\textrm{sp}})} \mathrm e^{-\mathrm i\left(S^{\mu}(\textbf{k}_{\textrm{sp}},t_{\textrm{sp}},s_{\textrm{sp}})-\omega t_{\textrm{sp}}\right)}+\textrm{c.c.} \end{align} \tag{ 72 }$$

with an additional Hessian factor $H(\textbf{k}_{\textrm{sp}},t_{\textrm{sp}},s_{\textrm{sp}}) = \frac{1}{\sqrt{\det\left[2\pi \mathrm i\partial_{2}S^{\mu}|_{\textbf{k}_{\textrm{sp}},t_{\textrm{sp}},s_{\textrm{sp}}}\right]}}$ that accounts for the width of the complex-integration Gaussians. The term $\partial_{2}S^{\mu}$ is the Hessian matrix with element $\partial_{l}\partial_{m}S^{\mu}$ (l, $m = \{\textbf{k},t,s\}$). As discussed in section 2.2, the semiclassical picture of HHG is obtained in the scenario that the integral is approximated using the values of the integrand at stationary points of the phase term, based on which the classic correspondence between the electron trajectory and harmonic emission is established. Thus, the validity of the semiclassical picture rests on whether the saddle-point approximation is valid.

In atomic gases, the integral form of harmonic emission under strong field approximation involves a highly oscillatory term in the phase factor $\Theta(\textbf{p},t,s) = \omega t - \int_{s}^{t}\mathrm{d}\tau\left(\frac{\left[\textbf{p}+\textbf{A}(t)\right]^{2}}{2}+I_{p}\right)$ [22] with the canonical momentum p and atomic ionization potential I_p . One can examine the behavior of the phase in the simplest case where an intense monochromatic linearly polarized laser field $\textbf{F}(t) = \textbf{F}_{0}\cos(\omega_{0}t)$ is applied

$$\begin{align} \Theta(\textbf{p},t,s) & = \omega t-\int_{\omega s}^{\omega_{t}}\left(\frac{\left[p_{\|}-\frac{F_{0}}{\omega_{0}}\sin(\theta)\right]^2}{2}+I_{p}\right)\frac{\mathrm{d}\theta}{\omega_{0}} \nonumber\\ & = \omega t-\frac{F_{0}^{2}}{2\omega_{0}^{3}}\int_{\omega s}^{\omega_{t}}\left[\frac{\omega_{0}p_{\|}}{F_{0}}-\sin(\theta)\right]\mathrm{d}\theta+\frac{I_{p}}{\omega_{0}}\left(\omega_{0}t-\omega_{0}s\right) \nonumber\\ & = \omega t-\frac{U_{p}}{\omega_{0}}\int_{\omega s}^{\omega_{t}}\left[\frac{\omega_{0}p_{\|}}{F_{0}}-\sin(\theta)\right]\mathrm{d}\theta+\frac{I_{p}}{\omega_{0}}\left(\omega_{0}t-\omega_{0}s\right). \end{align} \tag{ 73 }$$

$U_{p} = \frac{F_{0}^{2}}{4\omega_{0}^{2}}$ is the ponderomotive energy of the electron under the action of the laser field, and $\frac{I_{p}}{\omega_{0}}$ is the number of photons necessary to ionize the target atom. The saddle-point approximation is asymptotically exact provided $\frac{U_{p}}{\omega_{0}}$ and $\frac{I_{p}}{\omega_{0}}$ are large enough, which is in general well satisfied with a strong low-frequency laser field.

The situation is however quite different for the interband HHG in solids. On the one hand, in contrast to the free-electron dispersion relevant for gas HHG, solid systems have more complicated electron band structures. Then, the variation of the integrand phase term actually depends on a coupling form of the laser and crystal parameters, and one needs to meticulously evaluate the applicability of the saddle-point approximation. On the other hand, previous works have suggested the important role of electron delocalization in solid HHG, e.g. the nonzero recollision threshold [108], and the delocalization of HHG emission [107, 109]. While the particle-like recollision models attempt to incorporate these properties, the wave-like performances are still difficult to be fully described. To shed light on these problems, we consider a representative example by considering the evolution of a wave packet

$$\begin{align} \Psi(x,t,t_{0}) = \int_{-\infty}^{\infty}f(k)\mathrm e^{\mathrm ikx-\mathrm i\varphi(k,t,t_{0})}\mathrm{d}k, \end{align} \tag{ 74 }$$

where $f(k) = \mathrm e^{-(k/k_{w})^{2}}$ is the Gaussian wavepacket in k-space, $\varphi(k,t,t_{0}) = \int_{t_{0}}^{t}\mathrm d\tau\varepsilon(k+A(\tau)-A(t_{0}))$ is the dynamical phase with energy dispersion ε, and $A(t) = -F_{0}/\omega_{0}\textrm{sin}(\omega_{0}t)$ is the vector potential of the laser field. The saddle-point approximation gives a classical picture that the center of the wave packet moves with group velocity $\nabla_{k}\varepsilon$, i.e. $x_{c}(t) = \int_{t_{0}}^{t}\mathrm d\tau\nabla_{k}\varepsilon(k+A(\tau)-A(t_{0}))$.

We evaluate the results from equation (74) with different dispersions: the free-electron (FE) dispersion (i.e. parabolic band) and a crystal energy dispersion (we take the first CB of ZnO crystal along the $\Gamma-M$ direction as an example). We use the same laser parameters as those in [82, 124], and shift the parabolic band to mimic the same band gap of ZnO, i.e. $I_{p} = E_{g} = 0.1213$ a.u.. The energy and corresponding velocity dispersions are shown in figures 8(a) and (b), respectively. One can see obvious nonlinear velocity dispersion for crystal ZnO in the region far away from the top of VB. Using equation (74), one can obtain the time-dependent distribution of the wavepacket $\rho(x,t) = \Psi(x,t,t_{0})^{*}\Psi(x,t,t_{0})$. The results are shown in figures 8(c) and (d) for FE and crystal ZnO. The conformal contour shows the time-dependent distribution of the wavepacket and the dashed black lines show the classical movement $x_\textrm{c}$. In the case of FE, it can be seen that the shape of the wavepacket is almost unchanged except for free diffusion. Moreover, the classical motion is always consistent with the center of the wavepacket (the locations for maximum wavepacket distribution marked by dashed pink lines). However, for a crystal energy dispersion, one can clearly see that the Gaussian wavepacket is distorted during evolution, and the classical motion fails to describe the locations of the maximum wavepacket distribution. Note that the discrepancy between $x_\textrm c$ and $x_{\max[\rho]}$ is closely related to the distortion of the electron wavepacket during evolution, which is typically a wave feature and cannot be described by treating an electron as a particle.

Zoom In Zoom Out Reset image size

Before we proceed, let us briefly recap the previous discussions. Literatures have shown that the recollision models are widely applied and work well for HHG in gases. Several particle-like recollision models have also been developed and used for HHG in solids to explore HHG features such as the emission time, harmonic cutoff, etc [106–109]. Despite being promising in some cases, our discussions above suggest that there are still challenges for the recollision picture to describe solid HHG considering the non-parabolic energy band and the delocalization of the valence electrons for general semiconductors, insulators, and dielectrics, such as the noticeable error in describing the emission time. This prevents us from extending the successful HHS from gases to solid systems.

The success and challenge of the particle-like recollision picture based on the saddle-point approximation are reminiscent of the use of geometric optics. Although the propagation of light should be accurately described as waves, one may approximately describe it in the form of rays, in analogy to the semiclassical trajectories in HHG, see figure 9. In fact, the geometric-optics approximation (or eikonal approximation) is just one of the applications of the saddle-point approximation (this can be seen in [115] and will be addressed later on in this review). However, when the size of objects and apertures is comparable to the wavelength of light, geometry optics is no more a good approximation. Diffraction effects become noticeable, which are essentially interference of wavelets, and one must revert to wave optics described by the Huygens–Fresnel principle. Likewise, when the saddle-point approximation is not good enough, one should turn to more accurate models that take into account the wave properties of the electron wavepackets during the HHG process. In the following section, we will introduce such kind of model in the spirit of the Huygens–Fresnel principle.

Zoom In Zoom Out Reset image size