Social influence in committee deliberation

Abstract

Committee protocols typically involve a deliberation stage in which members try to influence and convince other regarding the “right” decision. Beyond information exchange, such deliberations also aim to affect the preferences and the votes of other members. Using a model of social influence, we demonstrate how deliberation procedures affect the voting outcome and how different protocols of consultation by committees’ chairs may affect their decisions. We then analyze the ability of a “designer” to control the deliberation protocol and to manipulate the deliberation procedure to increase the probability that the outcome he favors will be selected.

Appendix: Proofs

Proof of Claim 1:

If g is monotonic in both arguments and $g(\alpha ,\alpha )\equiv \alpha$ then for $\alpha <\beta$, $\alpha =g(\alpha ,\alpha )\leqslant g(\alpha ,\beta )\leqslant g(\beta ,\beta )=\beta$. If, on the other hand, for some $\alpha$, $g(\alpha ,\alpha )<\alpha$, then by continuity for sufficiently small $\varepsilon >0$, $g(\alpha ,\alpha +\varepsilon )<\alpha$. Likewise, if $g(\alpha ,\alpha )>\alpha$ then $\alpha <g(\alpha -\varepsilon ,\alpha )$, a contradiction. $\square$

Proof of Claim4:

If committee members do not deliberate among themselves, then there is no change in their preferences and therefore $\beta ^{cb}=\alpha$ and $\beta _0^{cb}=g(\alpha _0,\alpha )$. When the n agents deliberate among themselves their equilibrium behavioral preference is given by $\beta ^{cm}=g(\alpha ,\beta ^{cm})$. By Claim 6 in FS, $\beta ^{cm}=g(\alpha ,\beta ^{cm})>\alpha$ if and only if $g(\alpha ,\alpha )>\alpha$. And since $g_2>0$, $\beta _0^{cm}=g(\alpha _0,\beta ^{cm})>g(\alpha _0,\alpha )=\beta _0^{cb}$. $\square$

Proof of Claim 5:

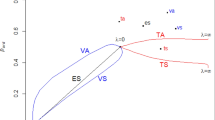
We start with the case db in which the chair deliberates with each adviser separately. Consider the behavioral preferences of each adviser which is a function of his core preferences and the behavioral preferences of the chair, $\beta (\alpha ,\beta _0)\equiv g(\alpha ,\beta _0)$. Given that $g_2>0$, this function is increasing in $\beta _0$. Also, $\beta _0(\alpha _0,\beta )\equiv g(\alpha _0,\beta )$ are the behavioral preferences of the chair given his core preferences and the behavioral preferences of the advisers. Figure 1 depicts both functions in a $(\beta \times \beta _0)$ space where $\alpha ,\alpha _0$ are fixed parameters. The intersection $(\beta ^{db}$,$\beta _0^{db})$ (point s in Fig. 1) is an equilibrium of the bilateral deliberation process as $\beta ^{db}=g(\alpha ,\beta _0^{db})$ and $\beta _0^{db}=g(\alpha _0,\beta ^{db})$. Note also that since $\alpha <\alpha _0$, it follows that the equilibrium point is above the $45^{\circ }$ line because in equilibrium $\beta ^{db}<\beta _0^{db}$ (see point (ii) at the end of Sect. 2.2).

Fig. 1

Proof of Claim 5

Examine now the equilibrium of the multilateral deliberation process. The function $\beta _0(\alpha _0,\beta )$ is the same as before. The function that determines the behavioral preferences of the advisers given the behavioral preferences of the chair is given now by $\beta =g(\alpha ,\frac{\beta _0+(n-1)\beta }{n})$.¹³ This curve is a left (anticlockwise) rotation of the curve $\beta (\alpha ,\beta _0)$ around the symmetric point r (which is the intersection of the $45^{\circ }$ line and the $\beta (\alpha ,\beta _0)$ curve). The reason is that when $\beta =\beta _0$, the two functions imply the same behavioral preferences. It is a left rotation because for all the points above the $45^{\circ }$ line $\beta <\beta _0$ and therefore the function for the multilateral procedure yields a lower value. The intersection q of the two curves, $\beta _0(\alpha _0,\beta )$ and $\beta =g(\alpha ,\frac{\beta _0+(n-1)\beta }{n})$ yields the equilibrium for the multilateral deliberation case. As depicted in Figure 1, comparing the two equilibrium points yields that $\beta _0^{db}>\beta _0^{dm}$. $\square$

Proof of Claim 6:

Under the consultation procedure, $\beta ^{cb}=\alpha$ and $\beta _0^{cb}=g(\alpha _0,\alpha )$, while under the deliberation procedure $\beta ^{db}=g(\alpha ,\beta _0^{db})$ and $\beta _0^{db}=g(\alpha _0,\beta ^{db})$. We show first that $\beta ^{db}>\alpha$. If the core preference of the chair is $\alpha$, then the advisers and the chair have the same core preferences and consequently the same behavioral preferences $\beta$. Given our SR assumption, $\beta$ must be larger than $\alpha$. They can obviously not equal $\alpha$, because $g(\alpha ,\alpha )>\alpha$. If $\beta <\alpha$, then since $g(\alpha ,\alpha )>\alpha$ and $g(\alpha ,\beta )=\beta$, we get

$$\begin{aligned}{} & {} \frac{g(\alpha ,\alpha )-g(\alpha ,\beta )}{\alpha -\beta }>\frac{\alpha -\beta }{\alpha -\beta }=1 \end{aligned}$$

In contradiction to the assumption that $g_2<1$. As $\alpha _0>\alpha$, the $\beta$ value of the chair is higher than when his core preferences are $\alpha$, and consequently, so is the $\beta$ values of the advisers.

Since $\beta _0^{b0}=g(\alpha _0,\beta ^{db})$ and $\beta ^{db}>\alpha$, it follows that $\beta _0^{db}>g(\alpha _0,\alpha )=\beta _0^{cb}$, hence the claim. $\square$

Proof of Claim 7:

If person 1 does not participate in the deliberation, then $\beta ^1_1=\alpha _1$. We show first that $\beta ^1_2>\beta _2$ and $\beta ^1_3>\beta _3$. Observe that by Claim 8 in FS, $\beta ^1_2>\alpha _2$. If $\beta _2\leqslant \alpha _2$, then clearly $\beta ^1_2>\beta _2$, and since $\beta _2 >\beta _1$,

$$\begin{aligned} \beta ^1_3=g(\alpha _3,\beta ^1_2)>g(\alpha _3,\dfrac{1}{2}[\beta _1+\beta _2])=\beta _3 \end{aligned}$$

Suppose that $\beta _2>\alpha _2$ but $\beta ^1_2\leqslant \beta _2$. Since by FS (2018) $\beta _1<\beta _3$ (see end of Sect. 2.2),

$$\begin{aligned}{} & {} \beta _2=g(\alpha _2,\dfrac{1}{2}[\beta _1+\beta _3])\geqslant \beta ^1_2=g(\alpha _2,\beta ^1_3) \Longrightarrow \nonumber \\{} & {} \dfrac{1}{2}[\beta _1+\beta _3]\geqslant \beta ^1_3\Longrightarrow \nonumber \\{} & {} \beta _3>\beta ^1_3 \end{aligned}$$

(2)

Also, since $g_2<1$,

$$\begin{aligned}{} & {} \left. \begin{array}{l} \beta _2=g(\alpha _2,\dfrac{1}{2}[\beta _1+\beta _3])> \\ \beta ^1_2=g(\alpha _2,\beta ^1_3) \end{array} \right\} \Longrightarrow \nonumber \\{} & {} \quad \beta _2-\beta ^1_2<\dfrac{1}{2}[\beta _1+\beta _3]-\beta ^1_3 \end{aligned}$$

(3)

Similarly, using inequality (2)

$$\begin{aligned}{} & {} \left. \begin{array}{l} \beta _3=g(\alpha _3,\dfrac{1}{2}[\beta _1+\beta _2])> \\ \beta ^1_3=g(\alpha _3,\beta ^1_2) \end{array} \right\} \Longrightarrow \nonumber \\{} & {} \quad \beta _3-\beta ^1_3<\dfrac{1}{2}[\beta _1+\beta _2]-\beta ^1_2 \end{aligned}$$

(4)

Combining inequalities (3) and (4) together and recalling that $\beta _1<\beta _2$, we get

$$\begin{aligned}{} & {} 2\beta _3-2\beta ^1_3<\beta _1+\beta _2-2\beta ^1_2<2\beta _2-2\beta ^1_2<\beta _1+\beta _3-2\beta ^1_3 \Longrightarrow \\{} & {} \beta _3<\beta _1 \end{aligned}$$

A contradiction, hence $\beta ^1_2>\beta _2$. And since $\beta _1<\beta _2$, it follows that $\beta ^1_2>\frac{1}{2}[\beta _1+\beta _2]$, hence $\beta ^1_3>\beta _3$. It thus follows that both unanimity rule (determined by person 3) and majority (determined by person 2) rule accept less projects than the case in which all members participate in the deliberation.

Suppose now that person 3 does not participate. Then by Claim 8 in FS, $\beta ^3_3=\alpha _3>\beta _3$ and the unanimity rule will accept less projects. Since $\beta ^3_2>\beta ^3_1$ (Claim 7 in FS), in order to show that the majority rule will accept more project it is enough to show that $\beta _2>\beta ^3_2$. Since by the aforementioned claim, $\alpha _2>\beta ^3_2$, this is clearly the case when $\beta _2\geqslant \alpha _2$. We therefore prove the impossibility of $\alpha _2>\beta ^3_2>\beta _2$. Otherwise,

$$\begin{aligned} \beta ^3_2=g(\alpha _2,\beta ^3_1)\geqslant \beta _2=g(\alpha _2,\dfrac{1}{2}[\beta _1+\beta _3])\Longrightarrow \beta ^3_1>\beta _1 \end{aligned}$$

Since $g_2<1$, we get

$$\begin{aligned}{} & {} \left. \begin{array}{l} \beta ^3_2-\beta _2<\beta ^3_1-\dfrac{1}{2}[\beta _1+\beta _3] \\ \beta ^3_1-\beta _1<\beta ^3_2-\dfrac{1}{2}[\beta _2+\beta _3] \end{array} \right\} \Longrightarrow \\{} & {} 2\beta _3<\beta _1+\beta _2 \end{aligned}$$

A contradiction to the fact that $\beta _3>\beta _2>\beta _1$. $\square$

Table 1 The effect of the order of deliberations

Proof of claim 8:

We use the following table

Person B is selected by a unanimity rule if and only if $M:=\min \{\beta _1,\beta _2,\beta _3\}\geqslant \gamma$.

(i):

1-2-3: For $i=1,2,3$, $\beta ^{(v)}_i\geqslant \beta ^{(i)}_1$, hence $M^{(v)}\geqslant M^{(i)}$.

(ii):

1-3-2: For $i=1,2,3$, $\beta ^{(v)}_i\geqslant \beta ^{(ii)}_1$, hence $M^{(v)}\geqslant M^{(ii)}$.

(iii):

2-1-3: For $i=1,2,3$, $\beta ^{(iv)}_i\geqslant \beta ^{(iii)}_1$, hence $M^{(iv)}\geqslant M^{(iii)}$.

(iv):

2-3-1: For $i=1,3$, $\beta ^{(v)}_i>\beta ^{(iv)}_i$. Consider two cases—

1.:

$g(\alpha _1,\alpha _3)<\alpha _2$. Then $\beta ^{(v)}_1=g(\alpha _1,\alpha _3)=g(g(\alpha _1,\alpha _3),g(\alpha _1,\alpha _3))<g(\alpha _2,g(\alpha _1,\alpha _3))\leqslant g(\alpha _2,\theta \alpha _3+(1-\theta )g(\alpha _1,\alpha _3))=\beta ^{(v)}_2<\beta ^{(v)}_3$, hence $M^{(v)}=\beta ^{(v)}_1>\beta ^{(iv)}_1\geqslant M^{(iv)}$.

2.:

$g(\alpha _1,\alpha _3)\geqslant \alpha _2$. Then $\beta ^{(v)}_2\geqslant \beta ^{(iv)}_2$ and since for $i=1,2,3$, $\beta ^{(v)}_i\geqslant \beta ^{(iv)}_i$, it follows that $M^{(v)}\geqslant M^{(iv)}$.

(vi):

3-2-1: $\beta ^{(vi)}_3>\beta ^{(vi)}_2>\beta ^{(vi)}_1$, hence $M^{(vi)}=\beta ^{(vi)}_1$. Obviously $M^{(vi)}\leqslant \beta ^{(v)}_1<\beta ^{(v)}_3$ and by definition, $M^{(vi)}\leqslant \beta ^{(vi)}_1$. We show next that for all $\alpha _2\in [\alpha _1,\alpha _3]$, $\beta ^{(vi)}_1\leqslant \beta ^{(v)}_2$. For $\alpha _2=\alpha _1$ we get $\beta ^{(vi)}_1=\beta ^{(v)}_2$. Differentiate both with respect to $\alpha _2$:

$$\begin{aligned} \frac{\partial \beta ^{(vi)}_1}{\partial \alpha _2}= & {} g_2(\alpha _1,\theta \alpha _3+(1-\theta )g(\alpha _2,\alpha _3))\times (1-\theta )g_1(\alpha _2,\alpha _3)\\ \frac{\partial \beta ^{(v)}_2}{\partial \alpha _2}= & {} g_1(\alpha _2,\theta \alpha _3+(1-\theta )g(\alpha _1,\alpha _3)) \end{aligned}$$

We assumed that $g_{12}<0$ (see end of Sect. 2.2), hence $g_1(\alpha _2,\alpha _3)\leqslant g_1(\alpha _2,\theta \alpha _3+(1-\theta )g(\alpha _1,\alpha _3))$ and since $g_2(\cdot ,\cdot )\leqslant 1$, $\frac{\partial \beta ^{(vi)}_1}{\partial \alpha _2}\leqslant \frac{\partial \beta ^{(v)}_2}{\partial \alpha _2}$, implying $\beta ^{(vi)}_1\leqslant \beta ^{(v)}_2$ for all $\alpha _2\in [\alpha _1,\alpha _3]$. As $M^{(vi)}\leqslant \beta ^{(v)}_i$ for $i=1,2,3$, it follows that $M^{(vi)}\leqslant M^{(v)}$.

Person B is selected by a majority rule if and only if L, the mid-value of $\beta _1,\beta _2,\beta _3$ satisfies $L\geqslant \gamma$. Using the above table, we get

(i):

1-2-3: For $i=1,2,3$, $\beta ^{(vi)}_i>\beta ^{(i)}_i$, hence $L^{(vi)}>L^{(i)}$.

(ii):

1-3-2: For $i=1,2,3$, $\beta ^{(vi)}_i>\beta ^{(ii)}_i$, hence $L^{(vi)}>L^{(ii)}$.

(iii):

2-1-3: $L^{(iii)}=\min \{\beta ^{(iii)}_2,\beta ^{(iii)}_3\}$. As $\beta ^{(vi)}_2>\beta ^{(iii)}_2$ and $\beta ^{(vi)}_3>\beta ^{(iii)}_3$, it follows that $L^{(vi)}>L^{(iii)}$.

(iv):

2-3-1: $L^{(vi)}=\beta ^{(vi)}_2>\max \{\beta ^{(iv)}_1,\beta ^{(iv)}_2\}\geqslant L^{(iv)}$.

(v):

3-1-2: $L^{(vi)}=\beta ^{(vi)}_2>\max \{\beta ^{(v)}_1,\beta ^{(v)}_2\}\geqslant L^{(v)}$.

$\square$