Debreu’s choice model

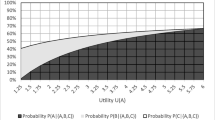
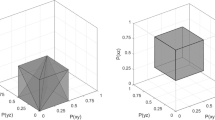
Abstract

Debreu (American Economic Review 50:186–188, 1960) famously criticized Luce (Individual choice behavior, Wiley, New York, 1959) choice model with what became known as the red-bus blue-bus example: if a choice set contains two distinct alternatives C (car) and B (blue bus) then adding a third alternative A (red bus) that is essentially identical to B does not affect the choice probability of C but reduces the choice probability of B by half. Debreu’s critique highlights the existence of substitution effects violating the principle of independence from irrelevant alternatives—the cornerstone of Luce (Individual choice behavior, Wiley, New York, 1959) choice model. This paper weakens this principle to construct a model of probabilistic choice satisfying Debreu’s critique.

Appendix

1.1 Proof of proposition 1

Multiplying conditions (5), (6), and (7) yields us Eq. (18) which is known as the product rule (e.g., Estes, 1960, p. 272; Luce & Suppes, 1965, definition 25, p. 341).

$$P\left(a,b\right)P\left(b,c\right)P\left(c,a\right)=P\left(a,c\right)P\left(c,b\right)P\left(b,a\right)$$

(18)

According to Theorem 48 in Luce and Suppes (1965, p. 350), binary choice probabilities satisfy the product rule (18) if and only if there exist a positive real-valued utility function $u$, unique up to multiplication by a positive constant, such that for any two choice alternatives a, b binary choice probability is given by (8).

Solving the system of Eqs. (1), (5), (6), and (7) yields us ternary choice probabilities (9)-(11), which are different from Luce (1959) choice model.

Q.E.D.

1.2 Proof of proposition 2

Proof by mathematical induction.

• Step 1. For n = 3 conditions (13)–(15) become (5)–(7) correspondingly and proposition 1 implies that there exist a real-valued utility function $u$, unique up to multiplication by a positive constant, such that binary choice probabilities take form (8) of binary Luce (1959) choice model. Ternary choice probabilities are then given by (9)–(11) and Proposition 2 is satisfied.

• Step 2. We assume that Proposition 2 holds for any n ≤ m-1.

• Step 3. We shall prove that Proposition 2 also holds for n = m.

If binary choice probabilities take form (8) of binary Luce (1959) choice model and probabilities $P\left({a}_{i}|S\backslash \left\{{a}_{i+1}\right\}\right)$ and $P\left({a}_{i+2}|S\backslash \left\{{a}_{i+1}\right\}\right)$ are given by (16) by step 2 then condition (13) can be rewritten as (19) for i ∊ {1, …, m-2}.

$$\frac{P\left({a}_{i}|S\right)}{P\left({a}_{i+2}|S\right)}=\frac{u\left({a}_{i+1}\right)u\left({a}_{i+2}\right)-{u\left({a}_{i}\right)}^{2}}{{u\left({a}_{i+2}\right)}^{2}-u\left({a}_{i}\right)u\left({a}_{i+1}\right)}\left[\frac{u\left({a}_{i+1}\right)+u\left({a}_{i+2}\right)}{u\left({a}_{i}\right)+u\left({a}_{i-1}\right)}\right]\frac{u\left({a}_{i+2}\right)+u\left({a}_{i+3}\right)}{u\left({a}_{i}\right)+u\left({a}_{i+1}\right)}\times \frac{{u\left({a}_{i}\right)}^{2}}{{u\left({a}_{i+2}\right)}^{2}}\left[\frac{u\left({a}_{i+2}\right)u\left({a}_{i+3}\right)-{u\left({a}_{i}\right)}^{2}}{{u\left({a}_{i+2}\right)}^{2}-u\left({a}_{i}\right)u\left({a}_{i-1}\right)}\right]\frac{{u\left({a}_{i+2}\right)}^{2}-{u\left({a}_{i-1}\right)}^{2}}{{u\left({a}_{i+3}\right)}^{2}-{u\left({a}_{i}\right)}^{2}}$$

(19)

Analogously, condition (14) becomes (18) and (15)–(19).

$$\frac{P\left({a}_{m}|S\right)}{P\left({a}_{2}|S\right)}=\frac{{u\left({a}_{m}\right)}^{2}-u\left({a}_{1}\right)u\left({a}_{2}\right)}{{u\left({a}_{m}\right)}^{2}-{u\left({a}_{1}\right)}^{2}}\left[\frac{u\left({a}_{1}\right)+u\left({a}_{2}\right)}{u\left({a}_{2}\right)}\right]\frac{u\left({a}_{2}\right)+u\left({a}_{3}\right)}{u\left({a}_{2}\right)}\left[\frac{u\left({a}_{m}\right)}{u\left({a}_{m}\right)+u\left({a}_{m-1}\right)}\right]\times \frac{\prod_{k=2}^{m-2}\frac{{u\left({a}_{m}\right)}^{2}-u\left({a}_{k}\right)u\left({a}_{k+1}\right)}{{u\left({a}_{m}\right)}^{2}-{u\left({a}_{k}\right)}^{2}}}{\prod_{j=3}^{m}\frac{u\left({a}_{j}\right)u\left({a}_{j-1}\right)-{u\left({a}_{2}\right)}^{2}}{{u\left({a}_{j}\right)}^{2}-{u\left({a}_{2}\right)}^{2}}}$$

(20)

$$\frac{P\left({a}_{m-1}|S\right)}{P\left({a}_{1}|S\right)}=\frac{{u\left({a}_{m}\right)}^{2}-{u\left({a}_{1}\right)}^{2}}{u\left({a}_{m}\right)u\left({a}_{m-1}\right)-{u\left({a}_{1}\right)}^{2}}\left[\frac{u\left({a}_{1}\right)+u\left({a}_{2}\right)}{u\left({a}_{1}\right)}\right]\frac{u\left({a}_{m-1}\right)}{u\left({a}_{m-1}\right)+u\left({a}_{m-2}\right)}\left[\frac{u\left({a}_{m-1}\right)}{u\left({a}_{m-1}\right)+u\left({a}_{m}\right)}\right]\times \frac{\prod_{k=1}^{m-2}\frac{{u\left({a}_{m-1}\right)}^{2}-u\left({a}_{k}\right)u\left({a}_{k+1}\right)}{{u\left({a}_{m-1}\right)}^{2}-{u\left({a}_{k}\right)}^{2}}}{\prod_{j=3}^{m-1}\frac{u\left({a}_{j}\right)u\left({a}_{j-1}\right)-{u\left({a}_{1}\right)}^{2}}{{u\left({a}_{j}\right)}^{2}-{u\left({a}_{1}\right)}^{2}}}$$

(21)

Solving the system of Eqs. (17)–(19) then yields

$$P\left({a}_{1}|S\right)=\frac{u\left({a}_{1}\right)}{u\left({a}_{1}\right)+u\left({a}_{2}\right)}\prod_{k=3}^{m}\frac{u\left({a}_{k-1}\right)u\left({a}_{k}\right)-{u\left({a}_{i}\right)}^{2}}{{u\left({a}_{k}\right)}^{2}-{u\left({a}_{i}\right)}^{2}}$$

$$P\left({a}_{m}|S\right)=\frac{u\left({a}_{m}\right)}{u\left({a}_{m}\right)+u\left({a}_{m-1}\right)}\prod_{j=1}^{m-2}\frac{{u\left({a}_{i}\right)}^{2}-u\left({a}_{j}\right)u\left({a}_{j+1}\right)}{{u\left({a}_{i}\right)}^{2}-{u\left({a}_{j}\right)}^{2}}$$

and

$$P\left({a}_{i}|S\right)=\frac{u\left({a}_{i}\right)}{u\left({a}_{i}\right)+u\left({a}_{i-1}\right)}\left[\frac{u\left({a}_{i}\right)}{u\left({a}_{i}\right)+u\left({a}_{i+1}\right)}\right]\prod_{j=1}^{i-2}\frac{{u\left({a}_{i}\right)}^{2}-u\left({a}_{j}\right)u\left({a}_{j+1}\right)}{{u\left({a}_{i}\right)}^{2}-{u\left({a}_{j}\right)}^{2}}\prod_{k=i+2}^{m}\frac{u\left({a}_{k-1}\right)u\left({a}_{k}\right)-{u\left({a}_{i}\right)}^{2}}{{u\left({a}_{k}\right)}^{2}-{u\left({a}_{i}\right)}^{2}}$$

for i  $\in$ {2, …, m-2}.

By mathematical induction Proposition 2 then holds for any finite n.

Q.E.D.