Feedback-based active reset of a spin qubit in silicon

Abstract

Feedback control of qubits is a highly demanded technique for advanced quantum information protocols such as fault-tolerant quantum error correction. Here we demonstrate active reset of a silicon spin qubit using feedback control. The active reset is based on quantum non-demolition (QND) readout of the qubit and feedback according to the readout results, which is enabled by hardware data processing and sequencing. We incorporate a cumulative readout technique to the active reset protocol, enhancing initialization fidelity above a limitation imposed by the single-shot QND readout fidelity. An analysis of the reset protocol implies a pathway to achieve the initialization fidelity sufficient for fault-tolerant quantum computation. These results provide a practical approach to high-fidelity qubit operations in realistic devices.

Introduction

Spin qubits based on silicon quantum dots are regarded as a powerful candidate for the building blocks of scalable quantum information processors owing to the high quantum-gate fidelities^{1,2,3,4,5,6,7,8,9}, high-temperature compatibility^10,11, and well-developed fabrication technologies^12,13,14. Fundamental technologies for a small number of qubits have matured as represented by the demonstration of a quantum error correction⁸, and technologies for scaling up toward quantum information processors have been attracting a lot of attention lately⁹. Feedback control where qubits are controlled conditionally on the results of quantum non-demolition (QND) measurements is one of the key technologies for scaling up, employed in a proposal of the surface code¹⁵. Active reset of a qubit is a basic feedback control and has been demonstrated in various qubit platforms^16,17,18. Very recently, active reset is also implemented in a silicon quantum-dot qubit system using single-shot QND measurements⁹. The fidelity of such a reset protocol can, however, be restricted by the fidelity of single-shot QND readout, which has shown limited values in past experiments in quantum-dot spin qubits except for recent reports oriented to reduction of readout errors in silicon^19,20 and in GaAs²¹. Improvement of the reset protocol to evade limitation imposed by the QND readout infidelity will facilitate achieving the initialization fidelity over the target value > 99.5% for a fault-tolerant quantum computer²².

In this work, we report feedback-based active reset of an electron spin qubit in a natural silicon quantum dot. The spin-qubit state is read out by QND measurements^8,9,23,24,25, whose outcome is used to generate a feedback pulse to reset the qubit. A combination of a digital signal processing (DSP) hardware²⁶ and a hardware sequencer (Keysight M3300A module with the option for hardware virtual instrument programming) enables us to reset the qubit much faster than spin relaxation. First, we have tested a simple reset protocol based on a single-shot QND measurement. Next, we have developed an active reset protocol based on a cumulative readout technique^23,24,25. The initialization fidelity of 98.3% has been obtained, much higher than the readout fidelity of the individual QND measurement (91.7%) which imposes a limitation for the simple reset protocol. We have also analyzed the reset protocol and propose a pathway to achieve an initialization fidelity of >99.5%. Feedback protocols based on cumulative readout are applicable even if a high-fidelity single-shot readout is not available owing to physical and hardware constraints, providing a practical approach to qubit operations in realistic devices.

Results

Active reset protocol

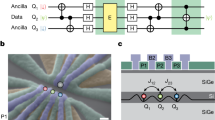
Figure 1a outlines an active reset protocol to initialize a qubit to the ground (spin-down) state. The protocol requires an auxiliary qubit (ancilla qubit) in addition to the qubit to be initialized (data qubit). We consider the initial two-qubit state represented as $\left|{0}_{{\rm{A}}}\right\rangle \left|{\psi }_{{\rm{D}}}\right\rangle$ where $\left|{s}_{X}\right\rangle$ denotes the spin-down (s_X = 0_X) and -up (s_X = 1_X) states of the ancilla (X = A) and data (X = D) qubits and $\left|{\psi }_{{\rm{D}}}\right\rangle$ represents an arbitrary superposition state $\alpha \left|{0}_{{\rm{D}}}\right\rangle +\beta \left|{1}_{{\rm{D}}}\right\rangle$ with |α|² + | β | ² = 1. We first apply a QND measurement (blue area) consisting of a controlled rotation (CROT) gate using the data qubit as the control bit and a subsequent destructive readout of the ancilla qubit. The two-qubit state is first entangled to $\alpha \left|{1}_{{\rm{A}}}\right\rangle \left|{0}_{{\rm{D}}}\right\rangle +{{\rm{e}}}^{{\rm{i}}\phi }\beta \left|{0}_{{\rm{A}}}\right\rangle \left|{1}_{{\rm{D}}}\right\rangle$ by the CROT gate (ϕ is the relative phase). The subsequent destructive measurement projects the entangled state to $\left|{0}_{{\rm{A}}}\right\rangle \left|{1}_{{\rm{D}}}\right\rangle$ or $\left|{1}_{{\rm{A}}}\right\rangle \left|{0}_{{\rm{D}}}\right\rangle$ with probabilities ${\left|\alpha \right|}^{2}$ and ${\left|\beta \right|}^{2}$, and yields an ancilla measurement outcome μ = 0 _A or 1 _A with minimal disturbance to the data-qubit state. While this outcome just reveals the ancilla-qubit state, the two-qubit entanglement induced by the CROT gate enables us to estimate the data-qubit state at the $\left|{0}_{{\rm{D}}}\right\rangle$ ($\left|{1}_{{\rm{D}}}\right\rangle$) state when μ = 1 _A (0 _A) is obtained. Thus the ancilla outcome μ = 0 _A (1 _A) is interpreted as a QND estimator m = 1_D (0_D) of the data-qubit state. We note that this interpretation is not unique; if the CROT gate is defined so as to entangle the qubits to $\alpha \left|{0}_{{\rm{A}}}\right\rangle \left|{0}_{{\rm{D}}}\right\rangle +{{\rm{e}}}^{{\rm{i}}\phi }\beta \left|{1}_{{\rm{A}}}\right\rangle \left|{1}_{{\rm{D}}}\right\rangle$, μ = 0 _A (1 _A) is interpreted as m = 0_D (1_D). When m = 1_D is obtained, a conditional π-rotation pulse is applied to the data qubit (yellow area). The data qubit is thus reset to the $\left|{0}_{{\rm{D}}}\right\rangle$ state deterministically, which can be used as an input for subsequent quantum circuit.

Fig. 1: Implementation of the feedback-based active reset of a spin qubit in silicon.

a Quantum circuit showing the basic reset protocol. The QND measurement of the data qubit is implemented by the CROT gate and a destructive measurement of the ancilla qubit (blue area). The destructive measurement yields an outcome μ ($\in \{{0}_{{\rm{A}}},{1}_{{\rm{A}}}\}$) revealing the ancilla-qubit state, and the data-qubit state is estimated at the QND estimator m ($\in \{{0}_{{\rm{D}}},{1}_{{\rm{D}}}\}$) according to μ (see bottom diagram). A π-rotation gate (yellow area) is applied to the data qubit when and only when the estimator m = 1_D. b Quantum circuit for cumulative readout. QND measurements are repeated N times, resulting in a set of outcomes {μ}_N = {μ₁, μ₂,…, μ_N}. A cumulative estimator M_N ($\in \{{0}_{{\rm{D}}},{1}_{{\rm{D}}}\}$) for the data qubit is obtained from {μ}_N (see bottom diagram). c Schematic diagram of the experiment setup. A scanning electron micrograph image of the two-qubit device is shown in the green dashed box. d, e Time-domain charge sensor signals of the destructive readout (d), and switch control signals output after the corresponding charge sensor signals in d (e). For clarity, curves are offset from one another by 0.05 for d and 0.1 for e. Black horizontal arrows indicate dips in the charge sensor signals due to reloading of the ancilla electron from the electron reservoir. As this electron reloading event is a sign of the $\left|{1}_{{\rm{A}}}\right\rangle$ state, we regard the presence (absence) of a dip as an ancilla measurement outcome μ = 1 _A (0 _A) as denoted in d. The obtained outcome μ is interpreted as a data-qubit estimator m. If the CROT gate entangles the ancilla and data qubit states to a form $\alpha \left|{1}_{{\rm{A}}}\right\rangle \left|{0}_{{\rm{D}}}\right\rangle +{{\rm{e}}}^{{\rm{i}}\phi }\beta \left|{0}_{{\rm{A}}}\right\rangle \left|{1}_{{\rm{D}}}\right\rangle$, μ = 1 _A (0 _A) is always interpreted as m = 0_D (1_D) as denoted in e. Switch control signal is raised to the high level from 210 μs to 220 μs (yellow area) when and only when m = 1_D is obtained. A π pulse applied in this time window as depicted in the top works as the conditional π pulse.

This reset protocol relies on the QND readout and the conditioned π rotation. The initialization fidelity relates to other fidelities as F_I = 1/2 + (2F_R − 1)F_G(2F_QND − 1)/2 (See Methods). Here, F_I is the initialization fidelity, F_R is the fidelity of the QND readout of the data qubit, F_QND is the state-preservation fidelity for the data qubit during the reset protocol (QND fidelity)²⁷, and F_G is the π-rotation fidelity. F_I, F_R, and F_QND are averaged over the input data-qubit states. F_R is degraded not only by errors in the destructive measurement and the preparation of the ancilla qubit but also by CROT-gate errors to map the data-qubit state on the ancilla-qubit state. In silicon spin qubits, F_R is typically much lower than F_G and F_QND; in the present experiments, F_R ≤ 92% and F_QND ≥ 99% for the reset protocol based on a single-shot QND measurement as shown later. In this regime, the relation between F_I and other fidelities is approximated by F_I ≈ F_R and thus F_I is expected to increase with F_R in the active reset protocol.

QND readout does not perturb the measured quantity, which is its important feature allowing us to improve F_R using cumulative readout techniques^23,24,25,28. To incorporate the cumulative readout to the active reset protocol, we design a quantum circuit (Fig. 1b) to replace the single-shot QND measurement in Fig. 1a. A repetition of the measurement provides a set of ancilla measurement outcomes {μ}_N (N is the number of repetition). A cumulative estimator M_N of the data-qubit state is obtained from the outcome set and used to condition the subsequent π-rotation gate. We note that the cumulative estimator M_N must be calculated in real time.

Qubit system and feedback control

The ancilla and data qubits are hosted by the left and right quantum dots in a double quantum dot device^2,24 (Fig. 1c, dashed box) with an adjacent charge sensor to detect charge occupations of the quantum dots (See Methods). An external magnetic field splits qubit levels by Zeeman energy of roughly 16 GHz (Figs. 2 and 4) or 19 GHz (Fig. 3). A micromagnet on top of the device induces a slanting magnetic field to couple the spin qubits to the microwave (MW) voltage applied to a gate (barrier gate), which drives the ancilla and data qubits at Rabi frequencies of 2-4 MHz. The micromagnet also induces a difference in the Zeeman splittings of the ancilla and data qubits of around 600 MHz large enough to address them individually. The exchange interaction between the qubits is turned on and off by a barrier-gate pulse (see Supplementary Note 1 for details of the experimental time sequence). As the exchange coupling in the on state (6-9 MHz) is much smaller than the Zeeman splitting difference, it is effectively an Ising-type interaction²⁴ which splits the $\left|{0}_{{\rm{A}}}\right\rangle \left|{0}_{{\rm{D}}}\right\rangle \leftrightarrow \left|{1}_{{\rm{A}}}\right\rangle \left|{0}_{{\rm{D}}}\right\rangle$ and $\left|{0}_{{\rm{A}}}\right\rangle \left|{1}_{{\rm{D}}}\right\rangle \leftrightarrow \left|{1}_{{\rm{A}}}\right\rangle \left|{1}_{{\rm{D}}}\right\rangle$ transition energies. A π rotation using a MW pulse resonant to one of these transitions works as a CROT gate. The $\left|{0}_{{\rm{A}}}\right\rangle \left|{0}_{{\rm{D}}}\right\rangle \leftrightarrow \left|{1}_{{\rm{A}}}\right\rangle \left|{0}_{{\rm{D}}}\right\rangle$ ($\left|{0}_{{\rm{A}}}\right\rangle \left|{1}_{{\rm{D}}}\right\rangle \leftrightarrow \left|{1}_{{\rm{A}}}\right\rangle \left|{1}_{{\rm{D}}}\right\rangle$) transition is used for the experiments in Figs. 1, 2, 4 (Fig. 3), and thus μ = 0 _A (1 _A) is interpreted as m = 1_D there. Here, the choice of the data-qubit projection axis in the QND measurement allows us to ignore conditional phase factors accumulated by pulsing exchange interaction. T₁ of the data qubit is >6 ms in this work. The sample is cooled down in a dilution refrigerator with a base temperature of 26 mK. The electron temperature is 36 mK measured by quantum-dot charge transition line width.

Fig. 2: Test of the active reset.

a Quantum circuit to test the reset protocol. The data and ancilla qubits are initialized at the beginning by reloading electrons from reservoirs. The data qubit is also subjected to a π/2 rotation before the active reset protocol. After the active reset, a θ rotation by a resonant MW burst for τ_b is applied to the data qubit. Finally, the data-qubit state is read out by a QND measurement (red area) and a subsequent destructive measurement to the data qubit (green square). The data-qubit state is estimated at an estimator m = 0_D (1_D) when the ancilla outcome μ = 1 _A (0 _A) is obtained by the ancilla destructive measurement. Separately, the data qubit is directly read out by the final destructive measurement, whose outcome is denoted m_d. b Rabi oscillations measured with and without the feedback as a function of τ_b. The red circles show the QND estimator <m> (<…> denotes ensemble averaging). The green and open circles show <m_d>. The solid and dashed curves are the fit curves for the data measured with and without the feedback, respectively.

Fig. 3: Active reset without electron reload to the data qubit and improvement of the readout fidelities by the repetitive QND measurements.

a Quantum circuit to test the reset protocol without access of the data-qubit to the electron reservoirs. The circuit repeats a cycle consisting of a QND measurement, a conditional π pulse, and a θ rotation pulse to the data qubit. The ancilla qubit is initialized after each destructive measurement using access to the reservoir. b Rabi oscillations measured with and without the feedback (solid and open circles, respectively). c Quantum circuit with a cumulative readout sequence (red area) to measure the final data-qubit state. In addition to the circuit in a, a 20-fold repetition of QND measurement is inserted before the single QND measurement to generate feedback. d QND fidelities after the nth QND measurement for the $\left|{0}_{{\rm{D}}}\right\rangle$ and $\left|{1}_{{\rm{D}}}\right\rangle$ states, F_QND,0 and F_QND,1, and their average F_QND, estimated by analyzing the joint probability. The solid lines are eye guides. The error bars represent 1σ confidence intervals obtained from fitting. e Rabi oscillations measured by the cumulative readout. Each plot is obtained by the Bayesian estimation using subsets {μ}_n (n = 1 and 20) of the set of repetitive measurement outcomes {μ}₂₀ (blue and orange, respectively). The solid curves are sinusoidal fit results. f Cumulative readout fidelities for the $\left|{0}_{{\rm{D}}}\right\rangle$ and $\left|{1}_{{\rm{D}}}\right\rangle$ states, F_R,0 and F_R,1, and their average F_R as a function of the subset size n. The solid lines are eye guides.

We test conditioning of the π-rotation gate to flip back the data-qubit state to $\left|{0}_{{\rm{D}}}\right\rangle$ using a feedback scheme based on the single-shot QND measurement in the actual experimental setup (Fig. 1c). The ancilla destructive readout is performed by a combination of spin-selective tunneling²⁹ and reflectometry charge sensing. Figure 1d shows typical time-domain signals in the measurement span between 30 and 130 μs after the CROT gate. Presence of a dip (arrows) in this time span is an indication of the $\left|{1}_{{\rm{A}}}\right\rangle$ state. The DSP hardware assigns each time trace to the ancilla measurement outcome of either μ = 1 _A or 0 _A using a single threshold value (see Fig. 1d), and then to a data-qubit estimator m of 1_D for μ = 0 _A and 0_D for μ = 1 _A, respectively (Fig. 1e). The state of a MW switch placed on the output port of a MW generator is decided by the value of m, enabling the conditional π-rotation gate on the data qubit in 210 μs. The time delay includes readout time (100 μs), sequencing time (80 μs), wait time to stabilize the charge sensor signal (20 μs), and wait times (10 μs in total). We note that these times are shortened in the following experiments (see Supplementary Note 1 for details of the experimental time sequence). Figure 1e shows the switch control signal following each of the readout signals shown in the same color as in Fig. 1d.

Implementation of the active reset using single-shot QND readout

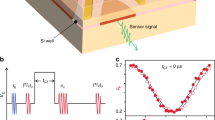
We now demonstrate the qubit reset protocol using the QND measurement and the feedback scheme. Figure 2a shows the quantum circuit used. Before the reset protocol, the ancilla and data qubits are prepared in the $\left|{0}_{{\rm{D}}}\right\rangle$ and $\left|{0}_{{\rm{A}}}\right\rangle$ states by reloading an electron with down spin to each quantum dot. The data qubit is subsequently subjected to a π/2 pulse, which makes a superposition state of the $\left|{0}_{{\rm{D}}}\right\rangle$ and $\left|{1}_{{\rm{D}}}\right\rangle$ states. The following QND measurement at the beginning of the reset protocol randomly projects the data-qubit state to $\left|{0}_{{\rm{D}}}\right\rangle$ or $\left|{1}_{{\rm{D}}}\right\rangle$, which works as an unbiased input state. The data qubit is then reset to the $\left|{0}_{{\rm{D}}}\right\rangle$ state using the active reset protocol described in the last section. To analyze the fidelity of the reset protocol, we apply a Rabi rotation with an angle θ to the data qubit by a resonant MW burst for duration τ_b. After the Rabi rotation, the data qubit is read out by two independent measurements, a QND measurement followed by a destructive one (see Fig. 2a). The QND measurement, which is performed in the same manner as that used to generate feedback, yields a QND estimator m of the data qubit. The destructive measurement of the data qubit, on the other hand, yields an outcome m_d directly revealing the data-qubit state. Analyzing the joint probabilities of m and m_d allows one to obtain the initialization and readout fidelities^23,24. Here time taken by the reset protocol τ_reset is 93.5 μs measured from the CROT gate to the conditional π rotation.

Figure 2b shows Rabi oscillations of the data qubit exhibited by the data-qubit destructive-measurement outcome <m_d> (green) and the QND estimator <m> (red). Here, <…> denotes ensemble averaging. For comparison, we also perform measurements without the conditional π-rotation pulse for the active reset (open circles). The data set with feedback shows clear Rabi oscillations with visibility of 44 ± 3% and 41 ± 2% for m_d and m, respectively (from fitting, solid curves). The oscillation offsets of <m_d> and <m> reflect the destructive measurement error rates of the ancilla and data qubits, respectively, and are thus slightly different. We note that the Rabi oscillation with a low visibility (3 ± 2%, dashed curve) is observed in m_d without the feedback because of a small remnant of bias in the initial data-qubit state. This result indicates successful initialization of the data qubit by the reset protocol.

The Rabi-oscillation visibility in <m> (<m_d>) depends not only on the initialization fidelity F_I but also on the QND (destructive) readout fidelities f_R,s (f_d,R,s), where the subscript s denotes the prepared data-qubit state ($\left|{0}_{{\rm{D}}}\right\rangle$ for s = 0 and $\left|{1}_{{\rm{D}}}\right\rangle$ for s = 1). To separately estimate these fidelities, we analyze the joint probabilities P(m,m_d) of obtaining a combination of m and m_d rather than the mean values <m_d> and <m>^23,24 (see Methods and Supplementary Note 2 for the joint probability analyses). We obtain F_I = 81.1 ± 0.6% along with the readout fidelities f_R,0 = 85.1 ± 0.9%, f_R,1 = 83 ± 1%, f_d,R,0 = 95 ± 1%, and f_d,R,1 = 70.6 ± 0.9%. The average fidelity F_R of the QND readout for feedback is (f_R,0 + f_R,1)/2 = 84 ± 1%. The F_I value close to F_R implies that F_I is limited by F_R.

The destructive measurement of the data qubit used in Fig. 2a requires an electron reservoir²⁹, which imposes geometrical constraints for scaling up. One of the benefits of the active reset protocol is that a qubit can be initialized without reloading an electron from reservoirs. To demonstrate this, we implement a quantum circuit shown in Fig. 3a without the destructive measurement of the data qubit. τ_reset is 93 μs out of 100 μs taken by each cycle. Figure 3b shows Rabi oscillations exhibited by m similarly to Fig. 2b. Clear difference between presence (blue) and absence (gray) of the reset pulse corroborates the success of the active reset protocol. The data qubit is free from electron reload throughout the experiment in contrast to Fig. 2a, while a note should be taken that the ancilla qubit still uses electron reload for a destructive measurement. The electron reload can be avoided completely by using Pauli spin blockade readout as demonstrated in ref. ⁹. although an additional ancilla spin is required for a QND measurement.

Feedback using cumulative readout

F_I obtained by the active reset protocol in Fig. 2a is limited by the low f_R value of the QND measurement. We attempt to incorporate a cumulative readout technique to improve the readout fidelity^23,24,25 in the active reset protocol. Increase of the readout fidelity by cumulative readout is tested using a quantum circuit shown in Fig. 3c. After the reset protocol and the spin rotation, the data qubit is read out 21 times (instead of once as in Fig. 3a) in a QND manner. Here we use only the last QND measurement outcome for active reset, but we use the rest of the ancilla readout outcomes, {μ}₂₀, to analyze the cumulative readout process.

A major drawback of cumulative readout is the time taken by the repetitive QND measurements, where spin relaxations can induce errors in preservation of the data-qubit state during the readout. Here we compare gains in the readout fidelity and losses of the QND fidelity in the cumulative readout process. First, fidelities of each QND measurement are extracted by analyzing joint probabilities P(m_k,m₂₀) where m_k (k = 1, 2,…, 20) is the estimator for the data-qubit state obtained from the single outcome μ_k. We obtain fidelities of the individual QND measurement for the $\left|{0}_{{\rm{D}}}\right\rangle$ and $\left|{1}_{{\rm{D}}}\right\rangle$ states, f_R,0 = 93.6 ± 0.1%, f_R,1 = 89.1 ± 0.2% (averaged over k), and their average f_R = 91.4 ± 0.1% (see Supplementary Note 2 for the joint probability analyses). From the k dependence of P(m_k,m₂₀), we can extract the initialization fidelity F_I = 87.8 ± 0.2% and the lifetimes of the $\left|{0}_{{\rm{D}}}\right\rangle$ and $\left|{1}_{{\rm{D}}}\right\rangle$ states, T_1,0 = 80 ± 20 ms and T_1,1 = 6.6 ± 0.1 ms. We can also extract the QND fidelities after n-fold repetition of the QND measurement for the $\left|{0}_{{\rm{D}}}\right\rangle$ and $\left|{1}_{{\rm{D}}}\right\rangle$ states, F_QND,0 and F_QND,1, and their average F_QND (Fig. 3d). Using a Bayesian estimation method taking these T₁ values into account, we calculate cumulative estimators M_n for the data-qubit state before the measurement from subsets {μ}_n = {μ₁, μ₂,…, μ_n} (n ≤ 20) of the {μ}₂₀ (see Supplementary Note 3 for the analyses of the repetitive measurement outcomes). Figure 3e shows the Rabi oscillations obtained from the estimators M_n for n = 1 and 20 (blue and orange). The Rabi-oscillation visibility for n = 20 is >n = 1, implying improved readout fidelities by cumulative readout. Given F_I = 87.8%, we can estimate the cumulative readout fidelities for the $\left|{0}_{{\rm{D}}}\right\rangle$ and $\left|{1}_{{\rm{D}}}\right\rangle$ states, F_R,0, and F_R,1, and their average F_R as a function of n (Fig. 3f). F_R increases with n for n < 10 and saturates to 97.1 ± 0.6% for higher n, and is indeed improved by the cumulative readout technique in comparison with single-shot QND readout. However, the F_QND values are much lower than F_R for n > 10 (F_QND = 92.6 ± 0.5% at n = 11). In this case, the fidelity of active reset may be limited by F_QND and hardly be improved by the incorporation of cumulative readout to the active reset protocol. To effectively incorporate cumulative readout to active reset, we improve F_QND by changing the experimental condition to prolong the data-qubit lifetimes.

Figure 4a shows an implementation of the active reset based on the cumulative readout. We change gate biases and find a condition with the longer spin relaxation times. The single-shot QND readout to generate feedback in Fig. 3c is replaced by an 11-fold repetition of the QND measurement. To cumulatively estimate the data-qubit state in real time on the hardware sequencer, we implement an online Bayesian-estimation block where the cumulative estimator is computed in the course of the repetitive measurement. Each ancilla outcome is used for the computation immediately after its acquisition, which reduces computational time after the measurement repetition and is also suitable for the hardware sequencer with a limited number of registers. These features are in contrast to the Bayesian estimation used in Fig. 3e, which is executed after all data have been recorded to standard computer storage. After the 11th QND measurement, the cumulative estimator M₁₁ is provided by the Bayesian-estimation block and used to generate feedback to condition the π rotation for active reset. The Bayesian-estimation block takes likelihood parameters into account but not T₁ values for the sake of simplicity. While the individual cycle of the repetition is reduced to 65 μs from 100 μs in Fig. 3c, τ_reset is increased to 708 μs due to the repetitive measurements. We also perform another 20-fold repetition of the QND measurements and acquire {μ}₂₀ for analysis.

Fig. 4: Feedback using a Bayesian-estimation logic.

a Quantum circuit to test the reset protocol using a cumulative QND readout. The difference from the circuit shown in Fig. 3c is that the single QND measurement to generate feedback is replaced by a 11-fold repetition of QND measurement (blue area). Outcomes {μ}₁₁ of the repetitive measurements are fed to the online Bayesian-estimation block (Box denoted B) and feedback is generated according to the resulting cumulative estimator M₁₁. After the data qubit is reset and rotated resonantly, another cumulative readout sequence with 20 QND measurements (red area) is carried out to measure the data-qubit state. b Rabi oscillations estimated by the Bayesian method using the set of ancilla measurement outcomes {μ}₂₀. The Bayesian estimation takes (T_1,0, T_1,1) = (130 ms, 19.8 ms) into account. c QND fidelities after the nth QND measurement for the $\left|{0}_{{\rm{D}}}\right\rangle$ and $\left|{1}_{{\rm{D}}}\right\rangle$ states, F_QND,0 and F_QND,1, and their average F_QND, estimated by analyzing the joint probability. The solid lines are eye guides. The error bars represent 1σ confidence intervals obtained from fitting. d, e Cumulative readout fidelities for the $\left|{0}_{{\rm{D}}}\right\rangle$ and $\left|{1}_{{\rm{D}}}\right\rangle$ states, F_R,0 and F_R,1, and their average F_R estimated with using (T_1,0, T_1,1) = (130 ms, 19.8 ms) (d) and (T_1,0, T_1,1) = (∞, ∞ ) (e). f Estimation fidelities for the data-qubit state after the nth QND measurement for the $\left|{0}_{{\rm{D}}}\right\rangle$ and $\left|{1}_{{\rm{D}}}\right\rangle$ states, F_P,0 and F_P,1, and their average F_P.

Joint probability analysis of {μ}₂₀ in the same manner as Fig. 3c-f reveals improved T_1,0 = 130 ± 30 ms and T_1,1 = 19.8 ± 0.7 ms together with the single-shot QND readout fidelity f_R of 91.7 ± 0.2% (f_R,0 = 89.9 ± 0.2% and f_R,1 = 93.5 ± 0.2%) comparable with that in Fig. 3. Along with these parameters, we obtain the F_I value of 98.33 ± 0.08% much >87.8% in Fig. 3c–e. This initialization fidelity is also higher than the single-shot QND readout fidelity f_R limiting F_I in the simple reset protocol (Figs. 2a and 3a, c), indicating the superior accuracy of the active reset protocol in Fig. 4a. We also note that this F_I value is comparable to a recent report of qubit preparation using real-time monitoring of negative-result measurements in silicon (98.9 ± 0.4%)³⁰. As a result of the improved initialization fidelity, we can observe Rabi oscillations with a higher visibility in Fig. 4b than in Fig. 3e. Incorporating cumulative readout to generate feedback certainly helps to improve the fidelity of the active reset protocol.

We review the effect of spin relaxation during the repetitive measurement, which is ignored in the online Bayesian estimation. Figure 4c shows the QND fidelities F_QND,0, F_QND,1, and F_QND extracted by the joint probability analysis. The observed F_QND (98.2 ± 0.4% at n = 11) is likely to limit F_I, while higher than Fig. 3d and the previous report²⁴. We also calculate the readout fidelities F_R,0, F_R,1, and F_R from the data set {μ}₂₀. Using T_1,0 = 130 ms and T_1,1 = 19.8 ms for a Bayesian estimation, the cumulative readout for the data-qubit state just after the θ rotation yields F_R = 98.7 ± 0.5% at n = 11 (Fig. 4d), which is slightly >F_QND. Notably, the saturation of fidelities at large n is attributed to QND errors, and thus the higher QND fidelities should improve F_R. Since the Bayesian method used to generate feedback does not take the QND errors into account, we also inspect the cumulative readout fidelities estimated by a Bayesian method assuming infinitely long T₁ values (Fig. 4e). While the F_R,0 and F_R,1 values deviate from each other, this estimation method provides a close F_R value to Fig. 4d (F_R = 98.6 ± 0.8% at n = 11). Based on these considerations, the initialization fidelity is now mainly limited by the spin relaxation effect and likely to further increase with the QND fidelities.

Online Bayesian estimation taking T₁ values into account, which is not implemented in this work, enables to estimate the data-qubit state after the repetitive measurement (posterior state)²⁴. Here, estimating the posterior state using the outcome set {μ}₂₀, we assess performance of the active reset protocol based on the online posterior-state estimation. Figure 4f shows the fidelities of the posterior-state estimation for the $\left|{0}_{{\rm{D}}}\right\rangle$ and $\left|{1}_{{\rm{D}}}\right\rangle$ states and their average, F_P,0, F_P,1, and F_P from the data set {μ}₂₀ in a similar way to ref. ²⁴. The evaluated F_P value (98.9 ± 0.8% at n = 11) is, however, comparable with the observed F_I value, indicating that active reset based on the posterior-state estimation does not improve F_I. The saturation of F_P at n ≥ 7 implies that the posterior-state estimation fidelity is poisoned by the QND errors (similarly to F_R for the large n values). The high QND fidelities are an essential requirement even for active reset based on the posterior-state estimation.

Discussion

Reduction of the time consumed by the reset protocol is important since a shorter reset time enables various applications. In this work, we can decrease τ_reset for the reset protocol using the single-shot QND measurement (Fig. 3a) to ≈60 μs, which is mainly limited by the destructive readout taking 40 μs. The energy-selective readout is generally limited in terms of the readout speed as it relies on stochastic electron exchange between a quantum dot and an electron reservoir. By employing the spin readout based on Pauli spin blockade, the readout time can be decreased to 1 μs with high fidelity^19,31,32,33. The second dominant limitation is the time taken by operation of the hardware sequencer. As this takes slightly >10 μs in the present setup, we reserve 15 μs before the application of the reset pulse (see Supplementary Note 1 for details of the experimental time sequence). We suppose this latency is due to the sequencing hardware and expect that it can be reduced to <1 μs as demonstrated in ref. ⁹. These potential improvements will decrease τ_reset for feedback based on a single-shot QND measurement to 2 μs or less.

Incorporation of the cumulative readout to the feedback-based reset is a reasonable way to enhance F_I exceeding the target value of 99.5% for fault-tolerant quantum computation²² for a given single-shot QND readout fidelity. While the time-consuming repetition of the QND measurement is a drawback of this scheme, a numerical simulation predicts that three-fold repetition provides F_R > 99.9% if the readout fidelity of the individual QND measurement is 99%²³. Together with the short readout time (1 μs) and the short sequencing time (<1 μs), this enables to perform high fidelity cumulative readout with τ_reset of 6 μs. Such a short τ_reset would yield F_QND > 99.98% using the T₁ values observed in Fig. 4. The fidelity of the active reset protocol is then expected to be F_I > 99.5% for F_G > 99.2%. As the single-qubit gate fidelity of 99.5% is routinely obtained in state-of-the-art spin qubits in silicon^{1,2,3,4,5,6,7,8,9}, the fidelity of the π-rotation gate rarely prevents F_I from reaching the target value. Therefore, we anticipate that F_I >99.5% is achievable by improving each QND readout fidelity and shortening the reset protocol.

In conclusion, we have demonstrated a deterministic initialization scheme of a spin qubit based on the QND measurement. Combination of fast data processing and sequencing enables us to implement feedback according to the QND-readout estimators before the data-qubit state relaxes. This scheme works properly regardless of isolation of a qubit from the electron reservoirs. We also demonstrate that cumulative readout techniques can be incorporated to improve the initialization fidelity by the reset protocol. This scheme opens a pathway to develop silicon spin quantum information architectures suitable for scaling up demanded for quantum information processors.

Methods

Initialization fidelity of the active reset protocol

The averaged initialization fidelity F_I of the active reset protocol to the $\left|{0}_{{\rm{D}}}\right\rangle$ state is expressed as follows:

$${F}_{{\rm{I}}}=\frac{{F}_{{\rm{I}},0}+{F}_{{\rm{I}},1}}{2},$$

(1)

$$\begin{array}{l}1-{F}_{{\rm{I}},0}={F}_{{\rm{R}},0}\left(1-{F}_{{\rm{QND}},0}\right)+\left(1-{F}_{{\rm{R}},0}\right){F}_{{\rm{G}}}{F}_{{\rm{QND}},0}\\\qquad\quad\quad\,\,\,+\left(1-{F}_{{\rm{R}},0}\right)\left(1-{F}_{{\rm{G}}}\right)\left(1-{F}_{{\rm{QND}},0}\right),\end{array}$$

(2)

$$\begin{array}{l}1-{F}_{{\rm{I}},1}=\left(1-{F}_{{\rm{R}},1}\right){F}_{{\rm{QND}},1}+{F}_{{\rm{R}},1}{F}_{{\rm{G}}}\left(1-{F}_{{\rm{QND}},1}\right)\\\qquad\quad\quad\,\,\,+{F}_{{\rm{R}},1}\left(1-{F}_{{\rm{G}}}\right){F}_{{\rm{QND}},1}.\end{array}$$

(3)

Here, F_I,s, F_R,s, and F_QND,s are the initialization, readout and QND fidelities for a given data-qubit state $\left|{s}_{{\rm{D}}}\right\rangle$ (s = 0, 1), respectively, and F_G is the fidelity of the conditional π rotation applied to the data qubit. Substituting the second and third equations to the first one, we obtain

$$\begin{array}{l}{F}_{{\rm{I}}}=\frac{1+{F}_{{\rm{QND}},0}-{F}_{{\rm{QND}},1}-{F}_{{\rm{G}}}\left(2{F}_{{\rm{QND}},0}-1\right)}{2}\\\qquad\,\,+\frac{1}{2}{F}_{{\rm{R}},0}{F}_{{\rm{G}}}\left(2{F}_{{\rm{QND}},0}-1\right)+\frac{1}{2}{F}_{{\rm{R}},1}{F}_{{\rm{G}}}\left(2{F}_{{\rm{QND}},1}-1\right).\end{array}$$

(4)

Using F_R = (F_R,0 + F_R,1)/2 and F_QND = (F_QND,0 + F_QND,1)/2,

$$\begin{array}{l}{F}_{{\rm{I}}}=\frac{1}{2}+\frac{1}{2}({2F}_{{\rm{R}}}-1){F}_{{\rm{G}}}\left(2{F}_{{\rm{QND}}}-1\right)\\\qquad\,\,+\frac{1}{2}\left\{\left({F}_{{\rm{R}},0}-{F}_{{\rm{R}},1}\right){F}_{{\rm{G}}}+\left(1-{F}_{{\rm{G}}}\right)\right\}({F}_{{\rm{QND}},0}-{F}_{{\rm{QND}},1}).\end{array}$$

(5)

According to the values of F_R and F_QND presented in the main text, the second term is comparable with 1/2 for F_G ≈ 1. We also find that F_R,0 – F_R,1 < < 1 (4.5% for the single-shot QND measurement in Figs. 3 and 1% for the cumulative readout based on 11 QND measurements in Fig. 4) and F_QND,0 – F_QND,1 < < 1 (1.4% in Figs. 3 and 2.8% in Fig. 4) in our experiments. Also assuming F_G ≈ 1, the third term is <10⁻³. Thus we neglect the third term and obtain

$${F}_{{\rm{I}}}=\frac{1}{2}+\frac{1}{2}({2F}_{{\rm{R}}}-1){F}_{{\rm{G}}}\left(2{F}_{{\rm{QND}}}-1\right).$$

(6)

In the above argument, we assume that the data-qubit state at the input to the reset protocol is prepared to the $\left|{0}_{{\rm{D}}}\right\rangle$ state or the $\left|{1}_{{\rm{D}}}\right\rangle$ state randomly with equal probability. This is not the case in the experiments presented in Figs. 3 and 4, since the input data-qubit state may be strongly correlated to the final data-qubit state of the previous cycle. For the case of general input data-qubit states, the initialization fidelity is represented by using the probability of the $\left|{1}_{{\rm{D}}}\right\rangle$ state before the reset protocol (denoted by the dashed vertical lines in Figs. 3a, c and 4a), p_0,1:

$${F}_{{\rm{I}}}^{{\prime} }=\left(1-\,{p}_{0,1}\right){F}_{{\rm{I}},0}+\,{p}_{0,1}{F}_{{\rm{I}},1}={F}_{{\rm{I}},0}+\,{p}_{0,1}\delta {F}_{{\rm{I}}},$$

(7)

using δF_I = F_I,1 − F_I,0. If the initialization fidelity is state dependent (δF_I ≠ 0), the second term must be considered in estimation of F_I. However, below we argue that the state dependence is negligible (δF_I = 0) in the present experiment. Since the data qubit is not subject to spin reload between each Rabi burst and reset protocol, p_0,1 is approximated as p_0,1 ≈ F_QND,1p₁(τ_b) + (1 – F_QND,0)(1 – p₁(τ_b)). Here, F_QND,0 and F_QND,1 are the values for 20-fold repetitive measurements to account for the QND fidelities in the red area in Figs. 3c and 4a while unity for Fig. 3a. p₁(τ_b) is the asymptotic value of the probability of the $\left|{1}_{{\rm{D}}}\right\rangle$ state just after the θ rotation, satisfying

$$\begin{array}{l}{p}_{1}\left({\tau }_{{\rm{b}}}\right)={F}_{{\rm{I}}}^{{\prime} }{\gamma }_{{\rm{Rabi}}}\left({\tau }_{{\rm{b}}}\right)+\left(1-{F}_{{\rm{I}}}^{{\prime} }\right)\left(1-{\gamma }_{{\rm{Rabi}}}\left({\tau }_{{\rm{b}}}\right)\right)\\\qquad\quad\,=\frac{1}{2}+\frac{1}{2}\left(2{F}_{{\rm{I}},0}+\,2{p}_{0,1}\delta {F}_{{\rm{I}}}-1\right)\left(2{\gamma }_{{\rm{Rabi}}}\left({\tau }_{{\rm{b}}}\right)-1\right),\end{array}$$

(8)

where γ_Rabi(τ_b) = 1/2 – cos(2πf_Rabiτ_b)exp(–τ_b/T_2,Rabi)/2 is the transition probability from the $\left|{0}_{{\rm{D}}}\right\rangle$ state to the $\left|{1}_{{\rm{D}}}\right\rangle$ state for the θ rotation. Solving this equation for p₁(τ_b), we obtain

$${p}_{1}\left({\tau }_{{\rm{b}}}\right)=\frac{1}{2}+\frac{1}{2}\frac{2{F}_{{\rm{I}}}-1+\delta {F}_{{\rm{I}}}\delta {F}_{{\rm{QND}}}}{1-\left(2{\gamma }_{{\rm{Rabi}}}\left({\tau }_{{\rm{b}}}\right)-1\right)\left(2{F}_{{\rm{QND}}}-1\right)\delta {F}_{{\rm{I}}}}\left(2{\gamma }_{{\rm{Rabi}}}\left({\tau }_{{\rm{b}}}\right)-1\right).$$

(9)

Here δF_QND = F_QND,1 – F_QND,0. The oscillating component γ_Rabi(τ_b) in the denominator induces higher harmonics of f_Rabi, which is apparent in the Taylor expansion of p₁(τ_b) for δF_I

$$\begin{array}{l}{p}_{1}\left({\tau }_{{\rm{b}}}\right)=\frac{1}{2}+\frac{1}{2}\left(2{F}_{{\rm{I}}}-1+\delta {F}_{{\rm{QND}}}\delta {F}_{{\rm{I}}}\right)\left(2{\gamma }_{{\rm{Rabi}}}\left({\tau }_{{\rm{b}}}\right)-1\right)\,\\ \qquad\qquad\,+\frac{1}{2}\left(2{F}_{{\rm{QND}}}-1\right)\left(2{F}_{{\rm{I}}}-1\right){\left(2{\gamma }_{{\rm{Rabi}}}\left({\tau }_{{\rm{b}}}\right)-1\right)}^{2}\delta {F}_{{\rm{I}}}+O\left(\delta {F}_{{\rm{I}}}^{2}\right).\end{array}$$

(10)

The $\left|{1}_{{\rm{D}}}\right\rangle$ probability shown in Figs. 3b, d, and 4b is described by this equation. However we do not observe 2f_Rabi oscillations attributed to the third term, indicating that δF_I is small in the experiments. We therefore neglect the state dependence of the initialization fidelity in the analysis of Figs. 3 and 4.

Experimental parameters

The device is a double quantum dot fabricated on a silicon/silicon-germanium heterostructure with the natural isotope abundance, which was investigated in previous reports^2,24. Charge occupations of the double dot are read by a radio-frequency reflectometry technique with the charge sensor neighboring the left quantum dot^31,32. The carrier frequency is 205 MHz and the carrier power at the output port of a radio-frequency signal generator is 13 dBm, which is attenuated to ≈−100 dBm before the device by an attenuator chain. The external magnetic field is 0.49 T (Figs. 2 and 4) or 0.60 T (Fig. 3). Zeeman splitting is 15.448 GHz (Fig. 2), 18.581 GHz (Fig. 3), and 15.438 GHz (Fig. 4) for the ancilla qubit when the exchange interaction is turned on, and is 16.006 GHz (Fig. 2), 19.156 GHz (Fig. 3), and 16.033 GHz (Fig. 4) for the data qubit when the exchange interaction is turned off. The difference in the Zeeman splittings of the ancilla and data qubits is around 600 MHz. The exchange coupling in the on state is 9.0 MHz (Fig. 2), 8.9 MHz (Fig. 3), and 6.1 MHz (Fig. 4). The Rabi frequency of the ancilla qubit is 2.8 MHz (Figs. 2), 2.2 MHz (Fig. 3), and 2.0 MHz (Fig. 4). The $\left|{0}_{{\rm{A}}}\right\rangle \left|{0}_{{\rm{D}}}\right\rangle \leftrightarrow \left|{1}_{{\rm{A}}}\right\rangle \left|{0}_{{\rm{D}}}\right\rangle$ and $\left|{0}_{{\rm{A}}}\right\rangle \left|{1}_{{\rm{D}}}\right\rangle \leftrightarrow \left|{1}_{{\rm{A}}}\right\rangle \left|{1}_{{\rm{D}}}\right\rangle$ transitions are used for the CROT gate in Figs. 2,4 and Fig. 3, respectively. The sizes of the exchange interaction and the ancilla Rabi frequency are not exactly tuned to cancel out the ancilla off-resonance drive in the CROT gate, which slightly decreases F_R of an individual QND measurement. In the experiments, the device is operated near the charge-symmetry point of the double dot to decouple the qubits from noise in energy level detuning. Dephasing time T₂^* is ~1 μs for both qubits.

Fundamentals of the joint probability analysis

Assuming that the destructive and the QND measurement in Fig. 2a is stochastically independent of each other, the joint probability P(m,m_d) is expressed in a form where the infidelities in initialization and readout of the qubit state are separated^23,24:

$$\begin{array}{l}P\left(m,{m}_{{\rm{d}}}\right)=\left\{1-p\left({\tau }_{{\rm{b}}}\right)\right\}{\varTheta }_{0,m}\left({f}_{{\rm{R}},0}\right){\varTheta }_{0,{m}_{{\rm{d}}}}\left({f}_{{\rm{d}},{\rm{R}},0}\right)\\\qquad\qquad\quad\,\,\,\,+p\left({\tau }_{{\rm{b}}}\right){\varTheta }_{1,m}\left({f}_{{\rm{R}},1}\right){\varTheta }_{1,{m}_{{\rm{d}}}}\left({f}_{{\rm{d}},{\rm{R}},1}\right).\end{array}$$

(11)

Here, Θ_0,m(x) = x for m = 0_D and Θ_0,m(x) = 1 – x for m = 1_D, and always Θ_1,m(x) = 1 – Θ_0,m(x). p(τ_b) is the $\left|{1}_{{\rm{D}}}\right\rangle$-state probability after the θ rotation induced by a resonant MW burst for duration τ_b, modeled as p(τ_b) = B − Acos(2πf_Rabiτ_b)exp(−τ_b/T_2,Rabi) using Rabi frequency f_Rabi satisfying θ = 2πf_Rabiτ_b, Rabi-oscillation decay time T_2,Rabi, amplitude A, and offset B. Fitting P(m,m_d) calculated from the acquired data to the above expression using a maximum likelihood method, we obtain A = 0.311 ± 0.006, B = 0.51 ± 0.01, f_R,0 = 85.1 ± 0.9%, f_R,1 = 83 ± 1%, f_d,R,0 = 95 ± 1%, f_d,R,1 = 70.6 ± 0.9%. The amplitude A relates solely to the initialization fidelity F_I as F_I = A + 1/2, yielding F_I = 81.1 ± 0.6%. The actual data of P(m,m_d) and fit results are shown in Supplementary Note 2 for details of joint probability analyses.

Error analysis

All uncertainties represent 1σ confidence intervals obtained from fitting.