Abstract
There is a plurality of formal constraints for aggregating probabilities of a group of individuals. Different constraints characterise different families of aggregation rules. In this paper, we focus on the families of linear and geometric opinion pooling rules which consist in linear, respectively, geometric weighted averaging of the individuals’ probabilities. For these families, it is debated which weights exactly are to be chosen. By applying the results of the theory of meta-induction, we want to provide a general rationale, namely, optimality, for choosing the weights in a success-based way by scoring rules. A major argument put forward against weighting by scoring is that these weights heavily depend on the chosen scoring rule. However, as we will show, the main condition for the optimality of meta-inductive weights is so general that it holds under most standard scoring rules, more precisely under all scoring rules that are based on a convex loss function. Therefore, whereas the exact choice of a scoring rule for weighted probability aggregation might depend on the respective purpose of such an aggregation, the epistemic rationale behind such a choice is generally valid.
Similar content being viewed by others
1 Introduction
Probability aggregation is the theory of how to adequately aggregate a set of probability distributions into a single probability distribution. For more than two decades now disciplines concerned with probabilistic reasoning and its rationale are undergoing a social turn, at least so it seems. This makes the problem of probability aggregation a highly relevant topic. Therefore, e.g., in philosophy of science recent research focusses a lot on the relation of scientific groups having gathered a different set of evidence, holding different theories, and providing alternative explanations (cf. Douven & Riegler 2010; Hartmann, Martini, & Sprenger 2009; Zollman 2007). Similarly, in epistemology core topics of social epistemology—namely, the problems of how to incorporate testimony, to resolve peer disagreement, to aggregate judgements—are very often framed in a probabilistic setting (cf., e.g., for testimony Goldman 1999; for peer disagreement Elga 2007; and for probabilistic judgement aggregation Dietrich & List 2016). It is clear that also there, the question of how to adequately aggregate probabilities pops up.
Probability aggregation is highly relevant for different domains. One of the reasons for this is that it has a multitude of interpretations. Wagner (2009, pp.336f) lists five usual roles of such an aggregation. It might serve as
-
1.
a rough summary of a set of individual probability distributions; or
-
2.
a compromise adopted by individuals; or
-
3.
a consensus to which all individuals have revised their initial probability distributions; or
-
4.
the probability distribution of a decision maker that is external to the group; or
-
5.
a revision of a particular individual probability distribution after the individual has learned about other “reasonable” probability distributions.
This list is, of course, not comprehensive and there are also further possibilities of dealing with other and more fine-grained group setups (cf., e.g., Dietrich 2019). Our suggestion for meta-inductive probability aggregation applies to all five domains of application; it is particularly intended for case 4, i.e., for generating a probability distribution of a decision maker that is in some sense external to a group; it might be that the decision maker is strictly external in the sense that she has the authority to make a decision and just has to think about how to best incorporate a group’s possibly diverse set of probability distributions (a case in point would be a policy-making agency that has to work on the bases of a diverse set of expert opinions). However, the decision maker might be also external in the weaker sense of simply having the advantage of receiving information from the group beforehand, while still competing with it (a case in point might be, e.g., weather forecasting competitions or any other forecasting competition with different time ranges for the announcement of the individual forecasts).
In a similar line as it is argued in social choice theory, also in the theory of probability aggregation general rationality constraints for probability aggregation methods are put forward; the aim then is to figure out which aggregation methods satisfy these constraints. Often the constraints put forward are not compatible with each other. This led to the famous impossibility results of social choice theory (cf. Arrow 1963) and the theory of judgement aggregation (cf. List & Pettit 2002). However, as it turned out, one can cluster these constraints in such a way that relevant subclasses are jointly satisfiable and characterise different families of aggregation methods. As we will see in the next section, broadly accepted constraints lead in particular to two common aggregation rules, namely, linear weighting and geometric weighting. Therefore, if one can figure out which constraints for probability aggregation are relevant for which domain of application, one seems to be able to give a partial solution to the problem of probability aggregation. However, even if one subscribes to such a purpose-dependent strategy (cf., e.g., List & Pettit 2011), the constraints put forward at most determine a family of aggregation methods, but no exact aggregation method. In particular, the choice of the weights—which is from the viewpoint of practical applications the most important factor—is undetermined by these constraints.
In this paper, we are going to argue for a new approach to determine such weights. We will do so by suggesting that—if available information permits it—to take in a dynamic perspective and employ optimality results of the so-called theory of meta-induction that show that a success-based determination of weights allows for proving long run optimality of probabilistic predictions. On one hand, this results in a more specific determination of the weights used for aggregating probabilities, and, on the other hand, it also provides an epistemic rationale for doing so.
The structure of the paper is as follows: in Sect. 2, we summarise the characterisation results of the theory of probability aggregation which lead to two families of aggregation functions, namely, the linear and the geometric weighting rules. Since the exact weights are not determined by these results, we briefly discuss solutions for determining weights and their problems in Sect. 3. There, we also outline our solution. The framework of prediction games, and the main results of the theory of meta-induction are presented in Sect. 4. This prepares the ground for Sect. 5, where we apply this framework to a probabilistic setting: We show how the meta-inductive optimality results can be transformed to the probabilistic case and provide a general epistemic rationale. We conclude in Sect. 6.
2 Underdetermined probability aggregation
Many investigations of probability aggregation were triggered by Leonard J. Savage’s seminal work on the Foundations of Statistics, where he introduced a model of group decision:
“Consider a group of people [...] supposed to have the same utility function, [...], but their personal probabilities are not necessarily the same. The group of people is placed in a situation in which it must choose an act [...] from a finite set of available acts [...]. The situation just described will be called a group decision problem.” (cf. Savage 1972, chpt.10.2)
A paradigmatic example mentioned by Savage is the decision-making by a legal jury. As it has to come to a conclusion as a jury, it needs to end up with a group opinion. The scheme of the problem is as follows (Russell, Hawthorne, & Buchak 2015, call this constraint ‘functionality’, cf. p.1290):
Here, \(Pr_1,\dots ,Pr_n\) are the probabilities of the members of a group, also called graded opinions, credences or graded predictions, f is an aggregation function, and \(Pr_{\{1,\dots ,n\}}\) is the respective group probability (graded group opinion, group credence or graded group prediction). In what follows, we assume that all the \(Pr_i\) as well as \(Pr_{\{1,\dots ,n\}}\) are probability functions over an algebra  of propositions, defined as the powerset of a finite set \(S = \{s_1,\ldots ,s_{m}\}\) of possible worlds or states \(s_i\) (we use ‘\(s_i\)’ and ‘S’ here for possible worlds/states and a set encompassing them, because later on we will use ‘\(w_i\)’ for the weights); thus, propositions (p) are subsets of S, and conjunctions and disjunctions of them are understood as set-theoretic intersection and union, respectively. We assume the cardinality of S is at least 3 (this assumption is needed for the characterisation of linear pooling). In later sections (beginning with Sect. 4), we will assume that the possible world propositions \(\{s_i\}\) are expressed by finite conjunctions of statements of the form \(X(i) = v\), where X is a random variable over a domain of discrete timepoints (\(i \in {\mathbb {N}}\), where \({\mathbb {N}}\) is the set of natural numbers), and
of propositions, defined as the powerset of a finite set \(S = \{s_1,\ldots ,s_{m}\}\) of possible worlds or states \(s_i\) (we use ‘\(s_i\)’ and ‘S’ here for possible worlds/states and a set encompassing them, because later on we will use ‘\(w_i\)’ for the weights); thus, propositions (p) are subsets of S, and conjunctions and disjunctions of them are understood as set-theoretic intersection and union, respectively. We assume the cardinality of S is at least 3 (this assumption is needed for the characterisation of linear pooling). In later sections (beginning with Sect. 4), we will assume that the possible world propositions \(\{s_i\}\) are expressed by finite conjunctions of statements of the form \(X(i) = v\), where X is a random variable over a domain of discrete timepoints (\(i \in {\mathbb {N}}\), where \({\mathbb {N}}\) is the set of natural numbers), and  is a value in the value space
is a value in the value space  of the random variable X.
of the random variable X.
As we have seen, according to Savage the group decision problem consists of the question of how to constrain the transmission from the individual to the group. A plurality of constraints for approaching the problem has been discussed. Such investigations are often performed in the line of the so-called axiomatic method, where one formulates general constraints for a good aggregation function in the form of axioms, and then asks which aggregation functions satisfy these if any at all (cf. Dietrich and List 2016, sect.3). A vast amount of literature evolved in this area (cf. Genest & Zidek 1986) and many impossibility results of constraints for aggregation have been proven in the past. Seminal is, e.g., Arrow (1963), where it is shown that some very basic constraints cannot be simultaneously satisfied in the comparative realm. List and Pettit (2002) prove a similar result for the qualitative realm of opinions, namely, belief and disbelief. However, many of the problems of the qualitative and comparative realm disappear in the quantitative realm. What is more, three axioms that lead to an impossibility result within the qualitative realm even characterise a plausible family of transformations or aggregation rules of the quantitative realm. As is discussed and shown in (Lehrer & Wagner 1981, chpt.6; and Genest & Zidek 1986, sect.3), the mentioned three conditions characterise the family of linear opinion aggregation rules:
-
(U)
Universal domain: The domain of the aggregation function f is the class of all (uncountably many) profiles of n probability measures, \((Pr_1,\dots , Pr_n)\), i.e., this domain is
 .
. -
(CP)
Certainty preservation: For all propositions
 , if everyone assigns a probability of 1 to it, so does the group, i.e.: if \(\forall i \in \{1, \dots , n \} Pr_i(p)=1\), then \(Pr_{\{1,\dots ,n\}}(p)=1\).
, if everyone assigns a probability of 1 to it, so does the group, i.e.: if \(\forall i \in \{1, \dots , n \} Pr_i(p)=1\), then \(Pr_{\{1,\dots ,n\}}(p)=1\). -
(I)
Propositionwise independece: the collective probability of any proposition depends solely on the individual probabilities of this proposition, or formally, for all propositions
 there exists a propositionwise aggregation function \(f_p: [0,1]^n \rightarrow [0,1]\), such that for all profiles \((Pr_1,\dots , Pr_n)\) in the domain, \(Pr_{\{1,\dots ,n\}}(p) = f_p(Pr_1(p),\dots ,Pr_n(p))\).
there exists a propositionwise aggregation function \(f_p: [0,1]^n \rightarrow [0,1]\), such that for all profiles \((Pr_1,\dots , Pr_n)\) in the domain, \(Pr_{\{1,\dots ,n\}}(p) = f_p(Pr_1(p),\dots ,Pr_n(p))\).
Linear opinion aggregation rules have the form of a weighted arithmetic mean:
It is interesting to note that comparative “versions” of the three constraints above lead to the famous impossibility results of social choice theory (cf. Arrow 1963). In the quantitative/probabilistic setup, however, these constraints turn out to determine an important family of functions, namely, linear opinion aggregation rules. Since many theorists consider (U), (CP), and (I) to be plausible constraints for probability aggregation, this family has been also proposed as a general framework for probability aggregation (cf. Lehrer & Wagner 1981).
Unfortunately, this characterisation has also some problems. One important drawback is that (U), (CP), and (I) are jointly incompatible with other further plausible constraints for aggregating probabilities. Well-known is, e.g., their incompatibility with the axiom of independence preservation (cf. Lehrer & Wagner 1983): This axiom demands that if all members of a group consider two propositions to be probabilistically independent: \(Pr_i(p_1|p_2)=Pr_i(p_1)\) (\(\forall i\in \{1,\dots ,n\}\)), then also the aggregation should be this way: \(Pr_{\{1,\dots ,n\}}(p_1|p_2)=Pr_{\{1,\dots ,n\}}(p_1)\). Connected with this is the problem that the constraint of aggregating Bayesian (cf. Genest & Zidek 1986, p.119) is not compatible with these conditions: Aggregating individual credences and then performing a Bayesian update by new evidence might be different from all individuals’ first performing a Bayesian update of their credences and then aggregating the updated credences (cf. Mongin 2001, p.320). In other words, linear probability aggregation does not satisfy the condition of the commutativity of aggregation and updating by Bayesian conditionalisation. The commutative update rule that holds for linear weighting is called “imaging” and differs in important respects from Bayesian updating (cf. Leitgeb 2016; the discussion of Leitgeb is based on the main result of Gärdenfors 1982).
However, there is another family of aggregation functions that allows one to satisfy the commutativity constraint while still upholding Bayesian orthodoxy: Genest (1984, p.1101) and Genest, McConway, & Schervish (1986, p.499) show that weak unanimity preservation (cf. Russell, Hawthorne, & Buchak 2015, p.1295,fn.8) and commutativity of aggregation and conditionalisation together with some further technical assumptions characterise the family of the logarithmic or geometric graded opinion aggregation rules. For lack of space, we will not discuss the technical assumptions here. The constraints of weak unanimity preservation and commutativity of aggregation and conditionalisation can be characterised as follows:
-
(P)
Weak unanimity preservation: For all profiles \((Pr_1,\ldots , Pr_n)\) in the domain: If \(Pr_1=\dots =Pr_n\), then \(Pr_{\{1,\dots ,n\}}=Pr_1=\dots =Pr_n\).
Our formulation of the following condition (CAC) on the commutativity of aggregation with learning is based on Dietrich (2019). We say that a probability function \(Pr^{*}\) arises from Pr by conditionalisation on a piece of evidence e iff \(Pr(e) > 0\) and for all  , \(Pr^{*}(p) = Pr(p|e):= \frac{Pr(p\cap e)}{Pr(e)}\):
, \(Pr^{*}(p) = Pr(p|e):= \frac{Pr(p\cap e)}{Pr(e)}\):
-
(CAC)
Commutativity of agregation and conditionalisation: For all propositions
 and profiles \((Pr_1, \dots , Pr_n)\) and \((Pr^{*}_1, \dots , Pr^{*}_n)\) in the domain, with corresponding aggregate functions \(Pr_{\{1,\dots ,n\}}\) and \(Pr^{*}_{\{1,\dots ,n\}}\), if each \(Pr^{*}_i\) arises from \(Pr_i\) by conditionalisation on e, then \(Pr_{\{1,\dots ,n\}}\) arises from \(Pr^{*}_{\{1,\dots ,n\}}\) by conditionalisation on e.
and profiles \((Pr_1, \dots , Pr_n)\) and \((Pr^{*}_1, \dots , Pr^{*}_n)\) in the domain, with corresponding aggregate functions \(Pr_{\{1,\dots ,n\}}\) and \(Pr^{*}_{\{1,\dots ,n\}}\), if each \(Pr^{*}_i\) arises from \(Pr_i\) by conditionalisation on e, then \(Pr_{\{1,\dots ,n\}}\) arises from \(Pr^{*}_{\{1,\dots ,n\}}\) by conditionalisation on e.
These two constraints characterise the normalised weighted geometric mean as defined below. Although initially the concern was voiced that the additional technical assumptions needed for proving a characterisation result of geometric pooling are in need of further justification, so that we “lack a fully compelling axiomatic characterisation of geometric pooling” (cf. Dietrich & List 2016, sect.6), new developments in this field resulted in further celebrated characterisation results for geometric averaging (cf. Russell, Hawthorne, & Buchak 2015) and could be even specified to different forms of geometric averaging as being characteristic for different forms of Bayesian learning situations (cf. Dietrich 2019).
The definition of the normalised weighted geometric mean of a family of probability functions is restricted to coherent profiles, where a profile \((\Pr _1, \dots , Pr_n)\) is called coherent iff there exists at least one world \(s \in S\) to which each \(Pr_i\) assigns a non-zero probability (cf. Dietrich 2019). Here is the definition: For all \(s \in S\) and all profiles \((\Pr _1, \dots , Pr_n)\) that are coherent:
This family of aggregation rules is technically quite demanding. By the coherence requirement, the denominator in the equation must be nonzero and guarantees normalisation: \(Pr_{\{1,\dots ,n\}}(s_1\cup \dots \cup s_{m})=Pr_{\{1,\dots ,n\}}(s_1)+\dots +Pr_{\{1,\dots ,n\}}(s_{m}) = 1\) (where m is the cardinality of S). Since the set of worlds is supposed to be finite, the equation above determines \(Pr_{\{1,\dots ,n\}}\) for arbitrary propositions, i.e., disjunctions of possible worlds, via \(Pr(s\cup s'):= Pr(s)+Pr(s')\) (with \(s,s'\in S\)). In Sect. 5.2, we will require a constraint for predictive propositions that is stronger than coherence, namely, \(\epsilon \)-regularity. More details of the family of geometric aggregation rules are discussed, e.g., in (Dietrich & List 2016, sect.6).
Regardless of the exact characterisation of arithmetic and geometric aggregation rules and the assessments of their advantages and disadvantages, these two families are amongst the most common pooling methods. And, although there is no general aggregation method that allows one to satisfy the constraints for aggregating probabilities as put forward here simultaneously, these two families allow one to satisfy reasonable subsets of these constraints. If one follows the line of reasoning of List and Pettit (2011) and makes the choice of the exact aggregation rule dependent on the context and purposes in question, then (AM) and (GM) may seem to be good candidates for solving the group decision problem (we think that particularly Dietrich 2019, is an excellent example in this vein of a context-dependent choice of aggregation). Hence, it should one make not wonder too much that these two families are also the two most prominent types of probability aggregation rules studied in the literature.
However, there is a problem underlying both (AM) and (GM): It is true that the characterisation results make clear which axioms determine the choice of which family of aggregation rules. Nevertheless, each family still allows for a wide range of different aggregations. In addition, as one can easily see when looking at the equations, this variance is due to the underdetermination of the weights by the aggregation constraints. Therefore, to provide an adequate answer to the group decision problem, one also has to address the problem of choosing the right weights.
3 The problem of choosing the weights
As we have indicated above, the constraints (U), (CP), and (I) determine the family of linear aggregation rules, (P), and (CAC) (and some technical assumptions not described here further) determine the family of geometric aggregation rules, but no set of the constraints allows one to determine a specific aggregation rule. Regarding the weights used for aggregation, these constraints remain undetermined. Now, it is sometimes suggested in the literature that there is no general objective account of justifying a specific choice of the weights: “The determination of the weights is a subjective matter, and numerous interpretations can be given to the weights” (Clemen & Winkler 2007, p.157). In addition, Genest (1984, p.1104) mentions this problem when stating his characterisation result of (GM): “The problem of choosing the weights \(w_i\) [...] remains and is not addressed here. This difficulty is common to most axiomatic approaches”.
Genest and McConway (1990) provide an overview of approaches to determine weights and briefly discuss their problems. We are going to mention just the most prominent approaches here.
According to the interpretation of veridical probabilities (cf. Bunn 1981, p.213), weights are considered to represent the probability of an individual probabilistic forecast to be right: “\(w_i\) represents the probability that \(Pr_i\) is the ‘true’ distribution” (cf. Genest & McConway 1990, p.56, notation adjusted) and “\(w_{i}\) would represent the probability of predictor i being the ‘true’ descriptive model of the underlying stochastic process” (cf. Bunn 1981, p.213, notation adjusted). Therefore, according to this approach the weights \(w_i\) represent the “decision maker’s” credence in \(Pr_i\) making an accurate prediction: \(Pr_{\{1,\dots ,n\}}(Pr_i=ch)\), where ch is the true chance distribution (cf. Bunn 1981, p.213). However, this approach faces the main problem that it is not clear how one can determine the relative veracity of competing opinions when one is ignorant about the true distribution in the world. Moreover, at any stage of evidence this account faces the problem of induction, i.e., of estimating the distribution over unobserved individuals from the observed individuals; and different priors give entirely different answers to this problem. Another objection against this account of weighting individuals by the probability that they have the ’true’ probability distribution is that we have to buy in a claim about the certainty that one of the individuals holds the ‘true’ probability distribution, because the weights sum up to one. In conclusion, the account fails to tell us what should be considered as adequate priors of \(Pr_{\{1,\dots ,n\}}\) in estimating that \(Pr_i\) is an accurate distribution. For this reason, so it seems, this approach fails to set foot on solid ground.
In a further approach, the weights are interpreted as outranking probabilities: “\(w_i\) should be interpreted as the probability that the next prediction made using opinion \(Pr_i\) will outperform predictions made from all other individual opinions in the group” (cf. Genest & McConway 1990, p.57, notation adjusted). An advantage of this interpretation is that such weights are operationally easier to grasp. “However, the main problem with this approach is that if the experts know in advance how their weights will be derived, they may experience them as scores and choose to report dishonest opinions to maximise their influence on the opinion pool”. This was the reason for introducing another interpretation of the weights, namely, weights being interpreted as scores: to avoid the problem of manipulation, proper scoring rules for weights were put forward, i.e., scoring rules which guarantee “that the distribution reported by each expert maximises his expected utility if he is honest and coherent”. However, also here a problem seems to show up: there is a plurality of proper scoring rules (quadratic, logarithmic, spherical etc.) and empirical investigations suggest that “weights [resulting from scores] are not quite satisfactory, because they seemed sensitive to the choice of scoring rule” (cf. Genest & McConway 1990, pp.56ff).
This is the point, where we think that meta-induction should enter the picture, because it allows for determining weights generally in a success-based way. Then, optimality results of meta-induction can be cashed out for providing a general rationale for such a determination. The main line of our argumentation is that at least for linear pooling the epistemological rationale provided by the optimality result of meta-induction is general enough to capture all relevant scoring rules. Therefore, to accommodate this rationale, no specific choice of a scoring rule is necessary. Rather, many of them can be justified generally and the exact choice of a scoring rule might be plausibly made dependent also on the context and purpose in question.
In the next section, we describe the optimality results for meta-inductive success-based weighting for the prediction of single events. Afterwards, in Sect. 5, we are going to generalise the approach to the probabilistic setting.
4 Meta-induction and determining weights
The theory of meta-induction generalises Hans Reichenbach’s best alternatives approach (cf. Reichenbach 1938, pp.348ff; and Schurz 2008, sect.2). Reichenbach proposed to consider the problem of induction not with respect to the strong requirement of proving that inductive methods are successful, but with respect to the much weaker, but epistemically still highly relevant, requirement of proving that inductive methods are the best methods accessible for making predictions. His solution to the problem of induction is a very simple, but also narrow one: If the world is predictable in the sense that for any distribution under investigation there is a limiting frequency, then a method that is defined as approaching this frequency in the limit (as, e.g., is guaranteed by the straight rule (cf. Howson 2003, p.72)), will “lead to the limit”. It is clear that the whole argument is analytic. The specific interpretation of ‘a series is predictable’ as ‘there exists a limit of the series’ some way or another smuggles the inductive uniformity of the series into the meaning of the ‘prediction of a series of events’.
However, one can try to weaken the assumption made by Reichenbach and prove that following an inductive method is still a necessary condition for predictive success, in the sense that all other accessible methods that are most successful converge with that inductive method. Exactly, this is done within the approach of meta-induction (cf. Schurz 2008; 2019). Here, the prediction problem is understood as the problem of providing a successful prediction of the outcome \(e_{t+1}\) of the next event based on information about the outcomes \(e_1,e_2,\dots ,e_t\) of the preceding events, with \(t = 0, 1, \dots \) as a discrete time variable. (Speaking of ‘outcomes of events’ means that we understand the events \(e_t\) as being generated by an event variable; see below.) Similar to Reichenbach’s proposal, induction is not justified in the account of Schurz (2008) in the sense of a ‘correct or true prediction’, but as ‘being optimal among all accessible alternatives’. Contrary to Reichenbach’s proposal, there are no constraints whatsoever on the series of events \(e_1,e_2,\dots \); there might be a limiting frequency of the distribution of properties within such a series or not—it might be predictable in the sense of Reichenbach or completely chaotic. In addition, different from Reichenbach’s framing of the problem, within the approach of meta-induction it is argued for the predictive optimality of induction on a meta-level instead of an object-level: whereas inductive rules at the object-level are applied to the series of events \(e_1,\dots ,e_t\) to predict the event \(e_{t+1}\), the meta-inductive method is applied to the series of predictions made by all available alternative methods and turns these predictions into a prediction of its own—this is the reason why it is called a ‘meta-method’. The underlying idea of the meta-inductive method is to select among predictions all those whose predicting methods were most successful in past—and to aggregate these predictions in an optimal way. It can be proven that there exists a meta-inductive selection-and-aggregation procedure which is most successful in the long run, i.e., its predictive success converges to that of the best prediction method, even if the best method permanently changes in an unforeseeable way, for example, because of unforeseeable changes of the environment. In this way one can say that the meta-inductive method infers from past success future success; it is successful induction over success rates.
Here are the details: The framework of meta-induction is formed by so-called prediction games. Graded (or real-valued) prediction games have the following ingredients (cf. Schurz 2008; 2019, sec. 5.5, notation adjusted):
-
\(e_1,e_2,\dots \) is an infinite series of events at discrete times or ‘rounds’ \(t = 1, 2, \dots \). The events are the actual outcomes of an event variable or random experiment E, taking for each time t a value in a fixed value space Val. More formally: \(E: {\mathbb {N}} \rightarrow Val\) and \(E(t):= e_t\). For graded (or real-valued) prediction games, Val is an interval of real numbers; to keep the number of possible world propositions finite (for any given time t) we assume that the real numbers representing events are of finite accuracy.
-
\(pr_{1,t},\dots ,pr_{n,t}\) are the predictions of the event value E(t), delivered by the n accessible prediction methods \(\{M_1,\dots M_n\}\), the so-called candidate methods, which are typically but not necessarily object-level methods. Thus the prediction \(pr_{i,t}\) stands more explicitly for the proposition “\(E(t) = pr_{i,t}\)” predicted by method \(M_i\). The predictions \(pr_{i,t}\) have to be elements of the real-valued interval [0, 1]. It is allowed to predict mixtures or weighted averages of event values; so the space of prediction values may be a superset of Val.
-
\(pr_{mi,t}\) is the prediction of \(e_t\) of the meta-inductive method \(M_{mi}\).
As we have said above, a meta-inductive method “cooks up” a prediction from the present predictions and past success rates of the candidate methods. The success rate of a method \(M_i\) at any given time t is determined as follows: First, one measures the loss of its predictions compared to the actual or ‘true’ event \(e_t\) for each time t—this loss is denoted as \(l(pr_{i,t},e_t)\). Next, one defines the score of a prediction as 1 minus its loss, and finally, one defines the success rate \(s_{i,t}\) of \(M_i\) at time t as the sums all of its scores up to time t divided by t (cf. Schurz 2019, sect.6.6):
The measure \(s_{i,t}\) represents the success rate, or average per-round success, of candidate method i up round t. The only assumption we make about the loss measure l is that it lies within the interval [0, 1], and that it is convex in its first argument, i.e., the loss of a weighted average of two predictions is lower than or equal to the weighted average of the losses of these two predictions. Or formally: \(l(w\cdot x+(1-w)\cdot y,z)\le w\cdot l(x,z)+(1-w)\cdot l(y,z)\) holds for all x, y and \(w\in [0,1]\). Important examples of convex loss functions are (i) the natural loss that identifies the loss with the absolute distance, \(l(pr_{i,u},e_u) = |pr_{i,u} - e_u|\), and (ii) the quadratic loss, \(l(pr_{i,u},e_u) = (pr_{i,u} - e_u)^2\), which is important for probabilistic prediction games (see below).
The same success measure (\(s_{mi,t}\)) applies to the predictions \(pr_{mi,t}\) of the meta-inductive method. Now, based on this success measure one can define a so-called attractivity measure. The idea of this measure is that the higher the past success of an attractive method, the higher is also its attractivity. Moreover, the attractivity measure cuts off those object-level methods that are not attractive, i.e., that have a lower average per-round success rate than the meta-level method has. Thus the weight of an object-level method \(M_i\) for the meta-level method \(M_{mi}\) regarding event \(e_t\) is defined as follows (as usual the denominator is needed for the purpose of normalisation):
provided t > 0 and the denumerator is non-zero; otherwise, we stipulate \(w_{i,t}=1/n\). Note that the denumerator becomes zero if \(M_{mi}\) outperforms all candidate methods, in which case \(s_{mi,t}\ge s_{i,t}\) holds for all \(i\in \{1,\dots ,n\}\).
Based on these weights, we can define a meta-inductive method which weights the predictions of the attractive methods according to their attractivities. Such a method generates predictions by the method of linear (arithmetic) aggregation as follows (cf. Schurz 2008, sect.7):
According to (AMI) \(M_{mi}\) with its predictions \(pr_{mi,t}\) is a meta-inductive method inasmuch as it bases its prediction on the predictions and weights of all accessible candidate methods, and it is a meta-inductive method inasmuch it is constructed out of candidate methods whose weight increases monotonically with their observed success rates. Note the recursive character of this definition: the meta-inductive prediction \(pr_{mi,t+1}\) depends on the weights \(w_{i,t}\) at earlier times which depend on the meta-inductive predictions at earlier times.
From the viewpoint of the meta-inductivist, attractivities are also called regrets; prediction methods based on regret-based weighting have been developed in a field of machine learning known as “online learning under expert advice” (Cesa-Bianchi & Lugosi 2006, chpt.1). A refined version of regret-based predictions uses weights based on an exponential success dependence; the definition of these weights ew is more complicated (cf. Cesa-Bianchi & Lugosi 2006, pp.14f; and Schurz 2019, p.144f.):
The exponential success-dependent meta-inductive predictor is defined similarly to the linear success-dependent meta-inductivist (AMI) by the method of weighted arithmetic average; thus:
Both methods (AMI) and (EAMI) prove to be very powerful regarding the task of justifying induction in a sense similar to that proposed by Reichenbach: There are quite narrow bounds of \(Pr_{mi}\) and \(Pr_{emi}\)’s relative worst-case regret, i.e., the loss of their success rates compared to the success rate of the actually best candidate method. Based on theorems in the machine learning literature (cf. Cesa-Bianchi & Lugosi 2006, sect.2.1f; and Schurz 2019, sect. 6.6) the following lower bounds of the regret hold:
As defined here, if \(n\ge 6\) the exponential success-dependent meta-level method (EAMI) has a better guaranteed lower bound. It should be noted also that (EAMI) is the best known long run access optimal meta-inductive method inasmuch as it approximates best the minimal lower bound that is achievable in principle, namely, \(\sqrt{\ln (n)/2t}\) (cf. Cesa-Bianchi & Lugosi 2006, p.62, thrm.3.7). On the other hand, (AMI) converges faster than (EAMI) to the maximal success rate of a game with a sustainably best method (cf. Schurz & Thorn 2022). However, what is most important in our context is that the relative regret of the two meta-inductive methods converges quickly to zero when t grows large. An important consequence of this fact is the following result about the so-called long run acccess-optimality of meta-induction:
-
Given l is convex (where l is used for determining s), then both meta-inductive prediction methods (AMI) and (EAMI) are optimal in the long run:
$$\begin{aligned} \lim \limits _{t\rightarrow \infty }max(s_{1,t},\dots ,s_{n,t})-s_{mi,t}~~\le ~~0~ \end{aligned}$$(AMI Optimality)$$\begin{aligned} \lim \limits _{t\rightarrow \infty }max(s_{1,t},\dots ,s_{n,t})-s_{emi,t}~~\le ~~0 \end{aligned}$$(EAMI Optimality)
Therefore, the meta-inductivist’s success rate and that of the best performing methods converge in the limit or the meta-inductivist even performs better. In the machine learning literature, such prediction methods are known as online learnable or no-regret algorithms (cf. Shalev-Shwartz & Ben-David 2014). This result expresses exactly what Reichenbach has described as a necessary condition for predictive success, though at the level of meta-induction. What is more, this result does not depend on any constraints of the event series under investigation and holds for all convex loss functions (underlying the success rates s).
It should be noted that the convexity of the loss function is an important ingredient of the meta-inductive optimality result explained in this section. We find the assumption also to be key in the general literature on the wisdom of the crowd (cf. Lyon forthcoming). At this venue, we cannot discuss in detail why we think that this assumption is justified. However, we want to hint at least at two points. First, for probabilistic predictions one standardly uses so-called proper scoring functions (for reasons to be explained in the next section), and the loss functions underlying them are always convex. Second, it is possible to transfer the meta-inductive optimality results to prediction games with arbitrary (possibly discrete, i.e., non-graded) events and arbitrary (possibly non-convex) loss functions, namely, by randomizing predictions and expressing optimality in terms of expected or average success; for details see (Schurz 2019, sec. 6.7).
In the next section, we are going to utilise the meta-inductive optimality result to determine the weights of linear and geometric probability aggregation and provide an epistemic rationale for such a determination.
5 Success-based probability aggregation
We now turn to probabilistic prediction games, which are an important subcase of prediction games in general. In these games, each forecaster or candidate method identifies the predicted real value with her credence of the predicted event conditional on her information about the past. First, let us ask: When is it reasonable to equate one’s real-valued prediction with one’s probability of the predicted event? According to a well-known result, this identification is not optimal if the loss function is natural or linear, even if one’s probability is close to the true statistical probability. Rather, under this assumption, the optimal prediction rule is the so-called maximum rule which predicts that event value v whose conjectured probability (i.e., so-far observed frequency \(freq_t\)) is maximal (cf. Rumelhart & Greeno 1971; Reichenbach 1938, pp.310f). For binary events, the maximum rule predicts 1 as long as \(freq_t(1)\ge .5\) and 0 otherwise.
The fact that with linear loss functions it is not optimal to predict the probabilities of discrete events does not at all imply that good estimations of the objective probabilities are unimportant for predictive purposes and all that one needs to know is which element of the value space has the maximal chance. One can see this, e.g., by the fact that the agreement of epistemic with objective probabilities is essential for objective Bayesian decision makers: they need to know the objective probabilities in order to choose an action with maximal average payoff. Moreover, knowledge of objective probabilities is necessary when one asks whether what is predicted by an optimal method should be believed as being true.
In many contexts one wants the predictor’s forecasts to reveal her epistemic probabilities. An example of such a context is weather forecasting. For this purpose, non-linear scoring rules have been devised having the property that the expected success of real-valued predictions in independent and identically distributed sequences (IID) is maximal exactly if the forecaster predicts her epistemic probability of the predicted event. These scoring rules are called proper. The loss function underlying a proper scoring rule for a binary event E with outcomes \(e \in \{0,1\}\) has the following property—where we abbreviate the prediction that the event e occurs with probability r simply as r:
-
(PS)
Proper scoring: A scoring rule for a binary event \(e \in \{0,1\}\)is proper iff it is based on a loss function l satisfying the following constraint:
The expected loss of the prediction r under probability Pr—defined as \(Pr(e=1)\cdot l(r,1)+Pr(e=0)\cdot l(r,0)\)—is minimal iff \(r=Pr(e=1)\).
Thus, if the accepted probability function of a rational forecaster is Pr and she is scored by a proper scoring rule. Then, she will predict her epistemic probabilities, because this maximises her expected success. Moreover, she will try to approximate the true statistical probabilities with her epistemic probabilities, because only this can guarantee that her expected success approximates the true average success.
While a linear loss function does not satisfy requirement (PS), certain non-linear but convex loss functions satisfy it. According to a famous result of Brier (1950), the quadratic loss function, \(l(r,e)=(r-e)^2\), constitutes a proper scoring rule. This is seen by differentiating \(Exp_{Pr}\) with respect to \(Pr(e=1)\) and setting it to zero: Let p abbreviate \(Pr(e=1)\). Then, \(d[p\cdot (r-1)^2+(1-p)r^2]/dr=d[p-2pr +r^2]/dr = -2p+2r !=0\); hence \(p=Pr(e=1)=r\).
In the following subsections, we are discussing implementations of meta-induction into the framework of probability aggregation. We will start with an implementation which allows for proving general optimality for linear pooling. By this, e.g., the quadratic loss function proposed by Brier (1950) is proven to be optimal. Then, we will go on with proving a more restricted optimality result for the much more complicated case of geometric pooling. Although scoring functions satisfying constraint (PS) seem to be the most adequate ones for probabilistic forecasts, the following considerations will hold for all convex scoring functions and are not restricted to proper ones.
5.1 Optimal arithmetic probability aggregation
To cash out the optimality result of meta-induction for probability aggregation we have to change our framework. A probabilistic prediction game contains the following ingredients:
-
As before, a series of events \(e_1, e_2, \dots \) that are represented as the outcomes of a random experiment or random variable \(E: {\mathbb {N}} \rightarrow Val\), taking at each time t a value E(t) in a finite value space \(Val = \{v_1,\dots , v_k\}\), where this time the possible values needed not to be graded but may also be discrete. In what follows, the constants \(e_i \in Val\) denote always the actual true outcome of a random experiment; i.e., \(E(t) = e_t\).
-
At each time or round, the candidate methods provide a full probability distribution over the possible outcomes of the next event in question. Thus, the predictions \(pr_{i,t}\) of the methods \(M_i\) for time t are now probability distributions over the possible values of the event variable E, representing the credences of the methods \(M_i\) for the possible outcomes \(E(t) = v_m\) (\(v_m \in Val\)). Or, more formally, \(pr_{i,t} = Pr_{i,t}:Val \rightarrow [0,1]\), where \(Pr_{i,t}\) satisfies the probability axioms.
-
The predictions of the meta-inductive methods AMI (short for arithmetically resp. linear weighted MI) and GMI (short for geometrically weighted MI) are also represented by a probability distribution over Val. They are denoted as \(Pr_{ami,t}\) and \(,Pr_{gmi,t}\), respectively, and defined as an arithmetically/geometrically weighted average of the \(Pr_{1,t},\dots ,Pr_{n,t}\); details are presented below.
It is important to highlight that the candidate methods can be constant methods, learning methods or any other kind of method whatsoever. Since the methods may conditionalise their predictions to observations of past events, the distribution \(Pr_{i,t}\) may be understood as implicitly conditionalised to the observed past events (and maybe to further method-specific information that we leave implicit). Therefore, “\(Pr_{i,t}(E_t=v)\)” is just a shorthand notation for “\(Pr_{i,t}(E_t=v|e_1,\dots ,e_{t-1})\)”. This implies formally that \(Pr_{i,t}\) runs over an algebra of propositions that contains \(\wp (Val)^t\) (the t-fold Cartesian product of the powerset of Val).
If we expand the meta-inductive framework of prediction games to the probabilistic setting we face a problem concerning the definition of the loss function: Now the predictions are real numbers, i.e., probabilities, but the event values are non-numeric values \(v_1,\dots ,v_k\). The problem of expanding meta-induction to the probabilistic setting was studied on another occasion (cf. Feldbacher-Escamilla & Schurz 2020). The problem is a two-fold tension: On one hand, if one tries to keep up with optimality in a too close-knit way, then one easily ends up with probabilistic inconsistency. Therefore, e.g., if one expands the meta-inductive framework, such that for each possible event value a single prediction game is launched, then the meta-inductive prediction for each event value will be optimal with respect to that event value. However, it will also be probabilistically incoherent, because the single predictions of the parallel meta-inductive game will (most of the time) not sum up to 1 (cf. Feldbacher-Escamilla & Schurz 2020, pp.723–726). On the other hand, if one tries to regain probabilistic consistency by, e.g., normalising the single meta-inductive predictions for each possible event value, then this comes at the cost of being no longer universally optimal (cf. Feldbacher-Escamilla & Schurz 2020, pp.726f). As we have also shown there, for the case of employing the Brier score, there is a possible way to apply the meta-inductive framework to the probabilistic setting: By defining an overall loss measure that averages the individual losses for all possible event values, one obtains meta-inductive weights that lead to a probabilistically coherent and at the same time optimal probabilistic prediction (the reason is that averaging the outcomes of a convex loss function results in a loss function that is itself convex; for details cf. the proof in the appendix of Feldbacher-Escamilla & Schurz 2020).
Here, we want to present another and even more general way of employing the meta-inductive framework for probability aggregation that does not face the dilemma of being either prone to inconsistency or suboptimality. The crucial idea is to define a success measure for each method that is not relative to the values of E’s value space. We do so by scoring a method for each time t by scoring its predicted probability for that value which was the true value in that round. We score the predicted probability \(Pr_{i,t}(e_t)\) of the true event outcome \(e_t\) by measuring its loss in regard to the truth value “1”, leading to the intended effect that the loss of \(Pr_{i,t}(e_t)\) is 0/1 iff \(e_t\) was predicted with probability 1/0. Let \(l(Pr_{i,t})\) denote the loss of a probabilistic prediction of the event distribution for time t, and \(s(Pr_{i,t}):= 1- l(Pr_{i,t})\) be the corresponding score. Then, the loss and the score are defined as follows:
Recall that \(e_t\) is that \(v_m\), such that \(E(t) = v_m\).
In particular, if l is the natural loss, this implies:
The same method of defining the success of a probabilistic forecaster is applied in sequential probability assignment (Cesa-Bianchi & Lugosi 2006, p.248), but restricted to the logarithmic loss function. Here, in the context of strategies of probability aggregation, we introduce this method in a more general way that applies to all convex loss functions. The schema of this approach is depicted in Fig. 1.
Example of a prediction game about single events using weights calculated out of predictions of those values which turned out to be true. The bars under ‘\(\Sigma \)’ indicate the sum of the meta-inductive’s probabilistic forecasts that add up to 1 in each round. Bars under ‘score’ represent the natural score in the given round (time) and indicate that the score for a probabilistic prediction is measured via its natural score in regard to the actual event in the given round (time t). The bars under ‘regret’ indicate proven upper bounds for the average per round regret. The probability forecast is optimal regarding the truth, as indicated by the guaranteed vanishing regret. Hence, we have a probabilistically coherent and optimal meta-inductive prediction method
We define the measure for the success rate based on the above loss and scoring function by adding up the scores and dividing them through t. We write this success rate of a candidate method \(M_i\) as  and the success rate of arithmetic (probabilistic) meta-induction as
and the success rate of arithmetic (probabilistic) meta-induction as  :
:

We can now define success-based weights, and, what is crucial, this is done without reference to a specific value of the value space:

with the same proviso as before, i.e., if \(t=0\) or the denominator is zero,  .
.
With the help of these weights we can define the meta-level probability aggregation function that aggregates the object-level probability functions by a success-based weighted arithmetic mean:

This probability aggregation function is an instance of the meta-inductive method (AMI). For this reason, the long run optimality result regarding \(Pr_{mi}\) of (AMI) can be simply transferred to the probability aggregation rule \(Pr_{\{1,\dots ,n\}}=Pr_{ami}\):
Theorem 1
Given that l is convex (where l is used for determining  as defined above), then the forecaster \(Pr_{ami}\) (as defined in (AMI\(^{p}\))) is long run access optimal:
as defined above), then the forecaster \(Pr_{ami}\) (as defined in (AMI\(^{p}\))) is long run access optimal:

with upper bounds for short run regrets:  \((\forall i\in \{1,\dots ,n\})\).
\((\forall i\in \{1,\dots ,n\})\).
The same strategy can be straightforwardly applied for defining the exponential version of probabilistic meta-induction based on arithmetic probability aggregation, resulting in improved upper bounds for short run regrets in accordance with (EAMI); we omit the details.
That the aggregated meta-inductive predictions are also probabilistically coherent follows from the well-known fact that the weighted average of individual probability functions is, again, a probability function. In conclusion, considering linear probability aggregation in a dynamical setting allows one to measure the scores by observing past success rates, then meta-inductive probability aggregation, as presented here, provides an epistemic rationale for using such success-based weights: It is simply because in doing so, one has a guarantee for approaching or even outperforming the best predictive probabilities accessible in the setting. We should highlight that the characterisation of weights as proposed above works only if the information base for aggregating probabilities is strong enough to contain details about the past performance of the different probabilistic methods in question. The results we presented here hinge on the assumption that we know the full track record. However, the meta-inductive account has been generalised also to prove optimality results for cases with a restricted information base. Therefore, e.g., there is the possibility to conditionalise success rates on those probabilistic prediction instances for which information about the individual performance is accessible. In these cases, the aggregated prediction is optimal with respect to conditional success (for details cf. the discussion of so-called “intermittent prediction games” in Schurz 2019, chpt.7). If there is no performance data available at all, then our account cannot be applied to specify the weights.
Up to now, we have achieved an epistemic rationale for choosing weights used in linear probability aggregation in a success-based way. In the following, we want to address the problem of providing an epistemic rationale for choosing weights used in geometric probability aggregation.
5.2 Optimal geometric probability aggregation
We have seen in the preceding subsection that there is a way of aggregating probabilities by arithmetic success-based weighting (AMI\(^{p}\)), which allows for optimality. In this subsection, we want to expand this result also to geometric success-based weighted probability aggregation (GM) (see sect. 2). It is clear that there is no direct implementation of the meta-inductive optimality results of sect. 4 for geometrical probability aggregation, because these optimality results are formulated only for linear success-based weighted predictions. We have already succeeded in transforming the optimality results from a set of predictions about single events to the probabilistic case. Now, we want to show how this result can be used further to allow also for proving the optimality of a geometrical rule that uses success-based weights. As a disclaimer, we should add that the result of this subsection is way more restricted than the result of the previous subsection. Whereas in the case of linear probability aggregation, we were able to show how the weights can be determined in a success-oriented way based on any convex loss function, in the case of geometric probability aggregation, we are only able to show that such a success-oriented way of determining the weights is possible for a specific set of loss functions. Since the matter becomes quite quickly quite technical, we present here the general scheme of our solution. The relevant technical details are provided in the attached appendix.
First, let us state what such a geometrical meta-level rule has to look like. In analogy to the instantiation of (AM) by the meta-level method (AMI\(^{p}\)), we aim at an instantiation of (GM) by the meta-level method \(GMI^p\):

Second, to transfer the optimality result from arithmetic probability aggregation to geometric probability aggregation, we want to highlight that the geometrical rule (GMI\(^p\)) can be re-stated as a linear rule similar to (AMI\(^{p}\)), by replacing probabilities by their logarithms and aggregating these logarithmic values:

Third, the main idea of our implementation is to transform the geometric prediction game into an arithmetic prediction game whose task is to predict the logarithms of the probabilistic forecasts of the geometric game. With the expression “geometric/arithmetic” game, we refer to a prediction game with geometric/arithmetic aggregation rule. The weights of the arithmetic-logarithmic prediction game in which we transform the geometric game will be success-based and they will allow for applying the meta-inductive optimality result as this was done for (AMI\(^{p}\)). Finally, the result is transferred back via the equation above to the geometrical aggregation rule (GMI\(^p\)) by defining suitable “geometrical” weights ( ) and success rates (
) and success rates ( ) (time index omitted). The schema of this approach is provided in Fig. 2.
) (time index omitted). The schema of this approach is provided in Fig. 2.
Schema of transferring the linear meta-inductive optimality result to the geometric aggregation rule. The \(^*\)–variables are the variables of a logarithmic prediction game which is a certain instance of (AMI\(^{p}\)). For this instance, the general meta-inductive optimality result holds, as was shown in sect. 5.1. One can equate this instance with (GMI\(^p\)). Now, via reverse engineering one can define success measures  which allow for geometric meta-inductive optimality in the probabilistic prediction game (\(^*\)–free variables)
which allow for geometric meta-inductive optimality in the probabilistic prediction game (\(^*\)–free variables)
Given such a procedure, an optimality result can also be proved for geometric probability aggregation as follows: In the spirit of geometric scoring, we define the absolute success of a method as the logarithm of the product of the scores achieved in each round. For this purpose we design the following geometric success measure for the probabilistic predictions of the candidate methods (cf. equation (6) in the technical appendix):

Here, \(\epsilon > 0\) is a small real number, such that \(Pr_{i,t}(E(t)=v_m)\) > 0 holds for all \(i \in \{1,\dots ,n\}\), \(t \in {\mathbb {N}}\) and \(v_m \in Val\). The latter requirement is called “epsilon-regularity” and is needed for logarithmic prediction games; a detailed justification is given in the appendix.
The normalised weights for the candidate methods are defined as usual (with the standard proviso that if t=0 or the denominator is zero,  ):
):

The success rate  of the geometric meta-inductive method \(Pr_{gmi}\) (GMI\(^p\)) is defined in the same way as the candidate method’s success rate (above), with one difference: there is the additional factor \(c_t\) that reverses the normalisation factor \(1/c_t\) in the definition of the geometric average (cf. equation (7) of the appendix):
of the geometric meta-inductive method \(Pr_{gmi}\) (GMI\(^p\)) is defined in the same way as the candidate method’s success rate (above), with one difference: there is the additional factor \(c_t\) that reverses the normalisation factor \(1/c_t\) in the definition of the geometric average (cf. equation (7) of the appendix):

That the success measure for the candidate methods must differ from that of the geometric meta-inductivist results from the fact that geometric averaging of probabilities requires the additional step of re-normalising the resulting probability function; this step is not needed in arithmetic averaging. Now, given this success measures it holds (the proof is given in the appendix):
Theorem 2
\(Pr_{gmi}\) as defined in (GMI\(^p\)) is long run access optimal, given the success rate  (as defined in (6) in the appendix) for the candidate methods and
(as defined in (6) in the appendix) for the candidate methods and  (as defined in (7) in the appendix) for the geometric meta-inductive method:
(as defined in (7) in the appendix) for the geometric meta-inductive method:

with the following short run bounds for the regrets: \(\forall i\in \{1,\dots ,n\}\):

A similar result is possible for the exponential version of (GMI\(^p\)); again, for a lack of space, we omit the details here. The result shows that also geometric probability aggregation can be performed in a success-based way, such that the long run access optimality as well as tight short run bounds of such aggregation can be guaranteed. This provides an epistemic rationale for geometric aggregation. Furthermore, as was the case for linear probability aggregation, also here the outcome is probabilistically coherent due to the normalisation of weights ( ) and the fact that the geometrically weighted average of individual probability functions results in a probability function again. Note, however, that due to the restrictions of geometrical pooling this result is much less general. Whereas for linear pooling with success-based weights we proved an optimality result that holds for the full range of convex loss functions, for geometrical pooling we were only able to show to prove optimality for a particular geometric loss and scoring function.
) and the fact that the geometrically weighted average of individual probability functions results in a probability function again. Note, however, that due to the restrictions of geometrical pooling this result is much less general. Whereas for linear pooling with success-based weights we proved an optimality result that holds for the full range of convex loss functions, for geometrical pooling we were only able to show to prove optimality for a particular geometric loss and scoring function.
6 Conclusion
In this paper we have argued for a new solution to the problem of weighted probability aggregation. We have seen that some general constraints determine families of aggregation rules. However, even if arguments can be put forward for deciding in favor of a particular family, in the classical approach the choice of an exact aggregation rule of the respective family remains epistemically undetermined. We have argued that a success-based calculation of weights—as is done in the framework of meta-induction—allows for a much more precise choice. Success-based weighting also provides a rationale for such a choice, since it guarantees long run optimality in probabilistic prediction tasks. As we have tried to make clear in this investigation, if we have a broad enough information basis that allows us to track the predictive success of the set of probability functions in question, we can employ this information to further determine the weights. Whereas the exact choice of the weights for linear and geometric probability aggregation might still depend on the context and purposes in question (e.g., depending on which loss function is used to measure success), such choices can be epistemically justified as long as the respective conditions of the optimality results are given. For the case of linear probability aggregation, we could justify a broad field of applications, namely, all those cases, where the success of a probabilistic forecast is measured via a convex loss function. For the case of geometric probability aggregation, our result is more restricted but proves at least the possibility of an optimal success-oriented determination of weights.
References
Arrow, K. J. (1963). Social choice and individual values (2nd ed.). Yale: Yale University Press.
Brier, G. W. (1950). Verification of forecasts expressed in terms of probability. Monthly Weather Review, 78(1), 1–3.
Bunn, D. W. (1981). Two methodologies for the linear combination of forecasts. Journal of the Operational Research Society, 32(3), 213–222. https://doi.org/10.1057/jors.1981.44
Cesa-Bianchi, N., & Lugosi, G. (2006). Prediction, Learning, and Games. Cambridge: Cambridge University Press. https://doi.org/10.1017/CBO9780511546921
Clemen, R. T., & Winkler, R. L. (2007). Aggregating probability distributions. Advances in decision analysis: from foundations to applications. Cambridge: Cambridge University Press.
Dietrich, F. (2019). A theory of bayesian groups. Noûs, 53(3), 708–736. https://doi.org/10.1111/nous.12233
Dietrich, F., & List, C. (2016). Probabilistic opinion pooling. In A. Hájek & C. Hitchcock (Eds.), The Oxford handbook of probability and philosophy. Oxford: Oxford University Press.
Douven, I., & Riegler, Al. (2010). Extending the Hegselmann- Krause model I. Logic Journal of the IGPL, 18(2), 323–335. https://doi.org/10.1093/jigpal/jzp059
Elga, A. (2007). Reflection and disagreement. Noûs, 41(3), 478–502. https://doi.org/10.1111/j.1468-0068.2007.00656.x
Feldbacher-Escamilla, C. J., & Schurz, G. (2020). Optimal probability aggregation based on generalized brier scoring. Annals of Mathematics and Artificial Intelligence, 88(7), 717–734. https://doi.org/10.1007/s10472-019-09648-4
Gärdenfors, P. (1982). Imaging and conditionalization. The Journal of Philosophy, 79(12), 747–760. https://doi.org/10.2307/2026039
Genest, C. (1984). A characterization theorem for externally Bayesian groups. The Annals of Statistics. https://doi.org/10.1214/aos/1176346726
Genest, C., & McConway, K. J. (1990). Allocating the weights in the linear opinion pool. Journal of Forecasting, 9(1), 53–73. https://doi.org/10.1002/for.3980090106
Genest, C., McConway, K. J., & Schervish, M. J. (1986). Characterization of externally bayesian pooling operators. The Annals of Statistics, 14(2), 487–501. https://doi.org/10.1214/aos/1176349934
Genest, C., & Zidek, J. V. (1986). Combining probability distributions: a critique and an annotated bibliography. Statistical Sciences, 1(1), 114–135.
Goldman, A. I. (1999). Knowledge in a Social World. Oxford: Oxford University Press.
Hartmann, S., Martini, C., & Sprenger, J. (2009). Consensual decision-making among epistemic peers. Episteme, 6(2), 110–129. https://doi.org/10.3366/E1742360009000598
Howson, C. (2003). Hume’s Problem. Oxford: Clarendon Press.
Lehrer, K., & Wagner, C. (1981). Rational consesus in science and society. A philosophical and mathematical study. Dordrecht: Reidel Publishing Company.
Lehrer, K., & Wagner, C. (1983). Probability amalgamation and the independence issue: a reply to Laddaga. Synthese, 55(3), 339–346. https://doi.org/10.1007/BF00485827
Leitgeb, H. (2016). Imaging all the people. Episteme. https://doi.org/10.1017/epi.2016.14
List, C., & Pettit, P. (2002). Aggregating sets of judgments: an impossibility result. Economics and Philosophy, 18(01), 89–110.
List, C., & Pettit, P. (2011). Group agency: the possibility, design, and status of corporate agents. Oxford: Oxford University Press.
Lyon, Aidan (forthcoming). “Collective Wisdom”. In: The Journal of Philosophy.
Mongin, P. (2001). The paradox of the Bayesian experts. Foundations of Bayesianism (pp. 309–338). Dordrecht: Springer Science+Business Media.
Reichenbach, H. (1938). Experience and prediction: an analysis of the foundations and the structure of knowledge. Chicago: University of Chicago Press.
Rumelhart, D. L., & Greeno, J. G. (1971). Similarity between stimuli: an experimental test of the Luce and Restle choice models. Journal of Mathematical Psychology, 8, 370–381.
Russell, J. S., Hawthorne, J., & Buchak, L. (2015). Groupthink. Philosophical Studies, 172(5), 1287–1309. https://doi.org/10.1007/s11098-014-0350-8
Savage, L. J. (1972). The foundations of statistics (2nd ed.). New York: Dover Publications.
Schurz, G. (2008). The meta-inductivist’s winning strategy in the prediction game: a new approach to Hume’s problem. Philosophy of Science, 75(3), 278–305. https://doi.org/10.1086/592550
Schurz, G. (2019). Hume’s problem solved. The optimality of meta-induction. Cambridge, Massachusetts: The MIT Press.
Schurz, G., & Thorn, P. (2022). Escaping the no free lunch theorem: a priori advantages of regret-based meta-induction. Journal of Experimental and Theoretical Artificial Intelligence. https://doi.org/10.1080/0952813X.2022.2080278
Shalev-Shwartz, S., & Ben-David, S. (2014). Understanding machine learning: from theory to algorithms. Cambridge: Cambridge University Press.
Wagner, C. (2009). Jeffrey conditioning and external Bayesianity. Logic Journal of the IGPL, 18(2), 336–345. https://doi.org/10.1093/jigpal/jzp063
Zollman, K. J. S. (2007). The communication structure of epistemic communities. Philosophy of Science, 74(5), 574–587. https://doi.org/10.1086/525605
Funding
Open Access funding enabled and organized by Projekt DEAL. Research of this paper was funded by the German Research Foundation (DFG), research group (FOR 2495), project A2.1 (SCHU 1566/11-2).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that there is no conflict of interest related to the research of this paper.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix: Optimality of geometric ggregation
Appendix: Optimality of geometric ggregation
Here, we provide details for our approach to geometric meta-inductive probability aggregation. Recall Fig. 2 of sect. 5.2. We go through it according to the following steps: we first define geometric pooling \(\textcircled {1}\), then device a game with predictions of logarithms of probabilities with an arithmetic meta-inductivist \(\textcircled {2}\), define the respective success measures of this game \(\textcircled {3}\), transform this game into a prediction game about probabilities with a geometric meta-inductivist \(\textcircled {4}\), define—via backwards engineering—the respective success measures of this game \(\textcircled {5}\), show that this is the success measure for geometric pooling and thus verify the optimality of the geometric meta-inductivist with respect to these success measures \(\textcircled {6}\).

\(\textcircled {1}\): We aim at the optimality of \(Pr_{gmi}\) as defined in (GMI\(^p\)).
We start with the geometric prediction game with predicted probabilities \(pr_{i,t} = Pr_{i,t}(E_t = v_m)\) (\(v_m \in Val\)). We transform this game into an ordinary arithmetic prediction game by designing an ordinary game whose task is to predict the logarithm of the predicted probabilities of the geometric game. There are three problems to be solved before we can start.
First, if the predicted probability is zero, its logarithm is negatively infinite, which is intractable. Therefore, we have to assume that the predicted probabilities are lower bounded by some arbitrarily small but positive value \(\epsilon > 0\), i.e., \(Pr_{i,t}(E(t)=v_m) > \epsilon \) holds for all \(i \in \{1,\dots ,n\}\), \(t \in {\mathbb {N}}\) and \(v_m \in Val\). The latter condition is called \(\epsilon \)-regularity. It is stronger than ordinary regularity, because there are infinitely many points in time. Moreover, (\(\epsilon \)-)regularity implies the condition of coherence from Sect. 2. Note that the condition of \(\epsilon \)-regularity would be too strong as a it general condition for probabilities that are implicitly conditionalised to evidence, because if the evidence e entails the negation of a hypothesis h then, obviously, \(Pr(h|e) = 0\). However, we require this condition only for the predicted probabilities of the next event, which are implicitly conditionalised at most on past events, but not on present events. For these probabilities, the predicted event is analytically independent of (implicitly) conditioning events, and therefore, the condition of \(\epsilon \)-regularity is reasonable.
Second, the logarithms of probabilities are zero or negative, but we want positive event values and predictions. A simple solution to this problem is suggested by the solution of our first problem: we just have to predict the logarithms of these probabilities viewed as multiples of \(\epsilon \), i.e., the probabilities divided by \(\epsilon \); the logarithms of them will always be positive and range between 0 and 1/\(\epsilon \).
Third, the so-defined predictions \(log\left( \frac{Pr_{i,t}(E(t)=v)}{\epsilon }\right) \) of our transformed arithmetic game do not range in the interval [0, 1] but in the interval \([0,log(1/\epsilon )]\). However, this does not matter, because we assume that the loss and scoring function of our transformed game is the natural one. For natural loss functions the optimality results for meta-induction can be transformed easily to any scoring interval of the form [0, b] (with scoring \(s(p,e) = b - |p-e|\), “p” for “prediction”). The long run optimality result stated in Sect. 4 applies directly, and the short-run bounds for (AMI) and (EAMI) hold if they are multiplied with the breath b of the scoring interval (cf. Schurz 2019, p.88).
We designate the parameters of the corresponding arithmetic-logarithmic prediction game by putting an asterix \(^*\) over the predictions and scores of this game. Therefore, for all candidate methods \(M_1,\dots ,M_n\) in the latter game, values \(v_m \in Val\) and times t it holds:
Note that the predictions \(pr^*_{i,t}\) of the logarithmic game are no longer probabilities.
\(\textcircled {2}\): Since the maximal score of a logarithmic prediction is \(\log (1/\epsilon )\), the loss of a logarithmic prediction \(pr^*_{i,t} = \log (Pr_{i,t}(e_t)/\epsilon )\) is given as
Therefore, the corresponding score is given as
The success rate of the candidate methods is denoted as  and thus given as follows:
and thus given as follows:

The same definition applies to the success rate of the meta-inductivist of the arithmetic-logarithmic game, denoted as  . Applying probabilistic meta-induction to the candidate methods of the logarithmic prediction game yields, according to (AMI\(^{p}\)):
. Applying probabilistic meta-induction to the candidate methods of the logarithmic prediction game yields, according to (AMI\(^{p}\)):

As before, the weights  are success-based (
are success-based ( ) as follows:
) as follows:

Since (3) is an instantiation of (AMI\(^{p}\)) and we assumed a convex loss function, it follows from our investigation in Sect. 5.1 that \(Pr^*_{ami}\) is long run access optimal. Therefore, we have defined the relevant success measures  for the logarithmic game \(\textcircled {3}\) \(\checkmark \).
for the logarithmic game \(\textcircled {3}\) \(\checkmark \).
We now transform the logarithmic predictions and scores of the arithmetic game into ordinary probabilistic predictions of a geometric game with suitably defined scores. Retransforming \(pr^*_i\) to \(Pr_i\) is possible by exponentiation, i.e., by defining \(Pr_{i,t}(v_m)=e^{pr^*_{i,t}(v_m)}\) (which is the inverse function of \(\log \), assuming that log is the natural logarithm). Similarly for the meta-inductive aggregation method:

Now, (5) resembles already (GMI\(^p\)), so \(\textcircled {4}\) \(\checkmark \). Only two things are different: First, the weights  are still based on the scores of the arithmetic-logarithmic game, and, second, the normalisation factor 1/c of the geometric aggregation rule (cf. (GMI\(^p\)) is missing.
are still based on the scores of the arithmetic-logarithmic game, and, second, the normalisation factor 1/c of the geometric aggregation rule (cf. (GMI\(^p\)) is missing.
We now define a corresponding scoring and success measure for the geometric game which allows us to achieve long run optimality together with short run bounds for the normalised geometric aggregation \(Pr_{gmi}\) accomplished by (GMI\(^p\)) based on the individual probabilities \(Pr_1,\dots ,Pr_n\). This is done as follows.
-
The score (s) of the probabilistic predictions \(Pr_{i,t}\) is defined as: \(s(Pr_{i,t}) = Pr_{i,t}(e_t)/\epsilon \), where this score is obtained by subtracting the corresponding loss \(l(Pr_{i,t}) = (1/\epsilon ) - (Pr_{i,t}(e_t)/\epsilon )\) from the maximal score \((1/\epsilon )\).
-
In the spirit of geometric aggregation, we define the absolute geometric success of a series of predictions as the logarithm of the product of their scores, i.e., as (\(\log \prod _{1\le u\le t} s(Pr_{i,u})\)). Alternatively, we could use a logarithmic loss function already for the one-round scores and define \(\log (Pr_{i,t}(e_t)/\epsilon )\) as the score of one round. In this case, the absolute success after t rounds would be given as the sum of these logarithmic scores. Both methods are equivalent. This is the reason why one finds both labels in the literature quite often used interchangeably: geometric pooling (due to the product) and ogarithmic pooling. The geometric success per round, abbreviated as
 , is obtained from the absolute geometric success by dividing through t:
, is obtained from the absolute geometric success by dividing through t:  (6)
(6) -
However, the result of (2) is identical with that of (6), and therefore, we get:

i.e., the average per round success of the logarithmic arithmetic game agrees with the average per round success of the geometric game. This promises that the optimality result is transferable from the logarithmic arithmetic to the geometric game, provided we apply the same transformation to the score of the meta-inductive method. However, this is not enough for the geometric meta-inductive method, since this method involves the additional (time-dependent) normalisation constant \(c_t\). For this reason, we have to define a scoring function gs and a success measure
 for geometric meta-inductive probability aggregation which “de-normalises”, i.e., gets rid of this constant, by implementing the normalisation factor \(c_t\) into the score:
for geometric meta-inductive probability aggregation which “de-normalises”, i.e., gets rid of this constant, by implementing the normalisation factor \(c_t\) into the score: 
Again, the standard proviso
 is assumed for t=0 or if the denominator should be zero.
is assumed for t=0 or if the denominator should be zero. -
Based on this “de-normalising” score we can define the de-normalised geometric success rate of \(Pr_{gmi}\) as
 (7)
(7)Therefore, we calculated the relevant success measures
 for the geometric game, hence \(\textcircled {5}\) \(\checkmark \).
for the geometric game, hence \(\textcircled {5}\) \(\checkmark \). -
We have already shown that the relative geometric success of a candidate method equals the relative success rate of this method in the logarithmic arithmetic game:
 . We also know that the meta-inductive predictions in the logarithmic arithmetic game, \(pr^*_{ami}\) with success rate
. We also know that the meta-inductive predictions in the logarithmic arithmetic game, \(pr^*_{ami}\) with success rate  , is long run access optimal and has short run bounds given by multiplying the short run bounds of (AMI) and (EAMI) of sect. 4 with the breath \(1/\epsilon \) of the scoring interval of the logarithmic scores (see the theorem below).
, is long run access optimal and has short run bounds given by multiplying the short run bounds of (AMI) and (EAMI) of sect. 4 with the breath \(1/\epsilon \) of the scoring interval of the logarithmic scores (see the theorem below). -
We show now that the geometrically aggregated meta-inductive predictions of the geometric game, \(Pr_{gmi}\) with success rates
 , are likewise long run access optimal and satisfy the same short run bounds, by showing that for all times \(t>0\),
, are likewise long run access optimal and satisfy the same short run bounds, by showing that for all times \(t>0\),  holds:
holds:-
By (7) the geometric success rate of the meta-inductive method is

-
According to (GMI\(^p\)):

so, the normalisation factor c cancels and we get:

.
-
Reformulation gives us:

-
which is identical with

since we identify the starred weights \(w^*_{i,t}\) with the weights of the geometric meta-inductivist
 . It follows that
. It follows that  .
. -
This completes the proof of theorem 2 at the end of sect. 5. \(\textcircled {6}\) \(\checkmark \).
We conjecture that this result can be generalised to other loss and scoring functions and that one could get rid of the “de-normalisation” in the success rate of \(Pr_{gmi}\). However, this is a very complex topic and work for future research.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Feldbacher-Escamilla, C.J., Schurz, G. Meta-Inductive Probability Aggregation. Theory Decis 95, 663–689 (2023). https://doi.org/10.1007/s11238-023-09933-z
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11238-023-09933-z


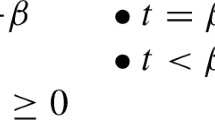


 .
. , if everyone assigns a probability of 1 to it, so does the group, i.e.: if
, if everyone assigns a probability of 1 to it, so does the group, i.e.: if  there exists a propositionwise aggregation function
there exists a propositionwise aggregation function  and profiles
and profiles 

 , is obtained from the absolute geometric success by dividing through t:
, is obtained from the absolute geometric success by dividing through t: 

 for geometric meta-inductive probability aggregation which “de-normalises”, i.e., gets rid of this constant, by implementing the normalisation factor
for geometric meta-inductive probability aggregation which “de-normalises”, i.e., gets rid of this constant, by implementing the normalisation factor 
 is assumed for t=0 or if the denominator should be zero.
is assumed for t=0 or if the denominator should be zero.
 for the geometric game, hence
for the geometric game, hence  . We also know that the meta-inductive predictions in the logarithmic arithmetic game,
. We also know that the meta-inductive predictions in the logarithmic arithmetic game,  , is long run access optimal and has short run bounds given by multiplying the short run bounds of (AMI) and (EAMI) of sect.
, is long run access optimal and has short run bounds given by multiplying the short run bounds of (AMI) and (EAMI) of sect.  , are likewise long run access optimal and satisfy the same short run bounds, by showing that for all times
, are likewise long run access optimal and satisfy the same short run bounds, by showing that for all times  holds:
holds:




 . It follows that
. It follows that  .
.