Interpolation-based decoding of folded variants of linearized and skew Reed–Solomon codes

Abstract

The sum-rank metric is a hybrid between the Hamming metric and the rank metric and suitable for error correction in multishot network coding and distributed storage as well as for the design of quantum-resistant cryptosystems. In this work, we consider the construction and decoding of folded linearized Reed–Solomon (FLRS) codes, which are shown to be maximum sum-rank distance (MSRD) for appropriate parameter choices. We derive an efficient interpolation-based decoding algorithm for FLRS codes that can be used as a list decoder or as a probabilistic unique decoder. The proposed decoding scheme can correct sum-rank errors beyond the unique decoding radius with a computational complexity that is quadratic in the length of the unfolded code. We show how the error-correction capability can be optimized for high-rate codes by an alternative choice of interpolation points. We derive a heuristic upper bound on the decoding failure probability of the probabilistic unique decoder and verify its tightness by Monte Carlo simulations. Further, we study the construction and decoding of folded skew Reed-Solomon codes in the skew metric. Up to our knowledge, FLRS codes are the first MSRD codes with different block sizes that come along with an efficient decoding algorithm.

1 Introduction

The sum-rank metric was first considered in [28] in the context of space-time coding and covers the Hamming metric as well as the rank metric as special cases. Alternative decoding metrics as the sum-rank metric are of great interest to the field of code-based cryptography (see e.g. [35]). Other applications range from error control in multishot network coding as described in [31] and [33] to the construction of locally repairable codes [32].

Martínez-Peñas introduced linearized Reed–Solomon (LRS) codes, which generalize the well-studied families of Reed–Solomon (RS) and Gabidulin codes, in [30]. LRS codes are maximum sum-rank distance (MSRD) codes, that is their minimum distance achieves the Singleton-like bound with equality.

While codewords of sum-rank-metric codes are commonly defined as tuples containing matrices of arbitrary sizes, most known constructions use the same number of rows for every matrix in the tuple. Some examples of MSRD codes with different numbers of rows for the matrices can be found in [11, 12]. Another construction for MSRD codes with this property is given in [14, 15]. However, no efficient decoding algorithm has been developed for such codes up to our knowledge. We address this by presenting the family of FLRS codes along with an efficient interpolation-based decoding algorithm that can be used for list and probabilistic unique decoding.

We further apply our results to the skew-metric regime where we fold skew Reed–Solomon (SRS) codes. SRS codes were introduced and studied in [9, 27] with respect to Hamming metric and rank metric. The work [30] defined the skew metric and analyzed SRS codes in this new context. In fact, it was shown that the sum-rank metric and LRS codes are the linearized version of the skew metric and SRS codes, respectively.

The idea of folding constructions in coding evolved in the Hamming-metric context with Parvaresh–Vardy codes [34] and folded Reed–Solomon codes [10, 19]. Folded Gabidulin codes and their efficient decoding in the rank metric were studied in [2, 3, 6].

Contributions Note that parts of this work were presented at WCC 2022: The Twelfth International Workshop on Coding and Cryptography (see [20]).

We define the family of FLRS codes and derive an interpolation-based decoding framework for these codes. In contrast to [20], we allow different block sizes in the underlying unfolded code as well as the usage of different folding parameters. This yields codes whose codewords are matrix tuples consisting of matrices having not the same size. We further lift the restriction to skew polynomials with zero derivation and also deal with nonzero derivations.

As in [20], we show how the decoding scheme can be used for list and probabilistic unique decoding and give bounds on the list size and the failure probability, respectively. We have performed several Monte Carlo simulations that verify the heuristic upper bound on the failure probability empirically. Moreover, new simulations show the reasonability of an assumption which is needed to obtain the heuristic bound.

A Justesen-like approach, which yields an improved interpolation-based decoding scheme for high-rate FLRS codes, and the discussion of implications for the skew metric are completely new topics in this work. More precisely, we introduce folded skew Reed–Solomon (FSRS) codes in the skew metric in a similar fashion as FLRS codes and show how the proposed FLRS decoding scheme can be applied.

Outline We start by giving some preliminaries in Sect. 2 before defining FLRS codes and studying their minimum distance in Sect. 3.

The main part of this paper is Sect. 4 in which we present and investigate an interpolation-based decoding scheme for FLRS codes. The decoder consists of an interpolation step and a root-finding step which are explained in detail in Sects. 4.1 and 4.2, respectively. Section 4.3 shows how the presented scheme can be used for list and probabilistic unique decoding. In particular, we derive an upper bound on the list size in the first case and on the failure probability in the latter. Section 4.4 introduces a variant of the decoding scheme that is tailored to high-rate codes by using a different set of interpolation points. Since the bound on the failure probability for probabilistic unique decoding from Sect. 4.3 is heuristic, we empirically verify its validity by simulations in SageMath in Sect. 4.5.

Section 5 deals with the implications of our results for the skew-metric setting. We give some background on the remainder evaluation of skew polynomials and the skew metric in Sect. 5.1 and introduce FSRS codes in Sect. 5.2. Section 5.3 shows how the presented decoder for FLRS codes in the sum-rank metric can be applied to FSRS codes in the skew metric.

Finally, Sect. 6 concludes the paper by summarizing our work and giving open problems and directions for further research.

2 Preliminaries

Let q be a prime power and let $\mathbb F_{q}$ be a finite field of order q. For any $m \in \mathbb {N}^{*}$, let $\mathbb F_{q^m}\supseteq \mathbb F_{q}$ denote an extension field with $q^m$ elements. We call $\alpha \in \mathbb F_{q^m}$ primitive in $\mathbb F_{q^m}$ if it generates the multiplicative group $\mathbb F_{q^m}^{*} :=\mathbb F_{q^m}\setminus \{0\}$.

An (integer) composition of $n\in \mathbb {N}^{*}$ into $\ell \in \mathbb {N}^{*}$ parts, which is also called an $\ell$-composition for short, is a vector $\textbf{n}= (n_{1}, \ldots , n_{\ell }) \in \mathbb {N}^{\ell }$ with $n_{i} > 0$ for all $1 \le i \le \ell$ that satisfies $n= \sum _{i=1}^{\ell } n_i$. We use the notation $\mathbb F_{q}^{\textbf{n}} :=\mathbb F_{q}^{n_{1}} \times \cdots \times \mathbb F_{q}^{n_{\ell }}$ to describe the space of $\mathbb F_{q}^{n}$-vectors that are divided into $\ell$ blocks with respect to a given $\ell$-composition $\textbf{n}$ of $n$. Similarly, we write $\mathbb F_{q}^{\textbf{o}\times \textbf{n}} :=\mathbb F_{q}^{o_{1} \times n_{1}} \times \cdots \times \mathbb F_{q}^{o_{\ell } \times n_{\ell }}$ for $\ell$-compositions $\textbf{o}$ of $o$ and $\textbf{n}$ of $n$. In the following, we always assume $\textbf{o}\le \textbf{n}$ with respect to the product order on $\mathbb {N}^{\ell }$, that is $o_{i} \le n_{i}$ holds for each $i = 1, \ldots , \ell$.

Definition 1

(Sum-Rank Metric) The sum-rank weight of a tuple $\textbf{X}= \left( {\textbf{X}}^{(1)}, \ldots , {\textbf{X}}^{(\ell )} \right) \in \mathbb F_{q}^{\textbf{o}\times \textbf{n}}$ is

$$\begin{aligned} {{\,\textrm{wt}\,}}_{\Sigma R}(\varvec{X}) :=\sum _{i=1}^{\ell } {{\,\textrm{rk}\,}}_q\left( \varvec{X}^{(i)}\right) \end{aligned}$$

and the vector ${\textbf{t}}= (t_1, \ldots , t_{\ell }) \in \mathbb {N}^{\ell }$ with $t_i :={{\,\textrm{rk}\,}}_q \left( \varvec{X}^{(i)} \right)$ for all $i = 1, \ldots , \ell$ is called the weight decomposition of $\textbf{X}$.

The sum-rank metric $d_{\Sigma R}$ is defined as

$$\begin{aligned} d_{\Sigma R}(\textbf{X}, \textbf{Y}) :={{\,\textrm{wt}\,}}_{\Sigma R}(\textbf{X}- \textbf{Y}) \end{aligned}$$

for two elements $\textbf{X}, \textbf{Y}\in \mathbb F_{q}^{\textbf{o}\times \textbf{n}}$.

A linear sum-rank-metric code $\mathcal {C}$ is an $\mathbb F_{q}$-linear subspace of the metric space $(\mathbb F_{q}^{\textbf{o}\times \textbf{n}}, d_{\Sigma R})$. Its minimum (sum-rank) distance is

$$\begin{aligned} d_{\Sigma R}(\mathcal {C})&= \min \{d_{\Sigma R}(\textbf{C}_1, \textbf{C}_2): \textbf{C}_1, \textbf{C}_2 \in \mathcal {C}, \textbf{C}_1 \ne \textbf{C}_2 \} \\&= \min \{ {{\,\textrm{wt}\,}}_{\Sigma R}(\textbf{C}) : \textbf{C}\in \mathcal {C}, \textbf{C}\ne 0 \}. \end{aligned}$$

If $\textbf{o}= (m, \ldots , m)$ for some $m \in \mathbb {N}^{*}$, we sometimes write codewords as $(m \times n)$-matrices over $\mathbb F_{q}$ instead of matrix tuples from $\mathbb F_{q}^{\textbf{o}\times \textbf{n}}$. Moreover, a code $\mathcal {C}$ in this ambient space has a vector-code representation $\mathcal {C}_{vec} :=\{ \text {ext}^{-1}_{\varvec{\gamma }}(\textbf{C}): \textbf{C}\in \mathcal {C} \} \subseteq \mathbb F_{q^m}^{n}$ over $\mathbb F_{q^m}$. Here, the map $\text {ext}^{-1}_{\varvec{\gamma }}$ is the inverse of the extension map $\text {ext}_{\varvec{\gamma }}$ that extends a vector $\textbf{a}\in \mathbb F_{q^m}^{n}$ to a matrix $\textbf{A}\in \mathbb F_{q}^{m \times n}$ with respect to a fixed ordered $\mathbb F_{q}$-basis $\varvec{\gamma }= (\gamma _1, \ldots , \gamma _m)$ of $\mathbb F_{q^m}$. Namely,

$$\begin{aligned} \text {ext}_{\varvec{\gamma }}: \quad \mathbb F_{q^m}^{n}&\rightarrow \mathbb F_{q}^{m \times n}, \\ \textbf{a}= (a_1, \ldots , a_{n})&\mapsto \textbf{A}= \begin{pmatrix} a_{1 1} &{} \ldots &{} a_{1 n} \\ \vdots &{} \ddots &{} \vdots \\ a_{m 1} &{} \ldots &{} a_{m n} \end{pmatrix} \text { with } a_i = \sum _{j=1}^{m} a_{j i} \gamma _j \text { for } 1 \le i \le n. \end{aligned}$$

Note that we omit the index $\varvec{\gamma }$ if the particular choice of the basis is irrelevant.

The Frobenius automorphism of the field extension $\mathbb F_{q^m}/ \mathbb F_{q}$ is the map $\theta : \mathbb F_{q^m}\rightarrow \mathbb F_{q^m}$ with $\theta (x) = x^q$ for all $x \in \mathbb F_{q^m}$. It is $\mathbb F_{q}$-linear, fixes $\mathbb F_{q}$ elementwise, and generates the group of all $\mathbb F_{q}$-linear automorphisms on $\mathbb F_{q^m}$ with respect to function composition. We focus on an arbitrary $\mathbb F_{q}$-linear automorphism $\sigma$ on $\mathbb F_{q^m}$ in the following. In particular, $\sigma = \theta ^{u}$ holds for a $u\in \{0, \ldots , m-1\}$. A $\sigma$-derivation is a map $\delta : \mathbb F_{q^m}\rightarrow \mathbb F_{q^m}$ satisfying

$$\begin{aligned} \delta (a + b) = \delta (a) + \delta (b) \quad \text {and} \quad \delta (ab) = \delta (a)b + \sigma (a)\delta (b) \quad \text {for all } a, b \in \mathbb F_{q^m}. \end{aligned}$$

Since we work over finite fields, any $\sigma$-derivation is an inner derivation which means that $\delta = z({{\,\mathrm{\text {Id}}\,}}- \sigma )$ for a $z\in \mathbb F_{q^m}$ and the identity ${{\,\mathrm{\text {Id}}\,}}$ (see [30, Prop. 44]).

Two elements $a, b \in \mathbb F_{q^m}$ are called $(\sigma , \delta )$-conjugate if there is a $c \in \mathbb F_{q^m}^{*}$ such that ${a}^{c} :=\sigma (c) a c^{-1} + \delta (c) c^{-1} = b$. This is an equivalence relation and $\mathbb F_{q^m}$ is hence partitioned into conjugacy classes $\mathcal {C}(a) :=\big \{ a^c: c \in \mathbb F_{q^m}^{*} \big \}$ for $a \in \mathbb F_{q^m}$ (see e.g. [21, 22]). A counting argument shows that there are $q^{\gcd (u, m)}$ distinct conjugacy classes and all except $\mathcal {C}(z)$ are called nontrivial. If $\delta = 0$ (i.e., $z= 0$) and $\sigma = \theta$, the powers $1, \alpha , \ldots , \alpha ^{q-2}$ of a primitive element $\alpha \in \mathbb F_{q^m}^{*}$ are representatives of all $q^{\gcd (1,m)}-1 = q-1$ distinct nontrivial conjugacy classes.

The skew polynomial ring $\mathbb F_{q^m}[x;\sigma ,\delta ]$ is defined as the set of polynomials $\sum _i f_i x^i$ with finitely many nonzero coefficients $f_i \in \mathbb F_{q^m}$. It forms a non-commutative ring with respect to ordinary polynomial addition and multiplication determined by the rule $x f_i = \sigma (f_i) x + \delta (f_i)$ for all $f_i \in \mathbb F_{q^m}$. We define the degree of a skew polynomial $f(x) = \sum _i f_i x^i$ as $\deg (f) :=\max \{i: f_i \ne 0\}$ and write $\mathbb F_{q^m}[x;\sigma ,\delta ]_{<k} :=\{ f \in \mathbb F_{q^m}[x;\sigma ,\delta ]: \deg (f) < k \}$ for the set of skew polynomials of degree less than $k \ge 0$.

We further introduce the operator $\mathcal {D}_{a}(b) :=\sigma (b) a + \delta (b)$ for any $a, b \in \mathbb F_{q^m}$ and we write $\mathcal {D}_{a}^{i}(b) :=\mathcal {D}_{a}(\mathcal {D}_{a}^{i-1}(b))$ for its i-th power with $i \in \mathbb {N}^{*}$. Let $\textbf{n}= (n_{1}, \ldots , n_{\ell }) \in \mathbb {N}^{\ell }$ be an $\ell$-composition of $n\in \mathbb {N}^{*}$. For a vector $\textbf{x}= \left( \textbf{x}^{(1)}, \ldots , \textbf{x}^{(\ell )}\right) \in \mathbb F_{q^m}^{\textbf{n}}$, a vector $\textbf{a}= (a_1, \ldots , a_\ell ) \in \mathbb F_{q^m}^{\ell }$, and a parameter $d \in \mathbb {N}^{*}$ the generalized Moore matrix $\mathfrak {M}_{d}(\textbf{x})_{\textbf{a}}$ is defined as

$$\begin{aligned} \mathfrak {M}_{d}(\textbf{x})_{\textbf{a}}&:=\left( \mathfrak {m}_{d}(\textbf{x}^{(1)})_{a_1}, \ldots , \mathfrak {m}_{d}(\textbf{x}^{(\ell )})_{a_\ell } \right) \in \mathbb F_{q^m}^{\textbf{d}\times \textbf{n}},\\ \text {where } \mathfrak {m}_{d}(\textbf{x}^{(i)})_{a_i}&:=\begin{pmatrix} x^{(i)}_1 &{} \cdots &{} x^{(i)}_{n_{i}}\\ \mathcal {D}_{a_i}(x^{(i)}_1) &{} \cdots &{} \mathcal {D}_{a_i}(x^{(i)}_{n_{i}})\\ \vdots &{} \ddots &{} \vdots \\ \mathcal {D}_{a_i}^{d-1}(x^{(i)}_1) &{} \cdots &{} \mathcal {D}_{a_i}^{d-1}(x^{(i)}_{n_{i}}) \end{pmatrix} \quad \text {for } 1 \le i \le \ell \nonumber \end{aligned}$$

(1)

and $\textbf{d}:=(d, \ldots , d) \in \mathbb {N}^{\ell }$. If $\textbf{a}$ contains representatives of pairwise distinct nontrivial conjugacy classes of $\mathbb F_{q^m}$ and ${{\,\textrm{rk}\,}}_{q}\left( \textbf{x}^{(i)}\right) = n_{i}$ for all $1 \le i \le \ell$, we have by [30, Thm. 2] and [22, Thm 4.5] that ${{\,\textrm{rk}\,}}_{q^m}\left( \mathfrak {M}_{d}(\textbf{x})_{\textbf{a}}\right) = \min (d, n)$.

The generalized operator evaluation of a skew polynomial $f \in \mathbb F_{q^m}[x;\sigma ,\delta ]$ at $b \in \mathbb F_{q^m}$ with respect to the evaluation parameter $a \in \mathbb F_{q^m}$ is defined as ${f}(b)_{a} = \sum _{i} f_i \mathcal {D}_{a}^{i}(b)$ and can be written in vector–matrix form using the generalized Moore matrix from (1). For $\textbf{a}= (a_1, \ldots , a_{\ell }) \in \mathbb F_{q^m}^\ell$ and $\textbf{x}= ({\textbf{x}}^{(1)}, \ldots , {\textbf{x}}^{(\ell )}) \in \mathbb F_{q^m}^\textbf{n}$ we use the shorthand notation

$$\begin{aligned} {f}(\textbf{x})_{\textbf{a}} :=({f}({\textbf{x}}^{(1)})_{a_1}, \ldots , {f}({\textbf{x}}^{(\ell )})_{a_\ell }) \in \mathbb F_{q^m}^\textbf{n}. \end{aligned}$$

Let $a_1, \ldots , a_{\ell }$ be representatives of distinct nontrivial conjugacy classes of $\mathbb F_{q^m}$ and consider $n_{i}$ $\mathbb F_{q}$-linearly independent elements $\zeta _1^{(i)}, \ldots , \zeta _{n_{i}}^{(i)} \in \mathbb F_{q^m}$ for each $i = 1, \ldots , \ell$. Then any nonzero $f \in \mathbb F_{q^m}[x;\sigma ,\delta ]$ satisfying ${f}(\zeta _j^{(i)})_{a_i} = 0$ for all $1 \le j \le n_{i}$ and all $1 \le i \le \ell$ has degree at least $\sum _{i=1}^{\ell } n_{i}$ (see e.g. [13]).

Definition 2

(Linearized Reed–Solomon Codes [30, Def. 31]) Let $\textbf{a}= (a_1, \ldots , a_\ell ) \in \mathbb F_{q^m}^{\ell }$ contain representatives of pairwise distinct nontrivial conjugacy classes of $\mathbb F_{q^m}$ and consider an $\ell$-composition $\textbf{n}:=(n_1, \ldots , n_\ell ) \in \mathbb {N}^{\ell }$ of $n \in \mathbb {N}$. Let the vectors $\varvec{\beta }^{(i)} = (\beta _1^{(i)}, \ldots , \beta _{n_i}^{(i)}) \in \mathbb F_{q^m}^{n_i}$ contain $\mathbb F_{q}$-linearly independent elements for all $i = 1, \ldots , \ell$ and define $\varvec{\beta }:=(\varvec{\beta }^{(1)}, \ldots , \varvec{\beta }^{(\ell )}) \in \mathbb F_{q^m}^{\textbf{n}}$. A linearized Reed–Solomon code of length n and dimension $k \le n$ is defined as

$$\begin{aligned} \textrm{LRS}[\varvec{\beta },\textbf{a};\textbf{n},k] :=\left\{ {f}(\varvec{\beta })_{\textbf{a}}: f \in \mathbb F_{q^m}[x;\sigma ,\delta ]_{<k} \right\} \subseteq \mathbb F_{q^m}^{\textbf{n}}. \end{aligned}$$

Observe that the parameter restrictions in Definition 2 also imply restrictions on the length that LRS codes can achieve. Since the evaluation parameters $a_1, \ldots , a_{\ell }$ have to belong to distinct nontrivial conjugacy classes, the number of blocks $\ell$ is upper bounded by the number of these classes. As we know from Sect. 2, $\mathbb F_{q^m}$ has $q^{\gcd (u,m)}-1$ distinct nontrivial conjugacy classes, where $u \in \{0, \ldots , m-1\}$ is defined by the equality $\sigma = \theta ^u$ for the Frobenius automorphism $\theta$ of $\mathbb F_{q^m}/\mathbb F_{q}$. Thus, $\ell \le q^{\gcd (u,m)}-1$ has to apply. At the same time, the code locators ${\varvec{\beta }}^{(i)}$ of the i-th block have to contain $\mathbb F_{q}$-linearly independent elements for all $i = 1, \ldots , \ell$ which implies $n_{i} \le m$. This means that the length n of an LRS code is always bounded by $n \le (q^{\gcd (u,m)}-1) \cdot m$.

The next lemma is taken from [11, Lemma III.12] and lays the foundation for a Singleton-like bound for sum-rank-metric codes with different block sizes.

Lemma 1

Consider an $\ell$-composition $\textbf{n}= (n_{1}, \ldots , n_{\ell })$ of $n\in \mathbb {N}$ and a vector $\textbf{o}= (o_{1}, \ldots , o_{\ell }) \in \mathbb {N}^{\ell }$ with $o_{1} \ge \cdots \ge o_{\ell } > 0$ and $\textbf{n}\le \textbf{o}$. Define the set

$$\begin{aligned} \mathcal {U}_z :=\left\{ \textbf{z}= (z_1, \ldots , z_{\ell }) \in \mathbb {N}^{\ell }: \textbf{z}\le \textbf{n}\text { and } \sum _{i=1}^{\ell } z_i = z \right\} \end{aligned}$$

for each $z \in \{0, \ldots , n\}$. If we denote by $j\in \{1, \ldots , \ell \}$ and $\lambda \in \{0, \ldots , n_{j} - 1\}$ the unique integers that satisfy $\sum _{i=1}^{j- 1} n_{i} + \lambda = z$, then it holds

$$\begin{aligned} \max \left\{ \sum _{i=1}^{\ell } o_{i} z_i: (z_1, \ldots , z_{\ell }) \in \mathcal {U}_z \right\} = \sum _{i=1}^{j- 1} o_{i} n_{i} + o_{j} \lambda . \end{aligned}$$

We can think about this result in the context of a matrix tuple from $\mathbb F_{q}^{{\textbf {o}}\times {\textbf {n}}}$ where we are allowed to mark z columns. Our goal is then to maximize the number of marked entries which is given as $\sum _{i=1}^{\ell } o_{i} z_i$. Since the matrices are sorted descendingly with respect to their number of rows, the logical strategy is to mark the first z columns. The index $j$ then corresponds to the first block for which we cannot mark every column anymore.

Theorem 1

(Singleton-like Bound [11, Thm. III.2]) Let $\textbf{o}= (o_{1}, \ldots , o_{\ell })$ and $\textbf{n}= (n_{1}, \ldots , n_{\ell })$ be integer vectors with $o_{1} \ge \cdots \ge o_{\ell } > 0$ and $0 < n_{i} \le o_{i}$ for all $i \in \{1, \ldots , \ell \}$. Consider a sum-rank-metric code $\mathcal {C} \subseteq \mathbb F_{q}^{\textbf{o}\times \textbf{n}}$ with $\vert \mathcal {C} \vert \ge 2$ and $d_{\Sigma R}(\mathcal {C}) = d$. Then,

$$\begin{aligned} \vert \mathcal {C} \vert \le q^{\sum _{i = j}^{\ell } o_{i} n_{i} - o_{j} \lambda }, \end{aligned}$$

(2)

where $j\in \{1, \ldots , \ell \}$ and $0 \le \lambda < n_{j}$ are the unique integers such that $d - 1 = \sum _{i=1}^{j- 1} n_{i} + \lambda$ holds.

Note that Theorem 1 generalizes the statements [30, Prop. 34] and [32, Cor. 2] that were derived for codes with $o_{1} = \cdots = o_{\ell }$.

3 Folded linearized Reed–Solomon codes

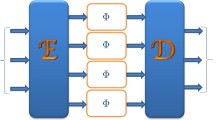
Code classes obtained by a folding construction have been considered starting from RS and Gabidulin codes in [19] and [3, 6], respectively. Let us describe the folding process for a codeword $\textbf{c}$ of length n and a folding parameter h that divides n. We obtain the folded codeword by subdividing $\textbf{c}$ into $\frac{n}{h}$ pieces of length h and using them as columns of a matrix of size $h \times \frac{n}{h}$. The folded code is simply the collection of all folded codewords.

The folding operation can be expressed by means of the folding operator

$$\begin{aligned} \mathcal {F}_{h}: \qquad \qquad \qquad \mathbb F_{q^m}^{n}&\rightarrow \mathbb F_{q^m}^{h\times N} \\ (x_1, \ldots , x_{n})&\mapsto \begin{pmatrix} x_1 &{} x_{h+ 1} &{} \cdots &{} x_{n- h+ 1} \\ x_2 &{} x_{h+ 2} &{} \cdots &{} x_{n- h+ 2} \\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ x_{h} &{} x_{2 h} &{} \cdots &{} x_{n} \end{pmatrix} \end{aligned}$$

where $n, N\in \mathbb {N}^{*}$ denote the length of the unfolded and folded vector, respectively, and where the folding parameter $h\in \mathbb {N}^{*}$ divides $n$ with $N= \frac{n}{h}$. Its inverse allows to unfold a matrix and is denoted by $\mathcal {F}_{h}^{-1}$.

This paper focuses on folding LRS codes which are a generalization of both RS and Gabidulin codes. Since LRS codes are naturally equipped with a block structure, we apply the described folding mechanism blockwise to obtain FLRS codes. Observe that since the length of the blocks may vary, we may choose a different folding parameter for each block. This produces sum-rank-metric codes whose codeword tuples consist of matrices with different numbers of rows and columns. A visual representation of the folding construction for a particular block of an LRS codeword is given in Fig. . A formal description is the following generalization of the above discussed folding operator:

$$\begin{aligned} \mathcal {F}_{\varvec{h}}: \qquad \qquad \qquad \mathbb F_{q^m}^{\textbf{n}}&\rightarrow \mathbb F_{q^m}^{\varvec{h}\times \textbf{N}} \\ \left( {\textbf{x}}^{(1)}, \ldots , {\textbf{x}}^{(\ell )} \right)&\mapsto \left( \mathcal {F}_{h_{1}}({\textbf{x}}^{(1)}), \ldots , \mathcal {F}_{h_{\ell }}({\textbf{x}}^{(\ell )}) \right) . \end{aligned}$$

Here, vectors of length $n$ are divided into $\ell$ blocks according to the $\ell$-composition $\textbf{n}$ and the vector $\varvec{h}= (h_{1}, \ldots , h_{\ell })$ contains the different folding parameters for the blocks. The corresponding inverse map, i.e. the blockwise unfolding operation, is denoted by $\mathcal {F}_{\varvec{h}}^{-1}$.

Definition 3

(Folded Linearized Reed–Solomon Codes) Consider an LRS code $\mathcal {C} :=\textrm{LRS}[\varvec{\beta },\textbf{a};\textbf{n},k]$ with ${\varvec{\beta }}^{(i)} :=(1, \alpha , \ldots , \alpha ^{n_{i}-1}) \in \mathbb F_{q^m}^{n_{i}}$ for a primitive element $\alpha$ of $\mathbb F_{q^m}$ and all $i = 1, \ldots , \ell$. Choose a vector $\varvec{h}= (h_{1}, \ldots , h_{\ell }) \in \mathbb {N}^{\ell }$ of folding parameters satisfying $h_{i} {{\,\mathrm{|}\,}}n_{i}$ and $N_{i} :=\frac{n_{i}}{h_{i}} \le h_{i}$ for all $1 \le i \le \ell$ and write $\textbf{N}:=(N_{1}, \ldots , N_{\ell })$. The $\varvec{h}$-folded variant of $\mathcal {C}$ is the $\varvec{h}$-folded linearized Reed–Solomon code $\textrm{FLRS}[\alpha , \textbf{a}, \varvec{h}; \textbf{N}, k]$ of length $N:=\sum _{i=1}^{\ell } N_{i}$ and dimension k defined as

The ambient space of this code is $\mathbb F_{q^m}^{\varvec{h}\times \textbf{N}}$ and we can interpret the folded code as vector code of length $N$ over the field $\mathbb F_{q^d}$ with extension degree $d :=m \cdot {{\,\textrm{lcm}\,}}(h_{1}, \ldots , h_{\ell })$ over $\mathbb F_{q}$. However, linearity is only guaranteed with respect to the subfield $\mathbb F_{q^m}$ and due to the $\mathbb F_{q^m}$-linearity of the unfolded LRS code.

To make the above definition more explicit, note that there is a message polynomial for every codeword with

$$\begin{aligned}{} & {} \textbf{C}= \left( \textbf{C}^{(1)}(f), \ldots , \textbf{C}^{(\ell )}(f) \right) \nonumber \\{} & {} \text {and } \textbf{C}^{(i)}(f) :=\begin{pmatrix} {f}(1)_{a_i} &{} {f}(\alpha ^{h_{i}})_{a_i} &{} \cdots &{} {f}(\alpha ^{n_{i}-h_{i}})_{a_i}\\ {f}(\alpha )_{a_i} &{} {f}(\alpha ^{h_{i}+1})_{a_i} &{} \cdots &{} {f}(\alpha ^{n_{i}-h_{i}+1})_{a_i}\\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ {f}(\alpha ^{h_{i}-1})_{a_i} &{} {f}(\alpha ^{2h_{i}-1})_{a_i} &{} \cdots &{} {f}(\alpha ^{n_{i}-1})_{a_i} \end{pmatrix} \in \mathbb F_{q^m}^{h_{i} \times N_{i}} \end{aligned}$$

(3)

for all $i \in \{1, \ldots , \ell \}$.

We can further draw conclusions about the maximum length of FLRS codes, similar to the LRS case. Let us therefore assume that the parameters of the unfolded code are maximal. In other words, choose an LRS code $\mathcal {C}$ in Definition 3 with $\ell = q^{\gcd (u,m)} - 1$ same-sized blocks of length m and resulting overall code length $n= (q^{\gcd (u,m)} - 1) \cdot m$ (see Sect. 2 for the definition of u and the derivation of this statement). Since we want to maximize the length of the folded code, we choose $h_{i}$ for each $i = 1, \ldots , \ell$ as small as possible such that and hold. As all blocks have the same length, we select the same folding parameter h for each block and it has to satisfy $h {{\,\mathrm{|}\,}}m$ and $m \le h^2$. We cannot get any better than $h = \sqrt{m}$ and thus obtain the upper bound on the total length $N$ of FLRS codes.

Remark 1

Note that we only consider a subclass of LRS codes for folding. Namely, we choose the code locators as powers of a primitive element $\alpha \in \mathbb F_{q^m}^{*}$. This turns out to be crucial for the interpolation-based decoder that we present in Sect. 4.

Fig. 1

Illustration of the folding construction for a block $\textbf{c}^{(i)} = (c_1, \ldots , c_{12})$ of an LRS codeword $\textbf{c}= ({\textbf{c}}^{(1)}, \ldots , {\textbf{c}}^{(\ell )})$ using folding parameter $h_i=3$

Theorem 2

(Minimum Distance) Let be an FLRS code and assume without loss of generality that applies. The minimum sum-rank distance of $\mathcal {C}$ is

where $j\in \{1, \dots , \ell \}$ is the unique choice that satisfies

$$\begin{aligned} 0 \le d_{\Sigma R}(\mathcal {C}) - \sum _{i=1}^{j- 1} N_{i} - 1 < N_{j}. \end{aligned}$$

In particular, $\mathcal {C}$ achieves the Singleton-like bound (2) with equality if and only if $h_{j}$ divides both k and for all .

Proof

Let be the nonzero codeword corresponding to the message polynomial . Then there are with $z = \sum _{i=1}^{\ell } z_i$ such that and for . Let us denote by the blockwise-reduced column-echelon form of $\textbf{C}$ which is obtained by bringing each block ${\textbf{C}}^{(i)}$ independently in its reduced column-echelon form with respect to $\mathbb F_{q}$ as follows: first obtain a matrix ${\textbf{C}}^{(i)}_q \in \mathbb F_{q}^{m h_{i} \times n_{i}}$ by replacing each row of the block ${\textbf{C}}^{(i)}$ with its extended matrix that is obtained via $\text {ext}_{\varvec{\gamma }}$ for an arbitrary $\mathbb F_{q}$-basis $\varvec{\gamma }$ of $\mathbb F_{q^m}$. Next, bring ${\textbf{C}}^{(i)}_q$ in reduced column-echelon form (e.g. by Gaussian elimination) and finally apply the inverse operation $\text {ext}^{-1}_{\varvec{\gamma }}$ to the matrix blocks and get back a $(h_{i} \times n_{i})$-matrix over $\mathbb F_{q^m}$. Since $\text {ext}^{-1}_{\varvec{\gamma }}$ preserves the zero columns and ${{\,\textrm{rk}\,}}_q(\textbf{C}^{(i)}) = N_{i} - z_i$, the number of nonzero columns in the i-th block of ${{\,\textrm{RCEF}\,}}(\textbf{C})$ is $N_{i} - z_i$. Thus, the overall number of nonzero entries is certainly upper-bounded by $\sum _{i=1}^{\ell } h_{i} (N_{i} - z_i)$. We further obtain an upper bound on the last result by finding the vector $\textbf{z}= (z_1, \ldots , z_{\ell })$ that realizes

$$\begin{aligned} \max \left\{ \sum _{i=1}^{\ell } h_{i} (N_{i} - z_i): \textbf{N}- \textbf{z}\le \textbf{N}\text { and } N- z = \sum _{i=1}^{\ell } z_i \right\} \end{aligned}$$

for a fixed z. With Lemma 1, the maximum equals $\sum _{i=1}^{y- 1} h_{i} N_{i} + h_{y} \varepsilon$, where $y\in \{1, \ldots , \ell \}$ and $0 \le \varepsilon < N_{y}$ are the unique integers such that $N- z = \sum _{i=1}^{y- 1} N_{i} + \varepsilon$. When we shift the focus to the zero entries of ${{\,\textrm{RCEF}\,}}(\textbf{C})$, we naturally obtain the lower bound $\sum _{i=y}^{\ell } h_{i} N_{i} - h_{y} \varepsilon$ with y and $\varepsilon$ as before, since the number of zero and nonzero entries adds up to $\sum _{i=1}^{\ell } h_{i} N_{i}$.

Note that the $\mathbb F_{q^m}$-semilinearity of the generalized operator evaluation ensures that for each $1 \le i \le \ell$ the entries of the i-th block of ${{\,\textrm{RCEF}\,}}(\textbf{C})$ are still $\mathbb F_{q}$-linearly independent and can be expressed as evaluations of f with respect to the evaluation parameter $a_i$. Since the number of $\mathbb F_{q}$-linearly independent roots of f with respect to evaluation parameters from distinct nontrivial conjugacy classes is bounded by its degree and $\deg (f) \le k - 1$, we get

$$\begin{aligned} \sum _{i=y}^{\ell } h_{i} N_{i} - h_{y} \varepsilon \le k - 1 \quad \begin{gathered} \text {for } y\in \{1, \ldots , \ell \}, \varepsilon \in \{0, \ldots , N_{y} - 1\} \\ \text {unique with } N- z = \sum \nolimits _{i=1}^{y- 1} N_{i} + \varepsilon . \end{gathered} \end{aligned}$$

(4)

On the other hand, the Singleton-like bound for $\mathbb F_{q}$-linear sum-rank-metric codes (see Theorem 1) yields

$$\begin{aligned} k \le \sum _{i = j}^{\ell } h_{i} N_{i} - h_{j} \lambda \quad \begin{gathered} \text {for } j\in \{1, \ldots , \ell \}, \lambda \in \{0, \ldots , N_{j} - 1\} \\ \text {unique with } d_{\Sigma R}(\mathcal {C}) - 1 = \sum \nolimits _{i=1}^{j- 1} N_{i} + \lambda . \end{gathered} \end{aligned}$$

(5)

As we can choose a minimum-weight codeword $\textbf{C}$ in the above reasoning, we can replace $N- z$ by $d_{\Sigma R}(\mathcal {C})$ in (4). But then there are only two possibilities for the relationship between the indices $y$ and $j$ and the parameters $\varepsilon$ and $\lambda$. Namely,

• 1. $j= y$,      $\varepsilon \in \{1, \ldots , N_{y} - 1\}$, and  $\lambda = \varepsilon - 1$ or

• 2. $j= y- 1$,  $\varepsilon = 0$, and $\lambda = N_{y- 1} - 1$.

Let us focus on the first case. We get

$$\begin{aligned} \sum _{i=y}^{\ell } h_{i} N_{i} - h_{y} \left( d_{\Sigma R}(\mathcal {C}) - \sum _{i=1}^{y- 1} N_{i} \right) + 1 \le k \end{aligned}$$

(6)

by substituting $\varepsilon$ for the equality condition in (4). We then shift the first summand $h_{y} N_{y}$ of the first sum into the second sum, do some transformations, and finally use the integrality of the left-hand side as well as the fact for any real number x to obtain

(7)

Similarly, substituting $\lambda$ for the equality condition in (5) yields

(8)

As $j= y$ holds, the right-hand side of (7) is less than or equal to the left-hand side of (8). But since the left-hand side of (7) and the right-hand side of (8) are equal, all inequalities in the chain must be equalities and we get

(9)

where $j\in \{1, \ldots , \ell \}$ is unique with $0 \le d_{\Sigma R}(\mathcal {C}) - \sum \nolimits _{i=1}^{j- 1} N_{i} - 1 < N_{j}$.

Let us move on to the second case and recall that $\varepsilon = 0$. Therefore, we can replace the factor $h_{y}$ of $\varepsilon$ (i.e. of $d_{\Sigma R}(\mathcal {C}) - \sum _{i=1}^{y- 1} N_{i}$) in (6) with $h_{y- 1}$. Similar transformations as above and again the integrality of the left-hand side yield

(10)

Since we have $j= y- 1$ in this case, the right-hand side of (10) is less than or equal to the left-hand side of (8). But, as in the first case, the left-hand side of (10) and the right-hand side of (8) are equal. Hence, the inequalities are in fact equalities and we obtain (9).

The Singleton-like bound is met if and only if $h_{y}$ divides $k - \sum _{i=y+ 1}^{\ell } h_{i} N_{i}$, which is equivalent to $h_{y}$ dividing k as well as $h_{i} N_{i}$ for each $i = 1, \ldots , \ell$. This concludes the proof. $\square$

Remark 2

Theorem 2 needs an FLRS code to satisfy $h_{1} \ge \cdots \ge h_{\ell }$ for technical reasons. However, this is not a restriction since we can simply reorder the blocks of a sum-rank-metric code without changing its weight distribution or its minimum distance. Formally speaking, we choose a permutation $\pi$ from the symmetric group $\mathcal {S}_{\ell }$ for which $h_{\pi ^{-1}(1)} \ge \cdots \ge h_{\pi ^{-1}(\ell )}$ holds and consider

$$\begin{aligned} \tilde{\mathcal {C}} = \{ ({\textbf{C}}^{(\pi ^{-1}(1))}, \ldots , {\textbf{C}}^{(\pi ^{-1}(\ell ))}): ({\textbf{C}}^{(1)}, \ldots , {\textbf{C}}^{(\ell )}) \in \mathcal {C} \}. \end{aligned}$$

4 Interpolation-based decoding of folded linearized Reed–Solomon codes

In this section we derive an interpolation-based decoder for FLRS codes that is based on the Guruswami–Rudra decoder for folded Reed–Solomon (FRS) codes [19] and the Mahdavifahr–Vardy decoder for folded Gabidulin codes [29]. As channel model we consider an additive sum-rank channel that relates the input $\textbf{C}\in \mathbb F_{q}^{\varvec{h}\times \textbf{N}}$ to the received output $\textbf{R}\in \mathbb F_{q^m}^{\varvec{h}\times \textbf{N}}$ by adding an error $\textbf{E}\in \mathbb F_{q^m}^{\varvec{h}\times \textbf{N}}$, that is $\textbf{R}= \textbf{C}+ \textbf{E}$. The addition in $\mathbb F_{q^m}^{\varvec{h}\times \textbf{N}}$ is performed componentwise.

We denote the sum-rank weight of the error $\textbf{E}= ({\textbf{E}}^{(1)}, \ldots , {\textbf{E}}^{(\ell )}) \in \mathbb F_{q^m}^{\varvec{h}\times \textbf{N}}$ by ${{\,\textrm{wt}\,}}_{\Sigma R}(\textbf{E}) = t$ and its weight decomposition by ${\textbf{t}}= (t_1, \ldots , t_{\ell })$ with $t_i = {{\,\textrm{rk}\,}}_{q} ({\textbf{E}}^{(i)})$ for all $i = 1, \ldots , \ell$. $\textbf{E}$ is chosen uniformly at random from the set of all tuples in $\mathbb F_{q^m}^{\varvec{h}\times \textbf{N}}$ having a fixed weight t as well as a weight decomposition belonging to a prescribed set of decompositions.

Suppose we transmit a codeword $\textbf{C}\in \textrm{FLRS}[\alpha , \textbf{a}, \varvec{h}; \textbf{N}, k]$ and we receive the word $\textbf{R}= ({\textbf{R}}^{(1)}, \ldots , {\textbf{R}}^{(\ell )})$ with

$$\begin{aligned} {\textbf{R}}^{(i)} = \begin{pmatrix} r_1^{(i)} &{} r_{h_{i}+1}^{(i)} &{} \cdots &{} r_{n_{i}-h_{i}+1}^{(i)}\\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ r_{h_{i}}^{(i)} &{} r_{2h_{i}}^{(i)} &{} \cdots &{} r_{n_{i}}^{(i)} \end{pmatrix} \in \mathbb F_{q^m}^{h_{i} \times N_{i}} \quad \text {for all } i \in \{1, \ldots , \ell \}. \end{aligned}$$

(11)

Note that the decodability of a specific error will in general depend on its weight decomposition and not only on the chosen code, the error weight t, and the decoder’s parameters (see Theorem 3). When we consider codes using the same folding parameter $h\in \mathbb {N}^{*}$ for all blocks, only the error weight t decides if an error is decodable for the chosen code and decoder.

As is typical for interpolation-based decoding, our decoder consists of two steps that we will describe in the following: interpolation and root finding. In the first phase, we construct interpolation points from the received word $\textbf{R}$ and obtain a multivariate skew polynomial Q that satisfies certain conditions. In the second phase, we use the interpolation polynomial Q to find candidates for the message polynomial and hence for the transmitted codeword.

4.1 Interpolation step

We first choose an interpolation parameter $s\in \mathbb {N}^{*}$ satisfying

$$\begin{aligned} s\le \min _{i \in \{1, \ldots , \ell \}} h_{i}, \end{aligned}$$

(12)

where the constraint arises from the selection method of the interpolation points. The latter are elements of $\mathbb F_{q^m}^{s+ 1}$ whose last $s$ entries are obtained from the received word $\textbf{R}$ using a sliding-window approach. Namely, we place a window of size $s\times 1$ on the top left corner of $\textbf{R}$ and slide it down one position at a time as long as each position of the window covers an entry of $\textbf{R}$. Then the window is moved to the next column, starting the same process again from the top. The first entry of an interpolation point obtained in this way is the code locator corresponding to the window’s starting position, that is a power of the primitive element $\alpha$.

Formally speaking, we consider for each $i = 1, \ldots , \ell$ the two sets

$$\begin{aligned} \begin{aligned} \mathcal {W}_i&:=\left\{ (j-1) h_{i} + l: j \in \{1, \ldots , N_{i}\}, l \in \{1, \ldots , h_{i} - s+ 1\} \right\} \\ \text {and} \quad \mathcal {P}_i&:=\left\{ \left( \alpha ^{w-1}, r_{w}^{(i)}, r_{w+1}^{(i)}, \ldots , r_{w+s-1}^{(i)} \right) : w \in \mathcal {W}_i \right\} , \end{aligned} \end{aligned}$$

(13)

where $\mathcal {P}_i$ contains all interpolation points corresponding to the i-th block ${\textbf{R}}^{(i)}$ of $\textbf{R}$. The index set $\mathcal {W}_i$ consists of all eligible starting positions for the sliding window within ${\textbf{R}}^{(i)}$ and each interpolation point can be naturally identified with a tuple (w, i) with $w \in \mathcal {W}_i$ and $i \in \{1, \ldots , \ell \}$. Note that, by construction, the set of all interpolation points $\mathcal {P} :=\bigcup _{i=1}^{\ell } \mathcal {P}_i$ has cardinality

$$\begin{aligned} \vert \mathcal {P} \vert = \sum _{i=1}^{\ell } N_{i} (h_{i} - s + 1). \end{aligned}$$

Example 1

Consider an FLRS code with folding parameters $\varvec{h}= (3, 2)$ and folded block lengths $\textbf{N}= (2, 2)$. Choose $s= 2$ and denote $\textbf{R}$ according to (11), i.e.

$$\begin{aligned} \textbf{R}= \left( \begin{pmatrix} r_1^{(1)} &{} r_4^{(1)} \\ r_2^{(1)} &{} r_5^{(1)} \\ r_3^{(1)} &{} r_6^{(1)} \end{pmatrix}, \begin{pmatrix} r_1^{(2)} &{} r_3^{(2)} \\ r_2^{(2)} &{} r_4^{(2)} \end{pmatrix} \right) . \end{aligned}$$

Then the set of interpolation points is the union of

$$\begin{aligned} \mathcal {P}_1&= \Big \{ (1, r_1^{(1)}, r_2^{(1)}), (\alpha , r_2^{(1)}, r_3^{(1)}), (\alpha ^3, r_4^{(1)}, r_5^{(1)}), (\alpha ^4, r_5^{(1)}, r_6^{(1)}) \Big \}\\ \text {and} \quad \mathcal {P}_2&= \Big \{ (1, r_1^{(2)}, r_2^{(2)}), (\alpha ^2, r_3^{(2)}, r_4^{(2)}) \Big \}. \end{aligned}$$

We wish to find a multivariate skew interpolation polynomial Q that satisfies certain interpolation constraints and has the form

$$\begin{aligned} Q(x, y_1, \ldots , y_{s}) = Q_0(x) + Q_1(x) y_1 + \cdots + Q_{s}(x) y_{s}, \end{aligned}$$

(14)

where $Q_r(x) \in \mathbb F_{q^m}[x;\sigma ,\delta ]$ for all $r \in \{0, \ldots , s\}$. The generalized operator evaluation of such a polynomial $Q \in \mathbb F_{q^m}[x,y_1,\dots ,y_s;\sigma ,\delta ]$ at a given interpolation point $\textbf{p}= (p_0, \ldots , p_{s}) \in \mathbb F_{q^m}^{s+ 1}$ with respect to an evaluation parameter $a \in \mathbb F_{q^m}$ is defined as

$$\begin{aligned} \mathscr {E}_{Q}(\textbf{p})_{a} :={Q_0}(p_0)_{a} + {Q_1}(p_1)_{a} + \cdots + {Q_s}(p_{s})_{a}. \end{aligned}$$

Problem 1

(Interpolation Problem) Let a parameter $D\in \mathbb {N}^{*}$, a set $\mathcal {P} = \bigcup _{i=1}^{\ell } \mathcal {P}_i$ of interpolation points and evaluation parameters $a_1, \ldots , a_{\ell }$ be given. Find a nonzero $(s+1)$-variate skew polynomial Q of the form (14) satisfying

• 1. $\mathscr {E}_{Q}(\textbf{p})_{a_i} = 0$ for all $\textbf{p}\in \mathcal {P}_i$ and $i \in \{1, \ldots , \ell \}$ as well as

• 2. $\deg (Q_0) < D$ and $\deg (Q_r) < D - k + 1$ for all $r \in \{1, \ldots , s\}$.

Note that the evaluation parameters $a_1, \ldots , a_{\ell }$ are the entries of $\textbf{a}$ of the considered FLRS code $\textrm{FLRS}[\alpha , \textbf{a}, \varvec{h}; \textbf{N}, k]$.

Problem 1 can be solved using skew Kötter interpolation from [26] (similar as in [7, Sec. V]) requiring at most $\mathcal {O}({sn^2})$ operations in $\mathbb F_{q^m}$ in the zero-derivation case. There exist fast interpolation algorithms [4, 5] that can solve Problem 1 requiring at most $\widetilde{\mathcal {O}}\mathopen {}\left( s^\omega \mathcal {M}(n)\right) \mathclose {}$ operations in $\mathbb F_{q^m}$ in the zero-derivation case, where $\widetilde{\mathcal {O}}\mathopen {}\left( \cdot \right) \mathclose {}$ denotes the soft-O notation (which neglects log factors), $\mathcal {M}(n)\in \mathcal {O}({n^{1.635}})$ is the cost of multiplying two skew-polynomials of degree at most n and $\omega < 2.37286$ is the matrix multiplication exponent [24].

Since the second condition of the interpolation problem allows us to write

$$\begin{aligned} Q_0(x) = \sum _{j=0}^{D-1} q_{0, j} x^j \quad \text {and} \quad Q_r(x) = \sum _{j=0}^{D-k} q_{r, j} x^j \quad \text {for} \quad r \in \{1, \ldots , s\} \end{aligned}$$

(15)

with all coefficients from $\mathbb F_{q^m}$, we can also solve Problem 1 by solving a system of $\mathbb F_{q^m}$-linear equations whose coefficient matrix describes the first condition of the interpolation problem. We collect all interpolation points from $\mathcal {P}_i$ as rows in a matrix $\textbf{P}_i \in \mathbb F_{q^m}^{N_{i}(h_{i} - s+ 1) \times (s+ 1)}$ for each $1 \le i \le \ell$ and denote its columns by $\textbf{p}_{i, 0}, \ldots , \textbf{p}_{i, s}$. Define further $\textbf{p}_r = (\textbf{p}_{1, r}^{\top } \ | \ \cdots \ | \ \textbf{p}_{\ell , r}^{\top })$ for $0 \le r \le s$. Then, Problem 1 can be written as

$$\begin{aligned}{} & {} \textbf{S}\textbf{q}_I^{\top } = \textbf{0 }\\{} & {} \text {with} \quad \textbf{S}= \left( \begin{array}{c|c|c|c} \left( \mathfrak {M}_{D}(\textbf{p}_0)_{\textbf{a}}\right) ^{\top }&\left( \mathfrak {M}_{D-k+1}(\textbf{p}_1)_{\textbf{a}}\right) ^{\top }&\cdots&\left( \mathfrak {M}_{D-k+1}(\textbf{p}_s)_{\textbf{a}}\right) ^{\top } \end{array} \right) \nonumber \\{} & {} \text {and} \quad \textbf{q}_I = \left( q_{0, 0} \cdots q_{0, D-1} \ | \ q_{1, 0} \cdots q_{1, D-k} \ | \ \cdots \ | \ q_{s, 0} \cdots q_{s, D-k} \right) . \nonumber \end{aligned}$$

(16)

Example 2

Let us continue Example 1 with $k = 2$ and derive the corresponding interpolation matrix for the choice $D= 3$. As we will see shortly in Lemma 2, this choice guarantees the existence of a nonzero solution of (16). We get

$$\begin{aligned} \textbf{P}_1 = \begin{pmatrix} 1 &{} r_1^{(1)} &{} r_2^{(1)} \\ \alpha &{} r_2^{(1)} &{} r_3^{(1)} \\ \alpha ^3 &{} r_4^{(1)} &{} r_5^{(1)} \\ \alpha ^4 &{} r_5^{(1)} &{} r_6^{(1)} \end{pmatrix} \qquad \text { and } \qquad \textbf{P}_2 = \begin{pmatrix} 1 &{} r_1^{(2)} &{} r_2^{(2)} \\ \alpha ^2 &{} r_3^{(2)} &{} r_4^{(2)} \\ \end{pmatrix} \end{aligned}$$

and hence the interpolation matrix $\textbf{S}$ is given by

$$\begin{aligned} \left( \begin{array}{c|c|c} \mathfrak {M}_{3}(\textbf{p}_0)_{\textbf{a}}^{\top }&\mathfrak {M}_{2}(\textbf{p}_1)_{\textbf{a}}^{\top }&\mathfrak {M}_{2}(\textbf{p}_2)_{\textbf{a}}^{\top } \end{array} \right) = \left( \begin{array}{c|c|c} \mathfrak {m}_{3}(\textbf{p}_{1, 0})_{a_1}^{\top } &{} \mathfrak {m}_{2}(\textbf{p}_{1, 1})_{a_1}^{\top } &{} \mathfrak {m}_{2}(\textbf{p}_{1, 2})_{a_1}^{\top }\\ \mathfrak {m}_{3}(\textbf{p}_{2, 0})_{a_2}^{\top } &{} \mathfrak {m}_{2}(\textbf{p}_{2, 1})_{a_2}^{\top } &{} \mathfrak {m}_{2}(\textbf{p}_{2, 2})_{a_2}^{\top } \end{array} \right) ,\\ \text {i.e.} \quad \textbf{S}= \left( \begin{array}{ccc|cc|cc} 1 &{} \mathcal {D}_{a_1}(1) &{} \mathcal {D}_{a_1}^{2}(1) &{} r_1^{(1)} &{} \mathcal {D}_{a_1}(r_1^{(1)}) &{} r_2^{(1)} &{} \mathcal {D}_{a_1}(r_2^{(1)})\\ \alpha &{} \mathcal {D}_{a_1}(\alpha ) &{} \mathcal {D}_{a_1}^{2}(\alpha ) &{} r_2^{(1)} &{} \mathcal {D}_{a_1}(r_2^{(1)}) &{} r_3^{(1)} &{} \mathcal {D}_{a_1}(r_3^{(1)})\\ \alpha ^3 &{} \mathcal {D}_{a_1}(\alpha ^3) &{} \mathcal {D}_{a_1}^{2}(\alpha ^3) &{} r_4^{(1)} &{} \mathcal {D}_{a_1}(r_4^{(1)}) &{} r_5^{(1)} &{} \mathcal {D}_{a_1}(r_5^{(1)})\\ \alpha ^4 &{} \mathcal {D}_{a_1}(\alpha ^4) &{} \mathcal {D}_{a_1}^{2}(\alpha ^4) &{} r_5^{(1)} &{} \mathcal {D}_{a_1}(r_5^{(1)}) &{} r_6^{(1)} &{} \mathcal {D}_{a_1}(r_6^{(1)})\\ \hline 1 &{} \mathcal {D}_{a_2}(1) &{} \mathcal {D}_{a_2}^{2}(1) &{} r_1^{(2)} &{} \mathcal {D}_{a_2}(r_1^{(2)}) &{} r_2^{(2)} &{} \mathcal {D}_{a_2}(r_2^{(2)})\\ \alpha ^2 &{} \mathcal {D}_{a_2}(\alpha ^2) &{} \mathcal {D}_{a_2}^{2}(\alpha ^2) &{} r_3^{(2)} &{} \mathcal {D}_{a_2}(r_3^{(2)}) &{} r_4^{(2)} &{} \mathcal {D}_{a_2}(r_4^{(2)}) \end{array} \right) . \end{aligned}$$

Lemma 2

(Existence) A nonzero solution to Problem 1 exists if

(17)

Proof

A nontrivial solution of (16) exists if less equations than unknowns are involved. The number of equations corresponds to the number of interpolation points and hence the condition on the existence of a nonzero solution reads as follows:

$$\begin{aligned} \sum _{i=1}^{\ell } N_{i} (h_{i} - s + 1)&< D(s+ 1) - s(k - 1) \nonumber \\ \iff D&\ge \frac{\sum _{i=1}^{\ell } N_{i} (h_{i} - s + 1) + s(k - 1) + 1}{s+ 1}. \end{aligned}$$

(18)

Since $D$ is integral, the statement follows. $\square$

If the same folding parameter is used for each block, that is if there is a $h \in \mathbb {N}^{*}$ such that $h= h_{i}$ holds for all $1 \le i \le \ell$, this reduces to

which coincides with [20, Lemma 2]. Note that this is still true for different numbers of columns $N_{1}, \ldots , N_{\ell }$.

Lemma 3

(Roots of Polynomial) Define the univariate skew polynomial

$$\begin{aligned} \begin{aligned} P(x)&:=Q_0(x)+Q_1(x)f(x)+Q_2(x)f(x)\alpha +\cdots +Q_s(x)f(x)\alpha ^{s- 1} \\&= Q(x, f(x), f(x)\alpha , \ldots , f(x)\alpha ^{s-1}) \in \mathbb F_{q^m}[x;\sigma ,\delta ]\end{aligned} \end{aligned}$$

(19)

and write $t_i :={{\,\textrm{rk}\,}}_q(\varvec{E}^{(i)})$ for $1 \le i \le \ell$. Then there exist $\mathbb F_{q}$-linearly independent elements $\zeta _1^{(i)}, \ldots , \zeta _{(N_{i} - t_i)(h_{i} - s+ 1)}^{(i)} \in \mathbb F_{q^m}$ for each $i \in \{1, \ldots , \ell \}$ such that ${P}(\zeta _j^{(i)})_{a_i} = 0$ for all $1 \le i \le \ell$ and all $1 \le j \le (N_{i} - t_i) (h_{i} - s+ 1)$.

Proof

Since ${{\,\textrm{rk}\,}}_q(\varvec{E}^{(i)}) = t_i$, there exists a nonsingular matrix $\varvec{T}_i \in \mathbb F_{q}^{N_{i} \times N_{i}}$ such that $\varvec{E}^{(i)}\varvec{T}_i$ has only $t_i$ nonzero columns for every $i \in \{1, \ldots , \ell \}$. Without loss of generality assume that these columns are the last ones of $\varvec{E}^{(i)}\varvec{T}_i$ and define $\varvec{\zeta }^{(i)} = \textbf{L}\cdot \varvec{T}_i$ with $\textbf{L}\in \mathbb F_{q^m}^{h_{i} \times N_{i}}$ containing the code locators $1, \ldots , \alpha ^{n_{i}-1}$ (cp. (3)). Note that the first $N_{i} - t_i$ columns of $\textbf{R}^{(i)} \varvec{T}_i = \textbf{C}^{(i)}\varvec{T}_i + \textbf{E}^{(i)}\varvec{T}_i$ are noncorrupted leading to $(N_{i} - t_i)(h_{i} - s+ 1)$ noncorrupted interpolation points according to (13). Now, for each $1 \le i \le \ell$, the first entries of the $(N_{i} - t_i)(h_{i} - s+ 1)$ noncorrupted interpolation points (i.e. the top left submatrix of size $(N_{i} - t_i) \times (h_{i} - s+ 1)$ of $\varvec{\zeta }^{(i)}$) are by construction both $\mathbb F_{q}$-linearly independent and roots of P(x). $\square$

Theorem 3

(Decoding Radius) Let $Q(x,y_1,\ldots ,y_s)$ be a nonzero solution of Problem 1. If the error-weight decomposition ${\textbf{t}}= (t_1, \ldots , t_{\ell })$ satisfies

$$\begin{aligned} \sum _{i=1}^{\ell } t_i (h_{i} - s+ 1) < \frac{s}{s+1} \left( \sum _{i=1}^{\ell } N_{i} (h_{i} - s + 1) - k + 1 \right) , \end{aligned}$$

(20)

then $P \in \mathbb F_{q^m}[x;\sigma ,\delta ]$ defined in (19) is the zero polynomial, that is for all $x \in \mathbb F_{q^m}$

$$\begin{aligned} P(x)=Q_0(x)+Q_1(x)f(x)+\!\cdots \!+Q_s(x)f(x)\alpha ^{s-1}=0. \end{aligned}$$

(21)

Proof

By Lemma 3, there exist elements $\zeta _1^{(i)}, \ldots , \zeta _{(N_{i} - t_i)(h_{i} - s+ 1)}^{(i)}$ in $\mathbb F_{q^m}$ that are $\mathbb F_{q}$-linearly independent for each $i \in \{1, \ldots , \ell \}$ such that ${P}(\zeta _j^{(i)})_{a_i} = 0$ for $1 \le i \le \ell$ and $1 \le j \le (N_{i} - t_i)(h_{i} - s+ 1)$. By choosing

$$\begin{aligned} D\le \sum _{i=1}^{\ell } (N_{i} - t_i)(h_{i} - s+ 1), \end{aligned}$$

(22)

P(x) exceeds the degree bound from [13, Prop. 1.3.7] which is possible only if $P(x)=0$. Together with inequality (18), we get

$$\begin{aligned}&\frac{\sum _{i=1}^{\ell } N_{i} (h_{i} - s + 1) + s(k - 1)}{s+ 1}< D\le \sum _{i=1}^{\ell } (N_{i} - t_i)(h_{i} - s+ 1)\\&\iff \sum _{i=1}^{\ell } N_{i} (h_{i} - s + 1) + s(k - 1)< (s+ 1) \sum _{i=1}^{\ell } (N_{i} - t_i)(h_{i} - s+ 1)\\&\iff \sum _{i=1}^{\ell } t_i (h_{i} - s+ 1) < \frac{s}{s+1} \left( \sum _{i=1}^{\ell } N_{i} (h_{i} - s + 1) - k + 1 \right) . \end{aligned}$$

$\square$

Note that the left-hand side equals the number of erroneous interpolation points. Intuitively speaking, a rank error in a block with many rows is worse than one in a block with a small folding parameter because it creates more corrupted interpolation points. This is due to the fact that we can interpret a rank error in the i-th block as a symbol error over the extension field $\mathbb F_{q^{h_{i}}}$ corresponding to $h_{i}$ $\mathbb F_{q}$-errors.

Even though Theorem 3 describes the admissible decoding radius, the derived condition does not only depend on the sum-rank weight t of the error but also on its weight decomposition ${\textbf{t}}= (t_1, \ldots , t_{\ell })$. If we focus on the simpler special case of using the same folding parameter $h \in \mathbb {N}^{*}$ for all blocks, formula (20) simplifies to the same inequality as in [20, Thm. 1] that only depends on the error weight t. Namely,

$$\begin{aligned} t < \frac{s}{s+1} \left( \frac{N(h-s+1)-k+1}{h-s+1}\right) . \end{aligned}$$

(23)

This yields the desirable property that we can characterize all decodable errors simply as the ones lying in a sum-rank ball.

In this case, we derive the normalized decoding radius $\tau :=\frac{t}{N}$ from (23) as

$$\begin{aligned} \begin{aligned} \tau = \frac{t}{N}&< \frac{s}{s+1} \left( \frac{N(h- s+ 1) - k + 1}{N(h- s+ 1)} \right) \\&= \frac{s}{s+1} \left( 1 - \frac{hR - \frac{1}{N}}{h- s+ 1} \right) \xrightarrow {N\rightarrow \infty } \frac{s}{s+1} \left( 1 - \frac{h}{h- s+ 1} R \right) \end{aligned} \end{aligned}$$

(24)

where $R :=\frac{k}{hN}$ denotes the code rate.

In the more general case, we can imagine the set of decodable error patterns as a sum-rank ball with some additional bulges. We can derive from (24) that all errors with sum-rank weight t satisfying

$$\begin{aligned} t < \frac{s}{s+1} \frac{\sum _{i=1}^{\ell } N_{i} (h_{i} - s + 1) - k + 1}{h_{max} - s+ 1} \end{aligned}$$

(25)

for $h_{max} :=\max _{i \in \{1, \ldots , \ell \}} h_{i}$ can be decoded for sure. This corresponds to the ball. On the other hand, the buldges represent specific decodable error-weight decompositions having larger sum-rank weight. However, the worst-case bound

$$\begin{aligned} t < \frac{s}{s+1} \frac{\sum _{i=1}^{\ell } N_{i} (h_{i} - s + 1) - k + 1}{h_{min} - s+ 1} \end{aligned}$$

(26)

with $h_{min} :=\min _{i \in \{1, \ldots , \ell \}} h_{i}$ shows that the code can definitely not correct error patterns of weight t exceeding its right-hand side. Table contains some examples for codes and the error patterns they can decode.

Table 1 Decodable error-weight decompositions for codes of dimension $k = 2$ and decoder parameter $s= 2$

4.2 Root-finding step

By Theorem 3, the message polynomial $f \in \mathbb F_{q^m}[x;\sigma ,\delta ]_{<k}$ satisfies (21) if (20) holds for the error-weight decomposition ${\textbf{t}}= (t_1, \ldots , t_{\ell })$. Therefore, we consider the following root-finding problem.

Problem 2

(Root-Finding Problem) Let $Q \in \mathbb F_{q^m}[x,y_1,\dots ,y_s;\sigma ,\delta ]$ be a nonzero solution of Problem 1 and let the error-weight decomposition ${\textbf{t}}= (t_1, \ldots , t_{\ell })$ satisfy constraint (20). Find all skew polynomials $f \in \mathbb F_{q^m}[x;\sigma ,\delta ]_{<k}$ for which (21) applies.

Condition (21) is equivalent to all coefficients of the polynomial on the left-hand side of (21) being zero. Multiple application of $\sigma ^{-1}$ to the equations resulting from the coefficients allows to express Problem 2 as an $\mathbb F_{q^m}$-linear system of equations in the unknown

$$\begin{aligned} \textbf{f}:=(f_0, \sigma ^{-1}(f_1), \ldots , \sigma ^{-k+1}(f_{k-1}))^{\top }. \end{aligned}$$

As e.g. in [6, 37], we use a basis of the interpolation problem’s solution space instead of choosing only one solution Q of system (16). This improvement is justified by the following result.

Lemma 4

(Number of Interpolation Solutions) For $d_I :=\dim _{q^m} (\ker (\textbf{S}))$ with $\textbf{S}$ defined in (16), it holds

$$\begin{aligned} d_I \ge s(D- k + 1) - \sum _{i=1}^{\ell } t_i (h_{i} - s+ 1). \end{aligned}$$

Proof

The first $D$ columns of $\textbf{S}$ are given as $\left( \mathfrak {M}_{D}(\textbf{p}_0)_{\textbf{a}}\right) ^{\top }$. Since the $\ell$ blocks of $\textbf{p}_0$ consist of pairwise distinct powers of $\alpha$, the elements of a single block are $\mathbb F_{q}$-linearly independent. Hence ${{\,\textrm{rk}\,}}_{q^m}\left( \mathfrak {M}_{D}(\textbf{p}_0)_{\textbf{a}}\right) = \min (D, \sum _{i=1}^{\ell } N_{i} (h_{i} - s+ 1)) = D$, where the last equality follows from equation (22). In the absence of an error, the remaining columns consist of linear combinations of the first $D$ ones and do not increase the rank. If an error $\textbf{E}$ with ${{\,\textrm{wt}\,}}_{\Sigma R}(\textbf{E}) = t$ is introduced, at most $\sum _{i=1}^{\ell } t_i (h_{i} - s+ 1)$ interpolation points are corrupted according to Lemma 3. As a consequence, these columns can increase the rank of $\textbf{S}$ by at most $\sum _{i=1}^{\ell } t_i (h_{i} - s+ 1)$. Thus, ${{\,\textrm{rk}\,}}_{q^m}(\textbf{S}) \le D+ \sum _{i=1}^{\ell } t_i (h_{i} - s+ 1)$ and the rank-nullity theorem directly yields

$$\begin{aligned} d_I&:=\dim _{q^m} (\ker (\textbf{S})) = D(s+ 1) - s(k-1) - {{\,\textrm{rk}\,}}_{q^m}(\textbf{S}) \\&\ge D(s+ 1) - s(k-1) - \left( D+ \sum _{i=1}^{\ell } t_i (h_{i} - s+ 1) \right) \\&= s(D- k + 1) - \sum _{i=1}^{\ell } t_i (h_{i} - s+ 1). \end{aligned}$$

$\square$

Again we get a simpler bound when we consider the same folding parameter $h \in \mathbb {N}^{*}$ for each block (cp. [20, Lemma 4]):

$$\begin{aligned} d_I \ge s(D- k + 1) - t (h- s+ 1). \end{aligned}$$

Let now $Q^{(1)}, \ldots , Q^{(d_I)} \in \mathbb F_{q^m}[x,y_1,\dots ,y_s;\sigma ,\delta ]$ form a basis of the solution space of Problem 1 and denote the coefficients of $Q^{(u)}$ by $q_{i,j}^{(u)}$ for all $1 \le u \le d_I$ (cp. (15)). In other words, we write for all $u \in \{1, \ldots , d_I\}$

$$\begin{aligned} Q^{(u)}(x, y_1, \ldots , y_\ell ) = \sum _{j=0}^{D-1} q_{0, j}^{(u)} x^j + \Bigg ( \sum _{j=0}^{D-k} q_{1, j}^{(u)} x^j \Bigg )y_1 + \ldots + \Bigg ( \sum _{j=0}^{D-k} q_{s, j}^{(u)} x^j \Bigg )y_s. \end{aligned}$$

Define further the ordinary polynomials

$$\begin{aligned} B_j^{(u)}(x) = q_{1, j}^{(u)} + q_{2, j}^{(u)} x + \cdots + q_{s, j}^{(u)} x^{s-1} \in \mathbb F_{q^m}[x]\end{aligned}$$

(27)

for $j \in \{0, \ldots , D-k\}$ and $u \in \{1, \ldots , d_I\}$ as well as the additional notations

$$\begin{aligned} \textbf{b}_{j,a}&= \left( \sigma ^{-a}\left( B_j^{(1)}(\sigma ^{a}(\alpha ))\right) , \ldots , \sigma ^{-a}\left( B_j^{(d_I)}(\sigma ^{a}(\alpha ))\right) \right) ^{\top } \\ \text {and} \qquad \textbf{q}_a&= \left( \sigma ^{-a}\left( q_{0,a}^{(1)}\right) , \ldots , \sigma ^{-a}\left( q_{0,a}^{(d_I)}\right) \right) ^{\top } \end{aligned}$$

for $0 \le j \le D-k$ and $0 \le a \le D-1$. Then the root-finding system is given as

$$\begin{aligned}{} & {} \textbf{B}\cdot \textbf{f}= -\textbf{q}\nonumber \\{} & {} \text {with } \textbf{B}:=\begin{pmatrix} \textbf{b}_{0,0} &{} &{} &{} \\ \textbf{b}_{1,1} &{} \textbf{b}_{0,1} &{} &{} \\ \vdots &{} \textbf{b}_{1,2} &{} \ddots &{} \\ \textbf{b}_{D-k,D-k} &{} \vdots &{} &{} \textbf{b}_{0,k-1} \\ &{} \textbf{b}_{D-k,D-k+1} &{} &{} \textbf{b}_{1,k} \\ &{} &{} \ddots &{} \vdots \\ &{} &{} &{} \textbf{b}_{D-k,D-1} \end{pmatrix} \text { and } \textbf{q}:=\begin{pmatrix} \textbf{q}_0 \\ \vdots \\ \textbf{q}_{D-1} \end{pmatrix}. \end{aligned}$$

(28)

The root-finding system (28) can be solved by back substitution in at most $\mathcal {O}({k^2})$ operations in $\mathbb F_{q^m}$ since we can focus on (at most) k nontrivial equations from different blocks of $d_I$ rows. Observe that the transmitted message polynomial $f \in \mathbb F_{q^m}[x;\sigma ,\delta ]_{<k}$ is always a solution of (28) as long as ${\textbf{t}}= (t_1, \ldots , t_{\ell })$ satisfies the decoding radius in (20).

Example 3

Let us set up the root-finding problem for the FLRS code considered in Example 1 and Example 2. We obtain

$$\begin{aligned} P(x)&= \underbrace{q_{0, 0} + q_{0, 1}x + q_{0, 2}x^2}_{Q_0(x)} + \underbrace{(q_{1, 0} + q_{1, 1}x)(f_0 + f_1 x)}_{Q_1(x)f(x)}\\&\quad + \underbrace{(q_{2,0} + q_{2, 1}x)(f_0\alpha + f_1\sigma (\alpha )x)}_{Q_2(x)f(x)\alpha }\\ \text {with} \quad Q_1(x)f(x)&= q_{1, 0}f_0 + \left( q_{1, 0}f_1 + q_{1, 1}\sigma (f_0) \right) x + q_{1, 1}\sigma (f_1) x^2\\ \text {and} \quad Q_2(x)f(x)\alpha&= q_{2, 0}f_0\alpha + \left( q_{2, 0}f_1\sigma (\alpha ) + q_{2, 1}\sigma (f_0)\sigma (\alpha ) \right) x + q_{2, 1}\sigma (f_1)\sigma ^2(\alpha ) x^2. \end{aligned}$$

Now we define $B_j(x) :=q_{1, j} + q_{2, j}x \in \mathbb F_{q^m}[x]$ for $j \in \{0, 1, 2\}$ and write the coefficients of $P(x) = p_0 + p_1 x + p_2 x^2$ as follows:

$$\begin{aligned} p_0&= q_{0, 0} + f_0(q_{1, 0} + q_{2, 0} \alpha ) = q_{0, 0} + f_0 B_0(\alpha ) \\ p_1&= q_{0, 1} + f_1(q_{1, 0}+ q_{2, 0} \sigma (\alpha )) + \sigma (f_0)(q_{1, 1} + q_{2, 1} \sigma (\alpha )) \\&= q_{0, 1} + f_1 B_0(\sigma (\alpha )) + \sigma (f_0) B_1(\sigma (\alpha )) \\ p_2&= q_{0, 2} + \sigma (f_1)(q_{1, 1} + q_{2, 1} \sigma ^2(\alpha )) = q_{0, 2} + \sigma (f_1) B_1(\sigma ^2(\alpha )) \end{aligned}$$

Because $p_i = 0$ for all $i \in \{0, 1, 2\}$, application of $\sigma ^{-i}$ to the equation belonging to $p_i$ does not change the solution space of the above system of equations. Hence, we can equivalently solve the root-finding system

$$\begin{aligned} \begin{pmatrix} B_0(\alpha ) &{} \\ \sigma ^{-1}\left( B_1(\sigma (\alpha )) \right) &{} \sigma ^{-1}\left( B_0(\sigma (\alpha )) \right) \\ &{} \sigma ^{-2}\left( B_1(\sigma ^2(\alpha )) \right) \\ \end{pmatrix} \cdot \begin{pmatrix} f_0 \\ \sigma ^{-1}(f_1) \end{pmatrix} = - \begin{pmatrix} q_{0, 0} \\ \sigma ^{-1}(q_{0, 1}) \\ \sigma ^{-2}(q_{0, 2}) \end{pmatrix}. \end{aligned}$$

4.3 List and probabilistic unique decoding

The interpolation-based scheme from above is summarized in Algorithm 1 and can be used for list decoding or as a probabilistic unique decoder. In the first case, all solutions of (28) are returned as a list of candidate message polynomials. Note that this list contains all message polynomials corresponding to codewords having sum-rank distance less than the decoding radius from the actually sent codeword. However, there may also be some candidates in the list that lie outside of the sum-rank ball around the sent codeword. In the second case, the decoder returns the unique solution of (28) or declares a decoding failure if there are multiple candidates. Let us investigate the usage of our decoding scheme as list decoder and bound its output size as follows:

Lemma 5

(Worst-Case List Size) The list size is upper bounded by $q^{m(s-1)}$.

Proof

With $d_{RF} :=\dim _{q^m}(\ker (\textbf{B}))$, the list size equals $q^{m \cdot d_{RF}}$ and $d_{RF} = k - {{\,\textrm{rk}\,}}_{q^m}(\textbf{B})$ due to the rank-nullity theorem. Let $\textbf{B}_{\triangle }$ denote the lower triangular matrix consisting of the first $d_I k$ rows of $\textbf{B}$. Then, ${{\,\textrm{rk}\,}}_{q^m}(\textbf{B}) \ge {{\,\textrm{rk}\,}}_{q^m}(\textbf{B}_{\triangle })$ and the latter is lower bounded by the number of nonzero vectors on its diagonal. These vectors are $\textbf{b}_{0,0}, \ldots , \textbf{b}_{0,k-1}$ and we focus on their first components while neglecting application of $\sigma$. Observe that each of them is given as the evaluation of $B_0^{(1)}$ at another conjugate of $\alpha$. Since $B_0^{(1)}$ can have at most $s- 1$ roots, it follows that at most $s- 1$ of the vectors on the diagonal can be zero. Thus, ${{\,\textrm{rk}\,}}_{q^m}(\textbf{B}) \ge k - s+ 1$ and, as a consequence, $d_{RF} \le s- 1$. $\square$

Note that, despite the exponential worst-case list size, an $\mathbb F_{q^m}$-basis of the list can be found in polynomial time. Theorem 4 summarizes the results for list decoding of FLRS codes.

Theorem 4

(List Decoding) Consider an FLRS code $\textrm{FLRS}[\alpha , \textbf{a}, \varvec{h}; \textbf{N}, k]$ and a codeword $\textbf{C}$ that is transmitted over a sum-rank channel. Assume that the error has weight t and that its weight decomposition ${\textbf{t}}= (t_1, \ldots , t_{\ell })$ satisfies

$$\begin{aligned} \sum _{i=1}^{\ell } t_i (h_{i} - s+ 1) < \frac{s}{s+1} \left( \sum _{i=1}^{\ell } N_{i} (h_{i} - s + 1) - k + 1 \right) \end{aligned}$$

for an interpolation parameter $1 \le s\le \min _{i \in \{1, \ldots , \ell \}} h_{i}$. Then, a basis of an at most $(s- 1)$-dimensional $\mathbb F_{q^m}$-vector space that contains candidate message polynomials satisfying (21) can be obtained in at most $\mathcal {O}({sn^2})$ operations in $\mathbb F_{q^m}$.

Recall that the decoding radius can be described by (23) if the same folding parameter $h$ is used for all blocks.

A different concept is probabilistic unique decoding where the decoder either returns a unique solution or declares a failure. In our setting, a failure occurs exactly when the root-finding matrix $\textbf{B}$ is rank-deficient. Similar to [6], we now derive a heuristic upper bound on the probability $\mathbb {P}\left( {{\,\textrm{rk}\,}}_{q^m}(\textbf{B}) < k \right)$.

Lemma 6

(Decoding Failure Probability) Assume that the coefficients of the polynomials $B_0^{(u)}(x) \in \mathbb F_{q^m}[x]$ from (27) for $u \in \{1, \ldots , d_I\}$ are independent and have a uniform distribution among $\mathbb F_{q^m}$. Then it holds that

$$\begin{aligned} \mathbb {P}\left( {{\,\textrm{rk}\,}}_{q^m}(\textbf{B}) < k \right) \lesssim k \cdot \left( \frac{k}{q^m} \right) ^{d_I}, \end{aligned}$$

where $\lesssim$ indicates that the bound is a heuristic approximation.

Proof

Let $\textbf{B}_{\triangle }$ denote the matrix consisting of the first $d_I k$ rows of $\textbf{B}$ as in the proof of Lemma 5. Note that

$$\begin{aligned} \mathbb {P}\left( {{\,\textrm{rk}\,}}_{q^m}(\textbf{B})< k \right) \le \mathbb {P}\left( {{\,\textrm{rk}\,}}_{q^m}(\textbf{B}_{\triangle }) < k \right) \end{aligned}$$

holds and we can focus on finding an upper bound for the right-hand side. As lower triangular matrix, $\textbf{B}_{\triangle }$ has rank k if and only if $\textbf{b}_{0, 0}, \ldots , \textbf{b}_{0, k-1}$ are nonzero. Instead of these vectors, we investigate $\tilde{\textbf{b}}_{0,a} = \left( B_0^{(1)}(\sigma ^{a}(\alpha )), \ldots , B_0^{(d_I)}(\sigma ^{a}(\alpha )) \right) ^{\top }$ for $a \in \{0, \ldots , k-1\}$ because application of $\sigma$ can be neglected. Following ideas from [6, Lemma 8], we can now interpret the vector consisting of the u-th entries of $\tilde{\textbf{b}}_{0,0}, \ldots , \tilde{\textbf{b}}_{0,k-1}$ for each $1 \le u \le d_I$ as a codeword of a Reed–Solomon code $\mathcal {C}_{RS}$ of length k and dimension s. These $d_I$ codewords have a uniform distribution with respect to the codebook of $\mathcal {C}_{RS}$ due to our assumption on the distribution of the polynomial coefficients. Thanks to [16, Eq. (1)], we can approximate the probability that a random codeword has full weight k as

$$\begin{aligned} \frac{|\{ \textbf{c}\in \mathcal {C}_{RS}: {{\,\textrm{wt}\,}}_{H}(\textbf{c}) = k \}|}{|\mathcal {C}_{RS}|} \approx \frac{|\{ \textbf{v}\in \mathbb F_{q^m}^k: {{\,\textrm{wt}\,}}_{H}(\textbf{v}) = k \}|}{|\mathbb F_{q^m}^k|} = \left( 1 - \frac{1}{q^m} \right) ^k. \end{aligned}$$

Let us fix an $a \in \{0, \ldots , k-1\}$ and consider $\tilde{\textbf{b}}_{0,a}$. Then, any full-weight codeword induces a nonzero entry in $\tilde{\textbf{b}}_{0,a}$ and conversely, the probability that one entry of $\tilde{\textbf{b}}_{0,a}$ is zero is upper bounded by

$$\begin{aligned} 1 - \left( 1 - \frac{1}{q^m} \right) ^k < \frac{k}{q^m}, \end{aligned}$$

(29)

where the estimation uses the binomial theorem. Due to our independence assumption for the coefficients of $B_0^{(u)}(x)$ for $u \in \{1, \ldots , d_I\}$, the entries of $\tilde{\textbf{b}}_{0,a}$ are also independent and the probability that the whole vector is zero for a fixed a is bounded by the $d_I$-th power of the right-hand side of (29). Finally, the union bound deals with the probability that at least one vector is zero and yields

$$\begin{aligned} \mathbb {P}\left( \bigcup _{a=0}^{k-1} (\tilde{\textbf{b}}_{0,a} = \textbf{0}) \right) \le \sum _{a=0}^{k-1} \mathbb {P}\left( \tilde{\textbf{b}}_{0,a} = \textbf{0 }\right) \lesssim \sum _{a=0}^{k-1} \left( \frac{k}{q^m} \right) ^{d_I} = k \cdot \left( \frac{k}{q^m} \right) ^{d_I}. \end{aligned}$$

$\square$

Section 4.5 presents results that empirically verify the heuristic upper bound by Monte Carlo simulations. Moreover, further simulations show that the assumption that the coefficients of $B_0^{(u)}(x)$ for $u \in \{1, \ldots , d_I\}$ are uniformly distributed is reasonable.

Let us now introduce a threshold parameter $\mu \in \mathbb {N}^{*}$ and enforce $d_I \ge \mu$ by adapting the proof of Lemma 2 which results in the new degree constraint

(30)

We incorporate this threshold into the results we have shown so far and obtain Theorem 5 which provides a summary for probabilistic unique decoding of FLRS codes.

Theorem 5

(Probabilistic Unique Decoding) For an interpolation parameter $1 \le s\le \min _{i \in \{1, \ldots , \ell \}} h_{i}$ and a dimension threshold $\mu \in \mathbb {N}^{*}$, transmit a codeword $\textbf{C}$ of an FLRS code $\textrm{FLRS}[\alpha , \textbf{a}, \varvec{h}; \textbf{N}, k]$ over a sum-rank channel. Assume that the error weight t has a weight decomposition ${\textbf{t}}= (t_1, \ldots , t_{\ell })$ satisfying

$$\begin{aligned} \sum _{i=1}^{\ell } t_i (h_{i} - s+ 1) \le \frac{s}{s+1} \left( \sum _{i=1}^{\ell } N_{i} (h_{i} - s+ 1) - k + 1 \right) - \frac{\mu }{s+ 1} \end{aligned}$$

(31)

and that the coefficients of the polynomials $B_0^{(u)}(x)$ for $u \in \{1, \ldots , \mu \}$ are independent and uniformly distributed among $\mathbb F_{q^m}$. Then, $\textbf{C}$ can be uniquely recovered with complexity $\mathcal {O}({sn^2})$ in $\mathbb F_{q^m}$ and with an approximate probability of at least

$$\begin{aligned} 1 - k \cdot \left( \frac{k}{q^m} \right) ^{\mu }. \end{aligned}$$

Proof

The decoding radius follows when inequality (18) is replaced by

$$\begin{aligned} \sum _{i=1}^{\ell } N_{i} (h_{i} - s + 1) \le D(s+ 1) - s(k - 1) - \mu \end{aligned}$$

in the proof of Theorem 3. Since the degree constraint (30) enforces $d_I \ge \mu$, the heuristic upper bound on the failure probability from Lemma 6 attains the worst-case value for $d_I = \mu$. The success probability of decoding is hence at least $1 - k \cdot \left( \frac{k}{q^m} \right) ^{\mu }$.

The total complexity of $\mathcal {O}({sn^2})$ follows since at most $\mathcal {O}({sn^2})$ $\mathbb F_{q^m}$-operations are needed to solve the interpolation problem and the solution of the root-finding problem can be computed in $\mathcal {O}({k^2})$ operations. $\square$

For the same folding parameter $h$ for each block, we get the simplified degree constraint

and, as in [20, Thm. 3], the description of the decoding radius reads as

$$\begin{aligned} t \le \frac{s}{s+ 1} \left( \frac{N(h- s+ 1) - k + 1}{h- s+ 1} \right) - \frac{\mu }{(s+ 1)(h- s+ 1)}. \end{aligned}$$

4.4 Improved decoding of high-rate codes

The normalized decoding radius $\tau :=\frac{t}{N}$ of the interpolation-based decoder for codes using the same folding parameter for all blocks, which is given in (24), is positive only for code rates $R < \frac{h- s+ 1}{h}$. This is our motivation to now consider an interpolation-based decoder for FLRS codes that allows to correct sum-rank errors beyond the unique decoding radius for any code rate $R > 0$. The main idea behind this decoder is inspired by Justesen’s decoder for FRS codes [19, Sec. III-B], [10] and the Justesen-like decoder for high-rate folded Gabidulin codes [2, 3, 6]. Compared to the Guruswami–Rudra-like decoder from Sect. 4, the proposed Justesen-like decoder uses additional interpolation points to improve the decoding performance for higher code rates. In particular, we allow the sliding window of size $s+1$ to wrap around to the neighboring symbols (except for the last symbol in each block).

As before we choose an interpolation parameter $s\in \mathbb {N}^{*}$ satisfying (12). Then for each $i = 1, \ldots , \ell$ we get the index set $\mathcal {W}_i^\text {HR}$ and the corresponding interpolation-point set $\mathcal {P}_i^\text {HR}$ as

$$\begin{aligned} \begin{aligned} \mathcal {W}_i^\text {HR} :=&\left\{ (j-1) h_{i} + l: j \in \{1, \ldots , N_{i}-1\}, l \in \{1, \ldots , h_{i}\} \right\} \\ \cup&\left\{ (N_{i}-1) h_{i} + l: l \in \{1, \ldots , h_{i} - s+ 1\} \right\} \\ \text {and} \quad \mathcal {P}_i^\text {HR} :=&\left\{ \left( \alpha ^{w-1}, r_{w}^{(i)}, r_{w+1}^{(i)}, \ldots , r_{w+s-1}^{(i)} \right) : w \in \mathcal {W}_i^\text {HR} \right\} . \end{aligned} \end{aligned}$$

(32)

Remark 3

The additional interpolation points for each block $i = 1, \ldots , \ell$ compared to the Guruswami–Rudra-like decoder can be easily deduced by the equality

$$\begin{aligned} \mathcal {W}_i^\text {HR} = \mathcal {W}_i \cup \left\{ (j-1) h_{i} + l: j \in \{1, \ldots , N_{i} - 1\}, l \in \{h_{i} - s+ 2, \ldots , h_{i}\} \right\} . \end{aligned}$$

Example 4

When we consider the code from Example 1, the interpolation points for the high-rate decoder are

$$\begin{aligned} \mathcal {P}_1^\text {HR} = \mathcal {P}_1 \cup \Big \{ (\alpha ^2, r_3^{(1)}, r_4^{(1)}) \Big \} \qquad \text {and} \qquad \mathcal {P}_2^\text {HR} = \mathcal {P}_2 \cup \Big \{ (\alpha , r_2^{(2)}, r_3^{(2)}) \Big \}. \end{aligned}$$

Problem 3

(High-Rate Interpolation Problem) Solve Problem 1 with the input sets $\mathcal {P}_1^\text {HR}, \ldots , \mathcal {P}_{\ell }^\text {HR}$, where the i-th set is associated to evaluation parameter $a_i$.

Since the interpolation point set $\mathcal {P}^\text {HR} :=\bigcup _{i=1}^{\ell } \mathcal {P}_i^\text {HR}$ contains

$$\begin{aligned} \vert \mathcal {P}^\text {HR} \vert = \sum _{i=1}^{\ell } \left( N_{i}h_{i} - (s- 1)\right) = n- \ell (s- 1) \end{aligned}$$

interpolation points, we get the following condition for the existence of a nonzero solution of the high-rate interpolation problem:

Lemma 7

(Existence) A nonzero solution to Problem 3 exists if

(33)

Proof

Problem 3 forms a homogeneous linear system of $\sum _{i=1}^{\ell } \left( N_{i}h_{i} - (s- 1)\right)$ equations in $D(s+ 1) - s(k - 1)$ unknowns, which has a nontrivial solution if less equations than unknowns are involved. This is satisfied for (33). $\square$

The new choice $\mathcal {P}^{\text {HR}}$ of interpolation points yields at least as many uncorrupted interpolation points as $\mathcal {P}$. Hence, we also get at least as many $\mathbb F_{q}$-linearly independent zeros of the corresponding univariate polynomial P.

Lemma 8

(Roots of Polynomial) Define the univariate skew polynomial

and write $t_i :={{\,\textrm{rk}\,}}_q(\varvec{E}^{(i)})$ for $1 \le i \le \ell$. Then there exist $\mathbb F_{q}$-linearly independent elements $\zeta _1^{(i)}, \ldots , \zeta _{N_{i} h_{i} - (s-1) - t_i(h_{i} + s- 1)}^{(i)} \in \mathbb F_{q^m}$ for each $i \in \{1, \ldots , \ell \}$ such that ${P}(\zeta _j^{(i)})_{a_i} = 0$ for all $1 \le i \le \ell$ and all $1 \le j \le N_{i} h_{i} - (s-1) - t_i(h_{i} + s- 1)$.

Proof

Since ${{\,\textrm{rk}\,}}_q(\varvec{E}^{(i)}) = t_i$, there exists a nonsingular matrix $\varvec{T}_i \in \mathbb F_{q}^{N_{i} \times N_{i}}$ such that $\varvec{E}^{(i)}\varvec{T}_i$ has only $t_i$ nonzero columns for every $i \in \{1, \ldots , \ell \}$. Without loss of generality assume that these columns are the last ones of $\varvec{E}^{(i)}\varvec{T}_i$ and define $\varvec{\zeta }^{(i)} = \textbf{L}\cdot \varvec{T}_i$ with $\textbf{L}\in \mathbb F_{q^m}^{h_{i} \times N_{i}}$ containing the code locators $1, \ldots , \alpha ^{n_{i}-1}$ (cp. (3)). Note that the first $N_{i} - t_i$ columns of $\textbf{R}^{(i)} \varvec{T}_i = \textbf{C}^{(i)}\varvec{T}_i + \textbf{E}^{(i)}\varvec{T}_i$ are noncorrupted leading to $N_{i} h_{i} - (s-1) - t_i(h_{i} + s- 1)$ noncorrupted interpolation points according to (32). Now, for each $1 \le i \le \ell$, the first entries of the $N_{i} h_{i} - (s-1) - t_i(h_{i} + s- 1)$ noncorrupted interpolation points (i.e. the top left submatrix of size $(N_{i} - t_i) \times (h_{i} - s+ 1)$ of $\varvec{\zeta }^{(i)}$) are by construction both $\mathbb F_{q}$-linearly independent and roots of P(x). $\square$

This results in a different decoding radius, which is shown below.

Theorem 6

(Decoding Radius) Let $Q(x,y_1,\ldots ,y_s)$ be a nonzero solution of Problem 3. If the error-weight decomposition ${\textbf{t}}= (t_1, \ldots , t_{\ell })$ satisfies

$$\begin{aligned} \sum _{i=1}^{\ell } t_i (h_{i} + s- 1) < \frac{s}{s+1} \left( \sum _{i=1}^{\ell } N_{i}h_{i} - \ell (s- 1) - k + 1 \right) , \end{aligned}$$

(34)

then $P \in \mathbb F_{q^m}[x;\sigma ,\delta ]$ is the zero polynomial, that is for all $x \in \mathbb F_{q^m}$

$$\begin{aligned} P(x)=Q_0(x)+Q_1(x)f(x)+\!\cdots \!+Q_s(x)f(x)\alpha ^{s-1}=0. \end{aligned}$$

(35)

Proof

By Lemma 8, there exist elements $\zeta _1^{(i)}, \ldots , \zeta _{N_{i} h_{i} - (s-1) - t_i(h_{i} + s- 1)}^{(i)}$ in $\mathbb F_{q^m}$ that are $\mathbb F_{q}$-linearly independent for each $i \in \{1, \ldots , \ell \}$ such that ${P}(\zeta _j^{(i)})_{a_i} = 0$ for all $1 \le i \le \ell$ and $1 \le j \le N_{i} h_{i} - (s-1) - t_i(h_{i} + s- 1)$. By choosing

$$\begin{aligned} D\le \sum _{i=1}^{\ell } \left( N_{i} h_{i} - (s-1) - t_i(h_{i} + s- 1)\right) \end{aligned}$$

(36)

P(x) exceeds the degree bound from [13, Prop. 1.3.7] which is possible only if $P(x)=0$. By combining (36) with (33) we get

$$\begin{aligned} \sum _{i=1}^{\ell } \left( N_{i}h_{i} - (s- 1)\right) + s(k - 1)&< (s+ 1) \left( \sum _{i=1}^{\ell } \left( N_{i} h_{i} - (s-1) - t_i(h_{i} + s- 1)\right) \right) \\ \iff \qquad \sum _{i=1}^{\ell } t_i (h_{i} + s- 1)&< \frac{s}{s+1} \left( \sum _{i=1}^{\ell } N_{i}h_{i} - \ell (s- 1) - k + 1 \right) . \end{aligned}$$

$\square$

For the same folding parameter $h \in \mathbb {N}^{*}$ for all blocks the decoding radius in (34) simplifies to

$$\begin{aligned} t < \frac{s}{s+1} \left( \frac{Nh-\ell (s- 1)-k+1}{h+s-1}\right) \end{aligned}$$

(37)

which for $\ell =1$ coincides with the result for high-rate folded Gabidulin codes from [2, 3, 6].

Similar to (24), we also derive the normalized decoding radius $\tau :=\frac{t}{N}$ for codes with the same folding parameter $h$ for each block from (37) and obtain

$$\begin{aligned} \tau = \frac{t}{N}&< \frac{s}{s+1} \left( \frac{Nh- \ell (s- 1) - k + 1}{N(h+ s- 1)} \right) \nonumber \\&\xrightarrow {N\rightarrow \infty } \frac{s}{s+1} \frac{h}{h+ s- 1} \left( 1 - R \right) \end{aligned}$$

(38)

for the code rate $R :=\frac{k}{hN}$.

Theorem 6 shows that if the weight decomposition ${\textbf{t}}$ of the error satisfies (34), a list containing the message polynomial $f \in \mathbb F_{q^m}[x;\sigma ,\delta ]_{< k}$ can be obtained by finding all solutions of (35). This coincides with the root-finding problem from Sect. 4.2 and we can hence summarize the list decoder for high-rate FLRS codes as follows:

Theorem 7

(List Decoding) Consider an FLRS code $\textrm{FLRS}[\alpha , \textbf{a}, \varvec{h}; \textbf{N}, k]$ and a codeword $\textbf{C}$ that is transmitted over a sum-rank channel such that the error has weight t and its weight decomposition ${\textbf{t}}= (t_1, \ldots , t_{\ell })$ satisfies

$$\begin{aligned} \sum _{i=1}^{\ell } t_i (h_{i} + s- 1) < \frac{s}{s+1} \left( \sum _{i=1}^{\ell } N_{i}h_{i} - \ell (s- 1) - k + 1 \right) \end{aligned}$$

for an interpolation parameter $1 \le s\le \min _{i \in \{1, \ldots , \ell \}} h_{i}$. Then, a basis of an at most $(s- 1)$-dimensional $\mathbb F_{q^m}$-vector space that contains candidate message polynomials satisfying (35) can be obtained in at most $\mathcal {O}({sn^2})$ operations in $\mathbb F_{q^m}$.

By following the ideas of Lemma 4 we observe that the dimension of the $\mathbb F_{q^m}$-linear solution space of the interpolation system for the Justesen-like decoder satisfies

$$\begin{aligned} d_I \ge s(D- k + 1) - \sum _{i=1}^{\ell } t_i(h_{i} - s+ 1). \end{aligned}$$

Imposing the threshold $d_I \ge \mu$ yields to the degree constraint

which lets us provide a summary for probabilistic unique decoding of FLRS codes in Theorem 8.

Theorem 8

(Probabilistic Unique Decoding) For an interpolation parameter $1 \le s\le \min _{i \in \{1, \ldots , \ell \}} h_{i}$ and a dimension threshold $\mu \in \mathbb {N}^{*}$, transmit a codeword $\textbf{C}$ of an FLRS code $\textrm{FLRS}[\alpha , \textbf{a}, \varvec{h}; \textbf{N}, k]$ over a sum-rank channel. If the coefficients of the polynomials $B_0^{(u)}(x)$ for $u \in \{1, \ldots , \mu \}$ are independent and uniformly distributed among $\mathbb F_{q^m}$ and the error-weight decomposition ${\textbf{t}}= (t_1, \ldots , t_{\ell })$ satisfies

$$\begin{aligned} \sum _{i=1}^{\ell } t_i (h_{i} + s- 1) \le \frac{s}{s+1} \left( \sum _{i=1}^{\ell } N_{i}h_{i} - \ell (s- 1) - k + 1 \right) - \frac{\mu }{s+ 1}, \end{aligned}$$

$\textbf{C}$ can be uniquely recovered with complexity $\mathcal {O}({sn^2})$ in $\mathbb F_{q^m}$ with an approximate probability of at least

$$\begin{aligned} 1 - k \cdot \left( \frac{k}{q^m} \right) ^{\mu }. \end{aligned}$$

For the same folding parameter $h$ for each block, we get the decoding radius

$$\begin{aligned} t \le \frac{s}{s+ 1} \left( \frac{Nh- k + 1 - \ell (s- 1)}{h+ s- 1} \right) - \frac{\mu }{(s+ 1)(h+ s- 1)} \end{aligned}$$

which for $\ell = 1$ coincides with the probabilistic unique decoding radius for folded Gabidulin codes (cf. [6, Thm. 3]).

Figure  illustrates the normalized decoding radii of the presented Guruswami–Rudra- and Justesen-like decoders for FLRS codes. In particular, the significant improvement upon unique decoding is shown.

Fig. 2

Normalized decoding radius $\tau :=\frac{t}{N}$ vs. code rate $R :=\frac{k}{Nh}$ for an FLRS code with the same folding parameter $h= 25$ for each block and optimal decoding parameter $s\le h$ for each code rate

4.5 Simulation results

We ran simulations¹ in SageMath [36] to empirically verify the heuristic upper bound for probabilistic unique decoding that we derived in Theorem 5. We designed the parameter sets to obtain experimentally observable failure probabilities. Therefore, we considered codes with parameters

$$\begin{aligned} q = 3, \qquad m = 6, \qquad k = 2, \qquad \textbf{n}= (6, 6), \end{aligned}$$

and with two different vectors $\varvec{h}\in \{ (3, 3), (3, 2) \}$ of folding parameters. The code using $\varvec{h}= (3, 3)$ has minimum distance 4 which implies a unique-decoding radius of 1.5. In contrast, the proposed probabilistic unique decoder with $s= 2$ allows to correct errors of weight $t = 2$ for $\mu \in \{1, 2\}$. Namely, the bound (31) yields $t \le 2.17$ for $\mu = 1$ and $t \le 2$ for $\mu = 2$. We investigated the case $\mu = 1$ by means of a Monte Carlo simulation and collected 100 decoding failures within about $4.23 \cdot 10^7$ transmissions with randomly chosen error patterns of fixed sum-rank weight $t = 2$. This gives an observed failure probability of about $2.36 \cdot 10^{-6}$, while the heuristic yields an upper bound of $5.49 \cdot 10^{-3}$.

For $\varvec{h}= (3, 2)$, the code has the higher minimum distance 5 and a unique-decoding radius of 2. Its decodable error-weight decompositions with respect to the probabilistic unique decoder with $s= 2$ and $\mu \in \{1, 2, 3\}$ are

• (0, 1) and (1, 0), i.e. all possible patterns for weight $t = 1$,

• (0, 2) and (1, 1), i.e. two out of three possible patterns for weight $t = 2$,

• and (0, 3), i.e. one out of three possible patterns for weight $t = 3$.

Note that the error patterns are not equally likely. For example, being able to correct one out of two error-weight decompositions for a given weight does not necessarily mean that half of all errors of the given sum-rank weight can be corrected. We ran two Monte Carlo simulations for $t = 2$ and $t = 3$ and collected in both cases 100 failures for $\mu = 1$. The errors were chosen uniformly at random from the set of all vectors having the prescribed sum-rank weight as well as a decodable weight decomposition. The observed failure probability was $1.11 \cdot 10^{-3}$ for $t = 2$ (100 failures in about $9.03 \cdot 10^{4}$ runs) and $2.11 \cdot 10^{-5}$ for $t = 3$ (100 failures in $4.73 \cdot 10^{6}$ runs). In both scenarios, the heuristic upper bound is $5.49 \cdot 10^{-3}$ as for the first code.

Similar to results in [6, 37], our heuristic upper bound is based on the assumption that the coefficients of the polynomials $B_0^{(u)}(x) \in \mathbb {F}_{729}[x]$ with $1 \le u \le \mu$ defined in (27) are uniformly distributed among $\mathbb F_{729}$. Unfortunately, this assumption was not backed by evidence in former work. We thus decided to investigate experimentally observed distributions and compare them with the uniform distribution by means of the Kullback–Leibler (KL) divergence. The KL divergence (or relative entropy, see [17, Sec. 2.3]) is a tool to measure the distance between two probability distributions, that is often used in coding and information theory. Note that it is not a metric in the mathematical sense but provides sufficient insights for our purpose. In particular, it is an upper bound for other widely used statistical distance measures as e.g. the total variation distance [18].

The KL divergence of two probability mass functions u(x) and v(x), that are defined over a finite alphabet $\mathcal {A}$, is defined as

$$\begin{aligned} D_{KL}(u \,||\, v) :=\sum _{x \in \mathcal {A}} u(x) \log \left( \frac{u(x)}{v(x)} \right) . \end{aligned}$$

We understand $0 \cdot \log \big ( \frac{0}{q} \big ) :=0$ for any q and $p \cdot \log \big ( \frac{p}{0} \big ) :=\infty$ for any nonzero p by convention. We follow the common approach and consider the logarithm with base 2 and thus measure the Kullback–Leibler divergence in bits. Note that the divergence is always nonnegative and it equals zero if and only if the two considered probability mass functions are equal (see e.g. [17, Thm. 2.6.3])).

Denote the observed probability mass function of the coefficients of the polynomials $B_0^{(1)}(x) \in \mathbb {F}_{729}[x]$ from (27) after $10^{6}$ transmissions by $\chi$ and let ${{\,\textrm{unif}\,}}_{\mathbb F_{729}}$ be the probability mass function of the uniform distribution among $\mathbb F_{729}$. We obtained the KL divergence values

• $D_{KL}(\chi \,||\, {{\,\textrm{unif}\,}}_{\mathbb F_{729}}) \approx 3.32 \cdot 10^{-4}$ bits for $\varvec{h}= (3, 3)$ and $t = 2$,

• $D_{KL}(\chi \,||\, {{\,\textrm{unif}\,}}_{\mathbb F_{729}}) \approx 2.30 \cdot 10^{-4}$ bits for $\varvec{h}= (3, 2)$ and $t = 2$, and

• $D_{KL}(\chi \,||\, {{\,\textrm{unif}\,}}_{\mathbb F_{729}}) \approx 3.42 \cdot 10^{-4}$ bits for $\varvec{h}= (3, 2)$ and $t = 3$.

This shows that the measured distribution is in all cases remarkably close to the uniform distribution, which justifies the assumption in Theorem 5. The results are illustrated in more detail in Fig. , where the subfigures (a)–(c) show the probability mass functions $\chi$ of the coefficients that were observed within $10^{6}$ transmissions for $\varvec{h}= (3, 3)$ with error weight $t = 2$ and for $\varvec{h}= (3, 2)$ with error weight $t = 2$ and $t = 3$, respectively. The red line marks the (in fact discrete) probability mass function ${{\,\textrm{unif}\,}}_{\mathbb F_{729}}$ of the uniform distribution for reference. Subfigure (d) shows the evolution of the Kullback–Leibler divergence $D_{KL}(\chi \,||\, {{\,\textrm{unif}\,}}_{\mathbb F_{729}})$ over the $10^{6}$ runs for all investigated scenarios.

Fig. 3

Observed probability mass function of the coefficients of $B_0^{(1)}(x)$ after $10^{6}$ probabilistic unique decodings with $s= 2$ and $\mu = 1$ for codes with $q = 3$, $m = 6$, $k = 2$, $\textbf{n}= (6, 6)$ and either $\varvec{h}= (3, 3)$ and $t = 2$ or $\varvec{h}= (3, 2)$ and $t \in \{2, 3\}$ and evolution of its divergence with respect to the uniform distribution

5 Implications for folded skew Reed–Solomon codes

Motivated by the relation between LRS codes and SRS codes from [30], we now derive FSRS codes for the skew metric from FLRS codes. The skew metric is related to skew evaluation codes and was introduced in [30]. Decoding schemes for SRS codes that allow for correcting errors of skew weight up to the unique-decoding radius $\lfloor \frac{n-k}{2}\rfloor$ were presented in [1, 8, 27, 30].

In this section we consider decoding of FSRS codes with respect to the (burst) skew metric, which was introduced for interleaved skew Reed–Solomon (ISRS) codes in [5]. In the following, we restrict ourselves to evaluation codes constructed by $\mathbb F_{q^m}[x;\sigma ]$, i.e. to the zero-derivation case.

5.1 Preliminaries on remainder evaluation

Apart from the (generalized) operator evaluation (see Sect. 2) there exists the so-called remainder evaluation for skew polynomials, which can be seen as an analog of the classical polynomial evaluation via polynomial division.

For a skew polynomial $f\in \mathbb F_{q^m}[x;\sigma ]$ the remainder evaluation ${f}\!\left[ b\right]$ of f at an element $b\in \mathbb F_{q^m}$ is defined as the unique remainder of the right division of f(x) by $(x-b)$ such that (see [21, 22])

$$\begin{aligned} f(x)=g(x)(x-b)+{f}\!\left[ b\right] \quad \Longleftrightarrow \quad {f}\!\left[ b\right] = f(x) \; \textrm{mod}_\textrm{r} \;(x-b). \end{aligned}$$

We denote the evaluation of f at all entries of a vector $\varvec{b} = (b_1, \ldots , b_n)\in \mathbb F_{q^m}^n$ by ${f}\!\left[ \varvec{b}\right] =\left( {f}\!\left[ b_1\right] ,{f}\!\left[ b_2\right] ,\ldots ,{f}\!\left[ b_n\right] \right)$.

For any $a\in \mathbb F_{q^m}$, $b\in \mathbb F_{q^m}^*$ and $f\in \mathbb F_{q^m}[x;\sigma ]$ the generalized operator evaluation of f at b with respect to a is related to the remainder evaluation by (see [25, 30])

$$\begin{aligned} {f}\!\left[ \mathcal {D}_{a}(b)b^{-1}\right] ={f}(b)_{a}b^{-1}. \end{aligned}$$

(39)

The following notions were introduced in [21,22,23], and we use the notation of [31]. Let $\mathcal {A} \subseteq \mathbb F_{q^m}[x;\sigma ]$, $\Omega \subseteq \mathbb F_{q^m}$, and $a \in \mathbb F_{q^m}$. The zero set of $\mathcal {A}$ is defined as

$$\begin{aligned} \mathcal {Z}(\mathcal {A}):= \left\{ \alpha \in \mathbb F_{q^m}\,: \, {f}\!\left[ \alpha \right] = 0 \, \forall \, f \in \mathcal {A} \right\} \end{aligned}$$

and

$$\begin{aligned} I(\Omega ):= \left\{ f \in \mathbb F_{q^m}[x;\sigma ]\,: \, {f}\!\left[ \alpha \right] = 0 \, \forall \, \alpha \in \Omega \right\} \end{aligned}$$

denotes the associated ideal of $\Omega$. The P-closure (or polynomial closure) of $\Omega$ is defined by $\overline{\Omega }:= \mathcal {Z}(I(\Omega ))$, and $\Omega$ is called P-closed if $\overline{\Omega }=\Omega$. Note that a P-closure is always P-closed. All elements of $\mathbb F_{q^m}{\setminus } \overline{\Omega }$ are said to be P-independent from $\Omega$. A set $\mathcal {B} \subseteq \mathbb F_{q^m}$ is said to be P-independent if any $b \in \mathcal {B}$ is P-independent from $\mathcal {B} \setminus \{b\}$. If $\mathcal {B}$ is P-independent and $\Omega := \overline{\mathcal {B}} \subseteq \mathbb F_{q^m}$, we say that $\mathcal {B}$ is a P-basis of $\Omega$.

For any $\textbf{x}= (x_1,\ldots ,x_n) \in \mathbb F_{q^m}^n$ and any P-basis $\mathcal {B}=\{b_1,b_2,\ldots ,b_n\}$, there is a unique skew polynomial $\mathcal {I}_{\mathcal {B}, \textbf{x}}^{\textrm{rem}} \in \mathbb F_{q^m}[x;\sigma ]$ of degree less than n such that

$$\begin{aligned} {\mathcal {I}_{\mathcal {B}, \textbf{x}}^{\textrm{rem}}}\!\left[ b_j\right] = x_j \quad \forall \, j=1,\ldots ,n. \end{aligned}$$

We call this the remainder interpolation polynomial of $\textbf{x}$ on $\mathcal {B}$. The skew weight of a vector $\varvec{x}\in \mathbb F_{q^m}^n$ with respect to a P-closed set $\Omega =\overline{\mathcal {B}}$ with P-basis $\mathcal {B}=\{b_1,b_2,\ldots ,b_n\}$² is defined as (see [8])

The skew weight of a vector depends on $\Omega$ but is independent from the particular P-basis $\mathcal {B}$ (see [30, Prop. 13]) of $\Omega$. In order to simplify the notation for the skew weights of vectors, we indicate the dependence on $\Omega$ by a particular P-basis for $\Omega$ and use the notation ${{\,\textrm{wt}\,}}_{skew}(\cdot )$ whenever $\mathcal {B}$ is clear from the context. Similar to the rank and the sum-rank weight we have that ${{\,\textrm{wt}\,}}_{skew}(\varvec{x})\le {{\,\textrm{wt}\,}}_{H}(\varvec{x})$ for all $\varvec{x}\in \mathbb F_{q^m}^n$ (see [30]). The skew distance between two vectors $\varvec{x},\varvec{y}\in \mathbb F_{q^m}^n$ is defined as

$$\begin{aligned} d_{skew}(\varvec{x},\varvec{y}):={{\,\textrm{wt}\,}}_{skew}(\varvec{x}-\varvec{y}). \end{aligned}$$

5.2 Skew metric for folded matrices

By fixing a basis of $\mathbb F_{q^{mh}}$ over $\mathbb F_{q^m}$ we can consider a matrix $\textbf{X}\in \mathbb F_{q^m}^{h\times N}$ as a vector $\varvec{x}=(x_1,x_2,\ldots ,x_N)\in \mathbb F_{q^{mh}}^N$. Similarly, we consider a tuple $\textbf{X}\in \mathbb F_{q^m}^{\varvec{h}\times \textbf{N}}$ as a matrix in $\mathbb F_{q^m}^{h\times N}$ whenever the folding parameter $h$ is the same for each block, i.e. if $\varvec{h}=(h,\ldots ,h)$. Similar as for ISRS codes we define the skew weight of a matrix $\textbf{X}\in \mathbb F_{q^m}^{h\times N}$ (or a tuple $\textbf{X}\in \mathbb F_{q^m}^{\varvec{h}\times \textbf{N}}$) with respect to $\mathcal {B}$ as the skew weight of the vector $\textbf{x}=\text {ext}^{-1}_{\varvec{\gamma }}(\textbf{X})\in \mathbb F_{q^{mh}}^N$, i.e. as (see [5])

where the polynomial

is now from $\mathbb F_{q^{mh}}[\sigma ;x]$ since we have that $x_i\in \mathbb F_{q^{mh}}$ for all $i=1,\ldots ,N$.

Lemma 9

Define $\mathcal {N}_{i}(a) :=\prod _{k=0}^{i-1} \sigma ^{k}(a)$ for any $i \in \mathbb {N}$ and $a \in \mathbb F_{q^m}$, let $c \in \mathbb F_{q^m}$ and consider a skew polynomial $f \in \mathbb F_{q^m}[x;\sigma ]$. Then for any $b \in \mathbb F_{q^m}$ and $j \in \mathbb {N}$ we have that

$$\begin{aligned} {f}\!\left[ c^j b\right] = {\tilde{f}}\!\left[ b\right] \end{aligned}$$

where $\tilde{f}=\sum _{i=0}^{\deg (f)} f_i \mathcal {N}_{i}(c^j) x^i$.

Proof

By [22, Lemma 2.4] we have that

$$\begin{aligned} {f}\!\left[ c^j b\right] = \sum _{i=0}^{\deg (f)} f_i \mathcal {N}_{i}(c^j b) \overset{(*)}{=}\ \sum _{i=0}^{\deg (f)} f_i \mathcal {N}_{i}(c^j) \mathcal {N}_{i}(b) = {\tilde{f}}\!\left[ b\right] \end{aligned}$$

where $\tilde{f}=\sum _{i=0}^{\deg (f)} f_i \mathcal {N}_{i}(c^j) x^i$ and $(*)$ follows since $f \in \mathbb F_{q^m}[x;\sigma ]$.

The following result shows that each matrix can be represented as the remainder evaluation of a single skew polynomial over the large field $\mathbb F_{q^{mh}}$ at evaluation points from the small field $\mathbb F_{q^m}$.

Lemma 10

Let $\alpha$ be a primitive element of $\mathbb F_{q^m}$, define $\omega :=\sigma (\alpha )/\alpha$, let the folding parameter $h$ divide $n\le m$ and define $N:=\frac{n}{h}$. Consider an evaluation parameter $a\in \mathbb F_{q^m}^*$ and define the vector

$$\begin{aligned} \textbf{b}:=(\mathcal {D}_{a}(1)/1, \mathcal {D}_{a}(\alpha ^h)/\alpha ^h, \ldots , \mathcal {D}_{a}(\alpha ^{(N-1)h})/\alpha ^{(N-1)h}) \in \mathbb F_{q^m}^{N}. \end{aligned}$$

Then any matrix $\textbf{X}\in \mathbb F_{q^m}^{h\times N}$ can be represented as

$$\begin{aligned} \textbf{X}= \begin{pmatrix} {f}\!\left[ \textbf{b}\right] \\ {f}\!\left[ \omega \textbf{b}\right] \\ \vdots \\ {f}\!\left[ \omega ^{h-1} \textbf{b}\right] \end{pmatrix} = \begin{pmatrix} {f^{(1)}}\!\left[ \textbf{b}\right] \\ {f^{(2)}}\!\left[ \textbf{b}\right] \\ \vdots \\ {f^{(h)}}\!\left[ \textbf{b}\right] \end{pmatrix} \end{aligned}$$

for some $f, f^{(1)}, \ldots , f^{(h)} \in \mathbb F_{q^m}[x;\sigma ]_{<n}$. Further, we have that

$$\begin{aligned} \text {ext}^{-1}_{\varvec{\gamma }}(\textbf{X}) = {F}\!\left[ \textbf{b}\right] \end{aligned}$$

for some $F \in \mathbb F_{q^{mh}}[x; \sigma ]_{<n}$.

Proof

Let $\textbf{x}= \mathcal {F}_{h}^{-1}(\textbf{X})$ be the vector obtained by unfolding $\textbf{X}$ and define

$$\begin{aligned} \widetilde{\textbf{b}} :=\left( \mathcal {D}_{a}(1)/1, \mathcal {D}_{a}(\alpha )/\alpha , \ldots , \mathcal {D}_{a}(\alpha ^{(N-1)h})/\alpha ^{(N-1)h}\right) \in \mathbb F_{q^m}^{Nh}. \end{aligned}$$

Since $\alpha$ is a primitive element of $\mathbb F_{q^m}$ we have that the entries in $\widetilde{\textbf{b}}$ are P-independent. Let $f :=\mathcal {I}_{\widetilde{\textbf{b}}, \textbf{x}}^{\textrm{rem}} \in \mathbb F_{q^m}[x;\sigma ]_{< n}$ be the unique interpolation polynomial satisfying

$$\begin{aligned} {\mathcal {I}_{\widetilde{\textbf{b}}, \textbf{x}}^{\textrm{rem}}}\!\left[ \widetilde{b}_j\right] = x_j \quad \forall j=1,\ldots , hN. \end{aligned}$$

Due to the structure of the evaluation points in $\widetilde{\textbf{b}}$ we can write $\textbf{X}$ as

$$\begin{aligned} \textbf{X}= \mathcal {F}_{h}\left( {f}\!\left[ \widetilde{\textbf{b}}\right] \right) = \begin{pmatrix} {f}\!\left[ \textbf{b}\right] \\ {f}\!\left[ \omega \textbf{b}\right] \\ \vdots \\ {f}\!\left[ \omega ^{h-1} \textbf{b}\right] \end{pmatrix} \overset{(*)}{=} \begin{pmatrix} {f^{(1)}}\!\left[ \textbf{b}\right] \\ {f^{(2)}}\!\left[ \textbf{b}\right] \\ \vdots \\ {f^{(h)}}\!\left[ \textbf{b}\right] \end{pmatrix} \end{aligned}$$

where $(*)$ follows by Lemma 9. By fixing a basis $\varvec{\gamma }$ of $\mathbb F_{q^{mh}}$ over $\mathbb F_{q^m}$ we can represent $\textbf{X}$ over $\mathbb F_{q^{mh}}$ as

$$\begin{aligned} \text {ext}^{-1}_{\varvec{\gamma }}(\textbf{X}) = {F}\!\left[ \textbf{b}\right] \end{aligned}$$

where $F(x) = \sum _{i=0}^{n-1}F_i x^i$ with $F_i=\text {ext}^{-1}_{\varvec{\gamma }}\left( (f_i^{(1)}, f_i^{(2)}, \ldots , f_i^{(h)})^\top \right)$ for all $i = 1, \ldots , n-1$.

Theorem 9 shows that applying the elementwise $\mathbb F_{q^m}$-linear transformation from [30, Thm. 3] to unfolded matrices yields an isometry between the skew metric and the sum-rank metric for matrices obtained from folded vectors.

Theorem 9

Let $\alpha$ be a primitive element of $\mathbb F_{q^m}$ and consider $\ell \in \mathbb {N}^{*}$. Let $1\le n_{i} \le m$ for all $i=1,\ldots ,\ell$ and let $\textbf{a}=(a_1, \ldots , a_\ell )\in \mathbb F_{q^m}^\ell$ contain representatives from different conjugacy classes. Let the folding parameter $h$ divide $n_{i}$ for all $i=1,\ldots ,\ell$, define the $\ell$-composition $\textbf{N}=(N_{1}, N_{2}, \ldots , N_{\ell })$ with $N_{i}=\frac{n_{i}}{h}$ for all $i=1,\ldots ,\ell$ and define $\varvec{h}=(h, \ldots , h)\in \mathbb {Z}_{\ge 0}^\ell$. Let ${{\,\textrm{diag}\,}}(\varvec{\beta }^{-1})$ denote the diagonal matrix of the vector

$$\begin{aligned} \varvec{\beta }^{-1}:=\left( 1,\alpha ^{-1}, \ldots , (\alpha ^{n_1-1})^{-1} \mid \ldots \mid 1, \alpha ^{-1}, \ldots , (\alpha ^{n_\ell -1})^{-1}\right) \end{aligned}$$

and define the map

$$\begin{aligned} \varphi _{\alpha } \, : \, \mathbb F_{q^m}^{h\times N}&\rightarrow \mathbb F_{q^m}^{h\times N}, \\ ({\textbf{X}}^{(1)} \mid {\textbf{X}}^{(2)} \mid \dots \mid {\textbf{X}}^{(\ell )})&\mapsto \mathcal {F}_{\varvec{h}}(\mathcal {F}_{\varvec{h}}^{-1}(\textbf{X}) \cdot {{\,\textrm{diag}\,}}(\varvec{\beta }^{-1})). \end{aligned}$$

Then for any $\textbf{X}\in \mathbb F_{q^m}^{h\times N}$ we have that the mapping $\varphi _{\alpha }$ is an isometry between the skew metric and the sum-rank metric, i.e. we have that

$$\begin{aligned} {{\,\textrm{wt}\,}}_{skew}^\mathcal {B}(\varphi _{\alpha }(\textbf{X})) = {{\,\textrm{wt}\,}}_{\Sigma R}(\textbf{X}) \end{aligned}$$

where $\mathcal {B}=\{\mathcal {D}_{a_i}(\alpha ^{jh})/\alpha ^{jh}: j=0,\ldots n_{i}-1, i=1,\ldots ,\ell \}$.

Proof

The vectors ${\varvec{\alpha }}^{(i)} :=(1, \alpha ^h, \ldots , \alpha ^{(N_{i}-1)h})$ contain $\mathbb F_{q}$-linearly independent elements from $\mathbb F_{q^m}$ since $\alpha$ is a primitive element of $\mathbb F_{q^m}$ and $n_{i}=N_{i}h\le m$ for all $i=1,\ldots ,\ell$. Thus, by [22, Thm. 4.5] we have that the vectors

$$\begin{aligned} {\textbf{b}}^{(i)} = \left( \mathcal {D}_{a_i}(1), \mathcal {D}_{a_i}(\alpha ^h)/\alpha ^h, \ldots , \mathcal {D}_{a_i}(\alpha ^{(N_{i}-1)h})/\alpha ^{(N_{i}-1)h}\right) \end{aligned}$$

contain P-independent elements for all $i=1, \ldots , \ell$. Since $a_1, \ldots , a_\ell$ are representatives of different conjugacy classes of $\mathbb F_{q^m}$, we also have that the entries in $\textbf{b}=({\textbf{b}}^{(1)} \mid {\textbf{b}}^{(2)} \mid \dots \mid {\textbf{b}}^{(\ell )})$ are P-independent which implies that $\mathcal {B}$ is a P-independent set (cf. [31, Thm. 9] and [21, 22]).

By using the relation between the generalized operator evaluation and the remainder evaluation in (39) and the result of Lemma 10, we can write the blocks of the transformed tuple

$$\begin{aligned} \widetilde{\textbf{X}} :=\varphi _{\alpha }(\textbf{X})=\mathcal {F}_{\varvec{h}}\left( \mathcal {F}_{\varvec{h}}^{-1}(\textbf{X})\cdot {{\,\textrm{diag}\,}}(\varvec{\beta }^{-1})\right) \end{aligned}$$

in terms of the remainder evaluation as

$$\begin{aligned} {\widetilde{\textbf{X}}}^{(i)} :=\mathcal {F}_{h}\left( \mathcal {F}_{h}^{-1}({\textbf{X}}^{(i)})\cdot {{\,\textrm{diag}\,}}\left( ({\varvec{\beta }}^{(i)})^{-1}\right) \right) = \begin{pmatrix} {f}\!\left[ {\textbf{b}}^{(i)}\right] \\ {f}\!\left[ \omega {\textbf{b}}^{(i)}\right] \\ \vdots \\ {f}\!\left[ \omega ^{h- 1} {\textbf{b}}^{(i)}\right] \end{pmatrix} = \begin{pmatrix} {f^{(1)}}\!\left[ {\textbf{b}}^{(i)}\right] \\ {f^{(2)}}\!\left[ {\textbf{b}}^{(i)}\right] \\ \vdots \\ {f^{(h)}}\!\left[ {\textbf{b}}^{(i)}\right] \end{pmatrix}, \end{aligned}$$

where $({\varvec{\beta }}^{(i)})^{-1} :=(1,\alpha ^{-1},\ldots ,(\alpha ^{n_{i}-1})^{-1})$ for all $i=1,\ldots ,\ell$ such that $\varvec{\beta }^{-1}=(({\varvec{\beta }}^{(1)})^{-1} \mid \dots \mid ({\varvec{\beta }}^{(\ell )})^{-1})$ and $f^{(j)}=\sum _{l=0}^{n-1} f_l \mathcal {N}_{a_i}(\omega ^j) x^l$.

Hence we can write each transformed block ${\widetilde{\textbf{X}}}^{(i)}$ over $\mathbb F_{q^{mh}}$ as an evaluation of $F \in \mathbb F_{q^{mh}}[x; \sigma ]_{<n}$ at the P-independent elements from $\mathbb F_{q^m}$ in ${\textbf{b}}^{(i)}$, i.e. we have

$$\begin{aligned} {\widetilde{\textbf{x}}}^{(i)} :=\text {ext}^{-1}_{\varvec{\gamma }}({\widetilde{\textbf{X}}}^{(i)}) = {F}\!\left[ {\textbf{b}}^{(i)}\right] \quad \forall i = 1, \ldots , \ell . \end{aligned}$$

Define the vectors $\widetilde{\textbf{x}} :=({\widetilde{\textbf{x}}}^{(1)} \mid {\widetilde{\textbf{x}}}^{(2)} \mid \dots \mid {\widetilde{\textbf{x}}}^{(\ell )}) \in \mathbb F_{q^{mh}}^N$ and $\textbf{x}:=({\textbf{x}}^{(1)} \mid {\textbf{x}}^{(2)} \mid \dots \mid {\textbf{x}}^{(\ell )}) \in \mathbb F_{q^{mh}}^N$. Then it follows from [30, Thm. 3] that

$$\begin{aligned} {{\,\textrm{wt}\,}}_{skew}^{\mathcal {B}}(\widetilde{\textbf{x}}) = {{\,\textrm{wt}\,}}_{\Sigma R}(\textbf{x}). \end{aligned}$$

Example 5 illustrates the operator $\varphi _{\alpha }$.

Example 5

Consider a matrix $\textbf{X}=({\textbf{X}}^{(1)} \mid {\textbf{X}}^{(2)})\in \mathbb F_{q^m}^{h\times N}$ where $h=3$ and $\textbf{N}=(2,3)$. Then the operator $\varphi _{\alpha }$ applied to $\textbf{X}$ gives

$$\begin{aligned} \varphi _{\alpha }(\textbf{X})= \left( \begin{array}{cc|ccc} {x}^{(1)}_{1,1}/1 &{} {x}^{(1)}_{1,2}/\alpha ^3 &{} {x}^{(2)}_{1,1}/1 &{} {x}^{(2)}_{1,2}/\alpha ^3 &{} {x}^{(2)}_{1,3}/\alpha ^6\\ {x}^{(1)}_{2,1}/\alpha &{} {x}^{(1)}_{2,2}/\alpha ^4 &{} {x}^{(2)}_{2,1}/\alpha &{} {x}^{(2)}_{2,2}/\alpha ^4 &{} {x}^{(2)}_{2,3}/\alpha ^7\\ {x}^{(1)}_{3,1}/\alpha ^2 &{} {x}^{(1)}_{3,2}/\alpha ^5 &{} {x}^{(2)}_{3,1}/\alpha ^2 &{} {x}^{(2)}_{3,2}/\alpha ^5 &{} {x}^{(2)}_{3,3}/\alpha ^8 \end{array} \right) . \end{aligned}$$

Skew Reed–Solomon codes were proposed by Boucher and Ulmer in [9] and further investigated in [27, 30].

Definition 4

(Skew Reed–Solomon Codes [9]) Let $\textbf{b}=(b_1, b_2, \ldots , b_n) \in \mathbb F_{q^m}^n$ contain P-independent elements from $\mathbb F_{q^m}$. Then a skew Reed–Solomon code of length n and dimension $k \le n$ is defined as

$$\begin{aligned} \textrm{SRS}[\textbf{b}; n,k]=\{{f}\!\left[ \textbf{b}\right] : f \in \mathbb F_{q^m}[x;\sigma ]_{<k}\}. \end{aligned}$$

Definition 5

(Folded Skew Reed–Solomon Codes) Let $\alpha$ be a primitive element of $\mathbb F_{q^m}$ and define $\omega :=\sigma (\alpha )/\alpha$. Let $a_1,\ldots ,a_\ell$ be representatives of pairwise distinct nontrivial conjugacy classes of $\mathbb F_{q^m}$. Define $\textbf{b}=({\textbf{b}}^{(1)} \mid {\textbf{b}}^{(2)} \mid \dots \mid {\textbf{b}}^{(\ell )})$ with

$$\begin{aligned} {\textbf{b}}^{(i)} :=a_i \left( 1, \omega , \omega ^2, \ldots , \omega ^{n_{i}-1}\right) \in \mathbb F_{q^m}^{n_{i}} \quad \forall i = 1, \ldots , \ell . \end{aligned}$$

Choose a folding parameter $h\in \mathbb {N}$ satisfying $h\mid n_{i}$ for all $1 \le i \le \ell$ and $N_{i} :=\frac{n_{i}}{h} \le h$ for all $1 \le i \le \ell$ and write $\textbf{N}:=(N_{1}, \ldots , N_{\ell })$. Then an $h$-folded skew Reed–Solomon code of length $N:=\sum _{i=1}^{\ell } N_{i}$ and dimension k is defined as

$$\begin{aligned} \textrm{FSRS}[\textbf{b}, h; \textbf{N}, k] :=\left\{ \mathcal {F}_{h}({f}\!\left[ \textbf{b}\right] ): f \in \mathbb F_{q^m}[x;\sigma ]_{<k} \right\} . \end{aligned}$$

Remark 4

Equivalently, we can define FSRS codes as

$$\begin{aligned} \textrm{FSRS}[\textbf{b}, h; \textbf{N}, k] :=\left\{ \mathcal {F}_{h}(\textbf{c}): \textbf{c}\in \textrm{SRS}[\textbf{b}; n,k] \right\} \end{aligned}$$

where $\textbf{b}$ is defined as in Definition 5.

Note that any codeword $\textbf{C}\in \textrm{FSRS}[\textbf{b}, h; \textbf{N}, k] \subseteq \mathbb F_{q^m}^{h\times N}$ corresponding to a message polynomial $f \in \mathbb F_{q^m}[x;\sigma ]_{<k}$ has the form

$$\begin{aligned} \textbf{C}= \left( \textbf{C}^{(1)} \mid \dots \mid \textbf{C}^{(\ell )} \right) \end{aligned}$$

where

$$\begin{aligned} \textbf{C}^{(i)} = \begin{pmatrix} {f}\!\left[ a_i\right] &{} {f}\!\left[ \omega ^ha_i\right] &{} \cdots &{} {f}\!\left[ \omega ^{n_{i}-h} a_i\right] \\ {f}\!\left[ \omega a_i\right] &{} {f}\!\left[ \omega ^{h+1} a_i\right] &{} \cdots &{} {f}\!\left[ \omega ^{n_{i}-h+1} a_i\right] \\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ {f}\!\left[ \omega ^{h- 1} a_i\right] &{} {f}\!\left[ \omega ^{2h-1} a_i\right] &{} \cdots &{} {f}\!\left[ \omega ^{n_{i}-1} a_i\right] \end{pmatrix} \in \mathbb F_{q^m}^{h\times N_{i}} \end{aligned}$$

for all $i \in \{1, \ldots , \ell \}$.

Proposition 1

(Relation between FLRS and FSRS Codes) Let $\textrm{FSRS}[\textbf{b}, h; \textbf{N}, k]$ be an FSRS code whose parameters comply with Definition 5. Then,

$$\begin{aligned} \textrm{FSRS}[\textbf{b}, h; \textbf{N}, k] = \{\varphi _{\alpha }(\textbf{C}): \textbf{C}\in \textrm{FLRS}[\alpha , \textbf{a}, \varvec{h}; \textbf{N}, k]\} \end{aligned}$$

where the code $\textrm{FLRS}[\alpha , \textbf{a}, \varvec{h}; \textbf{N}, k]$ with $\varvec{h}= (h, \ldots , h)$ is considered as subset of $\mathbb F_{q^m}^{h\times N}$.

Proof

The result follows directly by using the relation between the generalized operator evaluation and the remainder evaluation in (39).

By using the isometry between the sum-rank metric and the skew metric from Theorem 9, we obtain the following corollary from Theorem 2.

Corollary 1

(Minimum Skew Distance) The minimum skew distance of an FSRS code $\mathcal {C} :=\textrm{FSRS}[\textbf{b}, h; \textbf{N}, k]$ of length $N=\sum _{i=1}^{\ell }N_{i}$ as defined in Definition 5 is

5.3 Interpolation-based decoding of folded skew Reed–Solomon codes

We now consider interpolation-based decoding of FSRS codes with respect to the skew metric. As a channel model we consider the skew error channel with input and output alphabet $\mathbb F_{q^m}^{h\times N}$, where the input $\textbf{C}$ is related to the output $\textbf{R}$ by

$$\begin{aligned} \textbf{R}= \textbf{C}+ \textbf{E}\end{aligned}$$

(40)

and $\textbf{E}$ with ${{\,\textrm{wt}\,}}_{skew}(\textbf{E})=t$ is chosen uniformly at random from all matrices from $\mathbb F_{q^m}^{h\times N}$ with skew weight t.

Suppose we transmit a codeword $\textbf{C}\in \textrm{FSRS}[\textbf{b}, h; \textbf{N}, k]$ over a skew error channel (40) and receive a matrix $\textbf{R}=({\textbf{R}}^{(1)} \mid {\textbf{R}}^{(2)} \mid \dots \mid {\textbf{R}}^{(\ell )})$. Let $\varphi ^{-1}_{\alpha }$ denote the inverse map of $\varphi _{\alpha }$. By using the isometry between the sum-rank metric and the relation between FLRS codes and FSRS codes, we can transform the received matrix $\textbf{R}$ to

$$\begin{aligned} \widetilde{\textbf{R}} :=\varphi ^{-1}_{\alpha }(\textbf{R}) = \varphi ^{-1}_{\alpha }(\textbf{C}) + \varphi ^{-1}_{\alpha }(\textbf{E}) \end{aligned}$$

where $\varphi ^{-1}_{\alpha }(\textbf{C})$ is in the corresponding FLRS code $\textrm{FLRS}[\alpha , \textbf{a}, \varvec{h}; \textbf{N}, k]$ (see Proposition 1) and $\varphi ^{-1}_{\alpha }(\textbf{E})$ has sum-rank weight t (see Theorem 9). Hence, the decoding problem for FSRS codes with respect to the skew metric is mapped to an equivalent decoding problem for FLRS codes in the sum-rank metric.

Therefore, we can use the interpolation-based decoding schemes for FLRS codes from Sect. 4 to decode FSRS codes in the skew metric as follows:

• 1. Compute $\widetilde{\textbf{R}} :=\varphi ^{-1}_{\alpha }(\textbf{R})$, which requires $\mathcal {O}({n})$ operations in $\mathbb F_{q^m}$.

• 2. Apply a decoder for FLRS codes in the sum-rank metric (e.g. Algorithm 1) to $\widetilde{\textbf{R}}$.

6 Conclusion

We introduced the family of FLRS codes whose members are MSRD codes for appropriate parameter choices. We further described an efficient decoding scheme to correct sum-rank errors in the context of list and probabilistic unique decoding with quadratic complexity in the length of the unfolded code. Up to our knowledge, this is the first explicit MSRD code construction that allows different block sizes and has an explicit efficient decoding algorithm. We analyzed the decoder and gave upper bounds on both list size and failure probability. Monte Carlo simulations verified that the observed failure probability is indeed below the derived bound and further experiments show that the assumption under which the upper bound was derived is reasonable. Since the proposed decoding scheme has a rate restriction, we investigated a Justesen-like improvement tailored to high-rate FLRS codes.

The focus of the second part of the paper was the skew metric for which we introduced FSRS codes in the zero-derivation setting. Moreover, we explained how the decoding scheme for FLRS codes in the sum-rank metric can be applied to the presented skew-metric codes.

Goals for further research could be the extension of FSRS codes to the nonzero-derivation case or to more general parameters as e.g. code locators. Moreover, it is tempting to study if there are other useful ways of folding codes in different metrics.