Article Highlights

  • This paper reviews previous methods to calculate the sensitivity kernels in time-domain viscoelastic full-waveform inversion

  • This research derives the Q sensitivity kernels directly following the adjoint-state method, which is theoretically more complete

  • The Q sensitivity kernels calculated using memory strain variables suffer from fewer trade-offs

1 Introduction

In recent decades, the technique of wave-equation-based full-waveform inversion/tomography (FWI/FWT) has been intensively investigated to obtain underground model properties with high accuracy and spatial resolution for the exploration of hydrocarbon resources and interpreting deep Earth structures (Tarantola 1984; Bunks et al. 1995; Pratt et al. 1998; Virieux and Operto 2009; Tape et al. 2009; Warner et al. 2013; Fichtner and Trampert 2011; Bozdağ et al. 2016). Seismic signals experience amplitude decay and phase distortions when propagating in the Earth due to intrinsic attenuation (Liu et al. 1976; Dahlen and Tromp 1998). Attenuation represents one important property for interpreting subsurface structures and compositions. The attenuation effects are commonly quantified with quality factor Q for a linear viscoelastic solid in geophysics community. Considering attenuation effects in seismic imaging (Innanen and Lira 2010; Dutta and Schuster 2014; Zhu 2015; Sun et al. 2015; Shen et al. 2018) and inversion (Malinowski et al. 2011; Brossier 2011; Moradi and Innanen 2016; Fabien-Ouellet et al. 2017; Yang et al. 2017; Trinh et al. 2018; Pan and Wang 2020; Kamath et al. 2020; Keating and Innanen 2020; Chen et al. 2021) has drawn significant attention. However, constructing accurate and high-resolution subsurface Q profiles reliably using FWI approaches is still a very complex and difficult problem remaining to be solved.

The damping effects of attenuation on propagating waves can be modeled using a phenomenological model, which can be constructed by parallel connection of N standard linear elements referred to as the generalized standard linear solid (GSLS) rheology (Carcione et al. 1988; Robertsson et al. 1994; Carcione 2004). In the frequency domain, the modeling of wave propagation in attenuating medium can be implemented easily by introducing complex velocity (Hak and Mulder 2011; Kamei and Pratt 2013; Operto and Miniussi 2018; Keating and Innanen 2019). However, for (very) large-scale 3D forward and inverse simulations in exploration and earthquake seismology, time-domain approaches are preferable and more frequently used. Under the GSLS formulation, Q is not involved explicitly in the rheological bodies of time-domain visco-elastodynamic wave equation (Blanch et al. 1995; Bohlen 2002). Instead, the relaxation parameters are obtained implicitly by minimizing an objective function with linear or nonlinear optimization methods (Emmerich and Korn 1987; Martin and Komatitsch 2009; Blanc et al. 2016). This impedes the derivation and calculation of Q sensitivity kernels, which are essential for iteratively updating Q models in viscoelastic FWI (Komatitsch et al. 2016). Furthermore, when simultaneously inverting for velocity and Q properties, the inverted Q models are easily damaged by trade-off (or crosstalk) artifacts caused by inaccurate velocities (Brossier 2011; Hak and Mulder 2011; Kamei and Pratt 2013; Pan and Innanen 2019; Keating and Innanen 2020). Taking attenuation mechanisms into account has become one of the most difficult and complex problems in FWI studies and applications.

Different theoretical frameworks have been suggested by previous researchers to calculate the sensitivity kernels in time-domain viscoelastic FWI based on the GSLS model (Charara et al. 2000; Tromp et al. 2005; Fichtner and van Driel 2014). In Charara et al. (2000), the attenuation parameters are defined as the differences between unrelaxed and relaxed moduli. The sensitivity kernels of unrelaxed moduli and attenuation parameters in viscoelastic FWI are derived with a perturbation approach based on Born approximation. The attenuation sensitivity kernels are formulated as the cross-correlation between forward strain memory variables and adjoint strain fields. Based on this theoretical framework, Bai et al. (2017) inverted for the attenuation parameters in anisotropic and viscoelastic medium. In Tromp et al. (2005), when deriving the sensitivity kernel for Q, the relation between shear modulus and quality factor defined in the Kolsky–Futterman model by Kolsky (1952) and Futterman (1962) is introduced. Using the Born scattering integral and the chain rule, the derived Q sensitivity kernel has the same expression as that of modulus sensitivity kernel but with a different frequency-domain adjoint source. In earthquake seismology, Zhu et al. (2013) used this approach to invert for the Q structures beneath Europe and the North Atlantic. In exploration seismology, Pan and Innanen (2019) have applied this approach to image subsurface Q profiles in a practical walk-away vertical seismic profiling survey for delineating hydrocarbon reservoirs. In this paper, the approaches given by Charara et al. (2000) and Tromp et al. (2005) are referred to as method I and II, respectively.

Based on the adjoint-state (or Lagrangian multiplier) method, sensitivity kernels in FWI can be constructed by cross-correlating the forward and adjoint wavefields, which avoids direct calculation of the Jacobian matrices for (very) large-scale inversion practices (Plessix 2006; Métivier et al. 2013). In this paper, following the adjoint-state method, we directly derive the sensitivity kernels for relaxation functions and Q in viscoelastic FWI. The moduli sensitivity kernels can be constructed by cross-correlating the forward strain fields with the adjoint stress fields (Liu and Tromp 2008). The Q sensitivity kernels can be formulated as the cross-correlation between forward strain fields and adjoint strain memory variables. The same GSLS model as that of method II by Tromp et al. (2005) is used in forward modeling and sensitivity kernel derivation within this approach, which is theoretically more complete. Furthermore, this method allows calculating the velocity and Q sensitivity kernels simultaneously without introducing additional adjoint sources.

In the numerical experiments, a simple example with separated velocity and Q anomalies in viscoelastic media is first given for sensitivity and trade-off analysis. The velocity and Q sensitivity kernels based on different methods are calculated for comparison and interparmeter trade-off quantification. Next, we give a surface acquisition survey example with topographic variations and complex velocity structures. Unstructured quadrilateral mesh is used to discretize the models while accounting for topographic effects. Surface waves (SWs) are extracted from the shorts to calculate the sensitivity kernels of S-wave velocity and quality factor (\(V_\textrm{S}\) and \(Q_\textrm{S}\)). Early arrivals of body waves (BWs) are used to calculate the sensitivity kernels of P-wave velocity and quality factor (\(V_\textrm{P}\) and \(Q_\textrm{P}\)). The influences of velocity errors on Q sensitivity kernels are evaluated based on the three methods. The velocity and Q models obtained by inversion of SWs and BWs are presented for comparison. In these numerical experiments, we have obtained a series of observations:

  1. 1.

    The velocity sensitivity kernels calculated using these three different methods do not show obvious differences;

  2. 2.

    When simultaneously inverting for velocity and Q models, these three methods can provide inversion results of comparable quality;

  3. 3.

    However, in the presence of velocity errors, the Q sensitivity kernels calculated using the memory strain variables with method I and the adjoint-state method suffer from fewer trade-offs. The inverted Q models are also more accurate than those obtained by method II;

  4. 4.

    Furthermore, method II appears to converge more slowly and is almost two times more expensive than the other methods for simultaneous velocity and Q estimation.

This paper is organized as follows. The basic principles of viscoelastic FWI and forward modeling based on the GSLS rheology are first given. Then, previous theories for constructing the attenuation sensitivity kernels are reviewed. An adjoint-state (or Lagrangian multiplier) method for deriving and calculating the viscoelastic FWI sensitivity kernels is introduced. In the numerical modeling section, two synthetic examples are provided to analyze the sensitivity kernels obtained by different methods and evaluate their performances for inversion.

2 Theory and Methods

2.1 Principle of Viscoelastic FWI and Forward Simulation

In a common FWI framework, underground parameters are gradually refined by minimizing the least-squared differences between modeled data \({\textbf {u}}\) and practical seismic recordings \({\textbf {d}}\). However, because the data fitting procedure is highly nonlinear, the standard waveform-difference objective function suffers from cycle skipping problem seriously. The envelope \({\textbf {E}}\) measures the instantaneous amplitude of a seismic signal \({\textbf {s}}\)

$$\begin{aligned} {\textbf {E}}=\sqrt{{\textbf {s}}^2+\left[ {\mathcal {H}}\left( {\textbf {s}}\right) \right] ^2}, \end{aligned}$$
(1)

where \({\mathcal {H}}\) represents Hilbert transform. In FWI studies and applications, the envelope-based objective functions are widely used to reduce cycle skipping difficulty (Wu et al. 2014; Yuan et al. 2015; Pan et al. 2019). Pan and Wang (2020) showed that the envelope-difference objective function exhibits stronger sensitivity to Q anomaly and can naturally balance the velocity and Q updates for effective inversion. Thus, in this study, an envelope-difference objective function \(\phi\) is introduced to invert for the velocity and Q models in viscoelastic FWI

$$\begin{aligned} \phi \left( {\textbf {m}}\right) =\frac{1}{2}\sum _{{{\textbf {x}}}_r} \int _0^{t_{\textrm{max}}}\int _{V}\Vert {\textbf {E}}\left( {\textbf {m}}\right) -{\textbf {E}}^{\textrm{obs}}\Vert _{2}^2\hbox {d}{} {\textbf {x}}\hbox {d}t, \end{aligned}$$
(2)

where \(\Vert \cdot \Vert _{2}\) represents \(l_{2}\) norm, \({\textbf {x}}_r\) represent the positions of seismometers, \({\textbf {m}}\) indicate physical properties (e.g., velocity or modulus) describing subsurface media, \(t_{\textrm{max}}\) is the length of recording time, V denotes the underground space, \({\textbf {E}}\) and \({\textbf {E}}^{\textrm{obs}}\) indicate the envelopes of synthetic and observed data, respectively. Because the model sizes and data sets in the inversion applications of exploration and global seismology are usually extremely large, the local Newton optimization approach is commonly used to solve the inverse problem. At each updating loop, the search direction \(\Delta {\textbf {m}}\) can be obtained by solving the Newton linear system

$$\begin{aligned} {\textbf {H}}\Delta {\textbf {m}}=-{\textbf {g}}, \end{aligned}$$
(3)

where \({\textbf {g}}=\nabla _{{{\textbf {m}}}}\phi\) and \({\textbf {H}}=\nabla ^2_{{{\textbf {m}}}}\phi\) are the gradient and Hessian matrix. The gradient in Eq. 3 can be derived as (Bozdağ et al. 2011; Pan and Wang 2020)

$$\begin{aligned} \nabla _{{{\textbf {m}}}}\phi \left( {\textbf {m}}\right) =\sum _{{{\textbf {x}}}_r}\int _{0}^{t_{\textrm{max}}}\int _{V} \frac{\partial {\textbf {u}}^{*}\left( {\textbf {m}}\right) }{\partial {\textbf {m}}} \delta {\textbf {E}}{} {\textbf {u}}-\frac{\partial {\textbf {u}}^{*} \left( {\textbf {m}}\right) }{\partial {\textbf {m}}}{\mathcal {H}} \left[ \delta {\textbf {E}}{\mathcal {H}}\left( {\textbf {u}}\right) \right] \hbox {d}{} {\textbf {x}}\hbox {d}t, \end{aligned}$$
(4)

where \(*\) indicates complex conjugate transpose, \(\delta {\textbf {E}}=\left( {\textbf {E}}-{\textbf {E}}^{\textrm{obs}}\right) /{\textbf {E}}\) is relative change of the envelope, and the Fréchet derivative wavefield \(\partial {\textbf {u}}/\partial {\textbf {m}}\) measures the wavefield perturbation due to the perturbations of model parameters. Thus, the adjoint source of the envelope-difference misfit function can be obtained as

$$\begin{aligned} {\textbf {f}}^{\dag }=\delta {\textbf {E}}{} {\textbf {u}}-{\mathcal {H}} \left[ \delta {\textbf {E}}{\mathcal {H}}\left( {\textbf {u}}\right) \right] . \end{aligned}$$
(5)

Following Tromp et al. (2005), we reformulate the gradient as

$$\begin{aligned} \nabla _{{{\textbf {m}}}}\phi \left( {\textbf {m}}\right) =-\frac{K_{{{\textbf {m}}}}}{{\textbf {m}}}, \end{aligned}$$
(6)

where \(K_{{{\textbf {m}}}}\) denotes the sensitivity kernel corresponding to relative model perturbation \(\Delta {\textbf {m}}/{\textbf {m}}\). For (very) large-scale inversion applications in earthquake and exploration seismology, explicitly calculating the Hessian matrix and/or its inverse is computationally unaffordable. In this type of gradient-based optimization methods, the Hessian matrix and/or its inverse is generally ignored. In truncated-Newton methods (Métivier et al. 2013; Yong et al. 2022), the linear system in Eq. 4 is approximately solved with conjugate-gradient algorithms. In this study, we use a quasi-Newton l-BFGS optimization method to construct the search direction \(\Delta {\textbf {m}}\), wherein the inverse Hessian is approximated by the gradient and model changes within a limited number of previous iterations (Nocedal and Wright 2006). The inverse Hessian approximation is applied to precondition the gradients using a “two-loop” recursion scheme (Nocedal and Wright 2006). At the \(\hat{k}\)th iteration, the underground properties are corrected by

$$\begin{aligned} {\textbf {m}}_{\hat{k}+1}={\textbf {m}}_{\hat{k}} +\alpha _{\hat{k}}\Delta {\textbf {m}}_{\hat{k}}, \end{aligned}$$
(7)

where \(\alpha _{\hat{k}}\) is the step length determined using a backtracking line search method.

In viscoelastic FWI, a larger number of forward simulations need to be performed for obtaining the synthetic data \({\textbf {u}}\). Seismic wave propagation in a linear viscoelastic solid is governed by the following momentum equation and constitutive law

$$\begin{aligned}&\rho \partial ^2_{t}{} {\textbf {u}}=\nabla \cdot \mathbf {\sigma }+{\textbf {f}}, \end{aligned}$$
(8a)
$$\begin{aligned}&\varvec{\sigma }\left( t\right) =\int _{0}^{t}{} {\textbf {c}}\left( t-t^\prime \right) : \partial _{t^\prime }\varvec{\varepsilon }\left( t^\prime \right) \hbox {d}t^\prime , \end{aligned}$$
(8b)

where \(\rho\) denotes the distribution of mass density, \({\textbf {f}}\) is the source term vector, : indicates double tensor contraction operation and, in a linear viscoelastic solid, the stress tensor \(\varvec{\sigma }\) is determined by the entire history of strain fields and can be formulated as the convolution between relaxation function \({\textbf {c}}\) and time derivative of the stress tensor \(\varvec{\varepsilon }\) (or displacement gradient \(\nabla {\textbf {u}}\)) (Liu et al. 1976; Robertsson et al. 1994). The relaxation function \({\textbf {c}}\) determines the anelastic behavior of the materials, which can be modeled using the phenomenological model represented mechanically by a combination of springs and dash spots. The system constructed by parallel connection of N standard linear elements is referred to as the GSLS rheology. The relaxation function of Zener model writes

$$\begin{aligned} {\textbf {c}}\left( t\right) ={\textbf {c}}^{R}\left[ 1-\frac{1}{N} \sum _{p=1}^{N}\left( 1-\frac{\varvec{\tau }^{\varepsilon p}}{\tau ^{\sigma p}}\right) e^{-t/\tau ^{\sigma p}}\right] H\left( t\right) , \end{aligned}$$
(9)

where \({\textbf {c}}^{R}\) is the relaxed modulus, \(H\left( t\right)\) is the Heaviside step function, and \(\varvec{\tau }^{\varepsilon p}\) and \(\tau ^{\sigma p}\) indicate the strain and stress relaxation times of the pth rheological body, respectively (Blanch et al. 1995; Bohlen 2002). However, the convolution in Hooke’s law impedes numerical simulation of the viscoelastic waves. To overcome this problem, we can apply time derivative to the stress tensor, leading to

$$\begin{aligned} \partial _{t}\varvec{\sigma }={\textbf {c}}^{R}: \frac{\varvec{\tau }^{\varepsilon p}}{\tau ^{\sigma p}}: \partial _{t}\varvec{\varepsilon }-\sum _{p=1}^{N}{} {\textbf {c}}^{R}: \left( \frac{\varvec{\tau }^{\varepsilon p}}{\tau ^{\sigma p}}-1\right) :\varvec{\epsilon }^p, \end{aligned}$$
(10)

where \(\varvec{\epsilon }^p\) refers to the tensor of memory strain variables, which describe anelastic characteristics of the wavefields

$$\begin{aligned} \varvec{\epsilon }^p\left( t\right) =\frac{1}{N\tau ^{\sigma p}} \int _{0}^{t}e^{-\left( t-t^\prime \right) /\tau ^{\sigma p}}H \left( t-t^{\prime }\right) \partial _{t^\prime }\varvec{\varepsilon } \left( t^{\prime }\right) \hbox {d}t^{\prime }, \end{aligned}$$
(11)

and the memory variables satisfy the following differential equation

$$\begin{aligned} \partial _t\varvec{\epsilon }^p=-\frac{\varvec{\epsilon }^p}{\tau ^{\sigma p}} +\frac{1}{N}\frac{\partial _t\varvec{\varepsilon }}{\tau ^{\sigma p}}. \end{aligned}$$
(12)

Thus, by introducing the memory strain variables, the damping effects of attenuation on propagating waves in a dissipative medium can be modeled by solving several equations numerically with the superposition of N parallel relaxation mechanisms (Blanch et al. 1995). In viscoelastic forward simulations and adjoint inversion, if different numbers of parallel relaxation mechanisms N are used, additional inversion uncertainties may be introduced. Thus, \(N=3\) is used for modeling the attenuation effects in all of the numerical experiments presented in this study. Considering isotropy in attenuating media, the relaxation function can be expressed with bulk modulus \(\kappa\) and shear modulus \(\mu\)

$$\begin{aligned} c_{ijkl}=\kappa \delta _{ij}\delta _{kl}+\mu \left( \delta _{ik} \delta _{jl}+\delta _{il}\delta _{jk}-\tfrac{2}{3}\delta _{ij}\delta _{kl}\right) , \end{aligned}$$
(13)

where \(\delta _{ij}\) is the Kronecker delta function, and i, j, k, l take on the values of x, z for 2D media.

In this study, we use a time-domain spectral element (SEM) method to simulate the viscoelastic wave propagation (Komatitsch and Tromp 1999). In SEM, the weak formulation of the momentum equation is solved on the mesh of hexahedral elements, on which the wavefield is discretized using high-degree Lagrange interpolants and integrated using the Gauss-Lobatto-Legendre (GLL) rule. Compared to the other forward modeling methods, SEM combines the flexibility of finite element methods for incorporating irregular topography with the high accuracy of pseudo-spectral methods.

2.2 Construct Q Model

Q is commonly used to quantify and describe the damping effects of intrinsic attenuation on propagating seismic waves. Smaller Q values imply stronger attenuation. In frequency-domain, \(\tilde{Q}\) is defined by

$$\begin{aligned} \tilde{Q}\left( \omega \right) =\frac{{\mathbb {R}} \left[ \tilde{{\textbf {c}}}\left( \omega \right) \right] }{{\mathbb {I}} \left[ \tilde{{\textbf {c}}}\left( \omega \right) \right] }, \end{aligned}$$
(14)

where \(\omega\) denotes angular frequency, \({\mathbb {R}}\) and \({\mathbb {I}}\) mean real and imaginary parts, respectively, and \(\tilde{{\textbf {c}}}\) indicates the time derivative of \({\textbf {c}}\) in frequency-domain

$$\begin{aligned} \tilde{{\textbf {c}}}\left( \omega \right) ={\mathcal {F}} \left[ \partial _t{\textbf {c}}\left( t\right) \right] ={\textbf {c}}^{R}\left( 1+\frac{\text {i}\omega }{N} \sum _{p=1}^{N}\frac{\varvec{\tau }^{p}\tau ^{\sigma p}}{1+\text {i} \omega \tau ^{\sigma p}}\right) , \end{aligned}$$
(15)

where \({\mathcal {F}}\) means forward Fourier transform, \(\text {i}\) denotes the imaginary unit, and \(\varvec{\tau }^{p}\) describes the strength of viscoelastic attenuation

$$\begin{aligned} \varvec{\tau }^{p}=\frac{\varvec{\tau }^{\varepsilon p}}{\tau ^{\sigma p}}-1. \end{aligned}$$
(16)

Thus, reciprocal of \(\tilde{Q}\) becomes

$$\begin{aligned} \frac{1}{\tilde{Q}\left( \omega \right) }=\frac{{\mathbb {I}} \left[ \tilde{{\textbf {c}}}\left( \omega \right) \right] }{{\mathbb {R}} \left[ \tilde{{\textbf {c}}}\left( \omega \right) \right] } =\frac{\varvec{\tau }^{p}\sum _{p=1}^N\frac{\omega \tau ^{\sigma p}}{1+\left( \omega \tau ^{\sigma p}\right) ^2}}{N+\varvec{\tau }^{p} \sum _{p=1}^N\frac{\left( \omega \tau ^{\sigma p}\right) ^2}{1+\left( \omega \tau ^{\sigma p}\right) ^2}}. \end{aligned}$$
(17)

To fit a given quality factor \(Q^{-1}_{0}\) over a range of angular frequencies \(\left[ \omega _{\textrm{min}}, \omega _{\textrm{max}}\right]\), the parameters of relaxation times \(\varvec{\tau }^{p}\) and \(\tau ^{\sigma p}\) can be obtained by minimizing the distance between \(Q^{-1}_{0}\) and Eq. 17 through a least-squares optimization process (Emmerich and Korn 1987). However, in the classical approach given in Emmerich and Korn (1987), the results of \(\varvec{\tau }^{\varepsilon p}<\tau ^{\sigma p}\) may be obtained, which is not suitable both physically and mathematically (Blanc et al. 2016). Thus, in this study, according to Blanc et al. (2016), the following objective function is introduced

$$\begin{aligned} {\mathcal {J}}\left( \varvec{\tau }^{p}, \tau ^{\sigma p}; N, R\right) =\sum _{r=1}^{R}\left\| \sum _{p=1}^{N}\frac{\omega _{r}\tau ^{\sigma p}Q_{0} \left( \omega _{r}\right) -\left( \omega _{r}\tau ^{\sigma p}\right) ^2}{1+\left( \omega _{r}\tau ^{\sigma p}\right) ^2}\frac{\varvec{\tau }^{p}}{N}-1\right\| _{2}^2, \end{aligned}$$
(18)

where \(r=1,...,R\) indicates the index of angular frequencies that are distributed linearly on a logarithmic scale of R points (Blanc et al. 2016). In this study, we minimize the objection function \({\mathcal {J}}\) using the nonlinear SolvOpt optimization algorithm with the positivity constraint of \(\varvec{\tau }^{\varepsilon p}>\tau ^{\sigma p}>0\) \(\forall p\) (p is integer) (Kappel and Kuntsevich 2000; Kuntsevich and Kappel 1997). This approach is more accurate than the classical linear optimization method.

2.3 Sensitivity Kernels of Different Methods for Viscoelastic FWI

Sensitivity kernels are essential for effective model updates in viscoelastic FWI. However, as described above, the attenuation effects are modeled by superimposing N standard linear damping mechanisms without explicit description of Q in the rheological bodies with the GSLS model. Instead, a finite and constant Q within seismic frequency band is approximated through an optimization procedure. Thus, it becomes problematic and complex to derive and construct the Q sensitivity kernels for viscoelastic FWI.

Based on the GSLS forward modeling engine in time-domain, different frameworks have been suggested to construct the viscoelastic FWI sensitivity kernels. However, discrepancies exist between these methods, which gives rise to the problem of determining the best approach for sensitivity kernels calculation. In the following sections, we first revisit the previous theories for calculating the viscoelastic sensitivity kernels and then introduce the adjoint-state method for deriving and calculating the sensitivity kernels.

2.3.1 Method I

Charara et al. (2000) derived the sensitivity kernels for unrelaxed moduli and attenuation parameters with a perturbation approach based on Born approximation. At time \(t=0^{+}\), the relaxation function \({\textbf {c}}\) reduces to the unrelaxed stiffness tensor \({\textbf {c}}^{U}\) corresponding to the high-frequency limit

$$\begin{aligned} {\textbf {c}}^{U}={\textbf {c}}^{R}\left[ 1+\frac{1}{N}\sum _{p=1}^{N} \varvec{\tau }^{p}\right] ={\textbf {c}}^{R}\left( 1+\varvec{\tau }^{p}\right) . \end{aligned}$$
(19)

The difference between relaxed and unrelaxed stiffness tensors is given by

$$\begin{aligned} \delta {\textbf {c}}={\textbf {c}}^{R}-{\textbf {c}}^{U}=-\varvec{\tau }^{p} {\textbf {c}}^{R}=-\frac{\varvec{\tau }^{p}}{\left( 1+\varvec{\tau }^{p}\right) }{} {\textbf {c}}^{U}. \end{aligned}$$
(20)

The stiffness difference \(\delta {\textbf {c}}\), which is proportional to \(\varvec{\tau }^{p}\), measures the attenuation magnitude and is defined as the attenuation parameter that remains to be estimated in this method. The relaxation function can be expressed in terms of \({\textbf {c}}^{U}\) and \(\delta {\textbf {c}}\)

$$\begin{aligned} {\textbf {c}}\left( t\right) =\left( {\textbf {c}}^{U}+\delta {\textbf {c}}\right) \left( 1+\frac{1}{N}\sum _{p=1}^{N}\varvec{\tau }^{p}e^{-t/\tau ^{\sigma p}}\right) H\left( t\right) . \end{aligned}$$
(21)

Within the seismic frequency band, the ratio of \({\textbf {c}}^{U}\) to \({\textbf {c}}^{R}\) can be assumed to be constant (Carcione 2004; Charara et al. 2000)

$$\begin{aligned} \frac{{\textbf {c}}^{U}}{{\textbf {c}}^{R}}=\frac{\varvec{\tau }^{\varepsilon p}}{\tau ^{\sigma p}}=\text {constant}. \end{aligned}$$
(22)

Thus, the first-order derivative of relaxation function with respect to time can be expressed as

$$\begin{aligned} \partial _t{\textbf {c}}\left( t\right) ={\textbf {c}}^U +\delta {\textbf {c}}\left( \frac{1}{N}\sum _{p=1}^N \frac{1}{\tau ^{\sigma p}}e^{-t/\tau ^{\sigma p}}\right) H\left( t\right) . \end{aligned}$$
(23)

Inserting Eq. 23 into the constitutive relation yields

$$\begin{aligned}&\varvec{\sigma }={\textbf {c}}^{U}:\varvec{\varepsilon }+\delta {\textbf {c}}:\sum _{n=1}^{N}{} {\textbf {r}}^{p}, \end{aligned}$$
(24a)
$$\begin{aligned}&{\textbf {r}}^p\left( t\right) =\frac{1}{N\tau ^{\sigma p}} \int ^{t}_{0}e^{-\left( t-t^\prime \right) /\tau ^{\sigma p}} H\left( t-t^\prime \right) \varvec{\varepsilon }\left( t^\prime \right) \hbox {d}t^\prime , \end{aligned}$$
(24b)

where \({\textbf {r}}^{p}\) is the tensor of memory strain variables. Note that \({\textbf {r}}^{p}\) is slightly different from \(\varvec{\epsilon }^p\) in Eq. 11, which involves the time derivative of the strain tensor.

Supposing that a viscoelastic anomaly is embedded in an infinite homogeneous background, the model perturbations are \(\Delta \rho\), \(\Delta {\textbf {c}}^{U}\) and \(\Delta \delta {\textbf {c}}\). The wavefield perturbation can be expressed as

$$\begin{aligned} \Delta {\textbf {u}}={\textbf {u}}-{\textbf {u}}^{0}, \end{aligned}$$
(25)

where \({\textbf {u}}^{0}\) indicates the displacement wavefield propagating in the unperturbed media. Inserting the perturbations of model properties and wavefield into the equation of motion (Eq. 8) gives

$$\begin{aligned}&\left( \rho +\Delta \rho \right) \partial ^2_t\left( {\textbf {u}} +\Delta {\textbf {u}}\right) -\nabla \cdot \left( \varvec{\sigma } +\Delta \varvec{\sigma }\right) ={\textbf {f}},\nonumber \\&\varvec{\sigma }+\Delta \varvec{\sigma }=\left( {\textbf {c}}^{U} +\Delta {\textbf {c}}^{U}\right) :\left( \varvec{\varepsilon } +\Delta \varvec{\varepsilon }\right) +\left( \delta {\textbf {c}} +\Delta \delta {\textbf {c}}\right) :\sum _{p=1}^{N} \left( {\textbf {r}}^{p}+\Delta {\textbf {r}}^{p}\right) . \end{aligned}$$
(26)

where \(\Delta \varvec{\sigma }\) and \(\Delta {\textbf {r}}^{p}\) refer to the perturbed stress tensor and memory strain variables, respectively. Under the Born approximation (or single scattering approximation), the high-order terms in Eq. 26 can be ignored, which gives the following wave equation

$$\begin{aligned}&\rho \partial ^2_t\Delta {\textbf {u}}-\nabla \cdot \left( {\textbf {c}}^{R}: \Delta \varvec{\varepsilon }+\delta {\textbf {c}}:\sum _{p=1}^{N} \Delta {\textbf {r}}^p\right) =\nabla \cdot \Delta {\textbf {M}} -\Delta \rho \partial ^2_t{\textbf {u}}, \end{aligned}$$
(27a)
$$\begin{aligned}&\Delta {\textbf {M}}=\Delta {\textbf {c}}^{R}:\varvec{\varepsilon } +\Delta \delta {\textbf {c}}:\sum _{p=1}^{N}{} {\textbf {r}}^{p}. \end{aligned}$$
(27b)

where \(\Delta {\textbf {M}}\) is the equivalent moment tensor source. As can be seen the propagation of the perturbed seismic waves caused by model changes is described by Eq. 27. Interaction of the incident wave with model perturbations on the right side of Eq. 27a serves as the virtual scattering source. Based upon integration by parts and applying far-field approximation, the solution of Eq. 27 can be written using Green’s function G with the representation theory (Charara et al. 2000; Pan et al. 2016)

$$\begin{aligned} \Delta {\textbf {u}}=-\int _{V}\int _0^{t_{\textrm{max}}} \left[ \Delta \rho \left( {\textbf {G}}\cdot \partial ^2_t {\textbf {u}}\right) +\nabla {\textbf {G}}:\Delta {\textbf {c}}^{U}: \varvec{\varepsilon }+\nabla {\textbf {G}}:\Delta \delta {\textbf {c}}: \sum _{p=1}^{N}{} {\textbf {r}}^{p}\right] \hbox {d}t \hbox {d}{} {\textbf {x}}. \end{aligned}$$
(28)

The isotropic and viscoelastic media can be described with the model parameters of density \(\rho\), unrelaxed bulk and shear moduli (\(\kappa ^{U}\) and \(\mu ^{U}\)), and the corresponding moduli differences \(\delta \kappa =\kappa ^{R}-\kappa ^{U}\) and \(\delta \mu =\mu ^{R}-\mu ^{U}\) (or attenuation parameters). Taking partial derivatives of the wavefield perturbation with respect to the perturbations of these model parameters, we can obtain the Fréchect derivative wavefields. Then, the sensitivity kernels can be derived as

$$\begin{aligned}&K_{\kappa ^{U}}=-\kappa ^{U}\left( \nabla \cdot {\textbf {u}}^{\dag }\right) \left( \nabla \cdot {\textbf {u}}\right) , \end{aligned}$$
(29a)
$$\begin{aligned}&K_{\mu ^{U}}=-2\mu ^{U} {\textbf {D}}^{\dag }:{\textbf {D}}, \end{aligned}$$
(29b)
$$\begin{aligned}&K_{\delta \kappa }=-\delta \kappa \left( \nabla \cdot {\textbf {u}}^{\dag }\right) \sum _{p=1}^{N}\hat{{\textbf {r}}}^{p}, \end{aligned}$$
(29c)
$$\begin{aligned}&K_{\delta \mu }=-2\delta \mu {\textbf {D}}^{\dag }: \sum _{p=1}^{P}\check{{\textbf {r}}}^{p}, \end{aligned}$$
(29d)

where \({\textbf {u}}^{\dag }={\textbf {G}}\otimes {\textbf {f}}^{\dag }\) is the adjoint displacement field, \(\otimes\) represents convolution, \({\textbf {D}}=\left[ \nabla {\textbf {u}}+\left( \nabla {\textbf {u}}\right) ^{T} \right] /2-\left( \nabla \cdot {\textbf {u}}\right) {\textbf {I}}/3\) (T means matrix transpose) and \({\textbf {D}}^{\dag }\) are the traceless strain deviator and its adjoint, \(\hat{{\textbf {r}}}^{p}\) and \(\check{{\textbf {r}}}^{p}\) are the trace and deviatoric parts of \({\textbf {r}}^{p}\). For sake of compactness, we ignore the integrations over time, volume, sources and receivers in Eq. 29. In this study, we ignore the influence of density for viscoelastic FWI and thus the density kernel \(K_{\rho }\) is not presented. We observe that in method I, the unrelaxed moduli sensitivity kernels \(K_{\kappa ^{U}}\) and \(K_{\mu ^{U}}\) are the same with the moduli sensitivity kernels in purely isotropic and elastic media. The sensitivity kernels \(K_{\delta \kappa }\) and \(K_{\delta \mu }\) for attenuation parameters can be constructed by cross-correlating the forward memory strain variables and adjoint displacement wavefields.

2.3.2 Method II

In this section, we follow the approach given by Tromp et al. (2005) to derive the Q sensitivity kernels for viscoelastic FWI. With the assumption that Q is constant over a wide range of seismic frequencies, in frequency domain, the modulus \(\tilde{W}\) is associated the corresponding quality factor \(\tilde{Q}_{W}\) by

$$\begin{aligned} \frac{\tilde{W}\left( \omega \right) }{\tilde{W}\left( \omega _0\right) } =1+\frac{2}{\pi \tilde{Q}_{W}}\text {ln}\frac{|\omega |}{\omega _0} -\text {i } \text {sgn}\left( \omega \right) \frac{1}{\tilde{Q}_{W}}, \end{aligned}$$
(30)

where \(\omega _0\) means reference angular frequency, the symbols ln and \(\text {sgn}\) indicate natural logarithm and step function, respectively (Kolsky 1952; Futterman 1962; Dahlen and Tromp 1998; Tromp et al. 2005). Variation of the modulus due to the perturbation of \(\tilde{Q}_{W}\) can be derived as (Pan and Wang 2020)

$$\begin{aligned} \Delta \tilde{W}\left( \omega \right) =\frac{\tilde{W} \left( \omega _0\right) }{\tilde{Q}^2_{W}}\left[ -\frac{2}{\pi } \text {ln}\frac{|\omega |}{\omega _0}+\text {i } \text {sgn}\left( \omega \right) \right] \Delta \tilde{Q}_{W}. \end{aligned}$$
(31)

Using the chain rule and frequency-domain Born scattering integral, the sensitivity kernels for moduli quality factors (\(Q_{\kappa }\) and \(Q_{\mu }\)) can be expressed in terms of the corresponding moduli sensitivity kernels

$$\begin{aligned}&K_{Q_{\kappa }}=-\frac{K^{\textrm{iso}}_{\kappa }}{Q_{\kappa }} =\frac{\kappa }{Q_{\kappa }}\left( \nabla \cdot {\textbf {u}}^{\dag }\right) \left( \nabla \cdot {\textbf {u}}\right) , \end{aligned}$$
(32a)
$$\begin{aligned}&K_{Q_{\mu }}=-\frac{K^{\textrm{iso}}_{\mu }}{Q_{\mu }}=\frac{2\mu }{Q_{\kappa }} \left( {\textbf {D}}^{\dag }:{\textbf {D}}\right) , \end{aligned}$$
(32b)

where \(K^{\textrm{iso}}_{\kappa }\) and \(K^{\textrm{iso}}_{\mu }\) are the moduli sensitivity kernels in purely isotropic and elastic media (Tromp et al. 2005). However, a different adjoint source \({\textbf {f}}^{\dag }_{Q}\) is needed for calculating the adjoint wavefields in Eq. 32

$$\begin{aligned} {\textbf {f}}^{\dag }_{Q}\left( t\right) =\frac{1}{2\pi }\int _{-\infty }^{+\infty } \left[ \underbrace{\frac{2}{\pi }\text {ln} \frac{|\omega |}{\omega _0}}_{\textrm{dispersion}} -\underbrace{{\textbf {i}}\text {sgn}\left( \omega \right) }_{\textrm{dissipation}}\right] \tilde{{\textbf {f}}}^{\dag }\left( \omega \right) e^{{{\textbf {i}}}\omega t}d\omega , \end{aligned}$$
(33)

where \(\tilde{{\textbf {f}}}^{\dag }\) is the regular adjoint source of envelope-difference objective function (Eq. 5) in frequency-domain (Tromp et al. 2005). The first term in adjoint source \({\textbf {f}}^{\dag }_{Q}\) involving \(\text {ln}\left( \omega /\omega _0\right)\) controls the physical dispersion of the seismic signals, whereas the second term is simply the Hilbert transform of the regular adjoint source \({\textbf {f}}^{\dag }\) measuring dissipation of the seismic amplitudes (Bozdağ et al. 2011). Under this formulation, the moduli sensitivity kernels \(K_{\kappa }\) and \(K_{\mu }\) are the same as those in purely isotropic and elastic media. It means that when simultaneously inverting for moduli and Q parameters, different adjoint sources are needed to construct the adjoint wavefields, which doubles the computational cost for sensitivity kernel calculation. Furthermore, we realize that the Q sensitivity kernels in Eq. 32 and adjoint source \({\textbf {f}}^{\dag }_{Q}\) are derived utilizing the attenuation physical mechanism defined by Kolsky (1952) and Futterman (1962), which is different from the GSLS rheology used in the viscoelastic forward modeling. The modeling errors between two different physical models may produce unexpected uncertainties for Q inversion in this method (Keating and Innanen 2019).

2.3.3 Adjoint-State Method

According to Fichtner and van Driel (2014), the relaxation parameters are selected by minimizing the objective function \({\mathcal {J}}\) (Eq. 18) such that \(\varvec{\tau }^{p}\) is approximately equal to the inverse of Q. Thus, the relaxation function can be expressed in terms of Q:

$$\begin{aligned} {\textbf {c}}\left( t\right) ={\textbf {c}}^{R}\left( 1+\frac{1}{N} \sum _{p=1}^{N}\frac{1}{Q}e^{-t/\tau ^{\sigma p}}\right) H\left( t\right) . \end{aligned}$$
(34)

In this condition, the Q sensitivity kernels in viscoelastic FWI can be directly derived following the standard adjoint-state method by inserting the above constitutive relation into the equation of motion (Eq. 8). The Lagrangian formulation of the envelope-difference objective function can be written as

$$\begin{aligned} \tilde{\phi }\left( {\textbf {m}}\right) =\frac{1}{2}\sum _{{{\textbf {x}}}_r} \int _0^{t_{\textrm{max}}} \Vert {\textbf {E}}\left( {\textbf {m}}\right) -{\textbf {E}}^{{{\textbf {obs}}}}\Vert _{2}^2\hbox {d}t-\int _0^{t_{\textrm{max}}} \int _{V}\varvec{\lambda }\cdot \left( \rho \partial ^2_t{\textbf {u}} -\nabla \cdot \varvec{\sigma }-{\textbf {f}}\right) \hbox {d}{} {\textbf {x}}\hbox {d}t, \end{aligned}$$
(35)

where \(\varvec{\lambda }\) is Lagrangian multiplier. In isotropic media, the quality factors \(Q_{\kappa }\) and \(Q_{\mu }\) can be incorporated into the constitutive relation with the enforcement of \(\tau _{\kappa }=Q^{-1}_{\kappa }\) and \(\tau _{\mu }=Q^{-1}_{\mu }\), yielding

$$\begin{aligned} \sigma _{ij}^{\textrm{iso}}\left( t\right)&=\kappa ^R\delta _{ij}\delta _{kl} \left[ 1+\frac{1}{N}\sum _{p=1}^N\frac{1}{Q_{\kappa }}e^{-t/\tau ^{\sigma p}}\right] H\left( t\right) \otimes \partial _t{\varepsilon }_{kl}\nonumber \\&\quad +\mu ^R\left( \delta _{ik}\delta _{jl}+\delta _{il}\delta _{jk} -\frac{2}{3}\delta _{ij}\delta _{kl}\right) \left[ 1+\frac{1}{N} \sum _{p=1}^N\frac{1}{Q_{\mu }}e^{-t/\tau ^{\sigma p}}\right] H \left( t\right) \otimes \partial _t{\varepsilon }_{kl}. \end{aligned}$$
(36)

Inserting Eq. 36 into Eq. 35 and following the derivation process in adjoint-state method with integration by parts and divergence theorem (Liu and Tromp 2006), the variation of the Lagrangian objective function due to the perturbations of the model parameters \(\rho\), \(\kappa\), \(\mu\), \(Q_{\kappa }\) and \(Q_{\mu }\) can be derived as

$$\begin{aligned} \Delta \tilde{\phi }\left( {\textbf {m}}\right)&=\int _0^{t_{\textrm{max}}} \int _{V}\sum _{{{\textbf {x}}}_r}\left[ {\textbf {E}}\left( {\textbf {m}}\right) -{\textbf {E}}^{{{\textbf {obs}}}}\right] \cdot \Delta {\textbf {E}}\hbox {d}{} {\textbf {x}}\hbox {d}t\nonumber \\&\quad -\int _0^{t_{\textrm{max}}}\int _{V}\left( \rho \partial ^2_t\varvec{\lambda }-\nabla \cdot \varvec{\sigma }^{\textrm{iso}}\right) \cdot \Delta {\textbf {E}}\hbox {d}{} {\textbf {x}}\hbox {d}t\nonumber \\&\quad -\int _0^{t_{\textrm{max}}}\int _{V}\Delta \rho \varvec{\lambda }\cdot \partial ^2_t {\textbf {u}}\hbox {d}{} {\textbf {x}}\hbox {d}t\nonumber \\&\quad -\int _0^{t_{\textrm{max}}}\int _{V}\left[ \left( \Delta \kappa \otimes \partial _t \hat{\tilde{\varvec{\varepsilon }}}\right) \nabla \cdot {\textbf {u}} +2\left( \Delta \mu \otimes \partial _t\check{\tilde{\varvec{\varepsilon }}}\right) : {\textbf {D}}\right] \hbox {d}{} {\textbf {x}}\hbox {d}t\nonumber \\&\quad +\int _0^{t_{\textrm{max}}}\int _{V}\left( \Delta Q_{\kappa } \frac{\kappa ^{R}}{Q^{2}_{\kappa }}\sum _{p=1}^{N}\tau ^{\sigma p} \hat{\tilde{\varvec{\epsilon }}}^{p}\right) \nabla \cdot {\textbf {u}}\hbox {d}{} {\textbf {x}}\hbox {d}t\nonumber \\&\quad +\int _0^{t_{\textrm{max}}}\int _{V}\left( \Delta Q_{\mu }\frac{\mu ^{R}}{Q^{2}_{\mu }} \sum _{p=1}^{N}\tau ^{\sigma p}\check{\tilde{\varvec{\epsilon }}}^{p}\right) : {\textbf {D}}\hbox {d}{} {\textbf {x}}\hbox {d}t, \end{aligned}$$
(37)

where \(\Delta {\textbf {E}}\) represents the perturbation of envelope due to model variation, \(\tilde{\varvec{\varepsilon }}=\nabla \varvec{\lambda }\) is the Lagrangian strain field, \(\hat{\tilde{\varvec{\varepsilon }}}\) and \(\check{\tilde{\varvec{\varepsilon }}}\) mean the trace and deviatoric parts of \(\tilde{\varvec{\varepsilon }}\), \(\hat{\tilde{\varvec{\epsilon }}}^{p}\) and \(\check{\tilde{\varvec{\epsilon }}}^{p}\) indicate the trace and deviatoric parts of Lagrangian memory strain variables \(\tilde{\varvec{\epsilon }}^{p}\):

$$\begin{aligned} \tilde{\varvec{\epsilon }}^{p}\left( t\right) =\frac{1}{N\tau ^{\sigma p}} e^{-t/\tau ^{\sigma p}}H\left( t\right) \otimes \partial _t\tilde{\varvec{\varepsilon }}. \end{aligned}$$
(38)

As described in Métivier et al. (2013), the Lagrangian is stationary with respect to \(\Delta {\textbf {E}}\) in the absence of the model perturbations. Thus, the adjoint-state equation can be obtained when the coefficient of \(\Delta {\textbf {E}}\) becomes zero

$$\begin{aligned} \rho \partial ^2_t\varvec{\lambda }-\nabla \cdot \varvec{\sigma }^{\textrm{iso}} =\delta {\textbf {E}}{} {\textbf {u}}-{\mathcal {H}}\left[ \delta {\textbf {E}}{\mathcal {H}}\left( {\textbf {u}}\right) \right] . \end{aligned}$$
(39)

We define the adjoint displacement field \({\textbf {u}}^{\dag }\) as time-reversed Lagrangian field \(\varvec{\lambda }\left( t_{\textrm{max}}-t\right)\). Then, the sensitivity kernels for the \(\kappa\), \(\mu\), \(Q_{\kappa }\) and \(Q_{\mu }\) models based on the adjoint-state method can be obtained as

$$\begin{aligned}&K_{\kappa }=-\left( \kappa \otimes \partial _t\hat{\varvec{\varepsilon }}^{\dag }\right) \nabla \cdot {\textbf {u}}, \end{aligned}$$
(40a)
$$\begin{aligned}&K_{\mu }=-\left( \mu \otimes \partial _t \check{\varvec{\varepsilon }}^{\dag }\right) :{\textbf {D}}, \end{aligned}$$
(40b)
$$\begin{aligned}&K_{Q_{\kappa }}=\left( \frac{\kappa ^{R}}{Q_{\kappa }}\sum _{p=1}^{N} \tau ^{\sigma p}\hat{\varvec{\epsilon }}^{p,\dag }\right) \nabla \cdot {\textbf {u}}, \end{aligned}$$
(40c)
$$\begin{aligned}&K_{Q_{\mu }}=\left( \frac{\mu ^{R}}{Q_{\mu }}\sum _{p=1}^{N}\tau ^{\sigma p} \check{\varvec{\epsilon }}^{p,\dag }\right) :{\textbf {D}}, \end{aligned}$$
(40d)

where \(\varvec{\varepsilon }^{\dag }\) indicate the adjoint strain fields defined as the time-reversed Lagrangian strain fields \(\nabla \varvec{\lambda }\left( t_{\textrm{max}}-t\right)\), \(\hat{\varvec{\varepsilon }}^{\dag }\) and \(\check{\varvec{\varepsilon }}^{\dag }\) are the trace and deviatoric parts of the adjoint strain fields \(\varvec{\varepsilon }^{\dag }\), \(\hat{\varvec{\epsilon }}^{\dag }\) and \(\check{\varvec{\epsilon }}^{\dag }\) are the trace and deviatoric parts of the adjoint memory strain variables \(\varvec{\epsilon }^{\dag }\). As can be seen, following the derivation process of adjoint-state (or Lagrangian multiplier) method, the Q sensitivity kernels can be calculated efficiently with the adjoint memory strain variables.

2.3.4 Sensitivity Kernels with Velocity-Q Model Parameterization

In the previous section, the sensitivity kernels of moduli and attenuation parameters are given for different methods. However, in practical FWI experiments, the viscoelastic media is commonly described using velocity-Q model parameterization, which is associated with density \(\rho\), velocity (P-wave velocity \(V_\textrm{P}\) and S-wave velocity \(V_\textrm{S}\)), and quality factor (P-wave quality factor \(Q_\textrm{P}\) and S-wave quality factor \(Q_\textrm{S}\)). In this section, we derive the sensitivity kernels in velocity-Q model parameterization for different methods.

In method I, Charara et al. (2000) derived the sensitivity kernels for \(\rho\), \(\kappa ^{U}\), \(\mu ^{U}\), \(\delta \kappa\) and \(\delta \mu\). Herein, with the enforcement of \(\tau _{\kappa }=Q_{\kappa }^{-1}\) and \(\tau _{\mu }=Q_{\mu }^{-1}\) given by Fichtner and van Driel (2014), the attenuation parameters \(\delta \kappa\) and \(\delta \mu\) are associated with \(Q_{\kappa }\) and \(Q_{\mu }\) by

$$\begin{aligned}&\delta \kappa =-\frac{\tau _{\kappa }}{1+\tau _{\kappa }}\kappa ^{U} =-\frac{1}{1+Q_{\kappa }}\kappa ^{U}, \end{aligned}$$
(41a)
$$\begin{aligned}&\delta \mu =-\frac{\tau _{\mu }}{1+\tau _{\mu }}\mu ^{U}=-\frac{1}{1+Q_{\mu }}\mu ^{U}. \end{aligned}$$
(41b)

Thus, the sensitivity kernels for \(Q_{\kappa }\) and \(Q_{\mu }\) in method I can be obtained as

$$\begin{aligned}&K_{Q_{\kappa }}=-\frac{Q_{\kappa }}{1+Q_{\kappa }}K_{\delta \kappa }, \end{aligned}$$
(42a)
$$\begin{aligned}&K_{Q_{\mu }}=-\frac{Q_{\mu }}{1+Q_{\mu }}K_{\delta \mu }. \end{aligned}$$
(42b)

According to Dahlen and Tromp (1998), \(Q_\textrm{P}\) and \(Q_\textrm{S}\) are related to \(Q_{\kappa }\) and \(Q_{\mu }\) by

$$\begin{aligned}&Q_{\kappa }=\frac{\upsilon ^2-1}{\upsilon ^2-\varrho }Q_\textrm{P}, \end{aligned}$$
(43a)
$$\begin{aligned}&Q_{\mu }=Q_\textrm{S}, \end{aligned}$$
(43b)

where \(\upsilon =V_\textrm{P}/V_\textrm{S}\) and \(\varrho =Q_\textrm{P}/Q_\textrm{S}\). Sensitivity kernels for \(V_\textrm{P}\), \(V_\textrm{S}\), \(Q_\textrm{P}\) and \(Q_\textrm{S}\) in velocity-Q model parameterization can be expressed in terms of the sensitivity kernels in modulus-Q parameterizaion (Pan and Wang 2020):

$$\begin{aligned}&K_{V_\textrm{P}}=\frac{6\upsilon ^2}{3\upsilon ^2-4}K_{\kappa } +\frac{2\upsilon ^2\left( 1-\varrho \right) }{\left( \upsilon ^2-1\right) \left( \upsilon ^2-\varrho \right) }K_{Q_{\kappa }}, \end{aligned}$$
(44a)
$$\begin{aligned}&K_{V_\textrm{S}}=2\left( K_{\mu }-\frac{4}{3\upsilon ^2-4}K_{\kappa }\right) +\frac{2\upsilon ^2\left( \varrho -1\right) }{\left( \upsilon ^2-1\right) \left( \upsilon ^2-\varrho \right) }K_{Q_{\kappa }}, \end{aligned}$$
(44b)
$$\begin{aligned}&K_{Q_\textrm{P}}=\frac{\upsilon ^2}{\upsilon ^2-\varrho }K_{Q_{\kappa }}, \end{aligned}$$
(44c)
$$\begin{aligned}&K_{Q_\textrm{S}}=K_{Q_{\mu }}-\frac{\varrho }{\upsilon ^2-\varrho }K_{Q_{\kappa }}. \end{aligned}$$
(44d)

The relationships in Eq. 44 work for all of the three methods. Thus, in the inversion process, the velocity and Q models can be updated and reconstructed.

3 Numerical Experiments

In this section, we first give a synthetic example with separated velocity and Q anomalies to analyze the sensitivity kernels of different methods and evaluate their inversion performances. Next, numerical experiments based on a modified Canadian Foothill model with topographic variations and complex structures are given to invert for near-surface velocity and Q structures using SWs and early arrivals of BWs. The numerical modeling and inversion experiments presented in this section are performed using the FWI code package of SeisElastic2D (Pan et al. 2020) based on SEM forward modeling method in viscoelastic medium.

3.1 Sensitivity Kernel Analysis with Separated Velocity and Q Anomalies

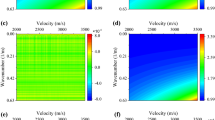
Figure 1 shows true velocity and Q models. A starting homogeneous \(V_\textrm{P}\) model is designed with a constant value of 5500 m/s. The target \(V_\textrm{P}\) structure is created by embedding one anomaly with \(+6\%\) perturbation in the upper parts of the homogeneous background, as shown in Fig. 1a. The true and initial \(V_\textrm{S}\) models are created from the true and initial \(V_\textrm{P}\) models with \(V_\textrm{P}/V_\textrm{S}=2\). The initial \(Q_\textrm{P}\) and \(Q_\textrm{S}\) models are homogeneous with \(Q_\textrm{P}=Q_\textrm{S}=150\). The true \(Q_\textrm{P}\) and \(Q_\textrm{S}\) models are created by embedding one attenuating anomaly (\(Q_\textrm{P}=Q_\textrm{S}=10\)) in the lower parts of the homogeneous background, as shown in Fig. 1c, d. The true and initial \(\rho\) models are homogeneous with a constant value of 3000 kg/m\(^3\). In the inversion experiments, the influence of \(\rho\) is ignored and the \(\rho\) model is kept unchanged. The model is 1000 m wide and 1000 m deep. A quadrilateral SEM mesh defined using 5 \(\times\) 5 GLL points with 35 and 35 elements in vertical and horizontal directions is used to discretize the models. A total of 32 sources and 194 receivers are regularly distributed along the left and right sides of the model with \(\Delta x_{s}=60\) m and \(\Delta x_{r}=10\) m, as indicated by the red stars and white triangles in Fig. 1. A Ricker wavelet with dominant frequency of 30 Hz is used as source for forward simulation. We set all boundaries of the model with absorbing boundary conditions to suppress the artificial reflections.

Fig. 1
figure 1

a, b are the true \(V_\textrm{P}\) and \(V_\textrm{S}\) models; the red stars and white triangles in a, b indicate the schematic distributions of the sources and receivers, respectively. c, d  are the true \(Q_\textrm{P}\) and \(Q_\textrm{S}\) models

Full size image

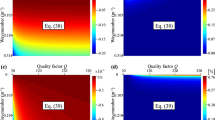
In the numerical experiments, to reduce the influences of P–S wave mode coupling, the P-waves are separated to calculate the sensitivity kernels of compressional velocity \(V_\textrm{P}\) and quality factor \(Q_\textrm{P}\). S-waves are separated to calculate the sensitivity kernels of shear velocity \(V_\textrm{S}\) and quality factor \(Q_\textrm{S}\). The sensitivity kernels are first calculated using the three different methods for comparison, as presented in Fig. 2. The velocity sensitivity kernels of different methods appear to be close. Some trade-off artifacts caused by the errors of attenuation models are observable in the lower parts of the velocity sensitivity kernels. However, the Q sensitivity kernels calculated using different methods differ obviously. In Fig. 2g, h, the \(Q_\textrm{P}\) and \(Q_\textrm{S}\) sensitivity kernels calculated using method II suffer from strong trade-off artifacts due to the velocity errors in the upper parts, as indicated by the arrows, whereas, in the \(Q_\textrm{P}\) and \(Q_\textrm{S}\) sensitivity kernels calculated using method I and the adjoint-state method, the trade-off artifacts are very weak, as shown in Fig. 2c, d, k, l. These observations suggest that compared to method II, the Q sensitivity kernels calculated with the memory strain variables in method I and the adjoint-state method can naturally suppress the trade-off artifacts, as the memory strain variables directly describe the anelastic characteristics of the seismic waves. The discrepancies between GSLS and Kolsky–Futterman models for modeling attenuation effects lead to the trade-offs in method II.

Fig. 2
figure 2

a–d are the velocity and Q sensitivity kernels (\(K_{V_\textrm{P}}\), \(K_{V_\textrm{S}}\), \(K_{Q_\textrm{P}}\) and \(K_{Q_\textrm{S}}\)) calculated using method I; e–h are the velocity and Q sensitivity kernels calculated using method II; i–l are the velocity and Q sensitivity kernels calculated using the adjoint-state method

Full size image

Synthetic inversion experiments are then performed. To evaluate the influences of velocity errors on Q inversion, we first only update the Q models based on the starting homogeneous velocity structures. The iterative inversion stops when the number of iterations reaches 12 or the relative data misfit decrease is smaller than 0.1%. The \(Q_\textrm{P}\) and \(Q_\textrm{S}\) models inverted using these methods are presented in Fig. 3. To test the performances of different methods further, we then carry out inversion experiments by simultaneously updating velocity and Q models, as presented in Fig. 4. The inversion stops when the number of iterations reaches 60 or the relative data misfit decrease is smaller than \(0.1 \%\). The well logs of inversion results at horizontal distance of 500 m are extracted for comparison, as plotted in Fig. 5a, b. Reductions of the normalized data misfits in the inversion experiments are plotted in Fig. 6. As can be seen, when using initial velocity models, the \(Q_\textrm{P}\) and \(Q_\textrm{S}\) models inverted by method II are contaminated more intensely by the trade-off artifacts of velocity errors, as indicated by the arrows in Fig. 3b, e. This is caused by the discrepancies between GSLS and Kolsky–Futterman models. Compared to method II, method I and the adjoint-state method allow obtaining better \(Q_\textrm{P}\) and \(Q_\textrm{S}\) models with stronger Q anomalies and fewer crosstalk artifacts, as shown in Fig. 3a, d, c, f. The data misfits in method I and the adjoint-state method also reduce faster, as shown in Fig. 6a. When simultaneously updating velocity and Q models, the three methods can resolve the velocity perturbations in the upper parts well. However, strong trade-off artifacts appear in the lower parts of the inverted velocity models caused by inaccurate Q models as indicated by the arrows in Fig. 5c, d. In the Q inversion results, some weak artifacts exist in the upper parts, as indicated by the arrows in Fig. 4g–l, whereas the Q anomalies in the lower parts are clearly discernable. In the simultaneous inversion experiments, data misfits of method II reduce slower than the other methods, as shown in Fig. 6b. Method II can produce comparable quality inversion results at the cost of higher computation requirements.

Fig. 3
figure 3

a–c are the \(Q_\textrm{P}\) models inverted using method I, II and the adjoint-state method with the initial velocity models, respectively; d–f are the \(Q_\textrm{S}\) models inverted by the three different methods

Full size image
Fig. 4
figure 4

a–c are the \(V_\textrm{P}\) models inverted using method I, II and the adjoint-state method, respectively; d–f are the \(V_\textrm{S}\) models inverted using method I, II and the adjoint-state method; g–i are the \(Q_\textrm{P}\) models inverted using method I, II and the adjoint-state method; j–l are the \(Q_\textrm{S}\) models inverted using method I, II and the adjoint-state method

Full size image
Fig. 5
figure 5

a, b are the comparison of well logs extracted from the inverted \(Q_\textrm{P}\) and \(Q_\textrm{S}\) models with the initial velocity models; c, d are the comparison of well logs extracted from the inverted \(V_\textrm{P}\) and \(V_\textrm{S}\) models in the simultaneous inversion experiments; e, f are the comparison of well logs extracted from the inverted \(Q_\textrm{P}\) and \(Q_\textrm{S}\) models in the simultaneous inversion experiments. The black and gray lines indicate initial and true models. The black dashed, black dash-dotted and gray dashed lines indicate method I, II and the adjoint-state method, respectively

Full size image
Fig. 6
figure 6

a shows the normalized data misfits reductions for Q inversion with the initial velocity models using method I, II and the adjoint-state method; b shows the normalized data misfits reductions when simultaneously inverting for velocity and Q models. The black dashed, black dash-dotted and gray dashed lines indicate method I, II and the adjoint-state method, respectively

Full size image

3.2 Canadian Foothill Model Example with Irregular Topography

In this part, we design a synthetic viscoelastic Canadian Foothill model with complex structures and irregular topography, which is closer to practical conditions in the subsurface (Pan et al. 2020; Pan et al. 2022). The three different methods are applied to computing the viscoelastic sensitivity kernels and inverting for velocity and Q models using both SWs and BWs. In Fig. 7, we present the true \(V_\textrm{S}\), initial \(V_\textrm{S}\) and true Q (\(Q_\textrm{P}=Q_\textrm{S}\)) models with topographic variations. The well log data at a horizontal distance of 325 m, as indicated by the white dashed lines in Fig. 7, are extracted from the models for presentation. The topographic surface is depicted by the black solid lines. The white area is the air layer. The initial \(V_\textrm{S}\) model, as presented in Fig. 7c, is created by smoothing the target \(V_\textrm{S}\) model using a 2D Gaussian function. The smoothing radii in horizontal and vertical directions are 20 m. The true and starting models for \(V_\textrm{P}\) are generated directly from the true and starting \(V_\textrm{S}\) models with the same structure variations and a constant value of \(V_\textrm{P}/V_\textrm{S}=3\). In practical conditions of the near-surface, the unconsolidated formations always have low velocity values and strong attenuation effects (small Q). Thus, we create the true \(Q_\textrm{P}\) and \(Q_\textrm{S}\) models by embedding strong Q anomalies (\(Q_\textrm{P}=Q_\textrm{S}=20\)) in the homogeneous background (\(Q_\textrm{P}=Q_\textrm{S}=150\)), which overlap with the low velocity zones at the near-surface, as shown in Fig. 7e. The density model is set with a constant value of 1800 kg/m\(^3\) and kept unchanged in the inversion experiments. The model size in the horizontal direction is 450 m. The maximum depth from the topographic surface to the model bottom is 150 m. To account for the effects caused by the irregular surface, an unstructured quadrilateral mesh is generated to discretize the model.

Fig. 7
figure 7

a, b are the true \(V_\textrm{S}\) model and well log (gray line) at horizontal distance of 325 m; c, d are the initial \(V_\textrm{S}\) model and corresponding well log (black line); e, f are the true Q (\(Q_\textrm{P}=Q_\textrm{S}\)) model and corresponding well log (gray line). The white dashed lines indicate the positions of well log. This figure is adapted from Fig. 10 in Pan et al. (2020)

Full size image

We arrange 33 sources and 151 receivers (\(\Delta x_\textrm{s}=12\) m and \(\Delta x_\textrm{r}=3\) m) regularly along the irregular surface. The source time function used in forward modeling is a Ricker wavelet with dominant frequency of 30 Hz. A free-surface boundary condition is applied on the topographic surface and absorbing boundary conditions are applied on the other sides of the model. In Fig. 8a, c, we present the observed shot gathers (black lines) of vertical (z) and horizontal (x) components calculated from the target models in comparison with the synthetic shot gathers (red lines) calculated from the initial models. Figure 8b, d shows the detailed comparison of the traces from 350 to 450 m in the horizontal distance. Figure 8e, f shows the corresponding data residuals of z (red lines) and x (gray lines) components. It can be seen that SWs in the short-offset profiles are much stronger than the BWs. Because the initial \(Q_\textrm{P}\) and \(Q_\textrm{S}\) models are homogeneous and do not contain the strong attenuation anomalies at the near-surface, the synthetic traces have larger amplitudes than the observed recordings. In the numerical experiments, we design time windows to separate SWs and BWs, which helps reduce the complex trade-offs between different model parameters. SWs are used to calculate the \(V_\textrm{S}\) and \(Q_\textrm{S}\) sensitivity kernels and update the \(V_\textrm{S}\) and \(Q_\textrm{S}\) models. BWs are used to calculate the \(V_\textrm{P}\) and \(Q_\textrm{P}\) sensitivity kernels and update the \(V_\textrm{P}\) and \(Q_\textrm{P}\) models. If the SWs and BWs are not separated, the \(V_\textrm{P}\) and \(Q_\textrm{P}\) models will be updated slowly and suffer from trade-offs artifacts seriously.

We first calculate the Q sensitivity kernels with the true velocity models within the frequency band of [3 Hz, 25 Hz] using different methods for comparison, as shown in Fig. 9. The Q sensitivity kernels constructed with different methods are very close with only small differences as indicated by the arrows in Fig. 9 and the attenuation anomalies at the near-surface can be imaged clearly without obvious artifacts. Then, we calculate the sensitivity kernels using the initial models obtained by smoothing the true models. Figure 10 presents the \(V_\textrm{S}\) and \(Q_\textrm{S}\) sensitivity kernels obtained by different methods using SWs when the initial velocity models are used (Pan et al. 2022). Figure 11 presents the \(V_\textrm{P}\) and \(Q_\textrm{P}\) sensitivity kernels calculated using BWs with by different methods. The velocity sensitivity kernels constructed with different frameworks do not exhibit obvious differences. However, the Q sensitivity kernels appear to contain more trade-off artifacts caused by velocity errors compared to those (Fig. 9) obtained with true velocity models. Furthermore, it is observed that the \(Q_\textrm{S}\) and \(Q_\textrm{P}\) sensitivity kernels calculated by method II suffer from stronger trade-off artifacts than those calculated by the other methods, as indicated by the arrows in Fig. 10d. The imaged Q anomaly structures appear distorted.

The \(Q_\textrm{S}\) and \(Q_\textrm{P}\) inversion results obtained using different methods with the true and initial velocity models are given in Figs. 12 and 13 for presentation, respectively. Stopping criteria of the inversion is that when the number of iterations reaches 12 or the relative data misfit decrease is smaller than \(0.1 \%\). Figure 14 shows the comparisons of well log data at horizontal distance of 325 m extracted from the \(Q_\textrm{S}\) and \(Q_\textrm{P}\) models inversion results. Figure 15 presents the reduction histories of data misfits and model errors after normalization in the Q inversion experiments with true and initial velocity models. It is observed that when the velocity models are correct, the three different methods can resolve the Q structures at the near-surface reliably and clearly. Due to illumination limitation of the early arrivals of BWs, some artifacts appear in deeper parts of the inverted \(Q_\textrm{P}\) models, as indicated by the arrow in Fig. 14b. Even though, the inverted \(Q_\textrm{P}\) model by method II appears to suffer from fewer artifacts, as indicated by the arrows in Fig. 12, these methods can provide inversion results of comparable quality, as indicated by the data misfits and model errors in Fig. 15a, c. However, in the presence of velocity errors, the inverted Q models are significantly damaged by the trade-off artifacts in the deeper parts, as indicated by the arrows in Fig. 14d. Furthermore, method II suffers from the trade-off errors more seriously compared to the other methods, as indicated by the data misfits and model errors in Fig. 15b, d. This may result from the fact that different physical models are used in forward modeling and Q sensitivity kernel calculation in method II. The Q sensitivity kernels calculated directly using the memory strain variables in method I and the adjoint-state method are more accurate and less prone to the trade-offs.

Fig. 8
figure 8

a, c show the comparison of observed data (black lines) and synthetic data (blue lines) calculated from the initial models of z and x components, respectively; b, d show the detailed comparisons of the data from 400 to 450 m in horizontal direction; e shows the corresponding data residuals of z (red lines) and x (gray lines) components; f shows the detailed data residuals

Full size image
Fig. 9
figure 9

a, b are the \(Q_\textrm{S}\) and \(Q_\textrm{P}\) sensitivity kernels (\(K_{Q_\textrm{S}}\) and \(K_{Q_\textrm{P}}\)) calculated using SWs and BWs with true velocity models by method I; c, d are the \(Q_\textrm{S}\) and \(Q_\textrm{P}\) sensitivity kernels calculated by method II; e, f are the \(Q_\textrm{S}\) and \(Q_\textrm{P}\) sensitivity kernels calculated by the adjoint-state method

Full size image
Fig. 10
figure 10

a, b are the \(V_\textrm{S}\) and \(Q_\textrm{S}\) sensitivity kernels (\(K_{V_\textrm{S}}\) and \(K_{Q_\textrm{S}}\)) calculated using SWs with initial wrong velocity models by method I; c, d are the \(V_\textrm{S}\) and \(Q_\textrm{S}\) sensitivity kernels calculated by method II; e, f are the \(V_\textrm{S}\) and \(Q_\textrm{S}\) sensitivity kernels calculated by the adjoint-state method

Full size image
Fig. 11
figure 11

a, b are the \(V_\textrm{P}\) and \(Q_\textrm{P}\) sensitivity kernels (\(K_{V_\textrm{P}}\) and \(K_{Q_\textrm{P}}\)) calculated using BWs with initial wrong velocity models by method I; c, d are the \(V_\textrm{P}\) and \(Q_\textrm{P}\) sensitivity kernels calculated by method II; e, f are the \(V_\textrm{P}\) and \(Q_\textrm{P}\) sensitivity kernels calculated by the adjoint-state method

Full size image
Fig. 12
figure 12

a, b are the inverted \(Q_\textrm{S}\) and \(Q_\textrm{P}\) models with the true velocity models by method I using SWs and BWs, respectively; c, d are the inverted \(Q_\textrm{S}\) and \(Q_\textrm{P}\) models by method II; e, f are the inverted \(Q_\textrm{S}\) and \(Q_\textrm{P}\) models by the adjoint-state method

Full size image
Fig. 13
figure 13

a, b are the inverted \(Q_\textrm{S}\) and \(Q_\textrm{P}\) models with the initial wrong velocity models by method I using SWs and BWs, respectively; c, d are the inverted \(Q_\textrm{S}\) and \(Q_\textrm{P}\) models by method II; e, f are the inverted \(Q_\textrm{S}\) and \(Q_\textrm{P}\) models by the adjoint-state method

Full size image
Fig. 14
figure 14

a, b show the comparisons of well logs extracted from the inverted \(Q_\textrm{S}\) and \(Q_\textrm{P}\) models (Fig. 12) with the true velocity models at horizontal distance of 325 m by different methods; c, d show the comparisons of well logs extracted from the inverted \(Q_\textrm{S}\) and \(Q_\textrm{P}\) models (Fig. 13) with the initial wrong velocity models by different methods. The black and gray solid lines indicate the true and initial models. The black dashed, black dash-dotted and gray dashed lines indicate the inverted models obtained by method I, II and the adjoint-state method, respectively

Full size image
Fig. 15
figure 15

a shows the reductions of normalized data misfits for \(Q_\textrm{S}\) and \(Q_\textrm{P}\) inversion using SWs and BWs with the true velocity models; b shows the reductions of normalized data misfits for \(Q_\textrm{S}\) and \(Q_\textrm{P}\) inversion using SWs and BWs with the initial velocity models; c, d show the corresponding reductions of normalized model errors for inversion of \(Q_\textrm{S}\) and \(Q_\textrm{P}\) models using SWs and BWs with true and initial velocity models, respectively. The black solid, black dashed and black dash-dotted lines indicate method I, II and the adjoint-state method for \(Q_\textrm{S}\) inversion with SWs. The gray solid, gray dashed and gray dash-dotted lines indicate method I, II and the adjoint-state method for \(Q_\textrm{P}\) inversion with BWs

Full size image
Fig. 16
figure 16

a, b show the simultaneously inverted \(V_\textrm{S}\) and \(Q_\textrm{S}\) models using SWs in stage I by method I; c, d are the inverted \(V_\textrm{S}\) and \(Q_\textrm{S}\) models in stage I by method II; e, f are the inverted \(V_\textrm{S}\) and \(Q_\textrm{S}\) models in stage I by the adjoint-state method

Full size image
Fig. 17
figure 17

a, b are the simultaneously inverted \(V_\textrm{P}\) and \(Q_\textrm{S}\) models using BWs in stage II by method I; c, d are the inverted \(V_\textrm{P}\) and \(Q_\textrm{P}\) models in stage II by method II; e, f are the inverted \(V_\textrm{P}\) and \(Q_\textrm{P}\) models in stage II by the adjoint-state method

Full size image

Finally, we perform inversion experiments for simultaneously determining the velocity and Q models by different methods. The inversion loops were ended when the number of iterations reaches 60 or the relative data misfit decrease is smaller than \(0.1 \%\). In stage I, SWs are extracted from the shot gathers to update \(V_\textrm{S}\) and \(Q_\textrm{S}\) models simultaneously. The inversion outputs are presented in Fig. 16. In stage II, BWs are extracted to update \(V_\textrm{P}\) and \(Q_\textrm{P}\) models simultaneously. The inversion outputs are plotted in Fig. 17. Well logs are extracted from the inversion results for comparison, as shown in Fig. 18. Figures 19 and 20 show the reduction histories of data misfits and model errors with normalization by inversion of SWs and BWs in stage I and II. Method II suffers from slower convergence rate because of the trade-off artifacts in the Q sensitivity kernels. As optimization progresses, the velocity models are iteratively improved and the trade-off artifacts in the Q models inverted are gradually suppressed. Even though, some small differences exist between the inverted models by different methods, as indicated by the arrows in Figs. 16 and 17, the final inversion results of method II are comparable to those obtained by method I and the adjoint-state method, as indicated by the model errors in Fig. 20a, b. However, because the adjoint wavefields in velocity and Q sensitivity kernels need to be constructed using different adjoint sources, method II is almost two times more expensive than the other two methods. Finally, the modeled data generated using the adjoint-state method inversion results is compared with the observations. It can be seen that amplitudes and travel time of the synthetics are consistent with the observations (Fig. 21).

Fig. 18
figure 18

a, b show comparisons of well logs extracted from the inverted \(V_\textrm{S}\) and \(Q_\textrm{S}\) models by inversion of SWs using different methods; c, d show comparisons of well logs extracted from the inverted \(V_\textrm{P}\) and \(Q_\textrm{P}\) models by inversion of BWs using different methods. The black and gray solid lines indicate the initial and true models. The black dashed, black dash-dotted and gray dashed lines indicate method I, II and the adjoint-state method, respectively

Full size image
Fig. 19
figure 19

Reductions of normalized data misfits for simultaneous inversion of velocity and Q models using SWs and BWs by different methods. The black solid, black dashed and black dash-dotted lines indicate method I, II and the adjoint-state method for inversion of SWs, respectively. The gray solid, gray dashed and gray dash-dotted lines indicate method I, II and the adjoint-state method for inversion of BWs, respectively

Full size image
Fig. 20
figure 20

a shows the reductions of normalized model errors for simultaneous inversion of \(V_\textrm{S}\) and \(Q_\textrm{S}\) models using SWs; The black solid, black dashed and black dash-dotted lines indicate method I, II and the adjoint-state method for \(V_\textrm{S}\) inversion. The gray solid, gray dashed and gray dash-dotted lines indicate method I, II and the adjoint-state method for \(Q_\textrm{S}\) inversion. b shows the reductions of normalized model errors for simultaneous inversion of \(V_\textrm{P}\) and \(Q_\textrm{P}\) models using BWs. The black solid, black dashed and black dash-dotted lines indicate method I, II and the adjoint-state method for \(V_\textrm{P}\) inversion. The gray solid, gray dashed and gray dash-dotted lines indicate method I, II and the adjoint-state method for \(Q_\textrm{P}\) inversion

Full size image
Fig. 21
figure 21

a, c show the comparison of observed data (black lines) and synthetic data (blue lines) calculated from the inverted models of z and x components, respectively; b, d show the detailed comparisons of the data from 350 to 450 m in horizontal direction; e shows the data residuals of z (red lines) and x (gray lines) components; f shows the detailed data residuals

Full size image

4 Discussion

In the first synthetic inversion example, an cross-well acquisition survey (as shown in Fig. 1) is designed for investigating the coupling effects between velocity and Q models. Ray coverage and source-receiver illumination for velocity and Q anomalies are the same. Transmission waves are mainly used for inversion. If a surface acquisition survey, in which sources and receivers are distributed on top surface of the model, is used for numerical experiments, the Q structures in deeper parts will be more difficult to be recovered. First, because offset of the surface acquisition survey is small, reflected waves are needed to invert for Q models in deep regions suffering from higher nonlinearity. The velocity structures at shallow parts are easier to be estimated benefiting from better ray coverage and source-receiver illumination. Furthermore, according to our experience and previous studies (Zhu 2014), velocity contrasts produce stronger influences on reflected seismic waves than Q contrasts. Compared to reflections, the transmission waves traveling through the attenuating zones are more sensitive to Q perturbations. This means that it is more difficult to decouple the velocity and Q models using reflected waves in the surface acquisition survey. In the second synthetic example for imaging the near-surface velocity and Q structures, the SWs and BWs of early arrivals can be considered as transmission waves. For further studies, it is necessary to provide more numerical experiments and detailed analysis about the influences of reflection and transmission waves in different acquisition settings (e.g., cross-well and vertical seismic profile acquisitions) for decoupling velocity and Q models.

Different physical mechanisms have been suggested to model the attenuation effects on propagating waves in viscoelastic media (Kolsky 1952; Futterman 1962; Carcione et al. 1988; Robertsson et al. 1994; Wang et al. 2019). Ursin and Toverud (2002) gave a comparison of different seismic dispersion and attenuation models and concluded that the standard linear solid (SLS) model shows behavior different to that of the Kolsky–Futterman model. In method II described in this study, the GSLS and Kolsky–Futterman models are used for forward simulations and calculating the Q sensitivity kernels, respectively. The discrepancies between GSLS model with \(N=3\) and the Kolsky–Futterman model increase the inversion trade-offs in method II. However, in method I and the adjoint-state method, the Q sensitivity kernels are calculated by involving memory strain variables, which characterize and capture the attenuation effects more effectively based on the GSLS model. Keating and Innanen (2019) investigated the modeling errors between SLS and Kolsky–Futterman models for viscoacoustic FWI in frequency-domain and showed that appropriate frequency band helps reduce the discrepancies between SLS and Kolsky–Futterman models. However, few researchers compare the behavior of GSLS model with different numbers of parallel relaxation mechanisms with that of the Kolsky–Futterman model. Hence, the appropriate frequency band and number of parallel relaxation mechanisms for reducing the modeling errors between GSLS and Kolsky–Futterman models remain to be determined in our future studies.

5 Conclusions

In this study, we revisit different methods for constructing the sensitivity kernels for time-domain viscoelastic FWI on the basis of GSLS rheology. In method I and the adjoint-state method, the Q sensitivity kernels are constructed with memory strain variables, whereas, in method II, an additional adjoint source is introduced based on the Kolsky–Futterman model and Born scattering integral. Synthetic inversion experiments with both cross-well and surface acquisition geometries are provided. Different methods are used to calculate the sensitivity kernels and invert for the models for comparison using transmission waves including SWs and BWs of early arrivals. The observations suggest that the Q sensitivity kernels constructed with memory strain variables are more accurate, suffering from fewer trade-off artifacts. When simultaneously inverting for the velocity and Q models, these different methods can provide inversion results of comparable quality. However, method II converges more slowly and is more expensive than the other methods.