Introduction

Various systems [1] in the real world, such as ecosystems, transportation systems, and social systems, can be abstracted into complex networks. Each element in the system is regarded as a node, and the relationship between elements can be equivalent to connecting edges. Nodes and the edges between nodes constitute the basic network structure of the system. In addition to certain structural characteristics, the states of the elements in the system in the real world often have certain rules. For example, in an ecosystem [2], to maintain the balance of the entire ecosystem, there will be certain changes in the numbers of different species. For humans, the number of individual states in the disease transmission network will also change over time. To describe the change in the state of each element in different systems, scholars in different fields use different dynamic [3] equations to describe the change law of the system state.

After the system is abstracted into a complex network and the dynamic equations are used to describe the state change process of the elements in the system, the relationship between the system structure and the dynamic process is established. A system without structure indicates that the elements in the system are isolated from each other, that is, there is no information exchange between elements; thus, there is no dynamic change process in the system. Such a system does not actually exist. Similarly, there is no system in which the elements do not interact. Therefore, the structure of the system is closely dependent on the dynamic system process [4]. After the network abstraction of the actual system, for the situation in which the dynamic process on the network is known and the network topology is unknown, the data-driven [5] method can be used to reconstruct the network topology. Many existing methods use the dynamic process data on the network to obtain the network topology by calculating the correlation between different nodes [6, 7], but in practice, the network is often large scale, and the dynamics on the network are nonlinear. It is often difficult to accurately reconstruct the network topology by simply calculating the correlation index between nodes.

Network reconstruction [8, 9] refers to inferring the network topology through the network dynamic process. It is an inverse problem of studying the network dynamic process according to the network topology. This problem has become a research hotspot in the field of network science. To date, related scholars have performed nuch work on this problem. Earlier related studies include Granger causality [10, 11], compress sensing [12,13,14], and the information theory method [15,16,17]. Due to the close dependence between the network topology and network dynamics, many scholars have studied how to reconstruct the network topology through the dynamic time series [18] of nodes on the network [19]. However, because it is difficult to obtain the complete time series data of network nodes, many works have studied network reconstruction under the condition of limited data. For example, Napoletani et al. [20] carried out network reconstruction for sparse networks with limited data. Zhang et al. [21] considered reconstructing the network topology in the case of insufficient data. In addition to network reconstruction through the time series of network nodes, the final state data of nodes can also be used to reconstruct the network topology. Based on the maximum-likelihood estimation framework, the network reconstruction method using the final state data of nodes was proposed in Ref. [22].

The problem of network reconstruction widely exists in different fields, and the network reconstruction methods are also different in combination with specific domain backgrounds. For human social networks, Eagle et al. [23] inferred the topology of friend relationship networks using the collected mobile phone data. There is also much research on biological networks [24] and gene regulatory networks [25]. Wang et al. [26] reviewed some methods for reconstructing biological networks with an emphasis on gene networks, including methods for reconstructing static gene networks and methods for modeling temporal changes in gene regulation in a dynamic network. Ceci et al. [27] proposed a semisupervised multiview machine learning framework for reconstructing gene regulatory networks. Timme et al. [28] reviewed the methods for inferring network topology from the perspective of nonlinear dynamics in different fields, including physical interaction networks, chemical and metabolic reaction networks, protein and gene regulation networks, and biological neural networks. When the network topology is partially known, inferring unknown nodes and edges is also a network reconstruction problem, which is also known as network completion [29] or hidden node detection [30]. In addition, Ching et al. [31] proposed a method for weighted network reconstruction, which is suitable for networks with linear and nonlinear dynamics. Peixoto et al. [32] found that there is a synergistic effect between network reconstruction and community detection. Angulo et al. [33] strictly deduced and proved the necessary conditions for network reconstruction, which provides an effective improvement theory for network reconstruction.

With the rapid development of artificial intelligence, researchers have begun to change their research methods and attempt to solve academic problems from the perspective of machine learning [34]. Neural networks have powerful learning and fitting capabilities. With the expansion of data volume and the improvement of computer performance, research ideas based on the combination of data-driven and neural networks have gradually become common in related scientific research fields. In this context, scholars also began to use graph neural networks [35] to solve the problem of network reconstruction. Kipf et al. [36] constructed a framework that can simultaneously learn network topology and dynamics, and this work improved the variational autoencoder framework, reconstructed the network topology using the encoder, and learned the network dynamics using the decoder. However, due to the complexity of the framework, the framework is only applicable to small-scale networks. Based on Ref. [36], Zhang et al. [37] further improved the scope of application of the model by simplifying the structure of the network framework. Chen et al. [38] proposed a novel data-driven deep learning model called the Gumbel graph network to solve network reconstruction and network completion problems. Zhang et al. [39] proposed a unified framework for automated interaction networks and dynamics discovery on various network structures and different types of dynamics.

In this paper, we propose to reconstruct the network through a data-driven approach using generative adversarial networks (GANs) [40]. The core idea of GANs is to make the samples generated by the generative network obey the real data distribution through adversarial training. In GANs, there are two adversarial training networks. One is the discriminative network, which is trained to judge as accurately as possible whether a sample comes from real data or is generated by a generative network. The other is the generative network, which is trained, so that the discriminative network cannot distinguish the source of the samples. These two networks with opposite goals are continuously and alternately trained. When the convergence state is reached, if the discriminative network cannot judge the real source of the sample, it means that the generative network meets the requirements of generating a distribution that conforms to the real data. Since GANs were proposed, many scholars have extended the application of GANs to various fields, such as 3D generation [41,42,43], text-to-image synthesis [44,45,46], image-to-image translation [47,48,49], sequence data generation [50, 51], and graph representation [52, 53]. Inspired by GANs, we use a generative network to generate the probability of an edge between two nodes in a network and use the discriminative network to evaluate whether the probability generated by the generative network conforms to the probability distribution of an edge connection between nodes in real networks. By alternately training the discriminative network and the generative network, a generative network that can generate the edge probability distribution of a real network is finally obtained. To the best of our knowledge, our work is the first method to reconstruct complex networks through a GAN-based approach.

The main novelties of this paper are summarized as follows:

  • A novel GAN-based deep learning framework for network reconstruction is proposed, which uses learning methods to capture the correlation between node state data rather than calculating a correlation index.

  • Different from network reconstruction methods that only target specific domains, we propose a general learning framework with a wider scope of application that can adapt to different network structures and network dynamics.

  • We conduct extensive experiments on networks of different scales with different dynamics. The experimental results show that our method can accurately reconstruct the topology of a network, and the accuracy is better than other network reconstruction methods.

The rest of this paper is organized as follows. In the “Deep learning framework of network reconstruction”, section we propose a deep learning framework based on a generative adversarial network. In the “Experimental design and analysis”, section we present the experimental results and analysis of network reconstruction under different networks and dynamics. Finally, we conclude the paper and propose some possible future work in the “Conclusion” section.

Deep learning framework of network reconstruction

Problem description

The network reconstruction problem can be divided into two categories. One is the network dynamic reconstruction problem with known network topology or not concerned with the network topology, that is, fitting the dynamic process on the network according to some known properties of the network. The other is the network topology reconstruction problem where the dynamics of the network are known or the network dynamics are not considered. We study the network topology reconstruction problem in this paper. For the convenience of description, we refer to network topology reconstruction as network reconstruction. Generally, network reconstruction uses the dynamic process on the network, that is, the state change law of each node in the network. In the case of unknown network dynamics, we can obtain the required dynamic process data through observation. For example, in the disease transmission network, we can record the law of disease transmission by counting the number of people infected with diseases in different areas at different times. When the network dynamics are known, we can obtain the state change data of each node on the network through simulation. According to whether the obtained network data are continuous, we can divide the network reconstruction problem into a discrete data-based network reconstruction problem and a network reconstruction problem based on continuous-time data. Discrete data indicate that there is no time sequence between the data, and the data are independent. Continuous-time data indicate that there is a sequence between data, that is, the data of a moment are related to the data of the previous moment. The problem studied in this paper is how to reconstruct the network topology according to the continuous-time data of each node on the network.

To more rigorously describe how to reconstruct the network topology based on continuous-time data, we express the state set of nodes on the network as \(X_i^T=\{x_i^{t_1},x_i^{t_2},\ldots ,x_i^T\}\), where \(x_i^t\) represents the state value of node i at time t, and T represents the total time length. After obtaining the state set of each node in the network, we can decompose the network reconstruction problem into how to predict the probability of the existence of an edge between two nodes according to the state set of two nodes, that is, \(P(E_{ij} |(X_i^T,X_j^T))\), where \(E_{ij}\) indicates that there is an edge between node i and node j. Furthermore, we assume that probability predictions of connecting edges between any two nodes are independent; thus, we denote the network reconstruction problem as \(P(A|(X_i^T,X_j^T))=\prod _{j\ne i=1}^N P(E_{ij}|(X_i^T,X_j^T))\), where N is the number of network nodes and A is the adjacency matrix of the network. We transform the state set of each node in the network into the state vector of the node and then transform the problem into calculating the correlation between the state vectors of two nodes using the correlation method to predict the probability of an edge between the two nodes. However, due to network complexity, including the complexity of network topology and the complexity of the dynamic process on a network, it is difficult to accurately measure the correlation between each node in the network using the correlation index. Therefore, this paper uses the deep learning method to judge the probability of the existence of an edge between two nodes by learning the intrinsic correlation between the state vectors of the two nodes.

Aiming at the problem of how to reconstruct the network topology through continuous-time data on the network, how to obtain the relevant data required for network reconstruction is the first problem we need to solve, and then, we need to design a suitable learning framework to capture the correlation between node state vectors. Finally, it is necessary to conduct experiments in real or simulated networks to verify the applicability and accuracy of the proposed method. This chapter focuses on the first two issues, and we describe and analyze the experimental results in the “Experimental design and analysis” section.

Data acquisition and processing

There are generally two methods for obtaining the data. One method is to directly obtain the data by adopting the corresponding observation method without knowing the network dynamic equation. For example, in a transportation network, we can use sensors to collect the number and speed data of vehicles at each intersection at different times. Another method is to obtain the state data of each node in the network at different times by means of simulation when the network dynamic equation is known. We consider the latter situation, that is, obtaining the dynamic process data on the network through simulation.

Differential equations can describe network dynamics. In this paper, we consider three continuous-time network dynamics from the fields of physics, ecosystems, and biology. The first dynamic is heat diffusion dynamics [54], and we can express the differential equation as \(\frac{dx_i(t)}{dt}=-k_{i,j}\sum _{j=1}^nA_{i,j}(x_i-x_j)\), where \(x_i\) represents the heat value of the node i, \(k_{i,j}\) is the heat coefficient, and \(A_{i,j}\) represents the value corresponding to the node in the network adjacency matrix, that is, \(A_{i,j}=1\) if there is an edge between node i and node j, and vice versa \(A_{i,j}=0\). The second dynamic is the mutualistic interaction dynamics between species in an ecosystem [55], which is expressed by the differential equation \(\frac{dx_i(t)}{dt}=b_i+x_i(1-\frac{x_i}{k_i})(\frac{x_i}{c_i}-1)+\sum _{j=1}^{n}A_{i,j}\frac{x_ix_j}{d_i+e_ix_i+h_jx_j}\), where \(x_i\) is the number of species i, \(b_i\) is the migration of alien species in the ecosystem, \(k_i\) is the species capacity, and \(c_i\) represents the species threshold. The third dynamic is gene regulation dynamics [56], and the differential equation is \(\frac{dx_i(t)}{dt}=-b_ix_i^f+\sum _{j=1}^{n}A_{i,j}\frac{x_j^h}{x_j^h+1}\), where f is the coefficient of the gene regulation mode and h is the Hill coefficient of regulating gene activation.

Based on knowing the dynamic equation of the network, we can obtain the state value of each node in the network at different times by solving the corresponding differential equation using neural ordinary differential equations [57, 58]. Taking the state data of each node in the network as a vector, we can obtain the state matrix \(W_{N\times T}\) of the network nodes. To facilitate the neural network learning the correlation between the node state vectors, we need to preprocess the obtained data. The data preprocessing includes two parts. One part concatenates the state vectors corresponding to the two nodes with connected edges according to the fact that there is an edge between the nodes in the network and marks the label as “1”. Accordingly, the concatenated vector of two nodes without edges is labeled with “0”. For the convenience of explanation, this paper refers to the sample labeled “1” as a positive sample, and the sample labeled “0” as a negative sample. The other part oversamples the data due to the sparse nature of real networks, that is, the number of nodes with connected edges in the network is small. If the state vectors between nodes are labeled according to the above method, we will obtain a large number of negative samples; that is, there is the problem of unbalanced sample data, which has no learning value for the neural network. For the imbalance of state vector samples between network nodes, we use the oversampling method to balance the sample data by expanding the number of positive samples. The specific method is to copy the positive samples according to the ratio of the number of negative samples to the number of positive samples. Then, the obtained positive samples and the original negative samples are combined and shuffled as the data needed for subsequent neural network training and testing. Finally, we use 80% of the combined data for model training, and use the remaining 20% for model testing. Since the state vectors of any two nodes in the network need to be concatenated and labeled, the complexity of data processing is \(O(N^2)\).

Deep learning framework

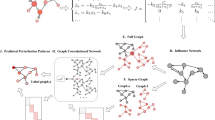
Inspired by generative adversarial network, this paper addresses the network reconstruction of continuous-time data in a similar way. Figure 1 shows the overall framework of the model, where \(\frac{dx(t)}{dt}=f(x(t))\) represents the differential equation of the network dynamics. By solving the differential equation, we obtain the state matrix \(W_{N\times T}\) of network nodes. By sampling, splicing, and labeling the initial state matrix, we finally obtain the data required by the model. The running process of the whole model is as follows. First, we train the discriminator D with the preprocessed training set data and obtain the real node connection probability \(P_{true} (E_{ij}|(X_i^T,X_j^T))\) by optimizing the loss function. Then, similarly, the preprocessed training set data are used to train the generator, and pass the output obtained by the generator is passed through the loss function in the discriminator and optimized, so that the predicted value obtained by the generator is as close as possible to the discriminator. Finally, we use the predicted value of the probability of connecting edges between nodes output by the generator as the probability of connecting edges between network nodes.

Fig. 1
figure 1

Deep learning framework based on generative adversarial network

Full size image

Generator module

We use a three-layer fully connected neural network with a sigmoid activation layer as the main structure of the generator module. First, the input layer receives the processed training data, i.e., the state vectors of different nodes. Then, the state vectors of different nodes are concatenated, and the concatenated vectors are mapped to the hidden layer. Finally, the obtained vector is reduced to one dimension through the mapping changes of multiple hidden layers and output through a sigmoid activation layer to obtain the probability value of the connection between the two nodes. We train the generator \(G(P_{pre} (E_{ij}|(X_i^T,X_j^T));\theta _G)\) using the loss function in the discriminator, so that the data input to the generator can obtain the prediction results of the edges, which are as close as possible to the edge connection probability obtained by the discriminator for the real data. Finally, we obtain the predicted value of the edge connection probability of the nodes in the network.

Discriminator module

Similar to the generator, we also use the three-layer fully connected neural network with a sigmoid activation layer as the main structure of the discriminator module. First, the input layer receives the processed training data, i.e., the state vectors of different nodes. Then, the state vectors of different nodes are concatenated, and the concatenated vectors are mapped to the hidden layer. Finally, the obtained vector is reduced to one dimension through the mapping changes of multiple hidden layers. Different from the generator, the output layer of the discriminator is connected to an MSE loss function for training the discriminator to improve the discriminator performance. The purpose of discriminator \(D(P_{true} (E_{ij}|(X_i^T,X_j^T));\theta _D)\) is to judge whether there is an edge between different nodes in the training data; that is, if there is an edge between two nodes, the probability \(P(E_{ij}|(X_i^T,X_j^T))\) output by the discriminator is as close as possible to 1; otherwise, the probability \(P(E_{ij}|(X_i^T,X_j^T))\) is as close as possible to 0. The loss function in the discriminator uses the MSE loss function and the Adam optimizer [59] for optimization.

Model training

First, we use the training set data obtained after preprocessing to train the discriminator \(G(P_{pre} (E_{ij}|(X_i^T,X_j^T));\theta _G)\), so that the output probability of the trainer is as close to the real value as possible. Even if the output of the discriminator is as consistent with the label value as possible, we use the Adam optimizer to optimize the loss function to obtain the training parameter \(\theta _D\) of the discriminator. Then, we train the generator \(G(P_{pre} (E_{ij}|(X_i^T,X_j^T));\theta _G)\) with the same training set data as the discriminator and obtain the training parameters of the generator. Since the generator and the discriminator share the same loss function, we can use the same training parameters as the training discriminator.

We separate the training data by batches, and the batch size is 2048. We train the discriminator and the generator for a maximum of 1000 epochs with learning rate 0.001. The algorithm is implemented through the Pytorch platform and the algorithm runs on RTX 3080 (32G).

Value function and parameter optimization

The generator and the discriminator can be regarded as two sides of an adversarial game. The purpose of the generator is to generate node edge data that are as similar to the real dataset as possible, and the purpose of the discriminator is to judge whether the obtained data come from the real dataset or are generated by the generator, so the generator and discriminator follow the value function of the following minmax game:

$$\begin{aligned} \min _{\theta _G}\max _{\theta _D}V(G,D)= & {} \sum _{i=1}^{N}(\mathbb {E}_{E_{ij}\sim P_{true}}[logD(E_{ij};\theta _D)]\nonumber \\{} & {} +\mathbb {E}_{E_{ij}\sim P_{pre}}[log(1-D(E_{ij};\theta _D))]). \end{aligned}$$
(1)

From the above formula, the parameters in the discriminator can be optimized as follows:

$$\begin{aligned} \nabla _{\theta _D}V(G,D)=\left\{ \begin{array}{ll}\nabla logD(E_{ij};\theta _D) &{}\quad \textit{if}\,E_{ij}\,from\,real\,data\\ \nabla log(1-D(E_{ij};\theta _D)) &{}\quad \textit{if}\,E_{ij}\,\textit{from generator}. \end{array} \right. \end{aligned}$$
(2)

The parameters in the generator are optimized as follows:

$$\begin{aligned} \begin{aligned} \nabla _{\theta _D}V(G,D)&=\nabla _{\theta _D}\sum _{i=1}^{N}\mathbb {E}_{E_{ij}\sim P_{true}}[log(1-D(E_{ij};\theta _D))]\\&=\sum _{i=1}^{N}\sum _{j=2,i\ne j}^{N}\nabla _{\theta _G}G(E_{ij};\theta _G)log(1-D(E_{ij};\theta _D))\\&=\sum _{i=1}^{N}\sum _{j=2,i\ne j}^{N}G(E_{ij};\theta _G)\nabla _{\theta _G}logG(E_{ij};\theta _G)\\&\quad log(1-D(E_{ij};\theta _D))\\&=\sum _{i=1,j=2,i\ne j}^{N}\mathbb {E}_{E_{ij}\sim P_{true}}[\nabla _{\theta _G}logG(E_{ij};\theta _G)\\&\quad log(1-D(E_{ij};\theta _D))]. \end{aligned} \end{aligned}$$
(3)

Algorithm 1 presents the pseudocode of the algorithm proposed in this paper, showing the input, output, and related parameter settings of our algorithm.

figure a

Experimental design and analysis

Experimental setup

To verify the applicability and accuracy of our model in this paper, we conduct experiments on BA scale-free networks [60] and WS small-world networks [61] with different node scales. Table 1 shows the topological characteristics of the network, where N is the number of network nodes, E is the number of network edges, \(<k>\) is the average degree of the network, C is the network clustering coefficient, and \(<l>\) is the average distance length of the network. Additionally, we use the network node state data generated by the three different dynamic equations described in the “Data acquisition and processing” section as the initial network data of the network, that is, heat diffusion dynamics, mutualistic interaction dynamics, and gene regulation dynamics. For each node, we sampled 100 snapshots \(\{X_{t1},\ldots ,X_{t100}\}\) through the dynamics as the state vector of the node. By preprocessing the obtained data, we obtain the training data and test data we need (see the “Data acquisition and processing” section). For our proposed deep learning model, we adopt the MSE loss function to evaluate the accuracy of the training results and used the Adam optimizer for optimization with a learning rate of 0.001.

Table 1 Basic topological characteristics of networks
Full size table

Evaluation indices of network reconstruction

To accurately evaluate the accuracy of the experimental results, we use ACC and F1 as indices to measure the effect of network reconstruction. As described in the “Data acquisition and processing” section, the samples with the label “1” are called positive samples, and the samples with the label “0” are called negative samples. Inferring whether there is an edge between any two nodes in the network according to the eigenvector of the network node can be regarded as a classification problem. Therefore, we can use the confusion matrix of the classification results to calculate the ACC and F1 indices of the network reconstruction. The confusion matrix of the classification results is defined as follows, as shown in Table 2.

Table 2 Classification confusion matrix
Full size table

TP is the number of true positive cases, that is, the number of positive cases with real data and positive prediction results, FP is the number of false-positive cases, that is, the number of negative cases with real data and positive prediction results, FN is the number of false-negative cases, that is, the number of positive cases with real data and negative prediction results, and TN is the number of true-negative cases, that is, the number of negative cases with real data and negative prediction results. According to the above definitions, precision (P) and recall (R) can be defined as follows:

$$\begin{aligned} P= & {} \frac{TP}{TP+FP} \end{aligned}$$
(4)
$$\begin{aligned} R= & {} \frac{TP}{TP+FN}. \end{aligned}$$
(5)

With precision and recall, the ACC and F1 indexes are defined as follows:

$$\begin{aligned} ACC= & {} \frac{TP+TN}{TP+TN+FP+FN} \end{aligned}$$
(6)
$$\begin{aligned} F1= & {} \frac{2\times P\times R}{P+R}. \end{aligned}$$
(7)
Table 3 Network reconstruction results under different dynamics on BA networks
Full size table
Table 4 Network reconstruction results under different dynamics on WS networks
Full size table

Effect and analysis of network reconstruction

On BA scale-free networks and WS small-world networks of different scales, we use the node state data obtained from heat diffusion dynamics, mutualistic interaction dynamics, and gene regulatory dynamics for network reconstruction experimental analysis, Tables 3 and 4 show the reconstruction effects of the three dynamics on the BA scale-free network and the WS small-world network. Figure 2 shows the experimental results of BA scale-free network reconstruction of different scales under heat diffusion dynamics, where the abscissa is the number of network nodes, and the ordinate is the index value. The left figure shows the ACC index results obtained by the model on the training set and test set data, and the right figure shows the F1 index results obtained by the model on the data of training set and test set data. From the experimental results, it can be found that the ACC index of the model on the data of the training set and test set is similar to that of the F1 index, which shows the applicability of the model to the data. With the increase in network scale, the average score of the ACC index and F1 index can be maintained above 0.95, which shows the effectiveness of the model for network reconstruction.

Figures 3 and 4 show the experimental results of mutualistic interaction dynamics and gene regulatory dynamics on BA scale-free networks, respectively, which are similar to the experimental results of heat diffusion dynamics on BA scale-free networks. We can see that the ACC index on the training dataset and the test dataset is relatively similar to the F1 index, and their scores fluctuate approximately 0.95. From Fig. 3, we can also find that there is no correlation between the accuracy of network reconstruction and the scale of the network; that is, the network reconstruction accuracy does not decrease with increasing of network scale, nor does it improve with decreasing network scale. This is different from traditional network reconstruction algorithms based on specific models. The traditional network reconstruction algorithm based on the correlation index is often sensitive to the network scale; that is, with an increase in the network scale, the model complexity will increase, which will affect the model accuracy. However, we use a network reconstruction model based on a learning framework, and the network reconstruction is data-driven. With the increase in network scale, the quantity of data in the network also increases, so the network reconstruction effect may improve. The experimental results in Fig. 4 verify this conclusion. Figures 5, 6, and 7 show the experimental results of network reconstruction of WS small-world networks with different scales under heat diffusion dynamics, mutualistic interaction dynamics, and gene regulatory dynamics, respectively.

To compare the effects of different network dynamics on network reconstruction on the same type of network, we plotted the network reconstruction results of heat diffusion dynamics, mutualistic interaction dynamics, and gene regulatory dynamics on BA scale-free networks and WS small-world networks at different scales. Figures 8 and 9 show the effect of BA scale-free network reconstruction under different network dynamics on the training set and test set, respectively. The network reconstruction effect under gene regulatory dynamics is relatively stable, the reconstruction effect under mutualistic interaction dynamics has a large fluctuation range, and the reconstruction effect under heat diffusion dynamics gradually stabilizes with increasing network scale. In general, the influences of the three dynamics on the network reconstruction of BA scale-free networks are quite different, and the possible reason is the result of the power-law distribution of the node degree values in the scale-free network. Figures 10 and 11 show the effect of WS small-world network reconstruction under different network dynamics on the training set and test set, respectively. Different from BA scale-free network reconstruction, the three dynamics have little difference in the impact of the WS small-world network reconstruction, and the network reconstruction effects under the three dynamics have a similar trend with the change in network scale. Compared with BA networks, in WS networks, the difference in the effect of network topology reconstruction under the three dynamics is not so great. The reason for this may be that WS networks is a network with a more uniform node degree value, and there is no large difference in the degree value of the nodes in BA networks. Therefore, the state values of the nodes generated by the dynamics on the network are more stable, and the relationship between the state values of the nodes is also more stable.

Fig. 2
figure 2

Network reconstruction of BA networks under heat diffusion dynamics

Full size image
Fig. 3
figure 3

Network reconstruction of BA networks under mutualistic interaction dynamics

Full size image
Fig. 4
figure 4

Network reconstruction of BA networks under gene regulatory dynamics

Full size image
Fig. 5
figure 5

Network reconstruction of WS networks under heat diffusion dynamics

Full size image
Fig. 6
figure 6

Network reconstruction of WS networks under mutualistic interaction dynamics

Full size image
Fig. 7
figure 7

Network reconstruction of WS networks under gene regulatory dynamics

Full size image
Fig. 8
figure 8

Network reconstruction effect of BA networks under different dynamics on training set

Full size image
Fig. 9
figure 9

Network reconstruction effect of BA networks under different dynamics on test set

Full size image
Fig. 10
figure 10

Network reconstruction effect of WS networks under different dynamics on training set

Full size image
Fig. 11
figure 11

Network reconstruction effect of WS networks under different dynamics on test set

Full size image

To further illustrate the feasibility and accuracy of the method proposed in this paper, we compare the method in this paper with five other traditional correlation indices: Euclidean distance, cosine similarity, Pearson correlation coefficient, Manhattan distance, and Mutual information. The calculation formulas of the five indices are as follows:

Euclidean distance, also known as the Euclidean metric, is a commonly used definition of distance, which refers to the true distance between two points in m-dimensional space, or the natural length of a vector, that is, the distance from the point to the origin. In the network reconstruction problem, the state vector of a node is regarded as the coordinate of the node, and the distance between two nodes can be measured using the Euclidean distance. The closer the distance is, the higher the probability that an edge exists between two nodes. The Euclidean distance can be calculated as

$$\begin{aligned} d_{Eculid}=\sqrt{\sum _{k=1}^{n}(x_{1k}-x_{2k})^2}. \end{aligned}$$
(8)

Cosine similarity refers to evaluating the similarity of two vectors by calculating the cosine value of the angle between them. The cosine of an angle of 0 degrees is 1, the cosine of any other angle is not greater than 1, and its minimum value is -1. Thus, the cosine of the angle between the two vectors determines whether the two vectors are pointing roughly in the same direction. When the two vectors have the same direction, the cosine similarity value is 1. When the angle between the two vectors is 90 degrees, the cosine similarity value is 0; when the two vectors point in completely opposite directions, the cosine similarity value is -1. For network reconstruction, the similarity between two nodes can be evaluated by calculating the cosine similarity between two node state vectors; that is, the greater the cosine similarity of the state vectors of the two nodes, the higher the probability that there is an edge between the two nodes. Cosine similarity is obtained by the following formula:

$$\begin{aligned} d_{\textrm{Cosine}}=\frac{\sum _{k=1}^{n} x_{1 k} x_{2 k}}{\sqrt{\sum _{k=1}^{n} x_{1 k}^{2}} \sqrt{\sum _{k=1}^{n} x_{2 k}^{2}}}. \end{aligned}$$
(9)

The Pearson correlation coefficient is widely used to measure the degree of correlation between two variables, and its value is between \(-1\) and 1. The Pearson correlation coefficient between two variables is defined as the quotient of the covariance and standard deviation between the two variables, and the larger the Pearson correlation coefficient is, the stronger the correlation between the two variables. In the network reconstruction problem, the Pearson correlation coefficient is used to measure the correlation between two nodes; that is, the larger the Pearson correlation coefficient is, the greater the probability of the existence of an edge between the two nodes. The Pearson correlation coefficient can be expressed as

$$\begin{aligned} d_{\textrm{Pearson }}=\frac{\sum _{k=1}^{n}\left( x_{1 k}-\bar{x}_{1}\right) \left( x_{2 k}-\bar{x}_{2}\right) }{\sqrt{\sum _{k=1}^{n}\left( x_{1 k}-\bar{x}_{1}\right) ^{2}} \sqrt{\sum _{k=1}^{n}\left( x_{2 k}-\bar{x}_{2}\right) ^{2}}}. \end{aligned}$$
(10)

Manhattan distance is a geometric term used in geometric metric spaces to indicate the sum of the absolute wheel distances of two points in a standard coordinate system. Similar to the Euclidean distance, the Manhattan distance can be used to measure the distance between two coordinate points, but the calculation is more efficient. Similarly, for network reconstruction problems, the Manhattan distance can be used to evaluate the similarity between two nodes. The calculation formula of the Manhattan distance is

$$\begin{aligned} d_{\textrm{Manhattan }}=\sum _{k=1}^{n}\left| x_{1 k}-x_{2 k}\right| , \end{aligned}$$
(11)

where \(x_{1k}\) and \(x_{2k}\) represent the state value of the kth dimension of the two nodes, and \(\overline{x}_1\) and \(\overline{x}_2\) represent the average value of the state of the two nodes. The smaller the Euclidean distance and the Manhattan distance between the nodes are, the greater the correlation between the two nodes, that is, the more likely the two nodes are to be connected.

Fig. 12
figure 12

Comparison of network reconstruction effect of BA networks under heat diffusion dynamics

Full size image
Fig. 13
figure 13

Comparison of network reconstruction effect of WS networks under heat diffusion dynamics

Full size image
Fig. 14
figure 14

Comparison of network reconstruction effect of BA networks under mutualistic interaction dynamics

Full size image
Fig. 15
figure 15

Comparison of network reconstruction effect of WS networks under mutualistic interaction dynamics

Full size image
Fig. 16
figure 16

Comparison of network reconstruction effect of BA networks under gene regulatory dynamics

Full size image

Mutual information [62, 63] is a measure of the degree of interdependence between random variables, which can be used to calculate the correlation between node state vectors, that is, the greater the mutual information between the state vectors of two nodes, the greater the probability of connecting edges between the two nodes. The formula for calculating mutual information is as follows:

$$\begin{aligned} I(X;Y)=\sum _{y\in Y}\sum _{x\in X}p_{(X,Y)}(x,y)log\left( \frac{p_{(X,Y)}(x,y)}{p_{X}(x)p_{Y}(y)}\right) , \end{aligned}$$
(12)

where X and Y represent the state vectors of different nodes, respectively, and x and y represent the specific state values in different state vectors.

Figures 12 and 13 show the network reconstruction effects of different methods on BA networks and WS networks under heat diffusion dynamics, respectively. It can be found that the method proposed in this paper is significantly better than other methods in terms of ACC and F1 indices. The method is relatively stable on BA networks and WS networks under heat diffusion dynamics.

Figures 14 and 15 show the network reconstruction effects of different methods on the BA networks and WS networks, respectively, under the mutualistic interaction dynamics. It can be found that the method proposed in this paper is still significantly better than other methods in terms of ACC and F1 indices. Different from the network topology reconstruction under the heat diffusion dynamics, except for the method in this paper, the performance of the other five methods on different networks under the mutualistic interaction dynamics fluctuates greatly.

Figures 16 and 17 show the network reconstruction effects of different methods on BA networks and WS networks under gene regulatory dynamics, respectively. It can be found that the method proposed in this paper is still significantly better than other methods in ACC and F1 indices. Similar to the network topology reconfiguration under heat diffusion dynamics, different methods performed relatively stably on BA networks and WS networks under gene regulatory dynamics.

Fig. 17
figure 17

Comparison of network reconstruction effect of WS networks under gene regulatory dynamics

Full size image

Conclusion

We propose an effective deep learning-based continuous-time data network topology reconstruction framework, which uses the learning method to capture the correlation between node state data. Different from the network reconstruction methods that only target specific domains, we propose a general learning framework that has a wider range of applications and can adapt to different network topologies, different network scales and different network dynamics. In addition, different from the modeling methods that require deep domain knowledge, we propose a data-driven model. Since our method requires the state vector of the node, our method may not obtain accurate network topology when the complete state vector data of the node cannot be obtained. This problem can be regarded as a network reconstruction problem under the condition of missing data, which will be more difficult to address. Of course, we will conduct follow-up research work on this problem in future work and try to propose a network reconstruction learning framework that can be applied to the condition of missing data.

At present, this paper only considers the reconstruction of static network topology, while in real life, the topology of many networks will change over time. These networks, such as social networks, are called temporal networks [64]. How to reconstruct the topology of temporal networks, including data acquisition and the design of learning architecture, is a research topic that is both meaningful and challenging. the nodes in the network considered in this paper do not have attributes, or the nodes all have the same attributes. In reality, many nodes in the network often have different attributes, such as citation networks and e-commerce networks. These networks can be regarded as heterogeneous networks [65]. How to reconstruct the topology of heterogeneous networks is also a new problem with important research value.