1 Introduction

With the development of new wireless communication technologies and the increasing popularity of low-cost communication equipment, wireless multi-hop networks are expected to play an important role in the "Internet of Everything" communication world because of their strong scalability and distributed self-organization. As one of the most critical topics in wireless multi-hop networks, access technology has important research significance.

The multi-hop networks have some intrinsic shortcomings such as insufficient network capacity, high latency and low energy efficiency. This is mainly due to the emergence of large-scale network nodes, and the access between nodes is prone to collisions, resulting in the decrease of overall network performance. At present, wireless transmission technology mainly includes IEEE 802.11x, Bluetooth, ZigBee, etc., are usually used for data transmission in multi-hop networks. Channel competition can lead to fluctuation in the wireless link and decrease in the probability of successfully sending packets. In the wireless network, there are some traditional methods, such as ALOHA, CSMA, TDMA, etc., used to access control for decreasing the interference. However, with the increase of the number of nodes, the probability of competing to access the same channel is greatly improved, and as a result, packets are constantly retransmitted. Also, the network energy consumption increases.

Stochastic differential games and MFGs are often applied to wireless network communication scenarios. The stochastic differential game is a dynamic game, which consists of multiple game stages. In each stage, there is a certain degree of randomness in the state of the decision maker. In [1], the interference problem of dynamic interaction among users is formulated as a random game model by using random game theory. A completely distributed online anti-interference channel selection algorithm based on random learning is designed. It is proved that the algorithm converges to Nash equilibrium and can effectively suppress interference in a distributed dynamic environment. The authors in [2] studied the spectrum sensing routing to prevent malicious nodes from attacking in multi-hop, multi-channel cognitive radio networks. According to the location and time-varying path delay information, the sensing process was modeled as a non-cooperative random game model. In the Markov decision making process, the model is decomposed into a series of stage games. For each stage of the game, this paper proposes a distributed strategy learning mechanism based on stochastic differential games, which can be used in limited information exchange and potential external attacks. Under these conditions, the joint relay channel selection makes an equalization strategy. Although the stochastic differential game can effectively solve the problems in the network, when the number of decision makers in the game increases, the dimensionality of the entire model will be too large. It will increase the complexity of solving the Nash equilibrium and add to the performance overhead. Therefore, traditional game theory is not suitable for scenarios with a large number of nodes.

The MFG is a non-zero-sum stochastic differential game, which is mainly used in the modeling and analysis of large-scale game systems [3]. By using MFG, the influence of other nodes is uniformly averaged, and the result of the average value is replaced with the sum of the influence of each node. The node only uses the local information and the average information of the mean field to make decisions. This not only simplifies the analysis and reduces the complexity, but as the number of nodes increases, the result of the mean field becomes more and more accurate. In [4], the network energy efficiency is maximized through scheduling and power allocation for ultra-dense cell networks. For the power allocation problem, the authors obtained Nash balance to get the best power allocation strategy by MFG [5] investigated an energy-aware wireless network anti-jamming problem based on the MFG, which maximizes transmission time and the sum of the user's remaining energy.

When dealing with the problem of initial sensitivity and difficulty in solving the partial differential equations in the MFG, [6] utilized reinforcement learning to achieve the mean field equilibrium [7] used the mean field approximation theory and convert the dynamic stochastic game into MFG, in which the game equilibrium is analyzed by solving two tractable partial differential equations, from the global and individual perspectives [8] modeled the energy efficiency and coverage optimization problem for ultra-dense network as a MFG and considered the base stations (BSs) as the main performance metrics and evaluate the optimal strategy that can be adopted by the BSs in an ultra-dense networking setting.

It is seen that the existing literatures seldom use the MFG to resolve the access problem of large scale distributed wireless networks. Therefore, in this paper we apply MFG to model the channel access problem of distributed wireless networks with a large number of nodes to improve the throughput and energy efficiency of the networks. The main contributions of this paper are as follows:

  • The problem of large-scale nodes competing for access to multiple channels in a distributed wireless network is modeled as a stochastic differential game. With the goal of maximizing energy efficiency, all competing nodes choose their optimal strategy interactively.

  • The MFG is introduced to this model where the interaction between nodes is transformed into the interaction between nodes and the mean field, and the numerical solution is carried out to obtain the Nash equilibrium. Based on the results, an intelligent access algorithm is designed to optimize the competitive access of multiple nodes and improve the energy efficiency of nodes.

  • A backoff strategy based on Markov model is proposed with the analysis of node backoff. Due to the limitation of the number of channels, when a node chooses a behavior strategy, some nodes can adopt a backoff strategy to avoid conflicts in the system.

The rest of this paper is structured as follows. In Sect. 2, we give the system mode. In Sect. 3, the channel access optimization problem of large-scale wireless networks is modeled by the MFG theory, and a backoff strategy based on the Markov model is presented in Sect. 4. In Sect. 5, simulation and analysis of the proposed algorithm are presented. Finally, conclusions are given in Sect. 6.

2 System model

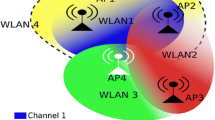
In this paper, we consider a large scale multi-hop wireless networks, as shown in Fig. 1, where all nodes can transmit data via WiFi, Bluetooth, Zigbee, etc., and access channels in a competitive mode with each other. We assume that all nodes are agents with certain perception and computing capabilities capable of perceiving channel state information (CSI).

Fig. 1
figure 1

Scenario of distributed wireless networks

Full size image

The set of all nodes in the network is represented as \(\mathcal{N}=\{\mathrm{1,2},\dots ,N-1,N\}\), the set of all feasible transmit powers is \({\mathcal{P}}_{i}=\{{p}_{1},{p}_{2},\dots ,{p}_{l}\}\), and the state set of all available channels is \(\mathcal{H}=\{{h}_{1},{h}_{2},\dots ,{h}_{k}\}\). It is reasonable that the energy consumption of nodes is mainly for transmission, operation and idle states. Let \({\mathcal{E}}_{i,loss}\left(t\right)={p}_{i}\left(t\right)+{p}_{i,oper}+{p}_{i,idle}\) denote the energy consumption of node \(i\) at moment \(t\), where \({p}_{i}(t)\) represents the transmit power of node \(i\), \({p}_{i,oper}\) represents energy consumption of node \(i\) at runtime, and \({p}_{i,idle}\) represents energy consumption when the node is idle. Hence, the energy consumption model of node \(i\), \({\mathcal{E}}_{i}\), is defined as

$${\mathcal{E}}_{i}\left(t+1\right)={\mathcal{E}}_{i}\left(t\right)-{\mathcal{E}}_{i,loss}\left(t\right)$$
(1)

It is seen that the residual energy \(\mathcal{E}\) of node \(i\) is mainly affected by the transmission power \({p}_{i}\left(t\right)\), and hence the residual energy state equation of node \(i\) in the time period \(T\) is defined as

$$d\mathcal{E}=-{p}_{i}\left(t\right)dt, 0\le t\le T$$
(2)

It is known that if nodes \(i\) and \(j\) communicate on the same frequency a neighbor node \(k\) of node \(j\) is also transmitting on this frequency, node \(k\) will interfere with node \(j\). Here, the path loss model of nodes \(i\) and \(j\) is defined as

$$ \ell _{{i,j}} = {\text{min}}\left( {1,d_{{i,j}}^{{ - \left( \alpha \right)}} } \right) $$
(3)

where \({d}_{i,j}\) represents the Euclidean distance between nodes \(i\) and \(j\), \(\mathrm{and} \alpha \ge 2\) represents the path loss parameter. Hence, the channel fading dynamic equation is defined as

$$d{\mathcal{g}}_{i,j}\left(t\right)=\frac{1}{2}\left(\lambda -{\mathcal{g}}_{i,j}\left(t\right)\right)dt+\varepsilon d{W}_{i,j}\left(t\right)$$
(4)

where \(\lambda \) and \(\varepsilon \) are constants greater than zero, and \({W}_{i,j}\left(t\right)\) represents a Wiener process. Based on the path loss model (3) and channel fading model (4), the wireless channel gain \({|{h}_{i,j}^{f}|}^{2}\) is defined as follows

$${\left|{h}_{i,j}(t)\right|}^{2}={\mathcal{l}}_{i,j}\times {\left|{\mathcal{g}}_{i,j}\left(t\right)\right|}^{2}$$
(5)

Therefore, the interference caused by adjacent node \(k\) on the same frequency can be obtained, namely

$${\mathrm{I}}_{j}\left(t\right)=\sum_{k}{p}_{k}{\left|{h}_{k,j}(t)\right|}^{2}$$
(6)

The SINR of node \(i\) is expressed as

$${SINR}_{i}=\frac{{p}_{i}{\left|{h}_{i}(t)\right|}^{2}}{{\sigma }^{2}+\gamma \sum_{j\ne i}^{N}\overline{{p }_{j}}{\left|\overline{{h }_{j}}(t)\right|}^{2}}$$
(7)

where \({\sigma }^{2}\) represents Gaussian white noise, \(\gamma \) is a constant, \(p\) represents the transmit power, and \({\left|h(t)\right|}^{2}\) represents the channel gain. Also we let \(\beta \) denote the minimum signal quality threshold. If node \(j\) successfully accesses the node, it needs to meet the following requirement as

$${SINR}_{j}(a)\ge \beta $$
(8)

where \(a\) represents node behavior strategy.

It can be seen from the above analysis that the channel access for a node is not only determined by its own state and behavior decision, but also related to other competing nodes. Therefore, the states and behavior decision of neighboring nodes interact with each other. In order to reduce the interference between nodes and maximize the income of channel access, the channel access optimization problem between competing nodes is modeled as a stochastic differential game model. In the stochastic differential game, all decision makers make different behavioral decisions based on their own and other decision makers' states, so as to improve their own benefits while meeting the channel access requirements. In this game, we let \({G}_{i}=\left\{\mathcal{N},\mathcal{A},\mathcal{S},\mathcal{R}\right\}\) denote the situation of node \(i\), where

  • \(N\) represents the set of competing nodes.

  • \(A\) represents the behavior strategy space of node \(i\), including all feasible transmit powers and different channels, then the behavior strategy of the node is \({a}_{i}(t)=\left({p}_{i},{h}_{i}\left(t\right)\right)\), where \({p}_{i}\) represents the transmit power, and \({h}_{i}\) represents the state of the channel.

  • \(S\) represents the state space of node \(i\). It defines the state of the node including backoff state, energy and interference. At time \(t\), the state of the node is \({s}_{i}\left(t\right)=\left({{\mathcal{B}}_{i}\left(t\right),\mathcal{E}}_{i}\left(t\right),{\mathcal{I}}_{i}\left(t\right)\right)\). Among them, \({\mathcal{B}}_{i}\left(t\right)\) represents the backoff state of node \(i\) at moment \(t\), which is a discrete value, that is, \({\mathcal{B}}_{i}\left(t\right)=k,k=\{\mathrm{0,1},\dots ,K\}\), \({\mathcal{E}}_{i}\) represents energy space, and \({\mathcal{I}}_{i}\) represents the interference space, which mainly includes channel interference and competition interference. The competition interference represents the interference of the current data service type of the node, and the purpose of introducing it is to send data with more important service types before other types of data.

  • \(R\) represents the benefit function of node \(i\) in a period of time, which is defined as

$${\mathcal{R}}_{i}=E \left[{\int }_{0}^{T}{\mathbb{I}}_{\left\{{SINR}_{i}\left({a}_{i}\left(t\right)\right) \ge \beta \right\}}*{\mathcal{r}}_{i}\left(t\right)dt\right]$$
(9)

where \( {\mathbb{I}}_ {A} = \left\{ {\begin{array}{*{20}c} {1,} & {P\left( A \right) = 1} \\ {0,} & {others} \\ \end{array} } \right.\) represents an indicator function, if event \(A\) is true, its value is 1, otherwise it is 0. \({\mathcal{r}}_{i}\left(t\right)\) represents the energy efficiency function of node \(i\) under the behavior strategy \({a}_{i}\)(t),

$${\left.{\mathcal{r}}_{i}\left(t\right)\right|}_{{a}_{i}(t)}=\frac{{R}_{b}}{p}=\frac{w*{\mathrm{log}}_{2}\left(1+SINR\left({a}_{i}\left(t\right)\right)\right) }{{p}_{i}\left(t\right)+{p}_{i,oper}}$$
(10)

where \(w\) is the channel bandwidth. When the node chooses a certain strategy \(a(t)\), if the node meets the access requirements under this behavior strategy, that is, \(SINR\ge \beta \), then the benefit of the node is related to energy efficiency, otherwise the benefit is 0.

Based on the stochastic differential game model, the channel access optimization problem \({\mathcal{q}}_{1}\) of large-scale competing nodes can be expressed as

$$\begin{array}{*{20}c} {{\mathcal{q}}_{1} :} & {\mathop {{\text{max}}}\limits_{{a_{i} \left( {0 \to T} \right)}} {\mathcal{R}}_{i} \left( {s_{i} ,a_{i} ,s_{{ - i}} } \right)} \\ {s.t.} & {SINR\left( {a_{i} } \right){ > }\beta } \\ \end{array} $$
(11)

where \({a}_{i}(0\to T)\) represents a behavioral strategy within a limited period of time, and \({s}_{-i}\) represents the state of the remaining competing nodes.

According to dynamic programming theory [9], an optimization problem in a finite time period \([0,T]\) can be decomposed into sub-problems of multiple periods \([t,T]\) in reverse time sequence, and then the sub-problems are solved separately, and finally get the overall solution. Therefore, the value function of node \(i\) in the time slot \(t\) is defined as \({u}_{i}\left({s}_{i}(t),t\right)\), which represents the maximum energy efficiency of the node in the time period \([t,T]\), namely

$${u}_{i}\left({s}_{i}(t),t\right)=\underset{\mathit{ }{a}_{i}(t\to T)}{\mathrm{ max}} E\left[{\int }_{t}^{T}{\mathcal{r}}_{i}\left(\tau \right)d\tau +{\mathcal{r}}_{i}\left(T\right)\right], t\in [0,T]$$
(12)

where \({\mathcal{r}}_{i}\left(T\right)\) represents the energy efficiency at the final moment \(T\).

A Nash equilibrium point NE is an N-tuple that can maximize the benefits of the mixed strategy of the decision maker when the strategies of the other decision makers remain unchanged. According to the theory of stochastic optimal control [10], the HJB stochastic differential equations are solved by the inverse induction method. For any node \(i\), if there is a solution of the equations (ie. the value function), then NE must exist. First, we derive the HJB equation [11]. Assuming that \(dt\) is a time interval that is infinitely near to zero, according to the Bellman optimality principle [12], the formula (13) can be obtained on \(t\to t+dt\), which can be expressed by

$$u\left({s}_{0},{t}_{0}\right)=\underset{a({t}_{0})}{\mathrm{max}} \left\{\mathrm{E}u\left({s}_{0}+ds+\sigma d{B}_{t},{t}_{0}+dt\right)+\mathcal{r}\left({s}_{0},a,{t}_{0},{s}_{-}\right)dt\right\}$$
(13)

where \(\sigma =(0,{\sigma }_{\mathcal{I}})\), \({B}_{t}=(0,{B}_{t}^{\mathcal{I}})\) represents Brownian motion. The formula (13) is expanded by using Taylor's formula, and the formula (14) is obtained by using Ito's lemma as

$$u\left({s}_{0}+ds+\sigma d{B}_{t},{t}_{0}+dt\right)=u\left({s}_{0},{t}_{0}\right)+\frac{\partial u\left({s}_{0},{t}_{0}\right)}{\partial t}dt+{\nabla }_{\mathcal{E}}u\left({s}_{0},{t}_{0}\right)d\mathcal{E}+{\nabla }_{\mathcal{I}}u\left({s}_{0},{t}_{0}\right)\left(d\mathcal{I}+{\sigma }_{\mathcal{I}}d{B}_{t}^{\mathcal{I}}\right)+\frac{1}{2}{\sigma }_{\mathcal{I}}^{2}\frac{{\partial }^{2}u\left({s}_{0},{t}_{0}\right)}{\partial {\mathcal{I}}^{2}}dt+o$$
(14)

where \(\nabla \) represents the gradient operator, \(o\) is the high-order infinitesimal, and \(d\mathcal{E}\) represents the energy lost by the node in a period of time, which can be obtained from the formula (2), \(d\mathcal{I}=\frac{\partial \mathcal{I}\left({s}_{0},{t}_{0}\right)}{\partial t}dt=\mathcal{J}({h}_{0},{s}_{0},{t}_{0})dt\), where \(\mathcal{J}\left({h}_{0},{s}_{0},{t}_{0}\right)=\left(f\left({h}_{0},{t}_{0}\right)+g\left({{h}_{0},s}_{0},{t}_{0}\right)\right)\), \(f\left({h}_{0},{t}_{0}\right)\) represents channel interference, specifically node perceived channel state probability density function, \(g\left({s}_{0},{t}_{0}\right)\) represents competition interference, specifically the importance of the current service type of the node. Ignore the high-order infinitesimal part in the formula (14), and calculate the expected value on both sides of the formula, namely

$$E\left[u\left({s}_{0}+ds+\sigma d{B}_{t},{t}_{0}+dt\right)\right]=u\left({s}_{0},{t}_{0}\right)+\frac{\partial u\left({s}_{0},{t}_{0}\right)}{\partial t}dt+{\nabla }_{\mathcal{E}}u\left({s}_{0},{t}_{0}\right)d\mathcal{E}+{\nabla }_{\mathcal{I}}u\left({s}_{0},{t}_{0}\right)d\mathcal{I}+E\left[{\nabla }_{\mathcal{I}}u\left({s}_{0},{t}_{0}\right){\sigma }_{\mathcal{I}}d{B}_{t}^{\mathcal{I}}\right]+\frac{1}{2}{\sigma }_{\mathcal{I}}^{2}\frac{{\partial }^{2}u\left({s}_{0},{t}_{0}\right)}{\partial {\mathcal{I}}^{2}}dt$$
(15)

According to the nature of Brownian motion, it is a normal random variable with an expectation of zero, \(E\left[d{B}_{t}^{\mathcal{I}}\right]=0\). Therefore, by simplifying the formula (15), we can get

$$E\left[u\left({s}_{0}+ds+\sigma d{B}_{t},{t}_{0}+dt\right)\right]=u\left({s}_{0},{t}_{0}\right)+\frac{\partial u\left({s}_{0},{t}_{0}\right)}{\partial t}dt+{\nabla }_{\mathcal{E}}u\left({s}_{0},{t}_{0}\right)d\mathcal{E}+{\nabla }_{\mathcal{I}}u\left({s}_{0},{t}_{0}\right)d\mathcal{I}+\frac{1}{2}{\sigma }_{\mathcal{I}}^{2}\frac{{\partial }^{2}u\left({s}_{0},{t}_{0}\right)}{\partial {\mathcal{I}}^{2}}dt$$
(16)

Jointly consider formulas (16) and (13), we get

$$u\left({s}_{0},{t}_{0}\right)=\underset{a\left({t}_{0}\right)}{\mathrm{max}}\left\{\begin{array}{c}u\left({s}_{0},{t}_{0}\right)+\frac{\partial u\left({s}_{0},{t}_{0}\right)}{\partial t}dt-{\nabla }_{\mathcal{E}}u\left({s}_{0},{t}_{0}\right)p\left({s}_{0},{t}_{0}\right)dt \\ +{\nabla }_{\mathcal{I}}u\left({s}_{0},{t}_{0}\right)J({h}_{0},{s}_{0},{t}_{0})dt+\frac{1}{2}{\sigma }_{\mathcal{I}}^{2}\frac{{\partial }^{2}u\left({s}_{0},{t}_{0}\right)}{\partial {\mathcal{I}}^{2}}dt \\ +r\left({s}_{0},a,{t}_{0},{s}_{-}\right)dt\end{array}\right\}$$
(17)

We reformulate (17) and get

$$\frac{\partial u\left({s}_{0},{t}_{0}\right)}{\partial t}dt+\underset{a\left({t}_{0}\right)}{\mathrm{max}}\left\{\begin{array}{c}J\left({h}_{0},{s}_{0},{t}_{0}\right){\nabla }_{\mathcal{I}}u\left({s}_{0},{t}_{0}\right)-{p\left({s}_{0},{t}_{0}\right)\nabla }_{\mathcal{E}}u\left({s}_{0},{t}_{0}\right)\\ +\frac{1}{2}{\sigma }_{\mathcal{I}}^{2}\frac{{\partial }^{2}u\left({s}_{0},{t}_{0}\right)}{\partial {\mathcal{I}}^{2}}+r\left({s}_{0},a,{t}_{0},{s}_{-}\right) \end{array}\right\}=0$$
(18)

Then, the HJB equation for any individual \(i\in \mathcal{N}\) is expressed as

$$\frac{\partial {u}_{i}\left({s}_{i}(t),t\right)}{\partial t}+\underset{\mathit{ }{a}_{i}\left(t\right)}{\mathrm{ max}} \left\{\mathcal{L}{u}_{i}\left({s}_{i}\left(t\right),t\right)+{\mathcal{r}}_{i}\left({s}_{i}\left(t\right),{a}_{i}\left(t\right),t,{s}_{-i}\left(t\right)\right)\right\}=0$$
(19)

where \(\mathcal{L}{u}_{i}\left({s}_{i}\left(t\right),t\right)\) represents the differential operator of the value function [13], which can be expressed as

$$\mathcal{L}{u}_{i}\left({s}_{i}\left(t\right),t\right)=\mathcal{J}\left({h}_{i}\left(t\right),{s}_{i}\left(t\right),t\right){\nabla }_{\mathcal{I}}{u}_{i}\left({s}_{i}\left(t\right),t\right)-{p\left({s}_{i}\left(t\right),t\right)\nabla }_{\mathcal{E}}{u}_{i}\left({s}_{i}\left(t\right),t\right)$$
(20)

To obtain the optimal behavior strategy in NE, the N HJB Eq. (19) coupled with each other should to be solved. However, in a large-scale network environment, the number of nodes \(N\) far exceeds the normal network environment, and the computational complexity is extremely large when solving high dimensional coupling equations. Moreover, nodes need to observe the state of each other. The exchange of information generates a huge amount of communication overhead. Therefore, we will introduce the MFG theory, converge to NE through an iterative method, and solve the channel access optimization problem of large-scale nodes with lower computational complexity and communication overhead.

3 An intelligent access algorithm based on MFG

3.1 Model formulation

In the application scenario of a distributed wireless network, for the problem of effective competition for access by large-scale nodes, the traditional game theory will generate serious computational overhead and complexity due to the huge number of nodes, so it is not suitable to be used in this scenario. Therefore, this paper will introduce the mean field theory and transform the established stochastic differential game model into an MFG model. The state of each node in the environment can be approximated by the average state of the entire environment, represented by a probability distribution function, which can greatly reduce the number of original coupling equations and thus system complexity and performance overhead.

Generally, the establishment of the MFG needs to satisfy the following hypotheses [14]: (1) all nodes are rational and can make reasonable decisions to maximize revenue; (2) the set of node states is continuous and consistent, that is, the mean field has continuity; (3) the node state is exchangeable, that is, the order of node exchange will not affect the final game result; (4) the interaction between nodes has mean field characteristics, which is equivalent to the interaction between nodes and mean field.

According to the proposed optimization problem, for the first hypothesis, it is a necessary condition for the existence of all game models, which ensures that all nodes can make the best decision. For the second hypothesis, in a large-scale network scenario, the number of nodes is sufficient to ensure continuity. For the third hypothesis, the nodes are in a competitive relationship and are independent of each other. Therefore, the order of exchanging nodes will not affect the final result of the entire game. For the fourth hypothesis, each node interacts with the mean field, and there is no need to observe and interact with the state of other nodes.

Based on the four hypotheses of the MFG, the original stochastic differential game model can be transformed into an MFG model. The state and strategy of each decision maker are homogeneous. Therefore, in the MFG model, we take a general node as the research object. For the convenience of further research, the subscript \(i\) of the node is omitted for now. It is known from the fourth hypothesis, the interaction between nodes can be replaced by the statistical distribution of its own state \(s(t)\) and the state of all nodes in the entire environment. First, we define the mean field distribution \(m\left(t,s\left(t\right)\right)\) as

$$m\left(t,s\left(t\right)\right)=\underset{N\to \infty }{\mathrm{lim}} \frac{1}{N}{\sum }_{i=1}^{N}{\mathbb{I}}_{\left({s}_{i}\left(t\right)=s\left(t\right)\right)}$$
(21)

where \({s}_{i}\left(t\right)=\left({{\mathcal{B}}_{i}\left(t\right),E}_{i}\left(t\right),{I}_{i}\left(t\right)\right)\) represents the node state. It can be seen from this formula that the mean field distribution is the probability distribution of the states of all nodes participating in the game. \(m\left(t,s\left(t\right)\right)\) is obtained by the FPK partial differential equation [15], namely

$$\frac{\partial m\left(t,s\left(t\right)\right)}{\partial t}+\sum_{k=1}^{3}{G}_{k}\left(t,{\dot{s}}_{k}\left(t\right),a(t)\right)*\frac{\partial m\left(t,s\left(t\right)\right)}{\partial {\dot{s}}_{k}}-\sum_{k=1}^{3}\frac{{\sigma }_{k}^{2}}{2}*\frac{{\partial }^{2}m\left(t,s\left(t\right)\right)}{\partial {\dot{s}}_{k}^{2}}=0$$
(22)

where \(G\left(t\right)\) is the function of time, state and behavioral strategy. \({\dot{s}}_{i,k}\left(t\right)\) represents the \({k}_{th}\) state factor of the state of the node \(i\). Calculate formula (22) to get

$$0=\frac{\partial m\left(t,s\left(t\right)\right)}{\partial t}+\mathcal{J}\left(h\left(t\right),s\left(t\right),t\right){\nabla }_{\mathcal{I}}m\left(t,s\left(t\right)\right)-{p\left(s\left(t\right),t\right)\nabla }_{\mathcal{E}}m\left(t,s\left(t\right)\right)$$
(23)

Based on the mean field distribution, the average state \(\overline{s }\left(t,\overline{\mathcal{B} }\left(t\right),\overline{\mathcal{E} }(t),\overline{\mathcal{I} }\left(t\right)\right)\) of other nodes in the mean field can be represented by \(m\left(t,s\left(t\right)\right)\), which is

$$\left\{\begin{array}{c}\overline{\mathcal{B} }\left(t\right)=\int \mathcal{B}\left(t\right)m\left(t,s\left(t\right)\right)d\mathcal{B}\\ \overline{\mathcal{E} }\left(t\right)=\int \mathcal{E}\left(t\right)m\left(t,s\left(t\right)\right)d\mathcal{E}\\ \overline{\mathcal{I} }\left(t\right)=\int \mathcal{I}\left(t\right)m\left(t,s\left(t\right)\right)d\mathcal{I}\end{array}\right.$$
(24)

According to the mean field distribution and average state, each node can make corresponding behaviour strategies by knowing the approximate state of the rest of the nodes based only on its own state and mean field distribution. Therefore, the goal of each node can also be expressed as an optimization problem \({\mathcal{q}}_{2}\), namely

$$\begin{gathered} {\mathcal{q}}_{2} :\quad \mathop {{\text{max}}}\limits_{{a(0 \to T)}} {\mathcal{R}}\left( {s,a,m} \right) \hfill \\ s.t.\quad SINR\left( a \right){ > }\beta \hfill \\ \end{gathered} $$
(25)

It can be seen from formulas (11) and (18) that the parameters of problem \({\mathcal{q}}_{2}\) have changed, in which the state \({s}_{-}\) of other nodes in the stochastic differential game has become the mean field distribution \(m\). Then, the solution of problem \({\mathcal{q}}_{2}\) is obtained by solving the HJB equation, namely

$$\frac{\partial u\left(s(t),t\right)}{\partial t}+\underset{\mathit{ a}\left(p,h\left(t\right)\right)}{\mathrm{ max}}\left\{\begin{array}{c}J\left(h\left(t\right),s\left(t\right),t\right){\nabla }_{\mathcal{I}}u\left(s\left(t\right),t\right)-p\left(s\left(t\right),t\right){\nabla }_{\mathcal{E}}u\left(s,t\right)\\ +r\left(s\left(t\right),a\left(p,h\left(t\right)\right),m\left(s\left(t\right),t\right),t\right)\\ +\frac{1}{2}{\sigma }_{\mathcal{I}}^{2}\frac{{\partial }^{2}u\left(s(t),t\right)}{\partial {\mathcal{I}}^{2}}\end{array}\right\}=0$$
(26)

The second term in formula (26) is the Hamiltonian term. By solving this term, the current optimal behavior strategy \(a\left(p,h\left(t\right)\right)\) of the node can be obtained.

So far, the derivation of the HJB equation and the FPK equation has been completed, and the HJB equation system has changed from the N equations coupled with each other in the stochastic differential game model to an independent equation. Then, until the end of the iteration, we can solve the formula (26) by the inverse induction method to obtain the value function \(u\left(s(t),t\right)\), and solve the formula (23) by the forward induction method to obtain the mean field distribution \(m\left(s\left(t\right),t\right)\), and this pair of solutions \(\left(u\left(s(t),t\right),m\left(s\left(t\right),t\right)\right)\) constitutes the Nash equilibrium.

3.2 Solving the HJB and FPK equations

In this paper, we adopt the finite difference method and Lax-Friedrichs method to solve the HJB-FPK equation. First, discretize the time period \([0,T]\), the energy state space \([0,{\mathcal{E}}_{max}]\), and the interference state space \([0,{\mathcal{I}}_{max}]\). Define the iteration step of time and state as

$${\delta }_{t}=\frac{T}{X},{\delta }_{\mathcal{I}}=\frac{{\mathcal{I}}_{max}}{Y},{\delta }_{\mathcal{E}}=\frac{{\mathcal{E}}_{max}}{Z}$$
(27)

where X, Y and Z denotes the maximal discrete values of time, energy, and interference states, respectively. For the Lax-Friedrichs [16] method, it is a numerical method based on the finite difference method to solve hyperbolic partial differential equations. Assuming that the function \(v\left({x}_{i},{t}_{j}\right)={v}_{i}^{j}\), the iteration steps are \({\delta }_{t}\) and \({\delta }_{x}\) respectively, where \({x}_{i}=i{\delta }_{x}\), \({t}_{j}=j{\delta }_{t}\), and then the Lax-Friedrich operator is obtained, which is specifically expressed as

$$\frac{\partial {v}_{i}^{j}}{\partial t}=\frac{{v}_{i}^{j+1}-\frac{1}{2}\left({v}_{i+1}^{j}+{v}_{i-1}^{j}\right)}{{\delta }_{t}}$$
(28)
$$\frac{\partial {v}_{i}^{j}}{\partial x}=\frac{{v}_{i+1}^{j}-{v}_{i-1}^{j}}{2{\delta }_{x}}$$
(29)
$${\Delta }_{x}{v}_{i}^{j}={\nabla }_{x}\left({\nabla }_{x}{v}_{i}^{j}\right)=\frac{{v}_{i+2}^{j}-2{v}_{i}^{j}+{v}_{i-2}^{j}}{4{\delta }_{x}^{2}}$$
(30)

Because the time and the state of the nodes are discretized, the derivative of the function \(v(x,t)\) with respect to time can be expressed by the change of the function \(v(x,t)\) of adjacent time, and the derivative of the function \(v(x,t)\) is for each state can be expressed by the change of the function \(v(x,t)\) in two adjacent states. Substituting these into the formula (23), the mean field iterative equation can be obtained, namely

$$\frac{{m}_{i,j}^{t+1}-\frac{1}{2}\left({m}_{i+1,j+1}^{t}+{m}_{i-1,j-1}^{t}\right)}{{\delta }_{t}}+\mathcal{J}\left(h\left(t\right),s\left(t\right),t\right)\frac{\left({m}_{i+1,j}^{t}-{m}_{i-1,j}^{t}\right)}{2{\delta }_{\mathcal{I}}}-p\left(s\left(t\right),t\right)\frac{\left({m}_{i,j+1}^{t}-{m}_{i,j-1}^{t}\right)}{2{\delta }_{\mathcal{E}}}-\frac{1}{2}{\sigma }_{\mathcal{I}}^{2}\frac{\left({m}_{i+2,j}^{t}-2{m}_{i,j}^{t}+{m}_{i-2,j}^{t}\right)}{4{\delta }_{\mathcal{I}}^{2}}=0$$
(31)

where \(i\in (0,{\mathcal{I}}_{max})\), \(j\in (0,{\mathcal{E}}_{max})\).

For the HJB equation, some researchers have used the finite difference method to solve the equation [17]. Based on this method, the HJB equation is discretized, and the result is

$$\frac{{u}_{i,j}^{t}-{u}_{i,j}^{t-1}}{{\delta }_{t}}+\underset{\mathit{ a}\left(p,h\left(t\right)\right)}{\mathrm{ max}}\left\{\begin{array}{c}J\left(h\left(t\right),s\left(t\right),t\right)\frac{{u}_{i,j}^{t}-{u}_{i-1,j}^{t}}{{\delta }_{\mathcal{I}}}\\ -p\left(s\left(t\right),t\right)\frac{{u}_{i,j}^{t}-{u}_{i,j-1}^{t}}{{\delta }_{\mathcal{E}}} +\frac{1}{2}{\sigma }_{\mathcal{I}}^{2}\frac{{u}_{i+1,j}^{t}-2{u}_{i,j}^{t}-{u}_{i-1,j}^{t}}{{\delta }_{\mathcal{I}}^{2}}\\ +r\left(s(t),a\left(p,h\left(t\right)\right),m(s\left(t\right),t),t\right)\end{array}\right\}=0$$
(32)

Then, the behavior strategy \(a\left(p,h\left(t\right)\right)\) is solved by the Hamiltonian function, and the optimal behavior strategy of the node needs to meet the channel access requirements, namely

$$\begin{gathered} a\left( {p,h\left( t \right)} \right) = \mathop {{\text{argmax}}}\limits_{{a\left( {p,h\left( t \right)} \right)}} \left\{ {\begin{array}{*{20}c} {J\left( {h\left( t \right),s\left( t \right),t} \right)\frac{{u_{{i,j}}^{t} - u_{{i - 1,j}}^{t} }}{{\delta _{{\mathcal{I}}} }}} \\ { - p\left( {s\left( t \right),t} \right)\frac{{u_{{i,j}}^{t} - u_{{i,j - 1}}^{t} }}{{\delta _{{\mathcal{E}}} }} + \frac{1}{2}\sigma _{{\mathcal{I}}}^{2} \frac{{u_{{i + 1,j}}^{t} - 2u_{{i,j}}^{t} - u_{{i - 1,j}}^{t} }}{{\delta _{{\mathcal{I}}}^{2} }}} \\ { + r\left( {s\left( t \right),a\left( {p,h\left( t \right)} \right),m\left( {s\left( t \right),t} \right),t} \right)} \\ \end{array} } \right\} \hfill \\ s.t.\qquad \qquad SINR\left( {a\left( {p,h\left( t \right)} \right)} \right) \ge \beta \hfill \\ \end{gathered}$$
(33)

At this point, the HJB and FPK equations are solved, and then an intelligent access algorithm is designed based on the MFG model to optimize the multi-node competitive access while improving the energy efficiency of the nodes.

3.3 Intelligent access algorithm based on MFG

In this section, an intelligent access algorithm based on MFG is presented to address the problem of large-scale nodes contending for access channels in a dispersed wireless network, as illustrated in Table 1. All nodes interact with the mean field in order to make optimum behavior decisions, that is, to choose the best transmission power and channel for their needs while maximizing their own advantages with channel access fulfilled. The study in the preceding section shows that the optimal behavior decision \({a}^{*}\left({p}^{*},{h}^{*}\right)\) can be achieved by solving the FPK problem and the HJB equation.

Table 1 Intelligent access algorithm based on MFG
Full size table

In algorithm 1, since the HJB equation must be solved in the reverse time direction, and the FPK equation must be solved in the forward time direction, the value function and the mean field distribution of the state at the final moment are initialized first. According to the discrete value of each time and state, the Hamiltonian function is solved to obtain the behavior strategy \(a\left(p,h\left(t\right)\right)\). Then substitute the obtained \(a\left(p,h\left(t\right)\right)\) into the HJB equation to update, and get the parameter \({\mathrm{u}}_{:,:}^{\mathrm{t}-1}\) needed to solve the Hamiltonian function in the next cycle. Use the FPK equation and the initial state of the mean field to update the mean field. If the change of the mean field distribution of the two adjacent times is lower than the convergence accuracy, the algorithm is considered to have reached the state of convergence, at this time the algorithm ends and the optimal behavior strategy \({a}^{*}\left({p}^{*},{h}^{*}\right)\) is output; otherwise continue to execute loop iterations. Since the maximal discrete values of time, energy, and interference states are X, Y and Z, respectively, the complexity of algorithm 1 is \(O(XYZ)\).

4 Backoff strategy based on Markov model

The previous section proposed an intelligent access algorithm for multiple nodes in a distributed wireless networks based on the MFG model. In the algorithm, the Nash equilibrium is obtained by iterating the FPK-HJB equations, and all nodes adopt the optimal behavior strategy, that is, select the appropriate appropriate transmit power and channel access. However, due to the limited number of channels, some nodes need to adopt backoff strategies to avoid conflicts. Therefore, we will propose a backoff model based on the behavior strategy, and then give the analysis model.

4.1 Backoff analysis model

Assume that the maximum number of retransmissions for each node is \(K\), and varies depending on the data. Assuming that time is a discrete time slot, each node has a saturated data queue, each data packet is continuous, and the back-off time slots of all nodes are synchronized. Because a node's back-off state is tied to its behavior strategy and its own state. The node's future back-off state is only related to its present back-off state and has nothing to do with its prior back-off state. As a result, we may assume that the entire backoff process is governed by a Markov decision process.

The backoff state of each node \(i\) is \({\mathcal{B}}_{i}\), which is determined by the SINR, While the retransmission probability of this node in each time slot t is \({\mathcal{p}}_{i}\). When \({SINR}_{i}\left({a}_{i}\right)<\beta \), the node does not meet the channel access requirements. In order to avoid collision with the node that is transmitting data, it should enter the backoff state, which satisfies \({\mathcal{B}}_{i}\left(t+1\right)=Mod({\mathcal{B}}_{i}\left(t\right),K+1)\). After the current backoff state ends, the node re-selects the decision. If the decision meets the channel access requirements, that is, \(SINR({a}_{i})\ge \beta \), then the node exits the backoff state. However, if the decision still fails to match the conditions for successful channel access, the number of retransmissions of the node is increased by one. Each node can calculate its own retransmission times, which corresponds to the backoff state. For a Markov decision process, the behavioral decision of node \(i\) at time \(t\) mainly depends on the backoff state, which is represented by \({\pi }_{i}^{^{\prime}}({\mathcal{B}}_{i},t)\). Since time is converted into discrete time slots, at the beginning of each time slot, the value of the node's backoff waiting time is reduced by one. As a result we characterize the entire backoff process as a series of retransmissions and backoff waiting time. The discrete-time two-dimensional Markov model for the state variable, as shown in Fig. 2.

Fig. 2
figure 2

Backoff strategy based on Markov model

Full size image

In Fig. 2, \({\mathcal{T}}_{k}\) represents the backoff waiting time in the \({k}_{th}\) backoff process, which satisfies the following requirements

$${\mathcal{T}}_{j}=\frac{\mathcal{T}}{\lambda *{2}^{k-1}}$$
(34)

where \(k\in [1,K]\) represents the current number of retransmissions of the node, and \(\mathcal{T}\) represents the initial contention window size, which is equal to the maximum backoff count value here. \(\lambda \) is a multiplicative factor, which is related to the service type of the node. In the back-off strategy of the node, the back-off waiting time of the node should be different for service types. The more important the service data, the smaller the back-off waiting time.

Let \(p\) represent the likelihood of channel access failure. Figure 2 shows how to calculate the one-step state transition probability of nodes in the backoff process over the whole system.

$$\left\{\begin{array}{c}P\left(k,\mathcal{l}|k,\mathcal{l}+1\right)=1 \\ P\left(\mathrm{0,0}|k,0\right)=1-p \\ P\left(k,\mathcal{l}|k-\mathrm{1,0}\right)=p \end{array},k\in \left[1,K\right]\right.$$
(35)

In formula (35), the first term indicates that if the node has backoff, the value of the backoff waiting time will inevitably decrease by 1 at the beginning of each time slot; the second term indicates that in the \({k}_{th}\) backoff state, when the backoff count decreases to 0, if the node reselects the strategy to meet the access conditions, it will successfully access the channel, and the number of retransmissions will become 0; the third term indicates that the access to the channel fails at the \({k}_{th}\) order. The node waits for access on the next level, and recalculate the backoff waiting time.

4.2 Channel access collision probability and contention window

  1. (1)

    Probability of channel access failure

The probability of channel access failure of node \(i\) under the decision \({\pi }_{i}^{^{\prime}}({\mathcal{B}}_{i},t)\) is expressed as the probability of communication interruption, then \({p}_{i}\) can be expressed as

$${p}_{i}=\mathcal{F}\left({s}_{i},{a}_{i},{s}_{-i},t\right)*{\mathbb{P}}\left({SINR}_{i}\left({a}_{i}\right)<\beta |{{a}_{i}=\pi }_{i}^{^{\prime}}\left({\mathcal{B}}_{i},t\right)\right)$$
(36)

where \(\mathcal{F}\left({s}_{i},{a}_{j},{s}_{-i},t\right)\) reflects the node i's impact factor function when choosing an access channel. Since the success of a node's channel access is determined by its behavior decision under the effect of its own state and the state of other nodes, each decision has a distinct degree of influence deviation. The physical meaning of this formula is reflected in the communication process, if the random information transmission rate obtained is lower than a certain level, that is, the reliable service rate, then the communication link will have an "interruption" event, which means that the node fails to access the channel and the event presents a probability distribution.

  1. (2)

    Retreat waiting time

For the initial backoff waiting time \(\mathcal{T}\), we believe that its size should be related to the duration of the data packet being transmitted. Ideally, when a data transmission in the channel is completed, the following data packet should be transmitted instantly. Therefore, the duration of the data packet transmission is equal to the ratio of the data packet size to the channel transmission rate, that is

$$\mathcal{T}=\frac{E\left[P\right]}{E\left[{R}_{b}\right]}$$
(37)

where \(E[P]\) represents the expectation of the data packet size. Here, we assume that the size of all data packets is constant. \(E[{R}_{b}]\) represents the expectation of the channel transmission rate. Since the node judges whether it meets the access requirement based on the SINR, we can obtain the maximum transmission rate of the ideal channel based on the SINR, so \({R}_{b}\) satisfies the following conditions.

$${R}_{b}=w*{\mathrm{log}}_{2}(1+SINR)$$
(38)

where \(w\) is the channel bandwidth. Other nodes do not know the magnitude of a node's SINR when it successfully accesses the channel, hence the value of \({R}_{b}\) cannot be determined. However, we can use the threshold \(\beta \) to calculate the boundary \({R}_{b}^{*}\) that meets the access, that is

$${R}_{b}^{*}=w{\mathrm{log}}_{2}\beta $$
(39)

In this way, we can both reduce \({R}_{b}\) and increase the duration, which reduces the occurrence of collisions to a certain extent. Therefore, the back-off waiting time \(\mathcal{T}\) is further expressed as

$$\mathcal{T}=\frac{E\left[P\right]}{E\left[{R}_{b}^{*}\right]}$$
(40)

5 Performance analysis

In this section we will make simulation and analysis on the performance of the proposed algorithm. Assuming that each node’s channel gain satisfies Rayleigh fading, for any node \(i\), the probability density function of the channel gain \({\theta }_{i}={\left|{h}_{i}\right|}^{2}\) satisfies the following’

$$f\left({\theta }_{i}\right)=\left\{\begin{array}{c}\frac{1}{\lambda }\mathrm{exp}\left(-\frac{{\theta }_{i}}{{\lambda }^{2}}\right), {\theta }_{i}\ge 0\\ 0, others\end{array}\right.$$
(41)

Since the HJB equation is solved in reverse time, the value function \(u\left(t,s\left(t\right)\right)\) at the final time \(T\) needs to be initialized. According to the reference [17], in order to minimize the node's energy loss and maximize the node's residual energy at the end, the value function \(u\left(t,s\left(t\right)\right)\) at the final time \(T\) is \({u}_{i,j*\gamma s}^{T}=0.05*\mathrm{exp}(j*\gamma s)\). The suggested approach requires the mean field distribution to be initialized, that is, \({m}_{:,:}^{0}=1/(X+1)\). The simulation parameters are shown in Table 2.

Table 2 Simulation parameters
Full size table

Figure 3 shows the selection strategy considering the transmission power of nodes in different energy states. It can be seen from Fig. 3(a) that the transmit power of nodes with different energy states at different moments generally decreases with time. In order to observe the results more clearly, extract the transmission power selection strategy curves at time \(t=0s,t=0.5s and t=1s\) from Fig. 3(a), as shown in Fig. 3(b). It can be seen from the figure that the transmission power selection strategy adopted by the node is related to time and energy state. As time increases, the transmission power adopted by the nodes gradually decreases. This is because the energy of the node is gradually losing. In order to save energy, the node needs to use a lower transmit power to guarantee that its life cycle is as long as possible. In addition, at a certain moment, as the remaining energy of the node increases, so does its selected transmit power.

Fig. 3
figure 3

Node transmit power selection strategy

Full size image

Figure 4 shows that when the MFG reaches the Nash equilibrium, the node adopts the change of the mean field distribution with respect to time and energy state under the transmit power strategy at that moment. It can be seen from Fig. 4(a) that as time continues to grow, the proportion of nodes in a low-energy state in the network is increasing. This is because high-energy nodes carry more service transmissions, which causes their energy to be continuously consumed. Therefore, there are more and more low-energy nodes in the network. In order to show the results more clearly, we respectively take the energy state distribution of the nodes at time \(t=0s,t=0.5s and t=1s\), as shown in Fig. 4(b). It can be seen from the figure that as time goes by, more and more nodes are in the low-energy state in the network. The nodes in the high-energy state are gradually reduced. The remaining energy distribution curve of the nodes is generally toward the lower energy state.

Fig. 4
figure 4

Mean field distribution

Full size image

The revenue of the node is determined by the energy efficiency, according to the description of the intelligent access algorithm presented in this chapter. The average energy efficiency of the network at any given time may be approximated as

$$\sum_{s}m\left(s,t\right)\mathcal{r}\left(s,t\right)$$
(42)

The formula (42) expresses the average value of each state node's energy efficiency. As illustrated in Fig. 5, we examine network energy efficiency when the number of nodes N = 100, 300, and 500, respectively.

Fig. 5
figure 5

Energy efficiency performance of the network

Full size image

Figure 5 shows that as the number of iterations of the system rises, the network's energy efficiency steadily increases and eventually achieves its maximum value until it stabilizes during a given iteration. This is due to the fact that the benefit aim of nodes in the mean-field game model is to maximize energy efficiency, and the current optimum behavior strategy is determined in each iteration. The behavior approach employed by nodes steadily improves prior to convergence, resulting in increased energy efficiency. The figure also shows that the number of iterations for various nodes varies. For example, when N = 500, it starts to converge at the 6th time, while N = 100 it starts to converge at the 9th time. It can be concluded that the number of iterations increases with the number of networks. This indicates that the denser the network, the lower the computational complexity of the MFG. It also proves that the MFG can achieve very low complexity in a distributed wireless large-scale network.

We use the access delay as an indicator to compare the intelligent access algorithm based on the MFG proposed in this chapter with the new random access method (new random access, NRA) proposed in [18], and the ACB (LA-ACB) algorithm [19]. The node access delay mainly includes two parts, the iteration time \({T}_{1}\) for the MFG to reach the Nash equilibrium, and the backoff waiting time \({T}_{2}\) of the node after the failure of channel access. Therefore, the access delay \({T}^{*}\) can be expressed as

$${T}^{*}=\left(1-{\mathbb{P}}\left({SINR}_{i}\left({a}_{i}\right)<\beta |{a}_{i}\right)\right)*{T}_{1}+\sum_{k=1}^{K}{{\mathbb{P}}^{k}\left({SINR}_{i}\left({a}_{i}\right)<\beta |{a}_{i}\right)*({T}_{2}+T}_{1})$$
(43)

In (43), \({\mathbb{P}}\left({SINR}_{i}\left({a}_{i}\right)<\beta |{a}_{i}\right)\) is expressed as the probability of channel access failure of node \(i\) under behavior strategy \({a}_{i}\). This formula means that if the node successfully accesses the channel, the access delay only exists in \({T}_{1}\). If the channel access fails, the backoff waiting time \({T}_{2}\) will be added to \({T}_{1}\), and the node will reselect behavior decisions after the waiting time has passed. The process adds another iteration time \({T}_{1}\). There may be k such processes during this period, \(k\le N\).

Figure 6 shows the average access delay of the three access algorithms as the number of nodes increases. It can be seen from the figure that NRA lacks the access control of the ACB mechanism. Due to its low access success rate, the number of backoff retransmissions also increases, resulting in an increase in access delay. The LA-ACB algorithm sets the ACB factor, which can improve the access success rate of the node, so the overall performance of the LA-ACB algorithm is better than that of the NRA. However, as the number of nodes grows, the LA-ACB algorithm's performance tends to deteriorate. This is due to the two-step access method used by the LA-ACB algorithm when it meets tiny data services, which wastes access resources. When there are fewer nodes, the proposed access algorithm has a longer access time than previous algorithms. This is because the iterative process of the MFG takes a certain amount of time, and the results of the Nash equilibrium also have certain errors, leading to some node access fail. As the number of nodes increases and iterations decreases, the result of Nash equilibrium becomes more and more accurate. In addition, the access delay gradually stabilizes and is better than the other two algorithms. This figure also shows that the access delay of the proposed algorithm is affected by the SINR threshold \(\beta \). This is because the threshold \(\beta \) affects the successful channel access probability of the nodes. The larger the threshold, the smaller the successful access probability, hence the average access delay with a modest threshold is tiny overall. The rate of increase of the average delay is gradually decreasing and it will not converge to a fixed value when the number of nodes is large enough. The node density and the number of access requests are related to the rate of increase of the average delay.

Fig. 6
figure 6

The curve of average access delay as a function of the number of nodes

Full size image

6 Conclusion

In this paper we propose an intelligent access algorithm based on MFG to solve the problem of large-scale nodes competing for access to multiple channels in a distributed wireless network scenario. First, the nodes' competition process is described as a stochastic differential game, with maximizing energy efficiency as the benefit goal. All competing nodes select their optimal behavior decisions through interactive selection to obtain Nash equilibrium. However, as the number of competing nodes increases, the coupling relationship of the HJB equation becomes more complicated, making it very difficult to solve the equations. Therefore, by introducing the mean field theory, the stochastic differential game is approximately transformed into a MFG. The interaction between the nodes is transformed into the interaction between the nodes and the mean field. Then the HJB equation and FPK equation are derived and numerically solved to obtain the Nash equilibrium. Finally, we analyzed the backoff of nodes. A backoff strategy based on Markov model is proposed. Simulation shows that the approach is particularly effective at maximizing the competitive access of large scale multi hop networks.