1 Introduction

Towards the next generation of mobile and wireless networks, machine-to machine (M2M) communications [3] is envisioned to play a significant role that forms the basis for the future Internet of Things (IoT). It is anticipated that the number of M2M devices connected to a single cellular base station (BS) may exceed 5 million by the year 2030 [4]. In such a massive connectivity scenario, conventional random access and resource allocation schemes [5] are not sufficient to handle the massive amount of communication requests from the M2M devices, thereby posing significant challenges in the design and operation of the wireless networks.

For large-scale networks such as M2M communication networks, distributed resource allocation schemes are highly desired in order to alleviate the scaling issues due to massive connectivity [6]. In distributed schemes, each device decides semi-autonomously on which resources to access the channel, which results in a significant reduction of signaling overhead for coordination and information exchange between the devices and the BS. Moreover, considering the limited computing capability of the M2M devices [7], there is a strong need for low-complexity solutions that require relatively low computing power.

Apart from the massive number of devices, a key feature of the M2M traffic is that the device activity patterns are typically sporadic [8] so that at any given time instant each device has a low probability of being active. This results in a certain level of sparsity in the device activity. To this end, compressed sensing (CS) [9,10,11,12] is identified as an ideal framework in such scenarios since it provides tools for efficient reconstruction of high-dimensional signals with a sparse representation. Moreover, it is often observed that the messages sent by the M2M devices are strongly correlated, e.g., due to proximity, the same service type, and etc [7]. Therefore, it is in particular beneficial to partition a given set of all devices into a number of clusters such that similar requests can be handled jointly. Given this cluster-like behavior and the sparse nature of the M2M traffic, the activation pattern of the devices can be modeled as a block-sparse signal with an additional in-block structure [13] in CS-based applications.

The main objective of this study is to seek for an efficient resource allocation scheme to mitigate serious scaling problems resulting from massive connectivity, by exploiting the specific sparsity feature in the device activity. A special attention is attached to low overhead communication with enhanced spectral efficiency and reduced computational complexity. Towards this end, we propose a three-phase resource allocation scheme, where we use a distributed approach to reduce the communication overhead and a sketching algorithm to lower the computing load.

1.1 Related works

Conventional cellular networks are designed based on the scheduling of active users to orthogonal time or frequency resources. The excessive control overhead incurred by the massive number of sporadically active M2M devices, however, renders such kind of resource allocation schemes unrealistic. As an alternative, contention-based schemes, such as slotted ALOHA [14], have been proposed to deal with this issue. However, the main drawback of these schemes is the lack of deterministic performance guarantees, and in particular the performance deteriorates significantly under massive connectivity settings. In addition, the authors of [15] also raised concerns of energy efficiency in large-scale M2M networks, where systems with less computational complexity and lower power consumption are particularly desired for low-cost M2M devices with limited operational capability.

Taking sparsity in the activity pattern into account, access schemes using CS also receive a great deal of attention in recent years. To the best of our knowledge, the authors of [16] were the first to propose the idea of CS-based multi-user detection. They introduced a smart adaptive algorithm that switches between a CS-based reconstruction algorithm and a classical detection method depending on the sparsity level of the signals being detected. Reference [17] proposed greedy CS algorithms to facilitate a joint detection of device activity and transmitted data. The idea was further extended in [18] to include multicarrier access schemes and to provide higher spectral efficiency and more flexibility of such schemes. Furthermore, schemes for distributed compressed sensing were also widely studied (e.g. in [19]) to take advantage of both inter- and intra-signal correlations by jointly reconstructing signals that have been compressed independently. The concept of distributed compressed sensing has been applied by the authors of [20] to facilitate device detection in M2M communications, which shows significant performance gains expressed in terms of robustness.

However, none of the works mentioned above has exploited the particular cluster-like behavior of M2M devices, thereby ignoring the block sparsity structure in the activation pattern. In addition, greedy algorithms such as orthogonal matching pursuit (OMP) [21] are widely used in detection schemes owing to their low computational complexity. However, in many wireless applications including that considered in this study, even this reduced complexity is a bottleneck due to strictly limited computing resources on the M2M devices. Therefore, we employ a sketching algorithm in our proposed approach to further offload the computation burden incurred by massive M2M communications.

1.2 Main contribution

In this work, we present and analyze a novel distributed scheme for device detection and contention-free resource allocation in large-scale M2M communication networks. We partition the M2M devices into disjoint clusters in advance based on service type, and assign to each device a cluster-specific signature that active devices use for their initial access. In this paper, we use the following definition of an active cluster.

Definition 1

(Active cluster) We say that a cluster is active if there is at least one active device in this cluster.

The devices in each cluster are totally ordered according to some given criterion such as service priority. In other words, the set of devices in each cluster is a totally ordered set \({\mathcal {S}}\) so that if \(a,b\in {\mathcal {S}}, a\ne b\) and \(a\le b\), then \(a<b\). This order is a priori known at all cluster members and gives rise to what we call active ranking that determines the order within each cluster in which the active devices access the set of assigned resource blocks, i.e., an active device that is the i-th element in the active ranking accesses the i-th resource block.

Definition 2

(Active ranking) The active ranking associated with each active cluster is the totally ordered subset induced by the active devices in a cluster.

Motivated by the CS principle, the proposed scheme mainly consists of three phases:

  • Phase (i) Signal acquisition The active devices transmit simultaneously pre-equalized individual signatures, each of which indicates the membership to a particular cluster. Exploiting full-duplex transceivers,Footnote 1 all the devices and the BS obtain their individual measurements, which are the superposition of the transmitted signatures from the active devices.

  • Phase (ii) Detection at BS The BS detects the active clusters, the number of active devices in each cluster, and also the collision pattern in the received measurements. Then it broadcasts the detected information to the devices and assigns a sufficient amount of resources to each active cluster accordingly.

  • Phase (iii) Detection at devices Each active device detects the active ranking of its cluster, and then accesses the corresponding resource assigned by the BS based on its ranking position.

We study a particular signature design for the devices in each cluster to facilitate the detection process of phase (ii) at the BS side and that of phase (iii) at the device side. Moreover, based on the Count-Sketch procedure [23, 24], we develop a novel block sketching algorithm to perform phase (ii) and to bring down computational complexity induced by massive connectivity. Phase (iii) is performed using a conventional greedy algorithm such as OMP [21] except that we use feedback information from the BS to enhance robustness and to further reduce complexity. Furthermore, with the distributed ranking-based resource allocation scheme, each active device accesses autonomously a pool of resource blocks assigned by the BS in a contention-free manner without further control signaling, thus the communication overhead is significantly reduced. We show via theoretical analysis that the proposed scheme achieves a better scaling with increasing network size both in terms of communication overhead and computational complexity when compared with classical CS-based approaches. Moreover, the simulation results reveal a significantly enhanced robustness of the proposed scheme in the presence of Gaussian noise and inaccurate channel estimations.

1.3 Organization of the paper

The remainder of this paper is organized as follows. Section 2 introduces a mathematical model for the proposed scheme. In Sect. 3, we present the detection algorithms in detail. Section 4 is devoted to theoretical analysis of the proposed scheme, while Sect. 5 evaluates the performance with numerical simulation results. Finally, Sect. 6 concludes the paper with some final remarks.

1.4 Notational remarks

Throughout this work, matrices and vectors are denoted by uppercase and lowercase letters, respectively. The superscript \((\cdot )^T\) represents the transpose of a matrix or a vector, and \((\cdot )^H\) indicates the Hermitian transpose. \(A\circ B\) denotes the Hadamard product of matrices A and B. The field of binary, real and complex numbers are denoted by \({\mathbb {B}}\), \({\mathbb {R}}\) and \({\mathbb {C}}\). The cardinality of a set is given by \(|\cdot |\), and the \(\ell _{2}\)-norm is given by \(||\cdot ||\). Furthermore, \({\mathcal {O}}\) denotes “big-O” according to Knuth’s notation. Unless otherwise stated, all logarithms are assumed to be to base 2.

2 Methods

In this section, we introduce the underlying system model and formulate the problem which is addressed in this paper.

2.1 Transmitter side

We consider an M2M network consisting of N devices, which are partitioned into L clusters of equal size d according to the service type.Footnote 2 The members of each cluster are known both at the BS and at all devices, which can be achieved via device registration to the network. We assume that the devices have sporadic transmissions, which implies that at a given time instant, only a relatively small number of devices from a few clusters are activated to access the channel. Therefore, we define a twofold sparsity pattern to model the active status of the devices:

  • Block sparsity \(K_{B}\) The maximum number of active clusters at any time.

  • In-block sparsity \(K_{I}\) The maximum number of active devices in an active cluster.

Therefore, the total number of active devices in the network is \(K\le K_{B}K_{I}\). On the other hand, due to the sparsely-activated devices, we have \(K\le K_{B}K_{I}\ll N={\mathrm {Ld}}\).

We use a K-sparse binary sequence (or vector) \(x\in {\mathbb {B}}^N\) to model the activation pattern of the devices in the network, where entry “1” indicates that the corresponding device is active while an inactive device results in “0”. Furthermore, we use \(x_{\ell }\in {\mathbb {B}}^d,\ell \in \{1,\cdots ,L\}\) to denote the subsequence (or subvector) of x corresponding to cluster \(\ell\). In addition, the block support, denoted as \({\mathcal {S}}_{B}\), is defined to be the set of indices of the active clusters: \({\mathcal {S}}_{B}=\{\ell \in \{1,\cdots ,L\}:||x_{\ell }||_{0}\ne 0\}\). Similarly, the in-block support, denoted as \({\mathcal {S}}_{I,\ell }\), indicates the set of indices of the active devices in cluster \(\ell\): \({\mathcal {S}}_{I,\ell }=\{j\in \{1,\cdots ,d\}:x_{\ell ,j}=1\}\). By definition, we have \(|{\mathcal {S}}_{B}|\le K_{B}\) and \(|{\mathcal {S}}_{I,\ell }|\le K_{I}\) for all \(\ell \in \{1,\cdots ,L\}\). Thus, the activation pattern of the devices x is modeled as a sparse signal with block sparsity \(K_{B}\) and in-block sparsity \(K_{I}\), and we call signals of such a sparsity pattern \((K_{B}, K_{I})\) block-sparse.

Due to the sparsity in x, we use the CS theory [9,10,11] to reconstruct x based on measurements performed by the BS and the devices in the network. We use \(A\in {\mathbb {R}}^{M\times N}\) to denote the measurement matrix whose exact structure is defined later in Sect. 3.1. Each column of A, say column i denoted by \(a_{i}, i\in \{1,\cdots ,N\}\), corresponds to the unique signature sent by device i if it is active, whereas \(A_{-,\ell }\in {\mathbb {R}}^{M\times d}\) denotes a submatrix of A corresponding to the signatures sent by the devices from the \(\ell\)-th cluster.

2.2 Receiver side

Due to the superposition property of the wireless channel, each receiver observes a noisy superposition of signatures transmitted by the active devices. We assume that all frames are received synchronously at the aggregation node. In practical systems this can be ensured e.g. by a synchronization signal from the BS. Alternatively, the requirement for precise synchronization can be mitigated by using schemes such as that considered in [25] which is robust to the lack of synchronization and requires only a coarse synchronization. To this end, the received signal at the BS \(y\in {\mathbb {C}}^M\) is a noisy linear combination of the transmitted signatures given by

$$\begin{aligned} y=(A\circ H_{B})x+\epsilon _{B}, \end{aligned}$$
(1)

where \(H_{B}\in {\mathbb {C}}^{M\times N}\) is the channel matrix, and \(\epsilon _{B}\in {\mathbb {C}}^M\) denotes the additive noise which is assumed to be zero-mean with independent components of variance \(\sigma _{B}^{2}\). The Hadamard product is used here to model the effective channel when applied with advanced technologies such as frequency hopping [26], which is introduced in detail in Sect. 3.2.

In addition, the active devices also perform their own local measurements during the acquisition phase. The received signal \(y_{D}\in {\mathbb {C}}^M\) observed by a particular device at some given time instant is obtained as

$$\begin{aligned} y_{D}=(A\circ H_{D})x+\epsilon _{D}, \end{aligned}$$
(2)

where \(H_{D}\) is an \({M\times N}\) matrix representing the wireless channels between the devices, and \(\epsilon _{D}\in {\mathbb {C}}^M\) is the vector of independent noise components with zero mean and variance \(\sigma _{D}^{2}\).

Furthermore, we make the following assumption on channel knowledge:

Assumption 1

Each device has the channel state information to the BS.

In current systems [5], the channel information can be obtained with pilot-signals from the network with no extra cost. Alternatively, it can also be possibly obtained via statistical channel knowledge [27], location-based estimation [28], channel reciprocity [29] or long-term observation [30]. We point out that the entries of \(H_{B}\) and \(H_{D}\) are in general not physical channels but rather effective channels that depend on the underlying transmission scheme. For instance, the effective channels of the energy-detection based scheme in [25] is related to channel power gains, which are much easier to acquire than complex-valued channel coefficients.

2.3 Problem formulation

Fig. 1
figure 1

Target problem formulation

Full size image

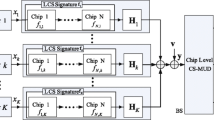
Figure 1 illustrates the transmission scenario and the problem of interest in this work. As a result of concurrent transmissions of the active devices, the BS observes a noisy superposition of the transmitted signatures given by (1), while the received signal at the devices is as in (2). Hereafter, we apply CS related techniques to reconstruct the (\(K_{B},K_{I}\)) block-sparse signal x with y at the BS and \(y_{D}\) at the devices. To be specific, the BS performs block support recovery to obtain an accurate estimation of the block support \(\tilde{{\mathcal {S}}}_{B}\) and the cardinality of the in-block support \(|\tilde{{\mathcal {S}}}_{I,\ell }|\) for each \(\ell \in \{1,\cdots ,L\}\). Subsequently, each active device from cluster \(\ell\) performs in-block support recovery to estimate the in-block support \(\tilde{{\mathcal {S}}}_{I,\ell }\) using the received signal \(y_{D}\) in (2) and side information broadcast by the BS.

In a typical massive connectivity scenario as in M2M communications, we need to find proper solutions of high efficiency and low computational complexity to the following problems.

  • Problem 1 Block support recovery at the BS with \({\mathbb {P}}\left( \tilde{{\mathcal {S}}}_{B}={\mathcal {S}}_{B}, \forall _{\ell \in \{1,\cdots ,L\}}|\tilde{{\mathcal {S}}}_{I,\ell }|=|{\mathcal {S}}_{I,\ell }| \right) \ge 1-\delta\), where \(\delta\) is a target error bound.

  • Problem 2 In-block support recovery at the active devices in cluster \(\ell\) with \({\mathbb {P}}\left( \tilde{{\mathcal {S}}}_{I,\ell }={\mathcal {S}}_{I,\ell }\right) \ge 1-\delta\).Footnote 3

3 Distributed ranking-based resource allocation

In this section, we present our algorithm design to tackle the target problems. In particular, this includes the structured signature model and the decoding procedures at the BS as well as at the devices, respectively.

3.1 Structured random signature model

The measurement matrix \(A\in {\mathbb {R}}^{M\times N}\) we design here is a structured random matrix, which is an extension of those utilized by the Count-Sketch procedure proposed in [23, 24]. These matrices are desired as they in general facilitate low computational complexity. We denote by \({\mathcal {A}}(R,T,L,d,\alpha )\) a particular distribution over matrices with RT rows and Ld columns, which is specified below, and we assume that the measurement matrix A is drawn from this distribution, i.e., \(A\sim {\mathcal {A}}(R,T,L,d,\alpha )\) with \(M={\mathrm {RT}}, N={\mathrm {Ld}}\).

Fig. 2
figure 2

Structure of the measurement matrix A

Full size image

As illustrated in Fig. 2, the measurement matrix A is composed of the vertical concatenation of T individual random matrices that we denote by \(A_{t,-}\in {\mathbb {R}}^{R\times N}\) for \(t\in \{1,\cdots ,T\}\), where \(A_{t,-}\) consists of the horizontal concatenation of L sub-matrices \(A_{t,\ell }\in {\mathbb {R}}^{R\times d}\) for \(\ell \in \{1,\cdots ,L\}\). Each \(A_{t,\ell }\) is a sparse matrix containing exactly d non-zero components – located on the same row and with the same value. The index of the row with non-zero elements is chosen uniformly at random from the set \(\{1,2,\cdots ,R\}\), and the non-zero components take either the value \(+\alpha\) or \(-\alpha\) with probability 1/2. For a given realization of \(A_{t,\ell }\), let \(q_{t,\ell }\in \{1,\cdots ,R\}\) denote the index of the row of \(A_{t,\ell }\) with non-zero entries, and \(s_{t,\ell }\in \{-\alpha ,+\alpha \}\) be the corresponding value of the non-zero components in \(A_{t,\ell }\). As each signature transmitted by the devices is the corresponding column of A, it is therefore a sparse sequence of length M with sparsity level T.

3.2 Block support recovery at BS

The objective of the decoding procedure at the BS is to obtain an accurate estimation of the block support \({\mathcal {S}}_B\) and the cardinality of the in-block support \(|{\mathcal {S}}_{I,\ell }|\) for each active cluster \(\ell \in \{1,\cdots ,L\}\) (see Problem 1 in Sect. 2.3).

The signal y received by the BS at some given time instant is given by (1). Since the channel state information \(H_{B}\) is assumed to be available at the devices, the active devices can perform a channel inversion before transmitting the signatures to indicate their active state. Particular variants of (generalized) inverses of the channel matrix may be taken at the transmitter side. For example, \(H_{B}\) can be inverted by simply taking the reciprocal of the non-zero elements whose magnitude is above certain threshold \(\theta\), which is given by

$$\begin{aligned} (H_{B})^{-1}_{i,j} = {\left\{ \begin{array}{ll} \frac{1}{(H_{B})_{i,j}}, \quad \text {if}\quad |H_{B}|_{i,j} \ge \theta \\ 0, \quad \quad \quad \text {else} \end{array}\right. },\text {for}\quad i=\{1,\cdots ,M\},j=\{1,\cdots ,N\}. \end{aligned}$$
(3)

In this case devices with weak links due to the near-far behavior may stay offline and avoid excessively large transmit power and strong interference to other nodes. Then the obtained measurements at the BS are given as

$$\begin{aligned} y = (A\circ H_{B}\circ H_{B}^{-1})x + \epsilon _{B}:= Ax+\epsilon _{B}. \end{aligned}$$
(4)

In this paper, for the sake of simplicity we develop a fast block sketching algorithm based on the Count-Sketch procedure proposed in [23, 24] to realize the decoding process at the BS. To be more precise, we use \(y_{t}\in {\mathbb {R}}^R\) to denote the subvector of y corresponding to the observations obtained via submatrix \(A_{t,-}\). So, we have

$$\begin{aligned} y_{t}=A_{t,-}x+\epsilon _{t}, \quad \text {for} \quad t\in \{1,\cdots ,T\}. \end{aligned}$$
(5)

Given \(y_{t}\) for each \(t\in \{1,\cdots ,T\}\), we form the signal estimate \({\tilde{x}}_{t}\in {\mathbb {R}}^N\) by indexing and scaling the entries of the corresponding observations \(y_{t}\) such that

$$\begin{aligned} {\tilde{x}}_{t}=A_{t,-}^Ty_{t}, \quad \text {for} \quad t\in \{1,\cdots ,T\}, \end{aligned}$$
(6)

where each \(A_{t,-}\) consists of the horizontal concatenation of L submatrices \(A_{t,\ell }\) for \(\ell \in \{1,\cdots ,L\}\). Further recall that each matrix \(A_{t,\ell }\) is a sparse matrix containing d non-zero components located on the same row \(q_{t,\ell }\in \{1,\cdots ,R\}\) and all the non-zero components have the same value \(s_{t,\ell }\in \{-\alpha , +\alpha \}\). As a result, the i-th entry \({\tilde{x}}_{t,i}\) of \({\tilde{x}}_{t}\) for the \(\ell\)-th block can be written as

$$\begin{aligned} {\tilde{x}}_{t,i}=s_{t,\ell }y_{t,\ell }, \quad \text {for} \quad i\in \{d\ell -d+1,\cdots ,d\ell \}, \ell \in \{1,\cdots ,L\}, \end{aligned}$$
(7)

where \(y_{t,\ell }=\left( y_{t}\right) _{q_{t,\ell }}\). We use \(a_{q_{t,\ell },i}\) to denote the entry in the \(q_{t,\ell }\)-th row and i-th column of \(A_{t,-}\), then we have

$$\begin{aligned} y_{t,\ell } = \sum _{k=1}^{L}\sum _{i=dk-d+1}^{dk}a_{q_{t,\ell },i}x_{i}+\epsilon _{t,\ell }, \quad \text {for} \quad t\in \{1,\cdots ,T\},\ell \in \{1,\cdots ,L\}. \end{aligned}$$
(8)

Since \(y_{t,\ell }\) is dominated by the non-zero entries on the \(q_{t,\ell }\)-th row of \(A_{t,-}\), we denote by \({\mathcal {S}}_{t,\ell }\) a set of indices of the clusters which have non-zero components on the same row as block \(\ell\), i.e., \({\mathcal {S}}_{t,\ell }=\{j=\{1,\cdots ,L\}:q_{t,j}=q_{t,\ell }\}\). Then \(y_{t,\ell }\) is given by

$$\begin{aligned} \begin{aligned} y_{t,\ell }&=\sum _{k\in {\mathcal {S}}_{t,\ell }}\sum _{i=dk-d+1}^{dk}s_{t,k}x_{i}+\epsilon _{t,\ell }\\&=\sum _{i=d\ell -d+1}^{d\ell }s_{t,\ell }x_{i}+\sum _{k\in {\mathcal {S}}_{t,\ell }\backslash \{\ell \}}\sum _{i=dk-d+1}^{dk}s_{t,k}x_{i}+\epsilon _{t,\ell }\\&\overset{(a)}{=}s_{t,\ell }\left( \sum _{i=d\ell -d+1}^{d\ell }x_{i}\right) +\sum _{k\in {\mathcal {S}}_{t,\ell }\backslash \{\ell \}}s_{t,k}\left( \sum _{i=dk-d+1}^{dk}x_{i}\right) +\epsilon _{t,\ell }\\&\overset{(b)}{=}s_{t,\ell }|{\mathcal {S}}_{I,\ell }|+\sum _{k\in {\mathcal {S}}_{t,\ell }\backslash \{\ell \}}s_{t,k}|{\mathcal {S}}_{I,k}|+\epsilon _{t,\ell }\\&\overset{(c)}{=}s_{t,\ell }|{\mathcal {S}}_{I,\ell }|+\sum _{k\in {\mathcal {S}}_{B}\cap {\mathcal {S}}_{t,\ell }\backslash \{\ell \}}s_{t,k}|{\mathcal {S}}_{I,k}|+\epsilon _{t,\ell }, \end{aligned} \end{aligned}$$
(9)

where (a) follows from the structure of \(A_{t,\ell }\) with equal non-zero elements on the same row, (b) is due to \(x_{i}\in \{0,1\}\), and (c) holds since \(|{\mathcal {S}}_{I,k}|=0\) if \(k\notin {\mathcal {S}}_{B}\).

Putting \(y_{t,\ell }\) in (9) into (7) yields

$$\begin{aligned} \begin{aligned} {\tilde{x}}_{t,i}&=s_{t,\ell }\left( s_{t,\ell }|{\mathcal {S}}_{I,\ell }|+\sum _{k\in {\mathcal {S}}_{B}\cap {\mathcal {S}}_{t,\ell }\backslash \{\ell \}}s_{t,k}|{\mathcal {S}}_{I,k}|+\epsilon _{t,\ell }\right) \\&=\alpha ^2|{\mathcal {S}}_{I,\ell }|+\underbrace{\sum _{k\in {\mathcal {S}}_{B}\cap {\mathcal {S}}_{t,\ell }\backslash \{\ell \}}s_{t,\ell }s_{t,k}|{\mathcal {S}}_{I,k}|}_{\Delta _{t,\ell }}+\underbrace{s_{t,\ell }\epsilon _{t,\ell }}_{\Xi _{t,\ell }},\\ \end{aligned} \end{aligned}$$
(10)

where \(\Delta _{t,\ell }\) is the interference term from other active blocks, and \(\Xi _{t,\ell }\) is the noise term with zero mean and variance \(\gamma ^2\).

To mitigate the interference \(\Delta _{t,\ell }\) from other blocks, we consider a block-wise estimate \({\bar{x}}_{\ell }\) for each \(\ell \in \{1,2,\cdots ,L\}\) given by

$$\begin{aligned} {\bar{x}}_{\ell } = \text {median} \{{\tilde{x}}_{t,i}\}_{t=1,i=d\ell -d+1}^{T,d\ell }, \quad \text {for} \quad \ell \in \{1,2,\cdots ,L\}. \end{aligned}$$
(11)

Notice that, instead of the mean, the estimate \({\bar{x}}_{\ell }\) for block \(\ell\) is equal to the median of \({\tilde{x}}_{t,i}\) over \({\mathcal {O}}(Td)\) samples. The rationale behind this approach is to make the estimates more robust against outliers, since large value elements in the data stream may spoil some subsets of the estimate if the mean is computed.

We show later in Sect. 4.1 that by taking the median value block-wisely among all individual estimations as in (11), each estimate \({\bar{x}}_{\ell }\) for the \(\ell\)-th block corresponds to \(|{{\mathcal {S}}}_{I,\ell }|\) with high probability (w.h.p.), and the cardinality of the in-block support set \(|{{\mathcal {S}}}_{I,\ell }|\) is obtained as

$$\begin{aligned} |{{\mathcal {S}}}_{I,\ell }|=\left[ \frac{1}{{\alpha }^2}\cdot {\bar{x}}_{\ell }\right] , \quad \text {for} \quad \ell \in \{1,2,\cdots ,L\}. \end{aligned}$$
(12)

Therefore, since \(|{{\mathcal {S}}}_{I,\ell }|\) indicates the number of active devices in cluster \(\ell \in \{1,2,\cdots ,L\}\), those clusters with \(|{{\mathcal {S}}}_{I,\ell }|>0\) are marked as “active” by the BS. For brevity, we assume that each device needs one resource block for transmission. Therefore, the number of resource blocks assigned by the BS to cluster \(\ell \in \{1,2,\cdots ,L\}\) equals to \(|{\mathcal {S}}_{I,\ell }|\).

In addition, for a given \(x_{i}\) from an active block \(\ell \in {\mathcal {S}}_{B}\), if an individual estimate \({\tilde{x}}_{t,i}\) in (7) is much larger than the block-wise estimate \({\bar{x}}_{\ell }\) in (11), i.e., \({\tilde{x}}_{t,i}\gg {\bar{x}}_{\ell }\), then we can conclude that the corresponding measurement might suffer strong interference from the other active clusters. That is, for a given \(x_{i}\) from block \(\ell\) and a particular \(t\in \{1,\cdots ,T\}\), the interference term \(\Delta _{t,\ell }\) in (10) is non-zero. In such a case, we mark the measurement as “collided” for cluster \(\ell\) and keep its index \(q_{t,\ell }\) in the collision pattern vector \(Q_{\ell }\) for the corresponding cluster.

The above approach provides the BS with an accurate estimate of \({\mathcal {S}}_{B}\) and \(|{\mathcal {S}}_{I,\ell }|\), and therefore it solves Problem 1. The detailed proof of the performance guarantee will be given in Sect. 4.1. In addition, it provides the collision patterns \(Q_{\ell }\) in the measurements for \(\ell \in \{1,2,\cdots ,L\}\). The BS broadcasts these information to the devices and assigns to each cluster, say cluster \(\ell \in \{1,2,\cdots ,L\}\), \(|{\mathcal {S}}_{I,\ell }|\) resource blocks to accommodate all active devices in this cluster.

3.3 In-block support recovery at devices

During the signal acquisition phase, each active device also collects its own measurements, which are linear combinations of the transmitted signatures from other active devices. In this section, we address Problem 2 in Sect. 2.3. The objective is to develop a scheme that enables each active device in cluster \(\ell \in \{1,\cdots ,L\}\) to reliably estimate the in-block support \({\mathcal {S}}_{I,\ell }\) with low computational complexity, based on its local measurements and the feedback from the BS as side information.

Given the measurement matrix A under the random structured model in Sect. 3.1 and the pre-channel correction in (4), the measurement \(y_{D}\) collected at an active device is given by

$$\begin{aligned} y_{D} = (A\circ H_{D}\circ H_{B}^{-1})x + \epsilon _{D} = {\tilde{A}}x+\epsilon _{D}. \end{aligned}$$
(13)

According to the specific structure of A, the corresponding submatrix \(A_{-,\ell }\) for cluster \(\ell \in \{1,\cdots ,L\}\) has only T rows with non-zero components. The indices of these rows are collected in the set \(D_{\ell }\). Furthermore, with the feedback information from the BS on the collision pattern \(Q_{\ell }\) for cluster \(\ell\) indicating those collided measurements to be discarded, we form an index set \(U_{\ell }=D_{\ell }\cap {\bar{Q}}_{\ell }\). Therefore, in order to perform the in-block support recovery of \(x_{\ell }\) at any device from cluster \(\ell\), we simply need to focus on \(y_{D,\ell }\) – a vector composed of the entries of \(y_{D}\) corresponding to \(U_{\ell }\). We denote \({\tilde{A}}_{D,\ell }\) as a \(|U_{\ell }|\times d\) submatrix of \({\tilde{A}}\) with vertical concatenation of rows corresponding to \(U_{\ell }\) and columns for block \(\ell\). Therefore, we have

$$\begin{aligned} y_{D,\ell } = {\tilde{A}}_{D,\ell }x_{\ell } + {\tilde{\epsilon }}_{D}. \end{aligned}$$
(14)

As introduced in Sect. 2.2, we use technologies such as frequency hopping [26] for the transmission where symbols are transmitted hopping over multiple subcarriers. Since the channels between the devices over different subcarriers are assumed to be i.i.d., we can conclude that \({\tilde{A}}_{D,\ell }\) has independent columns and row-blocks (e.g., to be i.i.d Subgaussian). Therefore, some classic CS decoding algorithms can be applied to perform the in-block support recovery. We argue in favor of the greedy algorithms such as OMP [21] due to their low complexity, which is particularly attractive to M2M-based applications where limited computational capability as well as energy consumption at the devices are important design criteria.

An example of the modification on OMP for in-block support recovery is summarized in Algorithm 1, where the modified steps are marked in boldface. By exploiting the broadcast information on the cardinality of the in-block support \(|{\mathcal {S}}_{I,\ell }|\) for cluster \(\ell\), the stopping criteria for implementing the greedy algorithms can be set by limiting the number of iterations to \(|{\mathcal {S}}_{I,\ell }|\), thereby leading to further reduced computational complexity. This is merely an illustrative example assuming that channel knowledge is available at the devices. However, this assumption can be further relaxed by using approximate message passing (AMP) algorithms as in [31].

figure a

To this end, Problem 2 is explicitly resolved. In Sect. 4.2, we prove conditions under which the in-block support \({\mathcal {S}}_{I,\ell }\) can be accurately reconstructed at the devices in cluster \(\ell\). Thus, the activation pattern \(x_{\ell }\) of the \(\ell\)-th cluster can be precisely reconstructed and detected by the active devices. Thereafter, each active device is able to learn the active ranking in its cluster and accesses the corresponding resource blocks assigned by the BS.

4 Theoretical performance analysis

This section provides a sufficient condition for the performance guarantees of our proposed scheme. In particular, we come with the following theorem.

Theorem 1

Suppose that the activation pattern of the devices is modeled as a \((K_{B}, K_{I})\) block-sparse signal \(x\in {\mathbb {B}}^N\) over block size d, and the signatures transmitted by the devices are modeled as a measurement matrix \(A\in {\mathbb {R}}^{M\times N}\) following the structure designed in Sect. 3.1. By applying the block sketching algorithm in Sect. 3.2 for decoding at the BS and the modified OMP in Sect. 3.3 for decoding at the devices, x can be reliably reconstructed by the proposed scheme with computational complexity of \({\mathcal {O}}(dK_{I}^{2}+\frac{N}{d}\log N)\) if the length of the transmitted signatures

$$\begin{aligned} M={\mathcal {O}}(\max \{K_{B}\log N, K_{B}K_{I}\log d\}). \end{aligned}$$
(17)

A rigorous proof of Theorem 1 will be presented in the following, considering both the block support recovery at the BS and in-block support recovery at the devices, respectively. And we also show that it achieves a better scaling when compared with classical CS-based approaches both in terms of communication overhead and computational complexity.

4.1 Block support recovery at BS

First, we analyze the recovery guarantee for the individual estimate \({\tilde{x}}_{t,i}\) in (7).

Lemma 1

Suppose that \(x\in {\mathbb {B}}^N\) is a \((K_{B}, K_{I})\) block-sparse signal over block size d, and \(A\in {\mathbb {R}}^{M\times N}\) is randomly drawn from \({\mathcal {A}}(R,T,L,d,\alpha )\). Given \(y\in {\mathbb {R}}^M\) in (4) and the estimate \({\tilde{x}}_{t,i}\) in (7) for a particular entry \(x_{i}\) from block \(\ell \in \{1,\cdots ,L\}\) and a given \(t\in \{1,\cdots ,T\}\), let \(\Gamma \left( {\tilde{x}}_{t,i}\right) :=\{|{\tilde{x}}_{t,i}-\alpha ^2|{\mathcal {S}}_{I,\ell }||\le 3\gamma \}\), where \(\gamma ^2\) is the variance of the noise term \(\Xi _{t,\ell }\) in (10). The probability of \(\Gamma ({\tilde{x}}_{t,i})\) is lower bounded by

$$\begin{aligned} {\mathbb {P}}\left( \Gamma ({\tilde{x}}_{t,i})\right) \ge 1-\frac{K_{B}-1}{R}. \end{aligned}$$
(18)

Proof

According to (10), for a particular estimate \({\tilde{x}}_{t,i}\) of \(x_{i}\) in block \(\ell\) with \(t\in \{1,\cdots ,T\}\), \(\Gamma ({\tilde{x}}_{t,i})\) holds w.h.p. if the corresponding interference term \(\Delta _{t,\ell }=0\), since the noise term \(\epsilon _{t,\ell }\) is randomly drawn from a Gaussian ensemble with zero mean and variance \(\gamma ^2\) [32]. A sufficient (but not necessary) condition for \(\Delta _{t,\ell }=0\) to hold is that the set \({\mathcal {S}}_{B}\cap {\mathcal {S}}_{t,\ell }\backslash \{\ell \}=\emptyset\), where \({\mathcal {S}}_{t,\ell }=\{j=\{1,\cdots ,L\}:q_{t,j}=q_{t,\ell }\}\). This implies that \(q_{t,\ell }\) is distinct from \(q_{t,{\bar{\ell }}}\) for all \({\bar{\ell }}\in {\mathcal {S}}_{B}\backslash \{\ell \}\). Therefore, we have

$$\begin{aligned} \begin{aligned} {\mathbb {P}}\left( \Gamma ({\tilde{x}}_{t,i})\right)&\ge {\mathbb {P}}(\Delta _{t,\ell }=0) \ge {\mathbb {P}}({\mathcal {S}}_{B}\cap {\mathcal {S}}_{t,\ell }\backslash \{\ell \}=\emptyset )\\&={\mathbb {P}}\left( \forall _{{\bar{\ell }}\in {\mathcal {S}}_{B}\backslash \{\ell \}}: q_{t,\ell }\ne q_{t,{\bar{\ell }}}\right) \overset{(a)}{=} \left[ {\mathbb {P}}(q_{t,\ell }\ne q_{t,{\bar{\ell }}})\right] ^{K_{B}-1}\\&=\left[ 1-{\mathbb {P}}(q_{t,\ell }= q_{t,{\bar{\ell }}})\right] ^{K_{B}-1} =\left( 1-\frac{1}{R}\right) ^{K_{B}-1}\\&\overset{(b)}{\ge } 1-\frac{1}{R}(K_{B}-1), \end{aligned} \end{aligned}$$
(19)

where (a) follows since the index of rows with non-zero entries \(q_{t,\ell }\) are drawn i.i.d. uniformly at random for each \(\ell \in \{1,\cdots ,L\}\) and \(|{\mathcal {S}}_{B}|=K_{B}\), and the inequality in (b) follows from the Bernoulli’s inequality [33]. \(\square\)

Then we look into the recovery guarantee for the block estimate \({\bar{x}}_{\ell }\) in (11) obtained via the median operator.

Lemma 2

Suppose that \(x\in {\mathbb {B}}^N\) is a (\(K_{B}, K_{I}\)) block-sparse signal over block size d, and \(A\in {\mathbb {R}}^{M\times N}\) is randomly drawn from \({\mathcal {A}}(R,T,L,d,\alpha )\). Given \(y\in {\mathbb {R}}^M\) in (4) and the block estimate \({\bar{x}}_{\ell }\) in (11) for a particular block \(\ell \in \{1,\cdots ,L\}\), let \(\Gamma ({\bar{x}}_{\ell }):=\{|{\bar{x}}_{\ell }-\alpha ^2|{\mathcal {S}}_{I,\ell }||\le 3\gamma \}\), where \(\gamma ^2\) is the variance of the noise term \(\Xi _{t,\ell }\) in (10). The probability of \(\Gamma ({\bar{x}}_{\ell })\) is lower bounded by

$$\begin{aligned} {\mathbb {P}}\left( \Gamma ({\bar{x}}_{\ell })\right) \ge 1-\frac{\delta }{L}, \end{aligned}$$
(20)

if \(R={\mathcal {O}}(K_{B})\) and \(T={\mathcal {O}}\left( \log \frac{N}{\delta }\right)\), where \(0<\delta <1\) is an arbitrary target error bound.

Proof

As in (11), the block estimate \({\bar{x}}_{\ell }\) is obtained by taking the median of the individual estimate \({\tilde{x}}_{t,i}\) over \({\mathcal {O}}(Td)\) samples for a given \(\ell \in \{1,\cdots ,L\}\). Suppose at least \(\frac{Td}{2}\) estimates \({\tilde{x}}_{t,i}\) fulfills the \(\Gamma\) condition of Lemma 1, then \(\Gamma ({\bar{x}}_{\ell })\) in Lemma 2 will follow affirmatively. We analyze in the following where \(\Gamma ({\tilde{x}}_{t,i})\) holds for at least \(\frac{Td}{2}\) individual estimates.

Let \(X_{1},\cdots ,X_{Td}\) be independent (0,1) Bernoulli random variables where \(X_{t}, 1\le t\le Td\) indicates whether the corresponding estimate \({\tilde{x}}_{t,i}\) of \(x_{i}\) satisfies the \(\Gamma\) condition of Lemma 1. As proved in Lemma 1, the probability of each \(X_{t}\) being equal to 1 is \(p\ge 1-\frac{K_{B}-1}{R}\). Then the probability that the number of simultaneous occurrence of the events \(\{X_{t}=1\}\) exceeds Td/2 is given by [32]

$$\begin{aligned} {\mathbb {P}}\left( \sum _{t=1}^{Td}X_{t}>\frac{Td}{2}\right) =\sum _{t=\left\lfloor \frac{Td}{2} \right\rfloor +1}^{Td} \left( \begin{array}{c} n\\ t \end{array} \right) p^t(1-p)^{Td-t}. \end{aligned}$$
(21)

A lower bound on this probability can be calculated using Chernoff’s inequality [34] to obtain

$$\begin{aligned} {\mathbb {P}}\left( \sum _{t=1}^{Td}X_{t}>\frac{Td}{2}\right) ={\mathbb {P}}\left( \frac{1}{Td}\sum _{t=1}^{Td}X_{t}>\frac{1}{2}\right) \ge 1-e^{-\frac{Td}{2p}(p-\frac{1}{2})^2}. \end{aligned}$$
(22)

The minimum bound can be easily found as achieved by \(p=1/2\). By setting a lower threshold \(\theta \in (\frac{1}{2}, 1)\) to the probability p, we have \(p\ge 1-\frac{K_{B}-1}{R}\ge \theta\) from which it follows that

$$\begin{aligned} R\ge \frac{1}{1-\theta }(K_{B}-1)={\mathcal {O}}(K_{B}). \end{aligned}$$
(23)

Footnote 4 Furthermore, (22) also implies that the lower bound of the probability scales as \(1-e^{-{\mathcal {O}}(Td)}\). By taking \(T=\log \left( \frac{Ld}{\delta }\right) ={\mathcal {O}}\left( \log \frac{N}{\delta }\right)\) into (22) proves Lemma 2. \(\square\)

Given the proof of Lemma 2, the overall performance guarantee for the block support recovery at the BS follows inherently.

Lemma 3

Suppose that \(x\in {\mathbb {B}}^N\) is a \((K_{B}, K_{I})\) block-sparse signal over block size d, and \(A\in {\mathbb {R}}^{M\times N}\) is randomly drawn from \({\mathcal {A}}(R,T,L,d,\alpha )\). Given \(y\in {\mathbb {R}}^M\) in (4) and the block estimate \({\bar{x}}_{\ell }\) in (11) for block \(\ell \in \{1,\cdots ,L\}\), the probability that \(\Gamma ({\bar{x}}_{\ell })\) in Lemma 2 satisfies for all blocks \(\ell \in \{1,\cdots ,L\}\) is lower bounded by

$$\begin{aligned} {\mathbb {P}}\left( \forall _{\ell \in \{1,\cdots ,L\}}: \Gamma ({\bar{x}}_{\ell })\right) \ge 1-\delta , \end{aligned}$$
(24)

if \(R={\mathcal {O}}(K_{B})\) and \(T={\mathcal {O}}\left( \log \frac{N}{\delta }\right)\), where \(0<\delta <1\) is an arbitrary target error bound.

Proof

Since the block estimate \({\bar{x}}_{\ell }\) for each block is i.i.d., the probability that \(\Gamma ({\bar{x}}_{\ell })\) in Lemma 2 holds for all \(\ell \in \{1,\cdots ,L\}\) is obtained as

$$\begin{aligned} \begin{aligned} {\mathbb {P}}\left( \forall _{\ell \in \{1,\cdots ,L\}}:\Gamma ({\bar{x}}_{\ell })\right)&=\left( {\mathbb {P}}\left( \Gamma ({\bar{x}}_{\ell })\right) \right) ^L\\&\ge \left( 1-\frac{\delta }{L}\right) ^L\\&\ge 1-L\cdot \frac{\delta }{L}\\&=1-\delta , \end{aligned} \end{aligned}$$
(25)

where the second inequality follows from Bernoulli’s inequality [33] since \(\delta /L\ll 1\). \(\square\)

Proposition 1

The computational complexity for reliable block support recovery at the BS is of \({\mathcal {O}}(\frac{N}{d}\log N)\).

Proof

According to (7), for a particular entry \(x_{i}\) of x from block \(\ell \in \{1,\cdots ,L\}\) and a given \(t\in \{1,\cdots ,T\}\), the calculation of its corresponding estimate \({\tilde{x}}_{t,i}\) only involves a single multiplication. Thereafter, the block-wise estimate \({\bar{x}}_{\ell }\) in (11) is obtained as the median of \({\tilde{x}}_{t,i}\) over \({\mathcal {O}}(Td)\) samples. The computational complexity for finding the median of an unsorted array with N elements is of \({\mathcal {O}}(N)\) by using the median-of-medians algorithm [35]. Moreover, since the submatrix \(A_{t,\ell }\) in (6) has same non-zero entries on the same row, the calculation cost for the block-wise estimate \({\bar{x}}_{\ell }\) can be further reduced to T times multiplication and \({\mathcal {O}}(T)\) operations to find the median, resulting in the computational complexity of \({\mathcal {O}}(T)\). To obtain the block-wise estimate \({\bar{x}}_{\ell }\) for all L blocks and by taking \(T={\mathcal {O}}(\log N)\) in Lemma 3, the overall computational complexity for reliable block support recovery at the BS is of \({\mathcal {O}}(TL)={\mathcal {O}}(\frac{N}{d}\log N)\). \(\square\)

Remark If the cluster size d scales linearly with the increasing network size N, i.e., \(d={\mathcal {O}}(N)\), the term \(\frac{N}{d}\) turns to be an arbitrary constant value. Thus, the algorithm achieves sublinear complexity of \({\mathcal {O}}(\log N)\) that scales significantly better than conventional approaches.

In short, the above analysis shows that by choosing R and T large enough, i.e., \(R={\mathcal {O}}(K_{B})\) and \(T={\mathcal {O}}(\log N)\) (for a total of \(M={\mathcal {O}}(K_{B}\log N)\) measurements), a reliable block support recovery at the BS can be guaranteed w.h.p. and the computational complexity is of \({\mathcal {O}}(\frac{N}{d}\log N)\).

4.2 In-block support recovery at devices

Lemma 4

Suppose that \(x\in {\mathbb {B}}^N\) is a (\(K_{B}, K_{I}\)) block-sparse signal over block size d, and \(A\in {\mathbb {R}}^{M\times N}\) is randomly drawn from \({\mathcal {A}}(R,T,L,d,\alpha )\). Given \(y_{D}\in {\mathbb {R}}^M\) in (13) and by applying the algorithm in Sect. 3.3, \(x_{\ell }\) for block \(\ell \in \{1,2,\cdots ,L\}\) can be reliably recovered with computational complexity of \({\mathcal {O}}(dK_{I}^{2})\) if \(R={\mathcal {O}}(K_{B})\) and \(T={\mathcal {O}}(K_{I}\log d)\).

Proof

As shown in (14), the effective measurements that can be used to perform the in-block support recovery of \(x_{\ell }\) for a given \(\ell \in \{1,\cdots ,L\}\) comprise only the entries of \(y_{D}\) indexed by \(D_{\ell }\backslash Q_{\ell }\), where \(D_{\ell }\) is the index set of rows with non-zero components in \(A_{-,\ell }\), and \(Q_{\ell }\) is the set of collided measurements feedback by the BS. By Lemma 1 and by the fact that the individual estimates are independent, it follows that the overall number of effective measurements \(T_{I}\) for the in-block support recovery of an active cluster \(\ell \in {\mathcal {S}}_{B}\) can be estimated as

$$\begin{aligned} T_{I}=T\cdot {\mathbb {P}}\left( \Gamma ({\tilde{x}}_{t,i})\right) \ge T\cdot \left( 1-\frac{K_{B}-1}{R}\right) . \end{aligned}$$
(26)

To elaborate the in-block support recovery at a device using Algorithm 1, for simplicity we assume that \({\tilde{A}}_{D,\ell }\) in (14) is real-valued and the system is noise-free. However, the scheme can be easily extended to complex settings and noisy cases as in [36]. Since \({\tilde{A}}_{D,\ell }\) has independent columns and row-blocks, it follows the column-independent model [37, p. 49] for Subgaussian matrices. Herein \({\tilde{A}}_{D,\ell }\) can be decomposed as \({\tilde{A}}_{D,\ell }=\Phi Q\) and we have \(y_{D,\ell }=\Phi Qx_{\ell } = \Phi {\tilde{x}}_{\ell }\), where \(\Phi\) is the column-normalized matrix of \({\tilde{A}}_{D,\ell }\) and Q is a diagonal matrix with each diagonal entry to be the original norm of the corresponding column. Furthermore, [38] provides a sufficient condition on the measurement matrix for uniform and robust sparse signal recovery, which is the well-known Restricted isometry property (RIP). Moreover, according to [37], random matrices with i.i.d. Subgaussian entries and normalized columns have optimal RIP, therefore \(\Phi\) follows the RIP condition and is admissible for reliable sparse signal recovery. It has been further investigated in [39] that a K-sparse signal of dimension N can be uniformly reconstructed using OMP with an admissible measurement matrix if its dimension lies in the regime \({\mathcal {O}}(K\log N)\). While the activation pattern \({\tilde{x}}_{\ell }\) to be reconstructed for cluster \(\ell\) is of dimension d and sparsity level \(K_{I}\), the support can be recovered w.h.p. if the number of effective measurements \(T_{I}\) satisfies

$$\begin{aligned} T_{I}\ge T\cdot \left( 1-\frac{K_{B}-1}{R}\right) ={\mathcal {O}}(K_{I}\log d). \end{aligned}$$
(27)

Recall that \(1-\frac{K_{B}-1}{R}\ge \theta , \theta \in (\frac{1}{2}, 1)\) should be satisfied for the block support recovery procedure at the BS with \(R={\mathcal {O}}(K_{B})\), then we have \(T={\mathcal {O}}(\frac{1}{\theta }K_{I}\log d)={\mathcal {O}}(K_{I}\log d)\) since \(\theta\) is a given constant.

It is further verified in [40] that the computational complexity is of \({\mathcal {O}}(NK^2)\) for sparse signal recovery via OMP. Thus, since the signal to be reconstructed for in-block support recovery at a device is of dimension d and sparsity level \(K_{I}\), \({\mathcal {O}}(dK_{I}^{2})\) operations are sufficient for decoding with the modified OMP algorithm. \(\square\)

4.3 Proof of Theorem 1

For a given realization of the measurement matrix, Lemma 3 guarantees that \(R={\mathcal {O}}(K_{B})\) and \(T={\mathcal {O}}(\log N)\) are sufficient for reliable block support recovery at the BS, while Lemma 4 shows that \(R={\mathcal {O}}(K_{B})\) and \(T={\mathcal {O}}(K_{I}\log d)\) measurements are required for the in-block support recovery at the devices. Taking the maximum value of both cases yields a sufficient condition on the required number of measurements

$$\begin{aligned} M = {\mathcal {O}}(\max \{K_{B}\log N, K_{B}K_{I}\log d\}). \end{aligned}$$
(28)

Furthermore, since the algorithms for block support recovery at the BS requires \({\mathcal {O}}(\frac{N}{d}\log N)\) operations and the in-block support recovery at the device side requires \({\mathcal {O}}(dK_{I}^{2})\) operations, the overall computational complexity is of \({\mathcal {O}}(dK_{I}^{2}+\frac{N}{d}\log N)\) for a successful detection process.

Remark If the signal is treated as a conventional K-sparse vector (where \(K=K_{B}K_{I}\)) as in [11] without exploiting knowledge of the block-sparse structure, a sufficient condition for reliable signal recovery using OMP would be \(M={\mathcal {O}}(K\log N)={\mathcal {O}}(K_{B}K_{I}\log N)\) with computational complexity is of \({\mathcal {O}}(NK^2)\). As M is the length of the unique signature transmitted by an active device, it is also an indication of the signal acquisition time or the communication overhead. Since \(d\ll N\) and \(K_{I}\ll K\), we can see that from the scaling point of view, both the communication cost and the computational complexity are significantly reduced by the proposed scheme.

5 Results and discussion

We conduct numerical experiments to verify the performance of the proposed distributed device detection and resource allocation scheme. Mapped into our mathematical model, the target problem is to reconstruct a K-sparse binary vector of length N from M distributed measurements obtained via the measurement matrix \(A\in {\mathbb {R}}^{M\times N}\) which is randomly drawn from \({\mathcal {A}}(R,T,L,d,\alpha )\) introduced in Sect. 3.1. We compare the performance of the proposed scheme to conventional CS-based approaches, among which we take the classic greedy algorithm OMP with random Gaussian measurements as the baseline. We assume for the baseline that the signal to be reconstructed is treated as a conventional K-sparse vector, and centralized decoding is performed without exploiting knowledge of the block-sparse structure.

In our simulations, we take the number of devices N in the network within the range \([10^3, 10^6]\) and they are partitioned into clusters with equal size \(d=100\). The sparsity level of the signal is set to be \(K=20\), with block sparsity \(K_{B}=4\) and in-block sparsity \(K_{I}=5\), respectively. For each plot we average over 1000 pairs of realizations of the measurement matrix and the block-sparse signal.

Fig. 3
figure 3

Performance comparison between the proposed scheme and standard OMP with Gaussian measurements

Full size image
Fig. 4
figure 4

Robustness of the proposed scheme compared with standard OMP

Full size image

Figure 3a and b give an intuitive comparison between the proposed scheme and standard OMP with Gaussian measurements for reliable signal recovery, in terms of both the length of signatures transmitted by the active devices and the number of operations conducted by the algorithms. It can be seen that the proposed scheme requires a significantly reduced signature length and computational complexity, especially when the number of devices in the network becomes excessively large. As the signature length also implies the signal acquisition time or communication overhead in distributed systems, the proposed scheme leads to a drastically reduced communication cost.

Figure 4a depicts the detection success probability as a function of the signature length for the proposed scheme and the baseline, while taking the network size \(N=10^4\). The performance is evaluated for the noise-free case. We can see that the proposed scheme significantly outperforms standard OMP, where less measurements are required by the proposed scheme to achieve the same detection success probability as the baseline. Figure 4b further extends the evaluation to noisy settings as well as with imperfect channel knowledge. The performance for the noisy case is evaluated by setting the signal-to-noise ratio (SNR) to 5 dB in the simulations. In addition, since the channel estimation error can be treated as a component that contributes as an additional source of distortion independent of noise [41], it is modeled as an additive noise term in the measurement matrix with the same variance as the white Gaussian noise. We can see that the proposed scheme achieves significantly higher detection success probability than the baseline under noisy conditions. The performance gain mainly comes from the reliable detection of in-block support cardinality of the active clusters using the sketching algorithm, which sets an appropriate stopping criteria for Algorithm 1 and minimizes the occurrence of false alarms in the detection. Therefore, the proposed scheme shows strong robustness in the presence of noise and imperfect channel knowledge.

We also compare performance of the proposed scheme with two classical random access schemes, namely the LTE RA procedure [5] and the conventional cluster-based approach [42] where a cluster head aggregates messages/requests for the rest of the devices in the cluster and initiates the RA procedure on behalf of the cluster members. We set the number of measurements M to be 839 bits in the simulation—same as the length of Zadoff-Chu sequence [5] used for the LTE RA procedure, thus the three schemes are running with the same signature length. The sparsity level \(K=K_{B}K_{I}\) is set within the range between 10 and 100.

Fig. 5
figure 5

Performance comparison between the proposed scheme, LTE RA procedure and conventional cluster-based approach [42]

Full size image

Figure 5a depicts the detection probability by the three schemes as a function of the number of active devices in the network (i.e., the sparsity level), and Fig. 5b plots the averaged access delay performance of the three schemes. It can be easily observed that the proposed scheme significantly outperforms the LTE RA procedure both in terms of higher detection success probability and reduced access delay, thus achieving much better scalability with the increasing network size and leading to more robustness in the detection process. Moreover, when compared with the cluster-based approach, the proposed scheme also achieves better detection performance if the sparsity level is sufficiently large (\(\le\) 70). Meanwhile, since the proposed distributed scheme is able to avoid the excessive communication and coordination between the devices as well as to the infrastructure as required by the cluster-based approach, the signaling overhead is substantially reduced and thus leading to significantly decreased access latency.

However, there are still some limitations on the proposed approach, especially on the requirement of perfect synchronization during the acquisition phase and priori knowledge of the channel state by the M2M devices. Further extensions to relax these limitations will be investigated in future work.

6 Conclusion

This work utilizes the framework of CS for detection of the network activation pattern to facilitate distributed resource allocation in large-scale M2M communication networks. The particular block-sparsity in the activation pattern of the M2M devices is exploited, thus mapping the objective into a support recovery problem for a particular block-sparse signal—with additional in-block structure—in CS based applications. The detection techniques are mainly based on sketching and greedy algorithms, which inherit the virtues of low computational complexity. Furthermore, by applying the distributed ranking-based resource allocation scheme, each active device decides autonomously on which resource to access the channel in a contention-free manner without further coordination, thus excessive control overhead is avoided. It has been verified via theoretical analysis that a (\(K_{B},K_{I}\)) block-sparse binary signal \(x\in {\mathbb {B}}^N\) over block size d can be reliably reconstructed using the proposed scheme with \({\mathcal {O}}(\max \{K_{B}\log N, K_{B}K_{I}\log d\})\) measurements and computational complexity of \({\mathcal {O}}(dK_{I}^{2}+\frac{N}{d}\log N)\), which achieves a better scaling compared with conventional CS based approaches. Furthermore, the simulation results also reveal the strong robustness of the proposed scheme under noisy conditions and with imperfect channel knowledge.