Abstract
This paper is devoted to studying non-commensurate fractional order planar systems. Our contributions are to derive sufficient conditions for the global attractivity of non-trivial solutions to fractional-order inhomogeneous linear planar systems and for the Mittag-Leffler stability of an equilibrium point to fractional order nonlinear planar systems. To achieve these goals, our approach is as follows. Firstly, based on Cauchy’s argument principle in complex analysis, we obtain various explicit sufficient conditions for the asymptotic stability of linear systems whose coefficient matrices are constant. Secondly, by using Hankel type contours, we derive some important estimates of special functions arising from a variation of constants formula of solutions to inhomogeneous linear systems. Then, by proposing carefully chosen weighted norms combined with the Banach fixed point theorem for appropriate Banach spaces, we get the desired conclusions. Finally, numerical examples are provided to illustrate the effect of the main theoretical results.
Similar content being viewed by others
1 Introduction
Fractional calculus and fractional order differential equations are research topics that have generated a great amount of interest in recent years. For details on their various applications in science and engineering, we refer the interested reader to the collections [2, 3, 16, 20, 21] and the references therein.
To our knowledge, the first contribution in the qualitative study of fractional order autonomous linear systems was published by Matignon [15]. In that paper, using Laplace transforms and the final value theorem, the author has obtained an algebraic criterion to ensure the attractiveness of solutions. The BIBO (bounded input, bounded output) stability for non-commensurate fractional order systems, i.e. for systems whose differential equations are not all of the same order, was investigated by Bonnet and Partington [4], and their result shows that the systems are stable if and only if their transfer function has no pole in the closed right hand side of the complex plane.
Starting from [4], a new difficult task appears: finding the conditions to ensure that the poles of the characteristic polynomial of the system lie on the open left side of the complex plane. Trigeassou et al. [22] have proposed a method based on Nyquist’s theorem. In particular, they have derived Routh-like stability conditions for fractional order systems involving at most two fractional derivations. Unfortunately, for higher numbers of differential operators, this approach seems to be unsuitable by its numerical implementation. After that, Sabatier et al. [18] have introduced another realization of the fractional system. This realization is recursively defined and involves nested closed-loops. Based on this realization, they have obtained a recursive algorithm that involves, at each step, Cauchy’s argument principle on a frequency range and removes the numerical limitation in [22] mentioned above.
In addition to the algorithmic approach as in [18], a number of analytic approaches have been used to investigate the zeros of characteristic polynomials of systems of fractional order systems. In [13], the stability and resonance conditions are established for fractional systems of second order in terms of a pseudo-damping factor and a fractional differentiation order. The method in [13] has been successfully extended in [28] for a wide class of second kind non-commensurate elementary systems. By the substitution method, a variation of constants formula and the properties of the Mittag-Leffler function in the stable domain, in [10], the authors have shown the asymptotic stability for fractional order systems with (block) triangular coefficient matrices. By combining a variation of constants formula, properties of Mittag-Leffler functions, a special weighted norm type and Banach’s fixed-point theorem, Tuan and Trinh [25] have proved the global attractivity and asymptotic stability for a class of mixed-order linear fractional systems when the coefficient matrices are strictly diagonally dominant and the elements on the main diagonal of these matrices are negative. Using the positivity of the system and developing a novel comparison principle, Shen and Lam [19] have considered the stability and performance analysis of positive mixed fractional order linear systems with bounded delays. Tuan et al. [26] have established a necessary and sufficient condition for the asymptotic stability of positive mixed fractional-order linear systems with bounded or unbounded time-varying delays.
Although there have been some articles on mixed fractional order systems as listed above, in our view, the qualitative theory of non-commensurate fractional order systems is still a challenging topic whose development is in its infancy. Even in the simplest case when the coefficient matrix is constant, the current results seem to be far away from a complete characterization of the stability of these systems. In particular, the entire theory for non commensurate systems is far less well developed than the corresponding theory for commensurate systems (i.e. systems all of whose associated differential equations are of the same order) that have been extensively discussed, e.g., in the papers mentioned above or in [7, 8] and the references cited therein.
For these reasons, we study in this paper the fractional-order planar system with Caputo fractional derivatives
where \(\alpha = (\alpha _1,\alpha _2) \in (0,1]^2\) is a multi-index, \(A\in {\mathbb {R}}^{2\times 2}\) is a square matrix and \(f :[0, \infty ) \times {\mathbb {R}}^2 \rightarrow {\mathbb {R}}^2\) is a vector valued continuous function. It is worth noting that for the case \(f=0\), in [6], by constructing a smooth parameter curve and using Rouché’s theorem, Brandibur and Kaslik have provided criteria for the asymptotic stability and for the instability of solutions, respectively. However, these conditions are not explicit and are quite difficult to verify. Motivated by [6], our aim is as follows. First, we want to give sufficient simple and clear conditions that can guarantee the Mittag-Leffler stability of the system (1.1) in the homogeneous case. Then, by establishing a variation of constants formula, estimates for general Mittag-Leffler type functions, and proposing new weighted norms, we show the asymptotic behaviour of the system when the vector field f is inhomogeneous or represents small nonlinear noise around its equilibrium point.
The paper is organized as follows. Section 2 contains a brief summary of existence and uniqueness results for solutions to multi-order fractional differential systems and a variation of constants formula for solutions to fractional order inhomogeneous linear planar systems. Section 3 deals with some properties of the characteristic function to a general fractional order homogeneous linear planar system whose coefficient matrix is constant. Section 4 is devoted to studying important estimates for special functions arising from the variation of constants formula for the solutions. Our main contributions are presented in Section 5 where we show the asymptotic behaviour of solutions to fractional-order linear planar systems and the Mittag-Leffler stability of an equilibrium point to fractional nonlinear planar systems. Numerical examples are provided in Section 6 to illustrate the main theoretical results.
To conclude the introduction, we present some notations that will be used throughout the rest of the paper. In \({\mathbb {R}}^2\), we define the norm \(\Vert \cdot \Vert \) by \(\Vert x\Vert := \max \{|x_1|,|x_2|\}\) for every \(x\in {\mathbb {R}}^2\). For any \(r>0\), the closed ball of radius r centered at the origin 0 in \({\mathbb {R}}^2\) is given by \(B(0,r):=\{x\in {\mathbb {R}}^2:\Vert x\Vert \le r\}\). The space of all continuous functions \(\xi :[0,\infty )\rightarrow {\mathbb {R}}^2\) is denoted by \(C([0,\infty );{\mathbb {R}}^2)\). For any \(\xi \in C([0,\infty );{\mathbb {R}}^2)\), let \(\Vert \xi \Vert _\infty :=\sup _{t\ge 0}\Vert \xi (t)\Vert \). Then, we use the notation \( C_\infty ([0,\infty );{\mathbb {R}}^2) := \{\xi \in C([0,\infty );{\mathbb {R}}^2): \Vert \xi \Vert _\infty <\infty \}\) to designate the subspace of \(C([0,\infty );{\mathbb {R}}^2)\) that comprises the bounded continuous functions on \([0, \infty )\).
For \(\alpha \in (0,1]\) and \(J = [0, T]\) or \(J = [0, \infty )\), we define the Riemann-Liouville fractional integral of a function \(f :J \rightarrow {\mathbb {R}}\) as
and the Caputo fractional derivative of the order \(\alpha \in (0,1]\) of a function \(f : J \rightarrow {\mathbb {R}}\) as
where \(\varGamma (\cdot )\) is the Gamma function and \(\frac{d}{dt}\) is the usual derivative. Letting \(\alpha = (\alpha _1,\alpha _2) \in (0,1]\times (0,1]\) be a multi-index and \(f = (f_1, f_2)\) with \(f_i : J \rightarrow {\mathbb {R}}\), \(i=1,2\), be a vector valued function, we write
See, e.g., [9, Chapter 3] and [27] for more details on the Caputo fractional derivative.
2 Preliminaries
2.1 Existence and uniqueness of global solutions and exponential boundedness of solutions
Consider the two-component incommensurate fractional-order initial value problem with Caputo fractional derivatives
where \(\alpha = (\alpha _1,\alpha _2) \in (0,1]^2\) is a multi-index and \(f :[0, \infty ) \times {\mathbb {R}}^2 \rightarrow {\mathbb {R}}^2\) is a continuous function. To make the exposition of this paper self-contained, we recall two important results about the solutions to this two-dimensional initial value problem.
Theorem 1
(Existence and uniqueness of global solutions) Suppose that the function \(f:[0, \infty ) \times {\mathbb {R}}^2 \rightarrow {\mathbb {R}}^2\) is continuous and that, for some constant \(L > 0\), it satisfies the Lipschitz condition
with respect to its second variable. Then, for any initial value \(x^0 \in {\mathbb {R}}^2\), the two-component incommensurate fractional-order system (2.1) has a unique global solution \(\varphi (\cdot ,x^0)\) on the interval \([0,\infty )\).
Proof
See [24, Theorem 2.2 and Remark 2.3]. \(\square \)
Theorem 2
(Exponential boundedness of global solutions) Suppose that the function f satisfies the assumptions of Theorem 1. Moreover, let there exist a constant \(\gamma > 0\) such that
Then, for any initial value \(x^0 \in {\mathbb {R}}^2,\) the two-component incommensurate fractional-order system (2.1) has a unique global solution \(\varphi (\cdot ,x^0) \in C\left( [0,\infty ),{\mathbb {R}}^2 \right) \) and
where M is some positive constant which depends on \(x^0.\)
Proof
See [24, Theorem 2.4]. \(\square \)
2.2 The variation of constants formula for the solutions
Consider the non-homogeneous two-component incommensurate fractional-order linear system
with initial condition
where \(\alpha = (\alpha _1, \alpha _2) \in (0,1]^2\), \(A = \left( a_{ij} \right) \in {\mathbb {R}}^{2 \times 2}\) is a square real matrix and \(f=(f_1,f_2)^{\mathrm{T}} :[0,\infty ) \rightarrow {\mathbb {R}}^2\) is a continuous function such that
for some \(M > 0\) and some \(\gamma > 0\). Then, we have
Due to Theorems 1 and 2, for any initial condition \(x^0 \in {\mathbb {R}}^2\), the system (2.2) has a unique exponentially bounded solution in \(C\left( [0, \infty ), {\mathbb {R}}^2 \right) \). Taking the Laplace transform on both sides of the system (2.2), we obtain the algebraic system
where \(X_i(s)\) and \(F_i(s)\), \(i=1,2\), are the Laplace transforms of \(x_i(t)\) and \(f_i(t)\), respectively. By Cramer’s rule, we see that
and
where \(Q(s) := s^{\alpha _1 + \alpha _2} - a_{11}s^{\alpha _2}-a_{22}s^{\alpha _1} +\det A. \) Put
with \(l(\alpha ): = \alpha _1 + \alpha _2.\) Then, with each \(i \in \left\{ 1,2 \right\} \), we obtain
where “\(*\)” is the Laplace convolution operator.
From the arguments above, we can derive our first new result that shows a precise analytic representation of the unique solution to the initial value problem (2.2).
Lemma 1
On the interval \([0, \infty )\), the non-homogeneous linear two-component incommensurate fractional-order system (2.2) has the unique solution
with
3 Some properties of the characteristic function
As mentioned in the introduction, in this paper we only focus on incommensurate systems, i.e. on systems of the form (1.1) with \(\alpha _1 \ne \alpha _2\), because the case \(\alpha _1 = \alpha _2\) has already been discussed in detail elsewhere. Thus, without loss of generality, we assume \(0<\alpha _1 < \alpha _2\le 1\). It will turn out, see Section 5, that such systems possess characteristic functions of the form
with certain \(a, b, c \in {\mathbb {R}}\) whose properties play an essential role in the analysis of the asymptotic behaviour of the solutions. In fact, we shall show in Section 5 that the crucial point is the location of the zeros of functions of this type: One needs to know whether or not all the function’s zeros are in the open left half of the complex plane. In this context, one result has already been shown by Brandibur and Kaslik [5]:
Lemma 2
Assume that \(a, b \le 0,\) and \(c > 0\). Then, all zeros of Q are in the open left-half complex plane regardless of \(\alpha _1\) and \(\alpha _2\).
Proof
See [5, Proposition 1(b)]. \(\square \)
The conditions of Lemma 2 are quite restrictive though, and therefore this statement can only be applied to a very limited class of systems. In the remainder of this section we shall therefore now develop some new alternative sufficient criteria for asserting a “good” distribution of the zeros of the characteristic function that can cover many further cases. Our first auxiliary statement in this context reads as follows.
Lemma 3
Let \(0<\alpha _1 < \alpha _2\le 1\) and \(a,b,c \in {\mathbb {R}}\). Then, the following statements hold for the function Q defined in (3.1).
-
(i)
If \( c < 0\) then Q has at least one positive real zero.
-
(ii)
If \(s \in {\mathbb {C}}\) is a zero of Q then its complex conjugate is also a zero of Q.
-
(iii)
Let \(0< \omega < \pi \). Then, Q has only a finite number of zeros in the set \({\mathcal {C}} = \{z \in {\mathbb {C}} : | \arg {(z)}| \le \omega \}\).
-
(iv)
If \(c > 0\), then \(s = i\omega \) with \(\omega > 0\) is a zero of Q if and only if
$$\begin{aligned}&{\left\{ \begin{array}{ll} &{} a= \rho _2 \omega ^{\alpha _1} -c\rho _1 \omega ^{-\alpha _2}, \\ &{} b = c\rho _2 \omega ^{-\alpha _1} -\rho _1 \omega ^{\alpha _2}, \end{array}\right. } \end{aligned}$$(3.2)where
$$\begin{aligned} \rho _1 = \frac{\sin \frac{\alpha _1 \pi }{2}}{\sin \frac{(\alpha _2 - \alpha _1)\pi }{2}} , \rho _2 = \frac{\sin \frac{\alpha _2 \pi }{2}}{\sin \frac{(\alpha _2 - \alpha _1)\pi }{2}}. \end{aligned}$$(3.3)
Proof
(i) and (ii) are obvious.
(iii) First, we assume that \(c\ne 0\). Then \(Q(0) \ne 0\). Due to the continuity of Q at 0, we can find \(\varepsilon \) which is small enough such that Q has no zero in \(\left\{ z\in {\mathbb {C}}: |z| < \varepsilon \right\} .\) Moreover, because \(|Q(s)| \ge |s|^{\alpha _1 + \alpha _2} - |a| \cdot |s|^{\alpha _2}-|b| \cdot |s|^{\alpha _1} -|c|,\) we have that \(\lim _{|s| \rightarrow \infty } |Q(s)| = \infty \) uniformly for all \(\arg s\). This implies that there is a positive real number R such that Q has no zero in the domain \(\left\{ z\in {\mathbb {C}}: |z| > R \right\} .\) Hence, all zeros of Q in \(\{z\in {\mathbb {C}}: | \arg {(z)}| \le \omega \}\) (if they exist) belong to the set \(\varOmega := \left\{ z\in {\mathbb {C}}: \varepsilon \le |z| \le R, |\arg {(z)}|\le \omega \right\} .\) Notice that \(\varOmega \) is a compact set and Q is analytic on this domain. If now Q has infinitely many zeros in \(\varOmega \) then, because of the compactness of \(\varOmega \), the set of zeros has a cluster point. This implies, in view of the analyticity of Q, that \(Q(s) = 0\) for all s which contradicts the definition of Q. Hence, Q has only a finite number of zeros in \(\varOmega \). This shows that Q has only a finite number of zeros in the domain \({\mathcal {C}}\) if \(c \ne 0\).
To deal with the case \(c=0\), we write
where \(P(s) = s^{\alpha _2} - as^{\alpha _2-\alpha _1}-b.\) By repeating the above arguments for P, the proof is complete.
(iv) See [5, Proposition 1, Part 3b]. \(\square \)
Corollary 1
Assume that \(a,b,c > 0\) and that one of conditions
-
(i)
\(c(\rho ^2_2 - \rho _1^2)< ab < c(\rho _2^2 + \rho _1^2)\),
-
(ii)
\(ab \le c\left( \rho _2 -\rho _1 \right) ^2\),
is satisfied where \(\rho _1,\rho _2\) are defined in (3.3). Then, the function Q defined in (3.1) has no purely imaginary zero.
Proof
Consider the system (3.2). Since \(\rho _2 \ne 0\), this system is equivalent to
Thus, we obtain
Setting \(X=\omega ^{\alpha _2}\), equation (3.5) takes the form
The discriminant of the quadratic equation (3.6) is
(i) Clearly, if \(c(\rho ^2_2 - \rho _1^2)< ab < c(\rho _2^2 + \rho _1^2),\) then \(\varDelta < 0.\) Hence, the quadratic equation (3.6) has no real roots. This implies that the system (3.2) has no root \(\omega >0\). This together with Lemma 3(ii) and 3(iv) shows that Q has no purely imaginary zero.
(ii) If \(ab \le c\left( \rho _2 -\rho _1 \right) ^2\), the quadratic equation (3.6) has two (not necessarily distinct) real roots. Because \( 0< \rho _1 < \rho _2,\) we have \(( \rho _2 -\rho _1 )^2 < \rho _2^2-\rho _1^2.\) This implies that \(ab - c(\rho _2^2-\rho _1^2) < 0\). Moreover, \(a,b,c, \rho _1 > 0,\) thus the two roots of the quadratic equation (3.6) are negative. Hence, in view of the relation \(X = \omega ^{\alpha _2}\) with \(0 < \alpha _2 \le 1\) between the solution X of (3.6) and the solution \(\omega \) of (3.2), the system (3.2) has no root \(\omega >0\). Using Lemmas 3(ii) and 3(iv), we see that Q has no purely imaginary zero. \(\square \)
Recall that if \(c \le 0,\) then Q has at least one non-negative real zero, which precludes any kind of stability. Thus, in this section, we only consider the case \(c >0\). As shown above, because Q has only a finite number of zeros in the domain \({\mathbb {C}}\), there exists a constant \(R > 0\) which is large enough such that Q has no zero in \(\left\{ z\in {\mathbb {C}}: |z|\ge R\right\} .\) On the other hand, Q is continuous at 0 with \(Q(0) > 0\), so we can find a small constant \(\varepsilon > 0\) such that \(Q(z)\ne 0\) in \(\left\{ z\in {\mathbb {C}}: |z| \le \varepsilon \right\} \). We define an oriented contour \(\gamma \) formed by four segments:
Clearly, if Q has no purely imaginary zero, then all zeros in the closed right hand side of the complex plane \(\{s=r(\cos \phi +i\sin \phi )\in {\mathbb {C}}: r\ge 0, \phi \in (-\pi ,\pi ]\}\) of Q (if they exist) must lie inside the contour \(\gamma \). Based on Cauchy’s argument principle in complex analysis, we see that \(n(Q(C), 0) = Z - P,\) where n(Q(C), 0) is the number of encirclements in the positive direction (counter-clockwise) around the origin of the the Nyquist plot \(Q(\gamma )\), Z and P are the number of zeros and number of poles of Q inside the contour \(\gamma \) in the s-plane, respectively. Due to the fact that Q is analytic inside \(\gamma \), we have \(P=0\) and thus \(n(Q(C), 0) = Z.\) This implies that if Q has no purely imaginary zero, then all roots of the equation \(Q(s) = 0\) lie in the open left-half complex plane if and only if \(n(Q(C), 0) = 0.\) Notice that \(Q(0)>0\), \(\lim _{|s|\rightarrow \infty }|Q(s)|=\infty \), \(\Re Q(i\omega ) = \Re Q(-i\omega )\) and \(\Im Q(i\omega ) = -\Im Q(-i\omega )\). It is easy to see that \(n(Q(C), 0) = 0\) if \(\Re Q(i\omega ) > 0\) for any \(\omega >0\) that satisfies \(\Im Q(i\omega ) = 0\). Consider \(\omega >0\) and put
If there exists some \(\omega > 0\) such that \(h_2(\omega ) = 0,\) then
Thus, the variable \(\omega >0\) satisfies the system
with
It is then clear from our assumptions on \(\alpha _1\) and \(\alpha _2\) that \(q_1, q_2 > 0\). Based on the analysis above, we obtain some sufficient conditions that ensure that the function \(Q(\cdot )\) has no zero lying in the closed right half of the complex plane.
Lemma 4
Let \(0< \alpha _1 < \alpha _2 \le 1\). Assume that \(a = 0\), \(b > 0\) and
Then, all zeros of Q lie in the open left-half of the complex plane.
Proof
Because \(a = 0\) and \(b > 0\), we see that \(h_2(\omega _0) = 0\) if and only if \(\omega _0 = \left( bq_1 \right) ^{1/\alpha _2}\). From (3.9), we have \(h_1(\omega _0) = c - \left( bq_1 \right) ^{\alpha _1/\alpha _2} b q_2\). By the assumption (3.11), we obtain \(h_1(\omega _0) > 0\). This implies that all zeros of Q lie in the open left-half of the complex plane. \(\square \)
Lemma 5
Let \(0< \alpha _1 < \alpha _2 \le 1.\) Assume that \(b = 0\), \(a > 0\) and
Then, all zeros of Q lie in the open left-half complex plane.
Proof
Since \(b = 0\) and \(a > 0\), it is easy to show that \(h_2(\omega _0) = 0\) if and only if \(\omega _0 = \left( aq_2 \right) ^{1/\alpha _1}\). From (3.9), it follows that \(h_1(\omega _0) = c - \left( aq_2 \right) ^{\alpha _2/\alpha _1}aq_1\). By the assumption (3.12), we see that \(h_1(\omega _0) > 0\) which implies that all zeros of Q lie in the open left-half of the complex plane. \(\square \)
Lemma 6
Let \(0< \alpha _1 < \alpha _2 \le 1.\) Assume that \(a, b, c > 0 \). Then, all zeros of Q are in the open left-half of the complex plane if one of the following conditions holds:
-
(i)
\( aq_2+bq_1 > 1\) and \(aq_2\left( (a+b)q_2 \right) ^{\alpha _2/\alpha _1} + b(a+b)q_2^2 \le c.\)
-
(ii)
\( aq_2+bq_1 \le 1\) and \( aq_1 + bq_2 < c.\)
Proof
We have
where
Notice that
It is not difficult to check that \(g_2'(\omega ) < 0\) in \((0,\omega _1)\) and \(g_2'(\omega ) > 0\) in \((\omega _1,\infty ),\) where \(\omega _1 = \left( \frac{\alpha _2-\alpha _1}{\alpha _1 + \alpha _2}aq_2 \right) ^{1/\alpha _1}.\) Due to the fact that \(g_2(0) = -\alpha _1 b \sin \frac{\alpha _1\pi }{2} < 0,\) and \(\lim _{\omega \rightarrow +\infty }g_2(\omega ) = +\infty ,\) the equation \(g_2(\omega ) = 0\) has a unique root \(\omega _2 \in (0, \infty ).\) Moreover \(g_2(\omega ) < 0\) in \((0,\omega _2)\) and \(g_2(\omega ) > 0\) in \((\omega _2, \infty ).\) Hence, \(h_2\) is decreasing in \((0,\omega _2)\) and increasing in \((\omega _2, \infty ).\) On the other hand, \(h_2(0) = 0\) and \(\lim _{\omega \rightarrow +\infty }h_2(\omega ) = +\infty \). This shows that the equation \(h_2(\omega ) = 0\) has a unique root \(\omega _3 \in (0,\infty )\) and then \(h_2(\omega ) < 0\) for all \(\omega \in (0,\omega _3)\) and \(h_2(\omega ) > 0\) for all \(\omega \in (\omega _3,\infty ).\)
(i) If \( aq_2+bq_1 > 1\), then \(h_2(1) < 0.\) This implies that \(\omega _3 > 1.\) Moreover, due to \(\alpha _1 < \alpha _2 \le 1\), we have
for every \(\omega > 1\), and thus \(h_2\left( \left( (a+b)q_2 \right) ^{1/\alpha _1} \right) > 0.\) This implies that \(1< \omega _3 < \left( (a+b)q_2 \right) ^{1/\alpha _1}.\) Hence, if
due to \(q_2> q_1 > 0,\) we obtain \(c > a\omega _3^{\alpha _2}q_1 + b\omega _3^{\alpha _1}q_2,\) which together with (3.9) leads to \(h_1(\omega _3) > 0.\) The proof of this part is complete.
(ii) If \( aq_2+bq_1 \le 1\), then \(h_2(1) \ge 0.\) This implies that \(0 < \omega _3 \le 1.\) Due to \( c > aq_1 + bq_2,\) we have \(c > a\omega _3^{\alpha _2}q_1 + b\omega _3^{\alpha _1}q_2\). This together with (3.9) shows that \(h_1(\omega _3) > 0.\) The proof is finished. \(\square \)
Lemma 7
Assume that \(a < 0\) and \(b, c > 0\). Then, all zeros of Q are in the open left-half complex plane if one of the following conditions holds:
-
(i)
\(a q_2+b q_1 > 1\) and \(\left( b q_1 \right) ^{\alpha _1/\alpha _2} b q_2 \le c.\)
-
(ii)
\(a q_2+b q_1 \le 1\) and \(b q_2 \le c\).
Proof
As shown in the proof of Lemma 6, we have \(h_2'(\omega ) = \omega ^{\alpha _1-1} g_2(\omega )\) where \(g_2\) is as in (3.14). Notice that
for \(\omega \in (0,\infty )\). Due to the facts that \(g_2(0) = -\alpha _1 b \sin \frac{\alpha _1\pi }{2} < 0\) and \(\lim _{\omega \rightarrow +\infty }g_2(\omega ) = +\infty ,\) the equation \(g_2(\omega ) = 0\) has a unique root \(\omega _1 \in (0, \infty )\). Moreover \(g_2(\omega ) < 0\) in \((0,\omega _1)\) and \(g_2(\omega ) > 0\) in \((\omega _1, \infty ).\) This shows that \(h_2\) is decreasing on \((0,\omega _1)\) and increasing on \((\omega _1, \infty )\). On the other hand, since \(h_2(0) = 0\) and \(\lim _{\omega \rightarrow +\infty }h_2(\omega ) = +\infty \), the equation \(h_2(\omega ) = 0\) has a unique root \(\omega _2 \in (0,\infty )\) and \(h_2(\omega ) < 0\) for all \(\omega \in (0,\omega _2)\) and \(h_2(\omega ) > 0\) for all \(\omega \in (\omega _2,\infty ).\)
(i) If \(aq_2+bq_1 > 1\) then \(h_2(1) < 0.\) Thus \(\omega _2 > 1\). Moreover, since \(a < 0,\) we have
and thus \(h_2\left( (bq_1)^{1/{\alpha _2}} \right) > 0\). This implies that \(1< \omega _2 < (bq_1)^{1/{\alpha _2}}.\) From that if
we obtain \(c > a\omega _2^{\alpha _2}q_1 + b\omega _2^{\alpha _1}q_2,\) which together with (3.9) leads to \(h_1(\omega _2) > 0.\)
(ii) If \( aq_2+bq_1 \le 1\), then \(h_2(1) \ge 0.\) Thus \(0 < \omega _2 \le 1.\) Due to \( c \ge bq_2\), we see that \(c > a \omega _2^{\alpha _2}q_1 + b\omega _2^{\alpha _1}q_2\). The proof is completed. \(\square \)
4 Estimates for the functions \({\mathcal {R}}^\lambda \) and \({\mathcal {S}}^\beta \)
This section is devoted to the derivation of some important and new estimates of the functions \({\mathcal {R}}^\lambda \) and \({\mathcal {S}}^\beta \) on \((0,\infty )\) and to some first applications of these estimates. We recall the definitions of these functions from (2.7), viz.
where \(l(\alpha ) = \alpha _1 + \alpha _2\) and \(Q(s) = s^{\alpha _1 + \alpha _2} -a_{11}s^{\alpha _2} - a_{22}s^{\alpha _1} + \det A\).
Lemma 8
Let \(\alpha _1, \alpha _2 \in (0, 1]\) and denote \( \nu = \min \{\alpha _1, \alpha _2 \}\). Assume there are no zeros of the characteristic function Q in the closed right-half complex plane. Then, the following estimates hold for \(\lambda \in \left\{ 0,\alpha _1, \alpha _2 \right\} \) and \(\beta \in \left\{ \alpha _1, \alpha _2 ,l(\alpha )\right\} \):
Moreover,
The proof of the lemma is quite lengthy and technical. Therefore, in order not to distract the reader and to make it easier to focus on the main results, we provide the proof in Appendix A at the end of the paper.
Our first application of Lemma 8 deals with estimates for the convolution of \({\mathcal {S}}^\beta \) and a continuous function.
Theorem 3
Let \(\alpha _1, \alpha _2 \in (0,1]\) and \(\beta \in \left\{ \alpha _1,\alpha _2,l(\alpha ) \right\} \). For each continuous function \(g : [0, \infty ) \rightarrow {\mathbb {R}}\), we put
and
Assume that all zeros of the characteristic function Q are in the open left-half complex plane. Then, the following statements hold.
-
(i)
If g is bounded then \({\bar{F}}_g^\beta \) and \(F_g^\beta \) are also bounded.
-
(ii)
If \(\lim _{t \rightarrow \infty } g(t) = 0\) then \(\lim _{t \rightarrow \infty } {\bar{F}}_g^\beta (t) = \lim _{t \rightarrow \infty } F_g^\beta (t) = 0\).
-
(iii)
If there exists some \(\eta \ge 0\) such that \(g(t) = O(t^{-\eta })\) for \(t \rightarrow \infty \) then
$$\begin{aligned} {\bar{F}}_g^\beta (t) = O(t^{-\mu }) \text{ and } F_g^\beta (t) = O(t^{-\mu }) \text{ for } t \rightarrow \infty \end{aligned}$$where \(\mu = \min \left\{ \alpha _1, \alpha _2, \eta \right\} .\)
Proof
We denote \(\nu = \min \{\alpha _1, \alpha _2 \}\). Since, by definition, \(|F_g^\beta (t)| \le {\bar{F}}_g^\beta (t)\), the claims for \(F_g^\beta \) immediately follow from those for \({\bar{F}}_g^\beta \), and therefore it suffices to explicitly prove the latter.
Statement (i) is merely the special case of \(\eta = 0\) of part (iii).
To prove (ii), we note that \({\bar{F}}_g^\beta (t) \ge 0\) by definition. Therefore, it is sufficient to show that for every \(\varepsilon > 0\) there exists a constant \({\widetilde{T}} = {\widetilde{T}}(\varepsilon )\) such that
Since this is trivially fulfilled if \(g(t) = 0\) for all t, we from now on assume that \(g(t) \ne 0\) for some t, and hence \(\Vert g \Vert _\infty > 0\).
Our first observation is then that, from (4.2) and (4.3), we know that there exists some constant \(C > 0\) such that
Given an arbitrary \(\varepsilon > 0\), due to our assumption on g we may then find some \({\hat{T}} > 0\) such that \(|g(t)| < \nu \varepsilon / (3 C)\) for all \(t > {\hat{T}}\). Using these values \({\hat{T}}\) and C, we then define
For \(t > {\widetilde{T}} \ge {\hat{T}} + 1\), we can then write
Our goal now is to show that, under these assumptions, \(F_j(t) \le \varepsilon /3\) for \(j = 1, 2, 3\), which implies (4.7) and thus suffices to prove part (ii) of the theorem. In this context, we see that
because here \(t - s \ge t - {\hat{T}} > {\widetilde{T}} - {\hat{T}} \ge 1\), so that we may use the first of the bounds given in (4.8). In the penultimate step, we have bounded the integral by the product of the length of the integration interval and the maximum of the integrand, and in the last step, we have used the fact that \(t > {\widetilde{T}}\) and the definition of \({\widetilde{T}}\).
Furthermore,
because here \(s \ge {\hat{T}}\), so that \(|g(s)| \le \nu \varepsilon / (3 C)\), and \(t-s \ge 1\), so we may once again use the first bound of (4.8).
Finally,
where now t and s are such that we may invoke the second bound of (4.8) but, as in the previous step, \(s \ge {\hat{T}}\), so that once again \(|g(s)| \le \nu \varepsilon / (3 C)\). This completes the proof of part (ii) of the theorem.
For the proof of (iii), we note that (4.8) is valid in this case too. Moreover, since we are interested in the asymptotic behaviour of \({\bar{F}}_g^\beta (t)\) for large t, we may assume without loss of generality that \(t \ge 2\). Then we write
and we need to show that \(F_j(t) = O(t^{-\mu })\) for \(j = 4, 5, 6, 7\).
In this connection, we first note that, by assumption,
with some \(C' > 0\), so that the upper branch of (4.8) implies
and
as well as
For the remaining part we need to invoke the second branch of (4.8) in combination with (4.11) to derive
thus completing the proof. \(\square \)
As an immediate application of Theorem 3(iii), we can conclude that
Moreover, assuming \(\nu < 1\) and setting
we can obtain (using Lemma 8 and the classical relation between the incomplete Beta function and the hypergeometric function \(_2 F_1\), cf. [1, eq. (6.6.8)]) the following bounds:
-
If \(t \ge 2\) then we have
$$\begin{aligned} \nonumber {\bar{F}}^\beta _{g_2}(t)&= \int _0^1 | {\mathcal {S}}^\beta (t-s) | (s^{-\nu }-1) ds \le C \int _0^1 (t-s)^{-\nu -1} s^{-\nu } ds \\ \nonumber&= C t^{-2\nu } B_{1/t} (1-\nu , -\nu ) \\&= \frac{C}{1-\nu } t^{-\nu -1} {} {}_2 F_1(1-\nu , 1+\nu ; 2-\nu ; t^{-1}) \le C' t^{-\nu -1} \end{aligned}$$(4.13)with some \(C' > 0\).
-
If \(t \in [1,2]\) then
$$\begin{aligned} \nonumber {\bar{F}}^\beta _{g_2}(t)&= \int _0^1 | {\mathcal {S}}^\beta (t-s) | (s^{-\nu }-1) ds \le C \int _0^1 (t-s)^{\nu -1} s^{-\nu } ds \\ \nonumber&= C B_{1/t} (1-\nu , \nu ) \\&= \frac{C}{1-\nu } t^{\nu -1} {} {}_2 F_1(1-\nu , 1-\nu ; 2-\nu ; t^{-1}) \le C'' t^{-\nu } \end{aligned}$$(4.14)with some \(C'' > 0\).
Since \({\bar{F}}^\beta _{g_1}(t) + {\bar{F}}^\beta _{g_2}(t) = {\bar{F}}^\beta _{g_1 + g_2}(t)\), we can summarize the observations of eqs. (4.12), (4.13) and (4.14) in the following way:
Remark 1
Assuming that \(\nu = \min \{ \alpha _1, \alpha _2\} < 1\), there exists a constant C such that, for all \(t \ge 1\) and \(\beta \in \left\{ \alpha _1, \alpha _2, l(\alpha ) \right\} \),
5 Asymptotic behaviour of solutions to non-commensurate fractional planar systems
In this section we will study the asymptotic behaviour of solutions to fractional-order linear planar systems and the Mittag-Leffler stability of an equilibrium point to fractional nonlinear planar systems, thus presenting the main new results of our work.
5.1 Asymptotic behaviour of solutions to fractional linear planar systems
Consider the non-homogeneous linear two-component incommensurate fractional-order system
where \(\alpha =(\alpha _1,\alpha _2)\in (0,1]\times (0,1]\) is a multi index, \(A = \left( a_{ij} \right) \in {\mathbb {R}}^{2 \times 2}\) is a square real matrix and \(f = (f_1, f_2)\) is a continuous vector valued function which is exponentially bounded on \([0,\infty )\).
Theorem 4
Suppose that all zeros of the characteristic function
of the problem (5.1a) lie in the open left-half of the complex plane. Then, the following statements hold.
-
(i)
If f is bounded, then for any \(x^0\in {\mathbb {R}}^2\) the solution to (5.1) is also bounded.
-
(ii)
If \(\lim _{t \rightarrow \infty } f(t) = 0\) then the solution to (5.1) tends to 0 when \(t \rightarrow \infty \) for any \(x^0\in {\mathbb {R}}^2\).
-
(iii)
If \(\Vert f(t) \Vert = O(t^{-\eta })\) as \(t \rightarrow \infty \) with some \(\eta > 0\) then every solution x of (5.1a) behaves as \(\Vert x(t) \Vert = O(t^{-\mu })\) for \(t \rightarrow \infty \) where \(\mu = \min \left\{ \alpha _1, \alpha _2, \eta \right\} .\)
Proof
The proof is straightforward by combining Lemmas 1 and 8 and Theorem 3. \(\square \)
Based on Theorem 4 and Lemmas 2, 4, 5, 6 and 7, we obtain the following corollary.
Corollary 2
Let
The statements of Theorem 4 (i), (ii) and (iii) are true if one of the following conditions is satisfied.
-
(i)
\(a_{11},a_{22}\le 0\) and \(\det A>0\).
-
(ii)
\(a_{11}=0\), \(a_{22}>0\), \(\det A>0\) and
$$\begin{aligned} (a_{22}q_1)^{\alpha _1/\alpha _2}a_{22}q_2< \det A. \end{aligned}$$ -
(iii)
\(a_{22}=0\), \(a_{11}>0\), \(\det A>0\) and
$$\begin{aligned} (a_{11}q_2)^{\alpha _2/\alpha _1}a_{11}q_1< \det A. \end{aligned}$$ -
(iv)
\(a_{11}, a_{22}, \det A > 0\) and one of the following conditions holds:
- (iv)\(_1\):
-
\(a_{11}q_2+a_{22}q_1 > 1\) and \(a_{11}q_2\left( (a_{11}+a_{22})q_2 \right) ^{\alpha _2/\alpha _1} + a_{22}(a_{11}+a_{22})q_2^2 \le \det A\);
- (iv)\(_2\):
-
\( a_{11}q_2+a_{22}q_1 \le 1\) and \( a_{11}q_1 + a_{22}q_2 < \det A.\)
-
(v)
\(a_{11} < 0\), \(a_{22}, \det A > 0\) and one of the following conditions holds:
- (v)\(_1\):
-
\( a_{11}q_2+a_{22}q_1 > 1\) and \(\left( a_{22}q_1 \right) ^{\alpha _1/\alpha _2}a_{22}q_2 \le \det A\);
- (v)\(_2\):
-
\( a_{11}q_2+a_{22}q_1 \le 1\) and \( a_{22}q_2 \le \det A\).
5.2 Mittag-Leffler stability of fractional nonlinear planar systems
We now look at a different class of systems. Specifically, we now allow the differential equations to contain nonlinearities, but we do require them to have the structure of an autonomous system, i.e., we consider a fractional nonlinear planar system of the form
where \(\alpha =(\alpha _1,\alpha _2)\in (0,1]\times (0,1]\) is a multi-index, \(A = \left( a_{ij} \right) \in {\mathbb {R}}^{2 \times 2}\) is a square real matrix, \(\varOmega \) is an open subset of \({\mathbb {R}}^2\) containing the origin and \(f:\varOmega \rightarrow {\mathbb {R}}^2\) is locally Lipschitz continuous at the origin such that \(f(0)=0\) and \(\lim _{r\rightarrow 0} l_f (r)=0\) with
In the context of first order differential equations, it is natural to talk about exponential stability; an appropriate generalization of this classical notion to the fractional order setting is the concept of Mittag-Leffler stability. In the case of a commensurate system, this can be defined as follows (cf., e.g., [14, Definition 4.1]):
Definition 1
The trivial solution of the system (5.2a) with \(\alpha _1 = \alpha _2 \in (0,1)\) is said to be Mittag–Leffler stable if there exist some \(b, \lambda >0\), some \(B \subset {\mathbb {R}}^2\) and some locally Lipschitz function \(m : B \rightarrow [0, \infty )\) with the property \(m(0) = 0\) such that, for all \(x^0 \in B\),
for all \(t \ge 0\), where \(\varphi (\cdot , x^0)\) denotes the solution of the initial value problem (5.2).
In view of the well known asymptotic properties of the Mittag-Leffler function for \(t \rightarrow 0\) and for \(t \rightarrow \infty \), [12, Section 3.4], the property (5.3) can essentially be reformulated in the form of the requirement that \(\Vert \varphi (t, x^0) \Vert \) remains bounded for \(t \rightarrow 0\) and exhibits an (at least) algebraic decay to zero as \(t \rightarrow \infty \) whenever \(x^0\) is sufficiently close to 0. Therefore, it seems natural to extend this definition to the case of non-commensurate fractional differential equation systems that is relevant in our context in the following way:
Definition 2
The trivial solution of (5.2a) is Mittag-Leffler stable if there exist positive constants \(\gamma ,m\) and \(\delta \) such that for any initial condition \(x^0\in B(0,\delta )\), the solution \(\varphi (\cdot , x^0)\) of the initial value problem (5.2) exists globally on the interval \([0,\infty )\) and
Our aim is to prove the following theorem.
Theorem 5
Suppose that all zeros of the characteristic function \(Q(s) =\) \(s^{\alpha _1+\alpha _2}-a_{11}s^{\alpha _2}-a_{22}s^{\alpha _1}+ \det A\) lie in the open left-half of the complex plane. Then, the trivial solution of differential equation (5.2a) is Mittag-Leffler stable. More precisely, there exist constants \(\delta , \varepsilon > 0\) such that for any \(\Vert x^0\Vert < \delta \), the unique solution \(\varphi (\cdot ,x^0)\) of the initial value problem (5.2) exists globally on \([0,\infty )\) and \(\sup _{t \ge 1} t^\nu \Vert \varphi (t,x^0)\Vert \le \varepsilon \) with \(\nu = \min \{\alpha _1, \alpha _2\}.\)
As shown above, we see that Lemmas 2, 4, 5, 6 and 7 give sufficient conditions which ensure that the characteristic function Q has no zero in the closed right hand side of the complex plane. Thus, by combining these lemmas and Theorem 5, we obtain the result below.
Corollary 3
Let
The statement of Theorem 5 is true if one of the following conditions is satisfied:
-
(i)
\(a_{11},a_{22}\le 0\) and \(\det A>0\).
-
(ii)
\(a_{11}=0\), \(a_{22}>0\), \(\det A>0\) and
$$\begin{aligned} (a_{22}q_1)^{\alpha _1/\alpha _2}a_{22}q_2< \det A. \end{aligned}$$ -
(iii)
\(a_{22}=0\), \(a_{11}>0\), \(\det A>0\) and
$$\begin{aligned} (a_{11}q_2)^{\alpha _2/\alpha _1}a_{11}q_1< \det A. \end{aligned}$$ -
(iv)
\(a_{11}, a_{22}, det A > 0\) and one of the following conditions holds:
- (iv)\(_1\):
-
\(a_{11}q_2+a_{22}q_1 > 1\) and \(a_{11}q_2\left( (a_{11}+a_{22})q_2 \right) ^{\alpha _2/\alpha _1} + a_{22}(a_{11}+a_{22})q_2^2 \le \det A\);
- (iv)\(_2\):
-
\( a_{11}q_2+a_{22}q_1 \le 1\) and \( a_{11}q_1 + a_{22}q_2 < \det A.\)
-
(v)
\(a_{11} < 0\), \(a_{22}, det A > 0\) and one of the following conditions holds:
- (v)\(_1\):
-
\( a_{11}q_2+a_{22}q_1 > 1\) and \(\left( a_{22}q_1 \right) ^{\alpha _1/\alpha _2}a_{22}q_2 \le \det A\);
- (v)\(_2\):
-
\( a_{11}q_2+a_{22}q_1 \le 1\) and \( a_{22}q_2 \le \det A\).
Proof of Theorem 5
From the assumption of the theorem that f is locally Lipschitz continuous at the origin, we can find a constant \(\varepsilon _0 > 0\) such that the function f is Lipschitz continuous on \(B(0,\varepsilon _0)\). Denote by \(\hat{f}\) a Lipschitz extension of f to \({\mathbb {R}}^2\). This means that \(\hat{f}\) is globally Lipschitz continuous and \(\hat{f}(x)=f(x)\) on \(B(0,\varepsilon _0)\). We now focus on the system
Then, for any \(x^0\in B(0,\varepsilon _0)\), its unique solution \({\hat{\varphi }}(\cdot ,x^0)=({\hat{\varphi }}_1(\cdot ,x^0),{\hat{\varphi }}_2(\cdot ,x^0))^{\!\mathrm T}\) on \([0,\infty )\) satisfies the relationships
To show the Mittag-Leffler stability of the trivial solution to the original system, we will prove that for any small initial value vector, the unique solution of the system (5.4) is contained in the space \(C_{\infty }([0,\infty );{\mathbb {R}}^2)\) which is equipped with the norm
It is easy to see that \(C_w([0,\infty );{\mathbb {R}}^2):=\{\xi \in C_{\infty }([0,\infty );{\mathbb {R}}^2):\Vert \xi \Vert _w<\infty \}\) is a Banach space with the norm \(\Vert \cdot \Vert _w\). For \(\varepsilon > 0\), let \(B_{C_w}(0,\varepsilon ) := \{\xi \in C_{\infty }([0,\infty );{\mathbb {R}}^2):\Vert \xi \Vert _w\le \varepsilon \}\).
Based on the representation in eq. (5.5), we establish a Lyapunov–Perron type operator \({\mathcal {T}}_{x^0}\) on the space \(C_w([0,\infty );{\mathbb {R}}^2)\) in the following way: For any \(\xi \in C_w([0,\infty );{\mathbb {R}}^2)\), let
On the interval [0, 1], we have
and
For \(t\in [1,\infty )\), we have
and
From (5.8) and (5.9), we obtain the estimates
and
where \(\Vert \xi \Vert _{w,1}\!:=\!\max \{\sup _{t\in [0,1]}|\xi (t)|,\sup _{t\ge 1}t^\nu |\xi (t)|\}\) for any \(\xi \!\in \! C_{\infty }([0,\infty );{\mathbb {R}})\) and \(M_{\beta }=\sup _{t\ge 1} t^\nu \int _0^t |{\mathcal {S}}^{\beta }(t-s)| s^{-\nu }ds\) for \(\beta \in \{ \alpha _1, \alpha _2, l(\alpha ) \}\). By (5.10) and (5.11), we see that
On the other hand, by virtue of the assumption that \(\lim _{r\rightarrow 0}l(r)=0\), we can choose \(\varepsilon \in (0,\varepsilon _0)\) so that
Take
then for any initial condition \(x^0\in B(0,\delta )\), we have
that is, \({\mathcal {T}}_{x^0}(B_{C_w}(0,\varepsilon ))\subset B_{C_w}(0,\varepsilon )\). Moreover, for every \(\xi ,{\hat{\xi }}\in B_{C_w}(0,\varepsilon )\),
Thus, the operator \({\mathcal {T}}_{x^0}\) is contractive on \(B_{C_w}(0,\varepsilon )\), and by Banach’s fixed point theorem, \({\mathcal {T}}_{x^0}\) has a unique fixed point \(\xi ^*\) in this set. Furthermore, this function is the unique solution to the system (5.4) in \(B_{C_w}(0,\varepsilon )\). Notice that if \(\xi ^*\in B_{C_w}(0,\varepsilon )\) then \(f(\xi ^*(t))=\hat{f}(\xi ^*(t))\) for every \(t\in [0,\infty )\), and thus \(\xi ^*\) is also a solution to the system (5.2). This completes the proof. \(\square \)
6 Numerical examples
To complete this paper, we now give some numerical examples to illustrate the main theoretical results. Specifically, Lemmas 2, 4, 5, 6(i), 6(ii), 7(i) and 7(ii) provide different sufficient criteria for the zeros of the characteristic function Q to be located in the desired part of the complex plane. To demonstrate the applicability of these criteria, we have included an example for each of them except for Lemma 2 because this result has already been known for some time now [5].
In all the examples below, we use the functions \(f_1\) and \(f_2\) with
For all cases, we have calculated numerical solutions to verify the theoretical findings. These solutions have been computed with Garrappa’s MATLAB implementation of the implicit trapezoidal method described in detail in [11]. This algorithm is known to have very favourable stability properties which makes it highly suitable for handling equations like ours over large intervals (which is required in this case to demonstrate the asymptotic behaviour). The step size has always been chosen as \(h = 1/200\). For each of the examples, we have provided two plots. The plots on the left always show the two components of the respective solution on their own. For these plots, the values of t range between 0 (the initial point) and 100. This interval is sufficiently large to provide a rough impression of the asymptotic behaviour of the functions and yet sufficiently small to still allow a reasonable view of their behaviour in the initial phase. To complement this, we have added (on the right of each figure) a plot of \(t^\beta x_j(t)\), \(j = 1, 2\), where the value of \(\beta \) is chosen such that, according to the theoretical considerations of Theorems 4 or 5 (whichever is applicable in the example under consideration), \(t^\beta x_j(t)\) is bounded as \(t \rightarrow \infty \) for both values of j. The range of t was chosen larger in this case (specifically, the displayed interval is [0, 300]) to clearly exhibit the boundedness (or lack thereof in the case of Fig. 3 where the conditions of Theorem 5 are not fulfilled).
Example 1
Consider the inhomogeneous two-component incommensurate fractional-order linear system
In this example, the characteristic function is \(Q(s) = s^{5/6} - s^{1/3} + 0.5.\) According to Lemma 4, all zeros of Q lie in the open left-half of the complex plane. Furthermore, the function f satisfies the assumption stated in Theorem 4. Hence, every solution to (6.1) tends to the origin as \(t\rightarrow \infty \) with the rate \(O(t^{-1/3})\). This property is illustrated in Fig. 1. The left graph shows that the components \(x_1(t)\) and \(x_2(t)\) decay to zero; the right graph visualizes the fact that \(t^{1/3} x_j(t)\) tends to a nonzero constant for \(t \rightarrow \infty \) and \(j = 1, 2\), thus demonstrating that the decay behaviour of \(x_j(t)\) is indeed \(O(t^{-1/3})\).
Example 2
Consider the two-component incommensurate fractional-order nonlinear system
It is not difficult to check that all conditions of Lemma 4 and Theorem 5 are verified. Thus, the trivial solution to (6.2) is Mittag-Leffler stable; more precisely, by Theorem 5, we have to expect an \(O(t^{-1/3})\) decay behaviour for nontrivial solutions with initial values sufficiently close to those of the trivial solution.
Definition 2 states that the boundedness of the solutions cannot be expected for all choices of the initial value any more (as had been the case in Example 1) but only for initial values sufficiently close to (0, 0). Indeed we can see this behaviour in Fig. 2 for the initial value \((0.1, -0.2)\), whereas Fig. 3 shows that this behaviour is not present for initial values farther away from (0, 0) such as, e.g., the initial value \((1,-1)\). In the latter case, the solutions still seem to be bounded, but the decay behaviour appears to be absent. If one moves the initial values even farther away from the equilibrium point, then one cannot even expect this boundedness any more.
Example 3
Consider the fractional linear system
The characteristic function of the system is \(Q(s) = s^{1.4} - s^{0.8} + 2.\) By Lemma 5, all zeros of Q lie in the open left-half of the complex plane and the assumptions of Theorem 4 are satisfied. Hence, every solution to this system converges to the origin as \(t\rightarrow \infty \) with an \(O(t^{-0.6})\) convergence rate. As in Example 1, we can also reproduce this behaviour numerically. The corresponding graphs are plotted in Fig. 4.
Example 4
Consider the system
Based on Lemma 5 and Theorem 5, we see that the trivial solution of (6.4) is Mittag-Leffler stable. As in Example 2, this is exhibited—together with the decay behaviour predicted by Theorem 5—in Fig. 5.
Example 5
Consider the inhomogeneous two-component incommensurate fractional-order linear system
The system (6.5) has the characteristic function \(Q(s) = s^{0.7} - s^{0.4} - s^{0.3} + 3\). From Lemma 6 (i) and Theorem 4, it follows that every solution of this system tends to the origin as \(t\rightarrow \infty \) as \(O(t^{-0.3})\). Once again, our numerical results, shown in Fig. 6, support this statement.
Example 6
Consider the two-component incommensurate fractional-order nonlinear system
Its characteristic function is \(Q(s) = s^{0.7} -0.1 s^{0.4} - 0.2 s^{0.3} + 0.3.\) It follows from Lemma 6(ii) and Theorem 5 that the trivial solution is Mittag-Leffler stable. Once again, we can visualize this observation on the basis of numerical results, cf. Fig. 7.
Example 7
Consider the two-component incommensurate fractional-order linear system
The system (6.7) has the characteristic function \(Q(s) = s^{0.9} + s^{0.5} - 4 s^{0.4} + 6.\) According to Lemma 7(i) and Theorem 4, its solution converges to the origin with a rate \(O(t^{-0.4})\). As above, the numerical data shown in Fig. 8 confirms this theoretical observation.
Example 8
Consider the two-component incommensurate fractional-order nonlinear system
Its characteristic function \(Q(s) = s^{0.9} + s^{0.5} - 2s^{0.4} + 2\). According to Lemma 7(ii) and Theorem 5, the trivial solution of (6.8) is Mittag-Leffler stable as illustrated graphically in Fig. 9.
7 Conclusion
In this paper, we have provided new insight into the behaviour of non-commensurate fractional order planar systems. The main new contributions are Theorem 4, Corollary 2, Theorem 5 and Corollary 3. In Theorem 4 and Corollary 2, we show sufficient conditions for the global attractivity of non-trivial solutions to fractional-order inhomogeneous linear planar systems. In Theorem 5 and Corollary 3, we obtain the Mittag-Leffler stability of an equilibrium point to fractional order nonlinear planar systems. To achieve these goals, our approach is as follows. Firstly, based on Cauchy’s argument principle in complex analysis, we obtain various explicit sufficient conditions for the asymptotic stability of linear systems whose coefficient matrices are constant. Secondly, by using Hankel type contours, we derive some important estimates of special functions arising from a variation of constants formula of solutions to inhomogeneous linear systems. Then, by proposing carefully chosen weighted norms combined with the Banach fixed point theorem for appropriate Banach spaces, we get the desired conclusions. We also provide numerical examples to illustrate the effect of the main theoretical results.
References
Abramowitz, M., Stegun, I.A.: Handbook of Mathematical Functions, 10th printing with corrections. National Bureau of Standards, Washington (1972)
Bǎleanu. D., Lopes, A.M.: Handbook of Fractional Calculus with Applications: Applications in Engineering, Life and Social Sciences, Part A. De Gruyter, Berlin (2019)
Bǎleanu. D., Lopes, A.M.: Handbook of Fractional Calculus with Applications: Applications in Engineering, Life and Social Sciences, Part B. De Gruyter, Berlin (2019)
Bonnet, C., Partington, J.R.: Coprime factorizations and stability of fractional differential systems. Systems and Control Letters 41(3), 167–174 (2000)
Brandibur, O., Kaslik, E.: Stability of two-component incommensurate fractional-order systems and applications to the investigation of a FitzHugh-Nagumo neuronal model. Math. Methods Appl. Sci. 41(17), 7182–7194 (2018)
Brandibur, O., Kaslik, E.: Exact stability and instability regions for two-dimensional linear autonomous multi-order systems of fractional-order differential equations. Fract. Calc. Appl. Anal. 24(1), 225–253 (2021). https://doi.org/10.1515/fca-2021-0010
Cong, N.D., Doan, T.S., Siegmund, S., Tuan, H.T.: Linearized asymptotic stability for fractional differential equations. Electron. J. Qualitative Theory Differ. Equations 39, 1–13 (2016)
Cong, N.D., Tuan, H.T., Trinh, H.: On asymptotic properties of solutions to fractional differential equations. J. Math. Anal. Appl. 484, 123759 (2020)
Diethelm, K.: The Analysis of Fractional Differential Equations. Springer, Berlin (2010)
Diethelm, K., Siegmund, S., Tuan, H.T.: Asymptotic behaviour of solutions of linear multi-order fractional differential systems. Fract. Calc. Appl. Anal. 20(5), 1165–1195 (2017). https://doi.org/10.1515/fca-2017-0062
Garrappa, R.: Numerical solution of fractional differential equations: A survey and a software tutorial. Mathematics 6, 16 (2018)
Gorenflo, R., Kilbas, A.A., Mainardi, F., Rogosin, S.: Mittag-Leffler Functions, Related Topics and Applications, 2nd edn. Springer, Berlin (2020)
Ivanova, E., Moreau, X., Malti, R.: Stability and resonance conditions of second-order fractional systems. J. Vibration and Control 24(4), 659–672 (2016)
Li, Y., Chen, Y.Q., Podlubny, I.: Stability of fractional-order nonlinear dynamic systems: Lyapunov direct method and generalized Mittag-Leffler stability. Comput. Math. Appl. 59(5), 1810–1821 (2010)
Matignon, D.: Stability results for fractional differential equations with applications to control processing. Comput. Eng. in Sys. Appl. 2, 963–968 (1996)
Petráš, I.: Handbook of Fractional Calculus with Applications: Applications in Control. De Gruyter, Berlin (2019)
Podlubny, I.: Fractional Differential Equations. Academic Press, San Diego (1999)
Sabatier, J., Farges, C., Trigeassou, J.-C.: A stability test for non-commensurate fractional order systems. Systems and Control Letters 62(9), 739–746 (2013)
Shen, J., Lam, J.: Stability and performance analysis for positive fractional-order systems with time varying delays. IEEE Transact. Automat. Control. 61(9), 2676–2681 (2016)
Tarasov, V.E.: Handbook of Fractional Calculus with Applications: Applications in Physics. Part A. De Gruyter, Berlin (2019)
Tarasov, V.E.: Handbook of Fractional Calculus with Applications: Applications in Physics. Part B. De Gruyter, Berlin (2019)
Trigeassou, J., Benchellal, A., Maamri, N., Poinot, T.: A frequency approach to the stability of fractional differential equations. Transact. on Systems, Signals and Devices 4(1), 1–25 (2009)
Tuan, H.T., Siegmund, S.: Stability of scalar nonlinear fractional differential equations with linearly dominated delay. Fract. Calc. Appl. Anal. 23(1), 250–267 (2020). https://doi.org/10.1515/fca-2020-0010
Tuan, H.T., Trinh, H.: A qualitative theory of time delay nonlinear fractional-order systems. SIAM J. Control Optimiz. 3, 1491–1518 (2020)
Tuan, H.T., Trinh, H.: Global attractivity and asymptotic stability of mixed-order fractional systems. IET Control Theory and Applications 14, 1240–1245 (2020)
Tuan, H.T., Trinh, H., Lam, J.: Necessary and sufficient conditions of the positivity and stability to mixed fractional-order systems. Internat. J. Robust and Nonlinear Control 31(1), 37–50 (2021)
Vainikko, G.: Which functions are fractionally differentiable? Z. Anal. Anwend. 35(4), 465–487 (2016)
Zhang, S., Liu, L., Xue, D., Chen, Y.Q.: Stability and resonance analysis of a general non-commensurate elementary fractional-order system. Fract. Calc. Appl. Anal. 23(1), 183–210 (2020). https://doi.org/10.1515/fca-2020-0007
Funding
Open Access funding enabled and organized by Projekt DEAL. Ha Duc Thai and Hoang The Tuan are supported by The International Center for Research and Postgraduate Training in Mathematics – Institute of Mathematics – Vietnam Academy of Science and Technology under the Grant ICRTM02_2022.02.
Author information
Authors and Affiliations
Contributions
The authors contributed equally to this work.
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix A: Proof of Lemma 8
Appendix A: Proof of Lemma 8
Proof of Lemma 8
Due to the fact that there are no zeros of the characteristic function Q in the closed right half of the complex plane, from Lemma 3(iii), we can find \(\delta > 0\) (which is small enough) such that all zeros of Q are not in the domain \(|\arg (s)| \le \frac{\pi }{2} + \delta .\) Let \(R > 0\) be a large enough constant such that
For \(\mu >0 \) and \(\theta \in (0,\pi ) \), we establish an oriented contour \(\gamma (\mu , \theta )\) formed by three segments:
-
\(\left\{ s\in {\mathbb {C}}: |s| \ge \mu , \arg s = \theta \right\} \),
-
\(\left\{ s\in {\mathbb {C}}: |s| = \mu , |\arg s| \le \theta \right\} \),
-
\(\left\{ s\in {\mathbb {C}}: |s| \ge \mu , \arg s = - \theta \right\} \).
(i) Because all zeros of Q (if they exist) lie on the left of the contour \(\gamma (R, \frac{\pi }{2} + \delta ),\) using the same argument as in [23, Lemma 4.1], we obtain the representation
Choose \(\varepsilon >0\) such that Q has no zero in the ball \(\left\{ s \in {\mathbb {C}}: |s| \le \varepsilon \right\} .\) From (A.2), we have
where \(\varLambda _t'\) is the clockwise oriented contour bounding the domain
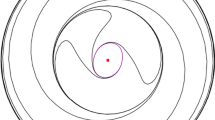
see Fig. 10. Notice that \((s^{l(\alpha )- \lambda -1} e^{st})/Q(s)\) is analytic on \(\varOmega _t \cup \varLambda _t'\) for all \(t \ge 1\). Thus, by applying Cauchy’s theorem, we obtain
The contours and sets used in the proof of Lemma 8: The radii of the green and magenta circular arcs are \(\varepsilon / t\) and R, respectively. The contour \(\gamma (R, \pi /2 + \delta )\) comprises the upper blue ray, the magenta circular arc, and the lower blue ray and is traversed from top to bottom; \(\varOmega _t\) is the open set bounded by the magenta and green boundary lines (so these magenta and green lines together form the contour \(\varLambda _t'\)). \(\varLambda _1\) comprises the upper blue ray and the upper green line; \(\varLambda _2\) denotes the union of the lower blue ray and the lower green line, and \(\varLambda _3\) is the green circular arc
Therefore, for each \(t \ge 1\), we see that
with
Put
For \(s \in \varLambda _1,\) \(s =re^{i(\frac{\pi }{2} + \delta )} = r( i\cos \delta - \sin \delta )\) with \(r \ge \varepsilon / t\), and therefore
Here, \(\widetilde{Q}(r) = Q(re^{i(\frac{\pi }{2}+ \delta )})\). From (A.5), we have the estimate \(|\widetilde{Q}(r)| \ge \eta \) for all \(r \ge \varepsilon / t\). This implies that
By the change of variable \(r = u/(t \sin \delta )\),
Hence,
Similarly, there is a \(C_{1,2}>0\) such that
For \(s \in \varLambda _3,\) \(s = (\varepsilon / t) e^{i\varphi }\) with \(|\varphi | \le \frac{\pi }{2} + \delta \), and so
where \({\hat{Q}}(\varphi ) = Q(\frac{\varepsilon }{t}e^{i\varphi })\). From (A.5), we know that \(|{\hat{Q}}(\varphi )| \ge \eta \) for all \(\varphi \in [-(\frac{\pi }{2}+ \delta ),\frac{\pi }{2}+ \delta ]\). Thus
From (A.4), (A.8), (A.9) and (A.11), we obtain
for all \(t \ge 1\) and all \(\lambda \in \left\{ 0,\alpha _1, \alpha _2 \right\} \), with \(C:=C_{1,1}+C_{1,2}+C_{1,3}\).
(ii) For the proof of the seocnd statement, we first look at the case \(\beta \in \left\{ \alpha _1, \alpha _2 \right\} \). Here, we apply the arguments as in the proof of the part (i) above to obtain
with each \(t \ge 1\). In the same way as above, we can find a constant \(C_{2,1}\) so that the estimate
holds for all \(t \ge 1\) and all \( \beta \in \left\{ \alpha _1, \alpha _2 \right\} \). Clearly, \(t^{l(\alpha )- \beta + 1 } \ge t^{\nu + 1}\) for all \(t \ge 1\) and all \(\beta \in \left\{ \alpha _1, \alpha _2 \right\} \). Thus,
Next, we consider the remaining case \(\beta = l(\alpha )\). For \(t \ge 1,\) we see
By using the same estimates as in the proof of the part (i) above, there exist constants \(C_{2,2}, C_{2,3}\) and \(C_{2,4}\) such that
On the other hand, by the change of variable \(s = \frac{u^{1/\mu }}{t}\) with some \(\mu \in (0,1)\), we find
the last equality being deduced from [17, eq. (1.52)]. Combining (A.15) and (A.16), for each \(t \ge 1\), we conclude
(iii) For each \(t \in (0,1)\) and \(\beta \in \left\{ \alpha _1,\alpha _2,l(\alpha ) \right\} \), we have
where \(\varPsi _t\) is the boundary of the domain \(U_t :=\big \{ s \in {\mathbb {C}} : R<|s| < R / t,\) \(|\arg s| < \frac{\pi }{2} + \delta \big \}\). Since \(s^{l(\alpha )- \beta } e^{st} / Q(s)\) is analytic on \(U_t \cup \varPsi _t\) for \(t \in (0,1)\), by applying Cauchy’s theorem, we obtain \(I_8(t) = 0\) for all \(t \in (0,1)\). Thus,
where
For \(s \in \varPsi _1,\) \(s =re^{i(\frac{\pi }{2} + \delta )} = r(- \sin \delta + i\cos \delta )\) with \(r \ge R/t\), and so
where \({\widetilde{Q}} (r) = Q(re^{i(\frac{\pi }{2} + \delta )})\). From (A.1), we have the estimate
This implies
The second inequality here is obtained by applying the relation \(e^{-x } \le 1/x\) for \(x > 0\). Similarly,
For \(s \in \varPsi _3\), \(s = (R/t) e^{i\varphi }\) with \(|\varphi | \le \frac{\pi }{2} + \delta \), thus
where \({\hat{Q}}(\varphi ) = Q(\frac{R}{t}e^{i\varphi })\). From (A.1), we have
for all \(\varphi \in [-(\frac{\pi }{2} + \delta ),\frac{\pi }{2} + \delta ]\), and thus
From (A.20), (A.23), (A.24) and (A.27), we obtain
Finally, (4.4) is an immediate consequence of (4.2) and (4.3). \(\square \)
Rights and permissions
This article is published under an open access license. Please check the 'Copyright Information' section either on this page or in the PDF for details of this license and what re-use is permitted. If your intended use exceeds what is permitted by the license or if you are unable to locate the licence and re-use information, please contact the Rights and Permissions team.
About this article
Cite this article
Diethelm, K., Thai, H.D. & Tuan, H.T. Asymptotic behaviour of solutions to non-commensurate fractional-order planar systems. Fract Calc Appl Anal 25, 1324–1360 (2022). https://doi.org/10.1007/s13540-022-00065-9
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s13540-022-00065-9
Keywords
- Non-commensurate fractional order planar systems
- Asymptotic behaviour of solutions
- Global attractivity
- Mittag-Leffler stability