An enhanced whale optimization algorithm with improved dynamic opposite learning and adaptive inertia weight strategy

Abstract

Whale Optimization Algorithm (WOA), as a newly proposed swarm-based algorithm, has gradually become a popular approach for optimization problems in various engineering fields. However, WOA suffers from the poor balance of exploration and exploitation, and premature convergence. In this paper, a new enhanced WOA (EWOA), which adopts an improved dynamic opposite learning (IDOL) and an adaptive encircling prey stage, is proposed to overcome the problems. IDOL plays an important role in the initialization part and the algorithm iterative process of EWOA. By evaluating the optimal solution in the current population, IDOL can adaptively switch exploitation/exploration modes constructed by the DOL strategy and a modified search strategy, respectively. On the other hand, for the encircling prey stage of EWOA in the latter part of the iteration, an adaptive inertia weight strategy is introduced into this stage to adaptively adjust the prey’s position to avoid falling into local optima. Numerical experiments, with unimodal, multimodal, hybrid and composition benchmarks, and three typical engineering problems are utilized to evaluate the performance of EWOA. The proposed EWOA also evaluates against canonical WOA, three sub-variants of EWOA, three other common algorithms, three advanced algorithms and four advanced variants of WOA. Results indicate that according to Wilcoxon rank sum test and Friedman test, EWOA has balanced exploration and exploitation ability in coping with global optimization, and it has obvious advantages when compared with other state-of-the-art algorithms.

Introduction

As engineering optimization problems have become more complex, previous deterministic methods are less effective to deal with complex practical problems. The meta-heuristic algorithms (MAs) inspired by natural phenomena are stochastic optimization strategies that do not require prior knowledge of the problem, which can be seen as a supplement to deterministic optimization techniques [1]. Different from deterministic methods iterating in one direction to the solution, MAs executes randomly and can find the approximate optimal solution of the problem through the parallel iterative optimization method of multiple search populations [2, 3], and it has been applied in practical engineering in many different fields [4].

Early researches on MAs with neighborhood searches such as hill-climbing [5] and simulated annealing (SA) [6] were proposed. As optimization problems become more complex, research on MAs is also advancing with the times. Under such circumstances, evolution-basd MAs and swarm-based MAs have also been developed [7]. There are some classic MAs in the early days: genetic algorithms (GA) [8], particle swarm optimization (PSO) [9] ant colony algorithm (ACO) [10], etc. Then new advanced MAs have been proposed in recent years: brain storm optimization (BSO) [11], bat algorithm (BA) [12], ant-lion optimization (ALO) [13], artificial bee colony (ABC) [14], biogeography-based optimization (BBO) [15], teaching-learning-based optimization (TLBO) [16], gray wolf optimization (GWO) [17], sine cosine algorithm (SCA) [18] moth-ame optimization (MFO) [19] and social group optimization (SGO) [20], etc. They have been widely used in many engineering applications, e.g., pattern recognition [21, 22], production scheduling [23, 24], control tuning [25, 26], time series forecasting [27, 28]. Among these recently proposed swarm-based MAs, WOA is a competitive algorithm inspired by humpback whales’ hunting behavior developed by Mirjalili and Lewis in [29]. The validation of the reference function experiments shows that WOA has better performance and fewer parameter settings against common algorithms [29], and it has been successfully used in flexible job shop scheduling [30], natural language processing [31] and optimal control [32], etc.

Although WOA can achieve better solutions than other algorithms in some problems, WOA still suffers from some shortcomings. Similar to most common MAs, it’s a challenge for WOA to balance exploration and exploitation stages better [33]. WOA can split the exploration and exploitation stages which contributes to escape from local optima [29]. The balance mechanism completely relies on the internal parameter a which is only determined by the number of iterations without considering the current convergence situation [34]. It leads to a poor trade-off between exploration and exploitation. Besides, due to the encircling prey mechanism used in the exploitation stage, WOA can easily converge to a local optima [35] and not update the search agents in an effective way [36]. Once the current prey is a local optimal solution, WOA is easy to fall into premature convergence. In view of this, more attempts have been made to enhance WOA, and it is very popular to combine it with a variety of learning strategies such as Lévy flight, inertia weight and opposition-based learning [37]. Among these strategies, Lévy flight was widely applied in various fields for optimization [38]. Ling et al. [39] proposed Lévy flight trajectory-based WOA (LWOA) to avoid falling into the local optimal by adding stochastic process at the end of the classical WOA. Sun et al. [40] introduced a modified WOA (MWOA) utilizing Lévy flight’s occasional long step-change feature to enhance the exploration ability when encircling preys. Yu et al. [41] exchanged the internal parameters of WOA with Lévy flight to tune the automatic carrier landing system controller. On the other hand, inertia weight is another learning strategy which can be flexibly embedded in each stage of WOA to improve the optimization effect and speed. Hu et al. [42] proposed an improved WOA based on inertia weight (IWOA), which introduced linearly decreasing inertia weight into the encircling prey stage to make IWOA convergence faster and more accurately. Chen et al. [43] proposed a random spare strategy and a double weighting strategy for the improvement of WOA (RDWOA), where two adaptive weights were used. Besides, the opposition-based learning (OBL) strategy is a competitive method for improving MAs which has been widely used for WOA. Since OBL was proposed by Tizhoosh [44], improvements to OBL have attracted more attentions. There are many existing variants of OBL, including quasi-opposition-based learning (QOBL) strategy [45], generalized opposition-based learning (GOBL) strategy [46], quasi-reflective based learning (QRBL) strategy [47] and elite opposition-based learning (EOBL)strategy [48], etc. All these are closer to the global optimum than OBL, and the improvement of WOA based on these variants is also worthy of research. HS Alamri et al. [49] proposed an opposition-based WOA (OWOA) to expand the initial population’s search space better. Based on OBL and GOBL, Luo et al. [50] proposed an EOBL-based WOA to enhance the convergence rate of WOA. In terms of application, an improved WOA with EOBL (EOWOA) was established in [51] to solve the problem of complexity and poor accuracy for parameter estimation of Muskingum model. Chen et al. [52] presented a WOA with a chaos mechanism based on quasi-opposition (OBC-WOA), which can improve convergence speed and enhance the global search ability. Kumar and Chaparala [53] presented a QOBL-based chaotic WOA to cluster the nodes in the wireless sensor network. Although OBL can be used to raise exploitation of WOA, the disadvantage that the OBL search space is symmetric leads to its weak exploration capability.

For this issue, the DOL strategy is presented in [54], which has been successfully used for improving MAs [55,56,57]. The search space of DOL is asymmetric and can be adjusted dynamically, which indicates that DOL has enough diversity to enhance the exploration capability of WOA. Although DOL has been applied to improve some common meta-heuristic algorithms, it still suffers from the problem of poor modes balance which relies on fixed, pre-tuned internal weights. Hence, this paper proposes an enhanced WOA (EWOA) to improve the search ability of WOA by introducing an improved DOL (IDOL) and a modified encircling prey stage with adaptive inertia weight (AIW). Among them, IDOL is a newly proposed enhanced learning strategy based on DOL, which plays an important role in the initialization part and the algorithm iterative process of EWOA. IDOL has two modes: in mode-one, the DOL-based stage is used to enhance the exploitation ability; in mode-two, an Lévy flight trajectory-based searching for prey stage is adopted to enhance the exploration ability. In particular, for the trade-off between exploration and exploitation, the two modes of IDOL are switched by an adaption switching rule by evaluating the optimal solution in the current population. On the other hand, AIW adjusted by current agents’ fitness is introduced into encircling pray stage to adaptive reform current prey position, which further enhances the search ability of EWOA’s exploitation phase and avoids premature convergence.

The main contributions of this paper are as follows:

• An improved DOL (IDOL) strategy is proposed and embedded in EWOA to achieve a better trade-off between exploration and exploitation. IDOL has two modes and can be adaptively switched with concerning the current convergence situation, and it has been introduced into WOA for performance improvement.

• The adaptive inertia weight (AIW), which is adaptively adjusted according to the current agent fitness situation, has been introduced into the encircling prey stage to avoiding local optima when this stage is executed.

• 30 benchmark problems selected from standard 16 functions and CEC 2014 as well as three well-known engineering problems are utilized to evaluate the improvements for EWOA. Some WOA variants and other advanced MAs are also used for comparison to confirm the advantages of the proposed EWOA.

The remainder of this paper is arranged as bellows. “Preliminaries of WOA and DOL” Section describes the concepts of WOA and DOL strategy. The proposed enhanced WOA algorithm was introduced in “The presented EWOA” section in detail. In “Experiment results and discussion” section, EWOA and compared MAs are evaluated by benchmark functions, and then the analysis of experiment results are presented. Besides, in this section the actual engineering problems are also used for test. The main conclusion of this study is presented in “Conclusion” section.

Preliminaries of WOA and DOL

The structure of a canonical WOA

The WOA simulates the hunting behavior of whale bubbles which including three stages: encircling prey, bubble-net attacking and search for prey. Firstly, the whale gradually acquires relevant information about the prey by searching for the prey. Then, the whale keeps approaching the prey by surrounding the prey and spiraling close to the prey, and the final prey found is the optimal solution of the algorithm.

Encircling prey

In this stage, whales identify the position of their prey and surround them. Since the optimal position in the search space is not known in advance, the WOA algorithm assumes that the current optimal individual position is the target prey, and other individuals continue to update their positions by approaching the prey. So that the whales constantly close to the prey by Eqs. (1) and (2).

$$\begin{aligned}&D = \left| {C\cdot {X^{*}}\left( t \right) - X\left( t \right) } \right| \end{aligned}$$

(1)

$$\begin{aligned}&X(t + 1) = {X^{*}}(t) - A \cdot D \end{aligned}$$

(2)

$$\begin{aligned}&A = 2a \cdot r - a \end{aligned}$$

(3)

$$\begin{aligned}&C = 2 \cdot r \end{aligned}$$

(4)

where $X^*$ is the position vector of the optimum solution acquired so far, X is the position vector, t denotes the current iteration, A and C are coefficient vectors calculated as Eqs. (3) and (4), respectively, the components of a is linearly decreased from 2 to 0, and r is a random number in (0,1).

Fig. 1

The search range of $X^{DO}$ under all possible relative positions of $X^{RO}$ and the boundary [a, b] [54]

Bubble-net attacking method

In the bubble-net attacking phase, the algorithm simulates that when a whale finds its prey, it continuously spirals close to the prey with the prey as the center. In this way, the prey is approached slowly and unconsciously to achieve the purpose of catching prey. As the whale spirals around, it firstly calculates the distance between it and the prey, and then approaches the prey in a spiral way. The mathematical model is as follows.

$$\begin{aligned} X(t + 1) = D^{'}\cdot {\mathrm{{e}}^{bl}} \cdot \cos (2\pi l) + {X^{*}}(t) \end{aligned}$$

(5)

where $D^{'}\mathrm{{ = }}\left| {C{X^{*}}\left( t \right) - X\left( t \right) } \right|$ denotes the distance of the $i^{th}$ whale to the optimum solution acquired so far, b represents a constant defining the spiral shape, l is a random number in $[-1,1]$. It is noting that when the whale moves around the prey in the outer circle, it will also reduce the enclosure radius.

Search for prey

The whales use the value A to control whether they are in the hunting stage or the encircling stage. When $|A|>1$ at this time, the whale cannot obtain the prey’s effective information, and it needs to make continuous attempts to find a trace of the prey’s clues through random ways. Its mathematical model of modified hunting strategy is shown as Eqs. (6) and (7), where $X^{rand}$ is a randomly selected whale position vector.

$$\begin{aligned}&D = \left| {C\cdot {X^{rand}}\left( t \right) - X\left( t \right) } \right| \end{aligned}$$

(6)

$$\begin{aligned}&X(t + 1) = {X^{rand}}(t) - A \cdot D \end{aligned}$$

(7)

The mechanism of DOL

The idea of OBL is that the search space can be dynamically expanded from a candidate to its opposite candidate, which makes it easier to approach the optimal value. However, due to the fixed location definition, it will inevitably converge to a local optimum. Given this deficiency, a DOL strategy is proposed [54]. The dynamic form of DOL strategy in one-dimensional space can be expressed as formulas (8) and Fig. 1.

$$\begin{aligned} {X^O}= & {} a + b - X\nonumber \\ {X^{RO}}= & {} r^1 {X^O}\nonumber \\ {X^{DO}}= & {} X + r^2 \left( {{X^{RO}} - X} \right) \end{aligned}$$

(8)

where $X^{O}, X^{R O}$ and $X^{D O}$ define the opposite number, random opposite number and the dynamic opposite number, respectively. $r^1$ and $r^2$ represent random values among (0,1). a denotes the low boundary and b denotes the high boundary while c is the center of [a,b]. The positions of all possible solutions of $X^{R O}$ and $X^{D O}$ relative to interval of [a,b] are illustrated in Fig. 1. If the calculation of $X^{D O}$ by Eq. (8) exceeds the boundary, a new $X^{D O}$ is reassigned a random number in [a, b]. By changing $X^{O}$ to $X^{R O}$, the search space becomes asymmetric and is conducive to improving exploration capabilities.

The presented EWOA

This section mainly focuses on the improvement of WOA. Firstly, a novel improved dynamic learning strategy basing DOL (IDOL) is proposed. Its exploration-exploitation modes consist of modified search strategy and DOL strategy, while adaptive mode switching rules are adopted to balance two modes. IDOL is executed in two stages of EWOA, including population initialization at the beginning of evolution and generation jumping. The AIW is then introduced to the encircling prey stage of EWOA, which enhances the exploration ability to avoid falling into a local optimum in the second half of the iteration. Two independent improvements for canonical WOA are named IDOLWOA and AIWWOA, respectively.

IDOL strategy

It can be seen from the mechanism of DOL that as the population converges iteratively, the search space gradually shrinks. To solve this problem, DOL introduces a preset fixed weight $w_{d}$ shown in Eq. (9), so that it can not only maintain the original convergence of OBL, but also improve the exploration ability. When $w_{d}$ is set larger, the difference between $X^{D O}$ and X also becomes larger and the diversity of populations increases accordingly. Nevertheless, the increase of $w_{d}$ will lead to low convergence speed and weak exploitation capability.

$$\begin{aligned} {X^{DO}} = X + r^2 w_{d} \left( {{X^{RO}} - X} \right) \end{aligned}$$

(9)

Different from DOL, IDOL can adaptively switch between the two modes to solve the above problems, instead of adopting a single mode based on a fixed pre-set weight $w_{d}$ in DOL. Mode-one is utilized to improve the exploitation and mode-two is used to raise exploration of $\mathrm {IDOL}$, respectively. The exploration-exploitation trade-off of IDOL is achieved by adopting an adaptive switching rule, which can be adjusted according to the current fitness situation.

Mode-one:DOL

IDOL improved the exploitation capability of WOA based on DOL by expanding the search space of group, where the weight of DOL is set to be 1. Hence, $X^{IDOL}$ is defined as Eq. (10).

$$\begin{aligned} X^{IDOL}=X+r^3 \left( r^4 X^{O}-X\right) \end{aligned}$$

(10)

where $X^{O}$ is obtained by Eq. (8) and $r^3$, $r^4$ are random numers among (0,1).

Mode-two:modified search strategy

This mode is inspired by the WOA searching for prey stage, which uses the information interaction between random individuals to expand the search range. To further enhance the mutation capability of this mode, the Lévy flight operator has also been introduced into this mode. Lévy distribution random number is widely used to improve MAs due to its occasional long-step mutation [58] . The simple power-law vision of Lévy flight is shown in (11).

$$\begin{aligned} L(s) \sim |s|^{-1-\beta }, 0<\beta \le 2 \end{aligned}$$

(11)

where $\beta =1.5$ and s is a random step size, which can be obtained approximately using Mantegna’s method [59] to generate random numbers with a step length similar to the Lévy distribution by Eq. (12). Both $\mu =N\left( 0, \sigma _{\mu }^{2}\right)$ and $\nu =N\left( 0, \sigma _{\nu }^{2}\right)$ obey normal stochastic distributions, where the value of $\sigma _{u}$ and $\sigma _{v}$ can be calculated as Eq. (13).

$$\begin{aligned}&s=\frac{\mu }{|\nu |^{1 / \beta }} \end{aligned}$$

(12)

$$\begin{aligned}&{\sigma }_{\mu }=\left[ \frac{\varGamma (1+\beta ) \times \sin (\pi \times \beta / 2)}{\varGamma (1+\beta / 2) \times \beta \times 2^{(\beta -1) / 2}}\right] ^{1 / \beta } \nonumber \\&{\sigma }_{\nu }=1 \end{aligned}$$

(13)

Based on Eq. (7), the original operator A is replaced by the Lévy flight operator s with higher mutation performance to form equation (14).

$$\begin{aligned} X^{IDOL}=X^{r}-r^5 s\left( X^{rand}-X\right) \end{aligned}$$

(14)

where $r^5$ is a random number among (0,1).

Adaptive IDOL mode switching rules

Since the algorithm will stagnate with iterations, it is necessary to switch modes to improve the search ability when stagnation. The IDOL mode switching rule plays an important role, which is formed by the iterative convergence parameter J and the mode switching threshold T. J and T are initialized to 0 at the beginning of operation, and then with iteration, whenever a better solution cannot be obtained after a round of iteration, J is accumulated following $J = J + 1$; when obtain better fitness, the iteration convergence parameter J is reset to 0; and when J exceeds T, the mode will be switched with J being reset to 0. Furthermore, the convergence speed of the algorithm will gradually decrease with the number of iterations increasing. Therefore, the threshold for switching modes should be increased to provide more iteration times for the current mode to prevent frequent switching when the iteration enters the later stage. In view of this, whenever switching modes, $T = T + \varDelta T$. Combining prior knowledge and experiment, $\varDelta T$ is set to 5. Under this parameter setting, IDOL-based WOA can obtain better performance.

AIW-based adaptive encircling prey stage

In canonical WOA’s encircling the prey stage, all agents approach the optimal agent at a random distance based on the A obtained by Eq. (3), and this value decreases linearly with iteration. However, due to the gradual decrease of the step size, the agent’s exploration performance will deteriorate at this stage. For increasing the diversity of the group and avoiding falling into local optima, this paper introduces the AIW into encircling stage. Multiply the AIW with the target prey of the current agent to form a new target, and adjust the AIW according to the fitness of the agents. The improved encircling prey stage is described as Eq. (15):

$$\begin{aligned} X_i(t + 1) = w_i(t) \cdot {X^\mathrm{{*}}}\left( t \right) - A \cdot \left| {C \cdot {X^\mathrm{{*}}}(t) - X_i(t)} \right| \end{aligned}$$

(15)

Among them, the adjustment of convergence is determined by the AIW operator $w_i(t), w_i(t) \in [0,1]$ which can be adjusted adaptively according to the current agent position. When the agent position in the solution space is more suitable, the AIW is maintained or increased. Specifically, when the agent’s fitness is better than the mean value of the whole population, the weight operator $w_i(t)$ of this agent is adjusted to the maximum value, so that they can converge to the current prey as soon as possible. On the other hand, $w_i(t)$ of the current agent will be assigned smaller value when its fitness is worse than average. The worse the performance is, the smaller the weight value is, which will weaken the prey’s impact on this group’ position update. Once the current prey is a local optima, then the search agent far away from the prey has a greater chance of escape from that to find global optima. Based on that, AIW strategy helps the group to have greater search ability and overcome premature convergence. At this point, the specific solution of AIW is determined following a mapping function basing the position proportion of the current agent’s fitness. There is a modified Versoria function [60] that can be used as a mapping function between fitness and AIW. Its curve is nonlinear while its computational complexity is lower than similarly shaped sigmoid functions and other nonlinear mapping functions. It has been successfully applied to adaptive inertial weight particle swarm optimization (AWPSO) [61, 62]. Based on the modified Versoria mapping function, w(t) can be formulated as Eq. (16).

$$\begin{aligned} w_i\left( t \right) = \left\{ {\begin{array}{*{20}{l}} {1 - \frac{1}{{\left( {\varphi \cdot {{\left( {a_i\left( t \right) - 1/2} \right) }^2} + 2} \right) }}}&{}{\text { if }\;\;a_i(t) \le 0.5}\\ {\frac{1}{{\left( {\varphi \cdot {{\left( {a_i\left( t \right) - 1/2} \right) }^2} + 2} \right) }}}&{}{\text { otherwise }} \end{array}} \right. \end{aligned}$$

(16)

where $a_i(t), a_i(t) \in [0,1]$ represents the current agent’s ranking in all agents between the minimum fitness and the average fitness, which is described as Eq. (17), and $\varphi$ is a regularization coefficient set to 300 in subsequent experiments.

$$\begin{aligned} f_{\text{ ave } }(t)= & {} \sum _{i=1}^{N_p} f_{i}(t) / N_p \nonumber \\ {f_{\min }}\left( t \right)= & {} \min \left\{ {{f_1}\left( t \right) ,{f_2}\left( t \right) ,...,{f_{Np}}\left( t \right) } \right\} \nonumber \\ a_i(t)= & {} \left( f_{i}(t)-f_{\min }(t)\right) /\left( f_{\text{ ave } }(t)-f_{\min }(t)\right) \end{aligned}$$

(17)

where $f_i(t)$ means the fitness of the i agent at the t iteration; $f_{\text{ ave } }(t)$ and $f_{\min }(t)$ denote the average value and minimum value of all Np size populations’ fitness.

The formation of EWOA

By embedding the IDOL strategy into AIWWOA, EWOA is formulated. In EWOA, the IDOL is embedded into the both population initialization and generation jumping processes. By comparing the fitness of the group generated by IDOL and the original group, the best group can be selected through the greedy rule.

IDOL initialization

In the initial generation, the population is generated randomly. To obtain a better initial population to speed up the convergence rate, the IDOL mode-one, which is inspired by the DOL’s dynamic asymmetric reconstruction space, is utilized after the random initialization of $X_{i, j}$ described as Eq. (18).

$$\begin{aligned} X^{IDOL}_{i,j}=X_{i,j}+r^3_{i} \left( r^4_{i} X^{O}_{i,j}-X_{i,j}\right) \end{aligned}$$

(18)

where $i = 1,2,\dots , Np$ is the population size, $j = 1,2,\dots , D$ is the dimension of agents, $r^1$ and $r^2$ are random numbers in (0,1), and $X^{O}_{i,j}$ is the opposite position of $X_{i, j}$ inside the search space. After the IDOL initialization process, the updated agent may exceed the boundary, so it is necessary to randomly generate a position for these individuals within the interval.

$$\begin{aligned} X_{i, j}^{IDOL}={\text {rand}}\left( a_{j}, b_{j}\right) , \text { if } X_{i, j}^{IDOL}<a_{j} \Vert X_{i, j}^{IDOL}>b_{j} \nonumber \\ \end{aligned}$$

(19)

where $a_{j}$ and $b_{j}$ are boundaries of search space. After the random initialization and IDOL initialization, Np fittest agents are selected from $X \bigcup X^{IDOL}$.

Improvement by AIW

The WOA is improved by the AIW, which utilizes Eq. (15) to update the positions of agents in the encircling stage. This equation includes the key factor: $w_i(t)$, introduced in Eq. (16).

IDOL generation jumping

By applying the adaptive learning strategy to the WOA algorithm generation, the appropriate IDOL mode is switched according to the current optimal solution’s update situation. This additional generation operation may lead to more accurate convergence or selection mutation to further increase population diversity, which enable the algorithm to find a better solution.

In each iteration, the population can be updated through IDOL. The convergence state parameter (J) is used to determine which mode IDOL executes. The IDOL is used to generate the jumping process while optimizing the position of the population, which is described as Eq. (20).

$$\begin{aligned} X_{i, j}^{IDOL}=\left\{ \begin{array}{ll} X_{i, j}+r^3_i \left( r^4_i \left( a_{j}+b_{j}-X_{i, j}\right) -X_{i, j}\right) &{} \text { if } \;\;\text {mode}>0 \\ X_{i, j}^{r a n d}-r^5_i s_i\left( X_{i, j}^{r a n d}-X_{i, j}\right) &{}\text {otherwise} \end{array}\right. \nonumber \\ \end{aligned}$$

(20)

where $X_{i, j}^{r a n d}$ is a randomly selected individual at the current generation $(i=1,2,\dots , Np$, $j=1,2,\dots , D$), $[a_{j}, b_{j}]$ is the search space of $j_{t h}$ dimension, $r^3_i$, $r^4_i$, $r^5_i$ denote random numbers among (0,1), and $s_i$ is a random step length vector generated by Eq. (12). Randomly select a mode at the beginning Eq. (21) firstly, switch mode by $\text {mode} = -\text {mode}$ if $J>T$ when convergence suffers from stagnation and reaches the threshold.

$$\begin{aligned} \text {mode} = \text {sign(rand(0, 1)}-0.5) \end{aligned}$$

(21)

After the IDOL process, for improving the performance of IDOL, search space’s boundaries are updated as Eq. (22):

$$\begin{aligned} a_{j}= & {} \min {\left\{ X_{1, j},X_{2, j},...,X_{Np, j}\right\} }\nonumber \\ b_{j}= & {} \max {\left\{ X_{1, j},X_{2, j},...,X_{Np, j}\right\} } \end{aligned}$$

(22)

Finally, Np better individuals will be selected from $X \bigcup X^{IDOL}$ . The IDOL genration jumping process is described in Algorithm 2.

Fig. 2

EWOA flowchart

Algorithm procedure

The pseudo-code of EWOA is shown as Algorithm 1, which is detailed described as follows:

• (1) Initialization basing IDOL: In this step, EWOA generates a dynamic opposition group of the original group according to the formula of DOL as Eq. 18, and all agents are evaluated together to obtain the optimal Np ones.

• (2) Update position with AIW-based WOA: In this step, EWOA updates the positions of each agent using either Eqs. 5, 6, or 15. If $p>0.5$, agents updating position as Eq. 5, otherwise one of the searching for prey stage and encircling the prey stage will be implemented according to $\left| A\right|$. Specifically, If $\left| A\right| <1$, the encircling prey period adopts the adaptive inertia weight strategy as Eq. 15. Otherwise, Eq. 6 will be used to update its position;

• (3) Apply the IDOL generation jumping stage as Algorithm 2: In this step, two modes of IDOL are introduced to enhance the WOA, it contains exploration and exploitation modes with an adaptive switching rule. Details of Algorithm 2 are shown as follows.

• (4) EWOA execution termination: The proposed EWOA algorithm repeats steps 2 and 3 maximal evolutionary iteration times or can be ended when obtaining the theoretically best solution.

IDOL generation jumping is a key stage of Algorithm 1, and it is shown in Algorithm 2. The details are as follows:

• (1) Update position following current IDOL mode: In this step, two IDOL modes are supplied to update positions as Eq.(20). They can both enhance exploration and exploitation ability of EWOA. When convergence suffers stagnation, proper mode will be conducted by judging the parameters of switching rule.

• (2) Fitness assessment: Best Np number search agents can be selected after checking boundaries and evaluating the 2Np size group consists of IDOL generation and original group.

• (3) Update IDOL parameters and modes: Modes can be switched adaptively referring the convergence situation by updating and judging the parameters of IDOL after each iteration. Parameter J records the times of stagnation during operating current mode, as it sums one if current mode cannot obtain better solution. T denotes the threshold of modes switching rule. Modes will not be switched until $J>T$. Ones mode switched, T is added $\varDelta T$ and J is reset to 0.

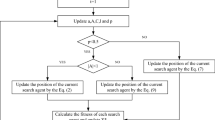
The workflow of the proposed EWOA can be summarized as follows and depicted in Fig. 2.

• (1) Initial the population using DOL and set parameters of IDOL generation jumping preparing to start iterating.

• (2) In each iteration, parameters a, A, C, l, p and w update for each search agent. And all the agents’ position are changed through one of the stages including Bubble-net attacking stage Search for prey stage and AIW-based adaptive encircling prey stage basing these parameters. Calculate fitness and update optimal agent $X^*$.

• (3) The IDOL generation jump stage adopts two modes and switching rules to be carried out after second step. Np number of optimal individuals are obtained through this stage and best agent $X^*$ is updated. The modes and parameters J and T will be updated according to the switching rules.

• (4) Repeat second and third steps until the theoretical optimal value is found or the maximum number of iterations is reached.

Experiment results and discussion

In this section, the performance of EWOA are verified by experiments on 30 benchmark functions and three engineering problems. The effective variants of WOA and many current advanced MAs are added to the comparison, and the accuracy and convergence of the results are analyzed afterward.

Test functions

The functions F1–F16 and F17–F30 used as benchmark functions in the optimization literature [63,64,65,66] and CEC 2014 [67] are divided into five categories: unimodal functions (F1–F6), multimodal functions (F7–F11), fixed-dimensional multimodal functions (F12–F16), hybrid functions (F17–F22) and composition functions (F23–F30). Unimodal functions are commonly used to evaluate the exploitation capabilities of optimization algorithms while the exploration capabilities of algorithms can be evaluated through multimodal and fixed-dimensional multimodal functions. Both hybrid functions and composition functions belong to multimodal functions, which have higher complexity after conversion and hybridization with other meta-functions. When solving complex problems, they can test the comprehensive capabilities of the algorithm for exploration, exploitation and the trade-off between them. The specific description of 30 functions is shown in Appendix 6 in the Table 12, where “HF” and “CF” represent hybrid functions and composition functions from CEC 2014, respectively, and “N” represents the number of basic functions that make up HF or CF. Besides, three engineering problems are used for evaluating EWOA’s ability to solve practical problems.

Table 1 Comparison of core operations in WOA, sub-variants of EWOA and EWOA

Table 2 Wilcoxon rank-sum tests between EWOA and other WOA variants

Parameter settings

To evaluate the performance of EWOA, numerical experiments on functions shown in Table 12 are performed. The three sub-variants of the proposed EWOA introduced in the Table 1, namely AIWWOA, DOLWOA and IDOLWOA, are added to the test. Then three classic MAs including TLBO, MFO and GWO, and three advanced MAs including the opposite learning artificial bee colony (OABC) [68], weighted PSO (wPSO) [69] and elite TLBO (ETLBO) [70], are compared with EWOA. Besides, there are four variants of WOA, including OWOA, IWOA, LWOA and RDWOA are also involved in comparison. These compared advanced MAs include the two improvement strategies that are also involved in EWOA, the opposition operator or inertia weight, to further prove that we can introduce these strategies into EWOA with the best effect.

The parameters of these compared MAs and numerical tests’ settings are as follows. For IDOLWOA and EWOA, the threshold increment step size $\varDelta T$ is set to 5; for DOLWOA, the DOL weight $w_{dol}$ has been pre-tuned and set to the optimal value 12 ; for IWOA, varying step is 0.1 from 0 to 1; for RDWOA weight adjustment factor s is set to 0; for ETLBO, the number of elites is set to 5; for wPSO, cognitive constant $C1=2$, social constant $C2=24$, inertia constant w decrease from 0.9 to 0.4; for OABC jump rate $J_r$ are set to 0.5; The rest algorithms’ parameter settings are subject to the original reference.

A large number of experiments can more accurately quantify the algorithm’s optimization ability in different types of problems and evaluate the comprehensive performance of the algorithms. In detail, for F1–F16 tests, set the population size and number of iterations to 30 and 2000, respectively; for F17–F30 (CEC 2014) tests and CEC 2019 tests, set the population size and number of iterations to 100 and 3000, respectively. And we performed 30 individual demonstrations of all experiments to establish a statistical sample of the algorithm. Besides, in the subsequent data display, the result of the CEC 2014 test is the final value of the evolution minus the theoretically optimal solution.

Accuracy analysis

In this section, the performance of EWOA is verified by comparing with WOA variants and other algorithms over all the benchmark functions. Table 2 lists the effect comparison between the improved optimized variants proposed in this paper, and Tables S1, S2 and S3 provided in the supplementary file depict the optimization effects of unimodal and multimodal functions with variety of different dimensions. Tables 13, 14, 15, 16 and 17 in Appendix 7 represent the statistic results of 11 compared algorithms with EWOA on all 30 functions. In the presented data, “Mean” and “Std” represent the mean and standard deviation of the results of 30 independent runs, and “Ranking” is the average ranking of “Mean”. Non-parametric tests for the performance of multiple algorithms, including the two-tailed Wilcoxon rank-sum tests [71] with a significance level of 0.05 and the Friedman test [72] with the Holm procedure, are shown in Tables 3, 4, 5 and 6.

To demonstrate the effect of independent improvement on WOA, i.e., IDOL and AIW, and the effect of improvement from DOL to IDOL, the performance comparison results of all the variants proposed in this paper, i.e., WOA, DOLWOA, AIWWOA, IDOLWOA and EWOA, are presented in Table 2. It lists the mean best fitness and the corresponding ARV (average ranking value) over all 30 functions (F1–F30) obtained by EWOA and other algorithms. The three columns below the algorithm names in Table 2 are the average optimal fitness of the algorithm, the statistical results of the Wilcoxon detection between EWOA and 4 algorithms, and the ranking based on the statistical results, respectively. The symbols “$+$” and “−” respectively indicate that EWOA is significantly better and worse than other algorithms through the Wilcoxon rank-sum tests; “=” indicates that there is no significant difference between them. Among them, EWOA is the optimal algorithm, IDOLWOA is better than DOLWOA, and all the improved algorithms are better than the canonical WOA. In detail, it can be observed AIWWOA perform better than WOA in solving complex problems from the test results of composition functions benefit from its more exploratory mechanism to encircle prey. Compared with DOLWOA, IDOLWOA can maintain outstanding exploitation ability in handling unimodal function, while avoiding local optima when calculating complex functions. The combination of IDOL and AIW in EWOA have all the above advantages.

Table 3 The results of Wilcoxon rank-sum tests for EWOA with WOA variants

Table 4 The results of Wilcoxon rank sum tests for EWOA with other advanced algorithms

Table 5 Statistical results of Wilcoxon rank-sum tests

Table 6 Friedman tests on unimodal/multimodal functions /fix-dimension functions F1–F16, hybrid functions /composition functions F17–F30 and all functions F1–F30

In order to study the optimization performance of EWOA in various dimensional problems, a multi-dimensional test was performed. The test included 6 unimodal functions and 5 multimodal functions, and compares with the other 11 functions in the mean and standard value of optimization results. In the subsequent tests in this paper, the default 30 dimensions are used. In this part of the different dimensional tests, the dimensions are set to 10, 50 and 100, and they are executed independently 30 times. From Tables S1, S2 and S3 in the supplementary material, it can be observed that EWOA can have strong competitiveness in both low-dimension and high-dimension tests, and rank first in the number of best solutions. It not only rank high among WOA variants, but also performs better than other optimization algorithms.

The results of experiments on unimodal, multimodal and fixed dimension functions are depicted in Tables 13, 14 and 15 given in Appendix 7. EWOA behaves best on unimodal functions F1–F4, multimodal functions F7–F9, second or third on F5, F6, F10, F11, and ranked first in the test of two functions, F15 and F16, while F13 and F14 ranked second and third. The hybrid and composition functions F17–F30 of CEC 2014 are more complex than unimodal and multimodal functions and are closer to optimization problems in the real world. For solving these problems, algorithms should appropriately balance exploration and exploitation. According to the results in Tables 16 and 17 given in Appendix 7, EWOA ranks first in terms of F18, F23–F25 and F27-30. Obviously, it performs best in the optimization problem of composition functions.

The overall significance analysis results on functions F1–F30 are also presented in this section. The optimization results of all algorithms on the test function are divided into two groups for comparison, the comparison with the WOA variant and the comparison with other advanced algorithms. To detect the significance of differences between algorithms, Wilcoxon rank-sum tests at the 5% level were conducted. Detailed data of the Wilcoxon rank-sum test results are shown in the Tables 3 and 4. where the values of p and h represent the difference significance indicators of EWOA compared with other algorithms. Specifically, if p is less than $5\%$, h will set to 1, which represents significance of the difference; otherwise h is set to 0, which means there is no significant difference between them. Statistical results of Wilcoxon rank-sum tests are shown in Table 5 When the difference in comparison is significant, the signs “Better” and “Worse” represent the times that EWOA performs better or worse on all functions, respectively.The sign “Same” means there is no significant difference between EWOA and compared algorithms. Besides, “Difference” denotes the value of “Better” minus “Worse”. Learn from the Wilcoxon test results, the value of “Better” is larger than 15 when compared to all compared algorithms except ETLBO, and it can be observed that the “Dierence” value is not less than 10 when compared with others. Moreover, the average excellent rate of EWOA can reach 66.7% $\left( \sum \nolimits _{i = 1}^{11} {\mathrm{Better}_i} /(30 \times 11) \right)$. In order to facilitate the visual comparison of the ranking of the algorithms, the two groups of ranking comparison are graphically depicted in Fig. 3. According to the Friedman test results in the fourth column of Table 6, EWOA has average rankings of 3.4062, 4.3214 and 3.85 on Simple (F1–F16) problems, complex (F17–F30) problems and overall 30 problems. The rankings of EWOA is smaller than all compared algorithms, and most of the null hypotheses are rejected based on Holm’s adjusted p-value. Through the overall data evaluation, i.e. the Wilcoxon rank-sum tests and the Friedman tests, EWOA is the top average ranking among all 12 comparison algorithms. In addition to the above 30 test problems, tests based on CEC 2019 benchmark functions are also performed. Detailed test functions information, accuracy analysis and convergence behavior are included in the supplementary file. The same Wilcoxon rank-sum and Friedman tests were used to evaluate the optimization ability of EWOA. Among them, the metrics that passed the Friedman test are summarized in Table 7. The “Average ranking” of EWOA is 1.4 which is superior than others. It indicates that the EWOA algorithm outperforms compared WOA variants, which further verifies the improvements of EWOA.

Fig. 3

Rank of mean best fitness of EWOA and other compared algorithms

Table 7 Friedman tests on CEC 2019

Actually, the above evaluation results can be predicted from the improved mechanism of EWOA. The comparison results with WOA show that EWOA maintains and improves the exploitation ability of WOA well in the unimodal function test, which benefits from the dynamic shrinking search space and opposite search properties of the IDOL strategy. In the test of complex functions, especially the hybrid and composition functions based on benchmark functions, EWOA can obtain more competitive results. The reason is that once a better solution cannot be found in the prey search stage, in the later stage of the iteration, the exploitation-based WOA will shrink the population to the vicinity of the optimal solution obtained in the previous stage. It is easy to get stuck in a local optimum. Differently, EWOA introduces AIW strategy to improve this phenomenon in the stage of encircling the prey. Groups that are far away from the current prey correspond to a smaller weight value, that is, they are less affected by the current prey to improve the diversity of the group, while groups that are close to the current prey correspond to a larger weight value and continue to maintain inertial encirclement. In addition, during the proposed IDOL generation jump stage, the appropriate mode is adaptively switched according to the current number of convergence stagnation to better balance exploration and exploitation. According to the overall data, EWOA adopts AIW and IDOL strategies to significantly improve the ability of exploration and exploitation, and has stronger global search ability, especially on the test of the most complex composition functions. EWOA can also significantly outperform WOA variants and other classical heuristics as well as some of their advanced variants.

Convergence analysis

Table 8 shows the comparison result (SP) of the algorithm convergence speed measured by the successful performance. The index is taken from [73] and is defined as the average FES and success rate (SR) of successful operations. SR is the ratio of successful runs when algorithms reache the value-to-reach (VTR) to the total number of runs. The SP value of the two algorithms and the algorithm’s convergence speed determine relative SP (RSP). Among all the expriments on F1–F16, the dimension is set to 30, and the VTR is set to $10^{-8}$.

Table 8 Comparison of the convergence speed of algorithms

Table 8 indicates that EWOA has the most vital ability to reach the theoretically optimal solution. The 10/16 test function can reach 100% to obtain the optimal solution, and the average success rate of all test functions is also the highest. At the same time, by comparing the iteration numbers needed for achieving the average optimal solution, it can be found that in the tests of functions other than F11, the number of iterations required by the comparison algorithm is mostly greater than that of EWOA, which shows that EWOA has faster convergence rate.

Fig. 4

Convergence trends of EWOA and advanced algorithms for some selected unimodal/multimodal/fixed dimension functions

Fig. 5

Convergence trends of EWOA and advanced algorithms for some selected hybrid and composition functions

Table 9 Results of the CD problem

Figures 4 and 5 illustrate the convergence trend of all compared algorithms and EWOA on the benchmark function tests. Two characteristic behaviors of EWOA can be observed in most convergence graphs. The fitness value decreases rapidly at the initial stage of the iteration, and a competitive value can be obtained at the end of the convergence. By observing the convergence of all tested functions, EWOA can converge to a small fitness faster than other algorithms at the beginning of optimization in almost most cases, which benefits from the exploration ability of IDOL through the initialization and jumping generation stages. For a special curve like F30, when EWOA encounters a convergence stagnation and mainly performs exploitation in the second half of the iteration, EWOA can still break the convergence stagnation and continue to reduce the fitness. This is because the adaptive inertia weight in AIW-based encircling prey play an important role in enabling the population to ensure diversity to escape the trap of local optima. On the other hand, from the final convergence results, EWOA gets the optimal fitness value at the end of the iteration on F1–F4, F7–F9, F15 and F16 and ranks among the top three on F5–F6, F10–12 and F14. For the tests on hybrid and the composite functions F18, F23–F25 and F27–F30, EWOA has the best final convergence results. The significant advantage of the final converged results reflects the EWOA algorithm’s ability to balance exploration and exploitation well. It benefits from IDOL’s enhancements in exploration and exploitation modes and corresponding adaptive switching rules.

Engineering problems experiments

To verify the effectiveness of EWOA when solving engineering constraint optimization problems, the EWOA and nine other algorithms including WOA, OWOA, IWOA, LWOA, RDWOA, SA, SCA, cfPSO [74] and SaDE [75] are applied to three well known standard engineering problems which are optimization design problems of tension/compression spring, cantilever beam and infinite impulse response (IIR) filter. Among them, the IIR filter design is a continuous optimization problem while the rest are constrained problems. A general death penalty function is used to deal with these constraints so that the algorithm automatically discards infeasible solutions during the optimization process. When solving these engineering optimization problems, each algorithm runs independently 30 times to select the best optimization design result.

Cantilever design problem

The structural cantilever design problem (CD) [76] is to minimize the weight of cantilever beams. A cantilever beam is composed of five hollow blocks, a variable represents each hollow block and the thickness is constant. Therefore, the problem has 5 design variables and 1 vertical displacement constraint.

$$\begin{aligned} \textit{Consider}\,\, \mathbf {x}= & {} \left[ {{x_1}\;\;{x_2}\;\;{x_3}\;{} \;{x_4}\;{} \;{x_5}} \right] ,\nonumber \\ \textit{Minimize}\,\, f\left( {\mathbf {x}} \right)= & {} 0.6224\left( {{x_1} + {x_2} + {x_3} + {x_4} + {x_5}} \right) ,\nonumber \\ \textit{Subject}\,\, {g_1}\left( {\mathbf {x}} \right)= & {} 61 / x_1^3 + 37 / x_2^3 + 19 / x_3^3\nonumber \\&+ 7 / x_4^3 + 1 / x_5^3 \le {1}.\nonumber \\ \textit{Variable ranges}\,\, 0.01\le & {} {x_1},{x_2},{x_3},{x_4},{x_5} \le 100. \qquad \nonumber \\ \end{aligned}$$

(23)

The results of the CD problem are depicted in Table 9, EWOA obtains the optimal when the five parameters are set to 6.2079, 4.8906, 4.4663, 3.7409, 2.4098 and outperforms other algorithms.

Tension/compression spring design problem

The purpose of the Tension/Compression Spring Design (TCSD) problem is to design a spring with the lightest weight [77]. This design includes three design variables: the wire diameter (d), the mean coil diameter (D) and the length (or number of coils) (N), and needs to meet the four constraints of deflection, shear stress, variable frequency and refractive index. The mathematical model of this problem is as follows:

Table 10 Results of the TCSD problem

Table 11 Results of the IIR problem

$$\begin{aligned}&Consider\quad \mathbf {x} = \left[ {{x_1}\;\;{x_2}\;\;{x_3}} \right] = \left[ {d\;\;D\;\;N} \right] ,\nonumber \\&Minimize\quad f\left( {\mathbf {x}} \right) = \left( {{x_3} + 2} \right) {x_2}x_1^2,\nonumber \\&Subject \quad {g_1}\left( {\mathbf {x}} \right) = 1 - \frac{{x_2^3{x_3}}}{{71785x_1^4}} \le 0,\nonumber \\&{g_2}\left( {\mathbf {x}} \right) = \frac{{4x_2^2 - {x_1}{x_2}}}{{12566\left( {{x_2}x_1^3 - x_1^4} \right) }}\nonumber \\&+ \frac{1}{{5108x_1^2}}-1 \le 0,\nonumber \\&{g_3}\left( {\mathbf {x}} \right) = 1 - \frac{{140.45{x_1}}}{{x_2^2{x_3}}} \le 0,\nonumber \\&{g_4}\left( {\mathbf {x}} \right) = \frac{{{x_1} + {x_2}}}{{1.5}} - 1 \le 0\nonumber \\&Variable \,ranges\quad 0.05 \le {x_1} \le 2.00,\nonumber \\&0.25 \le {x_2} \le 1.30,\nonumber \\&2.00 \le {x_3} \le 15.0. \end{aligned}$$

(24)

The results of EWOA are compared with other solutions and reported in Table 10. EWOA can generate the optimum cost of 0.012670417 when d, D and N are set to 0.0522, 0.3678 and 10.6985, which is superior to all other algorithms.

Infinite impulse response filter design problem

IIR filters have been widely used in system identification. When the process model is unknown or more complex, the simple finite impulse response (FIR) adaptive filter may not be able to fit the real model accurately. In these cases, it is natural to use IIR adaptive filters to model unknown systems [78]. In terms of system identification, when the filter order is determined, the key task is to configure appropriate filter parameters to minimize the difference between the filter and the real system output value. In this section, a fourth-order IIR is used to model a superior-order plant. The unknown plant and the IIR model hold the following transfer functions [79]:

$$\begin{aligned} H_{p}\left( z^{-1}\right)= & {} \frac{1-0.4 z^{-2}-0.65 z^{-4}+0.26 z^{-6}}{1-0.77 z^{-2}-0.8498 z^{-4}+0.6486 z^{-6}} \nonumber \\ H_{M}\left( z^{-1}\right)= & {} \frac{b_{0}+b_{1} z^{-1}+b_{2} z^{-2}+b_{3} z^{-3}+b_{4} z^{-4}}{1+a_{1} z^{-1}+a_{2} z^{-2}+a_{3} z^{-3}+a_{4} z^{-4}} \end{aligned}$$

(25)

These nine design variables are the simplest form of the transfer function of the fourth-order IIR model, which are represented by $a_{1}, a_{2}, a_{3}, a_{4}, b_{0}, b_{1}, b_{2}, b_{3}, b_{4} .$ The white noise sequence is taken as the input of the system u(t) and set 100 sample cases. d(t) and y(t) represent the output of the actual system and IIR model respectively.

$$\begin{aligned}&Consider\quad \mathbf {x}=\left[ a_{1} \;\; a_{2} \;\; a_{3} \;\; a_{4} \;\; b_{0} \;\; b_{1} \;\; b_{2} \;\; b_{3} \;\; b_{4}\right] ,\nonumber \\&Minimize\quad f(\mathbf {x})=\frac{1}{100} \sum _{t=1}^{100}(d(t)-y(t))^{2}, \nonumber \\&Variable\;ranges\quad -1 \le a_{1}, a_{2}, a_{3}, a_{4}, b_{0}, b_{1}, b_{2}, b_{3}, b_{4} \le 1 ,\nonumber \\&Where\;\quad u(t) \sim N(0,1),\nonumber \\&d(t)= 0.77 d(t-2)+0.8498 d(t-4) \nonumber \\&\quad +0.6486 d(t-6)+u(t)-0.4 u(t-2)\nonumber \\&\quad -0.65 u(t-4)+0.26 u(t-6) ,\nonumber \\&y(t)=\sum _{i=1}^{4} a_{i} \cdot y(t-i)+\sum _{j=0}^{4} b_{j} \cdot u(t-j).\nonumber \\ \end{aligned}$$

(26)

Statistics of the best solution data obtained by 10 algorithms in solving the IIR design problem is depicted in Table 11. It can be observed that EWOA can obtain the optimal fitting residual of 0.00105, which is lower than other algorithms.

According to the above engineering problems’ optimization results, EWOA can get the best optimal results in the CD, TCSD and IIR problems. It means that the optimal value of EWOA is better than WOA and its variants under the same iterative conditions. In optimizing specific engineering problems, EWOA is also competitive with other classic and advanced optimization algorithms.

Conclusion

This paper proposes an enhanced WOA (EWOA), which uses new IDOL and AIW strategies to overcome the problems encountered by canonical WOA, including the balance between exploitation and exploration, and easy to fall into local optima. Both IDOL and AIW strategies’ mechanisms to improve EWOA are presented in detail. In the proposed EWOA, IDOL plays an important role in population initialization and generation stages. This strategy is inspired by DOL, which not only has the characteristics of asymmetric and dynamically adjusting, but also works better in balancing exploration and exploitation. Inside IDOL, two modes are instructed to enhance the performance of exploration and exploitation, and the adaptive switching rules can choose the appropriate mode according to convergence situation. In another improvement method AIW, the inertia weight can be adaptively adjust referring to the current agents’ fittness, which increases the diversity of population in exploitation stage of EWOA.

The experiments consist of benchmark functions and engineering problems are used to evaluate the performance of EWOA. In combination with DOL, IDOL, AIW strategies, respectively, the inter-variants of EOWA, i.e. DOLWOA, IDOLWOA and AIWWOA’s are constructed and compared. The test results indicate that EWOA which combined with IDOL and AIW can achieve the best performance. Besides, all the combinations perform better than canonical WOA and the improvement from DOL to IDOL is significant. Canonical WOA, 3 sub-variants of EWOA and 10 advanced MAs are also for comparison, 30 functions including unimodal, multimodal, hybrid and composition are used for numerical testing to valid the exploitation, exploration and comprehensive capabilities of the EWOA. The results indicate that EWOA has consistently high performance in solving complex problems of different dimensions. Non-parametric tests’ results, i.e. Wilcoxon rank-sum tests and Friedman tests indicate that whether solving simple (F1–F16) or complex test functions (F17–F30) the comprehensive performance of EWOA is better than other algorithms. In addition to the default dimension 30, the variable dimension tests are also conducted. The test results of unimodal/multimodal functions in dimensions 10, 50, 100 indicate that EWOA outperforms other compared MAs when solving different dimensional problems. Convergence analysis depicts that the proportion of the theoretical optimal solution obtained by the EWOA is the highest and the number of iterations required for the average convergence except for individual test functions is the smallest. Besides, the engineering optimization results present that EWOA is very competitive in solving three practical engineering design problems.

Finally, there is still some potential research work to be done for IDOL and EWOA in the future. Given IDOL is first proposed and conducive to balance the exploration and exploitation, it has the potential to be extended to other MAs which suffering problem of trade-off. For the improvement of EWOA, the application of EWOA in multi-objective problems is also worth exploring.

Appendices

Appendix A

See Table 12.

Table 12 The test functions

Table 13 Results on unimodal functions F1–F6

Table 14 Results on multimodal functions F7–F11

Appendix B

See Tables 13,14,15,16 and 17.

Table 15 Results on fixed dimension functions F12–F16

Table 16 Results on hybrid functions F17–F22

Table 17 Results on composition functions F23–F30