1 Introduction

The Kerr spacetime [1,2,3,4,5,6], perhaps the pre-eminent exact solution of the Einstein equations of vacuum general relativity, is both a standard textbook exemplar [7,8,9,10,11,12,13,14], and is increasingly of central importance to both observational and theoretical astrophysics [15,16,17,18,19,20,21]. One key issue of particular importance is a full understanding of the geodesics — and the fact that despite the lack of spherical symmetry (the Kerr spacetime is merely stationary and axisymmetric, so that the Birkhoff theorem does not apply [22,23,24,25,26]), there are still a multitude of constant-r “quasi-circular” geodesics which are not confined to the equatorial plane. (Contrast, for example, the discussion in [27] with that of [28,29,30,31,32].) Sometimes these constant-r “quasi-circular” geodesics are referred to as “spherical geodesics”.

It should be noted that the non-equatorial constant-r null geodesics are particularly important tools for studying photon rings and black hole silhouettes [33,34,35,36,37,38]. Similarly non-equatorial constant-r timelike geodesics are particularly important tools for studying off-axis accretion disks and their related ISCOs and OSCOs [39,40,41,42,43].

In the current article we shall be interested is seeing how much of this qualitative structure survives once one moves away from the exact Kerr spacetime, specifically once one considers the Painlevé–Gullstrand version of the weak-field slow-rotation Lense–Thirring spacetime. The weak-field slow-rotation Lense–Thirring spacetime was originally introduced in 1918 [44, 45], while the current authors have recently introduced, and extensively explored, a novel Painlevé–Gullstrand variant [46,47,48,49,50,51] of the Lense–Thirring spacetime [52,53,54]. We shall soon see that the generic situation is as pictured in Fig. 1. The key physical reason underpinning the existence of these constant-r geodesics comes from the fact that the Kerr, Schwarzschild, and Painlevé–Gullstrand–Lense–Thirring spacetimes all possess a non-trivial Killing tensor and associated Carter constant.

Fig. 1
figure 1

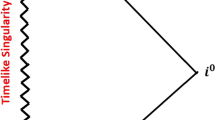
Schematic depiction of the generic situation, where the constant-r geodesics have incommensurate azimuthal and declination frequencies, and so sweep out a surface-filling symmetric equatorial band, (a spherical zone). The width of the equatorial band is controlled by a delicate interplay between the Carter constant and the azimuthal angular momentum

Full size image

2 Basic framework

The line-element of interest is [52,53,54]:

$$\begin{aligned} {\mathrm {d}}s^2 = - {\mathrm {d}}t^2 +\left\{ {\mathrm {d}}r+\sqrt{\frac{2m}{r}} \; {\mathrm {d}}t\right\} ^2 + r^2 \left\{ {\mathrm {d}}\theta ^2+\sin ^2\theta \; \left( {\mathrm {d}}\phi - {2J\over r^3} {\mathrm {d}}t\right) ^2\right\} \ . \end{aligned}$$
(2.1)

This line-element is somewhat related to the “river” model for black holes [55] — it exhibits both unit lapse [56], and flat spatial 3-slices [52,53,54] — the presence of flat spatial 3-slices being incompatible with the exact Kerr spacetime [57,58,59,60]. Furthermore this line element possesses a non-trivial Killing tensor [53, 54]:

$$\begin{aligned} K_{ab} \; {\mathrm {d}}x^a \; {\mathrm {d}}x^b = r^4\left\{ {\mathrm {d}}\theta ^2 + \sin ^2\theta \left( {\mathrm {d}}\phi - {2J\over r^3} {\mathrm {d}}t\right) ^2 \right\} . \end{aligned}$$
(2.2)

This Killing tensor was found by applying the algorithm presented in [61,62,63]. Once found, one can easily verify that \(\nabla _{(c}K_{ab)}= K_{(ab;c)} = 0\). For any affine parameter \(\lambda \), the (generalized) Carter constant is then [53, 54]:

$$\begin{aligned} \mathcal {C}=K_{ab}\;\frac{{\mathrm {d}}x^a}{{\mathrm {d}}\lambda }\,\frac{{\mathrm {d}}x^b}{{\mathrm {d}}\lambda }=r^4\left[ \left( \frac{{\mathrm {d}}\theta }{{\mathrm {d}}\lambda }\right) ^2 + \sin ^2\theta \left( \frac{{\mathrm {d}}\phi }{{\mathrm {d}}\lambda }-\frac{2J}{r^3}\frac{{\mathrm {d}}t}{{\mathrm {d}}\lambda }\right) ^2 \right] \ . \end{aligned}$$
(2.3)

By construction \(\mathcal {C}\ge 0\). Without loss of generality we choose \(\lambda \) to be future-directed, \({\mathrm {d}}t/{\mathrm {d}}\lambda > 0\).

In addition to the Carter constant, we have three other conserved quantities. Two (the energy and azimuthal component of angular momentum) come from the time-translation and axial Killing vectors [53, 54]:

$$\begin{aligned} E= & {} \left( 1-\frac{2m}{r}-\frac{4J^2\sin ^2\theta }{r^4} \right) \frac{{\mathrm {d}}t}{{\mathrm {d}}\lambda }-\sqrt{\frac{2m}{r}}\frac{{\mathrm {d}}r}{{\mathrm {d}}\lambda }+\frac{2J\sin ^2\theta }{r}\frac{{\mathrm {d}}\phi }{{\mathrm {d}}\lambda } \ ; \end{aligned}$$
(2.4)
$$\begin{aligned} L= & {} r^2\sin ^2\theta \frac{{\mathrm {d}}\phi }{{\mathrm {d}}\lambda } -\frac{2J\sin ^2\theta }{r}\frac{{\mathrm {d}}t}{{\mathrm {d}}\lambda } \ . \end{aligned}$$
(2.5)

The final conserved quantity, the “mass-shell constraint”, \(\epsilon \in \{0,-1\}\) for null and timelike geodesics respectively, comes from the trivial Killing tensor (the metric):

$$\begin{aligned} \begin{aligned} \epsilon =g_{ab}\frac{{\mathrm {d}}x^a}{{\mathrm {d}}\lambda }\frac{{\mathrm {d}}x^b}{{\mathrm {d}}\lambda }=&-\left( \frac{{\mathrm {d}}t}{{\mathrm {d}}\lambda }\right) ^2+\left( \frac{{\mathrm {d}}r}{{\mathrm {d}}\lambda }+\sqrt{\frac{2m}{r}}\frac{{\mathrm {d}}t}{{\mathrm {d}}\lambda }\right) ^2\\&+ r^2\left[ \left( \frac{{\mathrm {d}}\theta }{{\mathrm {d}}\lambda }\right) ^2+\sin ^2\theta \left( \frac{{\mathrm {d}}\phi }{{\mathrm {d}}\lambda }-\frac{2J}{r^3}\frac{{\mathrm {d}}t}{{\mathrm {d}}\lambda }\right) ^2\right] \ . \end{aligned} \end{aligned}$$
(2.6)

Simplify these four conserved quantities by re-writing them as follows [53, 54]:

$$\begin{aligned} L= & {} r^2\sin ^2\theta \left( \frac{{\mathrm {d}}\phi }{{\mathrm {d}}\lambda }-\frac{2J}{r^3}\frac{{\mathrm {d}}t}{{\mathrm {d}}\lambda }\right) \ ; \end{aligned}$$
(2.7)
$$\begin{aligned} \mathcal {C}= & {} r^4\left( \frac{{\mathrm {d}}\theta }{{\mathrm {d}}\lambda }\right) ^2 +{L^2\over \sin ^2\theta } \ ; \end{aligned}$$
(2.8)
$$\begin{aligned} \epsilon= & {} -\left( \frac{{\mathrm {d}}t}{{\mathrm {d}}\lambda }\right) ^2+\left( \frac{{\mathrm {d}}r}{{\mathrm {d}}\lambda }+\sqrt{\frac{2m}{r}}\frac{{\mathrm {d}}t}{{\mathrm {d}}\lambda }\right) ^2 +{\mathcal {C}\over r^2} \ ; \end{aligned}$$
(2.9)
$$\begin{aligned} E= & {} \left( 1-\frac{2m}{r}\right) \frac{{\mathrm {d}}t}{{\mathrm {d}}\lambda } - \sqrt{\frac{2m}{r}}\frac{{\mathrm {d}}r}{{\mathrm {d}}\lambda } + \frac{2J}{r^3}L \ . \end{aligned}$$
(2.10)

In particular \(L^2 \le \mathcal {C}\). For (generic) geodesic trajectories we have [53, 54]:

$$\begin{aligned}&\frac{{\mathrm {d}}r}{{\mathrm {d}}\lambda }= S_r \sqrt{X(r)} \ ; \end{aligned}$$
(2.11)
$$\begin{aligned}&\frac{{\mathrm {d}}t}{{\mathrm {d}}\lambda }= \frac{E-2JL/r^3+ S_r \sqrt{(2m/r)X(r)}}{(1-2m/r)} \ ; \end{aligned}$$
(2.12)
$$\begin{aligned}&\frac{{\mathrm {d}}\theta }{{\mathrm {d}}\lambda }= S_{\theta }\frac{\sqrt{\mathcal {C}-L^2/\sin ^2\theta }}{r^2} \ ; \end{aligned}$$
(2.13)
$$\begin{aligned}&\frac{{\mathrm {d}}\phi }{{\mathrm {d}}\lambda }= \frac{L}{r^2\sin ^2\theta } + 2J\; \frac{E-2JL/r^3 + S_{\phi }\sqrt{(2m/r)X(r)}}{r^3(1-2m/r)} \ . \end{aligned}$$
(2.14)

Here

$$\begin{aligned} S_r= & {} \left\{ \begin{array}{rl} +1 &{} \qquad \text{ outgoing } \text{ geodesic } \\ -1 &{} \qquad \text{ ingoing } \text{ geodesic } \end{array}\right. \ ; \end{aligned}$$
(2.15)
$$\begin{aligned}&\nonumber \\ S_{\theta }= & {} \left\{ \begin{array}{rl} +1 &{} \qquad \text{ increasing } \text{ declination } \text{ geodesic } \\ -1 &{} \qquad \text{ decreasing } \text{ declination } \text{ geodesic } \end{array}\right. \ ; \end{aligned}$$
(2.16)
$$\begin{aligned}&\nonumber \\ S_{\phi }= & {} \left\{ \begin{array}{rl} +1 &{} \qquad \text{ prograde } \text{ geodesic } \\ -1 &{} \qquad \text{ retrograde } \text{ geodesic } \end{array}\right. \ . \end{aligned}$$
(2.17)

Furthermore X(r) is explicitly given by the sextic Laurent polynomial:

$$\begin{aligned} X(r) =\left( E - \frac{2JL}{r^3}\right) ^2-\left( 1-\frac{2m}{r}\right) \left( -\epsilon + \frac{\mathcal {C}}{r^2}\right) \ ; \quad \lim _{r\rightarrow \infty } X(r) = E^2+\epsilon \ .\qquad \end{aligned}$$
(2.18)

In terms of the roots of this polynomial we can in the generic case write

$$\begin{aligned} X(r) = {E^2+\epsilon \over r^6} \;\prod _{i=1}^6 (r-r_i) \ . \end{aligned}$$
(2.19)

We shall now restrict attention to the constant-r orbits, \(r\rightarrow r_0\).

3 Location of possible constant-r geodesics

First let us analyze the lack of radial motion; this is not entirely trivial.

3.1 Generalities

Fix our r coordinate to take some fixed value \(r=r_0\). Hence, since \({\mathrm {d}}r/{\mathrm {d}}\lambda = S_r \sqrt{X(r)}\), we must have \(X(r_0)=0\). Furthermore, using the chain rule and the fact that \(S_r^2=+1\), we have

$$\begin{aligned} {{\mathrm {d}}^2r\over {\mathrm {d}}\lambda ^2}= S_r\,{{\mathrm {d}}\sqrt{X(r)}\over {\mathrm {d}}\lambda } = {1\over 2}\; X'(r) \ . \end{aligned}$$
(3.1)

So to remain at \(r_0\) we must also have \(X'(r_0)=0\). The two conditions

$$\begin{aligned} X(r_0)=0 \qquad \hbox {and} \qquad X'(r_0)=0 \end{aligned}$$
(3.2)

imply that \(r_0\) is a repeated root of X(r). The existence of a repeated root will put some constraint on the four geodesic constants E, L, \(\epsilon \), and \(\mathcal {C}\), (and the spacetime parameters m and J); they cannot all be functionally independent.

Higher derivatives do not lead to extra constraints, since

$$\begin{aligned}&{{\mathrm {d}}^3r\over {\mathrm {d}}\lambda ^3} = S_r\,{1\over 2} X''(r) \sqrt{X(r)} \ ; \end{aligned}$$
(3.3)
$$\begin{aligned}&{{\mathrm {d}}^4r\over {\mathrm {d}}\lambda ^4} = \left\{ {1\over 2} X'''(r) X(r) + {1\over 4} X''(r) X'(r)\right\} \ , \end{aligned}$$
(3.4)

and one sees inductively that all terms in all higher-order derivatives contain either \(\sqrt{X(r)}\) or \(X'(r)\) as a factor; quantities which we have already seen vanish at \(r\rightarrow r_0\). Finally we note that stability of the constant-r orbit is determined by considering

$$\begin{aligned} {{\mathrm {d}}\over {\mathrm {d}}r} \left( {{\mathrm {d}}^2r\over {\mathrm {d}}\lambda ^2}\right) = {1\over 2} \; X''(r) \ . \end{aligned}$$
(3.5)

Thence if \(X''(r_0) >0\) the constant-r orbit is unstable, if \(X''(r_0) =0\) the constant-r orbit is marginal, and if \(X''(r_0) <0\) the constant-r orbit is stable. So we are interested in evaluating \({\mathrm {sign}}\left( X''(r_0)\right) \). Let us now see what more we can say about the radial location of possible constant-r (“quasi-circular”) orbits.

3.2 Constant-r null geodesics

For massless particles following null geodesics we have \(\epsilon \rightarrow 0\), and without any loss of generality we can set \(E\rightarrow 1\). That implies that we can write

$$\begin{aligned} X(r)= & {} \left( 1 - \frac{2JL}{r^3}\right) ^2-\left( 1-\frac{2m}{r}\right) \frac{\mathcal {\mathcal {C}}}{r^2} \end{aligned}$$
(3.6)
$$\begin{aligned}= & {} {r^6 - \mathcal {C}r^4 +2(\mathcal {C}m-2 JL) r^3 + 4 J^2 L^2\over r^6}\ , \end{aligned}$$
(3.7)

while

$$\begin{aligned} X'(r) =2\; \frac{\mathcal {C}r^4 - 3(\mathcal {C}m-2JL)r^3 - 12 J^2 L^2 }{r^7} \ , \end{aligned}$$
(3.8)

and

$$\begin{aligned} X''(r) =6\; \frac{-\mathcal {C}r^4 + 4(\mathcal {C}m-2JL) r^3+28 J^2 L^2}{r^8} \ . \end{aligned}$$
(3.9)

Thence we are interested in simultaneously solving

$$\begin{aligned}&r_0^6 - \mathcal {C}r_0^4 +2(\mathcal {C}m-2 JL) r_0^3 + 4 J^2 L^2 =0\ ; \end{aligned}$$
(3.10)
$$\begin{aligned}&\mathcal {C}r_0^4 - 3(\mathcal {C}m-2JL)r_0^3-12 J^2 L^2 =0\ , \end{aligned}$$
(3.11)

and evaluating the sign of \(X''(r_0)\):

$$\begin{aligned} {\mathrm {sign}}\left( {X''(r_0)}\right) = {\mathrm {sign}}\left( { -\mathcal {C}r_0^4 + 4(\mathcal {C}m-2JL) r_0^3 + 28 J^2 L^2}\right) \ . \end{aligned}$$
(3.12)

The non-negativity of \(\mathcal {C}\ge 0\), applied to \(X(r_0)=0\), from Eq. (3.6) immediately implies that \(r_0 \ge 2m\). We also recall that \(L^2 \le \mathcal {C}\). The four quantities \(\mathcal {C}\), m, JL, and \(r_0\), are subject to two constraints, so only two of these four quantities are functionally independent. More on this point below.

Since we are interested in the sign of \(X''(r_0)\) at a location where \(X'(r_0)=0\), we can use that extra information to deduce

$$\begin{aligned} {\mathrm {sign}}\left( X''(r_0)\right) = {\mathrm {sign}}\left( \mathcal {C}r_0^4 + 36 J^2 L^2\right) = +1 \ . \end{aligned}$$
(3.13)

Thus there are no stable constant-r null geodesics. (And, as we shall soon see, there are no marginal constant-r null geodesics either, all of the constant-r null geodesics are unstable.)

Let us now consider several special case solutions to the radial part of the constant-r null geodesic conditions, \(X(r_0)=0=X'(r_0)\):

  1. (i)

    If \(JL=0\), corresponding either to a non-rotating source, or to a zero angular momentum geodesic (ZAMO), then one has the unique unstable constant-r null geodesic:

    $$\begin{aligned} r_0 = 3m; \qquad \mathcal {C}= 27 m^2; \qquad X''(r_0) = {2\over 3 m^2} = {6\over r_0^2} > 0. \end{aligned}$$
    (3.14)

    This is the situation familiar from Schwarzschild spacetime; an unstable photon orbit at \(r=3m\).

  2. (ii)

    If \(\mathcal {C}=0\), then \(L=0\), and there are no constant-r null orbits.

  3. (iii)

    If \(r_0=2m\) then this implies \(\mathcal {C}=0\). This is a sub-case of (ii) above.

  4. (iv)

    If \(r_0=3m\) then: either \(JL=0\) which is a sub-case of (i) above, or \(\mathcal {C}=0\) which is a sub-case of (ii) above.

  5. (v)

    If \(r_0= \root 3 \of {2JL}\ne 0\) then \(\mathcal {C}<0\), which is non-viable, and there are no constant-r null orbits.

  6. (vi)

    The generic case is \(JL\ne 0\), \(\mathcal {C}>0\) and \(2m < r_0 \not \in \{3m, \root 3 \of {2JL}\}\).

Now let us consider the generic case:

Treat m and \(r_0\) as the two independent variables; then we can explicitly solve for \(\mathcal {C}(m,r_0)\) and \(2JL(m,r_0)\). Let us proceed as follows: If \(JL\ne 0\) then first solve \(X'(r_0)=0\) to find \(\mathcal {C}(JL,m, r_0)\). We find

$$\begin{aligned} \mathcal {C}(JL,m, r_0) = {6(r_0^3-2JL) JL\over r_0^3 (3m-r_0)} \ne 0\ . \end{aligned}$$
(3.15)

Using this value of \(\mathcal {C}(JL,m, r_0)\), solve \(X(r_0)=0\) for \(2JL(m, r_0)\):

$$\begin{aligned} 2JL(m, r_0) = -{r_0^3\over 2}\, {(r_0-3m)\over (2r_0-3m)} . \end{aligned}$$
(3.16)

Third, substitute these values of \(JL(m, r_0)\) back into \(\mathcal {C}(JL,m, r_0)\) to yield \(\mathcal {C}(m, r_0)\):

$$\begin{aligned} \mathcal {C}(m, r_0) =9r_0^3\;{(r_0-2m)\over (2r_0-3m)^2} \ . \end{aligned}$$
(3.17)

Since we must always have \(\mathcal {C}> 0\) this limits the generic constant-r photon orbits to the range \(r_0 \in (2m,\infty )\). Finally, inserting this back into \(X''(r_0)\) we see:

$$\begin{aligned} X''(r_0) = {18\over r_0^2} \; {2(r_0-2m)^2+m^2\over (2r_0-3m)^2} >0. \end{aligned}$$
(3.18)

Since \(X''(r_0)>0\), we again see that all of these constant-r photon orbits are unstable. That is, instead of just having one unstable photon orbit at \(r=3m\), once we allow \(JL\ne 0\) we can arrange unstable photon orbits at arbitrary \(r_0 \in (2m,\infty )\).

3.3 Constant-r timelike geodesics

For massive particles following timelike geodesics \(\epsilon \rightarrow -1\), and E is unconstrained. That implies that we can write

$$\begin{aligned} X(r)= & {} \left( E - \frac{2JL}{r^3}\right) ^2-\left( 1-\frac{2m}{r}\right) \left( 1+\frac{\mathcal {\mathcal {C}}}{r^2}\right) \ ; \end{aligned}$$
(3.19)
$$\begin{aligned} X'(r)= & {} {12JL\over r^4}\left( E - \frac{2JL}{r^3}\right) + {2\mathcal {C}(r-3m)\over r^4} -{2m\over r^2}; \end{aligned}$$
(3.20)
$$\begin{aligned} X''(r)= & {} -{24JL\over r^5}\left( 2E-\frac{7JL}{r^3}\right) - {6\mathcal {C}(r-4m)\over r^5} +{4m\over r^3}. \end{aligned}$$
(3.21)

Rewrite this as

$$\begin{aligned} X(r)= & {} {(E^2-1)r^6 +2mr^5 - \mathcal {C}r^4 +2(\mathcal {C}m -2EJL) r^3+4J^2L^2 \over r^6} \ ; \end{aligned}$$
(3.22)
$$\begin{aligned} X'(r)= & {} - 2 \; {mr^5 -\mathcal {C}r^4 +3(\mathcal {C}m- 2 EJL) r^3 +12 J^2 L^2 \over r^7}; \end{aligned}$$
(3.23)
$$\begin{aligned} X''(r)= & {} 2 \; {2mr^5 -3\mathcal {C}r^4 +12(\mathcal {C}m- 2 EJL) r^3 +84 J^2 L^2\over r^8}. \end{aligned}$$
(3.24)

As before we are interested in solving \(X(r_0)=0=X'(r_0)\), and determining the sign of \(X''(r_0)\). So we are interested in studying

$$\begin{aligned}&(E^2-1)r^6 +2mr^5 - \mathcal {C}r^4 +2(\mathcal {C}m -2EJL) r^3+4J^2L^2=0; \end{aligned}$$
(3.25)
$$\begin{aligned}&mr^5 -\mathcal {C}r^4 +3(\mathcal {C}m- 2 EJL) r^3 +12 J^2 L^2 =0; \end{aligned}$$
(3.26)
$$\begin{aligned}&{\mathrm {sign}}\{2mr^5 -3\mathcal {C}r^4 +12(\mathcal {C}m- 2 EJL) r^3 +84 J^2 L^2\}. \end{aligned}$$
(3.27)

The five quantities E, \(\mathcal {C}\), m, JL, and \(r_0\) are subject to two constraints, so only three of these quantities can be functionally independent. The positivity of \((1+\mathcal {C}/r^2)>0\), applied to \(X(r_0)=0\), immediately implies \(r_0 \ge 2m\). There are several ways of proceeding.

Let us now consider several special case solutions to \(X(r_0)=0=X'(r_0)\):

  1. (i)

    If \(JL=0\), corresponding either to a non-rotating source, or to a zero angular momentum geodesic (ZAMO), then for constant-r orbits one has:

    $$\begin{aligned} \mathcal {C}= {mr_0^2\over r_0-3m} ; \qquad E^2 = {(r_0-2m)^2\over r_0(r_0-3m)}; \end{aligned}$$
    (3.28)

    and

    $$\begin{aligned} X''(r_0) = -{2m\over r_0^3} \; {r_0-6m\over r_0-3m}. \end{aligned}$$
    (3.29)

    Positivity of \(\mathcal {C}\) and/or \(E^2\) implies \(r_0\ge 3m\), and \(X''(r_0)\) changes sign at \(r_0=6m\). This is the situation familiar from Schwarzschild spacetime; an ISCO at \(r=6m\), stable orbits for \(r_0\in (6m,\infty )\), and unstable orbits for \(r_0\in (3m,6m)\). Note that for these constant-r orbits \(E<1\) for \(r_0>4m\), \(E=1\) for \(r_0=4m\), and \(E>1\) for \(r_0\in (3m,4m)\). Indeed \(E\rightarrow \infty \) as \(r_0\rightarrow (3m)^+\).

  2. (ii)

    If \(\mathcal {C}=0\), then automatically \(L=0\), and there is no consistent solution.

  3. (iii)

    If \(r_0<2m\) then \(X(r_0)\) is a sum of positive and non-negative terms, so there is no consistent solution.

  4. (iv)

    If \(r_0=2m\), then from \(X(r_0)=0\) we have \(E = JL/(4 m^2)\), but then from \(X'(r_0)=0\) we have \(\mathcal {C}=- 4 m^2 <0\), and so there is no consistent solution.

  5. (v)

    If \(r_0= \root 3 \of {2JL/E}\ne 0\) and \(r_0> 2m\) then \(X(r_0)=0\) implies \(1+\mathcal {C}/r_0^2=0\), so that \(\mathcal {C}=-r_0^2<0\) and there is no consistent solution.

  6. (vi)

    The generic case is \(JL\ne 0\), \(\mathcal {C}>0\) and \(2m < r_0 \ne \root 3 \of {2JL/E}\).

Now consider the general case:

Choose the three independent variables to be m, E, and \(r_0\). Let us solve for \(\mathcal {C}(m,E,r_0)\) and \(JL(m,E,r_0)\). First take linear combinations of (3.25) and (3.26) to obtain:

$$\begin{aligned} 3 (E^2-1) r_0^3 +5m r_0^2 - \mathcal {C}(2r_0 -3m) -6 E J L=0; \end{aligned}$$
(3.30)
$$\begin{aligned} 3 (E^2-1) r_0^6 +4m r_0^5 - \mathcal {C}r_0^4 -12 J^2 L^2=0. \end{aligned}$$
(3.31)

Solve the first of these equations for \(\mathcal {C}\) to find

$$\begin{aligned} \mathcal {C}(JL,m,E,r_0) = {3(E^2-1)r_0^3 + 5m r_0^2 - 6 EJL \over 2r_0-3m} \end{aligned}$$
(3.32)

Inserting this back into the second equation and solving for JL one finds

$$\begin{aligned} JL(m,E,r_0) = {\left( Er_0^2 \pm (r_0-2m) \sqrt{r_0\{[9E^2-8]r_0 +12m\}} \right) r_0^2\over 4 (2r_0-3m)} . \end{aligned}$$
(3.33)

Since JL must be real one in turn deduces \(E^2> {8\over 9} -{4m\over 3 r_0}> {2\over 9}\). However, the sign of JL is not constrained; so both roots (±) are valid.

Inserting this back into \(\mathcal {C}(JL,m,E,r_0)\) we see

$$\begin{aligned} \mathcal {C}(m;E,r_0)= & {} { (9E^2-12)r_0^4 -2(9E^2-19)m r_0^3 - 30 m^2 r_0^2 \over 2 (2r_0-3m)^2} \nonumber \\&\pm {3Er_0^2(r_0-2m)\sqrt{r_0\{[9E^2-8]r_0 +12m\}} \over 2 (2r_0-3m)^2}. \end{aligned}$$
(3.34)

The reality conditions for \(\mathcal {C}(m;E,r_0)\) are the same as they were for \(JL(m;E,r_0)\), that is, \(E^2> {8\over 9} -{4m\over 3 r_0}> {2\over 9}\). To enforce positivity of \(\mathcal {C}(m;E,r_0)\), both roots (±) are acceptable when \(E^2 \le {(3r_0-5m)^2\over 9r_0(r_0-2m)}\), but only the + root is acceptable outside this range.

Then to determine stability one must determine the sign of:

$$\begin{aligned} X''(m; E,r_0)= & {} {18E^2(3 r_0^2-10mr_0+9m^2)\over r_0^2(2r_0-3m)^2} -{2(12 r_0^2-37mr_0+30m^2)\over r_0^3(2r_0-3m)} \nonumber \\&\mp {6E(r_0-2m)\sqrt{r_0\{[9E^2-8]r_0 +12m\}} \over r_0^2 (2r_0-3m)^2}. \end{aligned}$$
(3.35)

That is:

$$\begin{aligned} {\mathrm {sign}}\left( X''(m; E,r_0)\right)= & {} {\mathrm {sign}}\Big \{ {18E^2(3 r_0^2-10mr_0+9m^2)r_0} \nonumber \\&-{2(12 r_0^2-37mr_0+30m^2)(2r_0-3m)} \nonumber \\&\mp {6Er_0(r_0-2m)\sqrt{r_0\{[9E^2-8]r_0 +12m\}}}\Big \}. \end{aligned}$$
(3.36)

In short, there will be many constant-r orbits, but determining the stability of these constant-r orbits as functions of the independent parameters \((m,E,r_0)\) will be extremely tedious.

4 General angular motion for constant-r orbits

Now that we have investigated acceptable values of the parameters \(\{\mathcal {C},JL,E,m\}\) and the radius \(r_0\) for constant-r orbits, we note that two of the the four constants of the motion reduce to

$$\begin{aligned} \epsilon= & {} -\left( 1-\frac{2m}{r_0} \right) \left( \frac{{\mathrm {d}}t}{{\mathrm {d}}\lambda }\right) ^2 +{\mathcal {C}\over r_0^2} \ ; \end{aligned}$$
(4.1)
$$\begin{aligned} E= & {} \left( 1-\frac{2m}{r_0}\right) \frac{{\mathrm {d}}t}{{\mathrm {d}}\lambda } + \frac{2JL}{r^3_0} \ . \end{aligned}$$
(4.2)

Thence for the constant-r geodesic trajectories

$$\begin{aligned}&\frac{{\mathrm {d}}r}{{\mathrm {d}}\lambda }= 0 = \frac{{\mathrm {d}}^2 r}{{\mathrm {d}}\lambda ^2}; \end{aligned}$$
(4.3)
$$\begin{aligned}&\frac{{\mathrm {d}}t}{{\mathrm {d}}\lambda }= \frac{E-2JL/r_0^3}{(1-2m/r_0)} \ ; \end{aligned}$$
(4.4)
$$\begin{aligned}&\frac{{\mathrm {d}}\theta }{{\mathrm {d}}\lambda }= S_{\theta }\frac{\sqrt{\mathcal {C}-L^2/\sin ^2\theta }}{r_0^2} \ ; \end{aligned}$$
(4.5)
$$\begin{aligned}&\frac{{\mathrm {d}}\phi }{{\mathrm {d}}\lambda }= \frac{L}{r_0^2\sin ^2\theta } + {2J\over r_0^3} \; \frac{E-2JL/r_0^3}{(1-2m/r_0)} \ . \end{aligned}$$
(4.6)

We immediately see that t is an affine parameter, that the declination \(\theta (\lambda )\) evolves independently of the azimuth \(\phi (\lambda )\), and that the azimuthal motion depends on a constant drift and a fluctuating term driven by the declination. Note that the angular motion is qualitatively unaffected by the difference between timelike and null.

5 Declination for constant-r orbits (\(L\ne 0\))

Consider the ODE controlling the evolution of the declination \(\theta (\lambda )\).

5.1 Forbidden declination range

The form of the Carter constant, Eq. (2.8), gives a range of forbidden declination angles for any given, non-zero values of \(\mathcal {C}\) and L. We require that \({\mathrm {d}}\theta /{\mathrm {d}}\lambda \) be real, and from Eq. (2.8) this implies the following requirement:

$$\begin{aligned} \left( r^2\frac{{\mathrm {d}}\theta }{{\mathrm {d}}\lambda }\right) ^2=\mathcal {C}-\frac{L^2}{\sin ^2\theta }\ge 0 \quad \Longrightarrow \quad \sin ^2 \theta \ge {L^2\over \mathcal {C}} \ . \end{aligned}$$
(5.1)

Then provided \(\mathcal {C}\ge L^2\), which is automatic in view of (2.8), we can define a critical angle \(\theta _* \in [0,\pi /2]\) by setting

$$\begin{aligned} \theta _* = \sin ^{-1}(|L|/\sqrt{\mathcal {C}}) \ . \end{aligned}$$
(5.2)

Then the allowed range for \(\theta \) is the equatorial band:

$$\begin{aligned} \theta \in \Big [ \theta _*, \pi -\theta _*\Big ] \ . \end{aligned}$$
(5.3)

  • For \(L^2=\mathcal {C}\) we have \(\theta =\pi /2\); the motion is restricted to the equatorial plane.

  • For \(L=0\) with \(\mathcal {C}>0\) the range of \(\theta \) is a priori unconstrained; \(\theta \in [0,\pi ]\).

  • For \(L=0\) with \(\mathcal {C}=0\) the declination is fixed \(\theta (\lambda )=\theta _{0}\), and the motion is restricted to a constant declination conical surface.

5.2 Evolution of the declination

As regards the declination angle \(\theta \), from Eq. (4.5), we find

$$\begin{aligned} \frac{{\mathrm {d}}\cos \theta }{{\mathrm {d}}\lambda }= & {} -S_{\theta } {\sqrt{\mathcal {C}\sin ^2 \theta -L^2}\over r_0^2} \nonumber \\= & {} -S_{\theta }\frac{\sqrt{\mathcal {C}}}{r_0^2}\sqrt{\sin ^2\theta -\sin ^2\theta _*}\; \nonumber \\= & {} -S_{\theta } \frac{\sqrt{\mathcal {C}}}{r_0^2}\sqrt{\cos ^2\theta _*-\cos ^2\theta } , \end{aligned}$$
(5.4)

implying

$$\begin{aligned} {{\mathrm {d}}\cos \theta \over \sqrt{\cos ^2\theta _*-\cos ^2\theta }} = -S_{\theta } \frac{\sqrt{\mathcal {C}}}{r_0^2}\,{\mathrm {d}}\lambda \ . \end{aligned}$$
(5.5)
Fig. 2
figure 2

Qualitative behaviour of the declination \(\theta (\lambda )/\pi \) as it oscillates back and forth between \(\theta _*/\pi \) and \((\pi -\theta _*)/\pi \)

Full size image

From this we see

$$\begin{aligned} {{\mathrm {d}}\cos ^{-1}\left( \frac{\cos \theta }{\cos \theta _*}\right) } = S_{\theta }\frac{\sqrt{\mathcal {C}}}{r_0^2}{\mathrm {d}}\lambda \ , \end{aligned}$$
(5.6)

that is

$$\begin{aligned} {\cos ^{-1}\left( \frac{\cos \theta }{\cos \theta _*} \right) } = {\cos ^{-1}\left( \frac{\cos \theta _0}{\cos \theta _*} \right) } + S_{\theta }\frac{\sqrt{\mathcal {C}}}{r_0^2} (\lambda -\lambda _0) \ . \end{aligned}$$
(5.7)

Without loss of generality we may allow the geodesic to reach the critical angle \(\theta _*\) at some affine parameter \(\lambda _*\), and then use that as our new initial data. This effectively sets \(\theta _0=\theta _*\), and gives us the following simple result:

$$\begin{aligned} \cos ^{-1}\left( \frac{\cos \theta }{\cos \theta _*}\right) = S_{\theta }\frac{\sqrt{\mathcal {C}}}{r_0^2}(\lambda -\lambda _*) \ . \end{aligned}$$
(5.8)

Thence, using the fact that cosine is an even function of its argument:

$$\begin{aligned} \cos \theta= & {} \cos \theta _*\;\cos \left( S_{\theta }\frac{\sqrt{\mathcal {C}}}{r_0^2}(\lambda -\lambda _*) \right) = \cos \theta _*\;\cos \left( \frac{\sqrt{\mathcal {C}}}{r_0^2}(\lambda -\lambda _*) \right) \ . \end{aligned}$$

For a qualitative plot of the declination angle as a function of affine parameter see Fig. 2. Note the motion is periodic, with period

$$\begin{aligned} \Delta \lambda = {2\pi r_0^2\over \sqrt{\mathcal {C}}}. \end{aligned}$$
(5.9)

In terms of the Killing time coordinate the period is

$$\begin{aligned} T_\theta = \frac{2\pi (E-2JL/r_0^3)}{\sqrt{\mathcal {C}}(1-2m/r_0)}. \end{aligned}$$
(5.10)

6 Azimuth for constant-r orbits (\(L\ne 0\))

Now consider the ODE for the evolution of the azimuthal angle \(\phi (\lambda )\). We have

$$\begin{aligned} \frac{d\phi }{d\lambda }= \frac{2J}{r_0^3}\; \left( {E-2JL/r_0^3\over 1-2m/r_0}\right) + { L\over r_0^2 \sin ^2\theta } \ , \end{aligned}$$
(6.1)

and

$$\begin{aligned} \cos \theta= & {} \cos \theta _*\;\cos \left( \frac{\sqrt{\mathcal {C}}}{r_0^2}(\lambda -\lambda _*) \right) \ . \end{aligned}$$

Thence

$$\begin{aligned} \phi (\lambda ) = \phi _* + \frac{2J}{r_0^3}\; \left( {E-2JL/r_0^3\over 1-2m/r_0}\right) (\lambda -\lambda _*) + {L\over r_0^2} \int _{\lambda _*}^\lambda {{\mathrm {d}}{\bar{\lambda }}\over 1-\cos ^2{\theta ({\bar{\lambda }})}}. \end{aligned}$$
(6.2)

The only tricky item here is evaluation of the integral

$$\begin{aligned} \int _{\lambda _*}^\lambda {{\mathrm {d}}{\bar{\lambda }}\over 1-\cos ^2{\theta ({\bar{\lambda }})}} = \int _{\lambda _*}^\lambda {{\mathrm {d}}{\bar{\lambda }}\over 1-\cos ^2(\theta _*) \cos ^2\left( (\sqrt{\mathcal {C}}/ r_0^2) ({\bar{\lambda }}-\lambda _*)\right) }. \end{aligned}$$
(6.3)

But it is easy to check that formally

$$\begin{aligned} \int {d\lambda \over 1- (A \cos ( B+ F\lambda ))^2} = {1\over F \sqrt{1-A^2}} \;\arctan \left( \tan (B+F\lambda )\over \sqrt{1-A^2}\right) \ . \end{aligned}$$
(6.4)

Note that the LHS above is monotone increasing, while the RHS naively exhibits discontinuities whenever the tangent passes through infinity. Thence the correct statement is to observe that

$$\begin{aligned} \int {d\lambda \over 1- (A \cos ( B+ F\lambda ))^2}= & {} {1\over F \sqrt{1-A^2}} \;\Bigg \{ \arctan \left( \tan (B+F\lambda )\over \sqrt{1-A^2}\right) \nonumber \\&+ \pi \; {\mathrm {floor}}\left[ { B+ F\lambda +\pi /2\over \pi } \right] \Bigg \}. \end{aligned}$$
(6.5)

Here \({\mathrm {floor}}[...]\) denotes the integer part (floor function) and the discontinuity in \({\mathrm {floor}}[...]\) exactly cancels the discontinuity due to the \(\arctan (...)\). In terms of the fractional part function \({\mathrm {frac}}[...]\) one has \(x = {\mathrm {floor}}[x] + {\mathrm {frac}}[x]\) so one could equally well write

$$\begin{aligned} \int {d\lambda \over 1- (A \cos ( B+ F\lambda ))^2}= & {} {1\over F \sqrt{1-A^2}} \;\Bigg \{ \arctan \left( \tan (B+F\lambda )\over \sqrt{1-A^2}\right) \nonumber \\&- \pi \; {\mathrm {frac}}\left[ { B+ F\lambda +\pi /2\over \pi } \right] + B+ F\lambda +\pi /2 \Bigg \}.\qquad \quad \end{aligned}$$
(6.6)

Thence

$$\begin{aligned}&\int _{\lambda _*}^\lambda {{\mathrm {d}}{\bar{\lambda }}\over \sin ^2(\theta ({\bar{\lambda }}))}\nonumber \\&\quad = {r_0^2\over \sqrt{\mathcal {C}} \sin \theta _*} {\Bigg \{ } \arctan \left( \tan (({\sqrt{\mathcal {C}}}/ r_0^2) (\lambda -\lambda _*))\over \sin \theta _*\right) \nonumber \\&\qquad { - \pi \; {\mathrm {frac}}\left[ {(\sqrt{\mathcal {C}}/ r_0^2) (\lambda -\lambda _*)+\pi /2\over \pi } \right] + (\sqrt{\mathcal {C}}/ r_0^2) (\lambda -\lambda _*)+\pi /2 \Bigg \}.\;\; } \end{aligned}$$
(6.7)

Finally, using \(\mathcal {C}= L^2/\sin ^2\theta {_*}\), we have

$$\begin{aligned} \phi= & {} \phi _* + {\Bigg \{} \frac{2J}{r_0^3}\; {E-2JL/r_0^3\over 1-2m/r_0}{ +{\sqrt{\mathcal {C}}\over r_0^2} \Bigg \} } (\lambda -\lambda _*) + \arctan \left( {1\over \sin \theta _*} \tan \left( \sqrt{\mathcal {C}} \;{\lambda -\lambda _*\over r_0^2}\right) \right) \nonumber \\&{ - \pi \; {\mathrm {frac}}\left[ {(\sqrt{\mathcal {C}}/ r_0^2) (\lambda -\lambda _*)+\pi /2\over \pi } \right] +{\pi \over 2}. } \end{aligned}$$
(6.8)

So the azimuthal motion is a constant drift (growing linearly in the affine parameter) with a superimposed oscillation. Specifically the oscillatory term is

$$\begin{aligned} { \phi _{oscillation}(\lambda ) }= & {} { \arctan \left( {1\over \sin \theta _*} \tan \left( \sqrt{\mathcal {C}} \;{\lambda -\lambda _*\over r_0^2}\right) \right) } \nonumber \\&{ - \pi \; {\mathrm {frac}}\left[ {(\sqrt{\mathcal {C}}/ r_0^2) (\lambda -\lambda _*)+\pi /2\over \pi } \right] +{\pi \over 2}. } \end{aligned}$$
(6.9)

Note the sensible limit for equatorial motion as \(\sin \theta _*\rightarrow 1\). See Fig. 3 for a qualitative plot of the oscillating term, and Fig. 4 for a qualitative plot of the total phase (drift plus oscillation).

Fig. 3
figure 3

Qualitative behaviour of the oscillatory part \(\phi _{oscillation}(\lambda )\) of the azimuthal evolution as a function of the affine parameter

Full size image
Fig. 4
figure 4

Qualitative behaviour of \(\phi (\lambda )\), the total azimuthal phase evolution (drift plus oscillation) as a function of the affine parameter

Full size image

The oscillatory contribution to the azimuthal evolution has the same period as the evolution in declination

$$\begin{aligned} \Delta \lambda _{oscillation} = {2\pi r_0^2\over \sqrt{\mathcal {C}}}, \end{aligned}$$
(6.10)

but the drift component has periodicity

$$\begin{aligned} \Delta \lambda _{drift} = 2\pi {\Bigg \{} \frac{2J}{r_0^3}\; {E-2JL/r_0^3\over 1-2m/r_0}{ +{\mathcal {C}\over r_0^2} \Bigg \}^{-1} } \end{aligned}$$
(6.11)

so that

$$\begin{aligned} (T_\phi )_{drift} = 2\pi \; {E-2JL/r_0^3\over 1-2m/r_0} \; {\Bigg \{} \frac{2J}{r_0^3}\; {E-2JL/r_0^3\over 1-2m/r_0}{ +{\mathcal {C}\over r_0^2} \Bigg \}^{-1} } \end{aligned}$$
(6.12)

This drift in azimuth periodicity is typically incommensurate with the periodicity in declination, so the geodesics are surface filling and will eventually cover the entire equatorial band \(\theta \in [\theta _*,\pi -\theta _*]\). (See Fig. 1 for a qualitative description.)

7 Angular motion for \(L=0\) (Constant-r ZAMOS)

If we now consider the special case of constant-r orbits where \(L=0\), then \(\sin \theta _*\rightarrow 0\), so we need to be careful. The equations of motion reduce even further to:

$$\begin{aligned} \left( \frac{d\phi }{d\lambda }\right) = \frac{2J}{r_0^3}\frac{E}{1-2m/r_0} \ ; \qquad \left( \frac{d\theta }{d\lambda }\right) = \pm {\sqrt{\mathcal {C}}\over r_0^2} \ . \end{aligned}$$
(7.1)

So in this special case we find

$$\begin{aligned} \phi =\phi _0 + \frac{2J}{r_0^3}\frac{E}{1-2m/r_0}(\lambda -\lambda _0) \ ; \qquad \theta =\theta _0\pm {\sqrt{\mathcal {C}}\over r_0^2} (\lambda -\lambda _0) \ . \end{aligned}$$
(7.2)

Now \(\phi \) is defined only modulo \(2\pi \), but \(\theta \) is naively in \([0,\pi ]\). However if we formally drive it outside this range we just need to reset \(\phi \) by \(\pi \). That is, we can identify the points \((\theta +\pi ,\phi ) \equiv (\pi -\theta , \phi +\pi )\).

In view of the fact that for constant-r orbits with \(L=0\) the quantity

$$\begin{aligned} {dt\over d\lambda } = {E\over 1-2m/r_0} \end{aligned}$$
(7.3)

is a constant, we can also rewrite angular dependence as

$$\begin{aligned} \phi =\phi _0 + \frac{2J}{r_0^3}(t-t_0) \ ; \qquad \theta =\theta _0\pm {\sqrt{\mathcal {C}}(1-2m/r_0)\over E r_0^2}\; (t-t_0) \ . \end{aligned}$$
(7.4)

Note the periodicities in azimuth and declination are

$$\begin{aligned} T_\phi = {\pi r_0^3\over J}, \qquad \hbox {and} \qquad T_\theta = {\pi E r_0^2\over \sqrt{\mathcal {C}}(1-2m/r_0)}. \end{aligned}$$
(7.5)

These are typically incommensurate, so these ZAMO curves are surface filling and will eventually cover the entire angular 2-sphere. (The equatorial band in Fig. 1 will expand to include both poles.)

8 Limit as \(J\rightarrow 0\)

Physically the limit \(J\rightarrow 0\) corresponds to switching off the angular momentum of the central object generating the gravitational field, so that the spacetime becomes Schwarzschild in Painlevé–Gullstrand coordinates; so for constant-r orbits we must recover the unstable photon sphere at \(r=3m\) and the ISCO at \(r=6m\). If not, something is very wrong.

For \(J\rightarrow 0\) the quantity X(r) simplifies to

$$\begin{aligned} X(r) \rightarrow E^2-\left( 1-\frac{2m}{r}\right) \left( -\epsilon + \frac{\mathcal {C}}{r^2}\right) \ . \end{aligned}$$
(8.1)

8.1 Photon spheres

For massless particles \(\epsilon \rightarrow 0\), and without loss of generality we can set \(E\rightarrow 1\). This implies

$$\begin{aligned}&X(r) \rightarrow 1-\left( 1-\frac{2m}{r}\right) \frac{\mathcal {C}}{r^2}; \end{aligned}$$
(8.2)
$$\begin{aligned}&X'(r) \rightarrow {2\mathcal {C}(r-3m)\over r^4}; \end{aligned}$$
(8.3)

and

$$\begin{aligned} X''(r) \rightarrow -\,{6\mathcal {C}(r-4m)\over r^5}. \end{aligned}$$
(8.4)

There is a unique photon sphere at \(r_0=3m\). Then \(X(r_0) = 0 = 1 -\mathcal {C}/(3 r_0^2)\), that is \(\mathcal {C}=3 r_0^2\). We then see that \(X''(3m) = 2\mathcal {C}/(243 m^4) = 2/(81 m^2)> 0\), these photon orbits are unstable. This is exactly as it should be.

8.2 Massive particle spheres

For massive particles \(\epsilon \rightarrow -1\), that implies

$$\begin{aligned}&X(r) \rightarrow E ^2-\left( 1-\frac{2m}{r}\right) \left( 1 + \frac{\mathcal {C}}{r^2}\right) ; \end{aligned}$$
(8.5)
$$\begin{aligned}&X'(r) \rightarrow {2\mathcal {C}(r-3m)-2mr^2\over r^4}. \end{aligned}$$
(8.6)

and

$$\begin{aligned} X''(r) \rightarrow \,{-6\mathcal {C}(r-4m) +4mr^2\over r^5}. \end{aligned}$$
(8.7)

Solve \(X'(r_0)=0\) to find \(\mathcal {C}(m,r_0)\):

$$\begin{aligned} \mathcal {C}(m,r_0)= {m r_0^2\over r_0-3m}. \end{aligned}$$
(8.8)

Since \(\mathcal {C}\ge 0\), there will now be many constant-r orbits, all the way from \(r_0=\infty \) down to \(r_0=3m\). Use this to evaluate \(X''(m,r_0)\):

$$\begin{aligned} X''(r_0,m) \rightarrow -\,{2m(r_0-6m)\over r_0^3(r_0-3m)}. \end{aligned}$$
(8.9)

Inspecting the sign of \(X''(m,r_0)\), the constant-r orbits are stable for \(r_0>6m\), marginal for \(r_0=6m\), and unstable for \(r_0<6m\). This is exactly as it should be.

9 Conclusions

We have explored the existence of and properties of the constant-r (“quasi-circular”) geodesics in the recently introduced Painlevé–Gullstand variant of the Lense–Thirring spacetime [52,53,54]. We emphasize that although the underlying spacetime is not spherically symmetric, (only stationary and axisymmetric), so that the Birkhoff theorem does not apply [22,23,24,25,26], one nevertheless encounters (partial) spherical shells of constant-r geodesics; notably this behaviour is not limited to the (exact) Kerr spacetime, but also persists in the Painlevé–Gullstand variant of the Lense–Thirring spacetime. The persistence of existence of these constant-r (“quasi-circular”) geodesics is intimately related to the persistence of existence of a non-trivial Killing tensor and the associated Carter constant. Overall, we see that the Painlevé–Gullstand variant of the Lense–Thirring spacetime [52,53,54] exhibits many useful and interesting properties, and is well-adapted to direct confrontation with observational astrophysics.

From a wider perspective, these considerations can be viewed as an element of the study of modified black holes — alternative black holes to the standard Schwarzschild–Kerr family that are nevertheless carefully formulated so as to pass the most obvious observational tests, and so provide useful templates for driving observational astrophysics [64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79].