Topographic effects on buoyancy driven flows along the slope

Abstract

The flow and descent of dense water masses formed in shallow regions of the ocean is an important leg in the global overturning circulation. The dense overflow waters tend to flow along the continental slopes as geostrophically balanced gravity plumes, but may be steered downslope by canyons and ridges cross-cutting the slopes. In that process, entrainment and mixing will be greatly enhanced. Ilicak et al. (Ocean Model 38:71–84, 2011) propose a parameterization to include the effects of corrugations in large scale models by increasing the vertical mixing locally. We re-visit the problem using the terrain-following Bergen Ocean Model and a DOME-inspired idealized topography. It is shown that the applied corrugations can move the core of the plume 800 m down the slope, while enhanced mixing raises the center of gravity by only 1–200 m. The overall effect of a corrugation is hence to lower the center of gravity, suggesting that the parameterization proposed by Ilicak et al. (Ocean Model 38:71–84) will act in the wrong vertical direction, if used on its own. A comparison of two bottom drag parameterizations, show that a parameterization consistent with a no-slip boundary condition is needed to correctly represent Ekman drainage, and that the Ekman drainage contribution to plume descent is comparable to that of the corrugation. Ridges are more effective in steering dense water downward than canyons, and we compare the dynamics between the two settings to explain the difference.

1 Introduction

The flow of dense water masses on a sloping bottom has been investigated in scientific contributions based on observations, laboratory experiments, theoretical analysis, and numerical model studies. The dense flows will tend to follow the continental slope in near geostrophic balance. The propagation of cold eddies is investigated in Nof [1] and time-dependent oscillatory migration is explained in Nof [2]. The dynamics of dense water flowing along slopes is investigated in Shapiro and Hill [3] and they later explain that the shape of a dense water lens can change from a head-up to a head-down state on the way along the slope [4]. Using laboratory experiments Cenedese et al. [5] investigated how the possible flow regimes depend on the governing physical parameters. Ezer and Weatherly [6] investigated numerically the interaction between dense water jets and the bottom boundary later, and downward migration due to Ekman transport is explained analytically in Wåhlin and Walin [7]. The importance of a proper representation of the Ekman drain in numerical models, using a no-slip boundary condition and high vertical resolution, is documented in Laanaia et al. [8], Wobus et al. [9], Berntsen et al. [10]. Even if downward migration due to Ekman transport is important it can be inhibited by buoyancy [11]. Eddies can form in dense water bodies. This is shown through laboratory experiments in Lane-Serff and Baines [12] and in numerical experiments [13] and they will affect mixing and plume paths [14].

In the real ocean, topographic features along the continental slopes will affect the propagation, structure, and mixing of dense water bodies. Boyer and Davies [15] gave an overview of laboratory studies of orographic effects that also include such effects on dense water flows along slopes. The flow through the Faroe bank Channel has been addressed in many papers. Johnson and Sanford [16] describe and explain the secondary circulation through this channel based on observational data. Ezer [17] used a numerical model to investigate the topographic influence on the overflow dynamics, and later the downstream dynamics were addressed in Seim et al. [18] using numerical modelling. A combination of laboratory and numerical model experiments was used in Cuthbertson et al. [19] to investigate the topographic effects in the Faroese Channels.

In particular, canyons and ridges cross the slopes and are known to play an important role in this puzzle. Allen and Durrieu de Madron [20] gave a review of the effects of submarine canyons. Wåhlin [21] analysed the topographic steering by canyons crossing the slope, and estimated the maximum downhill transport capacity of a canyon. Later laboratory experiments were used to study the effects of canyon and ridges on steering, mixing, and entrainment [22] and this has been followed up by numerical studies [23]. Wåhlin and Walin [7] and Darelius and Wåhlin [24] suggest that canyons and ridges can support a geostrophically balanced downslope flow where the along slope transport component is balanced by an oppositely directed Ekman transport in the bottom boundary layer. The transport capacity of a corrugation depends on the parameters of the topography, the slope steepness, and the strength of the reduced gravity. Laboratory experiments support the analytical results [25] and suggest that entrainment rates are increased due to the topography [22].

The setup from the DOME (Dynamics of Overflow Mixing and Entrainment http://www.rsmas.miami.edu/personal/tamay/DOME/dome.html) case has been used in many numerical investigations of dense water flows along slopes, see for instance Reckinger et al. [26] and Berntsen et al. [14] and references therein. In most of these investigations, dense water is flowing towards the deep ocean through inlets on the shelf, and the slopes are smooth in the along-flow direction.

The effects of corrugations on dense gravity currents were addressed in Ilicak et al. [27] using numerical experiments based on the DOME setup. They conclude that corrugations steer the plumes downslope, and they suggest a parameterization of vertical mixing based on a corrugation Burger number to include the effects of small scale ridges and canyons in large scale models. Corrugations will create enhanced mixing, which will lift the center of gravity of dense water upward. At the same time, corrugations will steer the dense water away from the coast and down the slope. A parameterization of the effects of corrugations using enhanced vertical mixing will always lift the center of gravity if the steering effect is ignored. In the present study, we investigate the effects of corrugations on the vertical center of gravity of a dense water plume flowing along a slope. If the net effect of a corrugation is to lift the center of gravity, a parameterization building on localized, enhanced vertical eddy diffusivity can be appropriate. If the net effect is to lower the center of gravity, a parameterization building on enhanced vertical eddy diffusivity is not adequate. In the present study, we also address the downward transports along a corrugation and compare the situation with a plume impinging on a ridge to that of of a plume impinging on a canyon.

Most DOME studies including Ilicak et al. [27] apply a constant drag coefficient. We have previously argued [10, 14] that when a constant drag coefficient is applied the Ekman drain is underestimated, and that a bottom boundary condition that is consistent with no-slip is necessary to model the flow in the Ekman layer correctly. Hence, for comparison, the numerical experiments are performed twice, first with a constant drag coefficient and thereafter with a bottom boundary condition giving no-slip.

2 Model and results

2.1 The numerical model and model setup

In the present study, a $\sigma$-coordinate ocean model named the Bergen Ocean Model (BOM) is used [28, 29]. The BOM has been used in two DOME-studies [10, 14]. Here the model setup follows Ilicak et al. [27]. The computational domain is 170 km in the along slope x-direction and 89 km in the cross slope y-direction. The lateral boundaries in the x-direction at $x=-10$ km and at $x = 160$ km are open, and $\frac{\partial u}{\partial x} = 0$, where u is the velocity component in the x-direction, at these boundaries. The origin in x is chosen to agree with the origin used in Ilicak et al. [27], and the domain is given in Fig. 1. At the lateral boundary at $y = 0$ km the velocity component in the y-direction, v is set to 0. At the lateral boundary at $y = 85$ km v is also set to 0, apart from in a channel starting at $x = 20$ km. Through this channel, dense water is injected, see below. The channel has a constant depth of 600  m, it is 10 km wide and 5 km long. The slope outside the channel is uniform with steepness $s = 0.08$ and the maximum depth is 7000 m. To study the effects of corrugations, three cases are investigated:

• (i) a reference case with no corrugations on the slope,

• (ii) a case with a V-shaped ridge with height 600 m and width 6000 m crossing the slope, and

• (iii) a case with a V-shaped canyon with height 600 m and width 6000 m crossing the slope.

In the horizontal, the grid size is 1  km. The Coriolis parameter f is negative and equal to $-1.4 \times 10^{-4}\,\hbox {s}^{-1}$.

Fig. 1

Horizontal view of the computational domain for the experiments with a ridge. The color-bars give depth in meters

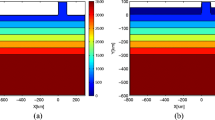
In the vertical 100 $\sigma$-layers are applied. This choice is based on the investigations in Berntsen et al. [10]. For studies of dense water flows, it is a requirement to resolve the bottom layer dynamics [8, 9]. The $\sigma$-transformation $\sigma = \frac{z-\eta }{H + \eta }$ where z is the vertical coordinate, $\eta$ the free surface elevation, and H is the depth, maps $(-H,\eta )$ on to $(-1,0)$ and by using a formulation from Lynch et al. [30] to distribute the $\sigma$-layers, a grid with fine resolution near the bottom ($\sigma$ close to $-1$) is obtained (Fig. 2). With this grid there are 34 layers over a 100 m thick layer near the bottom at 1000 m depth facilitating a proper representation of the dynamics in the Ekman layer.

Since the findings from the present study are compared to results from Ilicak et al. [27], the main differences in the models are summarized: The model used in Ilicak et al. [27] was isopycnal with 25 isopycnal layers and their horizontal grid size was 500 m whereas a $\sigma$-coordinate model with 100 $\sigma$-layers and a horizontal grid size of 1 km is used in the present investigations. The horizontal grid size had to be increased compared to Ilicak et al. [27] due to limited access to computer resources.

Fig. 2

The sigma layer thicknesses ($\varDelta \sigma$) for $\sigma \in [-1,0]$

A quadratic drag law

$$\begin{aligned} {\varvec{\tau }}_{\mathbf{b}} = C_D |\mathbf{U}_b | \mathbf{U}_b \, \end{aligned}$$

(1)

is applied as the bottom boundary condition. In Eq. (1), $\mathbf{U}_b$ is the velocity vector in the grid cell closest to the bottom, and $C_D$ is the bottom drag coefficient. The velocity $\mathbf{U}_b$ is a half-cell above the bottom in our staggered C-grid model.

The numerical experiments are performed with two choices of $C_D$ in Eq. (1). Firstly, the drag coefficient is set constant and equal to 0.002 as in Ilicak et al. [27]. This value is also a common choice in the DOME-literature [10, 26]. Secondly, the drag coefficient $C_D$ is computed from

$$\begin{aligned} C_D = \hbox {max}\left[ 0.002,\frac{\kappa ^{2}}{(\ln (z_b/z_0))^{2}}\right] \, , \end{aligned}$$

(2)

where $z_b$ is the distance of the nearest grid point to the bottom, the von Karman constant $\kappa =0.4$, and the bottom roughness parameter $z_0$ is set to 0.01 m [31]. By using the formulation above for $C_D$, the value of the drag coefficient will depend on the fraction $z_b/z_0$, and if $z_b/z_0$ tends towards unity, $C_D$ will tend to infinity, and near sea bed velocity profiles that agree with the logarithmic law of the wall profile can be obtained. Furthermore, solutions agree with the Ekman spiral’s exact solution near the bottom, assuming no-slip can be obtained [23]. For further discussions of the bottom boundary condition, see Laanaia et al. [8], Wobus et al. [9], Berntsen et al. [10, 14].

Each numerical experiment is integrated forward in time over 10 days. To follow the plume water, a passive tracer, $\tau$, is set to 1 in the inflowing dense water and 0 in the ambient water masses initially.

The Mellor–Yamada turbulence scheme [31, 32] is often applied in numerical investigations with $\sigma$-models, and it is also used in the present study to compute the vertical viscosity and the vertical diffusivity. To compute the horizontal viscosity $A_M$ a subgrid-scale parameterization based on Smagorinsky [33] is used

$$\begin{aligned} A_M = C_M (\varDelta x)^2 \;\left[ \left( \frac{\partial U}{\partial x}\right) ^2 +\frac{1}{2} \; \left( \frac{\partial V}{\partial x} +\frac{\partial U}{\partial y}\right) ^2 +\left( \frac{\partial V}{\partial y}\right) ^2\right] ^{\frac{1}{2}} . \end{aligned}$$

(3)

In Eq. (3), $C_M = 0.2$ is a non-dimensionless parameter, U is the velocity component in the x-direction, and V is the velocity component in the y-direction. The horizontal diffusion is set to zero. A superbee limiter TVD (Total Variance Diminishing) scheme [34] is used for the advection of density and momentum. There will be numerical diffusivity and numerical viscosity associated with the use of this scheme.

The density is initially constant (no stratification) and there is no motion. Dense water is injected into the domain through the coastal embayment using Eq. (3) in Ilicak et al. [27]

$$\begin{aligned} T_{in} = g^{\prime } H_{in}^2 / (2 f) \; . \end{aligned}$$

(4)

In this equation, $T_{in}$ is the transport, $g^{\prime }$ is the reduced gravity, and $H_{in}$ is the maximum interface thickness. The inflowing water is 0.2 kg m$^{-3}$ denser than the ambient water and $g^{\prime } = 0.0019$ m s$^{-2}$. Due to rotation, the interface in the embayment is tilted to achieve an approximate geostrophic balance, see Legg et al. [35]. The value of $T_{in}$ is 0.5 Sv for the present parameter values.

To investigate overall effects of a canyon or a ridge, the plume path

$$\begin{aligned} Y(x,t)\, = \, \frac{\int \int y \tau (x,y,z,t) dz dy}{\int \int \tau (x,y,z,t) dz dy} \, , \end{aligned}$$

(5)

the plume depth

$$\begin{aligned} Z(x,t)\, = \, \frac{\int \int z \tau (x,y,z,t) dz dy}{\int \int \tau (x,y,z,t) dz dy} \, , \end{aligned}$$

(6)

the plume thickness

$$\begin{aligned} H_0(x,t)\, = \, \frac{\int \int h(x,y,z,t) \tau (x,y,z,t) dz dy}{\int \int \tau (x,y,z,t) dz dy} \, , \end{aligned}$$

(7)

and the plume buoyancy

$$\begin{aligned} B(x,t)\, = \, \frac{\int \int b(x,y,z,t) \tau (x,y,z,t) dz dy}{\int \int \tau (x,y,z,t) dz dy} \, , \end{aligned}$$

(8)

where $\tau$ is the value of the tracer initially set to 1 in the inflowing dense water and to 0 elsewhere, are computed. The integrals in Eqs. (5) to (8) are taken over the whole domain in y and z for $\tau > 0.05$. In Eq. (7), h is height above bottom. In Eq. (8), $b = g(\rho _{ref} - \rho )/\rho _{ref}$, $\rho _{ref}$ is the density at the surface and is equal to 1022.0 kg m$^{-3}$, and B represents the mean buoyancy of the overflow water. In the plots, B is normalized by the maximum buoyancy that a water parcel can have, $\varDelta b = g(\rho _b -\rho _{ref})/\rho _{ref}$. For $\rho _b = 1022.2$ kg m$^{-3}$, $\varDelta b = 0.019$ ms$^{-2}$.

The plume transports in the x-direction $Tr_x(x,t)$ are computed as

$$\begin{aligned} Tr_x(x,t)\, = \, \int \int \tau (x,y,z,t) u(x,y,z,t) dz dy \, . \end{aligned}$$

(9)

In addition, the plume transports in the y-direction $Tr_y(y,t)$ are computed as

$$\begin{aligned} Tr_y(y,t)\, = \, \int \int \tau (x,y,z,t) v(x,y,z,t) dz dx \, . \end{aligned}$$

(10)

The integrals are computed for $\tau \, > \, 0.05$ and in Eq. (9) they are integrated for all y and z, and in Eq. (10) for all x and z. To investigate the down slope transport near the corrugations, the integral in Eq. (9) is also taken for $x_{topo} - 2W \,< \, x \, <x_{topo} + 2W$, where $x_{topo}$ is the location of the canyon/ridge in the x-direction, W is the width of the corrugation ($W = 6000$ m) and the transports are denoted as $Tr_{TOPOy}(x,t)$. The corresponding transports of added mass $\rho _{ref} - \rho$ are also computed by replacing $\tau$ with added mass in Eqs. (9) and (10), and denoted as $TrM_x$, $TrM_y$, $TrM_{TOPOy}$, respectively.

The numerical results produced with $\varDelta x = 1.0$ km are dominated by eddies and oscillatory motion. To illustrate this, the vertical component of the relative vorticity, averaged over the plume, ${\overline{\zeta }}$, is computed as

$$\begin{aligned} {\overline{\zeta }} = \frac{1}{H_{plume}} \int \left( \frac{\partial V}{\partial x} -\frac{\partial U}{\partial y} \right) dz \, . \end{aligned}$$

(11)

In addition, the divergence, averaged over the plume,${\overline{DIV}}$, is computed as

$$\begin{aligned} {\overline{DIV}} = \frac{1}{H_{plume}} \int \left( \frac{\partial U}{\partial x} +\frac{\partial V}{\partial y} \right) dz \, . \end{aligned}$$

(12)

In Eqs. (11) and (12), the vertical integrals are taken over the plume from the bottom and up to the threshold value of the tracer equal to 0.05. The thickness of the plume is denoted as $H_{plume}$ in the equations above.

2.2 Numerical results

The tracer fields are integrated vertically, and the values at the end of each experiment are shown in Fig. 3. In agreement with the statements by Ilicak et al. [27], the overall effect of the corrugations appears to be that they steer the plume away from the coast. The steering effect is stronger for ridges than for canyons. However, eddies are superimposed on the main dense water bodies, and it is difficult to identify the steering effects by comparing the fields at a specific time. Time-averages of the fields taken over the last 48 hours of each experiment are therefore computed, and the vertically-integrated tracer concentrations produced from the time-mean fields are given in Fig. 4. The use of time averaging of model fields can create an impression of dilution. The time-averaged model field given in Fig.  4a appears, for instance, to be more diluted than the instantaneous field given in Fig. 3a, and we should bear in mind that this is mainly due to time averaging rather than physical mixing. For the no-corrugation case, the time averaging filters out the oscillations. However, there are still signs of oscillations in the time-mean fields for the cases with canyons or ridges. This may indicate that the time averaging period is not appropriate and/or that the center of gravity of the overflows may overshoot/undershoot an equilibrium level when passing a ridge or a canyon. It may be mentioned that oscillations in the overflow paths around ridges are also seen in Fig. 10 in Ilicak et al. [27].

The cross-sections of the time mean tracer fields given in Fig. 5 illustrate that the upstream effects of the corrugations are minimal 10 km before the canyon or ridge. The tracer water is compressed in the vertical and spread out in the cross slope direction as the water crosses the ridge. After crossing the top of a ridge, the water will tend to follow the topography towards the coast, and the thickness of the plume will increase. As the plume water enters the canyon, the water will follow the isobaths towards the coast, and the plume thickness increases substantially. It may be noted that for a canyon, Ekman drainage will move dense fluid parcels towards the canyon’s center on both flanks of the canyon [21]. The time-averaged tracer field is diluted in the vertical and compressed in the cross slope direction as the plume crosses the canyon. By comparing the sections upstream and downstream of a corrugation (Fig. 5), the net effects of a canyon or a ridge are seen. The centers of mass in the time-averaged fields are moved away from the coast, and the plume is substantially spread out both horizontally and vertically. After crossing a corrugation, the plume path will continue along iso-baths. Downstream of a corrugation, there will be a drain of water downward and off the coast, and this drain will change the cross-sectional profiles, see Fig. 6, from a head-up towards a head-down state as discussed for instance in Shapiro and Hill [3, 4]. The effects of the bottom boundary conditions can be difficult to identify in the meandering tracer fields given in Figs. 3 and 4. However, by comparing the right and left panels of Fig. 6 it can be seen that the Ekman drain is substantially stronger when using the non-constant drag coefficient computed from Eq. (2). Especially for the ridge case, the core of the time-averaged tracer field is much further from the coast when using $C_D$ computed from Eq. (2).

From the plume paths (Fig. 7) it may be noticed that both the canyon and the ridge will steer the plume down the slope, and that the steering effect of the ridges is strongest. This is in agreement with the results in Ilicak et al. [27]. It may be seen by comparing the results for the cases without a corrugation with the corresponding results for the ridge cases that near the open exit boundary at $x = 150$ km the center of the plume is steered approximately 10 km further away from the coast and 800 m deeper when a ridge is present upstream. The plume water is meandering downstream of the topography and these values therefore vary with distance from the corrugation, see Figs. 7a and b. However, the center of mass is always further away from the coast and deeper in the ridge cases than in the no-corrugation cases. For $x \in [100,150]$ km, the vertical displacement is in the range from 400 m to 1000 m in the ridge cases. The plume thickness will increase with $100-200$ m over a ridge or a canyon, in agreement with corresponding results from Ilicak et al. [27]. The increase in plume thickness will contribute to raising the center of gravity of the plume, but this effect will be substantially smaller than the downslope steering effect, and downstream of the topographic feature, the plume thickness decrease towards the thickness of the undisturbed plume. As the plume water exits the coastal embayment, it mixes with the ambient water and reduces the negative buoyancy. This effect is strongest in the phase before a geostrophically balanced flow along the slope is established (Fig. 7d). The crossing of a corrugation will introduce further mixing and reduce the buoyancy, which again will affect the transports of dense water. By comparing the results computed with a constant value of $C_D$ rather than $C_D$ given by the drag law in Eq. (2), we find that with $C_D$ from Eq. (2) the plume water is systematically drained further down the slope, which is in agreement with the findings in Berntsen et al. [10].

The volume transports in the along slope direction increase substantially at the corrugations and this effect is gradually reduced towards the downstream open boundary (Fig. 8a). This is in qualitative agreement with Ilicak et al. [27]. The mass transport in the along slope direction is almost constant before the corrugations (Fig. 8b). The transport oscillates around the equilibrium level downstream, and for the ridge experiments, the mass transport is reduced towards the open boundary. The explanation is that part of the plume is diluted so that $\tau \, < \, 0.05$ and the integrals are computed for $\tau \, > \, 0.05$. The effect of the corrugation on the cross-slope volume and mass transport is evident, see Figs. 8c to 8f. The downslope transports extend approximately 800 m deeper when a corrugation is present, and this effect is larger in the ridge case. It may also be noticed that with $C_D$ computed from Eq. (2), the plume water is transported further away from the coast than with constant $C_D$. The added off-coast transport is located in the vicinity of the corrugations.

A theory for the transport capacity of a ridge or a canyon is given in Wåhlin [21] and Darelius and Wåhlin [24]. For the present topographic scales and value of the reduced gravity, the capacity is approximately 0.4 Sv suggesting that almost all the inflowing water can be transported downward and that the flux of dense water in the lee of the topography should be minimal. However, in our simulations all the dense water continues along the slope after crossing the topography. Also, in the simulations by Ilicak et al. [27] the plume water continues along the slope, and explanations for the apparent discrepancy with theory are given. We may add to this discussion that the estimate of 0.4 Sv is based on the reduced gravity $g^{\prime }$ of the dense water in the embayment. The transport capacity scales with $g^{\prime }$ and from Fig. 7d it may be seen that the negative buoyancy is substantially reduced in the numerical results as the plume water leaves the embayment, and there is an additional reduction in $g^{\prime }$ as the water impinges on the corrugation. There may be less mixing between the core plume water and the ambient water in the real ocean. The negative buoyancy can therefore be stronger as the plume water reaches the corrugation. The downward transport can accordingly be stronger. The discrepancy between the theory and the numerical results may thus be due to too much mixing in the numerical experiments performed with a resolution that possibly is not adequate for representing the mixing, see the discussion on the resolution in the next section. Having said this, it may be noticed from Fig. 8e that there is a downward flow along the corrugation of 0.2-0.4 Sv even if the flow does not continue down the slope.

As the along-slope current impinges a ridge, the plume will follow the iso-baths away from the coast and gain positive relative vorticity. The rotation will turn anti-clockwise over the top of the ridge and become anti-clockwise. In the lee of the ridge, the rotation turn clockwise again. The shift from clockwise to anti-clockwise over the top of the ridge is seen in Fig. 9c and d. In the areas where the rotation changes, we may notice areas with strong divergence, see Fig. 10c and d. When the water flows into or out of a canyon, the rotation will be anti-clockwise, and inside the canyon, the rotation will be clockwise, see Fig. 9e and f. There is an area of convergence along the canyon, but it is not as strong as for the ridge case, see Fig. 10e and f.

The asymmetry between the ridge and the canyon case discussed above can partly explain that the plume heights and the plume transports downstream of the corrugation become larger for the ridge case. To understand the asymmetry in off-coast steering for the two cases, we focus on the flow fields near the corrugations, see Figs. 11 and 12. As the water in the along slope currents approaches a ridge, it will first be steered away from the coast, and there will be a maximum in speed around the top of the ridge, and the flow away from the coast will be strong. With substantial off-coast inertia towards the top of the ridge, it will take time to turn the flow along the iso-baths towards the coast, and the flow towards the coast in the lee side will be much weaker. For the canyon case, the flow will be towards the coast as the water enters the canyon. This difference may explain that the total steering away from the coast becomes stronger when along slope gravity currents meet a ridge rather than a canyon. The effects of the bottom boundary condition on the Ekman drain may also be seen from Figs. 11 and 12. When using Eq. (2) to compute the bottom drag coefficient $C_D$, the drain of fluid from the core of the plume in the off-coast direction becomes stronger, and the magnitudes of the maximum speeds are reduced. The steering effects of using Eq. (2) to compute $C_D$ rather than a constant $C_D$ is of the same order of magnitude as the steering due to a ridge or a canyon, see Figs. 7 and 8.

Fig. 3

Vertically-integrated tracer concentrations after 10 days for runs with a–b no corrugation c–d a ridge and e–f a canyon. Results produced with a constant value of $C_D$ are given to the left. Results produced with $C_D$ computed from Eq. (2) are given to the right

Fig. 4

Vertically-integrated tracer time-averaged concentrations. The fields are averaged over the last 48 h of the experiments. The results for the no-corrugation case are given in the top panel, the results for the ridge case are given in the middle panel, and the results for the canyon case are given in the bottom panel. Results produced with a constant value of $C_D$ are given to the left, and results produced with $C_D$ computed from Eq. (2) are given to the right

Fig. 5

Cross sections of the time-averaged tracer concentrations taken 10 km upstream of the corrugations (in the x-direction) are given in the upper panel. Corresponding fields taken along the corrugations are given in the middle panel, and fields obtained 10 km downstream are given in the lower panel. The results for the ridge experiment are given to the left, and the results for the canyon are given to the right. The coordinate on the vertical axis $H_0$ is the height above the bottom. The results are produced with $C_D$ computed from Eq. (2)

Fig. 6

Cross sections of the time-averaged tracer concentrations taken 80 km downstream of the corrugations. The results for the ridge case are given in the upper panel, and the results for the canyon case are given in the bottom panel. The results produced with a constant value of $C_D$ are given to the left, and the results produced with $C_D$ computed from Eq. (2) are given to the right. The coordinate on the vertical axis $H_0$ is distance from the bottom

Fig. 7

Time means of Y(x, t), Z(x, t), $H_0(x,t)$, and normalized B(x, t), see Eqs. (5) to (8). The time means are taken over the last 48 hours of each experiment. The position of the canyon/ridge is marked with vertical green lines

Fig. 8

Time means of a $Tr_x(x,t)$, c $Tr_y(y,t)$, and e) $Tr_{TOPOy}(y,t)$, see Eqs. (9) to (10). The corresponding transports of added mass are given in b, d, and f. The time means are taken over the last 48 h of each experiment. The position of the canyon/ridge is marked with vertical green lines in Figs. a and b

Fig. 9

Time-averaged plume vorticity computed from Eq. (11) over the last 48 h of each experiment from runs with a–b no-corrugation c–d a ridge and e–f a canyon. The results produced with a constant value of $C_D$ are given to the left, and the results produced with $C_D$ computed from Eq. (2) are given to the right

Fig. 10

Time-averaged plume divergence computed from Eq. (12) over the last 48 h of each experiment from runs with a–b no corrugation, c–d a ridge, and e–f a canyon. Runs with a constant value of $C_D$ are given to the left, and runs with $C_D$ computed from Eq. (2) are given to the right

Fig. 11

Maximum flow speeds in the time-averaged velocity fields over the last 48 hours of each experiment from runs with a–b a ridge and c–d a canyon. Results produced with a constant value of $C_D$ are given to the left, and results produced with $C_D$ computed from Eq. (2) are given to the right

Fig. 12

The y-components of the time-averaged velocity fields taken at the depth with maximum flow speed over the last 48 hours of each experiment from runs with a–b a ridge and c–d a canyon. Results produced with a constant value of $C_D$ are given to the left, and results produced with $C_D$ computed from Eq. (2) are given to the right

3 Discussion

In the present set of simulations, the horizontal grid size is 1 km and 100 sigma-layers are used vertically. In the studies reported in Ilicak et al. [27], the grid size was 500 m horizontally and they applied 25 isopycnal layers vertically. However, none of the studies present grid-converged solutions, and the quality of the model outputs depends on the quality of the subgrid-scale parameterizations applied. We may also bear in mind a statement in the general introduction in Dickson et al. [36] where it is stated that “Climate models are inherently weak in the important subtleties of deep convection, interior diapycnal mixing, boundary currents, shelf circulations (climate models have no continental shelves!), downslope flows that entrain new fluid during their descent, thin cascading overflows, ...” In the present studies, the resolution is higher than in studies with climate models. However, there are still many processes that are not resolved or well represented. In the laboratory-scale investigations of dense water flow down a canyon, we conducted a series of experiments with a range of grid resolutions, see Berntsen et al. [23], and it was found that approximately 80 cells across the canyon and more than 300 layers vertically were needed to represent the dense water flow in the canyon appropriately.

Having the above in mind, we still consider findings from numerical investigations with different model systems that point in the same direction to be trustworthy. We find that many of the present results are in overall agreement with corresponding results given in Ilicak et al. [27]. For instance, it is found that both canyons and ridges give added mixing and steering, and these findings appear to be robust, and in overall agreement with the results from laboratory investigations [22, 24]. The off-coast steering by a ridge is also stronger than the corresponding steering by a canyon.

Global-scale climate models will not be able to represent ridges and canyons directly and possible effects of these topographic features on the density fields and the circulation need to be parameterized. We regard the parameterization suggested in Ilicak et al. [27] based on a corrugation Burger number to be a step in this direction. It is shown in Ilicak et al. [27] that by using this parameterization without the topographic feature, the increase in overflow thickness downstream of the location of the topography becomes comparable to the corresponding increase in experiments with the topography included. Qualitatively this is correct since increased vertical mixing will raise the center of gravity from the bottom. However, a quantitative test of the parameterization should be based on comparisons with grid converged solutions, see the discussion above.

A property of the suggested parameterization is that it will always lift the center of gravity. The center of gravity can be steered 10 km further away from the coast when a ridge is present. With a slope steepness of 0.08, this corresponds to a vertical displacement of the core of the plume of 800 m downwards, which is larger than the increase of plume thickness ($\sim$ 100-200 m). This effect of the topography on the transport of dense water flows towards the deep ocean can not be captured by increased vertical diffusivity. Parameterizations of the effects of interactions between topography and the large scale flow are discussed for instance in Holloway [37] and in the textbook by Haidvogel and Beckmann [38]. The present authors want to point out that the parameterizations suggested so far are inadequate for capturing the dominating steering effect, and that it is outside the scope of the present paper to suggest such a parameterization.

4 Conclusions

The present investigations are performed to follow up on earlier studies of dense water plumes on slopes impinging on corrugations. We have focused on the steering effects of canyons and ridges horizontally and especially vertically. The ridges appear to steer and mix more strongly than canyons, and we have tried to explain this asymmetry. Furthermore, the effects of the bottom boundary condition on the results are addressed.

Qualitatively our results confirm that both canyons and ridges will create more mixing and that the core of dense water plumes will be steered away from the coast. In the present study, we find that both ridges and canyons will steer the center of gravity of dense water plumes substantially downwards compared to the case with a flat slope. For the parameters used here and a slope steepness of 0.08, the downward displacement of the plume’s core can be approximately 800 m. The vertical mixing due to a ridge or a canyon will lift the center of gravity of the plume upwards but can only partially compensate for the downward steering. In order to get the geostrophically balanced dominating flows along slopes correct in large and global scale model systems, the density field in physical space must be correct. We argue accordingly that a parameterization of this steering, horizontally and vertically, is needed. Since the overall effect of a ridge or a canyon is to move the center of gravity down, the use of the parameterization suggested in Ilicak et al. [27] will work in the wrong vertical direction. In a density space, with the horizontal coordinates in the plane and density on the vertical axis, the mean height of the dense water can be correct with the Ilicak et al. [27] parameterization. However, as the plume will be shifted horizontally, also the internal pressure gradients and the geostrophically balanced flow will be shifted.

There will be divergence along the corrugation, and this divergence will be stronger in the ridge case, potentially explaining why there is more mixing near a ridge. When a dense gravity flow along a slope meets a cross-cutting ridge, the flow will essentially first be steered away from the coast along the iso-lines of the bathymetry. A flow meeting a canyon will first follow the iso-lines of the bathymetry towards the coast. This asymmetry will also create an overall asymmetry in the total steering.

All experiments are performed with a constant drag coefficient as in Ilicak et al. [27] and with a bottom drag parameterization that is consistent with no-slip. With no-slip, the down-slope steering is stronger and the additional steering due to the choice of parameterization of bottom-drag is of the same order of magnitude as the topographic steering effect.