1 Introduction

We consider a planar sloping boundary, immersed in a fluid that is density stratified. If the slope is cold relative to the stratified ambient fluid at the same horizontal level, then a down-slope ‘katabatic’ flow of denser slope-adjacent fluid is to be expected. Such down-slope flows are found commonly in applications with cooling of sloping terrain in a stratified atmosphere, see for example the review [1]. Similar weak flows can also be obtained for a stably salt-stratified fluid adjacent to a sloping boundary, driven by a zero-flux condition at the boundary, as discussed by Philips [2] and Wunsch [3].

If a constant potential temperature difference between the slope and the ambient fluid is maintained at all heights, then the buoyancy at the slope surface is spatially uniform and a solution exists due to Prandtl [4]. This solution will be explicitly discussed below and is given by Eq. (6); this is a parallel flow, with no motion in the slope-normal direction. In terms of the velocity field, the Prandtl solution shares some of the characteristics of a wall jet or gravity current, with a maximum downwards flow near the slope surface but the down-slope velocity profile is bi-directional. There is a maximum downwards flow near the slope surface with a return flow predicted at larger distances from the surface. The down-slope velocity profile and the buoyancy profile both oscillate and decay in the slope-normal coordinate, as illustrated in Fig. 1.

Later extensions to the Prandtl state included the effects of a height dependent diffusivity profile; see for example the formulation of Rao and Snodgrass [5] and later discussion of Grisogono and Oerlemans [6]. However, observations made in otherwise calm conditions remain reasonably close to both the Prandtl prediction and the slower decaying profiles of Rao and Snodgrass [5] but with some scatter particularly in the far field as shown in Fig. 3 of [7]. Depth-integrated models require assumptions to be made for entrainment and profile shapes, but have also been obtained by (for example) Manins and Sawford [8] or Kondo and Sato [7]. Reduced models of this form have been applied with some success to jets/plumes, however simple extensions to unsteady flows are known to be problematic, in some cases leading to ill-posed models as discussed in [9, 10].

It is worth noting that the role of Coriolis forcing in katabatic flow is not a trivial one. It is known, e.g. [11], that even for down slope flows induced by uniform surface buoyancy the effects of background rotation lead to unsteady thickening of the near-surface layer. This behaviour is akin to that observed in Ekman boundary layers on sloping surfaces in a stratified fluid; see for example the ‘growing boundary layer’ states identified by Duck et al. [12] and Hewitt et al. [13]. In what follows we will assume that Coriolis effects remain negligible throughout.

More recently Xiao and Senocak have described the stability of Prandtl solutions for katabatic [14], anabatic [15] and katabatic flows including ambient forcing [16], assuming a constant surface-buoyancy flux. In general the stability of these states is governed by three parameters associated with slope angle, Prandtl number and a measure of buoyancy forcing at the slope surface. By constructing numerical solutions of the linearised stability equations at finite values of a forcing parameter and at fixed slope angles and Prandtl numbers, critical values of buoyancy forcing are obtained for temporally neutral down-slope propagating waves or down-slope aligned vortices. Numerical results close to onset indicated that the propagating wave modes appear first for steep slopes, whilst vortex modes occur first for shallow slopes. We will return to these modes of instability in this work too.

Of some practical relevance are cases of katabatic flow with a non-uniform distribution of surface buoyancy. Such flows must be qualitatively different, leading to a “non-parallel” development (ie. the layer evolves with the down-slope coordinate) and necessitating a corresponding detrainment/entrainment of fluid between the ambient and the near-slope flow, required by mass conservation. The work of Shapiro and Fedorovich [17] considered spatially non-uniform forcing of down-slope flows under the assumption that the surface buoyancy increases/decreases linearly with the down slope coordinate. Their implicit assumption, and an issue we will explicitly address here, was that this simplified flow could find application to slowly varying surface buoyancy profiles or transition zones between regions of uniform surface buoyancy.

Fig. 1
figure 1

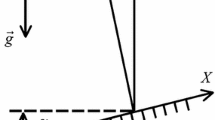
Katabatic flow down a sloping plane of angle \(\alpha\) to the horizontal. The dimensional coordinates (X, Z) are aligned with the downslope and slope-normal directions, with corresponding non-dimensional coordinates (x, z). The ambient fluid is stratified in the vertical \(Z^*\) direction, with buoyancy frequency N. The buoyancy distribution (red) varies across a layer of width \(\delta _0\) near the surface driving a downslope velocity (black). Both the buoyancy and velocity profile oscillate about zero as they decay into the ambient. Entrainment/detrainment into the layer is dependent on a down slope variation in the surface buoyancy on the L scale

Full size image

In what follows we begin by formulating a general boundary-layer approximation similar to that of Shapiro and Fedorovich [18] but applied to an arbitrary surface buoyancy forcing over a down-slope lengthscale that is substantially larger than the Prandtl depth. The resulting bi-directional parabolic problem for the two-dimensional katabatic flow is solved in Sect. 2 and results are compared to the self-similar predictions made in [17]. Having obtained the two-dimensional base flows we then go on to consider their stability in Sect. 3. By tackling the stability problem in the strongly-driven limit we can pick out the dominant mechanisms associated with the buoyancy-driven vortex perturbations and the inflectional wave perturbations. This approach also allows for a quasi-local treatment, allowing us to determine how the local velocity and buoyancy profiles in the non-uniformly cooled two-dimensional base state affect the stability compared to the uniform case of Xiao and Senocak [14]. A discussion is given in Sect. 4, with particular attention paid to describing the relative importance of the two main instability modes.

1.1 Formulation

We begin with the formulation of Shapiro and Fedorovich [17], using a Cartesian (X, Z) coordinate system that is aligned with a slope of angle \(\alpha\) (Fig. 1), where X is measured down the slope and Z is normal to the slope; in addition there is a vertical coordinate \(Z^*\) over which the ambient fluid’s density varies. We will denote the velocities in the directions of increasing (X, Z) by (U, W), whilst the pressure is P and buoyancy is B. In terms of the potential temperature \(\theta\), the buoyancy is \(B=g(\theta -\theta _\infty (Z^*))/\theta _r\), where g is the gravitational acceleration, \(\theta _\infty (Z^*)\) is the corresponding ambient value and \(\theta _r\) is a constant reference value. Similarly we work with a pressure that is measured relative to the ambient hydrostatic pressure, \(\Pi =P-P_\infty\).

The dimensional equations governing conservation of energy, momentum and mass are

$$\begin{aligned}&B_T + UB_X + WB_Z = N^2 \left( U\sin \alpha - W \cos \alpha \right) + \kappa \nabla ^2 B\,, \end{aligned}$$
(1a)
$$\begin{aligned}&U_T + UU_X + WU_Z = -\frac{1}{\rho _r} \Pi _X - B \sin \alpha + \nu \nabla ^2 U\,, \end{aligned}$$
(1b)
$$\begin{aligned}&W_T + UW_X + WW_Z = -\frac{1}{\rho _r} \Pi _Z + B \cos \alpha + \nu \nabla ^2 W\,, \end{aligned}$$
(1c)
$$\begin{aligned}&U_X + W_Z = 0\,, \end{aligned}$$
(1d)

where \(\nu\), \(\kappa\) are a constant kinematic viscosity and thermal diffusivity, \(\nabla ^2\) is the two-dimensional Laplacian and subscripts denote differentiation. Here

$$\begin{aligned} N= \sqrt{ \frac{g}{\theta _r} {\text{ d }{\theta _\infty } \over \text{ d }{Z^*}} }\,, \end{aligned}$$
(2)

is the buoyancy frequency, measured with respect to the vertical coordinate \(Z^*\) and is assumed to be constant.

The surface buoyancy \(B(X,Z=0,T)\) takes a value \(B_0\) at some reference location, and the spatial variation of B occurs over a known length scale L, down slope of this point. The coordinate system of (1) is then made non-dimensional via

$$\begin{aligned}&X=Lx\,,\quad Y=Ly\,,\quad Z=\delta _0 z\,, \quad T=\frac{t}{N\sin \alpha }\,,\quad \delta _0 = \sqrt{ \frac{ \nu }{N\sin \alpha } }\,. \end{aligned}$$
(3a)

We begin with solutions that are independent of the cross slope Y coordinate, but will return to more general behaviour in the context of the stability problem of Sect. 3. The slope-normal length scale, \(\delta _0\), is the depth of the Prandtl solution [4] when surface buoyancy is spatially uniform.

For the buoyancy, velocities and pressure we introduce

$$\begin{aligned}&B=\vert B_0 \vert \, b(x,z,t)\,,\quad U = U_0 \, u(x,z,t) \,, \end{aligned}$$
(3b)
$$\begin{aligned}&W = \epsilon U_0 \, w(x,z,t) \,,\quad \Pi = \epsilon L {\rho _r }\sin \alpha \vert B_0\vert \, p(x,z,t)\,, \end{aligned}$$
(3c)
$$\begin{aligned}&\epsilon = \delta _0/L\,,\quad U_0=\vert B_0 \vert /N\,, \end{aligned}$$
(3d)

where the given \(U_0\) is the appropriate velocity scale of the Prandtl solution assuming an O(1) Prandtl number; this solution is discussed more below and given explicitly by (6). Here \(\epsilon\) is an aspect ratio formed by the (slope-normal) Prandtl thickness (\(\delta _0\)) relative to the down slope lengthscale (L) over which the surface buoyancy is varying. In this choice of non-dimensionalisation we use the absolute value of the reference surface buoyancy \(\vert B_0\vert\), and a negative sign to drive a katabatic flow will be imposed explicitly in the surface boundary condition for B.

The governing dimensionless equations obtained via (1) and (3) become

$$\begin{aligned}&b_t + \text{ Fr }\,( ub_x + wb_z ) = \left( u - \frac{\epsilon }{\tan \alpha } w \right) + \frac{1}{\text{ Pr }}\, {\hat{\nabla }}^2 b\,, \end{aligned}$$
(4a)
$$\begin{aligned}&u_t + \text{ Fr }\,( uu_x + wu_z ) = - \epsilon p_x - b + {\hat{\nabla }}^2 u\,, \end{aligned}$$
(4b)
$$\begin{aligned}&\epsilon \left( w_t + \text{ Fr }\,( uw_x + ww_z) \right) = -p_z + \frac{b}{\tan \alpha } + \epsilon \, {\hat{\nabla }}^2 w\,, \end{aligned}$$
(4c)
$$\begin{aligned}&u_x + w_z = 0\,. \end{aligned}$$
(4d)

Here \(\text{ Fr }\) is an internal Froude number based on the Prandtl velocity scale \(U_0=\vert B_0\vert /N\) and the vertical lengthscale \(L\sin \alpha\),

$$\begin{aligned} \text{ Fr }= \frac{U_0}{NL\sin \alpha }=\frac{\vert B_0 \vert }{N^2 L \sin \alpha }\,, \end{aligned}$$
(4e)

\(\text{ Pr }\) is the corresponding Prandtl number (\(\nu /\kappa\)) and

$$\begin{aligned} {\hat{\nabla }}^2 \equiv \epsilon ^2 {\partial ^2 {}\over \partial {x^2}} + {\partial ^2 {}\over \partial {z^2}}\,. \end{aligned}$$
(4f)

1.2 Boundary and initial conditions

Our focus is initially on steady solutions to (4), where the boundary conditions are

$$\begin{aligned}&u=w=0\,,\quad b = b_s (x)\,\quad \text{ on } \quad z=0\,, \end{aligned}$$
(5a)
$$\begin{aligned}&u \sin \alpha - w \epsilon \cos \alpha \rightarrow 0\,, \quad b \rightarrow 0\, \quad \text{ as } \quad z \rightarrow \infty \,. \end{aligned}$$
(5b)

These correspond to no-slip, impermeability, a known buoyancy on the slope surface, and no buoyancy perturbation far from the surface. The constraint \(u \sin \alpha - w \epsilon \cos \alpha \rightarrow 0\) is consistent with no buoyancy perturbation, as can be seen from the form of (4a), and corresponds to a requirement for purely horizontal along-isentrope flow in the far field.

The function \(b_s(x)\) is any general distribution of surface buoyancy. If \(b_s\equiv -1\) for all x, then a non-entraining (\(w=0\)) steady solution exists, which is the classical x-independent Prandtl [4] solution \((u,w,b)=(U_p,0,B_p)\), where

$$\begin{aligned}&U_p(z) = \frac{1}{\sqrt{\text{ Pr }}} \exp \left( -\frac{z\,\text{ Pr}^\frac{1}{4}}{\sqrt{2}} \right) \sin \left( \frac{z\,\text{ Pr}^\frac{1}{4}}{\sqrt{2}} \right) \,, \end{aligned}$$
(6a)
$$\begin{aligned}&B_p(z) = - \exp \left( -\frac{ z\,\text{ Pr}^\frac{1}{4} }{\sqrt{2} } \right) \cos \left( \frac{z\,\text{ Pr}^\frac{1}{4} }{\sqrt{2}} \right) \,. \end{aligned}$$
(6b)

This parallel solution is independent of \(\text{ Fr }\) and any variation with the other parameters is already captured by (3).

Whilst (4) can be solved for arbitrary \(\epsilon\) our interest here is restricted to shallow flows for which \(\epsilon \ll 1\), and in this case the condition for u in (5) simplifies to \(u\rightarrow 0\) in the far field. In the shallow limit the equations are independent of the slope angle; any variation with \(\alpha\) is captured by the scaling factors of (3), which is consistent with the observations of Shapiro and Fedorovich [18]. Analogues of this \(\epsilon \ll 1\) boundary-layer system have been used in other related configurations, for example the Ekman layer on a sloping boundary in a stratified fluid as discussed in [12, 19], but in those cases driven by rotation rather than surface buoyancy.

2 Steady shallow katabatic flow

We now present solutions to the equations (4) subject to conditions (5) for shallow flows with \(\epsilon \ll 1\). Rather than uniform surface conditions associated with the Prandtl solution (6) we allow for more general surface buoyancy distributions. To this end, we consider the piece-wise distribution

$$\begin{aligned} b_s(x) ={\left\{ \begin{array}{ll} -1 &{} x<0\,, \\ -1+\gamma x &{} 0\le x \le 1\,, \\ -1+\gamma &{} x>1\,. \end{array}\right. } \end{aligned}$$
(7)

Here the unit length of the non-uniformly cooled region is set by our choice of non-dimensionalisation of x based on L, and we shall restrict attention to down-slope flows with \(b_s(x) \le 0\) by choosing \(\gamma \le 1\).

In the shallow-flow limit (\(\epsilon \ll 1\)) the governing system (4) becomes parabolic. However the problem is bi-directional with the down slope velocity u having both positive and negative regions. Therefore, the computational approach requires both up-slope and down-slope conditions, and in this case we assume that as \(\vert x \vert \rightarrow \infty\) the solution reverts to the appropriate x independent Prandtl state (6) with surface buoyancy values of \(-1\) far up the slope and \(-1+\gamma\) far down the slope. Any entrainment/detrainment where \(w\ne 0\) as \(z \rightarrow \infty\) therefore occurs only in the vicinity of the transition zone defined by (7), decaying both up (\(x\rightarrow -\infty\)) and down (\(x\rightarrow \infty\)) slope.

We obtain steady solutions to the nonlinear two-dimensional problem (4) by a second-order central finite-difference scheme and Newton iteration for the nonlinear terms. Solving for all x positions simultaneously in this way avoids issues with the bi-directionality, alternatively this can be dealt with by (for example) the zig-zag scheme [20]. For a non-uniformly spaced computational mesh with \(N_x \times N_z\) nodes, this leaves each Newton iteration to invert a \(3N_xN_z \times 3N_x N_z\) sparse linear system which is achieved using the MUMPS library [21]. The results we present are independent of \(N_x\), \(N_z\) and the domain truncation in both x and z.

Fig. 2
figure 2

Down-slope profiles of entrainment/detrainment from the katabatic surface layer when the surface buoyancy is given by (7). These results represent shallow (\(\epsilon \ll 1\)) solutions of (4), \(\text{ Fr }=1\) and \(\gamma = -0.8,-0.4,-0.2,0.2,0.4,0.8\) increasing in the direction of the arrow shown. Dashed lines indicate the corresponding x-independent values, \(w_l(z\rightarrow \infty )\), as predicted by the steady similarity solution (8)

Full size image

In Fig. 2 we show computational results for the x-dependent entrainment (negative) and detrainment (positive) velocity \(w(x,z \rightarrow \infty )\), as obtained for a range of \(\gamma\) and \(\text{ Fr }=1\). Here \(\gamma\) defines the down-slope gradient of surface buoyancy as given by the piece-wise profile (7). When \(0<\gamma <1\) the bulk (u) motion remains down-slope but decreases with x leading to a detrainment from the surface layer; if \(\gamma <0\) the down-slope flow increases with x and there is a corresponding entrainment from the ambient fluid. Sufficiently far up/down slope the flow returns to the parallel Prandtl solution (6) which has no entrainment or detrainment. Figure 2 shows that decay back to a Prandtl solution as x increases becomes slower for increasingly large negative values of \(\gamma\) and we address this behaviour below in Sect. 2.1.

Fig. 3
figure 3

Peak levels of non-dimensional entrainment/detrainment, as measured by the maximum/minimum of \(w(x,z\rightarrow \infty )\) taken over all x positions. The dimensional entrainment is \(\epsilon U_0 w(x,z\rightarrow \infty )\) as given by (3). Solid line: \(\epsilon \ll 1\) solutions of (4) subject to (7) with \(\text{ Fr }=1\) and variable \(\gamma\). Data points: the similarity solution (8), which only depends on the combination \(\gamma \text{ Fr }\). There is quantitative agreement in general, but this diverges rapidly in the region of \(\gamma \text{ Fr }\) near to unity

Full size image

A similarity solution to (4) was obtained by Shapiro & Fedorovich [17]. Their solution assumes an unbounded linear variation of the buoyancy at the surface of the slope, which replaces (7) with \(b_s(x) = \gamma (x-x_0)\) at all x locations, for some constant \(\gamma\). A solution to (4) can then be sought in the form

$$\begin{aligned}&u = (x-x_0) u_l (z) + \epsilon u_0(z)\,,\quad w = w_l(z)\,, \end{aligned}$$
(8a)
$$\begin{aligned}&b = (x-x_0) b_l(z) + \epsilon b_0(z)\,,\quad p = (x-x_0) p_l(z) + \epsilon p_0(z)\,, \end{aligned}$$
(8b)

where \(x_0\) is a constant associated with the choice of a reference position. As noted in [17], the subscript l terms give a standard stagnation-point form of solution; the \((u_0,b_0,p_0)\) terms are not present in the leading-order boundary-layer \(\epsilon \ll 1\) limit. Similar stagnation-point assumptions have been applied to problems of rotating stratified flow as in [13, 22]. The solution for \((u_l,w_l,p_l,b_l)\) only depends on the parameter combination \(\gamma \text{ Fr }\) because the lengthscale L is absent in the unbounded self-similar formulation.

The similarity solution leads to a constant x-independent entrainment/detrainment, which is \(w_l(z\rightarrow \ \infty )\) and represented in Fig. 2 by dashed horizontal lines. We can see that the similarity solution does give an effective quantitative prediction provided that \(\gamma \text{ Fr }>0\) is not too large. Figure 3 presents the ‘peak’ flow in/out of the katabatic layer (measured over all x positions) as a function of \(\gamma \text{ Fr }\) (solid line) and compares this to the simpler similarity solution (data points). Again the similarity solution remains predictive but diverges rapidly from the two-dimensional computations in the region of \(\gamma \text{ Fr }\approx 1\).

To explain the observed divergence from the self-similar prediction (as shown in Fig. 3) we consider further corrections to the assumed self-similar form (8) in the shallow limit via

$$\begin{aligned} u = (x-x_0) \left( u_l (z) + (x-x_0)^\lambda \tilde{u}_l(z) \right) \,,\quad w = w_l(z) + (x-x_0)^\lambda \tilde{w}_l(z)\,, \end{aligned}$$
(9)

with similar expressions for b and p. Linearisation of the tilde quantities gives a one-dimensional eigenvalue problem for \(\lambda\). Examination of the spectrum of eigenvalues for increasing values of \(\gamma \text{ Fr }\) shows that the real part of \(\lambda\) changes sign from positive to negative at \(\gamma \text{ Fr }\approx 0.9\) when \(\text{ Pr }=0.71\). The correction terms therefore grow near \(x_0\) when \(\lambda _r<0\) and this delineates the region of applicability of one-dimensional similarity solutions to the two-dimensional computational results.

In addition, the similarity solution has unsteady periodic states [17], which arise through a temporal instability via a supercritical Hopf bifurcation. However, this (self-similar) unsteady instability appears to have no relevance to the full problem defined by (4). Instead, katabatic flows become temporally unstable to modes of wavelength comparable to the short lengthscale \(\delta _0\) and that grow on a much faster timescale than that defined in (3). We return to describe these instabilities in Sect. 3 below.

2.1 Strongly decreasing surface buoyancy

When the surface buoyancy decreases rapidly in the down-slope direction (\(\vert \gamma \vert \gg 1\) with \(\gamma\) negative) the flow takes larger distances to equilibrate to the Prandtl solution. We can approach this limit directly, by noting that as \(\gamma \rightarrow -\infty\) the steady form of (4) (with \(\epsilon \ll 1\)) can be re-scaled via

$$\begin{aligned} b&= \vert \gamma \vert \,\bar{B}(x,\bar{Z})\,, \quad u = \vert \gamma \vert ^{1/2} \text{ Fr}^{-1/2} \,\bar{U}(x,\bar{Z})\,, \end{aligned}$$
(10a)
$$\begin{aligned} w&= \vert \gamma \vert ^{1/4} \text{ Fr}^{-3/4} \,\bar{W}(x,\bar{Z})\,, \quad \bar{Z} = \vert \gamma \vert ^{1/4}\text{ Fr}^{1/4}\, z \,. \end{aligned}$$
(10b)

This results in a slightly modified system,

$$\begin{aligned}&\bar{U} \bar{B}_x+\bar{W} \bar{B}_{\bar{Z}} = \frac{1}{Pr} \bar{B}_{\bar{Z} \bar{Z}} + O\left( \frac{\bar{U}}{\vert \gamma \vert \text{ Fr }} \right) \,, \end{aligned}$$
(10c)
$$\begin{aligned}&\bar{U} \bar{U}_x+ \bar{W} \bar{U}_{\bar{Z}} = -\bar{B} + \bar{U}_{\bar{Z} \bar{Z}}\,, \end{aligned}$$
(10d)
$$\begin{aligned}&\bar{U}_x+\bar{W}_{\bar{Z}} = 0\,, \end{aligned}$$
(10e)

to be solved subject to the same homogeneous boundary conditions, but with the re-scaled surface buoyancy \(\bar{B}(x,\bar{Z}=0)=x\) for \(x\in [0,1]\) and \(\bar{B}(x>1,\bar{Z}=0) = -1\). The only difference in this limit is the loss of the forcing term in the energy equation (10c), which is highlighted above by the \(O(\bar{U}/\vert \gamma \vert \text{ Fr})\) term.

Crucially, this leading-order solution differs from the general case in that \(\bar{U}\ge 0\) and \(\bar{B}\le 0\) for all \(\bar{Z} \ge 0\) and there is no oscillation with \(\bar{Z}\) as one approaches the ambient conditions. As we shall describe in the next section, this has consequences for the stability properties of solutions (10) compared to typical solutions of (4), and even (6).

An asymptotic description of (10) is possible (related to the solution of Pohlhausen [23]), which is valid sufficiently far down the slope (\(x\gg 1\)), past the non-uniformly cooled region. This solution thickens in the down-slope direction, increasing in magnitude and with a corresponding (decreasing) entrainment from the ambient fluid. The reduced equations are

$$\begin{aligned} \bar{U}(x,\bar{Z})&= \hat{U} (\hat{Z}) x^{1/2} \,, \quad \bar{W}(x,\bar{Z}) = \left( \hat{W}(\hat{Z}) +\frac{\hat{Z}}{4} \hat{U}(\hat{Z}) \right) x^{-1/4}\,, \end{aligned}$$
(11a)
$$\begin{aligned} \bar{B}(x,\bar{Z})&= \hat{B}(\hat{Z}) \,, \quad \bar{Z} = \hat{Z} x^{1/4}\,, \end{aligned}$$
(11b)

such that

$$\begin{aligned}&\hat{W} \hat{B}' = \text{ Pr}^{-1} \hat{B}''\,, \end{aligned}$$
(11c)
$$\begin{aligned}&\tfrac{1}{2}{\hat{U}^2} + \hat{W} \hat{U}' = -\hat{B} + \hat{U}''\,, \end{aligned}$$
(11d)
$$\begin{aligned}&\tfrac{3}{4}{\hat{U}} + \hat{W}' = 0\,; \end{aligned}$$
(11e)

where prime indicates differentiation with respect to the re-scaled coordinate \(\hat{Z}\).

We cannot neglect the term \(\bar{U}/\vert \gamma \vert \text {Fr}\) in (10c) at all x positions and when sufficiently far downstream from the non-uniformly cooled region it must be re-included for the solution to eventually recover down slope to a Prandtl state. The lengthscale at which this adjustment occurs can be determined from re-balancing the previously neglected term for large x, for example in (10c) we impose the balance

$$\begin{aligned} {\bar{B}}_{\bar{Z} \bar{Z}} \sim \frac{\bar{U}}{\vert \gamma \vert \text {Fr}} \end{aligned}$$

where from (11) we know that \(\bar{B} \sim O(1)\), \(\bar{Z} \sim O(x^{1/4})\), \(\bar{U} \sim O(x^{1/2})\). Therefore, eventually the neglected term must be reintroduced, which occurs when \(x = O(\vert \gamma \vert \text {Fr})\), at which point a down-slope x-invariant Prandtl solution (6) is recovered.

3 Instability in the shallow-flow limit

We can now consider the stability of the two-dimensional katabatic flows described in the previous section, to temporally growing small-amplitude perturbations. We are free to look for disturbances of any length scale, but if this disturbance length scale is comparable to the slope-normal scale \(\delta _0\) rather than the down slope scale L (with \(\delta _0\ll L\)) then the resulting stability problem is determined locally at each x position rather than globally. In addition, if we can find such unstable short waves, they have an associated fast time scale which means they grow rapidly. We therefore introduce

$$\begin{aligned} (\xi ,\eta ,\tau ) = \frac{1}{\epsilon } (x,y,t)\,. \end{aligned}$$
(12)

These perturbations are applied to a steady two-dimensional solution of (4) which varies on the slower downslope x scale of the non-uniform buoyancy forcing. We then seek a solution in the form

$$\begin{aligned}&\left( u(x,z),0,w(x,z),p(x,z),b(x,z)\right) \nonumber \\&\quad + \,\Delta \left( \hat{u}, \hat{v}, \frac{\hat{w}}{\epsilon }, \frac{\text{ Fr }}{\epsilon } \hat{p}, \hat{b} \right) \exp \left\{ i\left( \hat{k}_x\, \xi + \hat{k}_y \, \eta - \text{ Fr }\, \hat{\omega } \, \tau \right) \right\} \,, \end{aligned}$$
(13)

where \(\Delta \ll 1\) for small amplitude perturbations and \(\hat{u}, \hat{v}, \hat{w}, \hat{p}, \hat{b}\) are shape functions that depend on the slope-normal coordinate z. The base flow is two dimensional but we allow for a cross slope flow (\(\hat{v} \ne 0\)) in the stability problem.

After some rearrangement, the perturbation equations for \(\Delta \ll 1\) become

$$\begin{aligned}&i \hat{k}_x \hat{u} + i \hat{k}_y \hat{v} + \hat{w}' = 0\,, \end{aligned}$$
(14a)
$$\begin{aligned}&-i \hat{\omega } \hat{u} + i \hat{k}_x u \hat{u} + u_z \hat{w} = - i \hat{k}_x \hat{p} +\frac{\epsilon }{\text{ Fr }} \left\{ \hat{u}'' - \hat{k}_y^2 \hat{u} - \hat{k}_x^2 \hat{u} - \hat{b} \right\} \,, \end{aligned}$$
(14b)
$$\begin{aligned}&-i \hat{\omega } \hat{v} + i \hat{k}_x u \hat{v} = -i \hat{k}_y \hat{p} +\frac{\epsilon }{\text{ Fr }} \left\{ \hat{v}'' - \hat{k}_y^2 \hat{v} - \hat{k}_x^2 \hat{v} \right\} \,, \end{aligned}$$
(14c)
$$\begin{aligned}&-i \hat{\omega } \hat{w} + i \hat{k}_x u \hat{w} =- \hat{p}' + \frac{\epsilon }{\text{ Fr }} \left\{ \hat{w}'' -\hat{k}_y^2 \hat{w} - \hat{k}_x^2 \hat{w} +\frac{\hat{b}}{\tan \alpha } \right\} \,, \end{aligned}$$
(14d)
$$\begin{aligned}&-i \hat{\omega } \hat{b} + i\hat{k}_x u \hat{b} + b_z \hat{w} =\frac{\epsilon }{\text{ Fr }} \left\{ \frac{1}{\text{ Pr }} \left( \hat{b}'' -\hat{k}_y^2 \hat{b} - \hat{k}_x^2 \hat{b} \right) + \hat{u} - \frac{\hat{w}}{\tan \alpha } \right\} \,. \end{aligned}$$
(14e)

Here we have neglected x derivatives of the base katabatic flow since they are on a length scale much longer than the wavelength of the perturbation. Whilst the base flow equations (4) do not explicitly depend on the slope angle, this is not true for the linearised stability equations (14).

The combination \(\epsilon /\text{Fr }\) can be interpreted as an inverse Reynolds number based on the Prandtl solution velocity scale \(U_0\) (3d) and thickness \(\delta _0=\epsilon L\) (3a), so in what follows we use

$$\begin{aligned} \text{ Re }=\frac{\text{ Fr }}{\epsilon }\,. \end{aligned}$$
(15)

Apart from some notation differences, the linear stability problem (14) was presented in the recent work of Xiao and Senocak [14] applied to the classical (linear) one-dimensional solution of Prandtl (6), subject to a zero buoyancy flux condition at the boundary. Their approach determined a critical buoyancy flux (here this would be a critical value for \(\text{ Re }\)) for instability. In this work we will focus on the shallow-flow limit (\(\epsilon \ll 1\), \(\text{ Fr }=O(1)\)) which corresponds to \(\text{ Re }\gg 1\).

For simplicity, given the bi-directional nature of the base flow, we will restrict attention here to temporal stability, treating \(\hat{\omega }\) in (13) as an eigenvalue to be determined. We also restrict attention to two broad classes of disturbance (i) vortices aligned with the down-slope direction (\(\hat{k}_x=0\)) and periodic in the cross-slope direction (\(\hat{k}_y\ne 0\)), and (ii) waves that propagate up/down the slope (\(\hat{k}_x \ne 0\)) and are independent of the cross-slope coordinate (\(\hat{k}_y=0\)).

Fig. 4
figure 4

Down slope variation of the vortex growth rate (multiplied by \(\sqrt{\tan \alpha }\) where \(\alpha\) is the slope angle). These results are obtained from (17) with \(\text{ Fr }=1\) and \(\hat{k}_y = \pi\) and show a a decreasing (with x) surface buoyancy with \(\gamma =0.1,0.5,0.9\) leading to detrainment and b an increasing (with x) surface buoyancy with \(\gamma = -1,-2,-4,-8\) leading to entrainment

Full size image

Downslope vortices In the limit \(\text {Re}\gg 1\), requiring a balance of the unsteady/advection terms, pressure gradient and the buoyancy forcing term (\(\hat{b} / \tan \alpha\)) of (14d) reveals that

$$\begin{aligned} (\hat{v}, \hat{w}, \hat{\omega } ) = \text{ Re}^{-1/2} ( \tilde{v}, \tilde{w}, \Omega )\,, \end{aligned}$$
(16)

and we can reduce (14a) and (14c)–(14e) to

$$\begin{aligned} \tilde{w}''(z) - \hat{k}_y^2 \tilde{w}(z) = -\frac{\hat{k}_y^2}{\Omega ^2 \tan \alpha }{\partial {b} \over \partial {z}}\bigg \vert _{(x,z)} \tilde{w}(z)\,; \end{aligned}$$
(17)

where the down-slope x coordinate only appears parametrically via the local buoyancy gradient. This problem is to be solved subject to \(\tilde{w}=0\) at the boundary (\(z=0\)) and in the far field (\(z \rightarrow \infty\)).

For large wavenumber \(\hat{k}_y \gg 1\) the resulting small-wavelength vortex becomes spatially localised and offset from the slope surface. This localisation occurs in a thin layer around \(z=z_0\) which is of width \(O(\hat{k}_y^{-1/2})\), and \(z_0\) is the point at which the buoyancy gradient term \(-\partial b/\partial z\) is maximised. In this layer the second-derivative term in (17) is therefore \(O( \hat{k}_y)\) and the leading-order growth rate can be found directly from the other \(O(\hat{k}_y^2)\) terms. We therefore find that

$$\begin{aligned} \Omega _i \rightarrow \sqrt{ -\frac{\partial b}{\partial z} \bigg \vert _{(x,z_0)}\frac{1}{\tan \alpha } }\,, \end{aligned}$$
(18)

where \(z_0\) is an inflection point in the buoyancy profile with a negative buoyancy gradient. To determine the leading-order vortex shape and corrections to this growth rate requires continuation to higher order in the large \(\hat{k}_y\) expansion.

For the special case of a uniform surface buoyancy, the associated Prandtl solution given by (6) has a growth rate bounded above by

$$\begin{aligned} \sqrt{\frac{e^{-\pi }\text{ Pr}^{1/4}}{\sqrt{2}\,\tan \alpha }} \,, \end{aligned}$$
(19)

and the vortices are located at a distance \(z_0 =\sqrt{2}\,\pi \text{ Pr}^{-1/4}\) from the boundary.

Fig. 5
figure 5

The (inviscid) vortex disturbance obtained from (17), shown in the cross/normal-slope plane (y, z) as a velocity field for \(\text{ Fr }=1\) and \(\gamma =0.9\) at \(x=0.1,0.5,0.8,1.1\) with a cross-slope wavenumber of \(\hat{k}_y=\pi\). The colours show the velocity of the baseflow u(x, z) with red/blue for down/up-slope flow. The solid lines are at inflection points of the baseflow buoyancy \(\partial ^2 b/\partial z^2=0\), whilst dashed lines are at zeros of down/up-slope flow \(u=0\). For the Prandtl solution (6) the solid and dashed lines overlap

Full size image

In Fig. 4 we solve (17) at successive x positions, and present the variation of \(\Omega _i\sqrt{\tan \alpha }\) for a range of non-uniform surface buoyancy profiles, as defined by (7) for varying \(\gamma\). In this \(\text{ Re }\gg 1\) problem the dependence on the slope angle is entirely described by this \(\sqrt{\tan \alpha }\) factor. If the surface buoyancy increases with x (\(\gamma >0\)) the detraining slope flow becomes locally more unstable as seen in Fig. 4a before eventually readjusting to a slower and more stable down-slope Prandtl state. However, for surface buoyancy that decreases with x the entraining flow becomes locally more stable, as seen in Fig. 4b, before returning to a faster and more unstable Prandtl solution for large x.

Gradual stabilisation of the vortex mode for entraining flows is explained by the results of Sect. 2.1. The accelerating solution given by (10) is crucially free (at leading order) from any oscillation with the slope-normal coordinate z. In such a flow there is a monotonic decay of buoyancy flux from the cold surface and it is therefore stable to vortex modes.

In general the vortex is displaced from the boundary at a local minimum of the buoyancy gradient. For the special case of the Prandtl solution (6), this z-location is also where the down-slope flow first changes sign from positive (down the slope) to negative (up the slope). For non-uniform surface buoyancy, the vortex z-location varies with down-slope position. In such situations the vortex can be found in regions of up/down-slope flow, whilst still being correlated with a local minimum of the buoyancy flux.

In Fig. 5 we show an example of the vortex location for increasing x, in a non-uniform surface buoyancy solution of the type shown in Fig. 2. The colour contours show the down-slope flow (red for down-slope and blue for up-slope) whilst the vector field is the vortex mode’s velocity. The solid/dashed horizontal lines show where the katabatic flow changes sign (\(u=0\)) and where the buoyancy flux is a max/min (\(\partial ^2 b/\partial z^2=0\)). At lower values of x the vortex is located around \(u=0\) (Fig. 5a), but at \(x=0.8\) (Fig. 5c) the effects of the non-uniform buoyancy forcing are felt and the bulk of the vortex is found in the up-slope flow \(u<0\), before returning back to where \(u=0\) further down the slope (Fig. 5d).

For larger values of \(\hat{k}_y\), viscous effects in the thin vortex layer eventually act to restabilise the flow. The reader is referred to the related discussions in the centrifugal literature, for example Hall [24] or Denier et al. [25]. This restabilisation occurs when \(\hat{k}_y =O(\text{ Re}^{1/4})\).

Rayleigh waves In the inviscid limit \(\text{ Re }\gg 1\) with \(\hat{k}_y=\hat{v} = 0\) and \(\hat{k}_x=O(1)\) we recover a standard Rayleigh problem for the growth rate \(\hat{\omega }\)

$$\begin{aligned} \left( u\bigg \vert _{(x,z)} - \, \frac{\hat{\omega }}{\hat{k}_x} \right) \left( \hat{w}''(z) - \hat{k}_x^2 \hat{w}(z)\right) ={\partial ^2 {u}\over \partial {z^2}}\bigg \vert _{(x,z)} \hat{w}(z)\,; \end{aligned}$$
(20)

again to be solved subject to \(\hat{w} = 0\) at the boundary \(z=0\) and in the far field.

Sufficiently far down the slope we always recover the Prandtl solution (6) which is more/less unstable for increased/decreased down-slope flows associated with \(\gamma <0\) and \(\gamma >0\) respectively. For these Prandtl states the temporal growth rate \(\hat{\omega }_i\) peaks at wave numbers near \(\hat{k}_x \approx 0.25\).

Figure 6 shows the variation of the wave’s growth rate for a variety of solutions to (4). We typically find a monotonic increase/decrease of the growth rate, however, we must qualify this statement by noting that there is a very slight non-monotonic adjustment in the growth rate near to \(x=0\) just visible in Fig. 4b.

The vortex modes are strongly stabilised for accelerated/entraining down slope flows (Fig. 4b) because of a reduced oscillation in the buoyancy profile. However the Rayleigh waves ultimately owe their existence to inflectional down-slope velocity profiles, which persist even in the limiting solutions (10)–(11).

Fig. 6
figure 6

Down slope variation of the wave growth rate obtained from the Rayleigh problem (20) for \(\text{ Fr }=1\) and \(\hat{k}_x = 0.25\). Shown is a decreasing (with x) surface buoyancy \(\gamma =0.1,0.5,0.9\) leading to detrainment and b increasing (with x) surface buoyancy \(\gamma = -1,-2,-4,-8\) leading to entrainment

Full size image

4 Conclusion

Two-dimensional solutions have been obtained for a katabatic flow down a non-uniformly cooled slope, assuming that the down-slope length scale L over which the surface buoyancy varies is long compared to the boundary-layer thickness \(\delta _0 = \sqrt{\nu /N\sin \alpha }\). For a cooled slope surface, the main flow is down the slope, but there are regions of up-slope return flow. Both the buoyancy and down-slope velocity profiles approach the ambient conditions via a decaying spatial oscillation, which makes the parabolic boundary layer for shallow flows bi-directional.

We apply a numerical scheme to deal with this bi-directionality and compare our two-dimensional solutions with the one-dimensional similarity assumption of Shapiro and Fedorovich [17]. These similarity states are associated with an unbounded surface buoyancy that varies linearly with down-slope coordinate x. Nevertheless, the similarity solutions give good quantitative estimates for the entrainment/detrainment associated with the non-uniform buoyancy region. These estimates become poor beyond limiting value of \(\gamma \text{ Fr }\), where \(\gamma\) is the down-slope gradient of the surface buoyancy and \(\text{ Fr }\) is an internal Froude number. This limiting value varies with Prandtl number and can be found by an eigenvalue problem associated with the similarity states.

The temporal stability of two-dimensional non-uniformly cooled states (to small-amplitude three-dimensional disturbances) is assessed under the assumption that \(\text{ Fr }/\epsilon \gg 1\). In this limit there are (broadly) two types of (linear) temporal instability,

  1. (i)

    down-slope aligned stationary vortices that are periodic in the cross-slope direction, and of amplitude proportional to

    $$\begin{aligned} \exp \left\{ {\hat{\Omega }_i \, T } \, \left( \frac{\text{ Fr }}{\epsilon } \right) ^{1/2} \frac{N\sin \alpha }{\sqrt{\tan \alpha }} \,\right\} \,, \end{aligned}$$
  2. (ii)

    down-slope propagating Rayleigh waves of amplitude proportional to

    $$\begin{aligned} \exp \left\{ { \hat{\omega }_i \, T } \, \left( \frac{\text{ Fr }}{\epsilon } \right) \, N\sin \alpha \,\right\} \,, \end{aligned}$$

where \(\hat{\Omega }_i\), \(\hat{\omega }_i\) are the constants presented in Figs. 4 and 6 (for example), T is the dimensional timescale and N the stratification frequency. In this limit we are able to explicitly obtain the dependence of the growth rates on the slope angle (\(\alpha\)), something that is not possible for \(\text{ Fr }/\epsilon = O(1)\).

Unstable vortex modes are obtained even though the slope surface is being cooled because the buoyancy profile of katabatic flow is oscillatory (Fig. 1). This oscillation means that an unstable region still exists, but it is displaced away from the boundary (Fig. 5).

As can be seen from the above expressions, the wave modes always grow more quickly if \(\alpha =O(1)\) (steep slopes) but the growth rates are comparable on shallow slopes if

$$\begin{aligned} \alpha \sim \frac{\hat{\Omega }_i^2}{\hat{\omega }_i^2} \frac{\epsilon }{\text{ Fr }}\,. \end{aligned}$$

The growth rate results of Figs. 4 and 6 show that \(\hat{\Omega }_i\) can be an order of magnitude larger than \(\hat{\omega }_i\) making this balance plausible even when \(\text{ Fr }/\epsilon\) is large enough for the boundary-layer approximation to be useful. Of course combinations of the two modes in the form of oblique propagating waves are also possible.

The presence of both vortex and wave modes at finite values of \(\text{ Fr }/\epsilon\) (rather than the limiting behaviour described above) was demonstrated by the DNS results of Xiao and Senocak [14]. Of particular interest for katabatic flow is that the behaviour of fully developed turbulent states remains similar to the simple predictions of the Prandtl states (6) despite these instabilities. The role of nonlinearity for these disturbances is clearly a topic for future study.

Finally, while the vortex and wave modes develop with length scales comparable to the katabatic thickness \(\delta _0\) and corresponding time scales \(\delta _0/U_0\), there are also be non-growing perturbations on the (gravity wave) time scale associated with the stratification component \(1/N\sin \alpha\). These slower scale oscillations decay in entraining flows (and indeed for the Prandtl solution) but can be sustained in detraining flows, leading to a propagating and diffusing oscillation moving into the ambient as described in the appendix below.

This work was motivated by the time REH spent as a post-doc with Prof. PA Davies in the late 90s. Peter, your expertise, hospitality and humour over the intervening years are greatly appreciated!