Abstract
The Pythagorean fuzzy sets are more robust than fuzzy sets and intuitionistic fuzzy sets in dealing with the problems involving uncertainty. To compare two Pythagorean fuzzy sets, distance measures play a crucial role. In this paper, we have proposed some novel distance measures for Pythagorean fuzzy sets using t-conorms. We have also discussed their various desirable properties. With the help of suggested distance measures, we have introduced some new knowledge measures for Pythagorean fuzzy sets. Through numerical comparison and linguistic hedges, we have established the effectiveness of the suggested distance measures and knowledge measures, respectively, over the existing measures in the Pythagorean fuzzy setting. At last, we have demonstrated the application of the suggested measures in pattern analysis and multi-attribute decision-making.
Similar content being viewed by others
Introduction
Zadeh [1] introduced the concept of fuzzy sets (FSs) for handling deterministic uncertainty. Each element in a fuzzy set (FS) possesses a grade of membership \(\left(\mu \right)\) lying between 0 and 1. However, in an FS, the grade of non-membership \(\left(\vartheta \right)\) is by default taken as \(1-\mu \). So to assign an independent non-membership grade to an element, a novel extension of FSs known as intuitionistic fuzzy set (IFS) was given by Atanassov [2]. In an IFS, the sum of membership grades is less or equal to one i.e., \(\mu +\vartheta \le 1\). Though there are numerous applications of intuitionistic fuzzy sets (IFSs) but their scope is limited due to the restriction on sum of membership grades. The IFSs fail to handle those uncertain problems where \(\mu +\vartheta >1\). So, the concept of Pythagorean fuzzy set (PFS) was proposed by Yager [3] as an extension of intuitionistic fuzzy sets [2] (IFSs) and fuzzy sets [1] (FSs) for solving the problems involving uncertainty more precisely. Each element of a PFS has a membership grade \(\left(\mu \right)\) and a non-membership grade \(\left(\vartheta \right)\) with their square sum at most one \(\left({\mu }^{2}+{\vartheta }^{2}\le 1\right)\). The FSs and IFSs form a part of the space of PFSs and therefore the space of PFSs is wider than the space of FSs and IFSs.So, PFSs are more powerful than FSs and IFSs in handling uncertain problems. The technique for order of preference by similarity to ideal solution (TOPSIS) in the Pythagorean fuzzy (PF) setting and the concept of the Pythagorean fuzzy number were suggested by Zhang and Xu [4]. Various PF aggregation functions with their utility in decision-making were given by Yager [5]. Wei and Lu [6] introduced some power aggregation functions for PFSs. Using Einstein operations, Garg [7] proposed some new aggregation functions in the PF environment. Wei [8] suggested some PF interaction aggregation functions with their utility in multi-attribute decision-making (MADM). Many studies [9,10,11,12] concerning the PF aggregation functions with their various applications are available in the literature. The TODIM (an acronym in Portuguese for Interactive and Multicriteria Decision Making) method for PFSs was introduced by Ren et al. [13]. Peng et al. [14] proposed some information measures for PFSs. A novel PF distance measure was proposed by Peng and Dai [15]. Some PF measures of correlation with their utility were proposed by Singh and Ganie [16]. Various researchers [17,18,19,20,21,22,23,24] have studied PFSs and applied them in distinct uncertain situations. The current study is related to the development of some novel PF distance measures and knowledge measures.
The main contributions of this paper are as:
-
We suggest a new method of constructing the PF distance measures from t-conorms and introduce four new PF distance measures.
-
We discuss various desirable properties of the suggested PF distance measures.
-
We propose four weighted PF distance measures.
-
We suggest a general method of constructing the PF knowledge measures from the proposed PF distance measures and propose four new knowledge measures based on PFSs.
-
We compare the suggested PF measures of distance and knowledge with the available PF measures of compatibility.
-
We demonstrate the applicability of the suggested measures in pattern recognition and MADM.
Related work
Distance measures are very powerful in comparing two objects based on their inequality content. For FSs and IFSs there are a lot of studies [25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42] concerning distance measures along with their various applications. Karmakar et al. [43] suggested a Minkowski distance measure for Type-2 IFSs (T2IFSs) using the Hausdorff metric. Some recent studies related to Type 2 FSs and T2IFSs are given in [44,45,46]. The application of some PF measures of distance and similarity in MADM was shown by Zeng et al. [47]. Hussain and Yang [48] proposed some Hausdorff metric-based PF measures of distance and similarity with their applicability in PF TOPSIS. Some generalized measures of distance and their continuous versions for PFSs were given by Li and Lu [49]. They also proposed set-theoretic-based, matching function-based, and complement-based PF similarity measures. Based on the membership grades, Ejegwa [19] proposed some distance and similarity measures for PFSs. Some cosine function-based PF similarity measures were suggested by Wei and Wei [50]. Twelve PF measures of distance and similarity with their applicability were given by Peng et al. [14]. For PFSs Zhang [51] introduced a measure of similarity and its utility in decision-making. Some novel measures of similarity and distance for PFSs based on \({L}_{p}\) norm and level of uncertainty were given by Peng [52]. By combining the Euclidean distance measure and cosine similarity measures, Mohd and Abdullah [53] developed some novel PF similarity measures. Zhang et al. [54] proposed some exponential PF similarity measures and demonstrated their application in MADM, pattern analysis, and medical diagnosis. Some PF Dice similarity measures with application in decision-making were given by Wang et al. [55]. Verma and Merigo [56] developed some trigonometric function-based PF measures of similarity. The application of some multiparametric PF measures of similarity in classification problems was demonstrated by Peng and Garg [57]. Some novel PF similarity measures based on exponential function with their application in classification problems were given by Nguyen et al. [58]. Some recent studies related to PF distance measures along with their applications are given in [59,60,61,62,63,64].
The entropy of an FS is the ambiguous content present in it. Entropy measure is very essential for computing the weight of attributes in a MADM problem involving fuzzy data. The concept of fuzzy entropy was suggested by De Luca and Termini [65]. Some axiomatic requirements for a measure to be a fuzzy entropy measure were given by Ebanks [66]. Some more studies concerning fuzzy entropy measures and their utility are given in [67,68,69,70,71,72]. For IFSs Szmidt and Kacprzyk [73] suggested an entropy measure. Xue et al.[74] introduced the axiomatic definition of PF entropy measure and used the PF entropy measure in decision-making. Some probabilistic and non-probabilistic PF entropy measures were given by Yang and Hussain [75]. With the help of a new PF entropy measure, Thao and Smarandache [76] introduced the CORPAS MADM method in the PF environment.
Knowledge of an FS is the amount of precision present in it. Knowledge measure (KM) plays a great role in determining the weight of attributes in a MADM problem involving fuzzy data. Singh et al. [77] introduced the axiomatic definition of a fuzzy knowledge measure (FKM) and used it in decision-making. They also proposed a fuzzy accuracy measure and utilized it in image processing. Later on, Singh et al. [78] also introduced a one-parametric generalization of the FKM and discussed its various applications. A two-parametric fuzzy knowledge measure and accuracy measure with their applicability in decision-making and classification problems were given by Singh and Ganie [79]. For IFSs, there are various studies [80,81,82,83,84,85,86] regarding the knowledge measures (KMs) with their practical applications. Lin et al. [87] proposed a knowledge measure (KM) for picture fuzzy sets with its utility in decision-making. Some PF KMs with their various applications were introduced by Singh et al. [88]. For hesitant fuzzy sets, Singh and Ganie [89] introduced a generalized KM.
The following are the primary motivating aspects for this research:
-
There is no study concerning the generation of the PF distance measures and knowledge measures from t-conorms.
-
Axiomatic conditions are not met by several existing PF distance metrics.
-
When computing the distance between distinct PFSs, the majority of the existing PF distance metrics produce unacceptable results.
-
From the perspective of linguistic hedging, all of the known PF entropy/knowledge measurements are insufficient.
So, keeping the above facts in mind, we suggest some new distance measures and knowledge measures based on PFSs.
The rest of the paper is organized as: Sect. 3 is preliminary. Some novel t-conorm-based PF distance measures along with desirable properties are given in Sect. 4. Section 5 is devoted to the introduction of some distance-based PF knowledge measures. The comparison of the suggested PF distance measures and knowledge measures with the available PF measures of compatibility is shown in Sect. 6. Section 7 demonstrates the applicability of the suggested measures in pattern analysis and MADM. At last, the conclusion and future study are given in Sect. 8.
Preliminaries
Let \(W=\left\{{m}_{1}, {m}_{2}, \dots , {m}_{l}\right\}\) be the universe of discourse and \(PFS\left(W\right)\) be the set of all PFSs of \(W\).
Definition 1
[3] A PFS \({M}_{1}\) in \(W\) is given by
With \({\mu }_{{M}_{1}}\left({m}_{j}\right)\) and \({\vartheta }_{{M}_{1}}\left({m}_{j}\right)\) representing the membership and non-membership grades of the element \({m}_{j}\) in \({M}_{1}\) such that \(0\le {\mu }_{{M}_{1}}\left({m}_{j}\right), {\vartheta }_{{M}_{1}}\left({m}_{j}\right)\le 1\) and \(0\le {\mu }_{{M}_{1}}^{2}\left({m}_{j}\right)+{\vartheta }_{{M}_{1}}^{2}\left({m}_{j}\right)\le 1\). Also, \({\pi }_{{M}_{1}}\left({m}_{j}\right)=\sqrt{1-{\mu }_{{M}_{1}}^{2}\left({m}_{j}\right)-{\vartheta }_{{M}_{1}}^{2}\left({m}_{j}\right)}\) is the hesitancy grade of the element \({m}_{j}\) in \({M}_{1}.\)
Definition 2
[3] For two PFSs \({M}_{1}\) and \({M}_{2}\) in \(W\), some operations are given as:
-
\({M}_{1}\cup {M}_{2}=\left\{\begin{array}{c}\left(\begin{array}{c}{m}_{j}, max\left({\mu }_{{M}_{1}}\left({m}_{j}\right), {\mu }_{{M}_{2}}\left({m}_{j}\right)\right), \\ min\left({\vartheta }_{{M}_{1}}\left({m}_{j}\right), {\vartheta }_{{M}_{2}}\left({m}_{j}\right)\right)\end{array}\right)\\ |{m}_{j}\in W\end{array}\right\}.\)
-
\({M}_{1}\cap {M}_{2}=\left\{\begin{array}{c}\left(\begin{array}{c}{m}_{j}, min\left({\mu }_{{M}_{1}}\left({m}_{j}\right), {\mu }_{{M}_{2}}\left({m}_{j}\right)\right),\\ max\left({\vartheta }_{{M}_{1}}\left({m}_{j}\right), {\vartheta }_{{M}_{2}}\left({m}_{j}\right)\right)\end{array}\right)\\ |{m}_{j}\in W\end{array}\right\}.\)
-
\({M}_{1}\subseteq {M}_{2}\) iff \({\mu }_{{M}_{1}}\left({m}_{j}\right)\le {\mu }_{{M}_{2}}\left({m}_{j}\right)\) and \({\vartheta }_{{M}_{1}}\left({m}_{j}\right)\ge {\vartheta }_{{M}_{2}}\left({m}_{j}\right)\forall { m}_{j}\in W.\)
-
\({\left({M}_{1}\right)}^{c}=\left\{\begin{array}{c}\left({m}_{j}, {\vartheta }_{{M}_{1}}\left({m}_{j}\right), {\mu }_{{M}_{1}}\left({m}_{j}\right)\right)\\ |{m}_{j}\in W\end{array}\right\}.\)
Definition 4
[90] A function \(g:\left[0, 1\right]\times \left[0, 1\right]\to \left[0, 1\right]\) is called a t-norm if \(\forall x, y, z, t\in \left[0, 1\right]\)
-
\(g\left(x, y\right)=g\left(y,x\right);\)
-
\(g\left(x, y\right)\le g\left(z,t\right)\), whenever \(x\le z\) and \(y\le t;\)
-
\(g\left(x, 1\right)=x;\)
-
\(g\left(x, g\left(y, z\right)\right)=g\left(g\left(x, y\right), z\right)\).
Definition 5
[90] A function \(g:\left[0, 1\right]\times \left[0, 1\right]\to \left[0, 1\right]\) is called a t-conorm if \(\forall x, y, z, t\in \left[0, 1\right]\)
-
\(g\left(x, y\right)=g\left(y,x\right);\)
-
\(g\left(x, y\right)\le g\left(z,t\right)\), whenever \(x\le z\) and \(y\le t;\)
-
\(g\left(x, 0\right)=x;\)
-
\(g\left(x, g\left(y, z\right)\right)=g\left(g\left(x, y\right), z\right)\).
Definition 6
[14] A function \(S:PFS\left(W\right)\times PFS\left(W\right)\to \left[0, 1\right]\) is called a PF similarity measure if \(\forall { M}_{1}, {M}_{2}\) and \({M}_{3}\in PFS\left(W\right)\), we have:
(S1) \(0\le S\left({M}_{1}, {M}_{2}\right)\le 1;\)
(S2) \(S\left({M}_{1}, {M}_{2}\right)=S\left({M}_{2}, {M}_{1}\right);\)
(S3) \(S\left({M}_{1}, {M}_{2}\right)=1\) iff \({M}_{1}={M}_{2};\)
(S4) \(S\left({M}_{1}, {\left({M}_{1}\right)}^{c}\right)=0\) iff \({M}_{1}\) is a crisp set;
(S5) If \({M}_{1}\subseteq {M}_{2}\subseteq {M}_{3}\), then \(S\left({M}_{1}, {M}_{2}\right)\ge S\left({M}_{1}, {M}_{3}\right)\) and \(S\left({M}_{2}, {M}_{3}\right)\ge S\left({M}_{1}, {M}_{3}\right)\).
Definition 7
[14] A function \(D:PFS\left(W\right)\times PFS\left(W\right)\to \left[0, 1\right]\) is called a PF distance measure if \(\forall { M}_{1}, {M}_{2}\) and \({M}_{3}\in PFS\left(W\right)\), we have:
(D1) \(0\le D\left({M}_{1}, {M}_{2}\right)\le 1;\)
(D2) \(D\left({M}_{1}, {M}_{2}\right)=D\left({M}_{2}, {M}_{1}\right);\)
(D3) \(D\left({M}_{1}, {M}_{2}\right)=0\) iff \({M}_{1}={M}_{2};\)
(D4) \(D\left({M}_{1}, {\left({M}_{1}\right)}^{c}\right)=1\) iff \({M}_{1}\) is a crisp set;
(D5) If \({M}_{1}\subseteq {M}_{2}\subseteq {M}_{3}\), then \(D\left({M}_{1}, {M}_{2}\right)\le D\left({M}_{1}, {M}_{3}\right)\) and \(D\left({M}_{2}, {M}_{3}\right)\le D\left({M}_{1}, {M}_{3}\right)\).
Definition 8
[14] A function \(E:PFS\left(W\right)\to \left[0, 1\right]\) is called a PF entropy measure if \(\forall { M}_{1}\) and \({M}_{2}\in PFS\left(W\right)\), we have:
(E1) \(0\le E\left({M}_{1}\right)\le 1;\)
(E2) \(E\left({M}_{1}\right)=0\) iff \({M}_{1}\) is a crisp set;
(E3) \(E\left({M}_{1}\right)=1\) iff \({\mu }_{{M}_{1}}\left({m}_{j}\right)={\vartheta }_{{M}_{1}}\left({m}_{j}\right) \forall {m}_{j}\in W\);
(E4) \(E\left({M}_{1}\right)=E\left({\left({M}_{1}\right)}^{c}\right);\)
(E5) \(E\left({M}_{1}\right)\le E\left({M}_{2}\right)\) if \({\mu }_{{M}_{1}}\left({m}_{j}\right)\le {\mu }_{{M}_{2}}\left({m}_{j}\right)\le {\vartheta }_{{M}_{2}}\left({m}_{j}\right)\le {\vartheta }_{{M}_{1}}\left({m}_{j}\right)\) or \({\mu }_{{M}_{1}}\left({m}_{j}\right)\ge {\mu }_{{M}_{2}}\left({m}_{j}\right)\ge {\vartheta }_{{M}_{2}}\left({m}_{j}\right)\ge {\vartheta }_{{M}_{1}}\left({m}_{j}\right) \forall {m}_{j}\in W\).
Definition 9
[88] A function \(K:PFS\left(W\right)\to \left[0, 1\right]\) is called a PF knowledge measure if \(\forall { M}_{1}\) and \({M}_{2}\in PFS\left(W\right)\), we have:
(K1) \(0\le K\left({M}_{1}\right)\le 1;\)
(K2) \(K\left({M}_{1}\right)=1\) iff \({M}_{1}\) is a crisp set;
(K3) \(K\left({M}_{1}\right)=0\) iff \({\mu }_{{M}_{1}}\left({m}_{j}\right)={\vartheta }_{{M}_{1}}\left({m}_{j}\right) \forall {m}_{j}\in W\);
(K4) \(K\left({M}_{1}\right)=K\left({\left({M}_{1}\right)}^{c}\right);\)
(K5) \(K\left({M}_{1}\right)\ge K\left({M}_{2}\right)\) if \({\mu }_{{M}_{1}}\left({m}_{j}\right)\le {\mu }_{{M}_{2}}\left({m}_{j}\right)\le {\vartheta }_{{M}_{2}}\left({m}_{j}\right)\le {\vartheta }_{{M}_{1}}\left({m}_{j}\right)\) or \({\mu }_{{M}_{1}}\left({m}_{j}\right)\ge {\mu }_{{M}_{2}}\left({m}_{j}\right)\ge {\vartheta }_{{M}_{2}}\left({m}_{j}\right)\ge {\vartheta }_{{M}_{1}}\left({m}_{j}\right) \forall {m}_{j}\in W\).
In the next section, we introduce some novel t-conorm-based distance measures for PFSs along with their properties.
New measures of distance for PFSs
Here, we propose some PF measures of distance based on t-conorms.
Definition 10
Let \({M}_{1}\), \({M}_{2}\in PFS\left(W\right)\), then we define a function.
given by
where \(g\) is a t-conorm.
Theorem 1
The function \({D}_{G}\) given in Eq. (1) is a valid PF distance measure.
Proof
To prove that \({D}_{G}\) is a PF distance measure, we show that it satisfies the properties given in Definition 7.
(D1) Clearly \(0\le {D}_{G}\left({M}_{1}, {M}_{2}\right)\le 1\).
(D2) \({D}_{G}\left({M}_{1}, {M}_{2}\right)={D}_{G}\left({M}_{2}, {M}_{1}\right)\) is obvious.
(D3) \({D}_{G}\left({M}_{1}, {M}_{2}\right)=0\)
\(\iff \left|{\mu }_{{M}_{1}}^{2}\left({m}_{j}\right)-{\mu }_{{M}_{2}}^{2}\left({m}_{j}\right)\right|=0\) and \(\left|{\vartheta }_{{M}_{1}}^{2}\left({m}_{j}\right)-{\vartheta }_{{M}_{2}}^{2}\left({m}_{j}\right)\right|=0 \forall j, \)
\(\iff {\mu }_{{M}_{1}}^{2}\left({m}_{j}\right)={\mu }_{{M}_{2}}^{2}\left({m}_{j}\right)\) and \({\vartheta }_{{M}_{1}}^{2}\left({m}_{j}\right)={\vartheta }_{{M}_{2}}^{2}\left({m}_{j}\right) \forall j, \)
(D4) \({D}_{G}\left({M}_{1}, {M}_{1}^{c}\right)=1\)
\(\iff g\left(\begin{array}{c}\left|{\mu }_{{M}_{1}}^{2}\left({m}_{j}\right)-{\vartheta }_{{M}_{1}}^{2}\left({m}_{j}\right)\right|,\\ \left|{\vartheta }_{{M}_{1}}^{2}\left({m}_{j}\right)-{\mu }_{{M}_{1}}^{2}\left({m}_{j}\right)\right|\end{array}\right)=1\forall j\),
\(\iff \left|{\mu }_{{M}_{1}}^{2}\left({m}_{j}\right)-{\vartheta }_{{M}_{1}}^{2}\left({m}_{j}\right)\right|=1\) and \(\left|{\vartheta }_{{M}_{1}}^{2}\left({m}_{j}\right)-{\mu }_{{M}_{1}}^{2}\left({m}_{j}\right)\right|=1\forall j, \)
\(\iff \left|{\mu }_{{M}_{1}}^{2}\left({m}_{j}\right)-{\vartheta }_{{M}_{1}}^{2}\left({m}_{j}\right)\right|=1 \forall j\),
\(\iff {M}_{1}\) is a crisp set.
(D5) Let \({M}_{1}\subseteq {M}_{2}\subseteq {M}_{3}\), then \({\mu }_{{M}_{1}}^{2}\left({m}_{j}\right)\le {\mu }_{{M}_{2}}^{2}\left({m}_{j}\right)\le {\mu }_{{M}_{3}}^{2}\left({m}_{j}\right)\) and \({\vartheta }_{{M}_{1}}^{2}\left({m}_{j}\right)\ge {\vartheta }_{{M}_{2}}^{2}\left({m}_{j}\right)\ge {\vartheta }_{{M}_{3}}^{2}\left({m}_{j}\right) \forall j\). Therefore, we get
and
So,
and
Thus, \({D}_{G}\left({M}_{1}, {M}_{2}\right)\le {D}_{G}\left({M}_{1}, {M}_{3}\right)\) and \({D}_{G}\left({M}_{2}, {M}_{3}\right)\le {D}_{G}\left({M}_{1}, {M}_{3}\right)\).
Hence, \({D}_{G}\) is a valid PF measure of distance.
Theorem 2
The PF measure of distance \({D}_{G}\) given in Eq. (1) has the following properties:
-
1.
\({D}_{G}\left({M}_{1}^{c}, {M}_{2}^{c}\right)={D}_{G}\left({M}_{1}, {M}_{2}\right) \forall {M}_{1}, {M}_{2}\in PFS\left(W\right)\),
-
2.
\({D}_{G}\left({M}_{1}, {M}_{2}^{c}\right)={D}_{G}\left({M}_{1}^{c}, {M}_{2}\right) \forall {M}_{1}, {M}_{2}\in PFS\left(W\right)\),
-
3.
\({D}_{G}\left({M}_{1}, {M}_{1}^{c}\right)=0\) if and only if \({\mu }_{{M}_{1}}\left({m}_{j}\right)={\vartheta }_{{M}_{1}}\left({m}_{j}\right), \forall j\),
-
4.
\({D}_{G}\left({M}_{1}\cap {M}_{2}, {M}_{2}\right)\le {D}_{G}\left({M}_{1}, {M}_{2}\right)\) for every \({M}_{1}, {M}_{2}\in PFS\left(W\right)\),
-
5.
\({D}_{G}\left({M}_{1}\cup {M}_{2}, {M}_{2}\right)\le {D}_{G}\left({M}_{1}, {M}_{2}\right)\) for every \({M}_{1}, {M}_{2}\in PFS\left(W\right)\).
Proof 1. \({D}_{G}\left({M}_{1}^{c}, {M}_{2}^{c}\right)\)
2. \({D}_{G}\left({M}_{1}, {M}_{2}^{c}\right)\)
3. \({D}_{G}\left({M}_{1}, {M}_{1}^{c}\right)=0\)
and \(\left|{\vartheta }_{{M}_{1}}^{2}\left({m}_{j}\right)-{\mu }_{{M}_{1}}^{2}\left({m}_{j}\right)\right|=0 \, \forall \, j\),
4. \({D}_{G}\left({M}_{1}\cap {M}_{2}, {M}_{2}\right)=\)
We have the following cases:
(a) When \({\mu }_{{M}_{1}}\left({m}_{j}\right)\ge {\mu }_{{M}_{2}}\left({m}_{j}\right)\) and \({\vartheta }_{{M}_{1}}\left({m}_{j}\right)\ge {\vartheta }_{{M}_{2}}\left({m}_{j}\right) \forall j\), then
(b) When \({\mu }_{{M}_{1}}\left({m}_{j}\right)\ge {\mu }_{{M}_{2}}\left({m}_{j}\right)\) and \({\vartheta }_{{M}_{1}}\left({m}_{j}\right)\le {\vartheta }_{{M}_{2}}\left({m}_{j}\right) \forall j\), then
(c) When \({\mu }_{{M}_{1}}\left({m}_{j}\right)\le {\mu }_{{M}_{2}}\left({m}_{j}\right)\) and \({\vartheta }_{{M}_{1}}\left({m}_{j}\right)\ge {\vartheta }_{{M}_{2}}\left({m}_{j}\right) \forall j\), then
(d) When \({\mu }_{{M}_{1}}\left({m}_{j}\right)\le {\mu }_{{M}_{2}}\left({m}_{j}\right)\) and \({\vartheta }_{{M}_{1}}\left({m}_{j}\right)\le {\vartheta }_{{M}_{2}}\left({m}_{j}\right) \forall j\), then
5. \({D}_{G}\left({M}_{1}\cup {M}_{2}, {M}_{2}\right)\)
\(={\frac{1}{l}}\sum\limits_{j=1}^{l}g\left(\begin{array}{c}\left|max\left(\begin{array}{c}{\mu }_{{M}_{1}}^{2}\left({m}_{j}\right),\\ {\mu }_{{M}_{2}}^{2}\left({m}_{j}\right)\end{array}\right)-{\mu }_{{M}_{2}}^{2}\left({m}_{j}\right)\right|,\\ \left|min\left(\begin{array}{c}{\vartheta }_{{M}_{1}}^{2}\left({m}_{j}\right), \\ {\vartheta }_{{M}_{2}}^{2}\left({m}_{j}\right)\end{array}\right)-{\vartheta }_{{M}_{2}}^{2}\left({m}_{j}\right)\right|\end{array}\right). \)
We have the following cases:
(a) When \({\mu }_{{M}_{1}}\left({m}_{j}\right)\ge {\mu }_{{M}_{2}}\left({m}_{j}\right)\) and \({\vartheta }_{{M}_{1}}\left({m}_{j}\right)\ge {\vartheta }_{{M}_{2}}\left({m}_{j}\right) \forall j\), then
(b) When \({\mu }_{{M}_{1}}\left({m}_{j}\right)\ge {\mu }_{{M}_{2}}\left({m}_{j}\right)\) and \({\vartheta }_{{M}_{1}}\left({m}_{j}\right)\le {\vartheta }_{{M}_{2}}\left({m}_{j}\right) \forall j\), then
(c) When \({\mu }_{{M}_{1}}\left({m}_{j}\right)\le {\mu }_{{M}_{2}}\left({m}_{j}\right)\) and \({\vartheta }_{{M}_{1}}\left({m}_{j}\right)\ge {\vartheta }_{{M}_{2}}\left({m}_{j}\right) \forall j\), then
(d) When \({\mu }_{{M}_{1}}\left({m}_{j}\right)\le {\mu }_{{M}_{2}}\left({m}_{j}\right)\) and \({\vartheta }_{{M}_{1}}\left({m}_{j}\right)\le {\vartheta }_{{M}_{2}}\left({m}_{j}\right) \forall j\), then
Example 1
Some examples of PF distance measures are given in Table 1.
In most decision-making problems, the weights \({w}_{j}\) of the elements \({m}_{j}, j=1, 2, \dots , l\) are taken into consideration, so we introduce the weighted PF distance measures.
Definition 11
Let \({M}_{1}\), \({M}_{2}\in PFS\left(W\right)\), then we define a function
given by
where \(g\) is a t-conorm.
Theorem 3
The function \({D}_{G}^{W}\) given in Eq. (2) is a valid PF distance measure.
Proof
Similar to Theorem 1.
Example 2
Some examples of weighted PF distance measures are given in Table 2.
Next, we propose some novel PF measures of knowledge based on the proposed PF distance measures.
PF distance-based knowledge measures
The entropy measures are used to compute the amount of ambiguity present in a PFS, whereas the knowledge measures acting as the soft duals of entropy measures are used to calculate the amount of precision in a PFS. Here, we introduce a method of constructing PF knowledge measures from the PF distance measures.
Definition 12
Let \({M}_{1}\in PFS\left(W\right)\), then we define a function
given by
where \({D}_{G}\) is a PF distance measure.
Theorem 4
The function \({K}_{G}\) defined in Eq. (3) is a valid PF knowledge measure.
Proof
To show that the function \({K}_{G}\) is a PF measure of knowledge, we show it has the properties of a PF measure of knowledge given in Definition 9.
(K1) Clearly \(0\le {K}_{G}\left({M}_{1}\right)\le 1\) as \(0\le {D}_{G}\left({M}_{1}, {M}_{1}^{c}\right)\)
\(\le 1\).
(K2) \({K}_{G}\left({M}_{1}\right)=1\iff {D}_{G}\left({M}_{1}, {M}_{1}^{c}\right)=0\iff {M}_{1}\) is a crisp set.
(K3)
(K4) \({K}_{G}\left({M}_{1}^{c}\right)={K}_{G}\left({M}_{1}\right)\) is obvious.
(K5) Let \({M}_{1}\) be less fuzzy than \({M}_{2}\) i.e., \({\mu }_{{M}_{1}}\left({m}_{j}\right)\le {\mu }_{{M}_{2}}\left({m}_{j}\right)\le {\vartheta }_{{M}_{2}}\left({m}_{j}\right)\le {\vartheta }_{{M}_{1}}\left({m}_{j}\right)\) or \({\mu }_{{M}_{1}}\left({m}_{j}\right)\ge {\mu }_{{M}_{2}}\left({m}_{j}\right)\ge {\vartheta }_{{M}_{2}}\left({m}_{j}\right)\ge {\vartheta }_{{M}_{1}}\left({m}_{j}\right)\).
When \({\mu }_{{M}_{1}}\left({m}_{j}\right)\le {\mu }_{{M}_{2}}\left({m}_{j}\right)\le {\vartheta }_{{M}_{2}}\left({m}_{j}\right)\le {\vartheta }_{{M}_{1}}\left({m}_{j}\right)\), then we get
So, \({D}_{G}\left({M}_{1}, {M}_{1}^{c}\right)\)
Thus, \({K}_{G}\left({M}_{1}\right)\ge {K}_{G}\left({M}_{2}\right)\).
Similarly, when \({\mu }_{{M}_{1}}\left({m}_{j}\right)\ge {\mu }_{{M}_{2}}\left({m}_{j}\right)\ge {\vartheta }_{{M}_{2}}\left({m}_{j}\right)\ge {\vartheta }_{{M}_{1}}\left({m}_{j}\right)\), we get \({K}_{G}\left({M}_{1}\right)\ge {K}_{G}\left({M}_{2}\right)\). Hence the function \({K}_{G}\) given in Eq. (3) is a valid PF knowledge measure.
With the help of Eq. (3) and based on the suggested PF measures of distance, some PF measures of knowledge are given in Table 3 below:
Now, we compare the suggested PF measures of distance and knowledge with some available PF measures of information.
Comparative analysis
In this section, we show that our suggested PF measures of distance and knowledge give better results than most of the available PF measures of information.
Comparison of the proposed PF distance measures with various available PF measures of similarity/distance
To contrast the performance of the suggested PF measures of distance, we first list the PF measures of similarity/distance available in the literature as shown in Table 4.
Now we compare the suggested measures with the existing ones through some numerical examples related to the computation of the distance/similarity between different PFSs.
Example 3
Consider three different cases of PFSs with each case consisting of two different PFSs as shown below.
Case I: \(\left\{\begin{array}{c}{M}_{1}=\left\{\left({m}_{1}, 0.5, 0.5\right)\right\}\\ {M}_{2}=\left\{\left({m}_{1}, 0.0, 0.0\right)\right\}\end{array}\right.\)
Case II: \(\left\{\begin{array}{c}{M}_{1}=\left\{\left({m}_{1}, 0.4, 0.3\right)\right\}\\ {M}_{2}=\left\{\left({m}_{1}, 0.5, 0.3\right)\right\}\end{array}\right.\)
Case III: \(\left\{\begin{array}{c}{M}_{1}=\left\{\left({m}_{1}, 0.4, 0.3\right)\right\}\\ {M}_{2}=\left\{\left({m}_{1}, 0.5, 0.2\right)\right\}\end{array}\right.\)
The computed distance/similarity values for these three cases using the available measures of distance/similarity along with the suggested ones are shown in Table 5.
From Table 5, we have
-
1.
The PF distance measures \({D}_{PYY1}, {D}_{PYY4}, {D}_{PYY5}, D_{PYY6}, {D}_{PYY9}, {\mathrm{and }D}_{PYY10}\) gives the same distance for the two distinct cases (Case II and Case III).
-
2.
The PF distance measure \({D}_{PYY2}\) gives “0” as the distance between the two different PFSs (Case I) and thus fails to satisfy the axiom (D3) of the PF distance measure given in Definition 7.
-
3.
The PF distance measures \({D}_{PYY7}, {D}_{PYY8}, {D}_{PYY9}\), and \({D}_{PYY10}\) gives “1” as the distance between the two different PFSs (Case I) although they are not a complement of each other.
-
4.
The PF similarity measures \({S}_{PYY1}, {S}_{PYY4}, {{S}_{PYY5}, S}_{PYY6}, {S}_{PYY9}, {\mathrm{and }S}_{PYY10}\) give the same degree of similarity for the two distinct cases (Case II and Case III).
-
5.
The PF similarity measure \({S}_{PYY2}\) gives “1” as a similarity degree for the two different PFSs (Case I) and thus fails to satisfy the axiom (S3) of the PF measure of similarity given in Definition 6.
-
6.
The PF similarity measures \({S}_{PYY7}, {S}_{PYY8}, {S}_{PYY9}\), and \({S}_{PYY10}\) gives “0” as the similarity degree for the two different PFSs (Case I) although they are not a complement of each other.
-
7.
The similarity degree of the different PFSs (Case II and III) by the similarity measures \({S}_{PYY7}\) and \({S}_{PYY8}\) comes out to be negative, which is unreasonable.
-
8.
The proposed PF distance measures \({D}_{Gj}, 1\le j\le 4\) outperforms the majority of the available PF measures of distance/similarity.
Example 4
Consider six different cases of PFSs with each case consisting of two different PFSs as shown below.
Case I: \(\left\{\begin{array}{c}{M}_{1}=\left\{\left({m}_{1}, 0.4, 0.2\right)\right\}\\ {M}_{2}=\left\{\left({m}_{1}, 0.5, 0.2\right)\right\}\end{array}\right.\)
Case II: \(\left\{\begin{array}{c}{M}_{1}=\left\{\left({m}_{1}, 0.4, 0.2\right)\right\}\\ {M}_{2}=\left\{\left({m}_{1}, 0.5, 0.1\right)\right\}\end{array}\right.\)
Case III: \(\left\{\begin{array}{c}{M}_{1}=\left\{\left({m}_{1}, 0.5, 0.5\right)\right\}\\ {M}_{2}=\left\{\left({m}_{1}, 0, 0\right)\right\}\end{array}\right.\)
Case IV: \(\left\{\begin{array}{c}{M}_{1}=\left\{\left({m}_{1}, 1, 0\right)\right\}\\ {M}_{2}=\left\{\left({m}_{1}, 0, 0\right)\right\}\end{array}\right.\)
Case V: \(\left\{\begin{array}{c}{M}_{1}=\left\{\left({m}_{1}, 0.3, 0.4\right)\right\}\\ {M}_{2}=\left\{\left({m}_{1}, 0.4, 0.3\right)\right\}\end{array}\right.\)
Case VI: \(\left\{\begin{array}{c}{M}_{1}=\left\{\left({m}_{1}, 0.1, 0.9\right)\right\}\\ {M}_{2}=\left\{\left({m}_{1}, 0, 0\right)\right\}\end{array}\right.\)
The computed distance/similarity values for these six cases using the available measures of distance/similarity along with the suggested ones are shown in Table 6.
From Table 6, we have the following:
-
1.
The PF distance measures \({D}_{PYY1}, {D}_{PYY4},\)
\({D}_{PYY5}, {D}_{PYY6}, {D}_{PYY9},\) and \({D}_{PYY10}\) give the same distance for two distinct cases (Case I and Case II).
-
2.
The PF distance measure \({D}_{PYY2}\) gives “0” as the distance between the two unequal PFSs (Case III).
-
3.
The PF distance measures \({D}_{PYY7}, {D}_{PYY8},\)
\({D}_{PYY9},\) and \({D}_{PYY10}\) gives “1” as the distance between two PFSs \({M}_{1}\) and \({M}_{2}\) (Case III and Case VI) when neither \({M}_{1}\) is a crisp set nor \({M}_{1}={M}_{2}\). So, they fail to satisfy the axiom (D4) of Definition 7.
-
4.
The PF distance measure \({D}_{PYY3}\) indicates that the distance between the PFSs (Case IV and Case VI) is greater than “1” and therefore does not follow the axiom (D1) of definition 7.
-
5.
The PF distance measures \({D}_{PYY7}\) and \({D}_{PYY8}\) fail to compute the distance between the two PFSs (Case IV).
-
6.
The PF similarity measures \({S}_{PYY1}, {S}_{PYY4},\)
\({S}_{PYY5}, {S}_{PYY6}, {S}_{PYY9}\) and \({S}_{PYY10}\) give the same similarity for two distinct cases (Case I and Case II).
-
7.
The PF similarity measure \({S}_{PYY2}\) gives “1” as the similarity between the two unequal PFSs (Case III).
-
8.
The similarity between the different PFSs comes out to be negative (Case I, Case IV, Case V, and Case V) by the PF similarity measures \({S}_{PYY3}, {S}_{PYY7},\) and \({S}_{PYY8}\). So, these similarity measures fail to satisfy the axiom (S1) of Definition 6.
-
9.
The PF similarity measures \({S}_{PYY7}\) and \({S}_{PYY8}\) fails to compute the similarity between the PFSs (Case IV).
-
10.
The PF similarity measures \({S}_{PYY7}, {S}_{PYY8},\)
\({S}_{PYY9},\) and \({S}_{PYY10}\) gives “0” as the similarity between the PFSs \({M}_{1}\) and \({M}_{2}\) (Case III and Case VI), when neither \({M}_{2}={{M}_{1}}^{c}\) nor \({M}_{1}\) is a crisp set.
-
11.
The suggested PF distance measures \({D}_{Gj}, 1\le j\le 4\) computes the distance of all the PFSs without any counterintuitive results.
Thus, from Examples 3 and 4, we conclude that the suggested distance measures are more robust and effective than most of the available distance/similarity measures in PF theory.
Next, we compare the suggested PF knowledge measures with the available PF measures of entropy/knowledge.
Comparison of the suggested PF measures of knowledge with the available PF measures of entropy/knowledge
To contrast the performance of the newly introduced PF measures of knowledge, we first list the PF entropy/knowledge measures available in the literature.
Entropy measures due to Peng et al. [14]
Entropy measure due to Xue et al. [74]
Entropy measure due to Thao and Smarandache [76]
Entropy measure due to Yang and Hussain [75]
Knowledge measures due to Singh et al. [88]
Now, using linguistic hedges, we show the effectiveness of the suggested PF measures of knowledge.
Definition 13
[75] For any \({M}_{1}\in PFS\left(W\right)\), its modifier \({\left({M}_{1}\right)}^{\lambda }, \lambda >0\) is defined as
Then, we have the following PFSs:
\({M}_{1}\): LARGE; \({\left({M}_{1}\right)}^{2}\): very LARGE; \({\left({M}_{1}\right)}^{3}\): quite very LARGE; \({\left({M}_{1}\right)}^{4}\): very very LARGE; \({\left({M}_{1}\right)}^{\frac{1}{2}}\): more or less LARGE.
Since a PF entropy measure,\(E\) computes the ambiguous content in a PFS, it has to satisfy the following requirement:
Also, a PF knowledge measure \(K\) acts as a soft dual of a PF entropy measure and calculates the amount of precision in a PFS, so it has to satisfy the following requirement:
We now consider an example related to the ambiguous computation of the above-mentioned PFSs.
Example 5
Let \({M}_{1}\in PFS\left(W\right)\) be given as:
With the help of Definition 13, we construct the following PFSs:
The ambiguous content of these PFSs using the suggested PF knowledge measures and the existing ones is shown in Table 7.
From Table 7, we have the following:
Thus, it follows that all the available PF measures of entropy \({E}_{PLj}, 1\le j\le 8,{E}_{XXZT}, {E}_{TS}, {E}_{YH},\mathrm{ and}\) the PF knowledge measures \({K}_{SSGj}, j=1, 2, 3\) do not satisfy the requirements given in Eqs. (4) and (5) respectively. However, all our suggested PF knowledge measures \({K}_{Gj}, j=1, 2, 3, 4\), follow the desired requirement given in Eq. (5). This shows that from a linguistic hedge perspective, the suggested measures of knowledge are more robust than the available ones.
Now, we demonstrate the utility of the proposed PF distance and knowledge measures in pattern identification and decision-making.
Application of the proposed measures
In this section, we show how the suggested metrics can be used in pattern analysis and MCDM.
Pattern analysis
We demonstrate how the suggested PF distance metrics can be employed to solve pattern classification problems. An unfamiliar pattern is classed into one of the known patterns using compatibility measurements such as similarity measures, distance measures, correlation measures, and so on in pattern analysis. We also compare our findings to the existing compatibility measures.
Now, we solve some problems related to pattern analysis in the examples given below.
Example 6
(Nanometer material classification) The current nanometer materials collection \(M=\left\{{M}_{1}, {M}_{2}, {M}_{3}\right\}\) which stands for nanometer-ceramics, nanometer-film, and nanometer-fiber respectively. The following collection of parameters primarily describes the form features of the three-nanometer materials: \(W=\left\{{m}_{1} \left(\mathrm{odour}\right), {m}_{2} \left(\mathrm{layer}\right), {m}_{3} \left(\mathrm{color}\right)\right\}\).
The following are the standard model data for the form properties of the three-nanometer materials:
There is a nanometer material \(N\) that needs to be recognized in the following way:
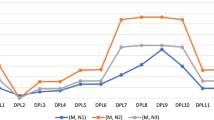
We need to find out the nanometer material that \(N\) belongs to. The similarity/distance between \(N\) and \({M}_{j}, j=1, 2, 3\) by various PF similarity/distance measures are shown in Table 8.
From Table 8, we see that the unknown nanometer is assigned to the pattern \({M}_{2}\) as shown by most of the PF distance/similarity measures. We also observe that the PF distance/similarity measures \({D}_{PYY8}, {D}_{PYY9}, {S}_{PYY8},\) and \({S}_{PYY9}\) fail to recognize the unknown nanometer \(N\).
Example 7
(Bacterial detection) \(M=\left\{{M}_{1}, {M}_{2}, {M}_{3}\right\}\) represents Salmonella, Shigella, and Escherichia coli, respectively, in the existing bacterial collection. The following set of numbers best describes the shape features of the three gut bacteria:
The following are the typical model data for the shape features of the three gut bacteria:
The following is the description of an unknown microbe \(N\) found in the laboratory:
Our aim is to find the bacteria to which \(N\) belongs. The similarity/distance between \(N\) and \({M}_{j}, j=1, 2, 3\) by various PF similarity/distance measures are shown in Table 9.
From Table 9, we observe that the unknown microbe \(N\) is assigned to \({M}_{1}\) as shown by most of the PF distance/similarity measures. We also observe that the PF distance/similarity measures \({D}_{PYY2}\) and \({S}_{PYY2}\) fail to recognize the unknown microbe \(N\).
Thus from Examples 6 and 7, it is clear that results due to the suggested PF distance measures are consistent with the existing ones and therefore are applicable in classification problems.
Multi-criteria decision-making
Here, we show that the suggested PF measures of knowledge and distance are useful for solving MCDM problems involving uncertainty and ambiguity. The main hurdle in an MCDM problem is the computation of criteria weights and we use the suggested knowledge measures for this purpose. For determining the best alternative, we take the help of the suggested distance measures. First, we give the algorithm for solving an MCDM problem having \(n\) alternatives \({M}_{j}, j=1, 2,\dots , n\) and \(k\) criteria \({N}_{k}, k=1, 2,\dots , m\) with \({w}_{k}, k=1, 2, \dots , m\) as criteria weights where \(0\le {w}_{k}\le 1\) and \(\sum\limits_{k=1}^{m}{w}_{k}=1\).
Algorithm
Step 1: Formulate the decision matrix \(D={\left[\left({\mu }_{jk}, {\vartheta }_{jk}\right)\right]}_{n\times m}\) expressing the information of the available alternatives with respect to the criteria.
Step 2: Formulate the normalized decision matrix \(E={\left[\left({\mu }_{jk}^{^{\prime}}, {\vartheta }_{jk}^{^{\prime}}\right)\right]}_{n\times m}\) where,
Step 3: Compute the criteria weights \({w}_{k}, k=1, 2, \dots , m\) as:
Here, \(K\) is a PF entropy measure.
Step 4: Determine the PF ideal solution \({M}^{*}=\left\{\left({\mu }_{1}^{*}, {\vartheta }_{1}^{*}\right), \left({\mu }_{2}^{*}, {\vartheta }_{2}^{*}\right), \dots , \left({\mu }_{m}^{*}, {\vartheta }_{m}^{*}\right)\right\}\) where \({\mu }_{k}^{*}=\underset{j}{\mathrm{max}}{\mu }_{jk}\) and \({\vartheta }_{k}^{*}=\underset{j}{\mathrm{min}}{\vartheta }_{jk}, k=1, 2, \dots , m\).
Step 5: Compute the distance of each alternative \({M}_{j}, j=1, 2,\dots , n\) from the PF ideal solution \({M}^{*}\) using the suggested weighted PF distance measures.
Step 6: Rank the alternatives as \({M}_{j}>{M}_{t}\) if \(D\left({M}_{j}, {M}^{*}\right)<D\left({M}_{t}, {M}^{*}\right)\), where \(D\) is a PF distance measure and \(1\le j, t\le n\).
Now, we solve an MCDM problem in the example given below.
Example 8
[91] Consider the problem of purchasing a house out of the five houses \({M}_{j}, j=1, 2, 3, 4, 5\) by considering the following criteria:
\({N}_{1}:\) ceiling height, \({N}_{2}:\) design, \({N}_{3}:\) location, \({N}_{4}:\) purchase price, \({N}_{5}:\) ventilation.
The information about the five houses with respect to the above-mentioned five criteria is expressed in the form of PFSs as shown by the decision matrix \(D\) below:
As the criteria \({N}_{4}\) is a cost attribute, so the normalized decision matrix \(E\) with the help of Step 2 is given below:
With the help of Step 3 and using the suggested entropy measure \({K}_{G1}\) given in Table 3, we obtain the criteria weights as:
\({w}_{1}=0.1744, {w}_{2}=0.1229, {w}_{3}=0.1813, {w}_{4}=0.2525,\) and \({w}_{5}=0.2688\).
Next, using Step 4, the PF ideal solution \({M}^{*}\) is given as:
The computed values of the distance of each alternative \({M}_{j}, j=1, 2, 3, 4, 5\) from the PF ideal solution \({M}^{*}\) using the suggested weighted distance measures \({D}_{Gj}^{w}, j=1, 2, 3, 4\) given in Table 2 are shown in Table 10.
The final ranking of alternatives with the help of Step 6 is shown in Table 11.
From Table 11, we conclude that \({M}_{2}\) is the most feasible alternative as all the suggested PF distance measures and the existing PF distance measures \({D}_{PYY1}\) and \({D}_{PYY4}\) indicate the same. Further, some existing q-rung orthopair correlation coefficients also indicate the same. This shows that the suggested distance measures are consistent with the existing distance measures.
Conclusion
With the use of t-conorms, this work offered a novel way of building some distance and knowledge metrics for PFSs. First, four new distance measures were presented using t-conorms, and then four new knowledge measures were developed using the proposed distance measures. In terms of the distance/similarity degree between distinct PFSs, the suggested distance measures are more successful than most of the known PF distance/similarity measures. The majority of the existing PF distance/similarity measures produce the same distance/similarity between distinct PFSs, and some of them fail to satisfy all of the axiomatic conditions. The suggested PF distance metrics, on the other hand, are devoid of these flaws. Furthermore, from the linguistic hedging perspective, the suggested measures of knowledge for PFSs are more resilient than the known PF entropy/knowledge measures. The proposed PF distance metrics have shown to be effective in pattern recognition challenges. Finally, in a multi-criteria decision-making situation, the recommended knowledge measures are used to compute the weight of attributes, and the distance measures are utilized to rank the alternatives. The results of the recommended measures are compatible with the available measures in pattern recognition and decision-making situations.
The advantages of this study are:
-
1.
The suggested method of constructing the distance measures from t-conorms can be utilized for obtaining the new distance measures for some recent generalizations of fuzzy sets.
-
2.
The distance-based knowledge measures can be used in computing the ambiguity content of Pythagorean fuzzy sets where the existing entropy measures lead to unreasonable results.
-
3.
The suggested distance measures can be applied to bidirectional approximate reasoning.
Our future studies include:
-
To demonstrate the applicability of the suggested distance measures in clustering and medical diagnosis.
-
To demonstrate the applicability of the suggested measures in real decision-making problems.
-
To introduce the t-conorm-based distance measures and knowledge measures for picture fuzzy sets [93], spherical fuzzy sets [94], T-spherical fuzzy sets [94], etc.
-
To introduce the parametric generalizations of the suggested measures along with their various applications.
References
Zadeh LA (1965) Fuzzy sets. Inf Control 8:338–353. https://doi.org/10.1016/S0019-9958(65)90241-X
Atanassov KT (1986) Intuitionistic fuzzy sets. Fuzzy Sets Syst 20:87–96. https://doi.org/10.1016/S0165-0114(86)80034-3
Yager RR (2013) Pythagorean fuzzy subsets. In: 2013 joint IFSA world congress and NAFIPS annual meeting (IFSA/NAFIPS). IEEE, pp 57–61
Zhang X, Xu Z (2014) Extension of TOPSIS to multiple criteria decision making with Pythagorean fuzzy sets. Int J Intell Syst 29:1061–1078. https://doi.org/10.1002/int.21676
Yager RR (2014) Pythagorean membership grades in multicriteria decision making. IEEE Trans Fuzzy Syst 22:958–965. https://doi.org/10.1109/TFUZZ.2013.2278989
Wei G, Lu M (2018) Pythagorean fuzzy power aggregation operators in multiple attribute decision making. Int J Intell Syst 33:169–186. https://doi.org/10.1002/int.21946
Garg H (2016) A new generalized Pythagorean fuzzy information aggregation using Einstein operations and its application to decision making. Int J Intell Syst 31:886–920. https://doi.org/10.1002/int.21809
Wei G (2017) Pythagorean fuzzy interaction aggregation operators and their application to multiple attribute decision making. J Intell Fuzzy Syst 33:2119–2132. https://doi.org/10.3233/JIFS-162030
Lu M, Wei G, Alsaadi FE et al (2017) Hesitant pythagorean fuzzy Hamacher aggregation operators and their application to multiple attribute decision making. J Intell Fuzzy Syst 33:1105–1117. https://doi.org/10.3233/JIFS-16554
Wei G, Lu M (2017) Dual hesitant Pythagorean fuzzy Hamacher aggregation operators in multiple attribute decision making. Arch Control Sci 27:365–395. https://doi.org/10.1515/acsc-2017-0024
Wei G, Lu M, Alsaadi FE et al (2017) Pythagorean 2-tuple linguistic aggregation operators in multiple attribute decision making. J Intell Fuzzy Syst 33:1129–1142. https://doi.org/10.3233/JIFS-16715
Garg H (2017) Generalized Pythagorean fuzzy geometric aggregation operators using Einstein t-norm and t-conorm for multicriteria decision-making process. Int J Intell Syst 32:597–630. https://doi.org/10.1002/int.21860
Ren P, Xu Z, Gou X (2016) Pythagorean fuzzy TODIM approach to multi-criteria decision making. Appl Soft Comput 42:246–259. https://doi.org/10.1016/j.asoc.2015.12.020
Peng X, Yuan H, Yang Y (2017) Pythagorean fuzzy information measures and their applications. Int J Intell Syst 32:991–1029. https://doi.org/10.1002/int.21880
Peng X, Dai J (2017) Approaches to Pythagorean fuzzy stochastic multi-criteria decision making based on prospect theory and regret theory with new distance measure and score function. Int J Intell Syst 32:1187–1214. https://doi.org/10.1002/int.21896
Singh S, Ganie AH (2020) On some correlation coefficients in Pythagorean fuzzy environment with applications. Int J Intell Syst 35:682–717. https://doi.org/10.1002/int.22222
Khan MSA, Abdullah S, Ali A, Amin F (2019) Pythagorean fuzzy prioritized aggregation operators and their application to multi-attribute group decision making. Granul Comput 4:249–263. https://doi.org/10.1007/s41066-018-0093-6
Rahman K, Ali A, Abdullah S (2020) Multiattribute group decision making based on interval-valued Pythagorean fuzzy Einstein geometric aggregation operators. Granul Comput 5:361–372. https://doi.org/10.1007/s41066-019-00154-w
Ejegwa PA (2020) Distance and similarity measures for Pythagorean fuzzy sets. Granul Comput 5:225–238. https://doi.org/10.1007/s41066-018-00149-z
Ejegwa PA (2020) Improved composite relation for pythagorean fuzzy sets and its application to medical diagnosis. Granul Comput 5:277–286. https://doi.org/10.1007/s41066-019-00156-8
Garg H (2019) Hesitant Pythagorean fuzzy Maclaurin symmetric mean operators and its applications to multiattribute decision-making process. Int J Intell Syst 34:601–626. https://doi.org/10.1002/int.22067
Garg H (2019) New logarithmic operational laws and their aggregation operators for Pythagorean fuzzy set and their applications. Int J Intell Syst 34:82–106. https://doi.org/10.1002/int.22043
Akram M, Ali G (2020) Hybrid models for decision-making based on rough Pythagorean fuzzy bipolar soft information. Granul Comput 5:1–15. https://doi.org/10.1007/s41066-018-0132-3
Khan MSA, Abdullah S, Ali A, Amin F (2019) An extension of VIKOR method for multi-attribute decision-making under Pythagorean hesitant fuzzy setting. Granul Comput 4:421–434. https://doi.org/10.1007/s41066-018-0102-9
Bhatia PK, Singh S (2013) On some divergence measures between fuzzy sets and aggregation operations. AMO Adv Model Optim 15:235–248
Xuecheng L (1992) Entropy, distance measure and similarity measure of fuzzy sets and their relations. Fuzzy Sets Syst 52:305–318. https://doi.org/10.1016/0165-0114(92)90239-Z
Mahanta J, Panda S (2021) A novel distance measure for intuitionistic fuzzy sets with diverse applications. Int J Intell Syst 36:615–627. https://doi.org/10.1002/INT.22312
Hao Z, Xu Z, Zhao H, Zhang R (2021) The context-based distance measure for intuitionistic fuzzy set with application in marine energy transportation route decision making. Appl Soft Comput 101:107044. https://doi.org/10.1016/J.ASOC.2020.107044
Gohain B, Dutta P, Gogoi S, Chutia R (2021) Construction and generation of distance and similarity measures for intuitionistic fuzzy sets and various applications. Int J Intell Syst 36:7805–7838. https://doi.org/10.1002/INT.22608
Garg H, Rani D (2022) Novel distance measures for intuitionistic fuzzy sets based on various triangle centers of isosceles triangular fuzzy numbers and their applications. Expert Syst Appl 191:116228. https://doi.org/10.1016/J.ESWA.2021.116228
Janis V, Tepavcevic A (2001) Distance generated by a fuzzy compatibility. Indian J Pure Appl Math 35:737–745
Sharma S, Singh S (2019) On some generalized correlation coefficients of the fuzzy sets and fuzzy soft sets with application in cleanliness ranking of public health centres. J Intell Fuzzy Syst 36:3671–3683. https://doi.org/10.3233/JIFS-181838
Bajaj RK, Hooda DS (2010) Generalized measures of fuzzy directed-divergence, total ambiguity and information improvement. J Appl Math Stat Inform 6:31–44
Montes S, Couso I, Gil P, Bertoluzza C (2002) Divergence measure between fuzzy sets. Int J Approx Reason 30:91–105. https://doi.org/10.1016/S0888-613X(02)00063-4
Mishra AR, Jain D, Hooda DS (2016) On fuzzy distance and induced fuzzy information measures. J Inf Optim Sci 37:193–211. https://doi.org/10.1080/02522667.2015.1103034
Montes I, Pal NR, Janis V, Montes S (2015) Divergence measures for intuitionistic fuzzy sets. IEEE Trans Fuzzy Syst 23:444–456. https://doi.org/10.1109/TFUZZ.2014.2315654
Baccour L, Alimi AM (2019) Distance measures for intuitionistic fuzzy sets and interval valued intuitionistic fuzzy sets. IEEE Int Conf Fuzzy Syst. https://doi.org/10.1109/FUZZ-IEEE.2019.8858789
Wang W, Xin X (2005) Distance measure between intuitionistic fuzzy sets. Pattern Recognit Lett 26:2063–2069. https://doi.org/10.1016/J.PATREC.2005.03.018
Singh S, Garg H (2017) Distance measures between type-2 intuitionistic fuzzy sets and their application to multicriteria decision-making process. Appl Intell 46:788–799. https://doi.org/10.1007/s10489-016-0869-9
Zhang H, Yu L (2013) New distance measures between intuitionistic fuzzy sets and interval-valued fuzzy sets. Inf Sci (N Y) 245:181–196. https://doi.org/10.1016/J.INS.2013.04.040
Zeng S, Zeng S (2011) Some intuitionistic fuzzy weighted distance measures and their application to group decision making. Gr Decis Negot 222(22):281–298. https://doi.org/10.1007/S10726-011-9262-6
He X, Li Y, Qin K, Meng D (2020) Distance measures on intuitionistic fuzzy sets based on intuitionistic fuzzy dissimilarity functions. Soft Comput 24:523–541. https://doi.org/10.1007/S00500-019-03932-5/TABLES/6
Karmakar S, Seikh MR, Castillo O (2021) Type-2 intuitionistic fuzzy matrix games based on a new distance measure: Application to biogas-plant implementation problem. Appl Soft Comput 106:107357. https://doi.org/10.1016/J.ASOC.2021.107357
Anusha V, Sireesha V (2022) A new distance measure to rank type-2 intuitionistic fuzzy sets and its application to multi-criteria group decision making. Int J Fuzzy Syst Appl 11:1–17. https://doi.org/10.4018/IJFSA.285982
Guerrero M, Valdez F, Castillo O (2022) A new Cuckoo search algorithm using interval type-2 fuzzy logic for dynamic parameter adaptation. Lect Notes Netw Syst 308:853–860. https://doi.org/10.1007/978-3-030-85577-2_98
Ontiveros-Robles E, Melin P, Castillo O (2021) An efficient high-order α-plane aggregation in general type-2 fuzzy systems using Newton-Cotes rules. Int J Fuzzy Syst 23:1102–1121. https://doi.org/10.1007/S40815-020-01031-4
Zeng W, Li D, Yin Q (2018) Distance and similarity measures of Pythagorean fuzzy sets and their applications to multiple criteria group decision making. Int J Intell Syst 33:2236–2254. https://doi.org/10.1002/int.22027
Hussian Z, Yang M (2019) Distance and similarity measures of Pythagorean fuzzy sets based on the Hausdorff metric with application to fuzzy TOPSIS. Int J Intell Syst 34:2633–2654. https://doi.org/10.1002/int.22169
Li Z, Lu M (2019) Some novel similarity and distance measures of Pythagorean fuzzy sets and their applications. J Intell Fuzzy Syst 37:1781–1799. https://doi.org/10.3233/JIFS-179241
Wei G, Wei Y (2018) Similarity measures of Pythagorean fuzzy sets based on the cosine function and their applications. Int J Intell Syst 33:634–652. https://doi.org/10.1002/int.21965
Zhang X (2016) A novel approach based on similarity measure for Pythagorean fuzzy multiple criteria group decision making. Int J Intell Syst 31:593–611. https://doi.org/10.1002/int.21796
Peng X (2019) New similarity measure and distance measure for Pythagorean fuzzy set. Complex Intell Syst 5:101–111. https://doi.org/10.1007/s40747-018-0084-x
Mohd WRW, Abdullah L (2018) Similarity measures of Pythagorean fuzzy sets based on combination of cosine similarity measure and Euclidean distance measure. In: AIP conference Proceedings. AIP Publishing LLC, p 030017
Zhang Q, Hu J, Feng J et al (2019) New similarity measures of Pythagorean fuzzy sets and their applications. IEEE Access 7:138192–138202. https://doi.org/10.1109/ACCESS.2019.2942766
Wang J, Gao H, Wei G (2019) The generalized Dice similarity measures for Pythagorean fuzzy multiple attribute group decision making. Int J Intell Syst 34:1158–1183. https://doi.org/10.1002/int.22090
Verma R, Merigó JM (2019) On generalized similarity measures for Pythagorean fuzzy sets and their applications to multiple attribute decision-making. Int J Intell Syst 34:2556–2583. https://doi.org/10.1002/int.22160
Peng X, Garg H (2019) Multiparametric similarity measures on Pythagorean fuzzy sets with applications to pattern recognition. Appl Intell 49:4058–4096. https://doi.org/10.1007/s10489-019-01445-0
Nguyen XT, Nguyen VD, Nguyen VH, Garg H (2019) Exponential similarity measures for Pythagorean fuzzy sets and their applications to pattern recognition and decision-making process. Complex Intell Syst 5:217–228. https://doi.org/10.1007/s40747-019-0105-4
Mahanta J, Panda S (2021) Distance measure for Pythagorean fuzzy sets with varied applications. Neural Comput Appl 33:17161–17171. https://doi.org/10.1007/S00521-021-06308-9/TABLES/9
Zhou F, Chen TY (2021) An extended Pythagorean fuzzy VIKOR method with risk preference and a novel generalized distance measure for multicriteria decision-making problems. Neural Comput Appl 33:11821–11844. https://doi.org/10.1007/S00521-021-05829-7/FIGURES/6
Ejegwa PA, Awolola JA (2019) Novel distance measures for Pythagorean fuzzy sets with applications to pattern recognition problems. Granul Comput 6:181–189. https://doi.org/10.1007/S41066-019-00176-4
Sarkar B, Biswas A (2021) Pythagorean fuzzy AHP-TOPSIS integrated approach for transportation management through a new distance measure. Soft Comput 25:4073–4089. https://doi.org/10.1007/S00500-020-05433-2/TABLES/20
Chen TY (2021) Pythagorean fuzzy linear programming technique for multidimensional analysis of preference using a squared-distance-based approach for multiple criteria decision analysis. Expert Syst Appl 164:113908. https://doi.org/10.1016/J.ESWA.2020.113908
Ejegwa PA, Onyeke IC (2021) A robust weighted distance measure and its applications in decision-making via Pythagorean fuzzy information. J Inst Electron Comput 3:87–97. https://doi.org/10.33969/JIEC.2021.31007
De Luca A, Termini S (1972) A definition of a nonprobabilistic entropy in the setting of fuzzy sets theory. Inf Control 20:301–312. https://doi.org/10.1016/S0019-9958(72)90199-4
Ebanks BR (1983) On measures of fuzziness and their representations. J Math Anal Appl 94:24–37. https://doi.org/10.1016/0022-247X(83)90003-3
Bhandari D, Pal NR (1993) Some new information measures for fuzzy sets. Inf Sci (N Y) 67:209–228. https://doi.org/10.1016/0020-0255(93)90073-U
Pal NR, Pal SK (1992) Higher order fuzzy entropy and hybrid entropy of a set. Inf Sci (N Y) 61:211–231. https://doi.org/10.1016/0020-0255(92)90051-9
Pal NR, Pal SK (1989) Object-background segmentation using new definitions of entropy. IEE Proc E Comput Digit Tech 136:284–295. https://doi.org/10.1049/ip-e.1989.0039
Kosko B (1986) Fuzzy entropy and conditioning. Inf Sci (N Y) 40:165–174. https://doi.org/10.1016/0020-0255(86)90006-X
Higashi M, Klir GJ (1982) On measures of fuzziness and fuzzy complements. Int J Gen Syst 8:169–180. https://doi.org/10.1080/03081078208547446
Yager RR (1979) On the measure of fuzziness and negation part I: membership in the unit interval. Int J Gen Syst 5:221–229. https://doi.org/10.1080/03081077908547452
Szmidt E, Kacprzyk J (2001) Entropy for intuitionistic fuzzy sets. Fuzzy Sets Syst 118:467–477. https://doi.org/10.1016/S0165-0114(98)00402-3
Xue W, Xu Z, Zhang X, Tian X (2018) Pythagorean fuzzy LINMAP method based on the entropy theory for railway project investment decision making. Int J Intell Syst 33:93–125. https://doi.org/10.1002/int.21941
Yang M-S, Hussain Z (2018) Fuzzy entropy for Pythagorean fuzzy sets with application to multicriterion decision making. Complexity 2018:1–14. https://doi.org/10.1155/2018/2832839
Thao NX, Smarandache F (2019) A new fuzzy entropy on Pythagorean fuzzy sets. J Intell Fuzzy Syst 37:1065–1074. https://doi.org/10.3233/JIFS-182540
Singh S, Lalotra S, Sharma S (2019) Dual concepts in fuzzy theory: entropy and knowledge measure. Int J Intell Syst 34:1034–1059. https://doi.org/10.1002/int.22085
Singh S, Sharma S, Ganie AH (2020) On generalized knowledge measure and generalized accuracy measure with applications to MADM and pattern recognition. Comput Appl Math 39:231. https://doi.org/10.1007/s40314-020-01243-2
Singh S, Ganie AH (2021) Two-parametric generalized fuzzy knowledge measure and accuracy measure with applications. Int J Intell Syst. https://doi.org/10.1002/INT.22705
Das S, Guha D, Mesiar R (2018) Information measures in the intuitionistic fuzzy framework and their relationships. IEEE Trans Fuzzy Syst 26:1626–1637. https://doi.org/10.1109/TFUZZ.2017.2738603
Farhadinia B (2020) A cognitively inspired knowledge-based decision-making methodology employing intuitionistic fuzzy sets. Cognit Comput 12:667–678. https://doi.org/10.1007/s12559-019-09702-7
Guo K (2016) Knowledge measure for Atanassov’s intuitionistic fuzzy sets. IEEE Trans Fuzzy Syst 24:1072–1078. https://doi.org/10.1109/TFUZZ.2015.2501434
Guo K, Xu H (2019) Knowledge measure for intuitionistic fuzzy sets with attitude towards non-specificity. Int J Mach Learn Cybern 10:1657–1669. https://doi.org/10.1007/s13042-018-0844-3
Lalotra S, Singh S (2018) On a knowledge measure and an unorthodox accuracy measure of an intuitionistic fuzzy set(s) with their applications. Int J Comput Intell Syst 11:1338. https://doi.org/10.2991/ijcis.11.1.99
Nguyen H (2015) A new knowledge-based measure for intuitionistic fuzzy sets and its application in multiple attribute group decision making. Expert Syst Appl 42:8766–8774. https://doi.org/10.1016/j.eswa.2015.07.030
Szmidt E, Kacprzyk J, Bujnowski P (2014) How to measure the amount of knowledge conveyed by Atanassov’s intuitionistic fuzzy sets. Inf Sci (N Y) 257:276–285. https://doi.org/10.1016/J.INS.2012.12.046
Lin M, Huang C, Xu Z (2020) MULTIMOORA based MCDM model for site selection of car sharing station under picture fuzzy environment. Sustain Cities Soc 53:101873. https://doi.org/10.1016/J.SCS.2019.101873
Singh S, Lalotra S, Ganie AH (2020) On some knowledge measures of intuitionistic fuzzy sets of type two with application to MCDM. Cybern Inf Technol 20:3–20. https://doi.org/10.2478/cait-2020-0001
Singh S, Ganie AH (2021) Generalized hesitant fuzzy knowledge measure with its application to multi-criteria decision-making. Granul Comput. https://doi.org/10.1007/s41066-021-00263-5
Weber S (1983) A general concept of fuzzy connectives, negations and implications based on t-norms and t-conorms. Fuzzy Sets Syst 11:115–134. https://doi.org/10.1016/S0165-0114(83)80073-6
Singh S, Ganie AH (2021) Some novel q-rung orthopair fuzzy correlation coefficients based on the statistical viewpoint with their applications. J Ambient Intell Humaniz Comput. https://doi.org/10.1007/s12652-021-02983-7
Du WS (2019) Correlation and correlation coefficient of generalized orthopair fuzzy sets. Int J Intell Syst 34:564–583. https://doi.org/10.1002/int.22065
Cuong BC, Kreinovich V (2013) Picture fuzzy sets—a new concept for computational intelligence problems. In: 2013 third world congress on information and communication technologies (WICT 2013). IEEE, pp 1–6
Mahmood T, Ullah K, Khan Q, Jan N (2019) An approach toward decision-making and medical diagnosis problems using the concept of spherical fuzzy sets. Neural Comput Appl 31:7041–7053. https://doi.org/10.1007/s00521-018-3521-2
Acknowledgements
The authors appreciate the Editor’s and anonymous reviewers' constructive remarks and recommendations, which have substantially improved the presentation of this paper.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
Authors declare that there is no conflict of interest.
Ethical approval
The present article does not contain any studies with human participants or animals performed by any of the authors.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Ganie, A.H. Some t-conorm-based distance measures and knowledge measures for Pythagorean fuzzy sets with their application in decision-making. Complex Intell. Syst. 9, 515–535 (2023). https://doi.org/10.1007/s40747-022-00804-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40747-022-00804-8