Demonstration of optimal non-projective measurement of binary coherent states with photon counting

Abstract

Quantum state discrimination is a central problem in quantum measurement theory, with applications spanning from quantum communication to computation. Typical measurement paradigms for state discrimination involve a minimum probability of error or unambiguous discrimination with a minimum probability of inconclusive results. Alternatively, an optimal inconclusive measurement, a non-projective measurement, achieves minimal error for a given inconclusive probability. This more general measurement encompasses the standard measurement paradigms for state discrimination and provides a much more powerful tool for quantum information and communication. Here, we experimentally demonstrate the optimal inconclusive measurement for the discrimination of binary coherent states using linear optics and single-photon detection. Our demonstration uses coherent displacement operations based on interference, single-photon detection, and fast feedback to prepare the optimal feedback policy for the optimal non-projective quantum measurement with high fidelity. This generalized measurement allows us to transition among standard measurement paradigms in an optimal way from minimum error to unambiguous measurements for binary coherent states. As a particular case, we use this general measurement to implement the optimal minimum error measurement for phase-coherent states, which is the optimal modulation for communications under the average power constraint. Moreover, we propose a hybrid measurement that leverages the binary optimal inconclusive measurement in conjunction with sequential, unambiguous state elimination to realize higher dimensional inconclusive measurements of coherent states.

Introduction

Quantum measurement theory provides a fundamental understanding of the limits on the achievable sensitivity for distinguishing quantum states^1,2,3. Physically realizable strategies that attain, or even approach, the ultimate sensitivity limits for distinguishing nonorthogonal coherent states have a wide range of applications in optical communication^4,5,6,7,8,9, cryptography^{10,11,12,13,14,15,16,17}, and quantum information processing^18,19,20. A central problem in quantum measurement theory and quantum information processing is the discrimination between two quantum states $\left|{\psi }_{1}\right\rangle$ and $\left|{\psi }_{2}\right\rangle$ with a certain optimal measurement given an optimality criterion, depending on the specific application^2,21,22.

Two fundamental measurement paradigms for quantum state discrimination involve either minimum error or unambiguous state discrimination. Minimum-error state discrimination (MESD) aims to achieve minimal probability of error P_E^{23,24,25,26,27,28,29,30,31,32,33,34}. The Helstrom bound²⁴ gives the ultimate limit for P_E, which is achieved by projective measurements onto complex superpositions of quantum states. Notably, the optimal MESD measurement for binary coherent states can be realized with linear optics, single-photon detection, and fast feedback^35,36. In contrast, unambiguous state discrimination (USD) allows for perfect discrimination with P_E = 0, but requires a non-zero probability of inconclusive results P_I ≠ 0. Such a non-projective measurement is described by a positive operator-valued measure (POVM) with three elements^2,37,38, and aims to achieve the smallest possible P_I^{39,40,41,42,43,44,45,46,47}. The realization of optimal USD of binary coherent states does not require feedback^12,48,49, allowing for simpler implementations^45,50 compared to optimal MESD.

While optimal projective measurements exist for certain binary discrimination tasks^2,24,51,52, quantum measurement theory allows for a broader class of generalized quantum measurements that are not projective. These generalized measurements provide a more powerful tool for quantum information processing and communications². Among these general quantum measurements, the optimal inconclusive measurement achieves the smallest possible error probability for a fixed probability of inconclusive results^37,53. This measurement is a non-projective measurement, and thus described by a non-projective POVM, that encompasses MESD and USD measurement paradigms. Moreover, non-projective quantum measurements allow for more exotic discrimination tasks such as quantum state elimination⁵⁴, state comparison^55,56,57, and discrimination with a fixed error margin⁵⁸. Furthermore, understanding optimal inconclusive measurements for binary states may provide a path for realizing arbitrary non-projective POVMs in a two-dimensional Hilbert space^59,60.

Theoretical work on quantum measurement theory has shown that it is possible to realize an optimal inconclusive measurement for a broad class of quantum states based on local operations and classical communications^58,61,62. However, the corresponding measurement operators for the discrimination of optical coherent states do not necessarily have a feasible physical realization. While suboptimal inconclusive measurements of coherent states can be realized based on linear optics and single-photon detection⁶³, their performance falls short of the performance of the optimal inconclusive measurement. Recent work in ref. ⁶⁴ proposed a physical realization of a strategy for the optimal inconclusive measurement of binary coherent states. It was shown that such a non-projective measurement can be realized using displacement operations, single-photon detection, and feedback⁶⁴, which are the same physical elements needed for implementing arbitrary binary projective measurements^52,65.

In this work, we experimentally demonstrate the optimal inconclusive measurement for binary coherent states⁶⁴. The measurement splits the energy of the input state into two temporal modes. It performs a MESD measurement in the first mode providing conclusive results with a certain probability of error, and an optimal inconclusive measurement in the single-state domain in the second mode determining whether the measurement result is inconclusive. Our demonstration uses low noise, high bandwidth real-time feedback conditioned on single-photon detections to prepare the optimal displacement operations required for the optimal inconclusive measurement. We further use this generalized optimal measurement to realize the optimal MESD for phase-coherent states, which is the optimal modulation for optical communications under the average power constraint, thus demonstrating the optimal quantum receiver for coherent optical communications. Lastly, we show that the binary optimal inconclusive measurement enables the realization of inconclusive discrimination of three coherent states when used together with measurements for unambiguous state elimination based on hypothesis testing. This proposed method can in principle be extended to high dimensional inconclusive measurement strategies of coherent states.

Results

Optimal inconclusive measurement

The optimal inconclusive measurement is a non-projective quantum measurement that encompasses the MESD and USD paradigms and optimizes the tradeoff between errors and inconclusive results^37,53. By construction, the optimal inconclusive measurement achieves the minimal error probability P_E for a specified inconclusive probability P_I^2,64. A feasible realization of the POVM for the optimal inconclusive measurement $\{{\hat{{{\Pi }}}}_{1},{\hat{{{\Pi }}}}_{2},{\hat{{{\Pi }}}}_{?}\}$ for binary coherent states was recently proposed in ref. ⁶⁴. Notably, this optimal non-projective measurement can in principle be realized by a generalization of the optimal receiver for MESD, called the Dolinar receiver. This optimal MESD receiver is based on displacement operations in phase space implemented by interfering the input state with a local oscillator (LO) field, single-photon detection, and feedback with an optimal feedback policy. The displacement has a magnitude given by an optimal waveform and a phase conditioned to photon detection^35,36,66.

Figure 1a shows the concept of the optimal inconclusive measurement. The input state $\left|\!\pm\! \alpha \right\rangle$ and strong LO field interfere on a high transmittance beam splitter to implement a displacement operation $\hat{D}(u(t))$. The receiver implements the optimal displacement waveform u(t), where the phase of the LO switches between 0 and π based on the photon detection outcomes from the single-photon detector (SPD) during the measurement time. In the proposal for the optimal inconclusive discrimination strategy⁶⁴, the generalized receiver performs optimal measurements in two temporal modes during the measuring time 0 ≤ t ≤ 1 using displacement operations, single-photon detection, and feedback. In the first temporal mode (0 ≤ t ≤ t₁), the receiver performs an optimal MESD measurement to discriminate between $\{\left|\!\pm\! \alpha \right\rangle \}$ with minimal error using the optimal displacement waveform^35,36,64,66. In the second temporal mode (t₁ < t ≤ 1), the receiver performs an optimal inconclusive measurement in the so-called single-state domain, where the measurement becomes a projective measurement such that the POVM element for the least probable state is zero, e.g., ${\hat{{{\Pi }}}}_{2}=0$^58,64. Without loss of generality, the most probable state after the first mode is $\left|\alpha \right\rangle$, and the non-zero POVM elements are ${\hat{{{\Pi }}}}_{1}$ and ${\hat{{{\Pi }}}}_{?}$. Therefore, the receiver in the second temporal mode attempts to determine whether the measurement result is inconclusive, i.e., the receiver realizes a MESD measurement between the correct and inconclusive outcomes. Reference ⁶⁴ shows that this projective measurement in the second temporal mode (single-state domain) can be realized by a Dolinar-like receiver with a different optimal displacement waveform, which is the key element that we leverage for demonstrating the optimal inconclusive measurement. The total displacement waveform u(t) that implements the optimal inconclusive measurement is given by⁶⁴:

$$u(t)=\left\{\begin{array}{ll}\frac{{(-1)}^{{N}_{1}(t)}\alpha }{\sqrt{1-4p(1-p){K}^{2t}}}&0\,\le \,t\,\le \,{t}_{1}\\ \frac{{(-1)}^{{N}_{2}(t)+{N}_{0}}\alpha }{\sqrt{1-4v(1-v){K}^{2(t-{t}_{1})}}}&{t}_{1} \,<\, t\,\le \,1.\end{array}\right.$$

(1)

Where N₁(t) and N₂(t) are the total number of photons detected up to time t for the first and second temporal mode, respectively, and N₀ ∈ {0, 1} based on ∣α∣², P_I, and p⁶⁴. The total optimal waveform u(t) is comprised of u₁(t) and u₂(t), each of which are optimal for the two temporal modes (see “Methods” section for details). The magnitude of u(t) is predetermined based on the values of ∣α∣², P_I, and p, but the sign of u(t) (phase of the LO) adaptively switches between positive and negative (LO phase of 0 and π) each photon detection due to the ${(-1)}^{{N}_{1}(t)}$ and ${(-1)}^{{N}_{2}(t)+{N}_{0}}$ terms.

Fig. 1: Implementation of the optimal inconclusive measurement.

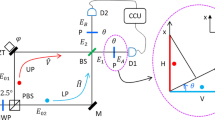
a Schematic of the generalized receiver for the optimal inconclusive measurement. The input states are displaced in phase space using an optimal waveform u(t) for the LO field and followed by a single-photon detector (SPD) and feedback operations. b Optimal waveform magnitudes ∣u(t)∣ for different mean photon numbers |α|² (top panel). The bottom panel shows an example of the waveform u(t) for a particular measurement record where the LO phase switches between 0 and π every photon detection (Photon Detections, middle panel). The circles along the x-axis show the current hypothesis for the input state as the measurement progresses. c Error probability P_E for the optimal inconclusive measurement as a function of the specified probability of inconclusive results P_I for ∣α∣²= 0.2, 0.4, and 0.6. The colored circles along the y-axis (P_I = 0) correspond to the smallest possible P_E in the paradigm of MESD, and the colored squares along the x-axis (P_E = 0) correspond to the smallest possible P_I in the paradigm of USD. d Experimental setup used for demonstrating the optimal inconclusive measurements of binary coherent states.

The top panel of Fig. 1b shows the displacement magnitude ∣u(t)∣ for the optimal inconclusive strategy with inconclusive probability P_I = 0.19 for ∣α∣² = 0.2, 0.4, and 0.6. The discrete jumps in ∣u(t)∣ for each ∣α∣² correspond to the time t₁ when the receiver switches between the measurements two temporal modes. The receiver implements a minimum-error measurement with a Dolinar receiver during 0 ≤ t ≤ t₁ with u₁(t) between $\left|\!\pm\! \alpha \right\rangle$. The receiver then implements the optimal inconclusive measurement in the single-state domain $\{{\hat{{{\Pi }}}}_{1},{\hat{{{\Pi }}}}_{?}\}$ with a Dolinar-like receiver during t₁ < t ≤ 1 with u₂(t). The final outcome of the measurement is either an inconclusive result with probability P_I, a correct discrimination result with probability P_C, or an error with probability P_E = 1 − P_C − P_I⁶⁴. The bottom panel of Fig. 1b shows the displacement amplitude u(t) for an example measurement record. The provisional hypothesis (circles) and the phase of the waveform change each time a photon is detected. The red dashed line (t₁ ≈ 0.70) shows where the receiver switches from MESD of the two input states in the first temporal mode, to MESD between the more likely state given the current detection record and the inconclusive outcome in the second temporal mode.

Figure 1c shows the resulting probabilities {P_I, P_E} of the optimal inconclusive measurement for equiprobable coherent states $\{\left|\!\pm\! \alpha \right\rangle \}$ with ∣α∣² = 0.2, 0.4, and 0.6, in blue, orange, and yellow, respectively. The colored circles along the y-axis (P_I = 0) correspond to the smallest possible P_E in the paradigm of MESD (Helstrom Bound), and the colored squares along the x-axis (P_E = 0) correspond to the smallest possible P_I in the paradigm of USD (sometimes referred to as the IDP bound^39,40,41). Thus, the optimal inconclusive measurement is the generalization of MESD and USD and interpolates between these measurement paradigms in an optimal way using more general non-projective measurements. In general, the optimal inconclusive measurement for the discrimination of two general quantum states $\{\left|{\psi }_{1}\right\rangle ,\left|{\psi }_{2}\right\rangle \}$ is represented by three POVM elements $\{{\hat{{{\Pi }}}}_{1},{\hat{{{\Pi }}}}_{2},{\hat{{{\Pi }}}}_{?}\}$ where a positive outcome of $\{{\hat{{{\Pi }}}}_{1,2}\}$ indicates that the state $\left|{\psi }_{1,2}\right\rangle$ is present, and ${\hat{{{\Pi }}}}_{?}=\hat{I}-{\hat{{{\Pi }}}}_{1}-{\hat{{{\Pi }}}}_{2}$ corresponds to an inconclusive result. Optimality indicates that this non-projective measurement achieves the minimum error for a fixed probability of inconclusive outcomes.

While the proposed implementation of this non-projective quantum measurement in ref. ⁶⁴ is in principle feasible, its demonstration requires a high degree of control for the preparation of optimal waveforms with high fidelity, and the ability to realize feedback measurements with high bandwidth and low noise (see Supplementary Note I). Moreover, the validation of optimal performance requires absolute power measurements at the single-photon level. In our experimental demonstration we address the issues to satisfy these stringent requirements, which allows us to demonstrate experimentally this complex quantum measurement with high fidelity. Figure 1d shows our experimental setup for the demonstration of the optimal inconclusive measurement for binary coherent states. We use an interferometric setup to generate the input states and local oscillator field, a single-photon detector (SPD), and an FPGA (Altera Cyclone IV, 50 MHz base clock) connected to a digital-to-analog converter (DAC) to implement the required optimal displacement waveform u(t) for the optimal inconclusive measurement using fiber-coupled amplitude (AM) and phase (PM) modulators (see “Experimental setup details”, “FPGA implementation”, and “Optical modulators” in the Methods section for details). We actively stabilize our interferometer using a second 780 nm laser and a feedback loop to maintain a well-defined relative phase (see “FPGA implementation” in the Methods section for details). Our implementation achieves an overall detection efficiency η = 0.72(1) (η = η_SPDη_sys where η_SPD = 0.82(1) is the SPD efficiency and η_sys = 0.88(1) is the system transmittance), interference visibility ξ = 0.998(1), and dark counts ν = 0.03(1) per pulse. The experiment operates at a 4 kHz repetition rate, alternating between experimental trials (1024 time bins, 160 ns each) and interferometer stabilization with a ≈66% duty cycle. We have also realized numerical investigations of the effects of realistic imperfections described in Supplementary Note I. Based on these studies, we observe that reduced detection efficiency degrades the achievable performance for all errors and inconclusive probabilities. Reduced interference visibility and increased dark counts mainly degrade the performance of strategies where the desired P_E or P_I are small, i.e., near the MESD and USD regimes.

Demonstration of the optimal inconclusive measurement

We implement the optimal inconclusive measurement for equiprobable coherent states. In our experimental demonstration, we obtain the time evolution of the error ${P}_{{{{\rm{E}}}}}^{\exp }(t)$, correct ${P}_{{{{\rm{C}}}}}^{\exp }(t)$, and inconclusive ${P}_{{{{\rm{I}}}}}^{\exp }(t)$ probabilities by reconstructing the results in post-processing, and compare them to the expected probabilities {P_E(t), P_C(t), P_I(t)}⁶⁴. The final inconclusive ${P}_{{{{\rm{I}}}}}^{\exp }(t=1)$ and error ${P}_{{{{\rm{E}}}}}^{\exp }(t=1)$ probabilities for a given ∣α∣² correspond to a single realization of the optimal inconclusive measurement. Figure 2a shows the experimental results for ∣α∣² = 0.2, 0.4, and 0.6 in blue, orange, and yellow, respectively. The points show the experimental data $\{{P}_{{{{\rm{I}}}}}^{\exp }(1),{P}_{{{{\rm{E}}}}}^{\exp }(1)\}$ and the error bars represent one standard deviation from five experimental runs of 5 × 10⁴ independent experiments each. The black lines show the theoretical expectation from Monte-Carlo simulations of the experiment incorporating experimental imperfections (See Supplementary Note IV). We note that we obtain the expected performance of our demonstration by directly simulating the experiment including experimental imperfections and other effects without requiring any fitting procedures. The dashed gray lines show the ideal (η = 1) performance for each mean photon number. The colored circles and squares on the y-axis and x-axis show the optimal P_E and P_I for ideal MESD and USD, respectively, for each ∣α∣².

Fig. 2: Experimental Results.

a Experimental results for the optimal inconclusive measurement for ∣α∣²= 0.2, 0.4, and 0.6, in blue, orange, and yellow, respectively. Each point corresponds to the measured values of $\{{P}_{{{{\rm{I}}}}}^{\exp }(1),{P}_{{{{\rm{E}}}}}^{\exp }(1)\}$ and the error bars represent one standard deviation from five sets of 5 × 10⁴ individual experiments each. The solid lines show the expected results and the dashed gray lines show the ideal performance for each ∣α∣². The colored circles and squares on the y-axis and x-axis show the optimal P_E and P_I for ideal MESD and USD, respectively. Inset (i): evolution of ${P}_{{{{\rm{E}}}}}^{\exp }$, ${P}_{{{{\rm{C}}}}}^{\exp }$, and ${P}_{{{{\rm{I}}}}}^{\exp }$ for ∣α∣²= 0.2 and and ${P}_{{{{\rm{I}}}}}^{\exp }$=0.31. b Experimental results (blue points) of an optimal MESD measurement, the Dolinar receiver, for phase coherent states $\{\left|\pm \alpha \right\rangle \}$. The gray and red solid lines show the Helstrom bound for η = 1.0 and η = 0.72, respectively, and the dashed lines show the corresponding error for a homodyne measurement.

We observe that our demonstration of the optimal inconclusive measurement with η = 0.72 for ∣α∣² = 0.2, 0.4, and 0.6 reaches errors below the ideal Helstrom bound when P_I ⪆ 0.18. This shows that a non-ideal implementation of the optimal inconclusive measurement can surpass the ideal Helstrom bound at the expense of having inconclusive results (We note that while the Helstrom bound is the minimum discrimination error that can be achieved by a deterministic measurement, this bound is not the lowest error for a general quantum measurement that allows for inconclusive results⁵³. As such, the optimal inconclusive measurement then allows for errors below the Helstrom bound for P_I ≠ 0, and achieves zero error at a rate of inconclusive results given by the IDP bound^39,40,41). The inset of Fig. 2a shows an example of the evolution of P_E(t) (blue), P_C(t) (orange), and P_I(t) (yellow) as the measurement progresses for ∣α∣² = 0.2 and P_I ≈ 0.31. The solid lines show the theoretical expectation including experimental imperfections and the points show the experimental results for ${P}_{{{{\rm{E}}}}}^{\exp }(t)$, ${P}_{{{{\rm{C}}}}}^{\exp }(t)$, and ${P}_{{{{\rm{I}}}}}^{\exp }(t)$ every 50-time bin steps. Note that the measurement switches from a MESD measurement to an optimal inconclusive measurement in the single-state domain at t₁ ≈ 0.57.

Optimal MESD of binary phase states

The optimal inconclusive measurement generalizes MESD and USD⁶⁴, and can be used to demonstrate the optimal MESD measurement, the Dolinar receiver³⁵, by setting P_I = 0. The previous work³⁶ demonstrated a Dolinar receiver for intensity-modulated coherent states $\{\left|0\right\rangle ,\left|\alpha \right\rangle \}$ and achieved performance below the shot noise limit after correcting for system losses and detection efficiency. However, phase-encoded coherent states $\{\left|\!\pm\! \alpha \right\rangle \}$ are the optimal modulation for binary coherent communications under the energy constraint. This is because this alphabet has the smallest overlap, and therefore the highest distinguishability, for a fixed average energy of the states^48,67,68. To this end, we use the optimal inconclusive measurement to demonstrate a Dolinar receiver for the phase-encoded binary coherent states, and thus demonstrate the optimal quantum receiver for coherent optical communications.

Figure 2b shows the experimental results (blue points) and the expected error probability (solid black) for the optimal MESD measurement, the Dolinar receiver, for phase-coherent states together with the Helstrom (solid) and homodyne limits (dashed). The Helstrom bound and the homodyne limits corrected to our overall efficiency (η = 0.72) are included for reference. We observe that our demonstration of the Dolinar receiver approaches the corrected Helstrom bound and shows an excellent agreement with the theoretical predictions (solid black line). We note that our implementation of the optimal MESD measurement for BPSK states with overall efficiency of η = 0.72 achieves P_E = 0.18 for ∣α∣² = 0.2, which is below the ideal homodyne limit that corresponds to the optimal Gaussian measurement for BPSK⁶⁷. This error rate is similar to the one achieved by a sub-optimal receiver without feedback in ref. ²⁷ using a high efficiency (η = 0.99) superconducting detector resulting on an overall system efficiency of η = 0.91. Thus, we conclude that the strategy demonstrated here based on complex adaptive measurements can potentially provide overall higher sensitivities than the sub-optimal strategy under the same loss and realistic experimental noise and imperfections. In principle, the optimal inconclusive measurement also allows for the construction of the optimal USD measurement where P_E = 0. However, the experimental imperfections such as dark counts and non-ideal interference visibility prevent the receiver from achieving P_E = 0 (see Fig. 2). Nevertheless, the above framework allows for finding the optimal waveform to implement this optimal measurement.

Higher dimensional inconclusive strategies

We investigate how to leverage the optimal inconclusive measurement of binary coherent states to enable inconclusive state discrimination of higher dimensional encodings. We propose a hybrid measurement that utilizes binary optimal inconclusive measurements in conjunction with unambiguous state elimination, which can realize such a non-projective inconclusive measurement of ternary phase-shift keyed (TPSK) states $\{\left|\alpha \right\rangle ,\left|\alpha {e}^{i2\pi /3}\right\rangle ,\left|\alpha {e}^{i4\pi /3}\right\rangle \}$, and can be extended to higher dimensions. This measurement first aims to eliminate all but two possible input states via hypothesis testing, and then utilizes the optimal inconclusive measurement in the remaining binary states. Figure 3a shows the measurement operations conditioned to single-photon detection, realized by the proposed high-dimensional inconclusive measurement. The receiver realizes an elimination measurement based on hypothesis testing (red region, Fig. 3a-i) for the state $\left|\alpha \right\rangle$ on a fraction f/3 of the total input state. This state elimination measurement is based on a displacement operation of $\left|\alpha \right\rangle$ to the vacuum state $\left|0\right\rangle$ and single-photon detection, such that detection of a photon unambiguously eliminates $\left|\alpha \right\rangle$ as a possible input state. If a photon is detected in the first stage (Stage 1), the receiver then performs an optimal binary inconclusive measurement (blue region, Fig. 3a-i) to optimally discriminate between $\left|\alpha {e}^{i2\pi /3}\right\rangle$ and $\left|\alpha {e}^{i4\pi /3}\right\rangle$ using the remaining fraction 1 − f/3 of the input energy. If no photons are detected during the first stage, the receiver then realizes a state elimination measurement for the input state $\left|\alpha {e}^{i2\pi /3}\right\rangle$ also using a fraction f/3 of the total input power (Fig. 3a-ii) . Now if a photon is detected in the second stage (Stage 2), an optimal inconclusive measurement discriminates between the remaining two possible input states using a fraction 1 − 2f/3 of the input power, where the factor of 2 comes from the first stage. If no photons are detected in the second stage, then the receiver tests for the state $\left|\alpha {e}^{i4\pi /3}\right\rangle$ in Stage 3, also using a fraction f/3 of the total input state (Fig. 3a-iii). If a photon is detected, an optimal inconclusive measurement discriminates between the remaining two states now using a fraction 1 − 3f/3 of the input power. If no photons are detected in the third hypothesis test for unambiguous state elimination, we define the measurement outcome to be inconclusive.

Fig. 3: Inconclusive discrimination of the ternary phase-shift keyed (TPSK) coherent states using the binary optimal inconclusive measurement.

a The proposed inconclusive measurement for TPSK states uses sequential unambiguous state elimination, followed by the optimal binary inconclusive measurement (See main text for details). b Conditional error probability P_E/(1 − P_I) as a function of inconclusive probability P_I for ∣α∣² = 0.2 (blue), 0.4 (orange), and 0.6 (yellow). We compare the proposed measurement with the parameter f = 0.66 (solid) and f = 0.90 (dashed) to the performance of ideal heterodyne detection (dotted). See text for details.

Figure 3b shows the simulation results for the proposed inconclusive measurement of TPSK states based on the optimal inconclusive measurement for binary states for mean photon numbers ∣α∣² = 0.2, 0.4, and 0.6. The x-axis corresponds to the inconclusive probability and the y-axis corresponds to the conditional error probability P_E/(1 − P_I), i.e., the error probability given that a conclusive outcome was obtained. The solid and dashed lines show the proposed inconclusive measurement of three coherent states with f = 0.66 and f = 0.90, respectively. The dotted lines show the result ${P}_{{{{\rm{E}}}}}^{{{{\rm{Het}}}}}/(1-{P}_{{{{\rm{I}}}}}^{{{{\rm{Het}}}}})$ for using ideal heterodyne detection, where measurement outcomes with the largest error probability are designated as inconclusive until the desired inconclusive probability is achieved as in ref. ⁴⁵. The optimal limits for USD and MESD for three states are represented with squares and circles in the x-axis (P_E = 0) and y-axis (P_I = 0), respectively^49,69.

The overall P_I achieved by this strategy contains two contributions ${P}_{{{{\rm{I}}}}}={P}_{{{{\rm{I}}}}}^{(1)}+{P}_{{{{\rm{I}}}}}^{(2)}$, where ${P}_{{{{\rm{I}}}}}^{(1)}$ comes from the state elimination stage, and ${P}_{{{{\rm{I}}}}}^{(2)}$ from the binary optimal inconclusive measurement. In the state elimination stage, the detection of vacuum during all three hypothesis tests results in an inconclusive outcome as each state is equally likely. This produces a lower bound (${P}_{{{{\rm{I}}}}}^{(1)}$) on the attainable inconclusive probability P_I depending on the values of f and ∣α∣². In the binary optimal inconclusive measurement stage, the proposed measurement defines a “target” inconclusive probability (${P}_{{{{\rm{I}}}}}^{(2)}$) which can be set for any ∣α∣² to achieve the desired overall P_I of the strategy. We observe that the proposed measurement with both values of the parameter f, which parameterizes the unambiguous state elimination stages, can outperform heterodyne detection. Moreover, we note that a smaller value of f = 0.66 achieves a smaller error probability, but this also puts a limit on the smallest attainable inconclusive probability of P_I ≈ 0.76, 0.58, and 0.45 for ∣α∣² = 0.2, 0.4, and 0.6, respectively. On the other hand, a larger value of f = 0.90 (dashed lines) allows for a smaller inconclusive probability but at the cost of a larger error probability compared to f = 0.66 (solid lines). This trade-off is due to the fact that a larger value of f results in a smaller contribution to P_I from the inconclusive outcome during the state elimination stage (detecting vacuum during all stages). However a larger value of f results in a smaller fraction of the total input energy of the state for the binary optimal inconclusive measurement, which results in a larger error probability. Then, the optimal choice of energy fraction f will depend on the particular application of this proposed measurement. For example, if we are willing to tolerate more inconclusive results P_I to achieve a given small target error threshold P_E such as for communications with error detection, correction, and erasures⁷⁰, we should choose a small value of f.

The proposed inconclusive measurement for three states can be extended to higher dimensions. Using this technique, an inconclusive measurement of M input coherent states can be realized through the implementation of M − 1 hypothesis testing stages for unambiguous state elimination^45,49, followed by the binary optimal inconclusive measurement. Given that the binary optimal inconclusive measurement can always achieve P_E = 0 for ${P}_{{{{\rm{I}}}}}^{(2)} \,<\, 1$, there is always a range of error probabilities for which this strategy will outperform heterodyne detection (note ${P}_{{{{\rm{E}}}}}^{{{{\rm{Het}}}}}=0$ only when ${P}_{{{{\rm{I}}}}}^{{{{\rm{Het}}}}}=1$), i.e., there is always an error regime where ${P}_{{{{\rm{I}}}}} \,<\, {P}_{{{{\rm{I}}}}}^{{{{\rm{Het}}}}}$. Ideally, this performance is achieved at the smallest possible value of P_I, which will depend on the number of possible states (See Supplementary Note III).

We note that the proposed measurement uses similar techniques in the state elimination stage as the Bondurant receiver for MESD of multiple states⁷¹, and the USD receiver based on feedback and state elimination⁴⁸. However, the proposed strategy in here makes use of the optimal inconclusive measurement of two states for allowing to transition between the measurement paradigms of MESD and USD to realize an optimized inconclusive measurement of multiple coherent states. While the performance of the strategy for more states will degrade due to the increased inconclusive probability in the state elimination stage, we expect that this strategy will serve as the basis for designing optimized inconclusive strategies in higher dimensions. A possible example for inconclusive measurement strategies could use hybrid measurement schemes combining Gaussian measurements, such as homodyne, with photon counting^72,73. In these schemes, the Gaussian measurement can eliminate a sub-set of the states, and photon counting would be used for state elimination in a smaller sub-set of states followed by the binary optimal inconclusive measurement.

Discussion

Optimal inconclusive measurements are generalized quantum measurements that encompass standard paradigms of state discrimination including MESD and USD. These non-projective measurements allow for diverse state discrimination tasks and provide a more powerful tool for classical and quantum information processing^17,63. In optical communication, inconclusive measurement results can be treated as an erasure channel, and optimal inconclusive measurements can be leveraged to increase the amount of information transfer by utilizing communication codes well suited for erasure channels⁷⁰. These optimal inconclusive measurements can also enable hybrid repeater schemes where inconclusive measurements of coherent states are used to entangle remote quantum memories^74,75. Recent advancements in quantum measurement theory showed that such complex quantum measurements for binary coherent states can be realized using single-photon detection and local operations and classical communication in a two-mode measurement⁶⁴. This measurement strategy splits the energy of the input state into two temporal modes. It performs a MESD measurement of the input state in the first mode with a certain probability of error, and an optimal inconclusive measurement in the single-state domain in the second mode determining whether the measurement result is inconclusive. The optimality of this measurement makes it possible to achieve minimal error for a given inconclusive probability. Moreover, such generalized quantum measurements can be realized with Dolinar-like optimal receivers for coherent states.

Here, we experimentally demonstrate the optimal inconclusive measurement proposed in⁶⁴. Our demonstration uses coherent displacement operations, single-photon detection, and fast feedback to implement these general non-projective quantum measurements with high fidelity in a real system. We further use this measurement to demonstrate the optimal MESD for phase-encoded binary coherent states, which is the optimal modulation for optical communications under the average power constraint. While our proof of principle demonstration of the optimal inconclusive measurement was realized at moderate measurement rates, future implementations based on integrated photonics with high-bandwidth optical modulation and processing⁷⁶ within small footprints, together with advancements in high-bandwidth integrated nanowire detectors will allow for demonstrations at GHz bandwidths. These results show that Dolinar-like receivers can be used to perform a wide variety of measurements within a two-dimensional Hilbert space with current technologies. Furthermore, we show how the binary optimal inconclusive measurement can be leveraged to perform inconclusive measurements in higher dimensions with hybrid measurements using sequential unambiguous state elimination of multiple states. Our work contributes to our understanding of the fundamental and practical limits of measurements based on single-photon detection, coherent displacement operations, and feedback, and can further our understanding of quantum measurement theory⁵⁹. Moreover, these measurement techniques can potentially allow for implementations of more general non-projective measurements in two-dimensional spaces using linear optics and single-photon detection.

Methods

Optimal displacement waveform

The optimal inconclusive measurement $\{{\hat{{{\Pi }}}}_{1},{\hat{{{\Pi }}}}_{2},{\hat{{{\Pi }}}}_{?}\}$ for binary coherent states can be realized with a generalized Dolinar receiver⁶⁴. In this modified strategy⁶⁴, the generalized receiver performs optimal measurements in two temporal modes during the measuring time 0 ≤ t ≤ 1. In the first temporal mode, 0 ≤ t ≤ t₁, the optimal inconclusive receiver performs an optimal MESD measurement to discriminate between $\{\left|\pm \alpha \right\rangle \}$ with minimal error using the optimal displacement waveform^35,36,64,66:

$${u}_{1}(0\,\le \,t\,\le \,{t}_{1})=\frac{{(-1)}^{{N}_{1}(t)}\alpha }{\sqrt{1-4p(1-p){K}^{2t}}},$$

(2)

Here ${K}^{2}=| \left\langle -\alpha | \alpha \right\rangle {| }^{2}={e}^{-4| \alpha {| }^{2}}$, p is the prior probability of the most likely state, and N₁(t) is the total number of detected photons in the first mode up to time t ≤ t₁, where N₁(0) = 0. Note that during the first temporal mode the phase of the LO displacement field (sign of u₁(t)) switches between 0 and π each time a photon is detected, similar to the Dolinar receiver⁷⁷. During the measurement in the first temporal mode, the provisional hypothesis for the input state at time t is $\left|\alpha \right\rangle$ if N₁(t) is even and $\left|-\alpha \right\rangle$ if N₁(t) is odd. The provisional probabilities for the two input states after the first temporal mode are $\{{P}_{{{{\rm{C}}}}}^{(1)},1-{P}_{{{{\rm{C}}}}}^{(1)}\}$ with:

$${P}_{{{{\rm{C}}}}}^{(1)}=\frac{1}{2}\left(1+\sqrt{1-p(1-p){e}^{-4{t}_{1}| \alpha {| }^{2}}}\right),$$

(3)

which corresponds to the Helstrom bound for the coherent states $\{\left|\pm \sqrt{{t}_{1}}\alpha \right\rangle \}$. The optimal waveform u₁(t) in Eq. (2) and the evolution of the probability of correct detection P_C(t) at t can be obtained using Bayesian updating^64,78,79 or optimal control⁶⁶.

In the second temporal mode (t₁ < t ≤ 1), the receiver performs an optimal inconclusive measurement in the so-called single-state domain, where P_I, ${P}_{{{{\rm{C}}}}}^{(1)}$, and (1 − t₁)∣α∣² are such that ${\hat{{{\Pi }}}}_{2}=0$^58,64. Without loss of generality, the most probable state is $\left|\alpha \right\rangle$, and the non-zero POVM elements are ${\hat{{{\Pi }}}}_{1}$ and ${\hat{{{\Pi }}}}_{?}$. This optimal inconclusive projective measurement in the single-state domain can be realized by a Dolinar-like receiver with optimal displacement waveform⁶⁴:

$${u}_{2}({t}_{1} \,<\, t\,\le \,1)=\frac{{(-1)}^{{N}_{2}(t)+{N}_{0}}\alpha }{\sqrt{1-4v(1-v){K}^{2t}}},$$

(4)

where p in Eq. (2) is replaced by the quantity v, which depends on P_I, p, and ∣α∣^2 64. N₂(t) is the number of photons detected in the second mode with N₂(t₁) = 0, and N₀ determines the phase of the LO at t₁: N₀ = 0 if v > 0.5 and N₀ = 1 otherwise.

The total displacement waveform for the optimal inconclusive receiver is thus a combination of u₁(t) in Eq. (2) and u₂(t) in Eq. (4) resulting on the total optimal displacement in Eq. (1) in main text. This strategy therefore implements a standard Dolinar receiver during the first mode 0 ≤ t ≤ t₁, and then a Dolinar-like receiver during t₁ < t ≤ 1 assuming the input states at t = t₁ have prior probabilities {v, 1 − v}⁶⁴.

Experimental setup details

In our experimental demonstration, optical pulses are generated from a Helium-Neon laser and a pulsed acousto-optic modulator (AOM), and then split into the signal arm (upper) and LO arm (lower), as shown in Fig. 1d. The input states are prepared with an attenuator (Att.) and a phase modulator (PM). The LO field is prepared by a PM with a multiplexer (MUX), and an amplitude modulator (AM) with a digital-to-analog converter (DAC). The input state and the LO field interfere on a 99/1 beam splitter (BS) to implement the optimal displacement waveforms $\hat{D}(u(t))$ conditioned on photon detection events using a single-photon detector (SPD). A field programmable gate array (FPGA) stores the magnitude of the optimal waveform ∣u(t)∣ in Eq. (1) in memory, prepares the amplitude and phase of the LO conditioned on N₁(t), N₂(t), and N₀, and implements the strategy for the optimal inconclusive measurement. We discretize time t into 1024 time bins of 160 ns each where a photon can be detected to approximate a continuous measurement. Our implementation achieves a feedback bandwidth of about 6 MHz, which is limited by the APD output latency, electronic bandwidth of controllers, switches and FPGA, accounting for about 50 ns and optical delays in the interferometric setup (100 ns). The FPGA processes and stores the photon detections during these time bins and sends the detection histories to a computer. We reconstruct the measurement probabilities in post-processing. The optimal inconclusive measurement requires very large values of the ratio between mean photon numbers of the displacement field and the input state, R = ∣u(t)∣²/∣α∣². However, experimentally there is a maximum ratio R that can be reliably implemented. In our demonstration, we set the maximum of this ratio to R = 50, which is limited by the extinction ratio (≈20 dB) of the AM in the LO arm of the setup. The impact of finite values for R and other experimental imperfections are discussed in Supplementary Notes I and II.

FPGA implementation

We use an Opal Kelly ZEM4310 to control the experiment, which is based on an Altera Cyclone IV FPGA and has a base clock rate of 50 MHz. We discretize the discrimination measurements into 1024 time bins of 160 ns each such that a single shot of the experiment corresponds to a pulse that is 163.8 μs long. The magnitude of the LO waveform for each of the 1024 time bins is pre-calculated for each ∣α∣² and inconclusive probability P_I and stored in a look-up table within the FPGA as an 8-bit value. The phase of the LO flips between 0 and π each time a photon is detected. This method for preparing the optimal LO waveform given by Eq. (1) allows us to efficiently implement the desired optimal inconclusive measurement in our demonstration.

The optimal inconclusive strategy requires precise and fast control of the LO phase. We control the phase of the LO by changing the voltage applied to the phase modulator between two values which correspond to a phase of 0 and a phase of π. Each time the phase of the LO changes, we ignore the output of the APD for 160 ns to avoid accidental photon detections. This “blanking time” is obtained by noting that the combined electrical and optical delay time between changing the modulation voltage and observing the corresponding photons at the APD is ~150 ns. This also has the benefit of reducing the effective after-pulsing probability to close to zero. Typically, the probability of detecting an after-pulse is at its maximum immediately after the dead-time of the APD (≈40 ns for our implementation), but this probability quickly decays with time. We note that without any blanking, the cumulative after-pulsing probability of our APD is P_AP ≈ 0.015 and P_AP < 0.001 with 100 ns of blanking.

Interferometer stabilization

In order to maintain a well-defined relative phase between the signal and LO fields, we actively stabilize the interferometer. We run the experiments with a 4 kHz repetition rate to give an experimental duty cycle of ≈66% (experiment time of ≈165 μs, locking time of ≈91 μs). During the part of the experimental duty cycle when the experiment is not taking place, the relative phase between the two arms of the interferometric setup actively stabilized with a feedback loop using a PID controller and a piezo on the back of a mirror in the signal arm, see Fig. 2. We obtain the error signal for stabilization of the interferometer using a narrow-band laser at 780 nm, which is actively stabilized in frequency to an atomic line in rubidium using saturated absorption spectroscopy. Light from this laser propagates in an opposite direction through the interferometer compared to the light at 633 nm, and is detected with a differential detector to measure the phase fluctuations. Slightly before the discrimination measurement begins, the feedback loop is paused and voltage to the piezo is fixed at its current value. The stabilization feedback loop resumes after the discrimination measurement is completed.

Optical modulators

The setup uses fiber-coupled Lithium-Niobate, amplitude and phase electro-optic modulators (AM and PM), with a 3 dB bandwidth of ≈1 GHz. The phase modulators (PMs) have a π-voltage of V_π = 1.5 V and the amplitude modulator (AM) has a π-voltage of V_π = 750 mV with an extinction ratio of ≈20 dB. The amplitude and phase of the LO and the phase of the signal fields are adjusted using three 8-bit digital-to-analog converters (DAC), voltage-controlled gain circuits, and summing amplifiers.