1 Introduction

The number of signals available from Global Navigation Satellite Systems (GNSS) increases rapidly as well as the demand for and the interest in multi-GNSS computations (Montenbruck et al. 2017; Steigenberger and Montenbruck 2019). Precise values for absolute receiver antenna phase centre corrections (PCC) are one prerequisite for high-quality (multi-)GNSS applications. They play a key role for the determination of consistent orbits, clocks, earth orientation parameters, atmospheric parameters and systematic biases estimates (Villiger et al. 2020). Here, absolute PCC means that these values are independent of any reference antenna.

Two independent methods are applied to obtain absolute PCC: chamber and robot calibration. The chamber method (Görres et al. 2006; Zeimetz and Kuhlmann 2008; Becker et al. 2010; Zeimetz 2010; Schupler and Clark 2001) provides corrections for a broad spectrum of GNSS frequencies determined from generic carrier signals in an anechoic chamber. The robot method (Menge et al. 1998; Wübbena et al. 1997; Böder et al. 2001) requires real modulated signals to determine the PCC.

The determined PCC of both methods are represented as correction grids following the conventions of the International GNSS Service (IGS) ANTenna EXchange format ANTEX (Rothacher and Schmid 2010).

Consistency issues occur when combining and mixing PCC from the two different absolute calibration methods. Only little research is available on this topic. Studies of Aerts et al. (2013), Baire et al. (2014) in the IGS network demonstrated that calibration values of individual antennas differ by several millimetres between the two methods (chamber and robot). These findings were used at the time for a preliminary discussion of the accuracy and consistency of estimates in the IGS network.

Kallio et al. (2018) applied special test set-up (revolver) to highlight the impact on the position domain. They found small differences between the robot calibrations from Geo++ and Institut für Erdmessung (IfE) below the 2 mm level. Inter-antenna PCC differences between chamber and robot were reported for the position domain to 2 mm and 4 mm for L1 and L2, respectively. An estimation of the effects on further geodetic parameters was not performed. Bergstrand et al. (2020) tilted the antennas under test and showed systematic inter-antenna differences for L1 and L2 of up to ± 4 mm. In addition, they determine an unbiased phase centre offset by a combination of inter-antenna differences and high-precision geometric measurements. Krzan et al. (2020) studied European Permanent Network (EPN) stations using a precise point positioning (PPP) approach and investigated position time series with the NAPEOS GNSS software (Springer and Dow 2009). They found deviations between chamber and robot calibrations of up to 20 mm for the ionosphere-free linear combination (L0) which are then transferred to position deviations, exceeding 5 mm height variations for some stations. Studies on the quality of individual absolute PCC for various signals and frequencies are made by Kröger et al. (2021) under laboratory conditions for a short baseline.

The analysis centres of the IGS (Johnston et al. 2017) are currently using absolute receiver antenna PCC type mean values for GPS and GlonassL1/L2 carrier frequencies to compute the routine IGS products; for repro3 (IGS-AC 2021), frequency-dependent multi-GNSS patterns are tested. The PCC values origin in majority from the calibration method robot. Contrary to the IGS, the EPN applies multi-GNSS receiver antenna correction data in its operational service (Bruyninx et al. 2019). In addition to the type mean values, the EPN network makes individual absolute PCC of ground stations separately available (EPN 2019). Furthermore, for selected EPN stations individual PCC are available that origin from both robot and chamber calibrations. They are studied in detail in this paper.

In this paper, we assess the effect of mixing absolute PCC values from different calibration strategies. We first develop and propose comparison methods of PCC obtained from different calibration methods. Next, taking the absolute individual PCC from robot (Geo++ company) and chamber (University of Bonn) from the EPN, we apply the proposed comparison strategy and study the impact of different PCC. Finally, we analyse a subset of EPN stations by double difference (DD) and PPP approaches to assess the impact of different PCC values.

2 Receiver antenna pattern—theory and practice

2.1 Carrier phase centre corrections

In this contribution, we name PCC the carrier phase centre corrections. By IGS convention, PCC are expressed in a left-handed antenna-fixed coordinate system. The positive z-axis is the vertical symmetry axis and the x-axis is in direction of the North marker of the antenna, which is usually the coaxial cable connector. The origin of the coordinate system is the antenna reference point (ARP) located at a mechanically accessible point, generally the antenna substructure or the 5/8\(^{\prime \prime }\) mounting threat. Details are given in the so-called antenna.gra file (IGS 2021). Spherical Harmonics (SH) expansion or a polynomial fit is used to estimate the PCC. The maximal degree and order of the development are varying, and a compromise must be made between the expected azimuthal and elevation-dependent oscillations of the pattern due to the antenna design and the number of parameters to be estimated. Often a development up to degree 8 and order 5 is used.

Traditionally, for each GNSS system s and each frequency f the PCC is subdivided into the 3\(\times \)1 carrier phase centre offset vector (\(\mathbf {PCO}\)) and the gridded phase centre variations (PCV) both expressed in an antenna body frame

$$\begin{aligned} \mathrm{PCC}_{s,f}(\phi ,\theta ) = -\mathbf{s}^\mathrm{T} \mathbf{PCO}_{s,f}+\mathrm{PCV}_{s,f}(\phi ,\theta ) +r_{s,f} \end{aligned}$$
(1)

with \(\phi ,\,\theta \) being the horizontal and vertical angle in the antenna body frame and \(\mathbf{s}\) the line-of-sight unit vector to the satellite. Experimental developments in the IGS reprocessing campaign repro3 consider no longer a system but only a frequency dependency.

The PCC determination has inherently one degree of freedom, expressed by the parameter \(r_{s,f}\), (Rothacher et al. 1995). This means that only the shape of the PCC can be determined but not the absolute size; a phase offset \(r_{s,f}\), constant for all directions, remains unsolvable. This corresponds, for example, to the 0th-order term of the SH development. The reason is that neither for method chamber nor for method robot absolute ranges can be measured. In the case of method chamber, the overall delays are not known at the picosecond level. For the method robot, only pseudo-ranges between satellite and receiver antenna pattern are observed by the carrier phases. Subsequently, we have to estimate (or eliminate in case of differences) the receiver clock bias—also when analysing the GNSS observations during calibrations. As a consequence, a specific datum has to be defined to overcome this rank deficiency. At IfE, the phase offset is set to zero for each system and each frequency, separately.

In addition, depending on calibration strategies used, strong correlations between the parameters (e.g. the SH coefficients) can be present (Kersten and Schön 2010). Various stabilisation methods (constrains, regularisation, process noise for Kalman filter or multi-step strategies) are applied but rarely documented. Numerical instabilities of the normal equation system are solved, for example, by constraining SH coefficients with odd sum of degree and order to zero (Willi et al. 2019; Kröger et al. 2021; Sutyagin and Tatarnikov 2020) or by re-parameterising the SH (Rothacher et al. 1995). In all cases, special care must be taken in order to not over-constrain and thus deform the resulting PCC.

2.2 Calibration strategies

GNSS receiver antennas for ground stations are successfully calibrated using different independent approaches. The first approach—method robot—is the absolute calibration in the field with a 5-axis precise robot from AMTEC/Schunk. This method was developed in a cooperation between the IfE and the company Geo++ (Menge et al. 1998; Wübbena et al. 1997). Currently, the system as described in Wübbena et al. (2019) is operated by Geo++, IfE, the State Survey Authority Berlin (SenStadtSW), and Geoscience Australia (Riddell et al. 2015). Zero difference carrier phase observations are input in a Kalman filter to estimate the PCC by SH of degree eight and order five. Typically, the PCV are set to zero at zenith (zero zenith constraint) to separate the PCC into PCO and PCV.

The US National Geodetic Survey (NGS) is developing their 2-axis robot system (Bilich et al. 2012) to a 6-axis system using a different robot and independent software implementation (Bilich et al. 2018) and a different SH expansion. At ETH Zurich, a KUKA robot is used in the field, too (Willi et al. 2019). Here, SH expansions up to degree and order 8 or 12 are proposed and the estimation is based on time-differenced double differences. Similar approaches are investigated at Wuhan University, China (Hu et al. 2015; Hu and Zhao 2018), and at the University at Warmia, Poland (Dawidowicz et al. 2021), as well as at Topcon using a robot from Stäubli (Sutyagin and Tatarnikov 2020).

At IfE, our group investigated an independent approach for method robot to estimate PCC for new signals with a SH expansion of degree and order 8 based on time-differenced single differences (Kersten and Schön 2010; Kersten 2014; Kröger et al. 2021). To precisely rotate and tilt the antenna under test (AUT) w.r.t the current satellite constellation, the same 5-axis robotic system as described in Wübbena et al. (2019) is used.

The approach at IfE was furthermore successfullyextended to determine code–phase centre corrections (CPC) sometimes also named group delay variations (GDV) that correct for the antenna specific receiving characteristic of the code ranges (Kersten et al. 2012; Kersten 2014). Depending on the AUT, the CPC have magnitudes of some decimetres (Kersten 2014; Wanninger et al. 2017; Garbin et al. 2018; Beer et al. 2019; Caizzone et al. 2019; Breva et al. 2019) and should be considered for code-only and code–carrier phase combined approaches (Kersten and Schön 2016).

The second PCC calibration approach—method chamber—is the absolute calibration using a network (vector) analyser (NA/NVA) in an anechoic chamber (Schupler 2001; Görres et al. 2006) to determine the PCC for a broad variety of possible GNSS frequencies using a synthetic unmodulated carrier wave. The development and operation is a cooperation of the University of Bonn and the District Government of Cologne (Zeimetz and Kuhlmann 2008). Since February 2009, the anechoic chamber is operable with the design described by Zeimetz (2010). Starting from 2010, anechoic chamber calibrations are officially approved by the IGS (Becker et al. 2010) as an alternative calibration method. Marginal hardware modifications are reported for July to November 2014. Between August 2016 and March 2017, the system was fully relocated to new laboratory now at the University of Bonn and is operational again with new hardware since October 2017 (GeoBasis.NRW 2018).

2.3 PCC representation by PCO and PCV

The resulting PCC are reported in the IGS ANTEX format which necessitates a separation in a mean phase centre offset vector \(\mathbf {PCO}\) and phase centre variations PCV, cf. Eq. (1). From a practical point of view, it would be advised to select a mean PCO vector that contains the information affecting the topocentric coordinates. This value would however vary with the geographic location and positioning application and would depend on the number of estimated parameters and the processing settings like the observation weighting and cut-off angle. Hence, a generally valid solution will be impossible to achieve.

For the majority of absolute PCC within the current ANTEX file (igs14.atx, cf. IGS 2021), the separation between the PCO Up-component and the PCV is performed by fixing the PCV to zero at zenith (zero zenith constraint). A minority of PCC is based on an estimation of a sphere with PCO as the centre and the PCV as corresponding residuals. In the latter approach, a zero mean constraint over the whole hemisphere of the antenna or just over some part is applied to the PCV in order to estimate the parameters. In most cases, the method chamber uses this second approach.

Any minimum constrained PCV can be transformed into a zero zenith constraint by applying:

$$\begin{aligned} \mathrm{PCV}(\theta =0^{\circ }) {\mathop {=}\limits ^{!}} 0 \end{aligned}$$
(2)

that corresponds to adding or subtracting a constant value from the whole PCV pattern, i.e. changing r. Such a change will not affect the coordinates but further parameters such as zero difference or also double difference ambiguities or the receiver clock parameter.

Since a unique set of PCO and PCV cannot be determined, PCO and PCV should be considered together as PCC:

$$\begin{aligned} \mathrm{PCC}(\phi ,\,\theta )= & {} -{\mathbf {s}}^\mathrm{T}\mathbf {PCO}_1 + \mathrm{PCV}_1(\phi ,\,\theta ) \end{aligned}$$
(3)
$$\begin{aligned}= & {} -{\mathbf {s}}^\mathrm{T}\mathbf {PCO}_2+ \mathrm{PCV}_2(\phi ,\,\theta ) \end{aligned}$$
(4)

where \(\mathbf {PCO}_1\) and \(\mathrm{PCV}_1\) as well as \(\mathbf {PCO}_2\) and \(\mathrm{PCV}_2\) denote two different representations of the identical PCC, respectively.

Figure 1 illustrates this arbitrary separation in a PCO and related PCV by Eqs. (3)–(4) as well as the impact of Eq. (2), which results in characteristic variations of the PCV component. For simplification, only elevation-dependent PCV and the PCO Up-component are used. For all the four depicted PCV and respective PCO Up-component, the identical coordinate results will be obtained as consistency is kept. The representation from Fig. 1 explained in detail reads:

  1. (1)

    Green Original PCV pattern (cf. Eq. (1)) with zero zenith constraint and a given PCO, here \(PCO_{Up}=0\),

  2. (2)

    Yellow Variation of the datum of (1), i.e. r, has to be compensated by a shift of the pattern. No deformation of the PCV nor change in the PCO occurs. This transformation will affect the ambiguities and receiver clock error.

  3. (3)

    Violet A change of the PCO Up-component of (1) by (\(-\Delta h\)) must be compensated by a change of the PCV of \(\Delta h \cdot \sin \theta \). The PCC and thus the estimated parameters are not affected by this step. The contribution of the changed PCO Up-component can be read at zenith direction and it is indicated by the superimposed \(\Delta h\, sin \theta \) pattern.

  4. (4)

    Orange Transforming the PCV of (3) to zero zenith constraint. Compared to (1), the contribution of the changed PCO Up-component can be read at zero elevation and it is indicated by the superimposed \(\Delta h\, (sin \theta - 1)\) pattern. Again, this transformation will affect the ambiguities and receiver clock error.

Fig. 1
figure 1

Representation of consistent PCC transformation illustrated exemplarily for elevation-dependent patterns

Full size image

2.4 Concepts of PCC comparison

2.4.1 General statements

Based on the results of the previous section, we propose the following comparison procedure (Schön and Kersten 2013, 2014):

  1. 1.

    PCV and PCO should be considered together in a consistent way as PCC for each frequency (e.g. L1, L2 or L5), cf. Eq. (3). It is worth noting that when forming linear combinations, the resulting PCC is generally amplified. This is especially true for ionosphere-free linear combinations (Dilssner et al. 2008; Schmid 2013).

  2. 2.

    The comparison of two PCC sets like, e.g. \(\mathrm{PCC}_i,\,\mathrm{PCC}_j\) is based on the difference pattern

    $$\begin{aligned} \Delta \mathrm{PCC} = \mathrm{PCC}_{i} - \mathrm{PCC}_{j}. \end{aligned}$$
    (5)

    The \(\Delta \mathrm{PCC}\) contains (i) potential differences in the PCO of the initial patterns, (ii) variations in the PCV and (iii) variations in the datum definition or constraints applied to separate between PCO and PCV of the patterns that are often not known. No further transformation of the \(\Delta \mathrm{PCC}\), like, for example, applying zero zenith constraints, is needed. Such transformation can improve the readability of graphical representation, but the transformation value should be stored for comparisons in the parameter domain.

  3. 3.

    Since the estimated parameters are of main interest in the analysis of GNSS data, the impact on the estimated parameters should be analysed. Due to high correlations among some of them (Weinbach and Schön 2011), all estimated parameters should be studied, i.e. coordinates, clock errors, tropospheric parameters, ambiguities, etc. It should be noted that parts of the pattern difference can also be mapped to the observation residuals during GNSS data analysis.

2.4.2 Scalar measures

In order to compare PCC patterns and to assess their similarity, different scalar measures can be used. An important property and requirement here should be that the quality measure is independent of a constant shift of the \(\Delta \mathrm{PCC}\), i.e. the selection of the datum or the constraint applied to separate PCO and PCV. In a preparation step, redundant values in the ANTEX files are eliminated in order to avoid too optimistic and misleading results. These are the redundant values for azimuth angle (\(\alpha \) = 0\(^\circ \) which equal those of \(\alpha \) = 360\(^\circ \)). The multiple entries for the zenith direction are reduced to a single entry. Potential scalar measures are functions of \(\Delta \mathrm{PCC}\) (1–2) or PCC (3–4):

  1. (1)

    Standard deviation \(\sigma _{\Delta \mathrm{PCC}}\) which measures the average quadratic deviation between the PCC.

  2. (2)

    Range \(r_{\Delta \mathrm{PCC}} = (max\{\Delta \mathrm{PCC}\} - min\{\Delta \mathrm{PCC}\})\) which measures the maximum range of the differences between the two patterns.

  3. (3)

    Spread \(s_{\Delta \mathrm{PCC}} := r_{\mathrm{PCC}_i} - r_{\mathrm{PCC}_j} \) which describes the difference in the range of values of the two patterns.

  4. (4)

    Correlation coefficient of two patterns, which measures the overall similarity between the patterns. A subtraction of a common PCO from both patterns is advised for meaningful results.

Common to all global comparison measures is that pattern structure or pattern difference gets lost, which, however, is required to assess their impact on the parameter domain.

Fig. 2
figure 2

Example of a NOAZI graphic: thick line: elevation-dependent mean differential receiver antenna pattern of a Leica AR25 antenna (station Lindenberg, LDB2) as chamber versus robot, shown for the ionosphere-free linear combination. Dashed lines show the minimum and maximum over the azimuthal range for each elevation bin

Full size image

2.4.3 Pattern-based measures

In order to incorporate more information about the pattern structure, further graphical measures are used.

  1. 1.

    NOAZI graphics. This representation refers to theANTEX entry NOAZI, where an elevation-dependent mean pattern is given. More generally, any scalar quantity per elevation bin can be depicted such as the standard deviation per bin, or min–max values, cf. also Menge (2003). Figure 2 shows an example of the mean and the min–max limits versus elevation for the ionosphere-free linear combination on station LDB2. It is mandatory to note that due to the degree of freedom the whole pattern or pattern difference can be shifted by an arbitrary value (cf. Fig. 1). Subsequently, it is not possible to associate a specific PCV value to a certain elevation angle, only the shape of the pattern is determined, not its absolute size. For new calibration facilities, the IGS antenna working group (IGS AWG) analyses the comparability of new results w.r.t the official IGS ANTEX file. Up to now, as a rule of thumb, the elevation-dependent variations of the type mean of GPS L1 PCV should agree within ± 1 mm for elevations above 10\(^{\circ }\). This procedure makes sense if the degree of freedom is fixed, for example, by constraining the pattern to zero at zenith.

  2. 2.

    Cumulative histograms. A second graphical measure is the cumulative histogram of a complete \(\Delta \mathrm{PCC}\) set (azimuth and elevation), which indicates the frequency of occurrence of certain deviations. Again for the interpretation special care must be put on how the degree of freedom was fixed for both patterns. Figure 3 addresses this issue in more detail. There, different sets of \(\Delta \)PCC patterns, based on different datum definitions or constraints that are used to separate into PCO and PCV, are depicted.

Fig. 3
figure 3

Comparison of patterns of a LEIAT504GG LEIT antenna as cumulative histogram of deviation for different datum definitions or constraints that are used to separate into PCO and PCV. Zero zenith indicates that \(\mathrm{PCV}(\phi ,0)=0\), zero mean refers to \(\int \mathrm{PCV} = 0\), and zero zenith \(\Delta \mathrm{PCC}\) means that after forming the PCC difference the resulting \(\Delta \mathrm{PCC}\) is set to zero at zenith

Full size image

To summarise, we highlight the results in terms of measures: The comparison of PCC using NOAZI is meaningful in combination with scalar metrics, such as range and spread, and the NOAZI should not be compared qualitatively in isolation from these metrics.

A graphical measure as depicted by Fig. 3 can provide useful insights and is particularly recommended when different sets with the same datum definitions or constraints are to be compared.

Table 1 Variation of estimated parameters when varying PCC patterns (introducing a radial component on all PCV values, or erroneous values for the Up-component with magnitudes of 10 mm and 20 mm)
Full size table

2.5 Impact of PCC on the estimated parameters

2.5.1 General assessment

The impact of PCC on the estimated parameters (coordinates, tropospheric wet delays, ambiguities and receiver clock estimates) is of most interest. This impact depends on the structure of the PCC in interaction with the geographic location and sampling of the pattern structure by the satellites distribution as well as various analysis parameter settings such as cut-off angle and observation weighting, and use of linear combinations. Finally, only the structure of the pattern that is not part of the null-space of \({\mathbf {A}}^\mathrm{T}{\mathbf {P}}\) will have an impact on the coordinates, with \({\mathbf {A}}\) being the design matrix of the positioning problem and \({\mathbf {P}}\) the observation weight matrix.

For some parts of the pattern the analysis is straight forward: the PCO or PCO differences will affect the topocentric coordinates, accordingly. A rough assessment on the impact of pattern differences can be made based on the scalar measures by the typical rule of thumb:

$$\begin{aligned} {\text {Impact on parameters}} = \mathrm{DOP} \cdot \sigma _{\Delta \mathrm{PCC}} \end{aligned}$$
(6)

2.5.2 PPP-based forward propagation

For more complex structures or elaborated analyses, a forward modelling technique is used, for example, by performing PPP-like solutions with different PCC settings in each run. We use this approach to highlight the necessity to check all estimated parameter in order to assess the impact of a pattern. To this end, we introduce errors in the PCC pattern of a EPN station (GOR2), namely (i) an offset to all PCV \(r = 10\) mm and (ii) a change in the PCO Up-component. We study a data set of 24 hours using identical processing strategies and just exchanging the ANTEX file.

We find that a common offset to all PCV (change of the parameter r, cf. Fig. 1 and Table 1) is completely absorbed in the zero differenced (float) ambiguities, as mainly the carrier phase observations are affected and the receiver clock error is estimated from both code and carrier phase observations.

Fig. 4
figure 4

Pattern difference \(\Delta \mathrm{PCC}\) of the ionosphere-free (L0) linear combination from chamber and robot calibrations for the station Lindenberg (LDB2). For the stereographic representation, the gridded PCC values from the ANTEX files (5\(^\circ \) resolution) were interpolated. a Full \(\Delta \mathrm{PCC}\), b \(\Delta \mathrm{PCC}\) weighted with the elevation-dependent weighting, c relative observation density per grid point and d taking into account the relative number of observations per grid point with the elevation-dependent weighting. Please note the differences in the colour bar

Full size image

A PCO height offset of \(\Delta h \sin \theta \) (with \(\Delta h=\) 10 mm and \(\Delta h=\) 20 mm) changes—as expected—the height component accordingly. In addition, however, also the receiver clock error and the ambiguities are affected. The reason is: In PPP, code and carrier phase observations are used to separate between the ambiguity terms and the receiver clock parameter. Since only the carrier phase observations are affected by the introduced error, the code observations get inconsistent. The average inconsistency of \(\Delta h \sin \theta \) over the elevation range (here \(8^{\circ }-90^{\circ }\)) equals 68.8% \(\Delta h\). It is absorbed in the ambiguity. which in turn has to be compensated by an offset in the receiver clock error for the carrier phase measurements and the residuals for the code. The ratio depends on the cut-off angle applied and possibly also the processing settings like the weight ratio between code and carrier phase observations.

Similar studies have been conducted by, for example, Menge (2003), Dilssner et al. (2008), Aerts (2011), Aerts et al. (2013), Schmid et al. (2007). Typical findings are amplification of the coordinate deviations when tropospheric parameters are estimated. The importance of individual calibration values for the consistent estimation of precise geodetic parameters is figured out in several contributions, among others by Schmid et al. (2015), Araszkiewicz and Völksen (2016).

We recommend that the patterns are compared in the parameter domain, w.r.t the IGS main products such as station coordinates, tropospheric delays as well as timing.

2.5.3 Generic patterns and analytic solutions

An alternative approach of assessing the impact is an analytical way. Geiger (1988) studied the impact of different generic parametric antenna models and proposed a method to analytically express the impact on the position domain based on the geometry of the positioning problem (Geiger 1988; Santerre 1991). Kersten et al. (2015) extended the numerical modelling and analysed the prediction model for the case of precise point positioning (PPP). In this way, predefined PCC structures can be linked to specific deviations in the estimated parameters. To this end, a satellite density is considered, which depends on the geographic location and weights the pattern structure as shown in Fig. 4c. The interaction of all influences makes a simple forward modelling of pattern contributions rather complex.

Fig. 5
figure 5

Structure of \(\Delta \mathrm{PCC}\) exemplarily shown for a Leica AR25.R4 choke ring antenna for the ionosphere-free linear combination; a most dominant pattern structure \({\mathbf {M}}_1\) corresponding to the maximum singular value, b pattern structure \({\mathbf {M}}_2\) corresponding to the second largest singular value, c pattern structure \({\mathbf {M}}_3\) corresponding to the third singular value, and d generic pattern (type chess board) as an indicator for corresponding error propagation. Please note the different scales on the colour tables

Full size image

Empirically, the structure of the PCC or \(\Delta \mathrm{PCC}\) can be analysed by its singular value decomposition (SVD). The PCC is considered as a rectangular data matrix where redundant information is eliminated (cf. discussion in Sect. 2.4.2). The decomposition reads

$$\begin{aligned} \Delta \mathrm{PCC} = {\mathbf {U}}{\mathbf {S}}{\mathbf {V}}^\mathrm{T} =\sum _{i} \mathbf {u_{i}} s_{i} \mathbf {v_{i}}^\mathrm{T} = \sum _{i} {\mathbf {M}}_{i} \end{aligned}$$
(7)

where \({\mathbf {U}}\) and \({\mathbf {V}}\) are orthogonal matrices of the left and right singular vectors, respectively, \({\mathbf {S}}\) the matrix of the singular values in decreasing order. Since the rectangular input matrix \(\Delta \mathrm{PCC}\) represents a map of the hemisphere, all grid points are equally weighted during the SVD, although grid points at low elevation angles represents a larger area of the spherical segment. However, this is rather a general drawback of the PCC mapping method.

Table 2 IGS/EPN stations equipped with conical choke ring antenna (LEIAR25, Rev. 3 &4, w/ and w/o radome LEIT) and individual calibration sets of both methods robot (Geo++) and chamber (Uni Bonn)
Full size table

The singular values \(s_i\) decrease rapidly. The first few matrices \({\mathbf {M}}_i\) represent the dominant structures. It should be noted, that the SVD produces chessboard-like structures if the order of magnitude of \(s_i\) is small, usually in the sub-millimetre level. Nevertheless, the most dominant structures provide a useful insight into the pattern’s structures.

Examples of the determined dominant structures of the differential pattern (L0) between robot and chamber calibration are depicted in Fig. 5 for a Leica AR25.R4 antenna. The first and most dominant pattern structure \({\mathbf {M}}_1\) contains in majority the elevation dependence induced by differences in the PCO as shown by Fig. 5a. The structures with generally azimuthal changes correspond to the second and following singular values. Here, these structures are depicted in Fig. 5b and c that reveal a chessboard-like structure with magnitudes of up to 1.5 mm in addition to the (mainly pure) elevation-dependent effect. A generic pattern of a chess board structure is depicted by Fig. 5d.

Fig. 6
figure 6

Differences of individual antenna pattern \(\Delta \mathrm{PCC}\) between calibration methods robot and chamber, shown for different frequencies and systems

Full size image

3 Pattern comparisons in the observation domain

3.1 Data sets from the EUREF permanent GNSS network

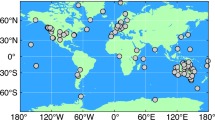
As of January 2019, 25 individual receiver antenna calibrations sets for were available for both robot (Geo++) and chamber (University of Bonn) calibration (Bruyninx and Legrand 2017), of which 19 were installed at operational EPN stations.

Calibration values for the method robot are from the years 2010–2016, whereas those from the method chamber were calibrated in the years 2010–2018. The spatial distribution of selected EPN stations is depicted in Fig. 9 and summarised with some metadata in Table 2. The majority of antenna PCC values of both calibration methods are provided by the German Federal Agency of Geodesy and Cartography (BKG, FSW) and the PCC of one antenna is from the Royal Observatory of Belgium (ROB). The main brand of receiver antenna is Leica AR25.R4 with radome (code LEIT). Additionally, four Leica AR25.R3 LEIT, one Leica AR25.R3 and one Leica AR25.R4 each without radome (code NONE) are part of the data set. For clarification: the revision number assigns the location of production (R3/Novatel and R4/Leica-Heerbrugg) with corresponding serial numbers and individual modifications (i.e. the L5 ring). Successive installed antennas at single stations in Table 2 are assigned by a four character identifier followed by numerical specifiers (e.g. AUBG-1, AUBG-2, etc.).

3.2 Differential phase centre corrections

Following the procedure of Sect. 2.3, differential phase centre corrections (\(\Delta \mathrm{PCC}\)) for GPS and Glonass L1 and L2 are computed and collected for all available 25 PCC sets in Fig. 6. For clarity of visualisation, all \(\Delta \mathrm{PCC}\) were set to zero at zenith. Individual antennas are colour-coded and referred to their specific station ID in the EPN. For this analysis, the method robot serves as reference.

The NOAZI representation of the elevation-only \(\Delta \)PCC shows differences up to ± 6 mm for GPS L1 and L2 (cf. Fig. 6a and b) at low elevation angles, while the maximum deviations for Glonass frequencies are slightly smaller (± 4 mm, cf. Fig. 6c and d). The rule of thumb that elevation-dependent \(\Delta \)PCC should agree within ± 1 mm for elevation angles above 10\(^{\circ }\) is not fulfilled for most of the patterns.

For further investigations, a classification of the PCC differences is carried out based on the scalar measures introduced in Sect. 2.4.2 and a visual inspection of the NOAZI representation. The results are depicted in Fig. 7 for GPS L1 (red), L2 (black) and the ionosphere-free linear combination L0 (blue). Rectangles indicate Bonn calibrations after 2013, circles show calibrations between 2013 and 2018. Based on these quantities, in total seven different categories of \(\Delta \)PCC can be found: I to VI and a residue class VII (cf. Table 2, column Category).

Fig. 7
figure 7

Scalar quality measures for \(\Delta \)PCC patterns between robot and chamber calibrations for GPS L1, L2 and the subsequent ionosphere-free linear combination L0. The \(\Delta \)PCC are formed as PCC (chamber)–PCC (robot)

Full size image

For all scalar measures, the different categories can be distinguished in a first step by the frequencies’ order (L1, L2 or L0), i.e. which frequency indicates the highest similarity between the two patterns. While for categories I and III to VI the L1 differences are principally smaller than the ones for L2, it is vice versa for category II. Secondly, the standard deviations and ranges of \(\Delta \)PCC differ quite clearly between the different categories. For categories I and II, a low similarity between the L0 calibrations, expressed by the higher scalar measures, is observed. While the categorisation for groups I to III is quite clear, the other groups are less well pronounced, i.e. a difference pattern could principally be classified in two different categories. As an example servers station DRES, where the characteristic values show a possible categorisation into category IV or V.

The so far presented categories are apparently related to the respective chamber calibration dates, the revision of the antenna (R3 or R4) and the serial number, cf. Table 2. All Leica AR25.R4 LEIT antennas are grouped into category I to IV, whereas the first three categories consist of antennas having a serial number starting with 72. Within each category, the chamber calibration dates are very homogeneous. It seems that they have an impact on the categorisation. This may be underlined by antenna S/N 725266 first installed at GELL (Cat I) and after chamber re-calibration installed as DILL-2 (Cat II). Category IV consist of two R4 antennas, having a different serial number (and chamber calibration date). In category V, all four R3 antennas can be found. The antenna mounted at station EUSK is in an own category (VI), since the scalar measures depicted in Fig. 7 show a different behaviour. This can be seen, for example, in the change of the L1 and L2 frequencies’ order for the maximum and standard deviation of the \(\Delta \)PCC. Correspondingly, this leads into highly similar spread and correlation coefficient values for L1 and L0. This is not observable for any of the other \(\Delta \)PCC.

In order to validate the determined categories, the type mean \(\Delta \)PCC pattern over all Leica AR25.R3/R4 LEIT antennas is calculated and subtracted from the individual \(\Delta \)PCC. Since the stations ISTA and DOUR are equipped with an antenna without a radome (NONE), they are not considered for the type mean calculation.

Figure 8 shows the resulting differences, again for GPS and Glonass L1, L2 and L0. Here, the individual differences to the type mean \(\Delta \)PCC are colour-coded w.r.t. their category. Thus, a direct link to the individual station differences it not given, but the consistency of each group can easily be assessed. It can be seen that the \(\Delta \)PCC of each group show a similar behaviour to the calculated type mean \(\Delta \)PCC. This does not hold true for category VII, since it is the residue class grouping pattern differences which do not match any of the other categories, visible for L2 and L0. Principally, the consistency of each group is higher for GPS L1. Nevertheless, a category-dependent behaviour is still observable for GPS L2 and L0.

Fig. 8
figure 8

Classification results for \(\Delta \)PCC: differences between individual \(\Delta \)PCC and the type mean \(\Delta \)PCC obtained by robot and chamber calibrations for Leica AR25.R3/R4 LEIT receiver antennas, colour-coded by categories of Table 2 (column category); a–c GPS and d–f Glonass. Please note the different scale on the y-axis for the ionosphere-free linear combinations

Full size image

In general, this analysis has shown that the scalar measures introduced in Sect. 2.4.2 are suitable for comparing different sets of PCC. This is especially true for the standard deviation, the range and the Pearson correlation coefficient. Since the maximum value depends on constant parts within the patterns, this measure should be handled with care. Further studies are needed for a generalisation to multiple antenna types.

4 Impact of phase centre corrections on GNSS estimates

4.1 Processing scheme

In order to verify the impact of individual antenna patterns on a network of GNSS stations, we reprocessed and analysed a subset of several EPN stations (Fig. 9) using the different carrier phase-based approaches. Separate solutions for all groups are processed using dedicated receiver antenna correction files (robot, chamber, mixed). Four settings are studied:

  1. 1.

    Star-shaped network of 16 stations with fixed coordinates of the station Lindenberg (LDB2) with consistent PCC patterns (chamber and robot method).

  2. 2.

    Star-shaped network of 16 stations with mixed PCC patterns with a 2/3 ratio of chamber and robot calibrations (cf. Fig. 9).

  3. 3.

    Minimum constraint network (17 stations) with consistent PCC antenna patterns (cf. setting 1) and minimum constraint network with mixed PCC patterns (cf. setting 2) and predefined baselines.

  4. 4.

    PPP processing of 17 stations with consistent PCC patterns (cf. setting 1).

The final comparisons assess the impact of different PCC patterns on position, troposphere estimates and the performance of carrier phase ambiguity resolution.

Fig. 9
figure 9

Regional sub-network of EPN used in this study. The spatial distribution corresponds to different orientations of the baselines w.r.t. one single reference point (setting 1–2). The provenance of PCC values are indicated by coloured triangles for scenarios when using PCC from different calibration methods (setting 2)

Full size image

4.1.1 Network processing set-up

The Bernese GNSS software 5.2 (Dach et al. 2015) and corresponding CODE (Centre of Orbit Determination in Europe) products (Dach et al. 2020) for GPS and Glonass are used to perform the DD processing. The network consists of GNSS stations with mean distances between 200 km and 600 km starwise referred to LDB2 (square symbol, Fig. 9). For the analysis, we use data from 6 January 2019 to 10 January 2019 by daily batches and a combined weekly solution. The Vienna mapping function (VMF1) with a resolution of two hours is applied to model the troposphere (Boehm et al. 2006) together with the gradient model proposed by Chen and Herring (1997). For the ambiguity resolution, different strategies were tested; here, results from the QIF strategy (Dach et al. 2015) are shown. An elevation cut-off angle of 10\(^\circ \) with an elevation-dependent weighting (COSZ model, Dach et al. 2015) is used.

4.1.2 PPP processing set-ups

We use our in-house Kalman filter-based processor (GNSS Toolbox V6.1) to generate PPP results. General settings are published in Krawinkel and Schön (2021). The toolbox enables us to track and access all intermediate steps of the data processing. In this context, we use the multi-GNSS products (COM) from CODE (Prange et al. 2020). The results are analysed for 24 hours of one day (8 January 2019). The refined discrete Vienna Mapping function (VMF3) (Landskron and Böhm 2017) applies with two hours resolution and estimation of horizontal gradients using the model of Chen and Herring (1997). An elevation cut-off angle of 8\(^\circ \) in combination with elevation-dependent weighting is used here, which was also applied in DD processing. Observation weighting has been performed by 1/100 (code/carrier), i.e. the a priori standard deviation equal one centimetre for the carrier phase and one metre for the code. Inter-system biases are modelled as a random walk process (tightly constrained).

4.2 Results of network analysis

4.2.1 Setting 1: star-shaped network with consistent PCC patterns

Deviations of position residuals for seven daily batches are compared for the processing using consistent PCC from both methods robot and chamber. Figure 10 summarises the results and indicates major deviations in the Up-component with magnitudes between − 0.3 mm (KARL) up to 12.7 mm (DIEP-1). Smaller variations are obtained for the horizontal components (below 2 mm) for all stations, which shows that the main effect is to find in the vertical component.

Fig. 10
figure 10

Position deviations for a regional EPN sub-network of star-shaped design using consistent antenna phase centre models (chamber or robot, cf. Sect. 4.2.1)

Full size image
Fig. 11
figure 11

Examples of GPS ionosphere-free linear combination (L0) on selected baselines w.r.t. LDB2, shown for categories I–III of \(\delta \Delta \)PCC patterns for DD approach. The use of elevation-only differences (a–c) gives a rough assessment of the complete behaviour of the \(\delta \Delta \)PCC patterns (d–f)

Full size image
Fig. 12
figure 12

Position deviations for a regional EPN sub-network of star-shaped design and obtained using mixed antenna phase centre models (chamber/robot) with respect to consistent reference solution (robot) (cf. Sect. 4.2.2)

Full size image

Correlations between the deviations and the \(\Delta \)PCC categories (cf. Table2) appear. For baselines where the reference antenna (LDB2) and the remote antenna are of the same category (III), smallest position deviations are obtained (GOR2, KARL). They do not exceed 2 mm, which is inside the noise of the used ionosphere-free linear combination. Higher deviations with magnitudes of up to 7–8 mm occur for category II (AUBG-2, BORJ, DILL-2, HEL2, HELG-2 and RANT). Highest deviations are identified at category I (DIEP-1, SAS-2) where the Up-component exceeds 10 mm. As discussed in Sect. 3.2, the classification of categories IV–VI is not stringent. Subsequently, these stations show low positive or larger negative deviations in the Up-component.

The \(\delta \Delta \)PCC deviations of the ionosphere-free linear combination on the individual baselines underline these findings:

$$\begin{aligned} \delta \Delta \mathrm{PCC} = \Delta \mathrm{PCC}_{i} - \Delta \mathrm{PCC}^{LDB2}, \end{aligned}$$
(8)

with i being the remote station. Figure 11 illustrates the deviations for selected baselines and PCC categories.

4.2.2 Setting 2: star-shaped network with mixed phase centre models

Figure 12 depicts the topocentric deviations for setting 2. Only the baselines with different PCC models are affected, i.e. BORJ, GOR2, KARL SAS2 and WARN (assigned with superscript c (chamber) and highlighted by transparent background). Identical effects in the Up-component occur again at BORJ (+ 8 mm) and SAS2 (+ 11 mm), which corresponds to the findings of Sect. 4.2.1. No network effect due to the mathematical correlations between baselines (Schön 2006), is visible, and each baseline could be treated separately concerning the impact of different PCC models.

4.2.3 Setting 3: minimum constraint network with different PCC patterns

In order to highlight the impact of different network datum selections, a minimum constraint solution (MCS) with the SHORT strategy (Dach et al. 2015) is performed with (i) common PCC sets of both methods (comparable to Sect. 4.2.1) and (ii) with mixed pattern distribution (comparable to Sect. 4.2.2).

Table 3 (5th–7th column) summarises the residuals after a three-translation Helmert transformation for both configurations. The results can be linked to scenario 1 by reducing the deviation at LDB2 (reference station) from all the other stations.

Table 3 Residuals of three-translation Helmert transformation for minimum constraint solution using either consistent robot or mixed chamber–robot PCC (setting 3, cf. Sect. 4.2.3)
Full size table

In addition, Table 3 (2nd–4th column) summarises the results of a MCS using a mixture of chamber–robot pattern, which is indicated in the table by a superscript c. Due to the chosen network datum, the affected antennas introduce a common offset of the whole network. This offset results as the value, introduced by all affected stations divided by the number of unaffected stations as suggested. This means in detail: The affected stations introduce an accumulated offset of + 13.0 mm (6 stations) that is divided by the number of all unaffected stations (11) and thus results into an offset of + 1.18 mm, which applies in this setting to all unaffected stations. Differences of 8.5 mm (BORJ) and 2.6 mm (GOR2) or − 8.7 mm (ISTA) are noticeable among others (cf. Table 3, column 2–4).

It is worth considering the differences of the corresponding tropospheric ZTD parameters shown in Fig. 13. There, the ZTDs of stations SAS2 and BORJ are on average offset by − 8 mm and − 6 mm relative to the other GNSS stations. The differences of the ZTDs at station ISTA, on the other hand, are on average − 2.1 mm smaller. The remaining stations in the network also show a common shift of approx. − 1.5 mm, indicated by a dashed line (cf. Fig. 13). Thus, the effects are pattern-specific and should not be interpreted in the same way as considering the rule of thumb 1:\(-\,3\) (Beutler et al. 1988; Schön 2006) between tropospheric error and upward component, since here the pattern and not the processing settings (i.e. solutions with/without estimation of tropospheric delays) were changed. The variations in the horizontal components are rather marginal, with magnitudes below 0.25 mm.

Fig. 13
figure 13

Differences between minimum constraint solution using robot or mixed chamber–robot PCC. Stations with chamber PCC are indicated by superscript c

Full size image
Table 4 Differences obtained for estimated parameters by a combined GPS and Glonass PPP processing using both, robot and chamber calibrations, solutions of robot are subtracted from chamber obtained solutions
Full size table

4.3 Results of PPP analysis

4.3.1 Setting 4: PPP processing with consistent PCC patterns

Findings from the PPP processing provide a comprehensive understanding of the impact of receiver antenna effects on all estimated parameters. For all 17 stations, differences in the estimates could be tracked, cf. Table 4. However, additional deviations could occur when code and carrier phase observations are not referring to the same reference point, as they affect the separation between clock and ambiguity, cf. Sect. 2.5.2. These deviations are linked by the observation equations of the ionosphere-free linear combination of code \(P_{0,r}^s\) and carrier phase \(\varphi _{0,r}^s\) such as

$$\begin{aligned}&P_{0,r}^{s} = \rho _{r}^{s} + c \Delta \delta t_{r}^{s} + T_{r}^{s} + \mathrm{PCC}_{r}^{*,s}(\phi ,\theta ) + \epsilon ^{s}_{r,c}\end{aligned}$$
(9)
$$\begin{aligned}&\varphi _{0,r}^{s} = \rho _{r}^{s} + c \Delta \delta t_{r}^{s} + T_{r}^{s} + \mathrm{PCC}_{r}^{s}(\phi ,\theta ) + b_{L0} + \epsilon ^{s}_{r,\varphi } \end{aligned}$$
(10)

with the geometric distance \(\rho _r^s\) between the receiver r and satellite s, the differential receiver clock estimate \(c \Delta \delta t_r^s\), the tropospheric delay \(T_r^s\), the float ambiguity term \(b_{L0}\), the correction \(\mathrm{PCC}_{r}^{*,s}(\phi ,\theta )\) to link the code observable to the phase centre of the receiving antenna, the carrier phase centre corrections \(\mathrm{PCC}_{r}^s(\phi ,\theta )\), and finally the residual effects and further corrections \(\epsilon ^s_{r,c}\) and \(\epsilon ^s_{r,\varphi }\) for code and carrier phase. In our study, the term \(T_r^s\) contains the a priori model (dry part, ZHD), the estimates (wet part, ZWD) and the horizontal gradients in north and east following Chen and Herring (1997).

n order to assess and understand the influence of possible differences between code and carrier phase observations on the impact on \(\Delta \mathrm{PCC}\) on the estimated parameters, we compare two separated cases based on differential PPP results (chamber–robot), cf. Fig. 14:

  1. (A)

    Orange we follow the IGS conventions and omit any correction to code observations, so \(\mathrm{PCC}_{r}^{*,s}\) are set to zero.

  2. (B)

    Blue the \(\mathrm{PCC}_{r}^{*,s}\) are set to the PCO component of ionosphere-free linear combination (PCO\(_{L0}\)), so that both observation types refer to the same mean receiver antenna phase centre (physical offset between ARP and receiver antenna element).

Figure14 depicts the differences of obtained PPP solution exemplarily for station LDB2 and AUG2; namely for float ambiguities, receiver clock error, and code as well as phase residuals of the ionosphere-free linear combination.

To summarise the findings: Case (A), the mean \(\Delta \)PCC induces a code–carrier difference, which results in a mean value of the differential float ambiguities \(\Delta b_{L0}\), (cf. Fig. 14b and e) and with marginal effect on the differential receiver clock estimate \(\Delta (\Delta \delta t_{r}^s)\), as depicted in Fig. 14a and d. Neither changes in troposphere estimates nor topocentric coordinates could be detected. Finally, the residuals of the code have to compensate the differential PCO (\(\Delta \)PCO) with a clear \(\Delta h \sin {\theta }\) superposition (cf. Fig. 14c and f). As the \(\Delta \)PCO is close to zero for the chamber–robot comparison at LDB2, the \(\Delta h \sin {\theta }\) contribution is also close to zero, cf. Fig. 14c. Contrary, the \(\Delta \)PCO is present at AUGB-2 and thus also detected in the differential code-based postfit residuals, cf. Fig. 14f.

In case (B), no code–carrier differences persist (except for the remaining PCV part), and thus, the \(\Delta b_{L0}\) are close to zero, cf. Fig. 14b and e. But the \(\Delta (\Delta \delta t^s_r)\) now show that offset, which was identified in case (A) for \(\Delta b_{L0}\), cf. Fig. 14b and e. We note at the end that the two terms are negatively swapped (1:-1) due to the different processing conventions. Corresponding to case (A), no effects are observed on other parameters, neither on the tropospheric delay (horizontal gradients or ZWD) nor on topocentric coordinates.

Fig. 14
figure 14

Summary of differential PPP results obtained using both chamber or robot PCC and their effect on all geodetic estimates on station LDB2 (a–c) and station AUBG-2 (d–f). These plots discuss the results for two different PPP processing schemes (either \(\mathrm{PCC}_{r}^{*,s}\) = PCO\(_{L0}\) on code observables or \(\mathrm{PCC}_{r}^{*,s}\) = 0)

Full size image
Table 5 Comparison between DD approach (Bernese processing) and in-house PPP processor (LUH-IfE) for selected sites, both processed as GPS/Glonass solution
Full size table
Fig. 15
figure 15

Summary of differential PPP code-based postfit residuals (\(\mathrm{PCC}_{r}^{*,s}\) = 0) and estimated height differences in relation to differences of DD and PPP (cf. Table 5) for antennas of different categories. The corresponding differential PCO offsets for ionosphere-free linear combination are listed in the legends, too

Full size image

Table 4 summarises the differences of PPP results for case (B) to keep consistency between carrier and code observables. Maximum deviations on the Up-component are obtained for ISTA (− 11.7 mm) and WRLG (− 6.7 mm). Maximum deviations in the East component for those PCC patterns of category III (approx. − 1.9 mm). Meanwhile, the ambiguities for GPS and Glonass as well as the horizontal troposphere gradients are not affected.

Finally, Table 5 lists the comparison of PPP and DD results. By referring to the last three columns of Table 5 a very good agreement of below 1 mm for all topocentric components show up at least for PCC patterns of category III and IV. This is explained by the features of the \(\Delta \)PCC patterns that has both a flat shape of azimuth differences and marginal differential PCO offsets, cf. Fig. 7. On the contrary, the deviations for categories I and II of Table 5 are obvious in the Up-component. Common to all stations are the small derivations in the horizontal components, whose variations do not exceed 0.5 mm.

The differences in the Up-component are explained by the different conventions of the code and carrier phase observable in the processing settings. Magnitudes of the differential Up-component agree with the magnitudes of the \(\Delta \)PCO of the ionosphere-free linear combination. The offsets in the Up-component between PPP and DD are found in the PPP code-based postfit residuals with a \(\Delta h\sin {\theta }\) character (cf. Fig. 15 and Table 5). Following the IGS conventions, in Bernese GNSS Software, no additional receiver antenna-related offset correction is applied to the code observable, (Dach et al. 2015). Our studies examine that for PPP a consideration of referring both the carrier and code observable to the antenna phase centre and, hence, a correction on code in terms of PCO is advantageous and consistent. This is shown by the results in Fig. 14. Furthermore, the different approach for the ambiguity resolution must be taken into account. While ambiguities are fixed to integer in DD processing, float ambiguities remain in our in-house PPP software.

Under these circumstances, the comparison between DD and PPP shows very good comparability, considering the different conditions in the processing.

4.4 Discussion

The findings of the studies conducted on the basis of different network geometries and different datum constraints have provided clear evidence of the impact of different antenna patterns on the geodetic parameters. Differences of more than 1 mm are mapped into the parameter domain, i.e. position as well as troposphere estimates and number of resolved carrier phase ambiguities (cf. Fig. 13).

In the case of the station ISTA, the mixed PCC patterns in scenario 2 (baseline of 1575 km length) affect both the horizontal position with up to 2 mm and the Up-component with approximately − 12 mm. This is explained by the different local horizon of the receiver antennas at both stations. Only a restricted number of common observations are achievable. Due to a baseline length of 1575 km, a variation of approximately 16\(^\circ \) in the elevation range is present.

Krzan et al. (2020) analysed the same network with PPP approach during a different time span during which the antenna calibration values changed. A very good agreement was found for those stations, where the identical antennas were mounted. Although different PPP processors have been used with different settings in terms of elevation mask, ambiguity resolution, troposphere model and analysed time span, the horizontal deviations between both solutions are below ± 0.2 mm in maximum. A common offset of approx. 1.5 mm is found at the Up-component. The comparability is explained by the similar processing approaches as for both NAPEOS and our in-house GNSS toolbox, the carrier and code observables are referred to the receiver antenna phase centre (Springer and Dow 2009). Furthermore, keeping in mind the different settings among the processing, we can summarise that the results are consistent and closely comparable.

5 Conclusions

A comparison strategy for receiver antenna calibration values is developed and applied to the comparison of robot and chamber calibrations using a set of individual and absolute calibrated Leica AR25 LEIT antennas from the EPN network. The comparison is separated into (1) a pattern-based comparison and (2) a study on the impact on parameters of interest, such as station coordinates for DD and PPP.

For the pattern-based comparison, we recommend a combined treatment of both ANTEX entities PCO and PCV as a phase centre correction value (PCC), as the separation in PCV and PCO is arbitrary. Allowed pattern transformations and their theoretical basis are highlighted.

We proposed scalar and graphical quality metrics to detect similarities of pattern differences. Based on this, the identification of seven categories is presented for 25 pairs of individual antenna calibration results (robot/chamber). The scalar and datum independent metrics such as range spread or the standard deviation turn out to be particular useful. The latter shows an average quadratic agreement that is better than the 1 mm level for all antennas on L1.

A solely elevation-dependent representation of pattern differences helps to assess the differences without adding too much complexity. For a qualitative comparison, however, additional scalar metrics are recommended. Differences between chamber and robot approaches for GPS and Glonass L1 and L2 frequencies are mostly below 2 mm at elevation angles larger than 20\(^\circ \) and up to 6 mm at elevation angles below 20\(^\circ \). These effects are generally altered for the ionosphere-free linear combination.

A singular value decomposition of the whole pattern or pattern difference gives insights in its main structures of dependencies in elevation and azimuth. Numerical limits of the SVD method should be considered.

The impact of PCC on the estimated parameters (coordinates, tropospheric wet delays, float ambiguities and receiver clock estimates) is of most interest. Hence, we recommend to study all of them, as some effects may be compensated or masked in different parameters. By case studies with relative positioning and PPP, we showed that the different processing methodologies lead to different effects. Depending on the antenna category, we found differences in parameter results between 1 mm and 12 mm for relative positioning. The ZWDs are affected by few mm for the majority of the stations and to up to 8 mm for few stations. The PPP analysis helped to trace the impact on all parameters. Here, the consistency of the reference point between code and phase observations adds additional effects on the impact of pattern differences on the parameters and residuals. This analysis underlines that an easy to use and general prediction of a pattern difference onto the parameters is difficult to achieve.