Introduction

A striking property of nature is that it is non-classical. Entanglement1,2, Bell nonlocality3, and steering4,5,6 are examples of quantum phenomena that can be observed experimentally7,8,9,10,11,12 and which cannot be explained by classical physics. Besides their foundational relevance, with the advent of quantum information theory we learned a valuable lesson: these seemingly bizarre quantum features can be exploited to process information more efficiently, even in ways that could never be possible with classical resources alone13,14,15.

A ubiquitous framework in which the scope of quantum advantage in information processing is explored is the so-called device-independent framework, where the parties executing protocols only rely on the classical inputs and outputs with which they operate their shared (and possibly quantum) devices. Such a framework is particularly well suited to the necessarily paranoid perspective on cryptographic tasks13, and is almost ubiquitously underpinned by a Bell nonlocality setup. A special milestone in the research of non-classical resources for device-independent information processing was the realisation that there exist correlations beyond what is quantumly admissible (a.k.a., post-quantum correlations), but which nonetheless are consistent with special relativity16. These so-called no-signalling correlations, moreover, were shown to be consistent with alternative theories of nature, confirming the necessity of their study. Exploring these general no-signalling correlations enabled, for example, the design of quantum cryptographic protocols that are robust against powerful adversaries that are not bounded by the laws of quantum theory17,18, and also the formulation of physical principles that a quantum world must satisfy16,19,20,21,22,23,24,25. These post-quantum correlations are hence studied beyond philosophical motivations, and from the perspective of the resources they provide for operational tasks.

Device-independent frameworks for information processing, however, are substantially demanding to implement experimentally. Indeed, for practical purposes, even if cryptographically secure, device-independent protocols are yet to move beyond ‘proof of principle’ applications into scalable and easily-accessible technologies. There are situations, however, where one may argue that the quantum description of some of the parties involved can be leveraged in the protocols: in the simplest case where two parties are involved and a single party is assigned a quantum description this is usually referred to as a one-way device-independent framework14,15. In such scenarios, the non-classical phenomenon providing quantum advantage is steering rather than Bell nonlocality. Recently, it has been shown that steering beyond that which quantum theory allows, whilst still consistent with special relativity, may exist26,27, which opens a new plethora of questions, such as (i) can post-quantum steering provide an advantage beyond what is possible with quantum theory for some information processing task?; (ii) is post-quantum steering just a mathematical curiosity, or may it emerge within alternative physical theories?

In this work, we tackle those two questions. First, we show that there are alternative theories beyond quantum which feature post-quantum steering, making the phenomenon physically relevant for post-quantum information processing and motivating its exploration. Second, we find a task for which post-quantum steering is a stronger-than-quantum resource: remote state preparation. Remote state preparation (RSP) is a task similar in spirit to teleportation: the goal is to transmit quantum states from one party to another distant party using only shared entanglement and classical communication. Unlike teleportation, though, in RSP the sender has knowledge of the transmitted state, which makes RSP protocols more economical than teleportation in terms of resources (e.g. classical communication) needed to succeed at the task28,29. In addition, RSP protocols do not necessarily require the ability to experimentally implement Bell (entangling) measurements, which makes them potentially more feasible experimentally30. The kind of RSP protocols that we focus on are so-called oblivious – namely those where no information about the state is leaked to the receiver, apart from the state itself, something that is relevant for certain applications such as blind quantum computation31. RSP is indeed an insightful task to explore from both a fundamental and applied viewpoint.

In order to prove our results, we define a generalised probabilistic theory (GPT) that we name Witworld, given its strong connection to entanglement witnesses. Witworld combines system types of three well-known GPTs (classical, quantum, and Boxworld) in a simple mathematical way, via the so-called max tensor product. Remarkably, even though Witworld cannot reproduce all the phenomenology of quantum theory, it does realise all quantum predictions for Bell and steering experiments. Hence, we can learn about the limitations of quantum advantage in one-sided and fully device-independent protocols by exploring the performance of Witworld. Despite its simplicity, Witworld displays powerful post-quantum features: not only can it realise all non-signalling correlations in Bell experiments, but it also displays post-quantum steering. As Witworld is a fully compositional theory, it comes equipped with an intuitive diagrammatic calculus32,33. This provides a convenient toolkit for exploring other applications of post-quantum phenomena for information processing.

The paper is organised as follows. In what remains of this section we present a brief introduction to the three main topics of this paper: generalised probabilistic theories, Bell nonlocality, and steering. Section “Witworld” presents the definition of Witworld, assuming basic knowledge of GPTs – the reader who is not familiar with them may consult Section A of the Supplementary Material. Section “Post-quantum phenomena: Bell non-classicalityand steering” discusses the post-quantum properties of Witworld with a focus on Bell and steering experiments, while section “Post-quantum advantage for informationprocessing” discusses how Witworld outperforms quantum theory at certain information processing tasks. Section “Post-quantum advantage for informationprocessing” also presents the first task where post-quantum steering outperforms quantum steering as a resource. Technicalities, as well as a brief review on steering, are included in the appendices.

Generalised probabilistic theories

The framework of generalised probabilistic theories34,35 provides tools with which to explore the operational features of candidate theories in a unified fashion. Classical theory, as well as quantum theory, may be recast within the language of GPTs34,35, which enables their unified and comparative study. The GPT framework has been proven useful not only from a foundational perspective (e.g. for developing axiomatic reconstructions of quantum theory33,35,36,37,38), but also when exploring the quantum information capabilities of post-quantum theories, such as their computational power39,40,41,42,43,44,45 or cryptographic security34,46,47,48,49.

Bell nonlocality

One example of a non-classical phenomenon of foundational and applied relevance is Bell nonlocality. Bell experiments are ubiquitous in the fields of quantum foundations and quantum information processing. On the one hand, Bell’s Theorem3 established a precise sense in which quantum theory requires a departure from a classical worldview, and violations of Bell inequalities provide a means for certifying the nonclassicality of nature. On the other hand, the correlations observed in a Bell test have become a resource for certain tasks13, and the violation of so-called Bell inequalities by these correlations has become a standard certification tool for security in cryptographic protocols17,18,50. In brief, a Bell scenario consists of a set of distant parties that perform space-like separated actions on their part of a physical system, and the objects of study are the correlations they observe among their measurement outcomes. In the case of a bipartite scenario, let \(x\in {\mathbb{X}}\) and \(a\in {\mathbb{A}}\) denote the classical variables that label the measurement choices and produced outcomes, respectively, corresponding to the first party (hereon, Alice), and, respectively, \(y\in {\mathbb{Y}}\) and \(b\in {\mathbb{B}}\) those for the second party (hereon, Bob). The correlations observed in this bipartite Bell experiment are captured by the conditional probability distribution {p(ab∣xy)}. It is therefore natural to ask ourselves which possible {p(ab∣xy)} may be generated, and at what cost. Given the space-like separation constraints, the largest set of correlations observable in a Bell scenario corresponds to those that satisfy the No-Signalling Principle, and it is known that correlations allowed by quantum theory are a strict subset of those correlations. Notably, a GPT colloquially referred to as Boxworld51,52 has been defined34, which can realise all the correlations compatible with the no-signalling principle via its bipartite states and local measurements.

Steering

Steering is another non-classical phenomenon of foundational and practical relevance, which was identified back in the 1930s4 but, unlike Bell nonlocality, only recently caught the attention of the quantum information community5,6. Steering captures the idea that Alice seemingly remotely ‘steers’ the state of a distant Bob, in a way which has no classical explanation. A main feature of a steering experiment is the asymmetric role that the parties play, which makes it particularly suitable as a resource for certain asymmetric information processing tasks14,15. In brief, the simplest steering experiment consist of two distant parties – Alice and Bob – which perform local actions on their part of a physical system. Unlike in a Bell experiment, though, the parties here perform different types of transformations in their labs: Alice performs a measurement, labelled by \(x\in {\mathbb{X}}\), on her system, and obtains a classical outcome \(a\in {\mathbb{A}}\), whereas Bob performs full tomography of the quantum system and so describes it via a density matrix \({\rho }_{a| x}^{{{{\rm{B}}}}}\) that is effectively prepared in his lab after Alice’s actions. In this way, the object of study in these experiments are the ensembles of ensembles (a.k.a. assemblages53) given by \({\{{\{{\sigma }_{a| x}\}}_{a\in {\mathbb{A}}}\}}_{x\in {\mathbb{X}}}\), where \({{{\rm{tr}}}}({\sigma }_{a| x})=p(a| x)\) and \({\sigma }_{a| x}=p(a| x)\,{\rho }_{a| x}^{{{{\rm{B}}}}}\). While nonclassical properties of steering within quantum theory have been considerably explored, not much is known about steering beyond quantum theory26,27,54,55. One main obstacle for this is the complexity of capturing fundamentally what could be post-quantum about an assemblage of quantum states. An operational recast of the steering phenomenon has been recently put forward26,27, which facilitates a way to articulate the concept of post-quantum assemblages. The study of post-quantum steering has only just begun, and, unlike for Bell nonlocality, important fundamental and practical questions are yet to be answered. One such question is: does there exist a GPT that realises all these post-quantum assemblages?

Results

Witworld

In this section, we provide a simple and concise introduction to Witworld, which should enable the understanding of the subsequent results. We moreover provide a detailed formal definition in Section B of the Supplementary Material.

In Witworld, there are three types of basic systems, which can be composed to construct more general system types. The basic systems are classical systems, quantum systems, and Boxworld systems34. (One could easily modify the theory to allow for further system types. However, it is not clear that this will provide any further benefit to the study of steering). Systems that are of one of those three types are called atomic. Witworld features a composition rule (which we define shortly) by which these simple system types can form new ones that are neither classical, quantum, nor Boxworld. We denote the atomic types diagrammatically with different types of wires by:

(1)

where \({{{{\mathcal{C}}}}}_{v}\) denotes a classical system of dimension v, \({{{{\mathcal{Q}}}}}_{d}\) denotes a quantum system of dimension d, and \({{{{\mathcal{B}}}}}_{n,k}\) denotes a Boxworld system of dimension (n, k) (These two integers relate to the input/output cardinality of the correlations in Bell scenarios that the system is tailored at34). Moreover, when we need to use a generic system type (which can be either simple or composite), we denote this by

(2)

We can also explicitly denote the components of a composite system by using parallel wires, for example:

(3)

corresponds to a system composed of a qubit, a (2, 2) Boxworld system, a qutrit, and a classical system of dimension 5.

The state space of a given system type is represented by a convex set living inside some real vector space. For instance, an atomic quantum system \({{{{\mathcal{Q}}}}}_{2}\) has states living inside a Bloch sphere in a 4-dimensional real vector space, an atomic classical state \({{{{\mathcal{C}}}}}_{3}\) has states living inside a triangle in a 3-dimensional vector space, and an atomic Boxworld system \({{{{\mathcal{B}}}}}_{2,2}\) has states inside a square in a 3-dimensional vector space. These examples are depicted in Fig. 1. Diagrammatically we denote a state σ of a system S by

(4)
Fig. 1: The geometry of states and effects.
figure 1

The geometry of the set of states (to the left) and effects (to the right) for (a) atomic quantum systems of dimension d = 2, (b) atomic classical systems of dimension v = 3, and (c) atomic Boxworld systems of dimension (n, k) = (2, 2).

Full size image

Regarding the effects, Witworld includes all the elements of the dual of the vector space which evaluate to valid probabilities for every state. That is, Witworld satisfies the no-restriction hypothesis (NRH)32. For example, for a system of the type \({{{{\mathcal{Q}}}}}_{2}\), the effects correspond to POVM elements and are represented as a particular region of \({({{\mathbb{R}}}^{4})}^{* }\). This region can be defined as the intersection of the cone of linear functionals which evaluate to positive reals on the set of state vectors with the set of linear functionals which evaluate to less than 1 for all state vectors. For \({{{{\mathcal{C}}}}}_{3}\), the effects live in a cube, and for \({{{{\mathcal{B}}}}}_{2,2}\), the effects live in an octahedron. A pictorial representation of these can be seen in Fig. 1. An effect e for a system S is diagrammatically denoted by

(5)

Since effects belong to the dual vector space, when we compose them with a state we obtain a real number, which, by assumption, must give a valid probability. That is, for all states σS and effects eS we have eS(σS) ∈ [0, 1]. Diagrammatically this is written as

(6)

As mentioned previously, we define Witworld to satisfy the NRH. This, however, is not the only simplifying assumption that we make in this construction. Additionally, we define the composition of systems to be via the so-called max tensor product46 and, hence, that the theory is locally tomographic35. Moreover, we demand that Witworld satisfies the generalised no-restriction hypothesis (GNRH). Intuitively, the GNRH is the NRH together with the requirement that every transformation that takes every element of a valid state space to an element of another valid state space is a valid transformation in the theory, that is, every completely positive transformation is considered valid.

The max tensor product (see Definition A.8 in the Supplementary Material) is a composition rule that assigns as valid states of a composite system A ⋅ B any vector in the product vector space (VA⋅B = VA ⊗ VB) that is consistent with the separable effects. Formally, ρAB is a valid state of the composite system AB if and only if, for every effect eA of A and \({e^{\prime} }^{B}\) of B, \({e}^{A}\otimes {e^{\prime} }^{B}({\rho }^{AB})\in [0,1]\). Diagrammatically we express this condition as:

(7)

From an intuitive point of view, the max tensor product gives rise to a GPT that somehow maximises the set of states that the system can be prepared in, whilst strongly restricting the set of measurements that one may perform on it. As a matter of fact, even though Witworld might appear to be a more general theory than quantum theory, these two are actually incomparable: quantum theory allows for measurements that Witworld systems cannot be acted upon with (with the latter having a more restricted set of measurements on collections of quantum atomic systems types), whilst Witworld allows for more states on which the composition of quantum atomic system types can be prepared (Witworld allows for two qubits to be prepared on a state mathematically corresponding to a quantum entanglement witness, whereas in quantum theory this is not an allowed state of a two-qubit system).

The fact that we have defined composition via the max tensor product and are demanding that the theory satisfies the GNRH, means that when we define the atomic states, we define the whole theory, since from the atomic states and max tensor product every possible state is defined, and from the states and GNRH the effects and transformations are also determined.

Finally, as mentioned above, the max tensor product is tomographically local, that is to say that its states can be uniquely determined by the information obtained from performing local measurements on its parts. Using the example above, this means that ρAB is completely determined by a set of values \({e}_{i}^{A}\otimes {e}_{j}^{B}({\rho }^{AB})\).

At this point, it is worth mentioning some further consequences of our definitions. The first one is that the use of the max tensor product to compose systems implies that every effect in Witworld is separable (see Lemma A.14 in the Supplementary Material). Therefore, an important feature of Witworld is that it does not contain entangling effects.

A second important fact about Witworld is that the combination of two atomic quantum systems yields systems whose states spaces are larger than the joint state space obtained from the standard quantum composition rule (see Theorems B.5 and B.6 in the Supplementary Material). For example, in the bipartite case, we have that the composite of \({{{{\mathcal{Q}}}}}_{n}\) and \({{{{\mathcal{Q}}}}}_{m}\), denoted by \({{{{\mathcal{Q}}}}}_{n}\cdot {{{{\mathcal{Q}}}}}_{m}\), has as its state space the set of entanglement witnesses (including density matrices56) for the quantum bipartite states, which strictly contains the set of bipartite quantum states \({{{{\mathcal{Q}}}}}_{nm}\). Therefore, whilst Witworld does contain arbitrary quantum systems, quantum theory is not a compositional subtheory within Witworld. Note that if one were to allow quantum systems in Witworld (where these quantum systems do not have the additional dynamics of Witworld quantum systems) to be composable both according to the standard quantum rule as well as to the Witworld composition rule, one could construct a protocol giving negative probabilities57. As such one cannot extend Witworld in such a manner as to contain quantum theory as a compositional subtheory.

A third important feature is that Boxworld-type (resp. classical-type) systems in Witworld compose exactly as they do in Boxworld (resp. classical theory). Therefore, both Boxworld and classical theory are indeed full subtheories of Witworld. Here, by full subtheory we mean that you can recover Boxworld or classical theory from Witworld by suitably restricting it to a particular collection of system types. This restriction recovers all and only the states, effects, transformations, and the composition rules of Boxworld or classical theory.

Finally, another important feature of Witworld is that because of the combination of GNRH and max tensor product, there is no difference between positive and completely positive maps (see Lemma A.15 in Supplementary Material). Of course, for systems that are not quantum, a more general notion (relative to that of positive operators in quantum theory) of positivity must be used in order to make that statement (see Definition A.6 in the Supplementary Material). Now, in the case of atomic quantum systems, this means that the valid Witworld transformations correspond to positive, but not necessarily completely positive, quantum transformations. Hence, this means that in Witworld there are more transformations available to local agents (i.e. to Alice and Bob) than would be available in quantum theory.

Post-quantum phenomena: Bell non-classicality and steering

In this section we explore the non-classical features that Witworld displays, starting with the case of Bell scenarios. One can readily see that Witworld can realise all non-signalling correlations in arbitrary Bell scenarios (see Fig. 2), since Boxworld is a full subtheory of Witworld. Therefore, one can leverage the Boxworld realisations of any non-signalling correlation, and translate them straightforwardly to a realisation within Witworld. For example, take the case of Popescu-Rohrlich (PR) correlations, which read \({p}_{PR}(ab| xy)=\frac{1}{2}{\delta }_{a\oplus b = xy}\) with a, b, x, y ∈ {0, 1} and ⊕ denoting modulo-2 addition; these correlations can be realised in Witworld as follows:

(8)

with the state sPR and controlled measurements MPR and \({M}_{{{{\rm{PR}}}}}^{\prime}\) as introduced in Ref. 34, whose explicit form we present in Eqs. (C8), (C3), and (C6) in the Supplementary Material. Note that for simplicity of notation we will often label the classical systems by an outcome or setting variable such as \({\mathbb{X}}\), in this case the relevant GPT system is \({{{{\mathcal{C}}}}}_{| {\mathbb{X}}| }\).

Fig. 2: Pictorial representation of the sets of correlations in Bell scenarios.
figure 2

The polytope of classical (Local Hidden State) correlations is depicted by the grey triangle. The convex set of quantum correlations is depicted by the red-bordered convex region. The set of Witworld correlations is depicted by the green transparent region. The polytope of no-signalling correlations is depicted by the black-bordered pentagon. The sets of no-signalling and Witworld correlations are equivalent. Witworld correlations strictly contain the quantum set, which strictly contains the classical set.

Full size image

The situation slightly changes when we instead focus on the non-classical phenomenon of steering (see Section D of the Supplementary Material for a comprehensive introduction). In brief, a traditional bipartite steering experiment consists of two distant parties, Alice and Bob, who share a physical system, perform space-like separated actions, and, unlike in Bell experiments, play asymmetric roles in the experiment. On the one hand, Alice (sometimes referred to as the black-box party in the steering literature) chooses a measurement labelled by \(x\in {\mathbb{X}}\) to perform on her share of the system, and obtains a classical outcome \(a\in {\mathbb{A}}\) with probability p(a∣x). Bob, on the other hand, merely characterises the quantum state \({\rho }_{a| x}^{B}\) to which his subsystem is steered. The information collected in this experiment (Alice’s probabilities and Bob’s conditional states) is expressed concisely as an assemblage53:

$${{{{\boldsymbol{\Sigma }}}}}_{{\mathbb{A}}| {\mathbb{X}}}={\left\{{\sigma }_{a| x}^{B}\right\}}_{a\in {\mathbb{A}},x\in {\mathbb{X}}}\,{{{\rm{where}}}}\,{\sigma }_{a| x}^{B}:= p(a| x)\,{\rho }_{a| x}^{B}.$$
(9)

Note that in Ref. 54 it is shown how assemblages can be equivalently represented by so-called ‘causal’ channels. With a slight abuse of notation we therefore diagrammatically represent the assemblage by the causal classical-quantum channel:

(10)

To see that this is indeed a good representation, note that we can extract the elements of the assemblage, i.e. the subnormalised steered states as:

(11)

and then the probabilities as:

(12)

where denotes the so-called unit effect (see Eq. (A11) and its preceding paragraph in the Supplementary Material), which in quantum theory corresponds to the partial trace of the relevant subsystem. Analogously, we can view non-signalling correlations as particular channels, in this case channels with classical inputs and outputs which correspond to stochastic maps. Using this we can rewrite Eq. (8) as

(13)

Beyond the traditional scenario, one may have steering experiments with more black-box parties also in a space-like separated configuration26,58, or even situations where Bob may influence the state preparation of his system by choosing a classical variable y (Bob-with-input scenarios)27.

In a similar fashion to Bell non-classicality, one can define what “classical” (a.k.a. LHS), quantum, and non-signalling assemblages are26,27. Notice that the differences in all these kinds of steering are not related to the type of system prepared in Bob’s lab, but rather to the types of shared resources that are used to prepare those quantum systems in Bob’s lab. From the point of view of Witworld, then, an assemblage in a steering experiment is produced by the parties performing local operations in a shared arbitrary composite multipartite system, which may include classical, quantum, and Boxworld systems. One fascinating property of Witworld is that it not only features all LHS and quantum assemblages (see Definitions D.5 and D.6, respectively, in the Supplementary Material), but may also realise post-quantum assemblages. That is, Witworld features post-quantum steering. In this section, we present a few key examples of this. Whether Witworld can realise all non-signalling assemblages is still an open question (see Fig. 3).

Fig. 3: Pictorial representation of the sets of assemblages in steering scenarios.
figure 3

The set of classical (Local Hidden State) assemblages is depicted by the grey ellipse. The set of quantum assemblages is depicted by the red-bordered region. The set of Witworld assemblages is depicted by the green transparent region. The set of no-signalling assemblages is depicted by the black-bordered ellipse. The set of Witworld assemblages strictly contains the quantum set, which strictly contains the LHS set. The set of no-signalling assemblages contains the Witworld set, and an open question (pictorially depicted by the question mark) is whether this inclusion is strict.

Full size image

The first example we present is in a tripartite steering scenario, since in traditional bipartite steering scenarios post-quantum steering is forbidden by the Gisin59 and Hughston, Josza and Wootters60 theorems. In a tripartite scenario, it is enough to consider the simplest setup with two black-box parties choosing among two dichotomic measurements each, so \({\mathbb{X}}={\mathbb{A}}=\{0,1\}\), and where Bob’s subsystem is a qubit. The particular assemblage we present is the PR-box assemblage, defined by

$${{{{\boldsymbol{\Sigma }}}}}_{{\mathbb{A}}{\mathbb{A}}| {\mathbb{X}}{\mathbb{X}}}^{{{{\rm{PR}}}}}={\left\{{\sigma }_{{a}_{1}{a}_{2}| {x}_{1}{x}_{2}}^{* B}\right\}}_{{a}_{j}\in {\mathbb{A}},{x}_{j}\in {\mathbb{X}},j\in \{1,2\}}\,,$$
(14)
$${{{\rm{with}}}}\,{\sigma }_{{a}_{1}{a}_{2}| {x}_{1}{x}_{2}}^{* B}={p}_{{{{\rm{PR}}}}}({a}_{1}{a}_{2}| {x}_{1}{x}_{2})\,\frac{{\mathbb{I}}}{2}\,.$$
(15)

This assemblage cannot be realised by the three parties sharing quantum resources26, i.e. it is post-quantum. \({{{{\boldsymbol{\Sigma }}}}}_{{\mathbb{A}}{\mathbb{A}}| {\mathbb{X}}{\mathbb{X}}}^{{{{\rm{PR}}}}}\) can however be realised within Witworld when the parties share the following mutipartite system: a bipartite Boxworld system of dimension (2, 2) on a PR state shared by the black-box parties, composed in parallel with a quantum state \({\rho }^{* B}=\frac{{\mathbb{I}}}{2}\) for Bob. Leveraging the realisation of PR-box correlations as in Eq. (8), the assemblage \({{{{\boldsymbol{\Sigma }}}}}_{{\mathbb{A}}{\mathbb{A}}| {\mathbb{X}}{\mathbb{X}}}^{{{{\rm{PR}}}}}\) can be realised by:

(16)

The second example we present is in a bipartite Bob-with-input steering scenario, where Alice has \({\mathbb{X}}={\mathbb{A}}=\{0,1\}\), Bob’s subsystem is a qubit, and Bob’s input is dichotomic (i.e. \(y\in {\mathbb{Y}}=\{0,1\}\)). The particular post-quantum assemblage \({{{{\boldsymbol{\Sigma }}}}}_{{\mathbb{A}}| {\mathbb{X}}{\mathbb{Y}}}^{* }\) we consider has elements defined by \({\sigma }_{a| xy}^{* B}=\frac{1}{2}(\left|a\right\rangle \left\langle a\right|{\delta }_{xy = 0}+\left|a\oplus 1\right\rangle \left\langle a\oplus 1\right|{\delta }_{xy = 1})\)27. This assemblage can be realised in Witworld by Alice and Bob sharing a bipartite Boxworld system of dimension (2, 2) prepared in a PR state, and implementing the following protocol. On the one hand, Alice performs the measurement MPR of Eq. (8) controlled on her classical input x, and obtains the output a. On the other hand, here the state preparation of Bob’s system further depends on Bob’s choice of a classical variable y which he inputs in a device. In this protocol, this device has a two-stage process: first it implements the measurement \({M}_{{{{\rm{PR}}}}}^{\prime}\) of Eq. (8) on the Boxworld system, conditioned on y; second, there is a controlled state preparation P which prepares the quantum state \(\left|b\right\rangle \left\langle b\right|\) conditioned on b, the classical output of \({M}_{{{{\rm{PR}}}}}^{\prime}\). Diagrammatically, the whole protocol reads:

(17)

One can readily see that Eq. (17) indeed holds, since the assemblage elements of \({{{{\boldsymbol{\Sigma }}}}}_{{\mathbb{A}}| {\mathbb{X}}{\mathbb{Y}}}^{* }\) can be rewritten as \({\sigma }_{a| xy}^{* B}=\frac{1}{2}\left|a\oplus xy\right\rangle \left\langle a\oplus xy\right|\), and PR-box correlations satisfy b = a ⊕ xy and \(\frac{1}{2}={\sum }_{b}{p}_{{{{\rm{PR}}}}}(ab| xy)\).

The third example we present is that of Gleason assemblages55. In short, Gleason assemblages are those that can be mathematically expressed in the language of quantum theory by having the parties measure a shared system whose state preparation is represented by a normalised quantum entanglement witness. Gleason assemblages are particularly useful, since there are constructions that yield provably post-quantum Gleason assemblages. More importantly, the post-quantumness of some Gleason assemblages is not implied by post-quantum Bell non-locality, which renders post-quantum steering as a genuinely new effect55. Witworld readily provides realisations of any Gleason assemblage, by noticing two facts: (i) any quantum entanglement witness is a valid state of composite quantum-type systems in Witworld (Theorem B.6), and (ii) in Witworld, any local quantum measurement is a valid Witworld measurement (Lemma 8.14). The explicit diagram for a Witworld realisation of a generic Gleason assemblage \({{{{\boldsymbol{\Sigma }}}}}_{{{\mathbb{A}}}_{1}{{\mathbb{A}}}_{2}| {{\mathbb{X}}}_{1}{{\mathbb{X}}}_{2}}^{{{{\rm{G}}}}}\) in a tripartite scenario with two black-box parties is:

(18)

The fourth example that we present is in a bipartite Bob-with-input steering scenario, with \({\mathbb{A}}={\mathbb{Y}}=\{0,1\}\) and \({\mathbb{X}}=\{1,2,3\}\). The particular post-quantum assemblage \({{{{\boldsymbol{\Sigma }}}}}_{{\mathbb{A}}| {\mathbb{X}}{\mathbb{Y}}}^{* * }\) here has elements defined by Sainz et al.27:

$${\sigma }_{a| xy}^{* * B}=\frac{1}{4}\left({\mathbb{I}}+{(-1)}^{a+{\delta }_{x,2}{\delta }_{y,1}}{{{\Sigma }}}_{x}\right)\,,$$
(19)

where (Σ1, Σ2, Σ3) are the Pauli X, Y, and Z operators, respectively. \({{{{\boldsymbol{\Sigma }}}}}_{{\mathbb{A}}| {\mathbb{X}}{\mathbb{Y}}}^{* * }\) is the first assemblage found in the Bob-with-input scenario whose post-quantumness cannot be proven directly from leveraging post-quantum Bell non-locality, which renders this type of post-quantum steering as a genuinely new effect. To see that Witworld can realise this assemblage, first notice that its elements can be mathematically written as \({\sigma }_{a| xy}^{* * B}={({\overline{\sigma }}_{a| xy}^{B})}^{{\top }_{y}}\), where \({\overline{\sigma }}_{a| xy}^{B}=\frac{1}{4}\left({\mathbb{I}}+{(-1)}^{a}{{{\Sigma }}}_{x}\right)\) are the elements of a quantum assemblage (see Definition D.6 in the Supplementary Material), and ⊤y is the identity operator for y = 0 and the Transpose operator (denoted ⊤) for y = 1. The final step is to observe that all of these mathematical objects are acceptable physical operations in Witworld: (i) the maximally entangled quantum state that realises \(\{{\overline{\sigma }}_{a| xy}^{B}\}\) is a valid Witworld state preparation for Alice and Bob by Theorem B.6, (ii) the quantum Pauli measurements for Alice that realise \(\{{\overline{\sigma }}_{a| xy}^{B}\}\) are valid Witworld measurements by Lemma A.14, where we denote the classically controlled Pauli measurement by PAULI, and (iii) the operations {⊤y}, which are positive quantum maps, are valid Witworld transformations by Theorem A.15, and, hence, so too is the controlled transformation c⊤ which implements ⊤ conditioned on a classical input system. Diagrammatically, this is represented as:

(20)

The final example that we consider is steering in the instrumental scenario27. This can be seen as an adaptation of the Bob-with-input scenario, in which Alice’s output a determines the setting y for Bob. The particular example of post-quantum steering in this scenario that we present here is given by modifying our previous example, by wiring Alice’s output to Bob’s input. That is, it can be shown that the assemblage

$${\sigma }_{a| x}^{IB}=\frac{1}{4}\left({\mathbb{I}}+{(-1)}^{a+{\delta }_{x,2}{\delta }_{a,1}}{{{\Sigma }}}_{x}\right)\,,$$
(21)

which is obtained by setting y = a in Eq. (19), is post-quantum27. It is then a simple modification of Eq. (20) to see that this too can be realised in Witworld:

(22)

where the small white circle splitting the classical system is the copy operation.

With this, we see that Witworld features a variety of non-classical and post-quantum properties, both in Bell and steering scenarios, and hence is the first GPT that has been shown to display post-quantum steering.

Post-quantum advantage for information processing

Post-quantum resources may outperform quantum ones for information processing tasks13,17,18,50,61,62. A natural question then is whether the post-quantum features of Witworld enable this theory to be more powerful than quantum theory in this respect. First, one can focus on device-independent information processing tasks, such as quantum cryptography17,18,50, which rely on the use of correlations in Bell scenarios. Here, it is known that Boxworld may outperform quantum theory, since it realises any non-signalling correlation. Since Boxworld is a subtheory of Witworld, then, the latter inherits these properties; that is, Witworld outperforms quantum theory in those device-independent information processing tasks. A more relevant question then is whether such advantage persists when moving on from device-independent tasks. Hence in this section, we investigate whether Witworld provides an advantage for tasks that go beyond the processing of Bell-type correlations.

There are two features of Witworld that go beyond Boxworld which are noteworthy when looking for an information task where Witworld is resourceful. One is the fact that Witworld has quantum systems as atomic system types, and the other is the fact that positive (but not necessarily completely positive) quantum operations are allowed physical operations in Witworld. Using these two facts we first show that Witworld outperforms Quantum Theory in the task of Remote State Preparation, and then we show that the resource underlying this advantage is post-quantum steering.

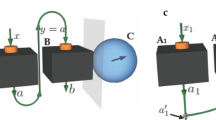
Remote State Preparation (RSP)28,29 is a protocol with a similar flavour to state teleportation. A main difference between teleportation and RSP is that in the former, Alice can send to Bob a state she knows nothing about, whereas in the latter she may require a complete classical description of \(\left|\psi \right\rangle\). We denote this complete classical description by ψ. In both cases, the main goal is for Alice to deterministically prepare a state \(\left|\psi \right\rangle\) in Bob’s lab, such that he gets no additional information about \(\left|\psi \right\rangle\). In RSP (see Fig. 4), however, Alice does not need to perform experimentally challenging entangling measurements (as in a full Bell-state analysis)30. Instead, she can directly encode the information about the state she wishes to send onto her share of an entangled state shared with Bob. When Alice and Bob use quantum resources, the minimum amount of classical information that she needs to send him for the protocol to succeed is \(2\log d\) bits of information, where d is the dimension of the Hilbert space containing \(\left|\psi \right\rangle\)29. Here we present a protocol using Witworld resources which may prepare an arbitrary qubit state in Bob’s lab using only 1 bit (instead of 2) of classical communication.

Fig. 4: Pictorial representation of the remote state preparation protocol.
figure 4

Alice performs \({U}_{A}(\left|\psi \right\rangle )\) on her share of a physical system – a unitary operation that depends on \(\left|\psi \right\rangle\) – and then a measurement (POVM). She sends a classical message m to Bob, who, in turn, performs an unitary transformation (which depends on m) on his share of the system. The outcome of the protocol is a quantum state on state \(\left|\psi \right\rangle\) on Bob's lab.

Full size image

Consider the following protocol in Witworld. Alice and Bob share the two qubit state \(\left|{{{\Phi }}}^{s}\right\rangle =(\left|01\right\rangle -\left|10\right\rangle )/\sqrt{2}\). Alice performs the unitary \({U}_{{{{\boldsymbol{\psi }}}}}=\left|0\right\rangle \left\langle {\psi }^{\perp }\right|+\left|1\right\rangle \left\langle \psi \right|\) on her qubit, which encodes the state \(\left|\psi \right\rangle\) to be sent. This effectively applies \({U}_{{{{\boldsymbol{\psi }}}}}^{{\dagger} }\) to Bob’s half of the state (the singlet state \(\left|{{{\Phi }}}^{s}\right\rangle\) transforms trivially under U ⊗ U; implying that \(({U}_{{{{\boldsymbol{\psi }}}}}\otimes {\mathbb{I}})\left|{{{\Phi }}}^{s}\right\rangle =({\mathbb{I}}\otimes {U}_{{{{\boldsymbol{\psi }}}}}^{{\dagger} })\left|{{{\Phi }}}^{s}\right\rangle\)). Next, she performs the measurement given by \(B=\{\left|0\right\rangle \left\langle 0\right|,\left|1\right\rangle \left\langle 1\right|\}\), whose outcome consists of one classical bit a which indicates exactly whether Bob now has the post measured state \(-\left|\psi \right\rangle\) (if a = 0) or \(\left|{\psi }^{\perp }\right\rangle\) (if a = 1). Then, Alice sends a to Bob, who now knows whether he is holding \(-\left|\psi \right\rangle\) or \(\left|{\psi }^{\perp }\right\rangle\). The task can be completed if Bob has access to a universal-NOT operation, which maps an arbitrary input \(\left|\phi \right\rangle\) into an orthogonal state to it (which is unique up to global phases for qubits). The universal-NOT operation is not valid in quantum theory since it is a positive transformation, but not a completely positive transformation. However, in Witworld, this is an allowable transformation. Thus in Witworld Bob can apply the universal-NOT gate when a = 1, leaving him with a perfect copy of \(\left|\psi \right\rangle\) (up to a physically irrelevant global phase). Diagrammatically, this protocol is represented as follows:

(23)

where cUNOT is the controlled-universal-NOT operation. The diagrammatic manipulations that prove that Eq. (23) holds are presented in Section E of the Supplementary Material. Through this protocol, Witworld performs RSP of a qubit deterministically with the transmission of only one classical bit from Alice to Bob, outperforming quantum theory at the task.

We now move on to unveiling what the critical resource is underlying the success of RSP in Witworld. For this, it is convenient to rewrite the diagram in the left hand side of Eq. (23) as:

(24)

where

(25)

is not the state \(\left|\psi \right\rangle\), but simply a classical label corresponding to it, used to determine the unitary Uψ that the transformation cU implements. In addition, B∘cU is the process that first implements the controlled unitary cU and then the measurement B.

The crucial step here is to notice that each term in the sum in Eq. (24) can be identified with an element of an assemblage {σa∣ψ} in an instrumental steering scenario (see Definition D.4 in the Supplementary Material) as follows:

(26)

where a denotes Alice’s dichotomic outcome, and ψ is the classical variable that denotes her measurement choice. That is, RSP is ultimately an instance of an instrumental steering scenario, and the possible assemblages that Alice can prepare dictates whether RSP is possible for the given cardinality of a. For the particular RSP protocol discussed above,

(27)

It is readily seen that the assemblage {σa∣ψ} has no quantum realisation: if this was instead the case, this assemblage would provide a quantum RSP protocol that succeeds deterministically with 1 bit of communication, which is fundamentally impossible.

We see therefore how instrumental steering powers RSP, and how the post-quantum steering featured in Witworld makes this theory more efficient than quantum theory at the task of Remote State Preparation.

Let us observe that quantum theory restricted to the reals63, which has mixed states given by symmetric matrices (a subset of quantum states), also requires a single bit of communication for RSP. A rebit (2 dimensional real quantum system) has mixed states given by the X − Z plane of the Bloch sphere (a disk). The universal NOT is just rotation by π around the Y axis, and is completely positive. Since the singlet state \(\left|{{{\Phi }}}^{s}\right\rangle \left\langle {{{\Phi }}}^{s}\right|\) is a real valued density operator (i.e. it is a symmetric matrix) it follows that it is a valid entangled state of two rebits. Hence the protocol outlined above in Witworld can be applied to real quantum theory as well, to give RSP with a single bit of communication.

Discussion

In this work, we explored the scope of post-quantum steering as a stronger-than-quantum resource for information processing. We particularly focused the search on tasks beyond device-independent ones or those that ultimately rely on Bell correlations (such as random access codes64,65 or device-independent quantum key distribution): we aimed at finding tasks that intrinsically leveraged quantum systems and non-classical steering. We discovered that remote state preparation of qubits systems provides a friendly proof-of-principle of a general phenomenology: steering assemblages in the instrumental scenario serve as a resource for the task, and post-quantum assemblages perform better than quantum ones at it. This is the first time that post-quantum steering – as opposed to post-quantum Bell non-classicality – has been identified as a resource powering information processing which can provably outperform quantum theory.

In order to prove our claims, we defined a generalised probabilistic theory, that we call Witworld, by combining classical, quantum, and Boxworld systems in a simple mathematical way, via the max tensor product. The intuitive formulation of Witworld allowed us to present its powerful post-quantum features in an accessible way: one can readily see how post-quantum Bell nonlocality, post-quantum steering, and post-quantum states emerge within Witworld. The task of remote state preparation can be studied diagrammatically within Witworld, and by doing so we showed how the post-quantum assemblages allowed by the theory makes Witworld perform better at it than quantum theory does.

A feature of Witworld is that, even though it is built in part on quantum systems, it does not contain quantum theory as a subtheory: there are tasks, such as quantum teleportation, that quantum theory can perform whilst Witworld cannot. The reason for this is the choice of composition rule: Witworld composes via the max tensor product, and hence no entangling measurements are allowed in the theory. Nonetheless, Witworld remarkably succeeds at reproducing all the quantum entangled states, quantum steering assemblages, and quantum correlations in Bell scenarios. That is, for the non-classical phenomena usually leveraged in quantum information tasks, Witworld is at least as good as quantum theory at manifesting them.

If we turn our attention to a particular subtheory of Witworld by restricting the system types to classical and quantum only – that is, by removing Boxworld from the theory – we find that this subtheory still features post-quantum properties, such as Bell non-classicality in multipartite scenarios (for example, by utilising the results of Ref. 56), as well as post-quantum steering and post-quantum states even in bipartite scenarios. Remarkably, the post-quantum advantage for remote state preparation is also featured by this subtheory of Witworld, since the post-quantum advantage provided by it stems from the enlarged set of operations allowed on local quantum systems. We leave it as an open question whether other previously defined GPTs (e.g. Refs. 66,67) may provide such an advantage for this information processing task.

It is worth noticing that Witworld’s simple formulation does not make the theory intrinsically groundbreaking from the perspective of generalised probabilitic theories, however its relevance is not grounded in its appeal as a standalone GPT. Rather, Witworld shows that there exists a compositional theory that could underpin post-quantum effects such as post-quantum steering. This shows that the latter phenomenon in not in principle un-realisable, and hence its study should not be simply dismissed.

Looking ahead, there are a variety of open questions that can be studied, especially about the extent to which post-quantum steering compatible with special relativity can be underpinned by some generalised theory. We know that Witworld may display post-quantum steering but, unlike the case of Bell non-classicality, it is still unknown whether any no-signalling assemblage may have a realisation within Witworld. Any answer to this question would be of interest: if Witworld can realise all no-signalling assemblages, then this theory becomes the first GPT to accommodate steering fully in a common-cause resource theoretic framework68; otherwise, understanding the reason behind the gap between no-signalling realisable and Witworld realisable assemblages may lead to an operational principle that could shed light on the characterisation of quantum phenomena.

Finally, the exploration of the information processing power of steering (quantum and beyond) has only just begun. Since Witworld is formulated in an intuitive way leveraging a diagrammatic representation32,33,69,70,71, there is plenty of scope for investigating other post-quantum advantages of this theory, and of post-quantum steering, for information processing.