Skip to main content
SpringerLink
Log in

Exact statistical inference for the Wasserstein distance by selective inference

Selective Inference for the Wasserstein Distance

  • Published:
Annals of the Institute of Statistical Mathematics Aims and scope Submit manuscript

Abstract

In this paper, we study statistical inference for the Wasserstein distance, which has attracted much attention and has been applied to various machine learning tasks. Several studies have been proposed in the literature, but almost all of them are based on asymptotic approximation and do not have finite-sample validity. In this study, we propose an exact (non-asymptotic) inference method for the Wasserstein distance inspired by the concept of conditional selective inference (SI). To our knowledge, this is the first method that can provide a valid confidence interval (CI) for the Wasserstein distance with finite-sample coverage guarantee, which can be applied not only to one-dimensional problems but also to multi-dimensional problems. We evaluate the performance of the proposed method on both synthetic and real-world datasets.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9

Similar content being viewed by others

Notes

  1. To make a distinction between random variables and observed variables, we use superscript \(^\mathrm{{obs}}\), e.g., \({\varvec{X}}\) is a random vector and \({\varvec{X}}^\mathrm{{obs}}\) is the observed data vector.

  2. We note that there always exists exactly one redundant equality constraint in linear equality constraint system in (7). This is due to the fact that sum of all the masses on \({\varvec{X}}^\mathrm{{obs}}\) is always equal to sum of all the masses on \({\varvec{Y}}^\mathrm{{obs}}\) (i.e., they are all equal to 1). Therefore, any equality constraint can be expressed as a linear combination of the others, and hence any one constraint can be dropped. In this paper, we always drop the last equality constraint (i.e., the last row of matrix S and the last element of vector \({\varvec{h}}\)) before solving (7).

  3. We suppose that the LP is non-degenerate. A careful discussion might be needed in the presence of degeneracy.

  4. We used dataset Lung_GSE7670 which is available at https://sbcb.inf.ufrgs.br/cumida.

References

  • Arjovsky, M., Chintala, S., Bottou, L. (2017). Wasserstein generative adversarial networks. International conference on machine learning, pp. 214–223. PMLR.

  • Bernton, E., Jacob, P. E., Gerber, M., Robert, C. P. (2017). Inference in generative models using the Wasserstein distance, 1(8), 9. arXiv preprint arXiv:1701.05146.

  • Chen, S., Bien, J. (2019). Valid inference corrected for outlier removal. Journal of Computational and Graphical Statistics, 29(2), 1–12.

    MathSciNet  MATH  Google Scholar 

  • Del Barrio, E., Cuesta-Albertos, J. A., Matrán, C., Rodríguez-Rodríguez, J. M. (1999). Tests of goodness of fit based on the l2-Wasserstein distance. Annals of Statistics, 27(4), 1230–1239.

    MathSciNet  MATH  Google Scholar 

  • Del Barrio, E., Gordaliza, P., Lescornel, H., Loubes, J.-M. (2019). Central limit theorem and bootstrap procedure for Wasserstein’s variations with an application to structural relationships between distributions. Journal of Multivariate Analysis, 169, 341–362.

  • Duy, V. N. L., Iwazaki, S., Takeuchi, I. (2020a). Quantifying statistical significance of neural network representation-driven hypotheses by selective inference. arXiv preprint arXiv:2010.01823.

  • Duy, V. N. L., Takeuchi, I. (2021a). More powerful conditional selective inference for generalized lasso by parametric programming. arXiv preprint arXiv:2105.04920.

  • Duy, V. N. L., Takeuchi, I. (2021b). Parametric programming approach for more powerful and general lasso selective inference. International conference on artificial intelligence and statistics, 901–909. PMLR.

  • Duy, V. N. L., Toda, H., Sugiyama, R., Takeuchi, I. (2020b). Computing valid p-value for optimal changepoint by selective inference using dynamic programming. Advances in neural information processing systems.

  • Evans, S. N., Matsen, F. A. (2012). The phylogenetic Kantorovich–Rubinstein metric for environmental sequence samples. Journal of the Royal Statistical Society: Series B (Statistical Methodology), 74(3), 569–592.

    Article  MathSciNet  MATH  Google Scholar 

  • Feltes, B. C., Chandelier, E. B., Grisci, B. I., Dorn, M. (2019). Cumida: An extensively curated microarray database for benchmarking and testing of machine learning approaches in cancer research. Journal of Computational Biology, 26(4), 376–386.

    Article  Google Scholar 

  • Fithian, W., Sun, D., Taylor, J. (2014). Optimal inference after model selection. arXiv preprint arXiv:1410.2597.

  • Frogner, C., Zhang, C., Mobahi, H., Araya-Polo, M., Poggio, T. (2015). Learning with a wasserstein loss. arXiv preprint arXiv:1506.05439.

  • Hyun, S., Lin, K., G’Sell, M., Tibshirani, R. J. (2018). Post-selection inference for changepoint detection algorithms with application to copy number variation data. arXiv preprint arXiv:1812.03644.

  • Imaizumi, M., Ota, H., Hamaguchi, T. (2019). Hypothesis test and confidence analysis with wasserstein distance with general dimension. arXiv preprint arXiv:1910.07773.

  • Kolouri, S., Park, S. R., Thorpe, M., Slepcev, D., Rohde, G. K. (2017). Optimal mass transport: Signal processing and machine-learning applications. IEEE Signal Processing Magazine, 34(4), 43–59.

    Article  Google Scholar 

  • Lee, J. D., Sun, D. L., Sun, Y., Taylor, J. E. (2016). Exact post-selection inference, with application to the lasso. The Annals of Statistics, 44(3), 907–927.

    Article  MathSciNet  MATH  Google Scholar 

  • Liu, K., Markovic, J., Tibshirani, R. (2018). More powerful post-selection inference, with application to the lasso. arXiv preprint arXiv:1801.09037.

  • Loftus, J. R., Taylor, J. E. (2015). Selective inference in regression models with groups of variables. arXiv preprint arXiv:1511.01478.

  • Murty, K. (1983). Linear Programming. New York: Wiley.

  • Ni, K., Bresson, X., Chan, T., Esedoglu, S. (2009). Local histogram based segmentation using the Wasserstein distance. International Journal of Computer Vision, 84(1), 97–111.

    Article  Google Scholar 

  • Ramdas, A., Trillos, N. G., Cuturi, M. (2017). On Wasserstein two-sample testing and related families of nonparametric tests. Entropy, 19(2), 47.

    Article  MathSciNet  Google Scholar 

  • Sugiyama, K., Le Duy, V. N., Takeuchi, I. (2021a). More powerful and general selective inference for stepwise feature selection using homotopy method. International conference on machine learning, 9891–9901. PMLR.

  • Sugiyama, R., Toda, H., Duy, V. N. L., Inatsu, Y., Takeuchi, I. (2021b). Valid and exact statistical inference for multi-dimensional multiple change-points by selective inference. arXiv preprint arXiv:2110.08989.

  • Suzumura, S., Nakagawa, K., Umezu, Y., Tsuda, K., Takeuchi, I. (2017). Selective inference for sparse high-order interaction models. Proceedings of the 34th international conference on machine learning, Vol. 70, pp. 3338–3347. JMLR.

  • Tanizaki, K., Hashimoto, N., Inatsu, Y., Hontani, H., Takeuchi, I. (2020). Computing valid p-values for image segmentation by selective inference. Proceedings of the conference on computer vision and pattern recognition, 9553–9562.

  • Tibshirani, R. J., Taylor, J., Lockhart, R., Tibshirani, R. (2016). Exact post-selection inference for sequential regression procedures. Journal of the American Statistical Association, 111(514), 600–620.

    Article  MathSciNet  Google Scholar 

  • Tsukurimichi, T., Inatsu, Y., Duy, V. N. L., Takeuchi, I. (2021). Conditional selective inference for robust regression and outlier detection using piecewise-linear homotopy continuation. arXiv preprint arXiv:2104.10840.

  • Villani, C. (2009). Optimal transport: Old and new (Vol. 338). Springer, Berlin.

  • Yang, F., Barber, R. F., Jain, P., Lafferty, J. (2016). Selective inference for group-sparse linear models. In Advances in neural information processing systems, 2469–2477.

Download references

Acknowledgements

We thank the authors of Imaizumi et al. (2019) for providing us with their software implementation. This work was partially supported by MEXT KAKENHI (20H00601, 16H06538), JST CREST (JPMJCR21D3), JST Moonshot R&D (JPMJMS2033-05), NEDO (JPNP18002, JPNP20006), RIKEN Center for Advanced Intelligence Project, and RIKEN Junior Research Associate Program.

Author information

Authors and Affiliations

  1. Nagoya Institute of Technology, Gokiso-cho, Showa-ku, Nagoya, Aichi, 466-8555, Japan

    Vo Nguyen Le Duy

  2. RIKEN, 2-1 Hirosawa, Wako, Saitama, 351-0198, Japan

    Vo Nguyen Le Duy & Ichiro Takeuchi

  3. Nagoya University, Furo-cho, Chikusa-ku, Nagoya, 464-8601, Japan

    Ichiro Takeuchi

Authors
  1. Vo Nguyen Le Duy
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Ichiro Takeuchi
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

We provide an exact (non-asymptotic) inference method for the Wasserstein distance. To our knowledge, this is the first method that can provide valid CI, called selective CI, for the Wasserstein distance that guarantees the coverage property in finite sample size. Another practically important advantage of this study is that the proposed method is valid when the Wasserstein distance is computed in multi-dimensional problem, which is impossible for almost all the existing asymptotic methods since the limit distribution of the Wasserstein distance is only applicable for univariate data. We conduct experiments on both synthetic and real-world datasets to evaluate the performance of the proposed method. Our implementation is available at https://github.com/vonguyenleduy/selective_inference_wasserstein_distance.

Corresponding author

Correspondence to Ichiro Takeuchi.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Appendices

A Proposed method in hypothesis testing framework

We present the proposed method in the setting of hypothesis testing and consider the case when the cost matrix is defined by using squared \(\ell _2\) distance.

Cost matrix We define the cost matrix \(C({\varvec{X}}, {\varvec{Y}})\) of pairwise distances (squared \(\ell _2\) distance) between elements of \({\varvec{X}}\) and \({\varvec{Y}}\) as

$$\begin{aligned} C({\varvec{X}}, {\varvec{Y}})&= \big [(x_i - y_j)^2 \big ]_{ij} \in \mathbb {R}^{n \times m}. \end{aligned}$$
(34)

Then, the vectorized form of \(C({\varvec{X}}, {\varvec{Y}})\) can be defined as

$$\begin{aligned} \begin{aligned} {\varvec{c}}({\varvec{X}}, {\varvec{Y}})&= \mathrm{{vec}} (C({\varvec{X}}, {\varvec{Y}})) \in \mathbb {R}^{nm}\\&= \left[ \varOmega {{\varvec{X}} \atopwithdelims (){\varvec{Y}}} \right] \circ \left[ \varOmega {{\varvec{X}} \atopwithdelims (){\varvec{Y}}} \right] , \end{aligned} \end{aligned}$$
(35)

where \(\varOmega \) is defined as in (5) and the operation \(\circ \) is element-wise product.

The Wasserstein distance By solving LP with the cost vector defined in (35) on the observed data \({\varvec{X}}^\mathrm{{obs}}\) and \({\varvec{Y}}^\mathrm{{obs}}\), we obtain the set of selected basic variables

$$\begin{aligned} \mathcal {M}_\mathrm{{obs}} = \mathcal {M}({\varvec{X}}^\mathrm{{obs}}, {\varvec{Y}}^\mathrm{{obs}}). \end{aligned}$$

Then, the Wasserstein distance can be re-written as (we denote \(W = W(P_n, Q_m)\) for notational simplicity)

$$\begin{aligned} W&= \hat{{\varvec{t}}}^\top {\varvec{c}}({\varvec{X}}^\mathrm{{obs}}, {\varvec{Y}}^\mathrm{{obs}}) \\&= \hat{{\varvec{t}}}_{\mathcal {M}_\mathrm{{obs}}}^\top {\varvec{c}}_{\mathcal {M}_\mathrm{{obs}}}({\varvec{X}}^\mathrm{{obs}}, {\varvec{Y}}^\mathrm{{obs}}) \\&= \hat{{\varvec{t}}}_{\mathcal {M}_\mathrm{{obs}}}^\top \Bigg [ \left[ \varOmega _{\mathcal {M}_\mathrm{{obs}}, :} {{\varvec{X}}^\mathrm{{obs}} \atopwithdelims (){\varvec{Y}}^\mathrm{{obs}}} \right] \circ \left[ \varOmega _{\mathcal {M}_\mathrm{{obs}}, :} {{\varvec{X}}^\mathrm{{obs}} \atopwithdelims (){\varvec{Y}}^\mathrm{{obs}}} \right] \Bigg ]. \end{aligned}$$

Hypothesis testing Our goal is to test the following hypothesis:

$$\begin{aligned} \mathrm{H}_0: \hat{{\varvec{t}}}_{\mathcal {M}_\mathrm{{obs}}}^\top \Bigg [ \left[ \varOmega _{\mathcal {M}_\mathrm{{obs}}, :} { {\varvec{\mu }}_{{\varvec{X}}} \atopwithdelims (){\varvec{\mu }}_{{\varvec{Y}}}} \right] \circ \left[ \varOmega _{\mathcal {M}_\mathrm{{obs}}, :} { {\varvec{\mu }}_{{\varvec{X}}} \atopwithdelims (){\varvec{\mu }}_{{\varvec{Y}}}} \right] \Bigg ] = 0. \end{aligned}$$

Unfortunately, it is technically difficult to directly test the above hypothesis. Therefore, we propose to test the following equivalent one:

$$\begin{aligned}&\mathrm{H}_0: \hat{{\varvec{t}}}_{\mathcal {M}_\mathrm{{obs}}}^\top \left[ \varTheta _{\mathcal {M}_\mathrm{{obs}}, :} { {\varvec{\mu }}_{{\varvec{X}}} \atopwithdelims (){\varvec{\mu }}_{{\varvec{Y}}}} \right] = 0 \\ \Leftrightarrow ~&\mathrm{H}_0: {\varvec{\eta }}^\top { {\varvec{\mu }}_{{\varvec{X}}} \atopwithdelims (){\varvec{\mu }}_{{\varvec{Y}}}} = 0 \end{aligned}$$

where \(\varTheta \) is defined as in (5) and \({\varvec{\eta }}= \varTheta _{\mathcal {M}_\mathrm{{obs}}, :}^\top \hat{{\varvec{t}}}_{\mathcal {M}_\mathrm{{obs}}}\).

Conditional SI To test the aforementioned hypothesis, we consider the following selective p-value:

$$\begin{aligned} p_\mathrm{{selective}} = \mathbb {P}_\mathrm{H_0} \left( \left| {\varvec{\eta }}^\top {{\varvec{X}} \atopwithdelims (){\varvec{Y}}} \right| \ge \left| {\varvec{\eta }}^\top {{\varvec{X}}^\mathrm{{obs}} \atopwithdelims (){\varvec{Y}}^\mathrm{{obs}}} \right| \mid \mathcal {E}\right) \end{aligned}$$

where the conditional selection event is defined as

$$\begin{aligned} \mathcal {E}= \left\{ \begin{array}{l} \mathcal {M}({\varvec{X}}, {\varvec{Y}}) = \mathcal {M}_\mathrm{{obs}}, \\ \mathcal {S}_{\mathcal {M}_\mathrm{{obs}}}({\varvec{X}}, {\varvec{Y}}) = \mathcal {S}_{\mathcal {M}_\mathrm{{obs}}}({\varvec{X}}^\mathrm{{obs}}, {\varvec{Y}}^\mathrm{{obs}}) \\ {\varvec{q}}({\varvec{X}}, {\varvec{Y}}) = {\varvec{q}}({\varvec{X}}^\mathrm{{obs}}, {\varvec{Y}}^\mathrm{{obs}}) \end{array} \right\} . \end{aligned}$$

Our next task is to identify the conditional data space whose data satisfies \(\mathcal {E}\).

Characterization of the conditional data space Similar to the discussion in Sect. 3, the data are restricted on the line due to the conditioning on the nuisance component \({\varvec{q}}({\varvec{X}}, {\varvec{Y}})\). Then, the conditional data space is defined as

$$\begin{aligned} \mathcal {D}= \Big \{ ({\varvec{X}} ~ {\varvec{Y}})^\top = {\varvec{a}} + {\varvec{b}} z \mid z \in \mathcal {Z}\Big \}, \end{aligned}$$

where

$$\begin{aligned} \mathcal {Z}= \left\{ z \in \mathbb {R}~ \Big | \begin{array}{l} \mathcal {M}({\varvec{a}} + {\varvec{b}} z) = \mathcal {M}_\mathrm{{obs}}, \\ \mathcal {S}_{\mathcal {M}_\mathrm{{obs}}}({\varvec{a}} + {\varvec{b}} z) = \mathcal {S}_{\mathcal {M}_\mathrm{{obs}}}({\varvec{X}}^\mathrm{{obs}}, {\varvec{Y}}^\mathrm{{obs}}) \end{array} \right\} . \end{aligned}$$

The remaining task is to construct \(\mathcal {Z}\). We can decompose \(\mathcal {Z}\) into two separate sets as \(\mathcal {Z}= \mathcal {Z}_1 \cap \mathcal {Z}_2\), where

$$\begin{aligned} \mathcal {Z}_1&= \{ z \in \mathbb {R}\mid \mathcal {M}({\varvec{a}} + {\varvec{b}} z) = \mathcal {M}_\mathrm{{obs}}\}, \\ \mathcal {Z}_2&= \{ z \in \mathbb {R}\mid \mathcal {S}_{\mathcal {M}_\mathrm{{obs}}}({\varvec{a}} + {\varvec{b}} z) = \mathcal {S}_{\mathcal {M}_\mathrm{{obs}}}({\varvec{X}}^\mathrm{{obs}}, {\varvec{Y}}^\mathrm{{obs}}) \}. \end{aligned}$$

The construction of \(\mathcal {Z}_2\) is as follows (we denote \({\varvec{s}}_{\mathcal {M}_\mathrm{{obs}}} = \mathcal {S}_{\mathcal {M}_\mathrm{{obs}}}({\varvec{X}}^\mathrm{{obs}}, {\varvec{Y}}^\mathrm{{obs}})\) for notational simplicity):

$$\begin{aligned} \mathcal {Z}_2&= \{ z \in \mathbb {R}\mid \mathcal {S}_{\mathcal {M}_\mathrm{{obs}}}({\varvec{a}} + {\varvec{b}} z) = {\varvec{s}}_{\mathcal {M}_\mathrm{{obs}}}\} \\&= \left\{ z \in \mathbb {R}\mid \mathrm{{sign}} \Big (\varOmega _{\mathcal {M}_\mathrm{{obs}}, :} ({\varvec{a}} + {\varvec{b}} z) \Big ) = {\varvec{s}}_{\mathcal {M}_\mathrm{{obs}}} \right\} \\&= \left\{ z \in \mathbb {R}\mid {\varvec{s}}_{\mathcal {M}_\mathrm{{obs}}} \circ \varOmega _{\mathcal {M}_\mathrm{{obs}}, :} ({\varvec{a}} + {\varvec{b}} z) \ge {\varvec{0}}\right\} , \end{aligned}$$

which can be obtained by solving the system of linear inequalities. Next, we present the identification of \(\mathcal {Z}_1\). Because we use squared \(\ell _2\) distance to define the cost matrix, the LP with the parametrized data \({\varvec{a}} + {\varvec{b}} z\) is written as follows:

$$\begin{aligned}&\min \limits _{{\varvec{t}} \in \mathbb {R}^{nm}} ~ {\varvec{t}}^\top [ \varOmega ({\varvec{a}} + {\varvec{b}} z) \circ \varOmega ({\varvec{a}} + {\varvec{b}} z)] ~ ~ \text {s.t.} ~ ~ S {\varvec{t}} = {\varvec{h}}, {\varvec{t}} \ge {\varvec{0}} \\ \Leftrightarrow&\min \limits _{{\varvec{t}} \in \mathbb {R}^{nm}} ~ ({\varvec{u}} + {\varvec{v}} z + {\varvec{w}} z^2)^\top {\varvec{t}} ~ ~ \text {s.t.} ~ ~ S {\varvec{t}} = {\varvec{h}}, {\varvec{t}} \ge {\varvec{0}}, \end{aligned}$$

where

$$\begin{aligned} {\varvec{u}}&= (\varOmega {\varvec{a}}) \circ (\varOmega {\varvec{a}}),\\ {\varvec{v}}&= (\varOmega {\varvec{a}}) \circ (\varOmega {\varvec{b}}) + (\varOmega {\varvec{b}}) \circ (\varOmega {\varvec{a}}), \\ {\varvec{w}}&= (\varOmega {\varvec{b}}) \circ (\varOmega {\varvec{b}}), \end{aligned}$$

and S and \({\varvec{h}}\) are the same as in (7). By fixing \(\mathcal {M}_\mathrm{{obs}}\) as the optimal basic index set, the relative cost vector w.r.t to the set of non-basic variables is defines as

$$\begin{aligned} {\varvec{r}}_{\mathcal {M}^c_\mathrm{{obs}}} = \tilde{{\varvec{u}}} + \tilde{{\varvec{v}}} z + \tilde{{\varvec{w}}} z^2, \end{aligned}$$

where

$$\begin{aligned} \tilde{{\varvec{u}}}&= \left( {\varvec{u}}_{\mathcal {M}^c_\mathrm{{obs}}}^\top - {\varvec{u}}_{\mathcal {M}_\mathrm{{obs}}}^\top S_{:, \mathcal {M}_\mathrm{{obs}}}^{-1} S_{:, \mathcal {M}^c_\mathrm{{obs}}} \right) ^\top , \\ \tilde{{\varvec{v}}}&= \left( {\varvec{v}}_{\mathcal {M}^c_\mathrm{{obs}}}^\top - {\varvec{v}}_{\mathcal {M}_\mathrm{{obs}}}^\top S_{:, \mathcal {M}_\mathrm{{obs}}}^{-1} S_{:, \mathcal {M}^c_\mathrm{{obs}}} \right) ^\top , \\ \text { and } ~~ \tilde{{\varvec{w}}}&= \left( {\varvec{w}}_{\mathcal {M}^c_\mathrm{{obs}}}^\top - {\varvec{w}}_{\mathcal {M}_\mathrm{{obs}}}^\top S_{:, \mathcal {M}_\mathrm{{obs}}}^{-1} S_{:, \mathcal {M}^c_\mathrm{{obs}}} \right) ^\top . \end{aligned}$$

The requirement for \(\mathcal {M}_\mathrm{{obs}}\) to be the optimal basis index set is \({\varvec{r}}_{\mathcal {M}^c_\mathrm{{obs}}} \ge {\varvec{0}}\) (i.e., the cost in minimization problem will never decrease when the non-basic variables become positive and enter the basis). Finally, the set \(\mathcal {Z}_1\) can be defined as

$$\begin{aligned} \mathcal {Z}_1&= \{ z \in \mathbb {R}\mid \mathcal {M}({\varvec{a}} + {\varvec{b}} z) = \mathcal {M}_\mathrm{{obs}}\}, \\ \mathcal {Z}_1&= \{ z \in \mathbb {R}\mid {\varvec{r}}_{\mathcal {M}^c_\mathrm{{obs}}} = \tilde{{\varvec{u}}} + \tilde{{\varvec{v}}} z + \tilde{{\varvec{w}}} z^2 \ge {\varvec{0}}\}, \end{aligned}$$

which can be obtained by solving the system of quadratic inequalities.

B Experiment on high-dimensional data

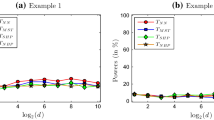
We generated the dataset \(X = \{{\varvec{x}}_{i, :} \}_{i \in [n]}\) with \({\varvec{x}}_{i, :} \sim \mathbb {N}({\varvec{1}}_d, I_d)\) and \(Y = \{{\varvec{y}}_{j, :} \}_{j \in [m]}\) with \({\varvec{y}}_{j, :} \sim \mathbb {N}({\varvec{1}}_d + \varDelta , I_d)\) (element-wise addition). We set \(n = m = 20, \varDelta = 2\), and ran 10 trials for each \(d \in \{100, 150, 200, 250\}\). The results in Fig. 10 show that the proposed method still has reasonable computational time.

Fig. 10
figure 10

Computational time of the proposed method when increasing the dimension d

Full size image

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Duy, V.N.L., Takeuchi, I. Exact statistical inference for the Wasserstein distance by selective inference. Ann Inst Stat Math 75, 127–157 (2023). https://doi.org/10.1007/s10463-022-00837-3

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10463-022-00837-3

Keywords

Search

Navigation