1 Introduction

The study of conservation laws for differential equations is beneficial to both the comprehension of the physical problem and to the analysis of the mathematical model. A conservation law relates the variation of a certain quantity within an arbitrarily small section of the space domain, to the amount of quantity that flows in and out. If the system is isolated, the total amount of the conserved quantity does not vary in the evolution of the process. The conserved quantity often has a physical meaning, such as mass, energy, momentum, electric charge. Thus, conservation laws provide further information on the physical properties of the problem with respect to the differential equation, which illustrates only the variation in time and space of a certain quantity (e.g. temperature, mass, concentration). On the side of the mathematical investigation, conservation laws represent a fundamental tool to study the existence, uniqueness and stability of analytical solutions, and to construct particular solutions of partial differential equations (PDEs).

Several mathematical techniques have been developed to construct conservation laws of classical PDEs involving integer order derivatives only, including methods based on Noether’s theorem, the direct method, the homotopy operator method, Ibragimov’s method [3, 4, 35, 52]. In addition, a great effort has been made for the numerical preservation of conservation laws [10, 13, 23, 25, 26, 44, 59] and to find structure preserving methods [6, 7, 14,15,16,17,18, 30, 34, 43, 55, 58]. Numerical methods that preserve conservation laws or the corresponding total invariants, not only have solutions that satisfy constraints that are inherited from the original problem, but also have favourable error propagation mechanisms on long term simulations [19, 22].

In the last decade, conservation laws for fractional differential problems have been derived by suitably extending some of these known methods for PDEs. In particular, techniques that rely on generalizations of Noether’s theorem and variational Lie point symmetries have been applied to find conservation laws of fractional differential equations (FDE) with a fractional Lagrangian [12, 39]. For nonlinearly self-adjoint FDEs that do not have a Lagrangian in the classical sense, a formal Lagrangian can be introduced and conservation laws are obtained by using modern techniques based on Lie group analysis of FDEs. This approach, proposed for the first time by Lukashchuk in 2015 [41], has been applied to time fractional PDEs [1, 12, 29, 36, 38,39,40,41, 47, 51] and more recently to time and space fractional PDEs (see [54, 56] and references therein).

However, to the best of our knowledge, the specialized literature still misses a study on the numerical preservation of conservation laws of fractional differential problems.

In the present paper we consider a time fractional diffusion equation. Equations of this kind have been used to investigate viscoelastic materials in mechanics [42], anomalous diffusion in complex systems [37], such as crowded liquids inside biological cells, solutions and melts of polymeric materials, lipid bilayer membranes, but also to model the dynamic behaviour of bone metastases, ion diffusion in an electrolytic cell through the electrical conductivity, diffusion in magnetic resonance imaging (MRI) of the brain, corrosion due to chloride ion diffusion in concrete structures. We refer to [57] and to the references therein for an overview on these and other applications of time fractional diffusion equations.

The purpose of this paper is threefold: finding conservation laws of the considered FDE, establishing conditions that a numerical scheme has to satisfy to have discrete counterparts of these conservation laws, proposing a numerical scheme with these conservative properties. In more details, the original contributions of this paper are as follows.

  1. 1.

    Conservation laws of diffusion equations of fractional order in time, \(\alpha \), with \(0<\alpha <1\) and \(1<\alpha <2\) have been obtained in [41]. This paper introduces sufficient conditions for identifying conservation laws of this equation for any value of \(\alpha \).

  2. 2.

    We show that if a numerical method satisfies discrete counterparts of the sufficient conditions introduced in the continuous setting, then it has discrete conservation laws that approximate the continuous ones. In the integer case, \(\alpha =1\), finite difference methods that preserve conservation laws have been introduced in [24].

  3. 3.

    We propose a mixed method that combines a finite difference scheme in space with a spectral time integrator. In particular, we consider the spectral time integrator proposed in [8] for time fractional PDEs of order \(\alpha \in (0,1)\) and extend its application to FDEs of arbitrary fractional order, \(\alpha \in (p-1,p)\), with \(p\in {\mathbb {N}}\). We show that the solutions of this method satisfy discrete versions of the conservation laws and derive their exact expressions for the two most relevant cases of subdiffusion (\(p=1\)) and superdiffusion (\(p=2\)) problems. Test examples are presented to highlight the conservation and convergence property of the scheme.

With respect to other methods for FDEs known in the literature (see e.g. [9, 20, 21, 45, 53, 60]), spectral methods present some advantages. In fact, step-by-step methods require at each time step a discretization of the long tail of the solution, arising from the hereditary nature of the fractional differential model. Thus, they are computationally expensive. Instead, spectral methods reflect the nonlocal nature of the fractional model and do not involve the discretization of the past history of the solution. Moreover, for a suitable choice of the function basis, spectral methods are exponentially convergent [62]. Within this class, we recall methods based on Chelyshkov polynomials [46, 48] and on Chebyshev polynomials [49, 50]. Pseudo-spectral methods based on fractional Lagrange or Müntz-Legendre polynomials have been introduced for the solution of time fractional PDEs, such as Fokker-Plank equation [31], Klein-Gordon equation [47], Black–Scholes equation [54], and a diffusion equation [32].

The rest of the paper is organized as follows. In Section 2, we give some basic material and definitions of fractional differential calculus that are used in the rest of the paper. In Section 3, we introduce sufficient conditions to have conservation laws in continuous and discrete settings. Section 4 generalizes the spectral time integrator in [8] to approximate Riemann-Liouville or Caputo derivatives of arbitrary order. Considering a Riemann-Liouville derivative, in Section 5, we apply this method to a finite difference discretization in space and derive its conservation laws. In Section 6, we verify the conservation laws and the accuracy of the numerical method on some numerical test examples. Finally, some conclusive remarks are drawn in Section 7.

2 Problem setting

Let us consider a time fractional diffusion PDE of the form

$$\begin{aligned} D_t^\alpha u-D_x^q K([u]_x)&=0, \end{aligned}$$
(2.1)

where the symbol \([u]_x\) denotes the function u and its integer derivatives in space and

$$\begin{aligned} p-1<\alpha <p,\qquad p,q\in {\mathbb {N}},\qquad u=u(x,t), \qquad (x,t)\in (a,b)\times (t_0,T). \end{aligned}$$

We assume that equation (2.1) is complemented by suitable Dirichlet boundary conditions,

$$\begin{aligned} u(a,t)=\chi _a(t),\qquad u(b,t)=\chi _b(t), \end{aligned}$$
(2.2)

and p initial conditions. Depending on the context, the symbol \(D_t^\alpha \) denotes either the Riemann-Liouville fractional derivative,

$$\begin{aligned} ^{\text {RL}}D_t^\alpha f=D_t^p(I_t^{p-\alpha }f), \end{aligned}$$
(2.3)

or the Caputo fractional derivative,

$$\begin{aligned} ^{\text {C}}D_t^\alpha f= \left. I_t^{p-\alpha }(D_t^p(f)),\right. \end{aligned}$$
(2.4)

where \(I_t^{p-\alpha }\) is the Riemann-Liouville integral,

$$\begin{aligned} I_t^{p-\alpha }f(x,t)=\frac{1}{\varGamma (p-\alpha )}\int _{t_0}^t\frac{f(x,\tau )}{(t-\tau )^{1-p+\alpha }}\,\mathrm {d}\tau , \end{aligned}$$

and \(\varGamma (z)\) is the Gamma function. These two definitions of fractional derivative are related by

$$\begin{aligned} ^{\text {C}}D_t^\alpha f(x,t)= {}^{\text {RL}}D_t^\alpha f(x,t) - {}^{\text {RL}}D_t^\alpha \left( \sum _{k=0}^{p-1}\frac{(t-t_0)^k}{k!}D_t^kf(x,t)_{\big \vert _{t=t_0}}\right) . \end{aligned}$$
(2.5)

Thus, if the initial configuration is of total rest the two definitions are equivalent. For more details on the theory of fractional derivatives, we refer the reader to [53].

If the fractional derivative in (2.1) is the Riemann-Liouville derivative defined by (2.3), the initial conditions assigned to (2.1) are [33]

$$\begin{aligned} D_t^{\alpha -k} u(x,t_0)=\gamma _k(x),\qquad k=0,\ldots ,p-1. \end{aligned}$$
(2.6)

Instead, if the fractional derivative is of Caputo type (2.4), the initial conditions specify the initial values of the integer derivatives

$$\begin{aligned} D_t^{k} u(x,t_0)=\gamma _k(x),\qquad k=0,\ldots ,p-1. \end{aligned}$$
(2.7)

Conservation laws for time fractional diffusion problems have been object of several papers, e.g. [12, 29, 38, 39, 41]. However, only papers [38, 41] treat equation of type (2.1) defined on a 3D and a 1D space, respectively.

3 Continuous and discrete conservation laws

3.1 Continuous setting

A conservation law of (2.1) is a total divergence,

$$\begin{aligned} D_x(F(x,t,[u]_\alpha ))+D_t(G(x,t,[u]_\alpha )), \end{aligned}$$
(3.1)

that vanishes on solutions of (2.1). Functions F and G are called the flux and the density of the conservation law (3.1), respectively. The symbol \([u]_\alpha \) denotes the function u, its fractional and integer derivatives and its fractional integrals. Differently from [41], in this paper we assume that G depends on fractional integrals of order \(p-\alpha \) only. In fact, integrals of higher order should be treated as new integral variables. Moreover, this is consistent with the limit case of \(\alpha \) integer, where F and G are assumed to depend on u and its partial derivatives but not on its integrals [52].

When the boundary conditions are conservative (e.g., periodic) integration in space of (3.1) yields,

$$\begin{aligned} D_t\int _a^b G(x,t,[u]_\alpha )\,\mathrm {d}x=0, \end{aligned}$$

therefore, the following integral,

$$\begin{aligned} \int _a^b G(x,t,[u]_\alpha )\,\mathrm {d}x, \end{aligned}$$

is a global invariant of equation (2.1). However, the local conservation law (3.1) holds true regardless of the specific boundary conditions.

The following theorem gives sufficient conditions to identify conservation laws of equation (2.1).

Theorem 1

If \(\rho (t)\) and \({\bar{G}}={{\bar{G}}}(x,t,[u]_\alpha )\) are two functions such that

$$\begin{aligned} \rho (t)D_t^\alpha u=D_t({{\bar{G}}}(x,t,[u]_\alpha )), \end{aligned}$$
(3.2)

then the quantities

$$\begin{aligned} x^k\rho (t)(D_t^\alpha u-D_x^q K([u])), \qquad k=0,\ldots , q-1. \end{aligned}$$
(3.3)

are conservation laws of (2.1).

Proof

The quantities in (3.3) all vanish when u is a solution of (2.1). Therefore, we only need to prove that these quantities can be written in the form (3.1).

Taking into account that \(\rho \) and \({\bar{G}}\) satisfy (3.2), we obtain,

$$\begin{aligned} x^k\rho (t)(D_t^\alpha u-D_x^q K([u]))=&\, D_t(x^k{{\bar{G}}}(x,t,[u]_\alpha ))-x^kD_x^q(\rho (t)K([u])), \end{aligned}$$

that, integrating by parts, can be written as a total divergence (3.1) with

$$\begin{aligned} F(x,t,[u])&=\sum _{\ell =0}^k (-1)^{\ell +1}\frac{k!}{(k-\ell )!}x^{k-\ell } D_x^{q-1-\ell }(\rho (t)K([u])),\nonumber \\ G(x,t,[u]_\alpha )&= x^k{{\bar{G}}}(x,t,[u]_\alpha ), \end{aligned}$$
(3.4)

and \(k=0,\ldots ,q-1\). \(\square \)

Corollary 1

Equation (2.1) with \(D_t^\alpha =\,^{\text {RL}}D_t^\alpha \) has at least \(p\cdot q\) conservation laws given by (3.1) where F and G are defined by (3.4) with

$$\begin{aligned} {{\bar{G}}}(x,t,[u]_\alpha )&=\sum _{i=0}^{j}(-1)^i\frac{j!}{(j-i)!}t^{j-i} D_t^{p-i-1}(I_t^{p-\alpha }u),\\ \rho (t)&= t^j,\qquad j=0,\ldots , p-1. \end{aligned}$$

Proof

It follows from the definition of Riemann-Liouville fractional derivative (2.3) that equation (2.1) is itself a conservation law. In fact, it can be written in the form (3.1) with

$$\begin{aligned} F(x,t,[u])&= -D_x^{q-1}K(u),\nonumber \\ G(x,t,[u]_\alpha )&= D_t^{p-1}(I_t^{p-\alpha }u) =\left\{ \begin{array}{ll} I_t^{1-\alpha }u,&{}\quad \text {if } p=1,\\ ^{RL}D_t^{\alpha -1}u,&{}\quad \text {if } p>1.\end{array}\right. \end{aligned}$$
(3.5)

As a consequence, Theorem 1 holds true with \(\rho (t)=1\) and \({{\bar{G}}}=G\). Hence, equation (2.1) has at least q conservation laws given in (3.3), and the statement is proved for \(p=1\). If \(p>1\),

$$\begin{aligned} \rho (t)D_t^\alpha u:= t^jD_t^\alpha u=t^jD_t^{p}(I_t^{p-\alpha }u)=D_t({{\bar{G}}}),\qquad j=1,\ldots , p-1, \end{aligned}$$
(3.6)

where the last equality is obtained after integrating by parts j times and holds true with

$$\begin{aligned} {{\bar{G}}}(x,t,[u]_\alpha )=\sum _{i=0}^{j}(-1)^i\frac{j!}{(j-i)!} t^{j-i}D_t^{p-i-1}(I_t^{p-\alpha }u), \,\quad j=1,\ldots ,p-1. \end{aligned}$$
(3.7)

Therefore, it follows from Theorem 1 that for each \(j=0,\ldots ,p-1,\) there are q conservation laws with flux and densities defined by

$$\begin{aligned} F(x,t,[u])&= \sum _{\ell =0}^k (-1)^{\ell +1}\frac{k!}{(k-\ell )!} x^{k-\ell }D_x^{q-1-\ell }(t^j K([u])),\nonumber \\ G(x,t,[u]_\alpha )&= x^k{{\bar{G}}}(x,t,[u]_\alpha ),\qquad k=0,1,\ldots ,q-1, \end{aligned}$$
(3.8)

with \({\bar{G}}\) given in (3.7), and so a total of at least \(p\cdot q\) conservation laws. \(\square \)

Remark 1

The function \({{\bar{G}}}\) in (3.7) can be equivalently written as

$$\begin{aligned} {{\bar{G}}}(x,t,[u]_\alpha )=\sum _{i=0}^{j}(-1)^i \frac{j!}{(j-i)!}t^{j-i}D_t^{\alpha -i-1}u, \end{aligned}$$

if \(j<p-1,\) or as

$$\begin{aligned} {{\bar{G}}}(x,t,[u]_\alpha )= \sum _{i=0}^{p-2}(-1)^i \tfrac{(p-1)!}{(p-i-1)!}t^{p-i-1}D_t^{\alpha -i-1}u + (-1)^{p-1}{(p-1)!}I_t^{p-\alpha }u, \end{aligned}$$

if \(j=p-1\).

Remark 2

For \(\alpha =p=1\) and \(q=2\), (3.2) and (3.3) with \(\rho (t)=1\) are the two conservation laws given in [35].

3.2 Discrete setting

In order to define a numerical approximation of (2.1) we define a uniform spatial grid with nodes,

$$\begin{aligned} x_i=a+i\varDelta x,\qquad i=0,\ldots ,M+1,\qquad \varDelta x=\frac{b-a}{M+1}. \end{aligned}$$
(3.9)

Considering that at the endpoints the solution is known from the boundary conditions (2.2), we define the vector of the approximations,

$$\begin{aligned} {\mathbf {u}}={\mathbf {u}}(t)\in {\mathbb {R}}^{M},\qquad {\mathbf {u}}_i(t)\simeq u(x_i,t),\quad i=1,\ldots ,M. \end{aligned}$$
(3.10)

We denote with \(D_{\varDelta x}\) the forward difference operator in space and with \(D^{(q)}_{\varDelta x}\) the second-order centred difference operator for the q-th derivative.

We consider here semidiscretizations of the form

$$\begin{aligned} D_t^\alpha {\mathbf {u}}-D_{\varDelta x}^{(q)}{\widetilde{K}}({\mathbf {u}})=0, \end{aligned}$$
(3.11)

where \({\widetilde{K}}\approx K\) is here arbitrary, and it can be defined in such a way to obtain accuracy in space of arbitrary order. In fact, high-order finite difference approximations of the q-th derivative are defined on larger stencils and are obtained combining \(D_{\varDelta x}^{(q)}\) with suitable averaging operators (see e.g. formulae in [2]).

Let be

$$\begin{aligned} t_0<t_1<\ldots<t_{N-1}<t_N=T, \quad t_{j+1}=t_j+\varDelta t_j, \quad j=0,\ldots ,N-1, \end{aligned}$$
(3.12)

the nodes in time and \(D_{\varDelta t_j}\) the forward difference operator with step \(\varDelta t_j\). For simplicity of notation, henceforth we omit the subscript j in the time difference operator. We denote with \(u_{i,j}\) and \(D_{\varDelta t}^\alpha u_{i,j}\) the approximations of \(u(x_i,t_j)\) and of \(D_{t}^\alpha u(x_i,t_j)\), respectively, obtained after applying a suitable time integrator to (3.11). Hence, the fully discrete scheme for (2.1) is

$$\begin{aligned} D_{\varDelta t}^\alpha u_{i,j}-D_{\varDelta x}^{(q)} {\widetilde{K}}(u_{i,j})=0. \end{aligned}$$
(3.13)

Theorem 2 will give sufficient conditions that method (3.13) has to satisfy to have discrete conservation laws in the form

$$\begin{aligned} D_{\varDelta x}{\widetilde{F}}(x_i,t_j,u_{i,j})+D_{\varDelta t}{\widetilde{G}}(x_i,t_j,u_{i,j})=0, \end{aligned}$$

where \({\widetilde{F}}\) and \({\widetilde{G}}\) are suitable discretizations of the flux and density of a selected continuous conservation law, respectively. This result is a discrete version of Theorem 1, and the main contribution in this section. For its proof, we recur to the following lemma that can be proved by straightforward calculations.

Lemma 1

For any two discrete functions f and g, the following discrete versions of Leibniz rule hold true:

$$\begin{aligned} -f_{i,j}D_{\varDelta x}^{(1)}g_{i,j}&= g_{i,j}D_{\varDelta x}^{(1)}f_{i,j} +D_{\varDelta x}(-\tfrac{1}{2}(f_{i-1,j}g_{i,j}+f_{i,j}g_{i-1,j})), \end{aligned}$$
(3.14)
$$\begin{aligned} -f_{i,j}D_{\varDelta x}^{(2)}g_{i,j}&= -g_{i,j}D_{\varDelta x}^{(2)}f_{i,j} +D_{\varDelta x}(\tfrac{1}{\varDelta x}(f_{i,j}g_{i-1,j}-f_{i-1,j}g_{i,j})). \end{aligned}$$
(3.15)

Moreover, for \(q>2\),

$$\begin{aligned} -f_{i,j}D_{\varDelta x}^{(q)}g_{i,j}=-(-1)^q g_{i,j}D_{\varDelta x}^{(q)}f_{i,j}+D_{\varDelta x}({\widetilde{F}}),\ \end{aligned}$$

where the function \({{\widetilde{F}}}\) is obtained by iterating (3.15) \(\lambda \) times, if \(q=2\lambda \), or (3.15) \(\lambda \) times and (3.14) once, if \(q=2\lambda +1\).

Theorem 2

For all \(\rho (t_j)\) and \({\bar{G}}={\bar{G}}(x_i,t_j,u_{i,j})\) such that

$$\begin{aligned} \rho (t_j)D_{\varDelta t}^\alpha u_{i,j}=D_{\varDelta t}({\bar{G}}(x_i,t_j,u_{i,j})), \end{aligned}$$
(3.16)

the quantities

$$\begin{aligned} x_i^k\rho (t_j)(D_{\varDelta t}^\alpha u_{i,j}-D_{\varDelta x}^{(q)} {{\widetilde{K}}}(u_{i,j})), \qquad k=0,\ldots , q-1, \end{aligned}$$
(3.17)

are conservation laws of (3.13) at the point \((x_i,t_j)\) that approximate their continuous counterparts with the same accuracy of the method.

Proof

The proof follows along similar lines as that of Theorem 1. Multiplying method (3.13) by \(x_i^k\rho (t_j)\), with \(k=0,1,\ldots ,q-1\), yields

$$\begin{aligned} x_i^k\rho (t_j)(D_{\varDelta t}^\alpha u_{i,j}-D_{\varDelta x}^{(q)}{\widetilde{K}}(u_{i,j})). \end{aligned}$$
(3.18)

These quantities clearly vanish on solutions of (3.13). Moreover, considering (3.16) and Lemma 1,

$$\begin{aligned}&x_i^k\rho (t_j)(D_{\varDelta t}^\alpha u_{i,j} - D_{\varDelta x}^{(q)} {\widetilde{K}}(u_{i,j})) \\&\quad = D_{\varDelta t}(x_i^k{\bar{G}}(x_i,t_j,u_{i,j})) - x_i^kD_{\varDelta x}^{(q)}(\rho (t_j){\widetilde{K}}(u_{i,j}))\\&\quad = D_{\varDelta t}(x_i^k{\bar{G}}(x_i,t_j,u_{i,j})) -((-1)^q D_{\varDelta x}^{(q)}x_i^k)\rho (t_j){{\widetilde{K}}}(u_{i,j}) + D_{\varDelta x}({{\widetilde{F}}}(x_i,t_j,u_{i,j})). \end{aligned}$$

Then, as the spatial grid is uniform and \(k<q\),

$$\begin{aligned} x_i^k\rho (t_j)(D_{\varDelta t}^\alpha u_{i,j}-D_{\varDelta x}^{(q)} {{\widetilde{K}}}(u_{i,j}))=D_{\varDelta t}({{\widetilde{G}}})+D_{\varDelta x}({{\widetilde{F}}}), \end{aligned}$$

where \({{\widetilde{G}}}=x_i^k{\bar{G}}\) and \({{\widetilde{F}}} \approx F\) in (3.4). As the function \(x_i^k\rho (t_j)\) is exactly evaluated at the nodes, a conservation law in the form (3.17) approximates its continuous limit (3.3) with the same accuracy of the scheme. \(\square \)

4 The time integrator

Given the space discretization (3.11), we perform the time integration by using the spectral method introduced in [8] for fractional problems of order \(\alpha \) with \(0<\alpha <1\). This method is here generalized to deal with equations of arbitrary fractional order. We separate the treatment of equations with fractional derivative satisfying Riemann-Liouville or Caputo definition with a focus on the particular case of zero initial conditions.

4.1 Riemann-Liouville fractional derivative

When the fractional derivative \(D_t^\alpha \) in (2.1) is the Riemann-Liouville derivative defined by (2.3), we look for time approximations of the solution (3.10) and of the initial conditions (2.6) at the node \(x_i\), in the form

$$\begin{aligned} u_N^i(t)&= \sum _{j=0}^{N+p} {{\hat{u}}}_j^i{\mathcal {P}}_j(t), \end{aligned}$$
(4.1)
$$\begin{aligned} D_t^{\alpha -k} u_N^i(t_0)&= \sum _{j=0}^{N+p} {{\hat{u}}}_j^iD_t^{\alpha -k} {\mathcal {P}}_j(t_0)=\gamma _k(x_i),\qquad k=0,\ldots ,p-1, \end{aligned}$$
(4.2)

respectively, where \(\{{\mathcal {P}}_j(t)\}_{j=0}^{N+p}\) is a suitable functional basis and \({{\hat{u}}}_j^i\) are unknown coefficients.

By considering the set of collocation points (3.12), we can equivalently write equation (4.1) as

$$\begin{aligned} u_N^i(t)=\sum _{k=0}^{N} \varphi _k(t)u_N^i(t_k)+\sum _{k=0}^{p-1}\varphi _{N+k+1}(t)\gamma _{k}(x_i), \end{aligned}$$
(4.3)

where the functions \(\varphi _k(t)\) are unknown. By defining

$$\begin{aligned} \psi _k(t)=D_t^\alpha \varphi _k(t),\qquad k=0,\ldots ,N+p, \end{aligned}$$

expansion (4.3) gives the following approximation of the time fractional derivative of \({\mathbf {u}}_i\) defined in (3.10) at the collocation points:

$$\begin{aligned} D_t^\alpha {\mathbf {u}}_i(t_j)&\approx D_t^\alpha u_N^i(t_j)\nonumber \\&=\sum _{k=0}^{N}\psi _k(t_j)u_N^i(t_k)+\sum _{k=0}^{p-1}\psi _{N+k+1}(t_j) \gamma _k(x_i)=: D_{\varDelta t}^\alpha u_{i,j}. \end{aligned}$$
(4.4)

In order to determine the functions \(\psi _k(t)\), and so to practically compute approximation (4.4), we define the following two vectors in \({\mathbb {R}}^{N+p+1}\),

$$\begin{aligned} {{\mathbf {u}}}_N^i&=\left( u_N^i(t_0),\ldots ,u_N^i(t_N),\gamma _0(x_i), \ldots ,\gamma _{p-1}(x_i)\right) ^T,\\ \hat{{\mathbf {u}}}^i&=\left( {{\hat{u}}}^i_0,\ldots ,{{\hat{u}}}_{N+p}^i\right) ^T, \end{aligned}$$

the matrices of dimension \(N+p+1\),

$$\begin{aligned} A=\left( \begin{array}{c} A_1\\ A_2 \end{array}\right) ,\qquad B=A^{-1}, \end{aligned}$$
(4.5)

with

$$\begin{aligned} {A}_1 = \left( \begin{array}{ccc} {\mathcal {P}}_0(t_0) &{} \cdots &{} {\mathcal {P}}_{N+p}(t_0)\\ \vdots &{} &{} \vdots \\ {\mathcal {P}}_0(t_N) &{} \cdots &{} {\mathcal {P}}_{N+p}(t_N) \end{array}\right) , \ {A}_2 = \left( \begin{array}{ccc} D_t^\alpha {\mathcal {P}}_0(t_0) &{} \cdots &{} D_t^{\alpha } {\mathcal {P}}_{N+p}(t_0)\\ \vdots &{} &{} \vdots \\ D_t^{\alpha -p+1} {\mathcal {P}}_0(t_0) &{} \cdots &{} D_t^{\alpha -p+1} {\mathcal {P}}_{N+p}(t_0)\\ \end{array}\right) , \end{aligned}$$

and the matrices

$$\begin{aligned} C=\left( \begin{array}{ccc} \psi _0(t_0) &{} \cdots &{} \psi _{N+p}(t_0)\\ \vdots &{} &{} \vdots \\ \psi _0(t_N) &{} \cdots &{} \psi _{N+p}(t_N) \end{array}\right) , \ {\mathcal {P}}=\left( \begin{array}{ccc} D_t^\alpha {\mathcal {P}}_0(t_0) &{} \cdots &{} D_t^\alpha {\mathcal {P}}_{N+p}(t_0)\\ \vdots &{} &{} \vdots \\ D_t^\alpha {\mathcal {P}}_0(t_N) &{} \cdots &{} D_t^\alpha {\mathcal {P}}_{N+p}(t_N) \end{array}\right) . \end{aligned}$$
(4.6)

Proposition 1

Matrix C can be computed as

$$\begin{aligned} C=\mathcal PB. \end{aligned}$$
(4.7)

Proof

By evaluating (4.1) at the nodes \(t_\ell \), with \(\ell =0,\ldots ,N\), we obtain a set of \(N+1\) equations that together with (4.2) forms an algebraic system that can be equivalently written as

$$\begin{aligned} {{\mathbf {u}}}_N^i=A\hat{{\mathbf {u}}}^i, \end{aligned}$$

therefore,

$$\begin{aligned} \hat{{\mathbf {u}}}^i=B{{\mathbf {u}}}_N^i, \end{aligned}$$

or, entry-wise,

$$\begin{aligned} {{\hat{u}}}^i_j=\sum _{k=0}^N B_{j+1,k+1}u_N^i(t_k)+\sum _{k=0}^{p-1} B_{j+1,N+k+2}\gamma _{k}(x_i),\qquad j=0,\ldots ,N+p. \end{aligned}$$

Substituting in (4.1),

$$\begin{aligned} u_N^i(t)&=\sum _{j=0}^{N+p} {\mathcal {P}}_j(t)\left( \sum _{k=0}^N B_{j+1,k+1}u_N^i(t_k)+\sum _{k=0}^{p-1}B_{j+1,N+k+2}\gamma _k(x_i)\right) \nonumber \\&=\sum _{k=0}^N\left( \sum _{j=0}^{N+p} B_{j+1,k+1}{\mathcal {P}}_j(t) \right) u_N^i(t_k) + \sum _{k=0}^{p-1}\left( \sum _{j=0}^{N+p}B_{j+1,N+k+2} {\mathcal {P}}_j(t) \right) \gamma _{k}(x_i). \end{aligned}$$
(4.8)

Comparing (4.3) and (4.8), we find that

$$\begin{aligned} \varphi _k(t)=\sum _{j=0}^{N+p} B_{j+1,k+1}{\mathcal {P}}_j(t), \qquad k=0,\ldots , N+p, \end{aligned}$$

and, differentiating,

$$\begin{aligned} \psi _k(t)=D_t^\alpha \varphi _k(t)=\sum _{j=0}^{N+p} B_{j+1,k+1}D_t^\alpha {\mathcal {P}}_j(t), \qquad k=0,\ldots , N+p. \end{aligned}$$
(4.9)

The values \(\psi _k(t_\ell )\) are then obtained as

$$\begin{aligned} \psi _k(t_\ell )=\sum _{j=0}^{N+p} B_{j+1,k+1}D_t^\alpha {\mathcal {P}}_j(t_\ell ), \qquad k=0,\ldots , N+p, \quad \ell =0,\ldots ,N.\nonumber \\ \end{aligned}$$
(4.10)

Equation (4.7) follows immediately. \(\square \)

Note that in order to compute \(\psi _k(t_j)\) in (4.10) we only need the values of the chosen basis \(\{{\mathcal {P}}_\ell (t)\}_{\ell =0}^{N+p}\) and its fractional derivatives at the collocation points. Therefore, the basis should be chosen such that it is easy to compute these fractional derivatives.

The fully discrete scheme for (2.1) is in the form (3.13) with the approximation of the fractional derivative (4.4) and

$$\begin{aligned} u_{i,j}:=u_N^i(t_j). \end{aligned}$$

Let us consider matrix C defined in (4.6) and let be \(C=[C_1,C_2]\), with \(C_1\) a square matrix of dimension \(N+1\) and \(C_2\) of dimension \( (N+1)\times p\). The numerical method can be written in matrix form as

$$\begin{aligned} C_1U=\frac{1}{\varDelta x^2}({\widetilde{K}}(U){\mathcal {M}}+{\mathcal {F}})-C_2\gamma , \end{aligned}$$
(4.11)

where the entries of \(U\in {\mathbb {R}}^{(N+1)\times M}\) and \(\gamma \in {\mathbb {R}}^{p\times M}\) are

$$\begin{aligned}&U_{k,i}=u_{i,k-1}, \quad \gamma _{\ell ,i}=\gamma _{\ell -1}(x_i),\quad k=1,\ldots ,N+1, \ i=1,\ldots ,M, \ \ell =1,\ldots p, \end{aligned}$$

respectively, matrix \({\widetilde{K}}(U)\) is obtained by applying \({\widetilde{K}}\) to the entries of matrix U, and

$$\begin{aligned} {\mathcal {M}}=\left( \begin{array}{ccccc} -2 &{} 1 &{} &{}&{} \\ 1 &{} -2 &{} 1 &{}&{}\\ &{}\ddots &{} \ddots &{} \ddots &{}\\ &{}&{}1 &{} -2 &{} 1 \\ &{}&{} &{} 1 &{}-2\end{array}\right) ,\quad {\mathcal {F}}=\left( \begin{array}{ccccc} {\widetilde{K}}(\chi _a(t_0)) &{} 0 &{}\ldots &{} 0 &{} {\widetilde{K}}(\chi _b(t_0))\\ \vdots &{} \vdots &{} &{}\vdots &{} \vdots \\ {\widetilde{K}}(\chi _a(t_N)) &{} 0 &{}\ldots &{} 0 &{} {\widetilde{K}}(\chi _b(t_N))\end{array}\right) , \end{aligned}$$

are matrices in \({\mathbb {R}}^{M\times M}\) and \({\mathbb {R}}^{(N+1)\times M},\) respectively.

Remark 3

In particular cases, the basis \(\{{\mathcal {P}}_j(t)\}_j\) can be chosen such that \(r\le p\) initial conditions (2.6) are satisfied by definition and do not need to be enforced on \(u_N^i\). In these cases, approximation (4.1) is taken in a projection space of dimension \(N+p+1-r\). Similarly, approximation (4.3) is replaced with

$$\begin{aligned} u_N^i(t)=\sum _{k=0}^{N} \varphi _k(t)u_N^i(t_k)+\sum _{k=0}^{p-1-r}\varphi _{N+k+1}(t)\gamma _{k}(x_i), \end{aligned}$$

where (after a suitable reordering of the indexes) the second sum includes only the values \(\gamma _k\) of the initial conditions to be imposed. Matrices A and B in (4.5) have then reduced dimension \(N+p+1-r\), and \({\mathcal {P}}\) in (4.6) has dimension \((N+1)\times (N+p+1-r)\). System (4.11) has still dimension \((N+1)\times M\) but matrices \(C_2\) and \(\gamma \) have dimension \((N+1)\times (p-r) \) and \((p-r)\times M\), respectively.

4.2 Caputo fractional derivative

We now adapt the method introduced in Section 4.1 to problems in the form (2.1) with the Caputo fractional derivative defined by (2.4). In this case the initial conditions are given by (2.7). In particular, the initial value of u at \(t=t_0\) is known, and in order to obtain a compatible system the approximated solution must be taken in a space of reduced dimension \(N+p\).

Therefore, equations (4.1) and (4.2) are replaced with

$$\begin{aligned} u_N^i(t)&=\sum _{j=0}^{N+p-1} {{\hat{u}}}_j^i{\mathcal {P}}_j(t), \end{aligned}$$
(4.12)
$$\begin{aligned} D_t^{k} u_N^i(t_0)&= \sum _{j=0}^{N+p-1} {{\hat{u}}}_j^iD_t^{k}{\mathcal {P}}_j(t_0)=\gamma _k(x_i),\qquad k=0,\ldots ,p-1, \end{aligned}$$
(4.13)

respectively. With collocation points,

$$\begin{aligned} t_1<\ldots <t_N=T,\qquad t_{j+1}=t_j+\varDelta t_j, \qquad j=1,\ldots ,N-1, \end{aligned}$$

equation (4.12) is equivalently written as

$$\begin{aligned} u_N^i(t)=\sum _{k=1}^{N} \varphi _k(t)u_N^i(t_k)+\sum _{k=0}^{p-1}\varphi _{N+k+1}(t)\gamma _{k}(x_i), \end{aligned}$$
(4.14)

where functions \(\varphi _k\) are unknown. Defining

$$\begin{aligned} \psi _k(t)=D_t^\alpha \varphi _k(t),\qquad k=1,\ldots ,N+p, \end{aligned}$$

the approximation of the fractional derivative is then given by

$$\begin{aligned} D_t^\alpha {\mathbf {u}}_i(t_j)\approx D_t^\alpha u_N^i(t_j)=\sum _{k=1}^{N}\psi _k(t_j)u_N^i(t_k)+\sum _{k=0}^{p-1} \psi _{N+k+1}(t_j)\gamma _k(x_i)=: D_{\varDelta t}^\alpha u_{i,j}.\nonumber \\ \end{aligned}$$
(4.15)

Following similar steps as in Section 4.1, the values

$$\begin{aligned} \psi _k(t_j),\qquad k=1,\ldots , N+p, \qquad j=1,\ldots ,N, \end{aligned}$$

can be obtained by solving (4.7) where matrices C and \({\mathcal {P}}\) have now dimension \(N\times (N+p)\) and are defined by deleting the first row and the first column and the first row and the last column, from the corresponding matrices in (4.6), respectively. Matrix B has dimension \((N+p)\times (N+p)\) and is defined as in (4.5) after removing from A the first row and the last column.

By splitting matrix C as \(C=[C_1,C_2]\) where \(C_1\) and \(C_2\) have dimension \(N\times N\) and \(N\times p\), respectively, and defining \(U\in {\mathbb {R}}^{N\times M}\) with entries \(U_{k,i}=u_N^i(t_k),\) \(k=1,\ldots ,N\), \(i=1,\ldots ,M\), the numerical method can be written in matrix form as

$$\begin{aligned} C_1 U=\frac{1}{\varDelta x^2}({\widetilde{K}}(U){\mathcal {M}}+{\mathcal {F}})-C_2\gamma , \end{aligned}$$
(4.16)

where \({\mathcal {M}}\), \(\gamma \) and \({\widetilde{K}}(U)\) are defined as in (4.11) and

$$\begin{aligned} {\mathcal {F}}=\left( \begin{array}{ccccc} {\widetilde{K}}(\chi _a(t_1)) &{} 0 &{}\ldots &{} 0 &{} {\widetilde{K}}(\chi _b(t_1))\\ \vdots &{} \vdots &{} &{}\vdots &{} \vdots \\ {\widetilde{K}}(\chi _a(t_N)) &{} 0 &{}\ldots &{} 0 &{} {\widetilde{K}}(\chi _b(t_N))\end{array}\right) \in {\mathbb {R}}^{N\times M}. \end{aligned}$$

We observe that the dimension of system (4.16) is lower than that of system (4.11).

Remark 4

If the basis \(\{{\mathcal {P}}_j(t)\}_j\) is chosen such that \(r\le p\) initial conditions (2.6) are satisfied by \(u_N^i\) a similar discussion as in Remark 3 holds considering a projection space of dimension \(N+p-r\).

4.2.1 The case of zero initial conditions

When the initial conditions are of total rest, i.e.,

$$\begin{aligned} D_t^k u(x,t_0)=0,\qquad k=0,\ldots p-1, \end{aligned}$$
(4.17)

the definitions of Caputo and Riemann-Liouville fractional derivative are equivalent. Since in this special case \(\gamma _k(x_i)=0\), approximation (4.15) reduces to

$$\begin{aligned} D_t^\alpha {\mathbf {u}}_i(t_j)\approx D_t^\alpha u_N^i(t_j)=\sum _{k=1}^{N}\psi _k(t_j)u_N^i(t_k)=: D_{\varDelta t}^\alpha u_{i,j}, \end{aligned}$$

and so only the values of \(\psi _k(t_j)\) for \(k=1\ldots ,N,\) and \(j=1\ldots ,N\) need to be calculated. The matrix form of the numerical method (4.16) reduces to

$$\begin{aligned} C_1 U=\frac{1}{\varDelta x^2}({\widetilde{K}}(U){\mathcal {M}}+{\mathcal {F}}), \end{aligned}$$
(4.18)

and so it is not necessary to calculate matrix \(C_2\). Matrix \(C_1\) is obtained from

$$\begin{aligned} C_1={{\mathcal {P}}} {{\bar{B}}}, \end{aligned}$$

where \({{\bar{B}}}\) is obtained removing from matrix B the last p columns.

Note that although the computation of the inverse of matrix A, having dimension \(N+p\), is still required, system (4.18) has reduced dimension, N.

Remark 5

The basis

$$\begin{aligned} \{{\mathcal {P}}_j(t)\}=\{(t-t_0)^{j\alpha }\}, \end{aligned}$$
(4.19)

identically satisfies all the initial conditions (4.17) for \(k=1,\ldots ,p-1,\) and so Remark 4 applies. In this case, then, matrix A has dimension \(N+1\).

5 Conservation laws of the fractional diffusion equation

Here and henceforth we consider equation (2.1) with \(q=2\) and Riemann-Liouville fractional derivative.

Although, as seen in Section 4, the general discussion holds for methods of arbitrary order in space, in order to give some specific results and explicit formulae of the preserved conservation laws, we focus here on second-order accurate schemes. Therefore, henceforth we set \({\widetilde{K}}=K\) and method (3.13) reduces to

$$\begin{aligned} D_{\varDelta t}^\alpha u_{i,j}-D_{\varDelta x}^{(2)} {K}(u_{i,j})=0. \end{aligned}$$
(5.1)

As stated in Corollary 1, when the fractional derivative is defined according to the definition of Riemann-Liouville there are always at least two conservation laws. The first one is equivalent to equation (2.1) and it is defined by (see (3.5))

$$\begin{aligned} F_1(x,t,u)=-D_x K(u),\qquad G_1(x,t,u)=D_t^{p-1}I_t^{p-\alpha }u. \end{aligned}$$
(5.2)

The second one is defined by (3.8) with \(k=1\) and \({\bar{G}}=G_1\), yielding,

$$\begin{aligned} F_2(x,t,u)= K(u)-xD_xK(u),\qquad G_2(x,t,u)=x G_1. \end{aligned}$$
(5.3)

We prove that method (5.1) preserves these conservation laws for any value of \(\alpha \) and p, and give their conserved approximations. According to Theorem 2, it suffices to prove (3.16), i.e. to find \({\widetilde{G}}_1\approx G_1\) such that

$$\begin{aligned} D_{\varDelta t}^\alpha u_{i,j}=D_{\varDelta t}({\widetilde{G}}_1(x_i,t_j,u_{i,j})). \end{aligned}$$
(5.4)

By integrating both sides in (2.3), we have

$$\begin{aligned} G_1(x,t,u)=D_t^{p-1}I_{t}^{p-\alpha }u(x,t)=\int _{t_0}^{t}D_\tau ^\alpha u(x,\tau )\,\mathrm {d}\tau . \end{aligned}$$

We define then

$$\begin{aligned} {{\widetilde{G}}}_1(x_i,t_{j},u_{i,j})=\varDelta t \sum _{\ell =0}^{j-1} D_{\varDelta t}^{\alpha }u_{i,\ell }, \end{aligned}$$
(5.5)

so that (5.4) is satisfied. Following the steps in the proof of Theorem 2, the remaining functions that define the two discrete conservation laws are

$$\begin{aligned} {\widetilde{F}}_1(x_i,t_{j},u_{i,j})=-D_{\varDelta x}{K}(u_{i-1,j}), \end{aligned}$$
(5.6)

and (see (3.15)),

$$\begin{aligned} {\widetilde{F}}_2(x_i,t_{j},u_{i,j})&= \displaystyle \,\tfrac{1}{\varDelta x} (x_iK(u_{i-1,j})-x_{i-1}K(u_{i,j})) \nonumber \\&= A_{\varDelta x}{K}(u_{i-1,j})A_{\varDelta x}(x_{i-1})D_{\varDelta x}K(u_{i-1,j}),\nonumber \\ {\widetilde{G}}_2(x_i,t_{j},u_{i,j})&= x_i{\widetilde{G}}_1(x_i,t_{j},u_{i,j}), \end{aligned}$$
(5.7)

respectively, where \(A_{\varDelta x}\) denotes the forward average operator,

$$\begin{aligned} A_{\varDelta x}(f(u_{i,j}))=\frac{f(u_{i+1,j})+f(u_{i,j})}{2}=f(u(x_i+\tfrac{\varDelta x}{2},t_j))+{\mathcal {O}}(\varDelta x^2). \end{aligned}$$

In the rest of this section, we focus on the two cases of subdiffusion and superdiffusion equations obtained setting \(p=1\) and \(p=2\), respectively. The continuous and discrete conservation laws obtained are listed in Table 1.

5.1 Subdiffusion-wave equation

When \(0<\alpha <1=p\) equation (2.1) defines a subdiffusion problem. Using Theorem 1 and Corollary 1 we can obtain only the two conservation laws defined by (5.2) and (5.3). Indeed, these two are the only independent conservation laws of the subdiffusion-wave equation in the generic form (2.1) with Riemann-Liouville fractional derivative [41]. As shown, for any value of p, method (5.1) has discrete counterparts of these conservation laws, defined by (5.5)–(5.7). Some extra conservation laws are given in [41] for special choices of the function K in (2.1), but these depend on integrals whose order is larger than \(p-\alpha \) that is a case that we do not consider in this paper.

5.2 Superdiffusion equation

Let us consider now the superdiffusion equation defined by (2.1) with \(1<\alpha <2=p\). In this case, according to Corollary 1, conservation laws are obtained from (3.3) with

$$\begin{aligned} \rho (t)=1\qquad \rho (t)=t, \end{aligned}$$

yielding four independent conservation laws. The first two are again (5.2) and (5.3) and these are preserved by method (5.1). The other two conservation laws are defined with (see (3.7)–(3.8)),

$$\begin{aligned} F_3(x,t,u)=-tD_xK(u),\qquad G_3(x,t,u)=tD_t^{\alpha -1}u-I_t^{2-\alpha }u, \end{aligned}$$
(5.8)

and

$$\begin{aligned} F_4(x,t,u)=tK(u)-xtD_xK(u),\qquad G_4(x,t,u)=xtD_t^{\alpha -1}u-xI_t^{2-\alpha }u. \end{aligned}$$
(5.9)

The density function in (5.8) can be equivalently written as,

$$\begin{aligned} G_3(x,t,u)=tG_1(x,t,u)-\int _{t_0}^tG_1(x,z,u)\,\mathrm {d}z. \end{aligned}$$

In fact, for \(p=2\),

$$\begin{aligned} D_t^{\alpha -1}u=D_tI_t^{2-\alpha }u=G_1(x,t,u), \end{aligned}$$

and integrating twice the Riemann-Liouville fractional derivative (2.3) yields,

$$\begin{aligned} I_t^{2-\alpha }u=\int _{t_0}^t\int _{t_0}^z D_\tau ^\alpha u(x,\tau )\,\mathrm {d}\tau \,\mathrm {d}z=\int _{t_0}^tG_1(x,z,u)\,\mathrm {d}z. \end{aligned}$$

We show that (3.16) is satisfied by the solutions of (5.1) with

$$\begin{aligned} \rho (t_j)=t_j,\quad {\bar{G}}={\widetilde{G}}_3(x_i,t_j,u_{i,j})=t_j{\widetilde{G}}_1(x_i,t_j,u_{i,j})-\varDelta t\sum _{r=0}^{j} {{\widetilde{G}}}_1(x_i,t_r,u_{i,r}),\nonumber \\ \end{aligned}$$
(5.10)

where \({\widetilde{G}}_1(x_i,t_j,u_{i,j})\) is given in (5.5). In fact, equation (5.4) yields

$$\begin{aligned} t_jD_{\varDelta t}^\alpha u_{i,j}&= t_jD_{\varDelta t}{{\widetilde{G}}}_1 (x_i,t_{j},u_{i,j}) = D_{\varDelta t}(t_j {{\widetilde{G}}}_1(x_i,t_{j},u_{i,j})) - {{\widetilde{G}}}_1(x_i,t_{j+1},u_{i,j+1})\\&=D_{\varDelta t}({{\widetilde{G}}}_3(x_i,t_{j},u_{i,j})). \end{aligned}$$

Therefore, it follows from Theorem 2 that method (5.1) has other two conservation laws that approximate (5.8) and (5.9), and that are defined by \({\widetilde{G}}_3\) in (5.10), and

$$\begin{aligned}&{\widetilde{F}}_3(x_i,t_j,u_{i,j})=-t_jD_{\varDelta x} ({K}(u_{i,j})),\qquad {\widetilde{F}}_4(x_i,t_{j},u_{i,j})=t_j{\widetilde{F}}_2(x_i,t_{j},u_{i,j}),\\&{\widetilde{G}}_4(x_i,t_{j},u_{i,j})=x_i{\widetilde{G}}_3(x_i,t_{j},u_{i,j}). \end{aligned}$$
Table 1 Continuous and discrete conservation laws
Full size table

6 Numerical tests

In this section we solve problem (2.1) with two different choices of function K that define a linear and a nonlinear problem, respectively. In both cases we set \(q=2\) and \((x,t)\in (0,1)\times (0,2)\), and we study the two cases of subdiffusion (\(p=1\)) and superdiffusion (\(p=2\)). We consider the boundary conditions

$$\begin{aligned} u(0,t)=u(1,t)=\frac{t^p}{p},\qquad t\in [0,2], \end{aligned}$$
(6.1)

and an initial configuration of total rest (4.17), i.e., if \(0<\alpha <1\) (subdiffusion case),

$$\begin{aligned} u(x,0)=0, \end{aligned}$$
(6.2)

whereas, if \(1<\alpha <2\) (superdiffusion case),

$$\begin{aligned} u(x,0)=\frac{\partial }{\partial t} u(x,0)=0. \end{aligned}$$
(6.3)

Therefore, the fractional derivative in (2.1) is equivalently defined by either equation (2.3) or equation (2.4).

The space grid is defined as in (3.9) with \(\varDelta x=0.005\), that is small enough to study the rate of convergence in time of the method. Inspired by [8] and by the spectral theory developed for the fractional Sturm-Liouville problem in [61], we choose the time nodes \(t_j\) equal to the Chebyshev nodes in [0, 2] and the basis \({\mathcal {P}}_j\) in (4.1)–(4.2) defined by the Jacobi polynomials in [0, 2] (see [5]),

$$\begin{aligned} {\mathcal {P}}_j(t)=P_{2,j}^{(0,p)}=\sum _{k=0}^j\frac{(-1)^{j+k} (j+k+p)!}{(k+p)!(j-k)!k!2^k}t^k, \qquad j=0,\ldots , N+p. \end{aligned}$$

Different choices, such as uniform nodes and the power basis (4.19), can also be considered. However, in the experiments below, choosing Chebyshev nodes and the Jacobi basis yields a matrix \(C_1\) in (4.18) with lower condition number and a faster rate of convergence, respectively.

6.1 Linear problem

We consider here the linear fractional PDE defined by (2.1) with \(K(u)=u\), i.e.,

$$\begin{aligned} D_t^\alpha u-D_x^2 u=0. \end{aligned}$$
(6.4)

The exact solution satisfying the boundary conditions (6.1) and the initial conditions (6.2) or (6.3) is given in [11] and amounts to

$$\begin{aligned} u_{\text {exact}}(x,t)&= \sum _{n=1}^\infty a_N(x,t)\\&= \sum _{n=1}^\infty \frac{-4t^p}{(2n-1)\pi }\sin {\left( (2n-1)\pi x\right) }E_{\alpha ,p+1}(-(2n-1)^2\pi ^2t^\alpha )+\frac{t^p}{p},\nonumber \end{aligned}$$
(6.5)

where

$$\begin{aligned} E_{\alpha ,\beta }(z)=\sum _{k=0}^\infty \frac{z^k}{\varGamma (\alpha k+\beta )}, \end{aligned}$$

is the Mittag-Leffler function with two parameters. A reference solution, \({\bar{u}}\), is calculated by truncating the infinite sum in (6.5) after R terms, where R is the smallest integer such that \(\Vert a_R\Vert <\text {tol} = 10^{-12}\), and by computing the Mittag-Leffler function using the Matlab routine \(\texttt {ml}\) [27, 28].

In order to show the convergence of the proposed numerical scheme, its spectral accuracy and its conservative properties, the error in the numerical solution and in the discrete conservation laws are calculated as

$$\begin{aligned} \text {Sol err}=\max _i\max _j \vert u_{i,j}-{{\bar{u}}}(x_i,t_j)\vert , \end{aligned}$$

and

$$\begin{aligned} \text {Err}_\ell =\max _i\max _j \vert D_{\varDelta t}{\widetilde{G}}_\ell (x_i,t_j,u_{i,j})+D_{\varDelta x}{\widetilde{F}}_\ell (x_i,t_j,u_{i,j})\vert , \quad \ell =1,\ldots ,p\cdot q, \end{aligned}$$
(6.6)

with functions \({{\widetilde{F}}}_\ell \) and \({{\widetilde{G}}}_\ell \) defined in Section 5.

Table 2 Linear problem
Full size table

In Table 2 we show the error in the solution and conservation laws given by method (5.1) with \(N=10\) applied to (6.4). We consider three different values of \(\alpha \) corresponding to subdiffusion problems. Two of these values are close to the integer cases (\(\alpha =0.1\) and \(\alpha =0.9\)). The third is an intermediate value (\(\alpha =0.5\)). Similarly, we consider three different superdiffusion problems (\(\alpha =1.1,1.5,1.9\)). The error in the solution is larger for values of \(\alpha \) that are closer to p. In all cases the error in the conservation laws is only due to the roundoffs. In particular, we verified that the errors in the conservation laws are comparable in magnitude to the residual of equation (4.18).

Fig. 1
figure 1

Linear problem. Numerical solution with \(N=10\), \(\varDelta x=0.005\), \(\alpha =0.5\) (left) and \(\alpha =1.5\) (right)

Full size image
Fig. 2
figure 2

Linear problem. Rate of convergence in time. \(\varDelta x=0.005\) (logarithmic scale on y-axis)

Full size image

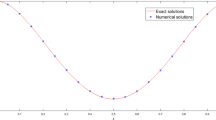
In Fig. 1 we show the solutions of method (5.1) with \(\alpha =0.5\) and \(\alpha =1.5\). These two graphs very well reproduce the behaviour of the exact solution shown in [11].

In Figure 2 we study the convergence of the method by plotting the logarithm of the error in the solution against N for \(N=2,\ldots ,18\). These graphs show that the convergence of the method is exponential in time.

6.2 Nonlinear problem

We consider now equation (2.1) with \(K(u)=\sqrt{u}\), therefore we solve equation

$$\begin{aligned} D_t^\alpha u-D_x^2 (\sqrt{u})=0, \end{aligned}$$
(6.7)

with boundary conditions (6.1) and initial conditions (6.2) if \(0< \alpha <1\) or (6.3) if \(1<\alpha <2\).

The exact solution of this problem is not known, and so we compute a reference solution, \({\bar{u}}\), setting \({{\bar{N}}}=13\). For \(N<{{\bar{N}}}\), the error in the solution at the final time is estimated by

$$\begin{aligned} \text {Sol err}=\sqrt{\sum _i \vert u_{i,N}-{{\bar{u}}}_{i,{{\bar{N}}}}\vert }. \end{aligned}$$

The error in the conservation laws is evaluated as in (6.6).

Table 3 Nonlinear problem
Full size table

Table 3 shows the solution error and the error in the conservation laws given by method (5.1) with \(N=10\) applied to (6.7). The error in the conservation laws is only due to the accuracy in the Newton method to solve the nonlinear system (4.18). As in the linear case, the error in the solution is larger for \(\alpha \) close to p, except that in this case the method exactly solves the subdiffusion problem with \(\alpha =0.5\).

Fig. 3
figure 3

Nonlinear problem. Numerical solution with \(N=10\), \(\varDelta x=0.005\), \(\alpha =0.5\) (left) and \(\alpha =1.5\) (right)

Full size image
Fig. 4
figure 4

Nonlinear problem. Rate of convergence in time. \(\varDelta x=0.005\) (logarithmic scale on y-axis)

Full size image

The numerical solutions obtained for \(\alpha =0.5\) and \(\alpha =1.5\) are shown in Figure 3. The convergence of the method is analysed in Figure 4 where we plot the logarithm of the error in the solution against N for \(N=2,\ldots ,12\). Also in this case the rate of convergence in time is exponential, except for \(\alpha =0.5\), where the method is exact for all values of N.

7 Conclusions

In the present paper we have investigated a class of time fractional diffusion PDEs of arbitrary fractional order. The purpose is twofold. On one hand, we have derived sufficient conditions to find conservation laws of a FDE of this kind, and derived a similar result for a numerical method to have discrete conservation laws. On the other hand, we have generalized the spectral method in [8] to approximate Caputo and Riemann-Liouville derivatives of arbitrary order. This method has been coupled with a finite difference approximation in space, and proved to have conservation laws. In the cases of subdiffusion and superdiffusion, we have derived the expressions of the conservation laws and performed numerical tests to confirm the theoretical findings and to show the convergence of the method.

Other promising approaches for the numerical solution of time fractional PDEs are pseudo spectral methods based on fractional Lagrange and Müntz-Legendre polynomials [31, 32, 47, 54]. A future development of this research could deal with the analysis of the conservative properties of these classes of methods and their experimental verification to make comparisons with the proposed approach.