1 Introduction

By adopting the simultaneous multi-beam (SM) working mode and exploiting the orthogonal signals, the collocated multi-input multi-output (C-MIMO) radar possesses the advantages such as waveform diversity [1], virtual aperture extension [2], and simultaneous multi-function [3], and has attracted much attention in recent years [1,2,3,4]. In practice, the limited resources are often the main factor restricting radar performance [5]. Therefore, in order to take full advantages of the C-MIMO radar system, the finite system resource should be efficiently managed.

Power allocation (PA) is a crucial theme in radar resource management for multiple target tracking (MTT). In many practical scenarios, the PA problem for MTT is mainly focused on: (1) Maximizing the overall tracking accuracy or the worst target tracking accuracy in all targets with the finite power budget [6,7,8,9,10]; (2) Minimizing the power consumption for given MTT performance requirements [11,12,13,14]. However, in practice, when combat missions are urgent, in order to guide more weapons to attack enemy objects accurately, the guidance radar system usually adopts in full power mode. In this case, the aforesaid PA strategies cannot be directly applied. In addition, for the guidance radar, the weapon launching conditions and enough guidance accuracy should be both satisfied [15]. Hence, the number of the effective tracking targets (ETTs) and the corresponding target tracking accuracy are both important performance indicators. Herein, the ETT denotes the target which satisfies the given tracking accuracy. However, to the best of our knowledge, the robust power allocation (RPA) strategy considering the above two optimization objectives is very limited.

Moreover, most of the existing studies on PA in the MIMO radar system are carried out under ideal detection condition, which is not common seen on the modern battlefields. Since the posterior Cramer–Rao lower bound (PCRLB) can provide a tight lower bound for any unbiased estimator [16,17,18], the PCRLB is usually used as the optimization metric in the resource allocation problems for MTT [5,6,7,8,9,10,11,12,13]. However, under the condition of electromagnetic interference, the process of target parameter estimation can be often very complex, which may cause the PCRLB cannot accurately quantify tracking accuracy. The MI is an information theoretic criterion, it has been proved that the more MI between radar echo and the target impulse response implies better capability of radar to estimate the target parameters [19]. In this case, the MI has been used in [20,21,22] for power allocation among the MIMO radars and jammers.

In this paper, the RPA strategy in the C-MIMO radar for multiple target guidance (MTG) application is studied under the blanket jamming environment. The MI between the reflected target signal and the path gain matrix is adopted to be the performance criterion for target parameter estimation. Based on the predicted MI, the RPA model is established to consider both the number of ETTs and their corresponding tracking accuracy, which formulated as a non-convex problem. In order to solve this problem, a two-step optimization algorithm based on benefit–cost ratio (BCR) [23] is proposed.

The rest of this paper is organized as follows: The system model of the C-MIMO radar along with the target motion model is demonstrated in Sect. 2. Section 3 derives the MI in terms of the PA and establishes a cognitive tracking scheme. In Sect. 4, the optimization model is formulated and an efficient solving algorithm is proposed. The numerical results and analysis are given in Sect. 5. Section 6 concludes this paper.

2 System model

Consider that a narrowband C-MIMO radar is located at (x0, y0). In order to track Q point-like enemy objects which carry with active oppressive jammers, a set of orthogonal and coherent pulse train signals are transmitted. In order to simplify the model analysis, we make the following assuptions:

  1. (1)

    The number and initial position of the tracked targets are known in advance as priori knwoledge;

  2. (2)

    Each target carries a self-defense jammer that continuously transmits jamming signal to the radar, which is modeled as Gaussian white noise;

  3. (3)

    The C-MIMO radar works in the SM pattern, and simultaneously transmits multiple orthogonal beams to track targets.

2.1 Radar signal model

Consider that the transmit signal for the qth target at the kth sample interval is normalized as \(s_{k,q} (t)\), and the number of transmit pulse trains in one measurement is \(L\), thus the lth pulse is [5]

$$s_{k,q,l} \left( t \right) = s_{k,q} \left[ {t^{\prime} + \left( {l - 1} \right)T_{{\text{p}}} } \right]$$
(1)

where Tp is the pulse repetition period, and \(t^{\prime}\) is the slow time. Moreover, the lth pulse in the received baseband signal is given by

$$r_{{k,q,l}} \left( t \right) = \delta _{{k,q}} h_{{k,q,l}} \sqrt {P_{{k,q}} } s_{{k,q}} \left[ {t - \left( {l - 1} \right)T_{p} - \tau _{{k,q}} } \right]e^{{ - j2\pi f_{{k,q}}^{{\text{d}}} t}} + n_{{k,q,l}} \left( t \right) + j_{{k,q,l}} \left( t \right)$$
(2)

where \(\delta_{k,q}\) denotes the attenuation of signal strength due to the path loss. \(h_{k,q,l} = h_{k,q,l}^{{\text{R}}} + h_{k,q,l}^{{\text{I}}}\) is the radar cross-section (RCS), modeled as a zero-mean white complex noise with variance \(\sigma_{k,q}^{2}\), denoted as \(h_{k,q,l} \sim CN(0,\sigma_{k,q}^{2} )\). \(P_{k,q}\) is the transient transmit power, the terms of \(\tau_{k,q}\) and \(f_{k,q}^{{\text{d}}}\) are the time delay and the Doppler frequency, respectively. \(n_{k,q,l} (t)\) represents the inherent environmental noise, modeled as \(n_{k,q,l} (t) \sim CN(0,\alpha_{k,q}^{2} )\), and \(j_{k,q,l} (t)\) denotes the oppressive jamming noise imposed by the jammer, distributed as \(j_{k,q,l} (t) \sim CN(0,\beta_{k,q}^{2} )\).

Aim at improving the echo signal–noise ratio (SNR), the coherent pulse accumulation technique is applied to the echo signal processing. Thus, the sampled signals of \(r_{k,q,l} (t)\) are

$${\hat{\mathbf{r}}}_{k,q,l} = {\hat{\mathbf{s}}}_{k,q,l} g_{k,q,l} + {\hat{\mathbf{n}}}_{k,q,l} + {\hat{\mathbf{j}}}_{k,q,l}$$
(3)

where \({\hat{\mathbf{s}}}_{k,q,l} \in {\mathbb{C}}^{M \times 1}\) denotes the sampling of \(s_{k,q,l} (t)\), and M indicates the sampling length. \({\hat{\mathbf{n}}}_{k,q,l} \in {\mathbb{C}}^{M \times 1}\) represents the sampling of \(n_{k,q,l} (t)\), \({\hat{\mathbf{j}}}_{k,q,l} \in {\mathbb{C}}^{M \times 1}\) is the sampling of \(j_{k,q,l} (t)\), and \(g_{k,q,l}\) dentoes the path gain coefficient, distributed as \(g_{k,q,l} \sim N(0,\gamma_{k,q}^{2} )\), with [7]

$$\gamma_{k,q}^{2} \propto P_{k,q} \sigma_{k,q}^{2} /R_{k,q}^{4}$$
(4)

where \(\propto\) is the proportional notation, and \(R_{k,q}\) is the distance from the qth target to the radar center at sample interval k.

Suppose that the C-MIMO radar continuously transmits \(N \le L\) pulses to the qth target at the kth sample interval, which means the number of coherent accumulation pulses in a detection is N. Then, the relevant echo signal can be denoted as

$$\begin{aligned} {\hat{\mathbf{R}}}_{k,q} & = \left( {{\hat{\mathbf{r}}}_{k,q,1} ,{\hat{\mathbf{r}}}_{k,q,2,} ...,{\hat{\mathbf{r}}}_{k,q,N} } \right) \\ & { = }{\hat{\mathbf{S}}}_{k,q} {\hat{\mathbf{G}}}_{k,q} + {\hat{\mathbf{N}}}_{k,q} + {\hat{\mathbf{J}}}_{k,q} \\ \end{aligned}$$
(5)

where

$$\left\{ {\begin{array}{*{20}l} {{\hat{\mathbf{S}}}_{k,q} = \left( {{\hat{\mathbf{s}}}_{k,q,1} ,{\hat{\mathbf{s}}}_{k,q,2} , \ldots ,{\hat{\mathbf{s}}}_{k,q,N} } \right)} \hfill \\ {{\hat{\mathbf{G}}}_{k,q} = {\text{diag}}\left( {g_{k,q,1} ,g_{k,q,2} , \ldots ,g_{k,q,N} } \right)} \hfill \\ {{\hat{\mathbf{N}}}_{k,q} = \left( {{\hat{\mathbf{n}}}_{k,q,1} ,{\hat{\mathbf{n}}}_{k,q,2} , \ldots ,{\hat{\mathbf{n}}}_{k,q,N} } \right)} \hfill \\ {{\hat{\mathbf{J}}}_{k,q} = \left( {{\hat{\mathbf{j}}}_{k,q,1} ,{\hat{\mathbf{j}}}_{k,q,2} , \ldots ,{\hat{\mathbf{j}}}_{k,q,N} } \right)} \hfill \\ \end{array} } \right.$$
(6)

In addition, to simplify the signal model, we assume that the transmit pulse waveforms are exactly the same. Thus, we have \({\hat{\mathbf{s}}}_{{k,q,1}} = {\hat{\mathbf{s}}}_{{k,q,2}} = \cdots = {\hat{\mathbf{s}}}_{{k,q,N}} = {\hat{\mathbf{s}}}_{{k,q}}\).

2.2 Target motion model

Without loss of generality, we assume that the target motion model can be described by the constant velocity (CV) model [6]. In this case, the qth target state is denoted by \({\mathbf{x}}_{k,q} = [x_{k,q} ,\dot{x}_{k,q} ,y_{k,q} ,\dot{y}_{k,q} ]^{{\text{T}}}\), where \([x_{k,q} ,y_{k,q} ]^{{\text{T}}}\) and \([\dot{x}_{k,q} ,\dot{y}_{k,q} ]^{{\text{T}}}\) represent the position and velocity at the kth sample interval in Cartesian coordinates. The target state transition model can be expressed by [7]

$${\mathbf{x}}_{k + 1,q} = {\mathbf{Fx}}_{k,q} + {\mathbf{w}}_{k,q}$$
(7)

where \({\mathbf{F}}\) denotes the state transition matrix of the CV model. The term of \({\mathbf{w}}_{k,q}\) represents an uncorrelated process noise sequence and is assumed to be a zero-mean Gaussian noise with the covariance matrix \({\mathbf{Q}}_{k,q}\). Herein, \({\mathbf{F}}\) and \({\mathbf{Q}}_{k,q}\) are given by [8]

$${\mathbf{F}} = \left[ {\begin{array}{*{20}c} 1 & {T_{{\text{s}}} } \\ 0 & 1 \\ \end{array} } \right] \otimes {\mathbf{I}}_{2}$$
(8)

and

$$\begin{aligned} {\mathbf{Q}}_{k,q} & = {\mathbb{E}}\left[ {{\mathbf{w}}_{k,q} \left( {{\mathbf{w}}_{k,q} } \right)^{{\text{T}}} } \right] \\ & = \left( {\int_{0}^{{T_{{\text{S}}} }} {m_{k,q} \left[ {\begin{array}{*{20}c} {T_{{\text{s}}} - t} \\ 1 \\ \end{array} } \right]} \left[ {\begin{array}{*{20}c} {T_{{\text{s}}} - t} & 1 \\ \end{array} } \right]{\text{d}}t} \right) \otimes {\mathbf{I}}_{2} \\ & { = }m_{k,q} \left[ {\begin{array}{*{20}c} {T_{{\text{s}}}^{{3}} /3} & {T_{{\text{s}}}^{{2}} /2} \\ {T_{{\text{s}}}^{{2}} /2} & {T_{s} } \\ \end{array} } \right] \otimes {\mathbf{I}}_{2} \\ \end{aligned}$$
(9)

where \(T_{{\text{s}}}\) is the sample interval, \({\mathbf{I}}_{2}\) denotes the second-order identity matrix, \(\otimes\) represents the Kronecker product operator, and \(m_{k,q}\) is the relevant process noise intensity [8].

2.3 Measurement model

According to the receive signal model in (2) and (5), the conditional probability density function (PDF) \(p({\hat{\mathbf{R}}}_{k,q} |{{\varvec{\upxi}}}_{k,q} )\) is given by

$$p\left( {\left. {{\hat{\mathbf{R}}}_{{k,q}} } \right|{\mathbf{\xi }}_{{k,q}} } \right) \propto \exp \left\{ { - \frac{1}{{\delta _{{k,q}}^{2} }}} \right.\int {|r_{{k,q,l}}^{{}} \left( t \right) - \alpha _{{k,q}}^{{}} h_{{k,q,l}}^{{}} } \left. {\sqrt {P_{{k,q}} } {\text{ }}s_{{k,q}} \left( {t - \tau _{{k,q}} } \right)e^{{ - j2\pi f_{{k,q}}^{{\text{d}}} t}} - j_{{k,q,l}}^{{}} \left( t \right)|{\text{d}}t} \right\}$$
(10)

where \({{\varvec{\upxi}}}_{k,q}^{{}} = [R_{k,q}^{{}} ,f_{k,q}^{{\text{d}}} ,\theta_{k,q}^{{}} ]^{{\text{T}}}\). Moreover, by adopting the maximum likelihood (ML) estimate method [24], the ML estimate of \({{\varvec{\upxi}}}_{k,q}^{{}}\) can be calculated as

$$\begin{aligned} \left\{ {{\hat{\mathbf{\xi }}}_{k,q}^{{}} } \right\}_{{{\text{ML}}}} & = \arg \left\{ {\mathop {\max }\limits_{{{{\varvec{\upxi}}}_{k,q} }} \left[ {\ln p\left( {\left. {{\hat{\mathbf{R}}}_{k,q} } \right|{{\varvec{\upxi}}}_{k,q} } \right)} \right]} \right\} \\ & = \arg \left\{ {\mathop {\max }\limits_{{{{\varvec{\upxi}}}_{k,q} }} \left[ {\sum\limits_{l = 1}^{L} {\left| {\int {r_{k,q,l}^{{}} \left( t \right) \times s_{k,q}^{ * } \left( {t - \tau_{k,q}^{{}} } \right)} } \right.} } \right.} \right.\left. {\left. {\left. { \times e^{{{ - j2\pi f_{k,q}{\text{d}}} t}} dt} \right|^{2} } \right]} \right\} \\ \end{aligned}$$
(11)

Therefore, the target information can be extracted from the receive signal, e.g., the time-delay, the Doppler frequency and the bearing angle. The measurement model can be expressed as

$${\mathbf{z}}_{k,q} = h\left( {{\mathbf{x}}_{k,q} } \right) + {{\varvec{\upnu}}}_{k,q}$$
(12)

where \(h({\mathbf{x}}_{k,q} ) = [R_{k,q} ,\dot{R}_{k,q} ,\theta_{k,q} ]^{{\text{T}}}\), \(R_{k,q}\), \(\dot{R}_{k,q}\) and \(\theta_{k,q}\) denote the range, radial velocity, and bearing angle of the qth target at the kth sample interval, respectively, i.e., given by

$$\left\{ {\begin{array}{*{20}l} {R_{k,q} = \sqrt {\left( {x_{k,q} - x_{0} } \right)^{2} + \left( {y_{k,q} - y_{0} } \right)^{2} } } \hfill \\ {\dot{R}_{k,q} = \left( {\dot{x}_{k,q} ,\dot{y}_{k,q} } \right)\left( \begin{gathered} x_{k,q} - x_{0} \hfill \\ y_{k,q} - y_{0} \hfill \\ \end{gathered} \right)/R_{k,q} } \hfill \\ {\theta_{k,q} = \arctan {{\left( {y_{k,q} - y_{0} } \right)} \mathord{\left/ {\vphantom {{\left( {y_{k,q} - y_{0} } \right)} {\left( {x_{k,q} - x_{0} } \right)}}} \right. \kern-\nulldelimiterspace} {\left( {x_{k,q} - x_{0} } \right)}}} \hfill \\ \end{array} } \right.$$
(13)

The measurement noise \({{\varvec{\upnu}}}_{k,q} \sim N({\mathbf{0}},{\mathbf{\Re }}_{k,q} )\), with \({\mathbf{\Re }}_{k,q} = {\text{diag}}(\sigma_{{R_{k,q} }}^{2} ,\sigma_{{\dot{R}_{k,q} }}^{2} ,\sigma_{{\theta_{k,q} }}^{2} )\). In addition, the elements in \({\mathbf{\Re }}_{k,q}\) are given by [9]

$$\left\{ {\begin{array}{*{20}l} {\sigma_{{R_{k,q} }}^{2} \propto \left( {\alpha_{k,q} P_{k,q} \left| {h_{k,q} } \right|^{2} \beta_{k,q}^{2} } \right)^{ - 1} } \hfill \\ {\sigma_{{\dot{R}_{k,q} }}^{2} \propto \left( {\alpha_{k,q} P_{k,q} \left| {h_{k,q} } \right|^{2} T_{k,q}^{2} } \right)^{ - 1} } \hfill \\ {\sigma_{{\theta_{{_{k,q} }} }}^{2} \propto \left( {\alpha_{k,q} P_{k,q} \left| {h_{k,q} } \right|^{2} /B_{{\text{w}}} } \right)^{ - 1} } \hfill \\ \end{array} } \right.$$
(14)

where \(\beta_{k,q}\) denotes the effective bandwidth, \(T_{k,q}\) is the effective time width, and \(B_{{\text{w}}}\) is the null-to-null beam width of receive antennas [25]. Moreover, it should be noted that all the elements in (14) are inversely linear with \(P_{k,q}\) [12], and thus, the measurement covariance can be rewritten as \({\mathbf{\Re }}_{k,q} = P_{k,q}^{ - 1} {{\varvec{\upchi}}}_{k,q}\). In this case, it is theoretically possible to achieve higher tracking accuracy by increasing the transmit power allocation for a certain target.

3 Cognitive tracking scheme based on MI under blanket jamming

3.1 Multi-beam target tracking with PSCKF

In the tracking process, the C-MIMO radar works in multi-beam mode and each beam operates in the “focused transmit focused receive” (FTFR) manner [13]. Therefore, the MTT task can be divided into a series of single target tracking [7]. In view of the nonlinear Gaussian state space model given in Sects. 2.2 and 2.3, the parallel square-root cubature Kalman filter (PSCKF) is adopted in target state estimation.

From the Bayesian theory perspective, based on recursive method, the PDF for target tracking is obtained by utilizing the known initial state probability density and system measurement value. In this case, after the system state transition model and the measurement model are probabilized, the state estimation of the nonlinear discrete system model (7) and (12) in the Gaussian domain can be normalized as

$$\left\{ {\begin{array}{*{20}l} {{\mathbf{x}}_{{k + 1\left| {k + 1,q} \right.}} = {\hat{\mathbf{x}}}_{{k + 1\left| {k + 1,q} \right.}} + {\mathbf{L}}_{k + 1,q} \left( {{\mathbf{z}}_{k + 1,q} - {\hat{\mathbf{z}}}_{k + 1,q} } \right)} \hfill \\ {{\mathbf{P}}_{{k + 1\left| {k + 1,q} \right.}} = {\mathbf{P}}_{{k + 1\left| {k,q} \right.}} - {\mathbf{L}}_{k + 1,q} {\mathbf{P}}_{k + 1,q}^{zz} {\mathbf{L}}_{k + 1,q}^{{\text{T}}} } \hfill \\ {{\mathbf{L}}_{k + 1,q} = {\mathbf{P}}_{k + 1,q}^{xz} \left( {{\mathbf{P}}_{k + 1,q}^{zz} } \right)^{ - 1} } \hfill \\ \end{array} } \right.$$
(15)

where \({\mathbf{P}}_{{k + 1\left| {k + 1,q} \right.}}\) is the state transition covariance matrix, \({\mathbf{P}}_{{k + 1\left| {k,q} \right.}}\) is the one-step predictive covariance matrix, \({\mathbf{L}}_{k + 1,q}\) is the Kalman gain, \({\mathbf{P}}_{k + 1,q}^{zz}\) is the measurement autocorrelation covariance matrix, and \({\mathbf{P}}_{k + 1,q}^{xz}\) is the state-measurement cross-correlation covariance matrix. To compute all the parameters in (15), the recursive calculation of PSCKF is given below.

FOR \(q = 1,2,...,Q\).

  1. (1)

    Time Update

Assume that the state transition covariance matrix \({\mathbf{P}}_{{k\left| {k,q} \right.}}\) is known, and the posterior density at the kth sample interval satisfies that \(p({\mathbf{x}}_{k,q} |{\mathbf{z}}_{k,q} )\sim N({\hat{\mathbf{x}}}_{{k\left| {k,q} \right.}} ,{\mathbf{P}}_{{k\left| {k,q} \right.}} )\). Then, we have.

Step 1.1: Cholesky decomposition.

$${\mathbf{P}}_{{k\left| {k,q} \right.}} = {\mathbf{S}}_{{k\left| {k,q} \right.}} \left( {{\mathbf{S}}_{{k\left| {k,q} \right.}} } \right)^{{\text{T}}}$$
(16)

Step 1.2: Calculate each cubature point and make one-step prediction.

$$\left\{ {\begin{array}{*{20}l} {{\mathbf{x}}_{{k\left| {k,q} \right.}}^{i} = {\hat{\mathbf{x}}}_{{k\left| {k,q} \right.}}^{{}} + {\mathbf{S}}_{{k\left| {k,q} \right.}} {{\varvec{\upxi}}}_{i} } \hfill \\ {{\mathbf{x}}_{{k + 1\left| {k,q} \right.}}^{i * } = {\mathbf{Fx}}_{{k\left| {k,q} \right.}}^{i} } \hfill \\ \end{array} } \right.$$
(17)

where \(i = 1,2,...,m\), \(m = 2n\), and n is the dimension of the state vector. Herein, \({{\varvec{\upxi}}}_{i} = \sqrt {m/2} [{\mathbf{1}}]\), where \([{\mathbf{1}}]\) is given by

$$\left[ {\mathbf{1}} \right] = \left\{ {\left( {\begin{array}{*{20}c} 1 \\ 0 \\ \ldots \\ 0 \\ \end{array} } \right),\left( {\begin{array}{*{20}c} 0 \\ 1 \\ \ldots \\ 0 \\ \end{array} } \right), \ldots \left( {\begin{array}{*{20}c} 0 \\ 0 \\ \ldots \\ 1 \\ \end{array} } \right),\left( {\begin{array}{*{20}c} { - 1} \\ 0 \\ \ldots \\ 0 \\ \end{array} } \right),\left( {\begin{array}{*{20}c} 0 \\ { - 1} \\ \ldots \\ 0 \\ \end{array} } \right), \ldots \left( {\begin{array}{*{20}c} 0 \\ 0 \\ \ldots \\ { - 1} \\ \end{array} } \right)} \right\}$$
(18)

Step 1.3: Estimate the square-root coefficient of the covariance matrix of state prediction value and state prediction error.

$$\left\{ {\begin{array}{*{20}l} {{\hat{\mathbf{x}}}_{{k + 1\left| {k,q} \right.}} = \frac{1}{m}\sum\limits_{i = 1}^{m} {{\mathbf{x}}_{k + 1\left| k \right.,q}^{i \, * } } } \hfill \\ {{\mathbf{S}}_{k + 1\left| k \right.,q} = {\text{Tria}}\left( {\left[ {{\mathbf{x}}_{k + 1\left| k \right.,q}^{ * } ,{\text{Chol}}\left( {{\mathbf{Q}}_{k,q} } \right)} \right]} \right)} \hfill \\ {{\mathbf{z}}_{{k + 1\left| {k,q} \right.}} = \frac{1}{\sqrt m }\left[ {{\mathbf{z}}_{{k + 1\left| {k,q} \right.}}^{1} - {\hat{\mathbf{z}}}_{{k + 1\left| {k,q} \right.}} ,{\mathbf{z}}_{{k + 1\left| {k,q} \right.}}^{2} - {\hat{\mathbf{z}}}_{{k + 1\left| {k,q} \right.}} , \ldots ,{\mathbf{z}}_{{k + 1\left| {k,q} \right.}}^{m} - {\hat{\mathbf{z}}}_{{k + 1\left| {k,q} \right.}} } \right]} \hfill \\ \end{array} } \right.$$
(19)

where \({\text{Tria(}} \cdot {)}\) and \({\text{Chol(}} \cdot {)}\) denote the QR decomposition operator and the Cholesky decomposition operator, respectively.

  1. (2)

    Measurement Update

Step 2.1: Estimate each cubature point and the square-root coefficient of the new covariance.

$$\left\{ {\begin{array}{*{20}l} {{\mathbf{x}}_{{k + 1\left| {k,q} \right.}}^{i} = {\hat{\mathbf{x}}}_{k + 1\left| k \right.,q}^{{}} + {\mathbf{S}}_{k + 1\left| k \right.,q} {{\varvec{\upxi}}}_{i} } \hfill \\ {{\mathbf{z}}_{k + 1\left| k \right.,q}^{i} = h\left( {{\mathbf{x}}_{k + 1\left| k \right.,q}^{i} } \right)} \hfill \\ {{\hat{\mathbf{z}}}_{k + 1\left| k \right.,q} = \frac{1}{m}\sum\limits_{i = 1}^{m} {{\mathbf{z}}_{k + 1\left| k \right.,q}^{i} } } \hfill \\ {{\mathbf{z}}_{k + 1\left| k \right.,q} = \frac{1}{\sqrt m }\left[ {{\mathbf{z}}_{k + 1\left| k \right.,q}^{1} - {\hat{\mathbf{z}}}_{k + 1\left| k \right.,q} ,{\mathbf{z}}_{k + 1\left| k \right.,q}^{2} - {\hat{\mathbf{z}}}_{k + 1\left| k \right.,q} , \ldots ,{\mathbf{z}}_{k + 1\left| k \right.,q}^{m} - {\hat{\mathbf{z}}}_{k + 1\left| k \right.,q} } \right]} \hfill \\ {{\mathbf{S}}_{k + 1\left| k \right.,q}^{ZZ} = {\text{Tria}}\left( {\left[ {{\mathbf{z}}_{k + 1\left| k \right.,q}^{{}} ,{\text{Chol}}\left( {{\mathbf{\Re }}_{k,q} } \right)} \right]} \right)} \hfill \\ \end{array} } \right.$$
(20)

Step 2.2: Calculate the new information covariance matrix and the cross-covariance matrix of state and measurement.

$$\left\{ {\begin{array}{*{20}l} {{\mathbf{P}}_{k + 1\left| k \right.,q}^{zz} = {\mathbf{S}}_{k + 1\left| k \right.,q}^{zz} \left( {{\mathbf{S}}_{k + 1\left| k \right.,q}^{zz} } \right)^{{\text{T}}} } \hfill \\ {{\mathbf{x}}_{k + 1\left| k \right.,q} = \frac{1}{\sqrt m }\left[ {{\mathbf{x}}_{k + 1\left| k \right.,q}^{1} - {\hat{\mathbf{x}}}_{k + 1\left| k \right.,q}^{{}} ,{\mathbf{x}}_{k + 1\left| k \right.,q}^{2} - {\hat{\mathbf{x}}}_{k + 1\left| k \right.,q} , \ldots ,{\mathbf{x}}_{k + 1\left| k \right.,q}^{m} - {\hat{\mathbf{x}}}_{k + 1\left| k \right.,q} } \right]} \hfill \\ {{\mathbf{P}}_{k + 1\left| k \right.,q}^{xz} = {\mathbf{x}}_{k + 1\left| k \right.,q} \left( {{\mathbf{z}}_{k + 1\left| k \right.,q} } \right)^{{\text{T}}} } \hfill \\ \end{array} } \right.$$
(21)

Step 2.3: Update the filter gain and compute the posterior state estimation.

$$\left\{ \begin{gathered} {\mathbf{L}}_{k + 1,q}^{{}} = {\mathbf{P}}_{k + 1\left| k \right.,q}^{xz} \left( {{\mathbf{P}}_{k + 1\left| k \right.,q}^{zz} } \right)^{ - 1} \hfill \\ {\hat{\mathbf{x}}}_{k + 1,q}^{{}} = {\hat{\mathbf{x}}}_{k + 1\left| k \right.,q}^{{}} + {\mathbf{L}}_{k + 1,q}^{{}} \left( {{\mathbf{z}}_{k + 1,q}^{{}} - {\hat{\mathbf{z}}}_{k + 1\left| k \right.,q}^{{}} } \right) \hfill \\ \end{gathered} \right.$$
(22)

Step 2.4: Recersion. Update the square-root coefficient of state error covariance matrix

$${\mathbf{S}}_{{k + 1\left| {k + 1} \right.,q}} = {\text{Tria}}\left( {\left[ {{\mathbf{x}}_{k + 1\left| k \right.,q}^{{}} - {\mathbf{L}}_{k + 1,q}^{{}} {\mathbf{z}}_{k + 1\left| k \right.,q}^{{}} ,{\mathbf{L}}_{k + 1,q}^{{}} {\text{Chol}}\left( {{\mathbf{\Re }}_{k,q} } \right)} \right]} \right)$$
(23)

Then, let \(k = k + 1\), and return to step 1.1.

3.1.1 END FOR.

3.2 MI derivation under blanket jamming

Assume that the transmit signal of \({\hat{\mathbf{s}}}_{k,q}\) is known, thus the pulse matrix \({\hat{\mathbf{S}}}_{k,q}\) can be obtained. Then, the MI between \({\hat{\mathbf{R}}}_{k,q}\) and \({\hat{\mathbf{G}}}_{k,q}\) can be expressed as [26]

$$\begin{aligned} I\left( {{\hat{\mathbf{R}}}_{k,q} ;{\hat{\mathbf{G}}}_{k,q} \left| {{\hat{\mathbf{S}}}_{k,q} } \right.} \right) & = H\left( {{\hat{\mathbf{R}}}_{k,q} \left| {{\hat{\mathbf{S}}}_{k,q} } \right.} \right) - H\left( {{\hat{\mathbf{R}}}_{k,q} \left| {{\hat{\mathbf{G}}}_{k,q} ,{\hat{\mathbf{S}}}_{k,q} } \right.} \right) \\ & { = }H\left( {{\hat{\mathbf{R}}}_{k,q} \left| {{\hat{\mathbf{S}}}_{k,q} } \right.} \right) - H\left( {{\hat{\mathbf{N}}}_{k,q} + {\hat{\mathbf{J}}}_{k,q} } \right) \\ \end{aligned}$$
(24)

where \(I({\hat{\mathbf{R}}}_{k,q} ;{\hat{\mathbf{G}}}_{k,q} |{\hat{\mathbf{S}}}_{k,q} )\) denotes the MI for the qth target. The term of \(H( \cdot )\) represents the differential entropy operator, which satisfies that, i.e., \(H({\mathbf{x}}) = - \int {p({\mathbf{x}})} \log p{(}{\mathbf{x}}{\text{)d}}{\mathbf{x}}\) and \(H({\mathbf{x}}\left| {\mathbf{y}} \right.) = - \int {\int {p({\mathbf{x}}\left| {\mathbf{y}} \right.)\log p{(}{\mathbf{x}}\left| {\mathbf{y}} \right.{\text{)d}}{\mathbf{x}}{\text{d}}{\mathbf{y}}} }\). Herein, \(p({\mathbf{x}})\) and \(p({\mathbf{x}}\left| {\mathbf{y}} \right.)\) are the PDF of \({\mathbf{x}}\) and the conditional PDF of \({\mathbf{x}}\) with respect to \({\mathbf{y}}\), respectively. In this case, \(p({\hat{\mathbf{R}}}_{k,q} |{\hat{\mathbf{S}}}_{k,q} )\) and \(p({\hat{\mathbf{N}}}_{k,q} + {\hat{\mathbf{J}}}_{k,q} )\) are given by

$$p\left( {{\hat{\mathbf{R}}}_{k,q} \left| {{\hat{\mathbf{S}}}_{k,q} } \right.} \right) = \frac{{\exp \left\{ { - {\text{tr}}\left[ {\left( {\gamma_{k,q}^{2} {\hat{\mathbf{s}}}_{k,q} {\hat{\mathbf{s}}}_{k,q}^{{\text{H}}} + \left( {\alpha_{k,q}^{2} + \beta_{k,q}^{2} } \right){\mathbf{I}}_{M} } \right)^{ - 1} {\hat{\mathbf{R}}}_{k,q} {\hat{\mathbf{R}}}_{k,q}^{{\text{H}}} } \right]} \right\}}}{{\pi^{MN} \left[ {\det \left( {\gamma_{k,q}^{2} {\hat{\mathbf{s}}}_{k,q} {\hat{\mathbf{s}}}_{k,q}^{{\text{H}}} + \left( {\alpha_{k,q}^{2} + \beta_{k,q}^{2} } \right){\mathbf{I}}_{M} } \right)} \right]^{N} }}$$
(25)

and

$$p\left( {{\hat{\mathbf{N}}}_{k,q} + {\hat{\mathbf{J}}}_{k,q} } \right) = \frac{{\exp \left\{ { - {\text{tr}}\left[ {\left( {\left( {\alpha_{k,q}^{2} + \beta_{k,q}^{2} } \right){\mathbf{I}}_{M} } \right)^{ - 1} \left( {{\hat{\mathbf{N}}}_{k,q} + {\hat{\mathbf{J}}}_{k,q} } \right)\left( {{\hat{\mathbf{N}}}_{k,q} + {\hat{\mathbf{J}}}_{k,q} } \right)^{{\text{H}}} } \right]} \right\}}}{{\pi^{MN} \left[ {\det \left( {\left( {\alpha_{k,q}^{2} + \beta_{k,q}^{2} } \right){\mathbf{I}}_{M} } \right)} \right]^{N} }}$$
(26)

Thus, \(H({\hat{\mathbf{R}}}_{k,q} |{\hat{\mathbf{S}}}_{k,q} )\) and \(H({\hat{\mathbf{N}}}_{k,q} + {\hat{\mathbf{J}}}_{k,q} )\) can be calculated as

$$\begin{aligned} H\left( {{\hat{\mathbf{R}}}_{k,q} \left| {{\hat{\mathbf{S}}}_{k,q} } \right.} \right) & = - \int {\int {p\left( {{\hat{\mathbf{R}}}_{k,q} \left| {{\hat{\mathbf{S}}}_{k,q} } \right.} \right)\log p\left( {{\hat{\mathbf{R}}}_{k,q} \left| {{\hat{\mathbf{S}}}_{k,q} } \right.} \right){\text{d}}{\hat{\mathbf{R}}}_{k,q} {\text{d}}{\hat{\mathbf{S}}}_{k,q} } } \\ & = - \int {p\left( {{\hat{\mathbf{R}}}_{k,q} \left| {{\hat{\mathbf{S}}}_{k,q} } \right.} \right)\log p\left( {{\hat{\mathbf{R}}}_{k,q} \left| {{\hat{\mathbf{S}}}_{k,q} } \right.} \right){\text{d}}{\hat{\mathbf{R}}}_{k,q} } \\ & = MN + N\log \left[ {\pi^{M} \det \left( {\gamma_{k,q}^{2} {\hat{\mathbf{s}}}_{k,q} {\hat{\mathbf{s}}}_{k,q}^{{\text{H}}} + \left( {\alpha_{k,q}^{2} + \beta_{k,q}^{2} } \right){\mathbf{I}}_{M} } \right)} \right] \\ \end{aligned}$$
(27)

and

$$\begin{aligned} H\left( {{\hat{\mathbf{N}}}_{k,q} + {\hat{\mathbf{J}}}_{k,q} } \right) & = - \int {p\left( {{\hat{\mathbf{N}}}_{k,q} + {\hat{\mathbf{J}}}_{k,q} } \right)\log p\left( {{\hat{\mathbf{N}}}_{k,q} + {\hat{\mathbf{J}}}_{k,q} } \right){\text{d}}{\hat{\mathbf{N}}}_{k,q} } \\ & \quad - \int {p\left( {{\hat{\mathbf{N}}}_{k,q} + {\hat{\mathbf{J}}}_{k,q} } \right)\log p\left( {{\hat{\mathbf{N}}}_{k,q} + {\hat{\mathbf{J}}}_{k,q} } \right){\text{d}}{\hat{\mathbf{J}}}_{k,q} \, } \\ & = MN + N\log \left[ {\pi^{M} \det \left( {\left( {\alpha_{k,q}^{2} + \beta_{k,q}^{2} } \right){\mathbf{I}}_{M} } \right)} \right] \\ \end{aligned}$$
(28)

Accordingly, combined with (24), (27) and (28), we have

$${\text{MI}}_{k,q} = N\log \frac{{\det \left( {\gamma_{k,q}^{2} {\hat{\mathbf{s}}}_{k,q} {\hat{\mathbf{s}}}_{k,q}^{{\text{H}}} + \left( {\alpha_{k,q}^{2} + \beta_{k,q}^{2} } \right){\mathbf{I}}_{M} } \right)}}{{\left( {\alpha_{k,q}^{2} + \beta_{k,q}^{2} } \right)^{M} }}$$
(29)

It can be seen from (4) and (29) that \(P_{k,q}\) is the only variable of \({\text{MI}}_{k,q}\) under the condition that the electromagnetic environment is regular and the pulse number is constant.

3.3 Cognitive tracking scheme based on transmit power

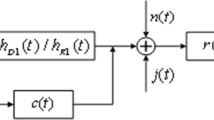
After obtaining the measurement information of all the tracked targets, the power-limited C-MIMO radar can calculate the power allocation results at the next tracking period according to the above steps. Hence, by feeding back the power allocation results to the C-MIMO radar transmitter, a close-loop feedback scheme for power allocation is established. The established cognitive tracking scheme is shown in Fig. 1.

Fig. 1
figure 1

Illustration of the proposed cognitive tracking scheme for RPA strategy

Full size image

4 Optimization model establishment and solution

In this section, we formulate the optimization problem of the RPA based on the MI. In order to solve the optimization problem, a two-step optimization scheme based on the idea of BCR is proposed.

4.1 Problem formulation

Since the MI between the echo signals and path gain matrix is closely related to the accuracy of parameter estimation [27, 28] and has an inverse relationship with mean square error (MSE) [29], we adopt the MI as the criterion of target tracking accuracy. Moreover, in order to establish a closed-loop tracking recursive cycle, the predicted MI should be calculated to guide PA. To be specific, by adopting the PSCKF, the target state estimation \({\tilde{\mathbf{x}}}_{k - 1,q}\) can be obtained. Then, the predicted MI is obtained by combining with the predicted target state \({\tilde{\mathbf{x}}}_{\left. k \right|k - 1,q} = {\mathbf{F}}{\tilde{\mathbf{x}}}_{k - 1,q}\). We consider finding the suboptimal RPA which combines with the effective tracking quantity and target tracking accuracy. Hence, the problem is formulated as

$$\begin{aligned} & {\text{max}}\left\{ {\sum\limits_{q = 1}^{Q} {\left[ {u_{k,q} \left. {{\text{MI}}_{k,q} \left( {P_{k,q} } \right)} \right|_{{{\tilde{\mathbf{x}}}_{\left. k \right|k - 1,q} }} } \right]} } \right\} \\ & \quad {\text{s.t.}}\left\{ {\begin{array}{*{20}l} {u_{k,q} = 1,} \hfill & {\left. {{\text{MI}}_{k,q} \left( {P_{k,q} } \right)} \right|_{{{\tilde{\mathbf{x}}}_{\left. k \right|k - 1,q} }} \ge {\text{MI}}_{0} } \hfill \\ {u_{k,q} = 0,} \hfill & {\left. {{\text{MI}}_{k,q} \left( {P_{k,q} } \right)} \right|_{{{\tilde{\mathbf{x}}}_{\left. k \right|k - 1,q} }} < {\text{MI}}_{0} } \hfill \\ \end{array} } \right. \\ & \quad \quad \sum\limits_{q = 1}^{Q} {P_{k,q} = P_{{{\text{total}}}} \, } ,\quad P_{\min } \le P_{k,q} \le P_{\max } \, \\ \end{aligned}$$
(30)

where \({\text{MI}}_{0}\) is the predetermined threshold of MI when each target is effectively tracked, \(P_{{{\text{total}}}}\) denotes the predefined total power budget, and the transient power bound of \([P_{\min } ,P_{\max } ]\) is set to keep the transmitter stay in an endurable interval.

4.2 Two-step optimization algorithm based on BCR

Since the existence of the binary variable \(u_{k,q}\), (30) is a non-convex optimization problem. In order to solve (20), we propose a two-step optimization algorithm based on BCR.

Step 1: Determine the targets in order of BCR when meet the ETT condition. Firstly, calculating the threshold power \(P_{k,q}^{\min }\), which satisfies that \({\text{MI}}_{k,q} (P_{k,q}^{\min } ) = {\text{MI}}_{0}\). Then, by introducing the idea of BCR [23], the ratio of virtual power and the relative MI of each target is sorted in descending order. Thus, we have

$${\mathbf{IX}}_{k} = {\text{sort}}\left( {E_{k,1} ,E_{k,2} , \ldots ,E_{k,Q} } \right)$$
(31)

where \({\mathbf{IX}}_{k}\) is the permutation vector of the BCR in terms of power from all the moving targets. Herein, \(E_{k,q}\) denotes the BCR in power, which is expressed as

$$E_{k,q} = \frac{{{\text{MI}}_{k,q} \left( {P_{k,q}^{\min } + P_{{{\text{set}}}} } \right)}}{{P_{k,q}^{\min } + P_{{{\text{set}}}} }}$$
(32)

where \(P_{set}\) is a preset constant. Finally, calculating the maximum \(N_{k}\), which satisfies that

$$\sum\limits_{{n = {\mathbf{cel}}_{k} \left( 1 \right)}}^{{{\mathbf{cel}}_{k} \left( {N_{k} } \right)}} {P_{k,n}^{\min } \le P_{{{\text{total}}}} } , \, \sum\limits_{{n = {\mathbf{cel}}_{k} \left( 1 \right)}}^{{{\mathbf{cel}}_{k} \left( {N_{k} + 1} \right)}} {P_{k,n}^{\min } > P_{{{\text{total}}}} }$$
(33)

where \({\mathbf{cel}}_{k}\) records the indices of the targets in \({\mathbf{IX}}_{k}\).

Step 2: Maximize the MI for the given ETT information. After obtaining the quantity \(N_{k}\) and the indices of all the effective tracking targets \({\mathbf{cel}}_{k}\), combining with the threshold power \(P_{k,q}^{\min }\), (30) can be converted into

$$\begin{aligned} & {\text{max }}\left\{ {\sum\limits_{{q = {\mathbf{cel}}_{k} \left( 1 \right)}}^{{{\mathbf{cel}}_{k} \left( {N_{k} } \right)}} {\left[ {\left. {MI_{k,q} \left( {P_{k,q} } \right)} \right|_{{{\tilde{\mathbf{x}}}_{\left. k \right|k - 1,q} }} } \right]} } \right\} \\ & \quad {\text{s.t.}} P_{k,q} = P_{k,q}^{\min } + P_{k,q}^{{{\text{reset}}}} \\ & \quad \,\,\quad \sum\limits_{{q = {\mathbf{cel}}_{k} \left( 1 \right)}}^{{{\mathbf{cel}}_{k} \left( {N_{k} } \right)}} {P_{k,q} = P_{{{\text{total}}}} \, } , \, P_{\min } \le P_{k,q} \le P_{\max } \\ & \quad \,\,\quad \sum\limits_{{{\mathbf{cel}}_{k} \left( 1 \right)}}^{{{\mathbf{cel}}_{k} \left( {N_{k} } \right)}} {P_{k,q}^{{{\text{reset}}}} = P_{{{\text{total}}}} - \sum\limits_{{{\mathbf{cel}}_{k} \left( 1 \right)}}^{{{\mathbf{cel}}_{k} \left( {N_{k} } \right)}} {P_{k,q}^{\min } } \, } \\ & \quad \,\,\quad 0 \le P_{k,q}^{{{\text{reset}}}} \le P_{{{\text{total}}}} - \sum\limits_{{{\mathbf{cel}}_{k} \left( 1 \right)}}^{{{\mathbf{cel}}_{k} \left( {N_{k} } \right)}} {P_{k,q}^{\min } } \, \\ \end{aligned}$$
(34)

where \(P_{k,q}^{{{\text{reset}}}}\) denotes the allocation of the remaining transmit power to the qth target at sample interval k. Technically, (34) can be easily solved by the particle swarm optimization (PSO) [30], and the final solution set is the suboptimal power set that can satisfy the robust tracking of each target.

5 Experiments and analysis

5.1 Parameter settings

In this section, numerous results are presented to demonstrate the effectiveness of the proposed RPA strategy. Consider that a C-MIMO radar is located at the origin point, and \(Q = 8\) targets follow the CV model and are widely separated, whose initial motion parameters are shown in Table 1. Moreover, the joint configuration of the C-MIMO radar and the tracked targets is demonstrated in Fig. 2. The number of coherent accumulation pulses in one illumination is set as \(L = 200\), and the pulse repetition period is \(T_{{\text{p}}} = 1\,{\text{ms}}\). The lower and upper bounds of power constraints for the tracked targets are \(P_{\min } = 0.05P_{{{\text{total}}}}\) and \(P_{\max } = 0.8P_{{{\text{total}}}}\), respectively. In addition, the targets not assigned for tracking are monitored by radar, with allocated power \(P_{{{\text{mon}}}} = 0.01P_{{{\text{total}}}}\). The preset power compensation is \(P_{\min } = 0.1P_{{{\text{total}}}}\), and the threshold of MI is set as \({\text{MI}}_{0} = 0.6\,{\text{nats}}\). It is assumed that the RCS of all targets is the Swerling I model [31] with mean being 1, and remains constant over the measurement interval. Suppose that all targets carry with self-defense jammers and transmit oppressive signals to the C-MIMO radar. The particle population is set as \(N_{{{\text{pop}}}} = 100\), the number of iterations is \(T_{\max } = 200\), and the upper and lower bounds of the inertial weights are \(w_{\max } = 0.9\) and \(w_{\min } = 0.2\), respectively. A sequence of 20 frames with sample interval \(T_{{\text{s}}} = 1\,{\text{s}}\) are utilized in each Monte Carlo trial, while the number of trials is set as \(N_{{{\text{sim}}}} = 1{00}\). To evaluate the tracking performance, we define the sum of RMSEs of the tracked targets as

$${\text{R}}_{{{\text{MSE}},k}} = \sum\limits_{{q = {\mathbf{cel}}_{k} \left( 1 \right)}}^{{{\mathbf{cel}}_{k} \left( {N_{k} } \right)}} {\sqrt {\frac{1}{{N_{{{\text{sim}}}} }}\sum\limits_{j = 1}^{{N_{{{\text{sim}}}} }} {{\text{tr}}\left[ {{{\varvec{\Lambda}}}\left( {{\mathbf{x}}_{k,q} -{\hat{\mathbf{x}}}_{k,q}^{j} } \right)\left( {{\mathbf{x}}_{k,q} -{\hat{\mathbf{x}}}_{k,q}^{j} } \right)^{{\text{T}}} {{\varvec{\Lambda}}}} \right]} } }$$
(35)

where \({\hat{\mathbf{x}}}_{k,q}^{j}\) denotes the results of target parameters estimation in the jth trail. The matrix \({{\varvec{\Lambda}}} = {\mathbf{I}}_{2} \otimes {\text{diag}}(1,0)\).

Table 1 Target moving parameters
Full size table
Fig. 2
figure 2

Joint configuration of the C-MIMO radar and the tracked targets

Full size image

5.2 Results and discussions

  1. 1)

    Scenario 1: Effect of Distance

In this scenario, the interference signal intensity of each jammer is assumed to be constant and the corresponding jam-signal ratio (JSR) is set as 12 dB. Hence, since the targets SNRs are only related to the radar-target distances and the transmit power results [32, 33], the distance factor becomes the major contributor in the PA problem.

In order to demonstrate the effectiveness of the proposed algorithm, two benchmarks are used as comparison: 1) Uniform allocation; 2) Sum-max optimize allocation. In the uniform allocation scheme, all power resources are evenly distributed to \(Q = 8\) targets. As for the sum-max optimize allocation scheme, the optimization objective is to maximize the sum of MIs of all targets, thus its optimization model can be expressed as

$$\begin{aligned} & {\text{max }}\left\{ {\sum\limits_{q = 1}^{Q} {\left. {MI_{k,q} \left( {P_{k,q} } \right)} \right|_{{{\tilde{\mathbf{x}}}_{\left. k \right|k - 1,q} }} } } \right\} \\ & \quad {\text{s.t.}} \sum\limits_{q = 1}^{Q} {P_{k,q} = P_{{{\text{total}}}} \, } \\ & \quad \quad \quad P_{\min } \le P_{k,q} \le P_{\max } \, \\ \end{aligned}$$
(36)

Moreover, (36) is solved by the PSO algorithm. Figure 3 demonstrates the effective tracking quantity comparison among the three resource allocation strategy. In general, the proposed RPA strategy performs best among all the adopted methods obviously. In addition, although the effective tracking quantity obtained by the sum-max optimize allocation scheme is less than that obtained by the average allocation method in the initial period of time, this situation changes with the improvement of the overall target tracking accuracy.

Fig. 3
figure 3

Performance comparison in terms of the effective tracking quantity in scenario 1

Full size image

Figure 4 further demonstrates the average PA results obtained by the proposed RPA strategy in scenario 1. Herein, the grid colors denote the ratio of allocated power towards different moving targets, which is given by

$$r_{{{\text{ave }}k,q}}^{{{\text{power}}}} = \frac{1}{{N_{{{\text{sim}}}} }}\sum\limits_{j = 1}^{{N_{{{\text{sim}}}} }} {\frac{{P_{k,q}^{j} }}{{P_{{{\text{total}}}} }}}$$
(37)

where \(P_{k,q}^{j}\) denotes the PA results in the jth trail. Moreover, the pinky white color represents that the ratio is zero, which means the corresponding target will not be tracked at this tracking interval. It should be noted that the target far from the radar is easily unable to meet the requirements of effective tracking under the given power resource budget due to the larger tracking error, so that the corresponding allocated power is less. Moreover, when the tracking error meets the effective tracking condition, the farther target from the radar is tend to allocated more power resource.

Fig. 4
figure 4

Average PA results obtained by the proposed RPA strategy in scenario 1

Full size image

Figure 5 shows the targets that meet the effective tracking condition at each frame for the three PA schemes. Obviously, target 4 and target 5 can be tracked more easily by radar due to their closer proximity. In addition, the proposed RPA strategy shows good robustness as the tracking time increases.

  1. 2)

    Scenario 2: Effect of Interference Intensity

Fig. 5
figure 5

Indices of the effective tracking targets. a Uniform allocation. b Sum-max optimize allocation. c Proposed RPA strategy

Full size image

In this senario, we will further study the influence of interference intensity on PA results. Therefore, we consider a time-varying JSR model. In the model, the JSR levels of target target q (q = 2, 3, 4, 5) are remain at 12 dB, which is consistent with that of scenario 1. In addition, it is assumed that the JSR levels of the rest of moving targets are time-varying, as shown in Fig. 6. As such, in addition to the distance factor, the interference intensity factor is also added to affect PA results.

Fig. 6
figure 6

Time-varying interference intensity model

Full size image

The effective tracking quantity performances among the three PA schemes in scenario 2 are compared and demonstrated in Fig. 7. Obviously, it can be seen from Fig. 7 that the proposed RPA strategy still performs best among the three algorithms. Due to the stronger inteference intensity, the effective tracking quantity is smaller in scenario 2 than in scenario 1. Moreover, in the long run, the sum-max optimize allocation strategy performs better than the uniform allocation method in increasing tracking performance in scenario 2.

Fig. 7
figure 7

Performance comparison in terms of the effective tracking quantity in scenario 2

Full size image

Figures 8 and 9 show the average PA results obtained by the proposed RPA strategy and the indices of effective tracking target for the three PA strategies, respectively. Compared with scenario 1, it can be noted that less power resources are allocated to targets (target 1 and target 8) with stronger interference intensity. In addition, due to the dual influence of longer radial distance and higher interference intensity, target 1 is abandoned due to the limitation of system power budget among the tracking process.

Fig. 8
figure 8

Average PA results obtained by the proposed RPA strategy in scenario 2

Full size image
Fig. 9
figure 9

Indices of the effective tracking targets. a Uniform allocation. b Sum-max optimize allocation. c Proposed RPA strategy

Full size image

6 Conclusions

In this paper, we proposed an RPA strategy in the C-MIMO radar system for MTG application under blanket jamming environment. Based on deriving and calculating the predicted MI and then setting the predetermined threshold of the MI, we formulated the RPA strategy as a non-convex optimization problem. In order to tackle the difficulty in solving this problem, a two-step optimization algorithm based on the BCR is utilized in the solving process. Numerical results showed that the distance from target to radar and the interference intensity have impact on the PA results. Additionally, in the proposed RPA strategy, those targets with low tracking accuracy are tend to be abandoned in exchange for higher tracking accuracy of other targets.