Introduction

Birefringent fluids are composed of optically anisotropic particles (colloidals) or macromolecules (polymers) (Merzkirch 2018). At rest, these particles or macromolecules are randomly orientated by Brownian motion and the fluid appears optically isotropic. When under the effect of shear, the particles align in a preferential direction and the fluid becomes birefringent. This phenomenon is also known as flow birefringence and has been studied ever since it was first described by Maxwell (1874). Flow birefringence and birefringent fluids are of interest for two reasons: the study of particles, macromolecules or polymer chains (Cerf and Scheraga 1952; Fuller 1995; Janeschitz-Kriegl 1983; Wayland 1964); and the visualization and study of flows and shear rates (Pih 1980). Macromolecular stretching and orientation as well as particle alignment lead to birefringence and influence the rheology. Birefringence is therefore linked to the rheological behavior and researchers have studied this relation. Several birefringent fluids have been researched. For example, the macromolecules of Xanthan gum solutions have been studied by means of flow birefringence (Chow and Fuller 1984; Meyer et al. 1993; Smyth et al. 1995; Yevlampieva et al. 1999). Flow-induced birefringence measurements have also been linked to the stress in the material by the so-called stress-optical rule (Fuller 1995; Janeschitz-Kriegl 1983). If this rule applies, birefringence is linearly proportional to the principal stress difference. Researchers apply the stress-optical rule to study the rheo-optical and structural behavior of fluids (Calabrese et al. 2021b; Ober et al. 2011).

Many flow visualization studies use Milling Yellow (Durelli and Norgard 1972; Peebles et al. 1964; Rankin et al. 1989; Schneider 2013; Sun et al. 1999), an industrial dye and a test fluid for simulating blood flows (Schmitz and Merzkirch 1984). Other fluids have also been successfully investigated (Funfschilling and Li 2001; Hu et al. 2009; Mackley and Hassell 2011; Martyn et al. 2000; Tomlinson et al. 2006).

Cellulose nanocrystals (CNCs) are currently attracting much attention, and several potential applications are being explored and discussed (Habibi et al. 2010; Lagerwall et al. 2014). CNCs are rod-like particles and have birefringent optical properties (Parker et al. 2018). Aqueous cellulose suspensions have been reported to be birefringent when the crystals are aligned magnetically (Frka-Petesic et al. 2015), electrically (Bordel et al. 2006) or mechanically (Calabrese et al. 2021b; Chowdhury et al. 2017; Ebeling et al. 1999; Hausmann et al. 2018). In this study, velocity gradients in laminar flows cause mechanical alignment. Flow birefringence has been used to study the birefringence relaxation of CNCs (Tanaka et al. 2019). The complex strain-optical coefficient was measured experimentally using a custom-built apparatus for oscillatory flow birefringence measurements (Tanaka et al. 2018) and was compared to theoretical values, for which the CNCs dimensions were measured by transmission electron microscopy. They concluded that birefringence relaxation is well-described by the theory for rigid rods and that flow birefringence is an efficient tool to determine the length distribution function of the CNCs. It was also noted that birefringence relaxation is less sensitive to internal motions such as tension and bending than to rotational motions.

In general, a birefringent fluid is characterized by two properties (Pindera and Krishnamurthy 1978). The first is the relationship between shear rate \(\dot{\gamma }\) and the magnitude of birefringence, expressed as \(\Delta n\,(\dot{\gamma })\), where \(\Delta n\) is the difference between the main refractive indices \(n_{1}\) and \(n_{2}\). If we define \(n_{1}\) as the refractive index associated with the fast axis, meaning \(n_{1} < n_{2}\), this gives \(\Delta n = n_{2} - n_{1}\). The second property refers to the orientation of the refractive index axes and is commonly described by the extinction angle \(\chi (\dot{\gamma })\). In order to measure optical properties, various polarized light imaging techniques have been proposed. Common experimental techniques use specially designed flow channels (Calabrese et al. 2021a), plate-plate geometries (Hausmann et al. 2018; Mykhaylyk et al. 2016) or Taylor-Couette type settings (Cerf and Scheraga 1952). The advantage of the latter is the straightforward identification of the extinction angle in the annular gap between the concentric cylinders. If two crossed linear polarizers are utilized in a Taylor-Couette type setting, one in front of the birefringent fluid and the other behind, an isoclinic cross appears, marking the orientation of the refractive index axes. The extinction angle is defined as the smaller of the two angles between the isoclinic cross and the linear polarizers. Possible values range between 0° and 45°.

If the refractive index of an ellipsoidal particle along the symmetry axis differs from the indices along the semi-axes, the optical response of one particle is similar to that of a uniaxial crystal with an extraordinary and an ordinary refractive index, \(n_{e}\) and \(n_{0}\), respectively. A uniaxial crystal is said to be positive if \(n_{e} > n_{o}\) and negative if \(n_{e} < n_{o}\). For rod-like CNC particles, studies have reported \(n_{e} > n_{o}\) (Frka-Petesic et al. 2015; Iyer et al. 1968; Klemm et al. 1998), making them optically positive. Peterlin (1938) and Peterlin and Stuart (1939a, 1939b) (in German) presented a three-dimensional distribution function of rigid rotational ellipsoidal particles in a laminar flow with a constant velocity gradient. Part of that theory was evaluated numerically (Cressely et al. 1985; Nakagaki and Heller 1975; Scheraga et al. 1951). Peterlin and Stuart (1939a, 1939b) applied the hydrodynamic equations of motion based on the work by Jeffery (1922) and added a rotational diffusion coefficient \(D_{r}\) to model the effect of Brownian motion. They showed that the extinction angle is a result of the distribution function and argue that the fluid behaves like a biaxial crystal. If the ellipsoidal particles are aligned electrically or magnetically, the fluid behaves like a uniaxial crystal with the optical axis in the direction of alignment. In a flow with a constant velocity gradient (gradient perpendicular to the flow direction), the particles align in a preferential direction within the flow plane but the in-plane alignment distribution is different to the out-of-plane distribution, resulting in the biaxial crystal behavior (three different main refractive indices). Peterlin and Stuart (1939a, 1939b) did not take particle–particle interactions into account. Therefore, their theoretical findings are limited. However, their conclusion that a sheared fluid behaves like a biaxial crystal due to the three-dimensional distribution function is thought to be transferable. Due to the symmetric setting here, one main refractive index axis is perpendicular to the flow plane.

A single rod-like particle in a fluid flow with constant velocity gradient is primarily oriented as indicated in Fig. 1 (Calabrese et al. 2021a; Cerf and Scheraga 1952; Mykhaylyk et al. 2016). The relation between alignment and rotational diffusion is described by the Péclet number \(Pe = {{\dot{\gamma }} \mathord{\left/ {\vphantom {{\dot{\gamma }} {D_{r} }}} \right. \kern-\nulldelimiterspace} {D_{r} }}\). Rotational diffusion is dominant when \(Pe < 1\) whereas the velocity gradient dominates when \(Pe > 1\). For \(Pe \approx 1\), the rods start to align in a preferential orientation, causing the onset of shear thinning and birefringence. At small velocity gradients (\(Pe \approx 1\)) the preferred orientation of the rods is x = 45° due to the hydrodynamic tensile and compression forces, which are at an angle of 45° to the direction of flow. With higher velocity gradients (\(Pe \gg 1\)), the longitudinal axis of the rods is increasingly parallel to the direction of flow, leading to \(\chi \to 0^\circ\) (Scheraga et al. 1951). For optically positive, rod-like particles, the extinction angle lies between the direction of flow and the slow refractive index axis \(n_{2}\) (\(n_{2} > n_{1}\)). This is because of the larger extraordinary optical index of the longitudinal axis of the particles \(n_{e} > n_{o}\).

Fig. 1
figure 1

Indicated position of an optically positive rod-like particle with \(n_{e} > n_{o}\). Dotted lines represent the laminar velocity field with a constant gradient

Full size image

The intention of this study is to present streaming birefringence measurements of CNC water suspensions. Utilizing a Taylor-Couette type setting, the optical properties \(\Delta n\,(\dot{\gamma })\) and \(\chi (\dot{\gamma })\) are determined as functions of the shear rate. The results are of interest for two reasons. First, they help characterizing aqueous CNC suspensions and are therefore of interest to researchers studying the suspension physics. Second, the measurements indicate that these types of birefringent fluids can be used to visualize and study fluid flows and could present an alternative to current birefringent fluids.

Materials and methods

Material

Aqueous CNC suspensions were prepared by dispersing CelluForce NCC® powder (CelluForce Inc., www.celluforce.com) in distilled water. Jakubek et al. (2018) measured the average length and width of CelluForce CNC (spray dried) by transmission electron microscopy (87 nm, 7.4 nm; axial ratio ∼11; longest reported length ∼250 nm) and atomic force microscopy (77 nm, 3.5 nm; axial ratio ∼22, longest reported length ∼200 nm). Bertsch et al. (2018) also use atomic force microscopy and arrive at similar results (79 nm, 4.8 nm; axial ratio ∼16; longest reported length ∼400 nm). Seven suspensions with different concentrations (weight percentage, wt%) CNC were studied: 0.7, 0.8, 0.9, 1.0, 1.1, 1.2, 1.3 wt%. The mixtures were allowed one week to settle before the experiments so that the nanocrystals could disperse homogeneously. The distilled water had a conductivity of < 0.07 \({{\mu S} \mathord{\left/ {\vphantom {{\mu S} {cm}}} \right. \kern-\nulldelimiterspace} {cm}}\) and the error in concentration is estimated to be \(\Delta c = \pm 0.03wt\%\).

Experimental setup

The experimental setup is shown in Fig. 2. It is the same apparatus as documented in Lane et al. (2021) with only small modifications. Unpolarized light from a halogen bulb (150 W EKE) is emitted through a 600 nm bandpass filter (600FS10-50 from Andover Corporation, HBW 10 nm). The light is then polarized by a linear polarizer (extinction ratio 10,000:1). The polarized light is collimated and redirected by a mirror upwards through a Taylor-Couette flow cell. The linear polarizer was placed in such a way that the light is fully p-polarized (electric field in the plane of incidence on the mirror). The Taylor-Couette experiment consists of a feedback-controlled DC motor with a tachometer and a 415:1 reduction gear rotating the inner cylinder at a selected angular velocity \(\Omega\), two glass windows at top and bottom enabling optical access and an outer cylinder sealing the setup. The height of the inner cylinder is 25 mm and the radius \(r_{inner} = 48mm\). The inner radius of the outer cylinder is \(r_{outer} = 49.5mm\), resulting in a gap width of 1.5 mm. The shear rate in a Taylor-Couette flow can be derived from (Davey 1962) and is given as

$$\left| {\dot{\gamma }(r)} \right| = \frac{2 \cdot \Omega }{{r^{2} }} \cdot \frac{{r_{inner}^{2} \cdot r_{outer}^{2} }}{{r_{outer}^{2} - r_{inner}^{2} }}$$
(1)
Fig. 2
figure 2

source is color filtered (600 nm), polarized and directed through the Taylor-Couette flow. A polarization camera measures the optical response in the gap. The figure is adapted from Lane et al. (2021)

Experimental setup of the Taylor-Couette flow. Light from a light

Full size image

We approximate the close to constant shear rate with the shear rate in the middle of the gap \(\dot{\gamma }(r_{middle} )\), where \(r_{middle} = {{(r_{inner} + r_{outer} )} \mathord{\left/ {\vphantom {{(r_{inner} + r_{outer} )} 2}} \right. \kern-\nulldelimiterspace} 2}\). The relative difference between inner and outer shear rate is

$$\frac{{\left| {\dot{\gamma }(r_{inner} ) - \dot{\gamma }(r_{outer} )} \right|}}{{\left| {\dot{\gamma }(r_{middle} )} \right|}} = \frac{{(r_{outer}^{2} - r_{inner}^{2} ) \cdot (r_{inner} + r_{outer} )^{2} }}{{4 \cdot r_{inner}^{2} \cdot r_{outer}^{2} }} \approx 6\%$$
(2)

With this design, shear rates between 0–31 1/s were tested. A monochrome polarization camera (Lucid Vision Labs Phoenix PHX050S-P, Nikon Nikkor 35–70 mm 1:3.3–4.5, applied f-number: f/3.3) placed above the setup measured the optical response. The default gain setting was used, and the exposure time was set to ensure a dynamic range of about 70%. The camera was not calibrated, as measurement errors are estimated to remain below 4% for this setting (Lane et al. 2022).

Using a linear polarizer has the advantage that phase differences up to \(\pi\) radians can be measured. However, only the relative positions of the refractive index axes can be determined, and no distinction between fast axis and slow axis is possible.

Optical characterization

The polarization camera used in this study is a division-of-focal-plane polarimeter that features small polarizers on every pixel. The polarizers have the directions 0°, 45°, 90°, 135° and vary in a regular pattern. The measured light intensities passing the corresponding polarizers are referred to as \(I_{0} ,I_{45} ,I_{90} ,I_{135}\). These intensities give the first three of the four Stokes parameters,

$$\begin{gathered} S_{0} = \frac{{I_{0} + I_{45} + I_{90} + I_{135} }}{2} \hfill \\ S_{1} = I_{0} - I_{90} \hfill \\ S_{2} = I_{45} - I_{135} \hfill \\ \end{gathered}$$
(3)

A polarization camera is therefore able to measure the Stokes parameters in (3) with a single snapshot. If light is only partially polarized, meaning that the light is composed of a polarized part and an unpolarized part, the fully polarized part can be expressed with the help of the degree of polarization (\(DOP \le 1\)). Applying the DOP and normalizing the Stokes parameters by \(S_{0}\) results in two normalized expressions for the fully polarized part of the light (Chipman 1995):

$$\begin{gathered} S_{{1_{N,P} }} = \frac{{S_{1} }}{{DOP \cdot S_{0} }} \hfill \\ S_{{2_{N,P} }} = \frac{{S_{2} }}{{DOP \cdot S_{0} }} \hfill \\ \end{gathered}$$
(4)

The DOP in the experiments was typically between 90 and 95%. By linking Stokes parameters to the birefringent properties of the flow, it is possible to optically characterize the fluid. The suspension is sheared due to the rotating inner cylinder and therefore becomes birefringent. The axis \(n_{2}\) is located at an angle \(\alpha\), and the extinction angle \(\chi\) describes the relative position between axis \(n_{2}\) and flow direction. The situation is schematically shown in Fig. 3. The drawing outlines the relation between extinction angle \(\chi\), angular coordinate \(\phi\) and absolute position \(\alpha\) of the slow axis \(n_{2}\):

$$\alpha = \phi + \chi$$
(5)
Fig. 3
figure 3

Relation between extinction angle \(\chi\), angular coordinate \(\phi\) and absolute position of the optical axes \(\alpha\)

Full size image

The Mueller matrix in Lane et al. (2021) relates \(\chi\) to the fast axis, which would be \(n_{1}\) in our case. However, as the method cannot distinguish between fast and slow axis, we relate \(\chi\) directly to \(n_{2}\), the correct reference axis. To make sure that this axis is the slower axis, we used a circular polarizer and analyzed the results following the theory described by Onuma and Otani (2014). This approach distinguishes fast and slow axis but can only measure phase differences up to \({\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-\nulldelimiterspace} 2}\) radians. The measurements were not used to quantify the optical properties but to determine the position of the fast and slow refractive index axes. The measurements confirmed that fast and slow axis are indeed located as indicated in Fig. 3. (It is worth mentioning that the mirror reverses the direction of circular polarization. Left-handed circularly polarized light is therefore right-handed circularly polarized after reflection. Also, if right-handed circular polarized light undergoes a phase shift of \(\pi\), it is left-handed circular polarized and the equations require a proper adaptation). The relationship between phase differences \(\delta\) and difference of the refractive indices is given as:

$$\Delta n = \frac{\lambda }{2\pi \,L}\delta$$
(6)

Here, \(\lambda\) is the wavelength of the light (600 nm) and \(L\) the optical path length, equalling the height of the inner rotating cylinder (25 mm).

We use the measurement technique described in a previous study (Lane et al. 2021) to characterize the birefringent fluid. At each position \(\phi\), the polarization camera records the intensities \(I_{0} (\phi ),I_{45} (\phi ),I_{90} (\phi ),I_{135} (\phi )\). The degree of polarization for each location is estimated when the fluid is at rest, hence not being birefringent:

$$DOP(\phi ) = \frac{{\sqrt {S_{1,rest}^{2} (\phi ) + S_{2,rest}^{2} (\phi )} }}{{S_{0,rest} (\phi )}}$$
(7)

With Eqs. (3) and (7), the normalized expressions in Eq. (4) can be measured at every position \(\phi\), giving \(S_{{1_{N,P} }} (\phi )\) and \(S_{{2_{N,P} }} (\phi )\). If we assume that the birefringent fluid can be approximated as a linear retarder with \(\delta\) being the phase difference and \(\alpha\) the position of an axis, theoretical expressions for the normalized Stokes parameters \(S_{{1_{N,P} }}\) and \(S_{{2_{N,P} }}\) are obtained by applying Mueller calculus. If the linear polarizer in Fig. 2 is in line and hence parallel to the \(I_{0}\) direction of the polarization camera, the normalized Stokes parameters resulting from Mueller calculus are:

$$\begin{gathered} S_{{1_{N,P} }} (\phi ) = 1 - \frac{1}{2}(1 - \cos [4(\phi + \chi )])\,(1 - \cos \delta ) \hfill \\ S_{{2_{N,P} }} (\phi ) = \frac{1}{2}\sin [(4(\phi + \chi )]\,(1 - \cos \delta ) \hfill \\ \end{gathered}$$
(8)

Measuring \(S_{{1_{N,P} }} (\phi )\) and \(S_{{2_{N,P} }} (\phi )\) as functions of the angular coordinate and fitting Eq. (8) to the measured distributions gives estimates for the extinction angle \(\chi\) and the phase difference \(\delta\). The distributions in Eq. (8) are periodic with period \({\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-\nulldelimiterspace} 2}\) in \(\chi\) and therefore the resulting extinction angle remains in the range between [0°, 90°]. For this reason, the distributions in Eq. (8) cannot distinguish between fast and slow axis. The results for the phase difference \(\delta\) using Eq. (8) are within the range [0,\(\pi\)]. Figure 4a, b show sample measurements of the Stokes parameters as function of the polar coordinate \(\phi\) and the correspondingly fitted distributions. In total, 200 measurement points with \(\phi\) varying between [− 3°, 154°] were analyzed. From the fits, parameters \(\chi\) and \(\delta\) are determined. Without any further information, it cannot be determined if the result for \(\delta\) is within the range [0,\(\pi\)] or within [\(\pi\),\(2\pi\)]. At the beginning of a measurement, the fluid is at rest and no birefringence occurs, corresponding to \(\delta = 0\). If the shear rate is increased by small enough steps, the measured phase differences that lie between [0,\(\pi\)] can be unwrapped to higher intervals. For example, the measurements \([0,{\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-\nulldelimiterspace} 2},\pi ,{\pi \mathord{\left/ {\vphantom {\pi {2,}}} \right. \kern-\nulldelimiterspace} {2,}}0,{\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-\nulldelimiterspace} 2},\pi ]\) correspond to \([0,{\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-\nulldelimiterspace} 2},\pi ,{{3\pi } \mathord{\left/ {\vphantom {{3\pi } 2}} \right. \kern-\nulldelimiterspace} 2},2\pi ,{{5\pi } \mathord{\left/ {\vphantom {{5\pi } {2,3\pi }}} \right. \kern-\nulldelimiterspace} {2,3\pi }}]\). With the unwrapping procedure, birefringence of multiple order retardance can be determined. This can be seen in Fig. 4c where the measured phase differences \(\delta\) are expanded to higher values. The measurement error resulting from the fitting procedure is discussed by Lane et al. (2021). For phase differences close to \(\delta = 0,2\pi ,...\), the measurement error for the extinction angle \(\chi\) is high. This becomes obvious when comparing Fig. 4a, b. The accuracy of the \(\chi\) measurements for the periodic distributions in Fig. 4a is significantly larger compared to the distributions shown in Fig. 4b. The reason for this is found in Eq. (8), indicating that the amplitude of the distributions is directly linked to the phase difference \(\delta\). If \(\delta\) is below a certain limit, we therefore neglect the corresponding \(\chi\) measurement. In this study, a limit of \(\delta \ge {\pi \mathord{\left/ {\vphantom {\pi 4}} \right. \kern-\nulldelimiterspace} 4}\) was chosen for which the measured extinction angles \(\chi\) are considered valid. Finally, we would like to note that the fitting of \(\delta\) appeared more robust compared to the fitting of \(\chi\). Many measurement points showed a strong discontinuity for \(\chi\) at \(\delta = 0,2\pi ,...\). The CNC suspensions are strongly birefringent and we assume that an unwanted re-alignment of the fluid at the top and bottom surfaces of the cylinder gap disturbs the measurements of \(\chi\). The optical influence of the unwanted alignment seems minimal in areas where the gap is parallel or perpendicular to the linear polarization of the incident light. Therefore, the presented measurements of \(\chi\) were obtained by only considering the 20 measurement points for which \(\phi\) is within [− 3°, 5°] or [86°, 94°]. For \(\delta\) however, all 200 measurement points were used, as depicted in Fig. 4.

Fig. 4
figure 4

Birefringence measurements with a linear polarizer. Suspension: 1.3 wt% CNC. a, b Results obtained by fitting Eq. (8) to the measured distributions of Eq. (4) are shown in (a) for \(\dot{\gamma } = 17.6\) and b for \(\dot{\gamma } = 7.6\). c The fitted results for \(\delta\) are between [0,\(\pi\)], sorting them according to the periodic nature gives the correct phase difference. Birefringence \(\Delta n\) is calculated with Eq. (6). d Measurement results for the extinction angle \(\chi\) using the measurement points for which \(\phi\) is between [− 3°,5°] or [86°,94°]

Full size image

Experimental procedure

Fifty different shear rates between 0 and 31 1/s were studied. Figure 4 shows the result for the suspension with 1.3 wt%. The first measurement was done at rest. After each stepwise increase, the shear rate was kept steady for five seconds before recording ten images and averaging them. From the mean image the corresponding parameters \(\delta ,\chi\) were derived. Phase differences were sorted following the procedure depicted in Fig. 4 (c). The relationship between birefringence \(\Delta n\), shear rate \(\dot{\gamma }\), and mass fraction \(w = {{w_{CNC} } \mathord{\left/ {\vphantom {{w_{CNC} } {w_{total} }}} \right. \kern-\nulldelimiterspace} {w_{total} }}\) is modeled as:

$$\Delta n = (A \cdot \dot{\gamma })^{n} \cdot w^{m}$$
(9)

Results and discussion

Measurement results for the extinction angle \(\chi\) are shown in Fig. 5a and are given in Table 1 in the appendix. All measurements that are considered valid (compare Fig. 4 for the distinction between valid and non-valid measurements) are within 23–40°. Increasing the shear rate tends to decrease the extinction angle, which is in line with common theory as discussed in the introduction. For all suspensions most of the decrease can be seen between 0 and 5 1/s. After 5 1/s, the extinction angle decreases rather slowly. We explain outliers such as the 35° measurement for 1.0 wt% at a shear rate of 24.9 1/s with measurement limitations and its uncertainties. Birefringence measurements \(\Delta n\) are shown in Fig. 5b–d. The values can be looked up in Table 2 in the appendix. It is important to note that measurement errors of \(\delta\) are high for phase differences close to \(\delta = 0,\pi ,2\pi\) (Lane et al. 2021). The non-zero values at zero shear rate in Table 2 are therefore thought to result from measurement inaccuracies. Equation (9) was fitted to the measurements and the result is plotted for comparison. The determined parameters are A = 0.1070 s, n = 0.537 and m = 2.445, giving a root-mean-square-error of 9e–7. Figure 5d shows the measurements and the fit in a base-10 logarithmic scale for the shear rates. We can see that the fit is working particularly well for the 1.1 wt% and 1.3 wt% suspension. Increasing the shear rate generally increases birefringence. The increase in birefringence per shear rate decreases for higher shear rates as the slope decreases. A rather sharp increase at low shear rates and a levelling off at higher velocity gradients has been similarly found for Xanthan gum solutions (Chow and Fuller 1984; Lane et al. 2021). Birefringence of Milling Yellow suspensions has been reported to be proportional to the shear rate at low shear rates but also shows a levelling off at higher shear rates (Peebles et al. 1964). The studied CNC suspensions display birefringence of magnitude 1e-5 and are in the same order as Xanthan gum (Lane et al. 2021) and Milling Yellow (Peebles et al. 1964). Hence CNC suspensions appear as an attractive alternative for flow visualization studies due to their stability, ease of preparation and low cost.

Fig. 5
figure 5

Steady state response as function of mass fraction and shear rate. a Extinction angle measurements. b Birefringence \(\Delta n\) measurements and fitted Eq. (9) with A = 0.1070 s, n = 0.537, m = 2.445 and a root-mean-square-error of 9e–7. c Measurement points and surface plot of Eq. (9). d Birefringence \(\Delta n\) measurements and fitted Eq. (9) in a base-10 logarithmic scale for the shear rates

Full size image

The critical concentration for interparticle interactions of aqueous CNC is reported to be 0.5 wt% and the critical volume fraction for the isotropic cholesteric phase transition is at about 3–4 wt% (Bertsch et al. 2019). Below a concentration of 0.5 wt%, CNCs are assumed to be isotropically oriented. Above 0.5 wt%, cholesteric tactoids are formed. The suspensions in this study are above 0.5 wt% and we hence expect interparticle interactions.

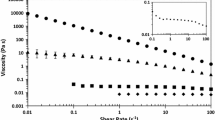
It was stated in the introduction that the relation between shear alignment and rotational diffusion is described by the Péclet number \(Pe = {{\dot{\gamma }} \mathord{\left/ {\vphantom {{\dot{\gamma }} {D_{r} }}} \right. \kern-\nulldelimiterspace} {D_{r} }}\). The rotational diffusion coefficient \(D_{r}\) for interacting rods decreases with increasing rod concentration (Doi and Edwards 1978; Maguire et al. 1980; Teraoka and Hayakawa 1989). This is because the rotational motion of a rod is increasingly restricted by its neighbors (Tao et al. 2005). Therefore, the required shear rate for the onset of particle alignment decreases with increasing concentration. It can be seen in Fig. 5d that the birefringence data seems to shift to the left with increasing concentration, which is in line with the theory. Shafiei-Sabet et al. (2012) report rheology measurements of aqueous CNC suspensions. Their 1 wt% CNC suspension is thought to be comparable to the suspensions used in this study (CNC powder dispersed in distilled water; average length: 100 nm, average width: 7 nm). The steady-state shear viscosity measurements for the 1wt% suspension show a Newtonian plateau at low shear rates (\(< \,\, \sim 10^{ - 2} {1 \mathord{\left/ {\vphantom {1 s}} \right. \kern-\nulldelimiterspace} s}\)), a shear thinning region at intermediate shear rates (\(\sim 10^{ - 2} {1 \mathord{\left/ {\vphantom {1 s}} \right. \kern-\nulldelimiterspace} s}\,\, - \,\, \sim 10^{0} {1 \mathord{\left/ {\vphantom {1 s}} \right. \kern-\nulldelimiterspace} s}\)); and a second plateau at higher shear rates. The onset of shear thinning is related to the onset of shear alignment (\(Pe \approx 1\)), and the shear rate corresponding to the onset of shear thinning can be taken as an estimate for the rotational diffusion coefficient (Corona et al. 2018). We therefore assume that all our measurements (except at zero shear rate) are taken in the shear aligned regime.

As expected, increasing the amount of CNC increases the birefringence response. Calabrese et al. (2021a) studied the birefringence of a 0.1 wt% CNC dispersion that had been similarly prepared (CNC purchased from CelluForce, diluted in deionized water). However, they purchased an aqueous dispersion (never-dried) from CelluForce whereas this study uses re-suspended CNC powder. The CNC dimensions reported by Calabrese et al. (2021a) are: average length 260 nm; average diameter 4.8 nm; aspect ratio ∼54; longest reported length ∼700 nm. Shear induced birefringence is reported to be \(\Delta n \approx 3 \cdot 10^{ - 6}\) (\(\dot{\gamma } \approx 100{{\,1} \mathord{\left/ {\vphantom {{\,1} s}} \right. \kern-\nulldelimiterspace} s}\)) and \(\Delta n \approx 9 \cdot 10^{ - 6}\) (\(\dot{\gamma } \approx 400{{\,1} \mathord{\left/ {\vphantom {{\,1} s}} \right. \kern-\nulldelimiterspace} s}\)). Compared to these values our birefringence results are much higher. This is plausible as we are using much higher CNC concentrations. For shear rates below 40 1/s the fluid from Calabrese et al. (2021a) is considered isotropic (\(\Delta n = 0\)). The onset of shear alignment and therefore equally the rotational diffusion (\(Pe \approx 1\)) is reported to be 40 1/s. The authors propose a proportionality of \(\Delta n\sim \dot{\gamma }^{0.9}\). The exponent 0.9 is significantly different to our result, 0.537. We consider several possible reasons for this difference. Calabrese et al. (2021a) are using a CNC suspension in the dilute regime and the relation between rotational diffusion coefficient \(D_{r0}\) (no particle interaction) and rod length is given as \(D_{r0} \sim l^{ - 3}\) (Doi and Edwards 1978). The suspensions in this study are thought to be above the dilute regime and hence particle interactions have to be considered. According to Maguire et al. (1980) the rotational diffusion coefficient for interacting rods is concentration and rod length dependent, giving \(D_{r} \sim c^{ - 2} l^{ - 9}\). Our different exponent could therefore be explained by a different particle interaction behavior due to the different concentrations and the shorter rod lengths. The morphological properties are dependent on the drying method (Peng et al. 2012) and this might also explain the difference.

Calabrese et al. (2021a) report that extensional forces, described by the extensional rate \(\dot{\varepsilon }\), are four times more effective in aligning CNCs than shear forces, stating \(\Delta n\sim \dot{\gamma }^{0.9} \sim (4 \cdot \dot{\varepsilon })^{0.9}\). As we only study shear forces in the Taylor-Couette flow this aspect has not been researched and it is not clear if the factor 4 is transferable to our suspensions.

Conclusion

The results presented in this study characterize the steady state birefringence response of aqueous CNC suspensions to shear, with concentrations between 0.7 and 1.3 wt%. The measurements show that the extinction angle decreases and birefringence increases with increasing shear rate. Measured birefringence is in the order of 1e–5, and a non-linear model has been fitted to the values with an accuracy estimated by a root-mean-square-error of 9e–7. The findings are in line with the theory on birefringent fluids and indicate that aqueous CNC suspensions could be used for flow birefringence studies.