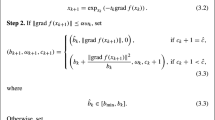An Accelerated First-Order Method for Non-convex Optimization on Manifolds

Abstract

We describe the first gradient methods on Riemannian manifolds to achieve accelerated rates in the non-convex case. Under Lipschitz assumptions on the Riemannian gradient and Hessian of the cost function, these methods find approximate first-order critical points faster than regular gradient descent. A randomized version also finds approximate second-order critical points. Both the algorithms and their analyses build extensively on existing work in the Euclidean case. The basic operation consists in running the Euclidean accelerated gradient descent method (appropriately safe-guarded against non-convexity) in the current tangent space, then moving back to the manifold and repeating. This requires lifting the cost function from the manifold to the tangent space, which can be done for example through the Riemannian exponential map. For this approach to succeed, the lifted cost function (called the pullback) must retain certain Lipschitz properties. As a contribution of independent interest, we prove precise claims to that effect, with explicit constants. Those claims are affected by the Riemannian curvature of the manifold, which in turn affects the worst-case complexity bounds for our optimization algorithms.

1 Introduction

We consider optimization problems of the form

$$\begin{aligned} \min _{x \in {\mathcal {M}}} f(x) \end{aligned}$$

(P)

where f is lower-bounded and twice continuously differentiable on a Riemannian manifold ${\mathcal {M}}$. For the special case where ${\mathcal {M}}$ is a Euclidean space, problem (P) amounts to smooth, unconstrained optimization. The more general case is important for applications notably in scientific computing, statistics, imaging, learning, communications and robotics: see for example [1, 27].

For a general non-convex objective f, computing a global minimizer of (P) is hard. Instead, our goal is to compute approximate first- and second-order critical points of (P). A number of non-convex problems of interest exhibit the property that second-order critical points are optimal [7, 11, 14, 24, 30, 36, 49]. Several of these are optimization problems on nonlinear manifolds. Therefore, theoretical guarantees for approximately finding second-order critical points can translate to guarantees for approximately solving these problems.

It is therefore natural to ask for fast algorithms which find approximate second-order critical points on manifolds, within a tolerance $\epsilon$ (see below). Existing algorithms include RTR [13], ARC [2] and perturbed RGD [20, 44]. Under some regularity conditions, ARC uses Hessian-vector products to achieve a rate of $O(\epsilon ^{-7/4})$. In contrast, under the same regularity conditions, perturbed RGD uses only function value and gradient queries, but achieves a poorer rate of $O(\epsilon ^{-2})$. Does there exist an algorithm which finds approximate second-order critical points with a rate of $O(\epsilon ^{-7/4})$ using only function value and gradient queries? The answer was known to be yes in Euclidean space. Can it also be done on Riemannian manifolds, hence extending applicability to applications treated in the aforementioned references? We resolve that question positively with the algorithm $\mathtt {PTAGD}$ below.

From a different perspective, the recent success of momentum-based first-order methods in machine learning [42] has encouraged interest in momentum-based first-order algorithms for non-convex optimization which are provably faster than gradient descent [15, 28]. We show such provable guarantees can be extended to optimization under a manifold constraint. From this perspective, our paper is part of a body of work theoretically explaining the success of momentum methods in non-convex optimization.

There has been significant difficulty in accelerating geodesically convex optimization on Riemannian manifolds. See “Related literature” below for more details on best known bounds [3] as well as results proving that acceleration in certain settings is impossible on manifolds [26]. Given this difficulty, it is not at all clear a priori that it is possible to accelerate non-convex optimization on Riemannian manifolds. Our paper shows that it is in fact possible.

We design two new algorithms and establish worst-case complexity bounds under Lipschitz assumptions on the gradient and Hessian of f. Beyond a theoretical contribution, we hope that this work will provide an impetus to look for more practical fast first-order algorithms on manifolds.

More precisely, if the gradient of f is L-Lipschitz continuous (in the Riemannian sense defined below), it is known that Riemannian gradient descent can find an $\epsilon$-approximate first-order critical point¹ in at most $O(\Delta _f L / \epsilon ^2)$ queries, where $\Delta _f$ upper-bounds the gap between initial and optimal cost value [8, 13, 47]. Moreover, this rate is optimal in the special case where ${\mathcal {M}}$ is a Euclidean space [16], but it can be improved under the additional assumption that the Hessian of f is $\rho$-Lipschitz continuous.

Recently in Euclidean space, Carmon et al. [15] have proposed a deterministic algorithm for this setting (L-Lipschitz gradient, $\rho$-Lipschitz Hessian) which requires at most ${{\tilde{O}}}(\Delta _f L^{1/2} \rho ^{1/4} / \epsilon ^{7/4})$ queries (up to logarithmic factors), and is independent of dimension. This is a speed up of Riemannian gradient descent by a factor of ${{\tilde{\Theta }}}(\sqrt{\frac{L}{\sqrt{\rho \epsilon }}})$. For the Euclidean case, it has been shown under these assumptions that first-order methods require at least $\Omega (\Delta _f L^{3/7} \rho ^{2/7} / \epsilon ^{12/7})$ queries [17, Thm. 2]. This leaves a gap of merely ${{\tilde{O}}}(1/\epsilon ^{1/28})$ in the $\epsilon$-dependency.

Soon after, Jin et al. [28] showed how a related algorithm with randomization can find $(\epsilon , \sqrt{\rho \epsilon })$-approximate second-order critical points² with the same complexity, up to polylogarithmic factors in the dimension of the search space and in the (reciprocal of) the probability of failure.

Both the algorithm of Carmon et al. [15] and that of Jin et al. [28] fundamentally rely on Nesterov’s accelerated gradient descent method (AGD) [40], with safe-guards against non-convexity. To achieve improved rates, AGD builds heavily on a notion of momentum which accumulates across several iterations. This makes it delicate to extend AGD to nonlinear manifolds, as it would seem that we need to transfer momentum from tangent space to tangent space, all the while keeping track of fine properties.

In this paper, we build heavily on the Euclidean work of Jin et al. [28] to show the following. Assume f has Lipschitz continuous gradient and Hessian on a complete Riemannian manifold satisfying some curvature conditions. With at most $\tilde{O}(\Delta _f L^{1/2} {{\hat{\rho }}}^{1/4} / \epsilon ^{7/4})$ queries (where ${{\hat{\rho }}}$ is larger than $\rho$ by an additive term affected by L and the manifold’s curvature),

• 1. It is possible to compute an $\epsilon$-approximate first-order critical point of f with a deterministic first-order method,

• 2. It is possible to compute an $(\epsilon , \sqrt{{{\hat{\rho }}} \epsilon })$-approximate second-order critical point of f with a randomized first-order method.

In the first case, the complexity is independent of the dimension of ${\mathcal {M}}$. In the second case, the complexity includes polylogarithmic factors in the dimension of ${\mathcal {M}}$ and in the probability of failure. This parallels the Euclidean setting. In both cases (and in contrast to the Euclidean setting), the Riemannian curvature of ${\mathcal {M}}$ affects the complexity in two ways: (a) because ${{\hat{\rho }}}$ is larger than $\rho$, and (b) because the results only apply when the target accuracy $\epsilon$ is small enough in comparison with some curvature-dependent thresholds. It is an interesting open question to determine whether such a curvature dependency is inescapable.

We call our first algorithm $\mathtt {TAGD}$ for tangent accelerated gradient descent,³ and the second algorithm $\mathtt {PTAGD}$ for perturbed tangent accelerated gradient descent. Both algorithms and (even more so) their analyses closely mirror the perturbed accelerated gradient descent algorithm (PAGD) of Jin et al. [28], with one core design choice that facilitates the extension to manifolds: instead of transporting momentum from tangent space to tangent space, we run several iterations of AGD (safe-guarded against non-convexity) in individual tangent spaces. After an AGD run in the current tangent space, we “retract” back to a new point on the manifold and initiate another AGD run in the new tangent space. In so doing, we only need to understand the fine behavior of AGD in one tangent space at a time. Since tangent spaces are linear spaces, we can capitalize on existing Euclidean analyses. This general approach is in line with prior work in [20], and is an instance of the dynamic trivializations framework of Lezcano-Casado [33].

In order to run AGD on the tangent space $\mathrm {T}_x{\mathcal {M}}$ at x, we must “pullback” the cost function f from ${\mathcal {M}}$ to $\mathrm {T}_x{\mathcal {M}}$. A geometrically pleasing way to do so is via the exponential map⁴$\mathrm {Exp}_x :\mathrm {T}_x{\mathcal {M}}\rightarrow {\mathcal {M}}$, whose defining feature is that for each $v \in \mathrm {T}_x{\mathcal {M}}$ the curve $\gamma (t) = \mathrm {Exp}_x(tv)$ is the geodesic of ${\mathcal {M}}$ passing through $\gamma (0) = x$ with velocity $\gamma '(0) = v$. Then, ${{\hat{f}}}_x = f \circ \mathrm {Exp}_x$ is a real function on $\mathrm {T}_x{\mathcal {M}}$ called the pullback of f at x. To analyze the behavior of AGD applied to ${{\hat{f}}}_x$, the most pressing question is:

To what extent does ${{\hat{f}}}_x = f \circ \mathrm {Exp}_x$ inherit the Lipschitz properties of f?

In this paper, we show that if f has Lipschitz continuous gradient and Hessian and if the gradient of f at x is sufficiently small, then ${{\hat{f}}}_x$ restricted to a ball around the origin of $\mathrm {T}_x{\mathcal {M}}$ has Lipschitz continuous gradient and retains partial Lipschitz-type properties for its Hessian. The norm condition on the gradient and the radius of the ball are dictated by the Riemannian curvature of ${\mathcal {M}}$. These geometric results are of independent interest.

Because ${{\hat{f}}}_x$ retains only partial Lipschitzness, our algorithms depart from the Euclidean case in the following ways: (a) at points where the gradient is still large, we perform a simple gradient step; and (b) when running AGD in $\mathrm {T}_x{\mathcal {M}}$, we are careful not to leave the prescribed ball around the origin: if we ever do, we take appropriate action. For those reasons and also because we do not have full Lipschitzness but only radial Lipschitzness for the Hessian of ${{\hat{f}}}_x$, minute changes throughout the analysis of Jin et al. [28] are in order.

To be clear, in their current state, $\mathtt {TAGD}$ and $\mathtt {PTAGD}$ are theoretical constructs. As one can see from later sections, running them requires the user to know the value of several parameters that are seldom available (including the Lipschitz constants L and $\rho$); the target accuracy $\epsilon$ must be set ahead of time; and the tuning constants as dictated here by the theory are (in all likelihood) overly cautious.

Moreover, to compute the gradient of ${{\hat{f}}}_x$ we need to differentiate through the exponential map (or a retraction, as the case may be). This is sometimes easy to do in closed form (see [33] for families of examples), but it could be a practical hurdle. On the other hand, our algorithms do not require parallel transport. It remains an interesting open question to develop practical accelerated gradient methods for non-convex problems on manifolds.

In closing this introduction, we give simplified statements of our main results. These are all phrased under the following assumption (see Sect. 2 for geometric definitions):

A 1

The Riemannian manifold ${\mathcal {M}}$ and the cost function $f :{\mathcal {M}}\rightarrow {{\mathbb {R}}}$ have these properties:

• ${\mathcal {M}}$ is complete, its sectional curvatures are in the interval $[-K, K]$, and the covariant derivative of its Riemann curvature endomorphism is bounded by F in operator norm; and

• f is lower-bounded by $f_{\mathrm {low}}$, has L-Lipschitz continuous gradient $\mathrm {grad}f$ and $\rho$-Lipschitz continuous Hessian $\mathrm {Hess}f$ on ${\mathcal {M}}$.

1.1 Main Geometry Results

As a geometric contribution, we show that pullbacks through the exponential map retain certain Lipschitz properties of f. Explicitly, at a point $x \in {\mathcal {M}}$ we have the following statement.

Theorem 1.1

Let $x \in {\mathcal {M}}$. Under A1, let $B_x(b)$ be the closed ball of radius $b \le \min \!\left( \frac{1}{4\sqrt{K}}, \frac{K}{4F} \right)$ around the origin in $\mathrm {T}_x{\mathcal {M}}$. If $\Vert \mathrm {grad}f(x)\Vert \le Lb$, then

• 1. The pullback ${{\hat{f}}}_x = f \circ \mathrm {Exp}_x$ has 2L-Lipschitz continuous gradient $\nabla {{\hat{f}}}_x$ on $B_x(b)$, and

• 2. For all $s \in B_x(b)$, we have $\Vert \nabla ^2 {{\hat{f}}}_x(s) - \nabla ^2 {{\hat{f}}}_x(0)\Vert \le {{\hat{\rho }}} \Vert s\Vert$ with ${{\hat{\rho }}} = \rho + L\sqrt{K}$.

(Above, $\Vert \cdot \Vert$ denotes both the Riemannian norm on $\mathrm {T}_x{\mathcal {M}}$ and the associated operator norm. Also, $\nabla {{\hat{f}}}_x$ and $\nabla ^2 {{\hat{f}}}_x$ are the gradient and Hessian of ${{\hat{f}}}_x$ on the Euclidean space $\mathrm {T}_x{\mathcal {M}}$.)

We expect this result to be useful in several other contexts. Section 2 provides a more complete (and somewhat more general) statement. At the same time and independently, Lezcano-Casado [35] develops similar geometric bounds and applies them to study gradient descent in tangent spaces—see “Related literature” below for additional details.

1.2 Main Optimization Results

We aim to compute approximate first- and second-order critical points of f, as defined here:

Definition 1.2

A point $x \in {\mathcal {M}}$ is an $\epsilon$-FOCP for (P) if $\Vert \mathrm {grad}f(x)\Vert \le \epsilon$. A point $x \in {\mathcal {M}}$ is an $(\epsilon _1, \epsilon _2)$-SOCP for (P) if $\Vert \mathrm {grad}f(x)\Vert \le \epsilon _1$ and $\lambda _{\mathrm {min}}(\mathrm {Hess}f(x)) \ge -\epsilon _2$, where $\lambda _{\mathrm {min}}(\cdot )$ extracts the smallest eigenvalue of a self-adjoint operator.

In Sect. 5, we define and analyze the algorithm $\mathtt {TAGD}$. Resting on the geometric result above, that algorithm with the exponential retraction warrants the following claim about the computation of first-order points. The $O(\cdot )$ notation is with respect to scaling in $\epsilon$.

Theorem 1.3

If A1 holds, there exists an algorithm ($\mathtt {TAGD}$) which, given any $x_0 \in {\mathcal {M}}$ and small enough tolerance $\epsilon > 0$, namely,

$$\begin{aligned} \epsilon&\le \frac{1}{144} \min \!\left( \frac{1}{K} {{\hat{\rho }}}, \frac{K^2}{F^2} {{\hat{\rho }}}, \frac{36 \ell ^2}{{{\hat{\rho }}}}\right) \nonumber \\ {}&= \frac{1}{144} \min \!\left( \frac{1}{K}, \frac{K^2}{F^2}, \left( \frac{12 L}{\rho + L\sqrt{K}}\right) ^2 \right) (\rho + L\sqrt{K}), \end{aligned}$$

(1)

produces an $\epsilon$-FOCP for (P) using at most a constant multiple of T function and pullback gradient queries, and a similar number of evaluations of the exponential map, where

$$\begin{aligned} T&= (f(x_0) - f_{\mathrm {low}}) \frac{{\hat{\rho }}^{1/4} \ell ^{1/2}}{\epsilon ^{7/4}} \log \!\left( \frac{16\ell }{\sqrt{{\hat{\rho }} \epsilon }}\right) ^{6} \\&= O\!\left( (f(x_0) - f_{\mathrm {low}}) (\rho + L\sqrt{K})^{1/4} L^{1/2} \cdot \frac{1}{\epsilon ^{7/4}} \log \!\left( \frac{1}{\epsilon }\right) ^6 \right) , \end{aligned}$$

with $\ell = 2L$ and ${{\hat{\rho }}} = \rho + L\sqrt{K}$. The algorithm uses no Hessian queries and is deterministic.

This result is dimension-free but not curvature-free because K and F constrain $\epsilon$ and affect ${{\hat{\rho }}}$.

Remark 1.4

In the statements of all theorems and lemmas, the notations $O(\cdot ), \Theta (\cdot )$ only hide universal constants, i.e., numbers like $\frac{1}{2}$ or 100. They do not hide any parameters. Moreover, ${\tilde{O}}(\cdot ), {\tilde{\Theta }}(\cdot )$ only hide universal constants and logarithmic factors in the parameters.

Remark 1.5

If $\epsilon$ is large enough (that is, if $\epsilon > \Theta (\frac{\ell ^2}{{{\hat{\rho }}}})$), then $\mathtt {TAGD}$ reduces to vanilla Riemannian gradient descent with constant step-size. The latter is known to produce an $\epsilon$-FOCP in $O(1/\epsilon ^2)$ iterations, yet our result here announces this same outcome in $O(1/\epsilon ^{7/4})$ iterations. This is not a contradiction: when $\epsilon$ is large, $1/\epsilon ^{7/4}$ can be worse than $1/\epsilon ^2$. In short: the rates are only meaningful for small $\epsilon$, in which case $\mathtt {TAGD}$ does use accelerated gradient descent steps.

In Sect. 6 we define and analyze the algorithm $\mathtt {PTAGD}$. With the exponential retraction, the latter warrants the following claim about the computation of second-order points.

Theorem 1.6

If A1 holds, there exists an algorithm ($\mathtt {PTAGD}$) which, given any $x_0 \in {\mathcal {M}}$, any $\delta \in (0, 1)$ and small enough tolerance $\epsilon > 0$ (same condition as in Theorem 1.3) produces an $\epsilon$-FOCP for (P) using at most a constant multiple of T function and pullback gradient queries, and a similar number of evaluations of the exponential map, where

$$\begin{aligned} T&= (f(x_0) - f_{\mathrm {low}}) \frac{{\hat{\rho }}^{1/4} \ell ^{1/2}}{\epsilon ^{7/4}} \log \!\left( \frac{d^{1/2} \ell ^{3/2} \Delta _f}{({{\hat{\rho }}} \epsilon )^{1/4} \epsilon ^2 \delta } \right) ^{6} + \frac{\ell ^{1/2}}{{{\hat{\rho }}}^{1/4} \epsilon ^{1/4}} \log \!\left( \frac{d^{1/2} \ell ^{3/2} \Delta _f}{({{\hat{\rho }}} \epsilon )^{1/4} \epsilon ^2 \delta } \right) \\&= O\!\left( (f(x_0) - f_{\mathrm {low}}) (\rho + L\sqrt{K})^{1/4} L^{1/2} \cdot \frac{1}{\epsilon ^{7/4}} \log \!\left( \frac{d}{\epsilon \delta }\right) ^6 \right) , \end{aligned}$$

with $\ell = 2L$, ${{\hat{\rho }}} = \rho + L\sqrt{K}$, $d = \dim {\mathcal {M}}$ and any $\Delta _f \ge \max (f(x_0) - f_{\mathrm {low}}, \sqrt{\epsilon ^3 / {\hat{\rho }}})$. With probability at least $1 - 2\delta$, that point is also $(\epsilon , \sqrt{{{\hat{\rho }}} \epsilon })$-SOCP. The algorithm uses no Hessian queries and is randomized.

This result is almost dimension-free, and still not curvature-free for the same reasons as above.

1.3 Related Literature

At the same time and independently, Lezcano-Casado [35] develops geometric bounds similar to our own. Both papers derive the same second-order inhomogenous linear ODE (ordinary differential equation) describing the behavior of the second derivative of the exponential map. Lezcano-Casado [35] then uses ODE comparison techniques to derive the geometric bounds, while the present work uses a bootstrapping technique. Lezcano-Casado [35] applies these bounds to study gradient descent in tangent spaces, whereas we study non-convex accelerated algorithms for finding first- and second-order critical points.

The technique of pulling back a function to a tangent space is frequently used in other settings within optimization on manifolds. See for example the recent papers of Bergmann et al. [9] and Lezcano-Casado [34]. Additionally, the use of Riemannian Lipschitz conditions in optimization as they appear in Section 2 can be traced back to [21, Def. 4.1] and [23, Def. 2.2].

Accelerating optimization algorithms on Riemannian manifolds has been well-studied in the context of geodesically convex optimization problems. Such problems can be solved globally, and usually the objective is to bound the suboptimality gap rather than finding approximate critical points. A number of papers have studied Riemannian versions of AGD; however, none of these papers have been able to achieve a fully accelerated rate for convex optimization. Zhang and Sra [48] show that if the initial iterate is sufficiently close to the minimizer, then acceleration is possible. Intuitively this makes sense, since manifolds are locally Euclidean. Ahn and Sra [3] pushed this further, developing an algorithm converging strictly faster than RGD, and which also achieves acceleration when sufficiently close to the minimizer.

Alimisis et al. [4,5,6] analyze the problem of acceleration on the class of non-strongly convex functions, as well as under weaker notions of convexity. Interestingly, they also show that in the continuous limit (using an ODE to model optimization algorithms) acceleration is possible. However, it is unclear whether the discretization of this ODE preserves a similar acceleration.

Recently, Hamilton and Moitra [26] have shown that full acceleration (in the geodesically convex case) is impossible in the hyperbolic plane, in the setting where function values and gradients are corrupted by a very small amount of noise. In contrast, in the analogous Euclidean setting, acceleration is possible even with noisy oracles [22].

2 Riemannian Tools and Regularity of Pullbacks

In this section, we build up to and state our main geometric result. As we do so, we provide a few reminders of Riemannian geometry. For more on this topic, we recommend the modern textbooks by Lee [31, 32]. For book-length, optimization-focused introductions see [1, 12]. Some proofs of this section appear in Appendices A and B.

We consider a manifold ${\mathcal {M}}$ with Riemannian metric $\left\langle {\cdot },{\cdot }\right\rangle _x$ and associated norm $\Vert \cdot \Vert _x$ on the tangent spaces $\mathrm {T}_x{\mathcal {M}}$. (In other sections, we omit the subscript x.) The tangent bundle

$$\begin{aligned} \mathrm {T}{\mathcal {M}}= \{ (x, s) : x \in {\mathcal {M}}{\text { and }} s \in \mathrm {T}_x{\mathcal {M}}\} \end{aligned}$$

is itself a smooth manifold. The Riemannian metric provides a notion of gradient.

Definition 2.1

The Riemannian gradient of a differentiable function $f :{\mathcal {M}}\rightarrow {{\mathbb {R}}}$ is the unique vector field $\mathrm {grad}f$ on ${\mathcal {M}}$ which satisfies:

$$\begin{aligned} \mathrm {D}f(x)[s]&= \left\langle {\mathrm {grad}f(x)},{s}\right\rangle _x&{\text { for all }} (x, s) \in \mathrm {T}{\mathcal {M}}, \end{aligned}$$

where $\mathrm {D}f(x)[s]$ is the directional derivative of f at x along s.

The Riemannian metric further induces a uniquely defined Riemannian connection $\nabla$ (used to differentiate vector fields on ${\mathcal {M}}$) and an associated covariant derivative $\mathrm {D}_t$ (used to differentiate vector fields along curves on ${\mathcal {M}}$). (The symbol $\nabla$ here is not to be confused with its use elsewhere to denote differentiation of scalar functions on Euclidean spaces.) Applying the connection to the gradient vector field, we obtain Hessians.

Definition 2.2

The Riemannian Hessian of a twice differentiable function $f :{\mathcal {M}}\rightarrow {{\mathbb {R}}}$ at x is the linear operator $\mathrm {Hess}f(x)$ to and from $\mathrm {T}_x{\mathcal {M}}$ defined by

$$\begin{aligned} \mathrm {Hess}f(x)[s]&= \nabla _s \mathrm {grad}f = \left. \mathrm {D}_t\mathrm {grad}f(c(t)) \right| _{t = 0}, \end{aligned}$$

where in the last equality c can be any smooth curve on ${\mathcal {M}}$ satisfying $c(0) = x$ and $c'(0) = s$. This operator is self-adjoint with respect to the metric $\left\langle {\cdot },{\cdot }\right\rangle _x$.

We can also define the Riemmannian third derivative $\nabla ^3 f$ (a tensor of order three), see [12, Ch. 10] for details. We write $\left\| {\nabla ^3 f(x)}\right\| \le \rho$ to mean $\left| \nabla ^3 f(x)(u, v, w)\right| \le \rho$ for all unit vectors $u, v, w \in \mathrm {T}_x{\mathcal {M}}$.

A retraction $\mathrm {R}$ is a smooth map from (a subset of) $\mathrm {T}{\mathcal {M}}$ to ${\mathcal {M}}$ with the following property: for all $(x, s) \in \mathrm {T}{\mathcal {M}}$, the smooth curve $c(t) = \mathrm {R}(x, ts) = \mathrm {R}_x(ts)$ on ${\mathcal {M}}$ passes through $c(0) = x$ with velocity $c'(0) = s$. Such maps are used frequently in Riemannian optimization in order to move on a manifold. For example, a key ingredient of Riemannian gradient descent is the curve $c(t) = \mathrm {R}_x(-t \mathrm {grad}f(x))$ which initially moves away from x along the negative gradient direction.

To a curve c, we naturally associate a velocity vector field $c'$. Using the covariant derivative $\mathrm {D}_t$, we differentiate this vector field along c to define the acceleration $c'' = \mathrm {D}_tc'$ of c: this is also a vector field along c. In particular, the geodesics of ${\mathcal {M}}$ are the curves with zero acceleration.

The exponential map $\mathrm {Exp}:{\mathcal {O}}\rightarrow {\mathcal {M}}$—defined on an open subset ${\mathcal {O}}$ of the tangent bundle—is a special retraction whose curves are geodesics. Specifically, $\gamma (t) = \mathrm {Exp}(x, ts) = \mathrm {Exp}_x(ts)$ is the unique geodesic on ${\mathcal {M}}$ which passes through $\gamma (0) = x$ with velocity $\gamma '(0) = s$. If the domain of $\mathrm {Exp}$ is the whole tangent bundle, we say ${\mathcal {M}}$ is complete.

To compare tangent vectors in distinct tangent spaces, we use parallel transports. Explicitly, let c be a smooth curve connecting the points $c(0) = x$ and $c(1) = y$. We say a vector field Z along c is parallel if its covariant derivative $\mathrm {D}_tZ$ is zero. Conveniently, for any given $v \in \mathrm {T}_x{\mathcal {M}}$ there exists a unique parallel vector field along c whose value at $t = 0$ is v. Therefore, the value of that vector field at $t = 1$ is a well-defined vector in $\mathrm {T}_y{\mathcal {M}}$: we call it the parallel transport of v from x to y along c. We introduce the notation

$$\begin{aligned} P_t^c :\mathrm {T}_{c(0)}{\mathcal {M}}\rightarrow \mathrm {T}_{c(t)}{\mathcal {M}}\end{aligned}$$

to denote parallel transport along a smooth curve c from c(0) to c(t). This is a linear isometry: $(P_t^c)^{-1} = (P_t^c)^*$, where the star denotes an adjoint with respect to the Riemannian metric. For the special case of parallel transport along the geodesic $\gamma (t) = \mathrm {Exp}_x(ts)$, we write

$$\begin{aligned} P_{ts} :\mathrm {T}_x{\mathcal {M}}\rightarrow \mathrm {T}_{\mathrm {Exp}_x(ts)}{\mathcal {M}} \end{aligned}$$

(2)

with the meaning $P_{ts} = P_t^\gamma$.

Using these tools, we can define Lipschitz continuity of gradients and Hessians. Note that in the particular case where ${\mathcal {M}}$ is a Euclidean space we have $\mathrm {Exp}_x(s) = x + s$ and parallel transports are identities, so that this reduces to the usual definitions.

Definition 2.3

The gradient of $f :{\mathcal {M}}\rightarrow {{\mathbb {R}}}$ is L-Lipschitz continuous if

$$\begin{aligned} \Vert P_s^* \mathrm {grad}f(\mathrm {Exp}_x(s)) - \mathrm {grad}f(x)\Vert _x&\le L \Vert s\Vert _x&{\text { for all }} (x, s) \in {\mathcal {O}}, \end{aligned}$$

(3)

where $P_s^*$ is the adjoint of $P_s$ with respect to the Riemannian metric.

The Hessian of f is $\rho$-Lipschitz continuous if

$$\begin{aligned} \Vert P_s^* \circ \mathrm {Hess}f(\mathrm {Exp}_x(s)) \circ P_s - \mathrm {Hess}f(x)\Vert _x&\le \rho \Vert s\Vert _x&{\text { for all }} (x, s) \in {\mathcal {O}}, \end{aligned}$$

(4)

where $\Vert \cdot \Vert _x$ denotes both the Riemannian norm on $\mathrm {T}_x{\mathcal {M}}$ and the associated operator norm.

It is well known that these Lipschitz conditions are equivalent to convenient inequalities, often used to study the complexity of optimization algorithms. More details appear in [12, Ch. 10].

Proposition 2.4

If a function $f :{\mathcal {M}}\rightarrow {{\mathbb {R}}}$ has L-Lipschitz continuous gradient, then

$$\begin{aligned} \left| f(\mathrm {Exp}_x(s)) - f(x) - \left\langle {\mathrm {grad}f(x)},{s}\right\rangle _x \right|&\le \frac{L}{2} \Vert s\Vert _x^2&{\text { for all }} (x, s) \in {\mathcal {O}}. \end{aligned}$$

If in addition f is twice differentiable, then $\left\| {\mathrm {Hess}f(x)}\right\| \le L$ for all $x \in {\mathcal {M}}$.

If f has $\rho$-Lipschitz continuous Hessian, then

$$\begin{aligned}&\left| f(\mathrm {Exp}_x(s)) - f(x) - \left\langle {\mathrm {grad}f(x)},{s}\right\rangle _x - \frac{1}{2} \left\langle {s},{\mathrm {Hess}f(x)[s]}\right\rangle _x \right| \\&\quad \le \frac{\rho }{6} \Vert s\Vert _x^3 \quad {\text { and}} \\&\quad \left\| P_{s}^* \mathrm {grad}f(\mathrm {Exp}_x(s)) - \mathrm {grad}f(x) - \mathrm {Hess}f(x)[s] \right\| _x \\&\quad \le \frac{\rho }{2} \Vert s\Vert _x^2 \quad {\text { for all }} (x, s) \in {\mathcal {O}}.&\end{aligned}$$

If in addition f is three times differentiable, then $\left\| {\nabla ^3 f(x)}\right\| \le \rho$ for all $x \in {\mathcal {M}}$.

The other way around, if f is three times continuously differentiable and the stated inequalities hold, then its gradient and Hessian are Lipschitz continuous with the stated constants.

For sufficiently simple algorithms, these inequalities may be all we need to track progress in a sharp way. As an example, the iterates of Riemannian gradient descent with constant step-size 1/L satisfy $x_{k+1} = \mathrm {Exp}_{x_k}(s_k)$ with $s_k = -\frac{1}{L}\mathrm {grad}f(x_k)$. It follows directly from the first inequality above that $f(x_k) - f(x_{k+1}) \ge \frac{1}{2L} \Vert \mathrm {grad}f(x_k)\Vert ^2$. From there, it takes a brief argument to conclude that this method finds a point with gradient smaller than $\epsilon$ in at most $2L(f(x_0) - f_{\mathrm {low}})\frac{1}{\epsilon ^2}$ steps. A similar (but longer) story applies to the analysis of Riemannian trust regions and adaptive cubic regularization [2, 13].

However, the inequalities in Proposition 2.4 fall short when finer properties of the algorithms are only visible at the scale of multiple combined iterations. This is notably the case for accelerated gradient methods. For such algorithms, individual iterations may not achieve spectacular cost decrease, but a long sequence of them may accumulate an advantage over time (using momentum). To capture this advantage in an analysis, it is not enough to apply inequalities above to individual iterations. As we turn to assessing a string of iterations jointly by relating the various gradients and step directions we encounter, the nonlinearity of ${\mathcal {M}}$ generates significant hurdles.

For these reasons, we study the pullbacks of the cost function, namely, the functions

$$\begin{aligned} {{\hat{f}}}_x&= f \circ \mathrm {Exp}_x :\mathrm {T}_x{\mathcal {M}}\rightarrow {{\mathbb {R}}}. \end{aligned}$$

(5)

Each pullback is defined on a linear space, hence we can in principle run any Euclidean optimization algorithm on ${{\hat{f}}}_x$ directly: our strategy is therefore to apply a momentum-based method on ${\hat{f}}_x$. To this end, we now work towards showing that if f has Lipschitz continuous gradient and Hessian then ${{\hat{f}}}_x$ also has certain Lipschitz-type properties.

The following formulas appear in [2, Lem. 5]: we are interested in the case $\mathrm {R}= \mathrm {Exp}$. (We use $\nabla$ and $\nabla ^2$ to designate gradients and Hessians of functions on Euclidean spaces: not to be confused with the connection $\nabla$.)

Lemma 2.5

Given $f :{\mathcal {M}}\rightarrow {{\mathbb {R}}}$ twice continuously differentiable and (x, s) in the domain of a retraction $\mathrm {R}$, the gradient and Hessian of the pullback ${{\hat{f}}}_x = f \circ \mathrm {R}_x$ at $s \in \mathrm {T}_x{\mathcal {M}}$ are given by

$$\begin{aligned} \nabla {{\hat{f}}}_x(s)&= T_s^* \mathrm {grad}f(\mathrm {R}_x(s))&{\text { and }}&\nabla ^2 {{\hat{f}}}_x(s)&= T_s^* \circ \mathrm {Hess}f(\mathrm {R}_x(s)) \circ T_s + W_s, \end{aligned}$$

(6)

where $T_s$ is the differential of $\mathrm {R}_x$ at s (a linear operator):

$$\begin{aligned} T_s&= \mathrm {D}\mathrm {R}_x(s) :\mathrm {T}_{x}{\mathcal {M}}\rightarrow \mathrm {T}_{\mathrm {R}_x(s)}{\mathcal {M}}, \end{aligned}$$

(7)

and $W_s$ is a self-adjoint linear operator on $\mathrm {T}_x{\mathcal {M}}$ defined through polarization by

$$\begin{aligned} \left\langle {W_s[\dot{s}]},{\dot{s}}\right\rangle _x&= \left\langle {\mathrm {grad}f(\mathrm {R}_x(s))},{c''(0)}\right\rangle _{\mathrm {R}_x(s)}, \end{aligned}$$

(8)

with $c''(0) \in \mathrm {T}_{\mathrm {R}_x(s)}{\mathcal {M}}$ the (intrinsic) acceleration on ${\mathcal {M}}$ of $c(t) = \mathrm {R}_x(s+t\dot{s})$ at $t = 0$.

Remark 2.6

Throughout, $s, \dot{s}, \ddot{s}$ will simply denote tangent vectors.

We turn to curvature. The Lie bracket of two smooth vector fields X, Y on ${\mathcal {M}}$ is itself a smooth vector field, conveniently expressed in terms of the Riemannian connection as $[X, Y] = \nabla _X Y - \nabla _Y X$. Using this notion, the Riemann curvature endomorphism R of ${\mathcal {M}}$ is an operator which maps three smooth vector fields X, Y, Z of ${\mathcal {M}}$ to a fourth smooth vector field as:

$$\begin{aligned} R(X, Y) Z&= \nabla _X \nabla _Y Z - \nabla _Y \nabla _X Z - \nabla _{[X, Y]} Z. \end{aligned}$$

(9)

Whenever R is identically zero, we say ${\mathcal {M}}$ is flat: this is the case notably when ${\mathcal {M}}$ is a Euclidean space and when ${\mathcal {M}}$ has dimension one (e.g., a circle is flat, while a sphere is not).

Though it is not obvious from the definition, the value of the vector field R(X, Y)Z at $x \in {\mathcal {M}}$ depends on X, Y, Z only through their value at x. Therefore, given $u, v, w \in \mathrm {T}_x{\mathcal {M}}$ we can make sense of the notation R(u, v)w as denoting the vector in $\mathrm {T}_x{\mathcal {M}}$ corresponding to R(X, Y)Z at x, where X, Y, Z are arbitrary smooth vector fields whose values at x are u, v, w, respectively. The map $(u, v, w) \mapsto R(u, v)w$ is linear in each input.

Two linearly independent tangent vectors u, v at x span a two-dimensional plane of $\mathrm {T}_x{\mathcal {M}}$. The sectional curvature of ${\mathcal {M}}$ along that plane is a real number K(u, v) defined as

$$\begin{aligned} K(u, v)&= \frac{\left\langle {R(u, v)v},{u}\right\rangle _x}{\Vert u\Vert _x^2\Vert v\Vert _x^2 - \left\langle {u},{v}\right\rangle _x^2}. \end{aligned}$$

(10)

Of course, all sectional curvatures of flat manifolds are zero. Also, all sectional curvatures of a sphere of radius r are $1/r^2$ and all sectional curvatures of the hyperbolic space with parameter r are $-1/r^2$—see [32, Thm. 8.34].

Using the connection $\nabla$, we differentiate the curvature endomorphism R as follows. Given any smooth vector field U, we let $\nabla _U R$ be an operator of the same type as R itself, in the sense that it maps three smooth vector fields X, Y, Z to a fourth one denoted $(\nabla _U R)(X, Y)Z$ through

$$\begin{aligned} (\nabla _U R)(X, Y)Z&= \nabla _U(R(X, Y) Z) - R(\nabla _U X, Y) Z \nonumber \\&\quad - R(X, \nabla _U Y) Z - R(X, Y) \nabla _U Z. \end{aligned}$$

(11)

Observe that this formula captures a convenient chain rule on $\nabla _U(R(X, Y) Z)$. As for R, the value of $\nabla R(X, Y, Z, U) \triangleq (\nabla _U R)(X, Y)Z$ at x depends on X, Y, Z, U only through their values at x. Therefore, $\nabla R$ unambiguously maps $u, v, w, z \in \mathrm {T}_x{\mathcal {M}}$ to $\nabla R(u, v, w, z) \in \mathrm {T}_x{\mathcal {M}}$, linearly in all inputs. We say the operator norm of $\nabla R$ at x is bounded by F if

$$\begin{aligned} \Vert \nabla R(u, v, w, z)\Vert _x&\le F \Vert u\Vert _x \Vert v\Vert _x \Vert w\Vert _x \Vert z\Vert _x \end{aligned}$$

for all $u, v, w, z \in \mathrm {T}_x{\mathcal {M}}$. We say $\nabla R$ has operator norm bounded by F if this holds for all x. If $F = 0$ (that is, $\nabla R \equiv 0$), we say R is parallel and ${\mathcal {M}}$ is called locally symmetric. This is notably the case for manifolds with constant sectional curvature—Euclidean spaces, spheres and hyperbolic spaces—and (Riemannian) products thereof [41, pp. 219–221].

We are ready to state the main result of this section. Note that ${\mathcal {M}}$ need not be complete.

Theorem 2.7

Let ${\mathcal {M}}$ be a Riemannian manifold whose sectional curvatures are in the interval $[{K_{\mathrm {low}}}, {K_{\mathrm {up}}}]$, and let $K = \max (|{K_{\mathrm {low}}}|, |{K_{\mathrm {up}}}|)$. Also assume $\nabla R$—the covariant derivative of the Riemann curvature endomorphism R—is bounded by F in operator norm.

Let $f :{\mathcal {M}}\rightarrow {{\mathbb {R}}}$ be twice continuously differentiable and select $b > 0$ such that

$$\begin{aligned} b \le \min \!\left( \frac{1}{4\sqrt{K}}, \frac{K}{4F} \right) . \end{aligned}$$

Pick any point $x \in {\mathcal {M}}$ such that $\mathrm {Exp}_x$ is defined on the closed ball $B_x(b)$ of radius b around the origin in $\mathrm {T}_x{\mathcal {M}}$. We have the following three conclusions:

• 1. If f has L-Lipschitz continuous gradient and $\Vert \mathrm {grad}f(x)\Vert _x \le Lb$, then ${{\hat{f}}}_x = f \circ \mathrm {Exp}_x$ has 2L-Lipschitz continuous gradient in $B_x(b)$, that is, for all $u, v \in B_x(b)$ it holds that $\Vert \nabla {{\hat{f}}}_x(u) - \nabla {{\hat{f}}}_x(v)\Vert _x \le 2L \Vert u - v\Vert _x$.

• 2. If moreover f has $\rho$-Lipschitz continuous Hessian, then $\Vert \nabla ^2 {{\hat{f}}}_x(s) - \nabla ^2 {{\hat{f}}}_x(0)\Vert _x \le {{\hat{\rho }}} \Vert s\Vert _x$ for all $s \in B_x(b)$, with ${{\hat{\rho }}} = \rho + L \sqrt{K}$.

• 3. For all $s \in B_x(b)$, the singular values of $T_s = \mathrm {D}\mathrm {Exp}_x(s)$ lie in the interval [2/3, 4/3].

A few comments are in order:

• 1. For locally symmetric spaces ($F = 0$), we interpret K/F as infinite (regardless of K).

• 2. If ${\mathcal {M}}$ is compact, then it is complete and there necessarily exist finite K and F. See work by Greene [25] for a discussion on non-compact manifolds.

• 3. If ${\mathcal {M}}$ is a homogeneous Riemannian manifold (not necessarily compact), then there exist finite K and F, and these can be assessed by studying a single point on the manifold. This follows directly from the definition of homogeneous Riemannian manifold [32, p. 55].

• 4. All symmetric spaces are homogeneous and locally symmetric [32, Exercise 6–19, Exercise 7–3 and p. 78] so there exists finite K and $F = 0$. Let ${\text {Sym}}(d)$ be the set of real $d \times d$ symmetric matrices. The set of $d\times d$ positive definite matrices

  $$\begin{aligned} {\mathcal {P}}_d = \{P \in {\text {Sym}}(d) : P \succ 0\} \end{aligned}$$

  endowed with the so-called affine invariant metric

  $$\begin{aligned} \left\langle {X},{Y}\right\rangle _P = \mathrm {Tr}(P^{-1} X P^{-1} Y) \quad \text {for } P \in {\mathcal {P}}_d \text { and } X, Y \in \mathrm {T}_P {\mathcal {P}}_d \cong {\text {Sym}}(d) \end{aligned}$$

  is a non-compact symmetric space of non-constant curvature. It is commonly used in practice [10, 37, 38, 43]. One can show that $K = \frac{1}{2}$ and $F=0$ are the right constants for this manifold.

• 5. The following statements are equivalent: (a) ${\mathcal {M}}$ is complete; (b) $\mathrm {Exp}$ is defined on the whole tangent bundle: ${\mathcal {O}}= \mathrm {T}{\mathcal {M}}$; and (c) for some $b > 0$, $\mathrm {Exp}_x$ is defined on $B_x(b)$ for all $x \in {\mathcal {M}}$. In later sections, we need to apply Theorem 2.7 at various points of ${\mathcal {M}}$ with constant b, which is why we then assume ${\mathcal {M}}$ is complete.

• 6. The properties of $T_s$ are useful in combination with Lemma 2.5 to relate gradients and Hessians of the pullbacks to gradients and Hessians on the manifold. For example, if $\nabla {{\hat{f}}}_x(s)$ has norm $\epsilon$, then $\mathrm {grad}f(\mathrm {Exp}_x(s))$ has norm somewhere between $\frac{3}{4}\epsilon$ and $\frac{3}{2}\epsilon$. Under the conditions of the theorem, $W_s$ (8) is bounded as $\Vert W_s\Vert _x \le \frac{9}{4} K \Vert \nabla {{\hat{f}}}_x(s)\Vert _x \Vert s\Vert _x$.

• 7. We only get satisfactory Lipschitzness at points where the gradient is bounded by Lb. Fortunately, for the algorithms we study, whenever we encounter a point with gradient larger than that threshold, it is sufficient to take a simple gradient descent step.

To prove Theorem 2.7, we must control $\nabla ^2 {{\hat{f}}}_x(s)$. According to Lemma 2.5, this requires controlling both $T_s$ (a differential of the exponential map) and $c''(0)$ (the intrinsic initial acceleration of a curve defined via the exponential map, but which is not itself a geodesic in general). On both counts, we must study differentials of exponentials. Jacobi fields are the tool of choice for such tasks. As a first step, we use Jacobi fields to investigate the difference between $T_s$ and $P_s$: two linear operators from $\mathrm {T}_x{\mathcal {M}}$ to $\mathrm {T}_{\mathrm {Exp}_x(s)}{\mathcal {M}}$. We prove a general result in Appendix A (exact for constant sectional curvature) and state a sufficient particular case here. Control of $T_s$ follows as a corollary because $P_s$ (parallel transport) is an isometry.

Proposition 2.8

Let ${\mathcal {M}}$ be a Riemannian manifold whose sectional curvatures are in the interval $[{K_{\mathrm {low}}}, {K_{\mathrm {up}}}]$, and let $K = \max (|{K_{\mathrm {low}}}|, |{K_{\mathrm {up}}}|)$. For any $(x, s) \in {\mathcal {O}}$ with $\Vert s\Vert _x \le \frac{\pi }{\sqrt{K}}$,

$$\begin{aligned} \Vert (T_s - P_s)[\dot{s}]\Vert _{\mathrm {Exp}_x(s)}&\le \frac{1}{3} K \Vert s\Vert _x^2 \Vert \dot{s}_\perp \Vert _x, \end{aligned}$$

(12)

where $\dot{s}_\perp = \dot{s} - \frac{\left\langle {s},{\dot{s}}\right\rangle _x}{\left\langle {s},{s}\right\rangle _x}s$ is the component of $\dot{s}$ orthogonal to s.

Corollary 2.9

Let ${\mathcal {M}}$ be a Riemannian manifold whose sectional curvatures are in the interval $[{K_{\mathrm {low}}}, {K_{\mathrm {up}}}]$, and let $K = \max (|{K_{\mathrm {low}}}|, |{K_{\mathrm {up}}}|)$. For any $(x, s) \in {\mathcal {O}}$ with $\Vert s\Vert _x \le \frac{1}{\sqrt{K}}$,

$$\begin{aligned} \sigma _{{\text {min}}}(T_s)&\ge \frac{2}{3}&{\text { and }}&\sigma _{{\text {max}}}(T_s)&\le \frac{4}{3}. \end{aligned}$$

(13)

Proof

By Proposition 2.8, the operator norm of $T_s - P_s$ is bounded above by $\frac{1}{3} K \Vert s\Vert _x^2 \le \frac{1}{3}$. Furthermore, parallel transport $P_s$ is an isometry: its singular values are equal to 1. Thus,

$$\begin{aligned} \sigma _{{\text {max}}}(T_s)&= \sigma _{{\text {max}}}(P_s + T_s - P_s) \le \sigma _{{\text {max}}}(P_s) + \sigma _{{\text {max}}}(T_s - P_s) \le 1 + \frac{1}{3} = \frac{4}{3}. \end{aligned}$$

Likewise, with min/max taken over unit-norm vectors $u \in \mathrm {T}_x{\mathcal {M}}$ and writing $y = \mathrm {Exp}_x(s)$,

$$\begin{aligned} \sigma _{{\text {min}}}(T_s)&= \min _{u} \Vert T_s u\Vert _y \ge \min _{u} \Vert P_s u\Vert _y - \Vert (T_s - P_s)u\Vert _y \\&= 1 - \max _{u} \Vert (T_s - P_s)u\Vert _y \ge \frac{2}{3}. \end{aligned}$$

$\square$

We turn to controlling the term $c''(0)$ which appears in the definition of operator $W_s$ in the expression for $\nabla ^2 {{\hat{f}}}_x(s)$ provided by Lemma 2.5. We present a detailed proof in Appendix B for a general statement, and state a sufficient particular case here. The proof is fairly technical: it involves designing an appropriate nonlinear second-order ODE on the manifold and bounding its solutions. The ODE is related to the Jacobi equation, except we had to differentiate to the next order, and the equation is not homogeneous.

Proposition 2.10

Let ${\mathcal {M}}$ be a Riemannian manifold whose sectional curvatures are in the interval $[{K_{\mathrm {low}}}, {K_{\mathrm {up}}}]$, and let $K = \max (|{K_{\mathrm {low}}}|, |{K_{\mathrm {up}}}|)$. Further assume $\nabla R$ is bounded by F in operator norm.

Pick any $(x, s) \in {\mathcal {O}}$ such that

$$\begin{aligned} \Vert s\Vert _x&\le \min \!\left( \frac{1}{4\sqrt{K}}, \frac{K}{4F} \right) . \end{aligned}$$

For any $\dot{s} \in \mathrm {T}_x{\mathcal {M}}$, the curve $c(t) = \mathrm {Exp}_x(s + t \dot{s})$ has initial acceleration bounded as

$$\begin{aligned} \Vert c''(0)\Vert _{\mathrm {Exp}_x(s)}&\le \frac{3}{2} K \Vert s\Vert _x \Vert \dot{s}\Vert _x \Vert \dot{s}_\perp \Vert _x, \end{aligned}$$

where $\dot{s}_\perp = \dot{s} - \frac{\left\langle {s},{\dot{s}}\right\rangle _x}{\left\langle {s},{s}\right\rangle _x} s$ is the component of $\dot{s}$ orthogonal to s.

Equipped with all of the above, it is now easy to prove the main theorem of this section.

Proof of Theorem 2.7

Consider the pullback ${{\hat{f}}}_x = f \circ \mathrm {Exp}_x$ defined on $\mathrm {T}_x{\mathcal {M}}$. Since $\mathrm {T}_x{\mathcal {M}}$ is linear, it is a classical exercise to verify that $\nabla {{\hat{f}}}_x$ is 2L-Lipschitz continuous in $B_x(b)$ if and only if $\Vert \nabla ^2 {{\hat{f}}}_x(s)\Vert _x \le 2L$ for all s in $B_x(b)$. Using Lemma 2.5, we start bounding the Hessian as follows:

$$\begin{aligned} \Vert \nabla ^2 {{\hat{f}}}_x(s)\Vert _x&\le \sigma _{{\text {max}}}(T_s^*) \sigma _{{\text {max}}}(T_s) \Vert \mathrm {Hess}f(\mathrm {Exp}_x(s))\Vert _{\mathrm {Exp}_x(s)} + \Vert W_s\Vert _x, \end{aligned}$$

with operator $W_s$ defined by (8). Since $\mathrm {grad}f$ is L-Lipschitz continuous, $\Vert \mathrm {Hess}f(y)\Vert _y \le L$ for all $y \in {\mathcal {M}}$ (this follows fairly directly from Proposition 2.4). To bound $W_s$, we start with a Cauchy–Schwarz inequality then we consider the worst case for the magnitude of $c''(0)$:

$$\begin{aligned} \Vert W_s\Vert _x&\le \Vert \mathrm {grad}f(\mathrm {Exp}_x(s))\Vert _{\mathrm {Exp}_x(s)} \cdot \max _{\dot{s} \in \mathrm {T}_x{\mathcal {M}}, \Vert \dot{s}\Vert _x = 1} \Vert c''(0)\Vert _{\mathrm {Exp}_x(s)}. \end{aligned}$$

Combining these steps yields a first bound of the form

$$\begin{aligned} \Vert \nabla ^2 {{\hat{f}}}_x(s)\Vert _x&\le \sigma _{{\text {max}}}(T_s)^2 L \nonumber \\&\quad + \Vert \mathrm {grad}f(\mathrm {Exp}_x(s))\Vert _{\mathrm {Exp}_x(s)} \cdot \max _{\dot{s} \in \mathrm {T}_x{\mathcal {M}}, \Vert \dot{s}\Vert _x = 1} \Vert c''(0)\Vert _{\mathrm {Exp}_x(s)}. \end{aligned}$$

(14)

To proceed, we keep working on the $W_s$-terms: use Proposition 2.10, L-Lipschitz-continuity of the gradient, and our bounds on the norms of s and $\mathrm {grad}f(x)$ to see that:

$$\begin{aligned} \Vert W_s\Vert _x&\le \max _{\dot{s} \in \mathrm {T}_x{\mathcal {M}}, \Vert \dot{s}\Vert _x = 1} \Vert c''(0)\Vert _{\mathrm {Exp}_x(s)} \cdot \Vert \mathrm {grad}f(\mathrm {Exp}_x(s))\Vert _{\mathrm {Exp}_x(s)} \nonumber \\&\le \frac{3}{2} K \Vert s\Vert _x \cdot \Vert P_s^*\mathrm {grad}f(\mathrm {Exp}_x(s)) - \mathrm {grad}f(x) + \mathrm {grad}f(x)\Vert _{x} \nonumber \\&\le \frac{3}{2} K \Vert s\Vert _x \cdot \left( L \Vert s\Vert _x + \Vert \mathrm {grad}f(x)\Vert _x \right) \nonumber \\&\le 3KLb\Vert s\Vert _x \le \frac{3}{4} L \sqrt{K} \Vert s\Vert _x \le \frac{3}{16}L. \end{aligned}$$

(15)

Returning to (14) and using Corollary 2.9 to bound $T_s$ confirms that

$$\begin{aligned} \Vert \nabla ^2 {{\hat{f}}}_x(s)\Vert _x&\le \frac{16}{9} L + \frac{3}{16} L < 2L. \end{aligned}$$

Thus, $\nabla {{\hat{f}}}_x$ is 2L-Lipschitz continuous in the ball of radius b around the origin in $\mathrm {T}_x{\mathcal {M}}$.

To establish the second part of the claim, we use the same intermediate results and $\rho$-Lipschitz continuity of the Hessian. First, using Lemma 2.5 twice and noting that $W_0 = 0$ so that $\nabla ^2 {{\hat{f}}}_x(0) = \mathrm {Hess}f(x)$, we have:

$$\begin{aligned} \nabla ^2 {{\hat{f}}}_x(s) - \nabla ^2 {{\hat{f}}}_x(0)&= P_s^* \circ \mathrm {Hess}f(\mathrm {Exp}_x(s)) \circ P_s - \mathrm {Hess}f(x) \\&\quad + (T_s - P_s)^* \circ \mathrm {Hess}f(\mathrm {Exp}_x(s)) \circ T_s \\&\quad + P_s^* \circ \mathrm {Hess}f(\mathrm {Exp}_x(s)) \circ (T_s - P_s) \\&\quad + W_s. \end{aligned}$$

We bound this line by line calling upon Proposition 2.8, Corollary 2.9 and (15) to get:

$$\begin{aligned} \Vert \nabla ^2 {{\hat{f}}}_x(s) - \nabla ^2 {{\hat{f}}}_x(0)\Vert _x&\le \rho \Vert s\Vert _x + \frac{4}{9} L K \Vert s\Vert _x^2 + \frac{1}{3} L K \Vert s\Vert _x^2 + 3LKb\Vert s\Vert _x \\&\le \left( \rho + \frac{1}{9} L \sqrt{K} + \frac{1}{12} L \sqrt{K} + \frac{3}{4} L \sqrt{K} \right) \Vert s\Vert _x \\&\le \left( \rho + L \sqrt{K} \right) \Vert s\Vert _x. \end{aligned}$$

This shows a type of Lipschitz continuity of the Hessian of the pullback with respect to the origin, in the ball of radius b. $\square$

3 Assumptions and parameters for $\mathtt {TAGD}$ and $\mathtt {PTAGD}$

Our algorithms apply to the minimization of $f :{\mathcal {M}}\rightarrow {{\mathbb {R}}}$ on a Riemannian manifold ${\mathcal {M}}$ equipped with a retraction $\mathrm {R}$ defined on the whole tangent bundle $\mathrm {T}{\mathcal {M}}$. The pullback of f at $x \in {\mathcal {M}}$ is ${{\hat{f}}}_x = f \circ \mathrm {R}_x :\mathrm {T}_x{\mathcal {M}}\rightarrow {{\mathbb {R}}}$. In light of Sect. 2, we make the following assumptions.

A 2

There exists a constant $f_{\mathrm {low}}$ such that $f(x) \ge f_{\mathrm {low}}$ for all $x \in {\mathcal {M}}$. Moreover, f is twice continuously differentiable and there exist constants $\ell$, ${{\hat{\rho }}}$ and b such that, for all $x \in {\mathcal {M}}$ with $\Vert \mathrm {grad}f(x)\Vert \le \frac{1}{2} \ell b$,

• 1. $\nabla {{\hat{f}}}_x$ is $\ell$-Lipschitz continuous in $B_x(3b)$ (in particular, $\Vert \nabla ^2 {{\hat{f}}}_x(0)\Vert \le \ell$),

• 2. $\Vert \nabla ^2 {{\hat{f}}}_x(s) - \nabla ^2 {{\hat{f}}}_x(0)\Vert \le {{\hat{\rho }}} \Vert s\Vert$ for all $s \in B_x(3b)$, and

• 3. $\sigma _{{\text {min}}}(T_s) \ge \frac{1}{2}$ with $T_s = \mathrm {D}\mathrm {R}_x(s)$ for all $s \in B_x(3b)$,

where $B_x(3b) = \{ u \in \mathrm {T}_x{\mathcal {M}}: \Vert u\Vert \le 3b \}$. Finally, for all $(x, s) \in \mathrm {T}{\mathcal {M}}$ it holds that

• 4. ${{\hat{f}}}_x(s) \le {{\hat{f}}}_x(0) + \langle {\nabla {{\hat{f}}}_x(0)},{s}\rangle + \frac{\ell }{2}\Vert s\Vert ^2$.

The first three items in A2 confer Lipschitz properties to the derivatives of the pullbacks ${{\hat{f}}}_x$ restricted to balls around the origins of tangent spaces: these are the balls where we shall run accelerated gradient steps. We only need these guarantees at points where the gradient is below a threshold. For all other points, a regular gradient step provides ample progress: the last item in A2 serves that purpose only, see Proposition 5.2.

Section 2 tells us that A2 holds in particular when we use the exponential map as a retraction and f itself has appropriate (Riemannian) Lipschitz properties. This is the link between Theorems 1.3 and 1.6 in the introduction and Theorems 5.1 and 6.1 in later sections.

Corollary 3.1

If we use the exponential retraction $\mathrm {R}= \mathrm {Exp}$ and A1 holds, then A2 holds with $f_{\mathrm {low}}$, and

$$\begin{aligned} \ell&= 2L,&{{\hat{\rho }}} = \rho + L\sqrt{K},&b = \frac{1}{12}\min \!\left( \frac{1}{\sqrt{K}}, \frac{K}{F}\right) . \end{aligned}$$

(16)

With constants as in A2, we further define a number of parameters. First, the user specifies a tolerance $\epsilon$ which must not be too loose.

A 3

The tolerance $\epsilon > 0$ satisfies $\sqrt{{{\hat{\rho }}} \epsilon } \le \frac{1}{2}\ell$ and $\epsilon \le b^2 {{\hat{\rho }}}$.

Then, we fix a first set of parameters (see [28] for more context; in particular, $\kappa$ plays the role of a condition number; under A3, we have $\kappa \ge 2$):

$$\begin{aligned} \eta&= \frac{1}{4\ell },&\kappa&= \frac{\ell }{\sqrt{{{\hat{\rho }}} \epsilon }},&\theta&= \frac{1}{4\sqrt{\kappa }},&\gamma&= \frac{\sqrt{{{\hat{\rho }}} \epsilon }}{4},&s&= \frac{1}{32} \sqrt{\frac{\epsilon }{{{\hat{\rho }}}}}. \end{aligned}$$

(17)

We define a second set of parameters based on some $\chi \ge 1$ (as set in some of the lemmas and theorems below) and a universal constant $c > 0$ (implicitly defined as the smallest real satisfying a finite number of lower-bounds required throughout the paper):

$$\begin{aligned} r&= \eta \epsilon \chi ^{-5}c^{-8},&{\mathscr {T}}&= \sqrt{\kappa }\chi c,&{\mathscr {E}}&= \sqrt{\frac{\epsilon ^3}{{\hat{\rho }}}}\chi ^{-5}c^{-7},\nonumber \\ {\mathscr {L}}&= \sqrt{\frac{4\epsilon }{{\hat{\rho }}}} \chi ^{-2}c^{-3},&{\mathscr {M}}&= \frac{\epsilon \sqrt{\kappa }}{\ell }c^{-1}. \end{aligned}$$

(18)

When we say “with $\chi \ge A \ge 1$” (for example, in Theorems 5.1 and 6.1), we mean: “with $\chi$ the smallest value larger than A such that ${\mathscr {T}}$ is a positive integer multiple of 4.”

Lemma C.1 in Appendix C lists useful relations between the parameters.

4 Accelerated Gradient Descent in a Ball of a Tangent Space

The main ingredient of algorithms $\mathtt {TAGD}$ and $\mathtt {PTAGD}$ is $\mathtt {TSS}$: the tangent space steps algorithm. Essentially, the latter runs the classical accelerated gradient descent algorithm (AGD) from convex optimization on ${{\hat{f}}}_x$ in a tangent space $\mathrm {T}_x{\mathcal {M}}$, with a few tweaks:

• 1. Because ${{\hat{f}}}_x$ need not be convex, $\mathtt {TSS}$ monitors the generated sequences for signs of non-convexity. If ${{\hat{f}}}_x$ happens to behave like a convex function along the sequence $\mathtt {TSS}$ generates, then we reap the benefits of convexity. Otherwise, the direction along which ${{\hat{f}}}_x$ behaves in a non-convex way can be used as a good descent direction. This is the idea behind the “convex until proven guilty” paradigm developed by Carmon et al. [15] and also exploited by Jin et al. [28]. Explicitly, given $x \in {\mathcal {M}}$ and $s, u \in \mathrm {T}_x{\mathcal {M}}$, for a specified parameter $\gamma > 0$, we check the negative curvature condition (one might also call it the non-convexity condition) (NCC):

  $$\begin{aligned} {\hat{f}}_x(s) < {\hat{f}}_x(u) + \langle {\nabla {\hat{f}}_x(u)},{s - u}\rangle - \frac{\gamma }{2}\left\| {s - u}\right\| ^2. \end{aligned}$$

  (NCC)

  If (NCC) triggers with a triplet (x, s, u) and s is not too large, we can exploit that fact to generate substantial cost decrease using the negative curvature exploitation algorithm, $\mathtt {NCE}$: see Lemma 4.4. (This is about curvature of the cost function, not the manifold.)

• 2. In contrast to the Euclidean case in [28], our assumption A2 provides Lipschitz-type guarantees only in a ball of radius 3b around the origin in $\mathrm {T}_x{\mathcal {M}}$. Therefore, we must act if iterates generated by $\mathtt {TSS}$ leave that ball. This is done in two places. First, the momentum step in step 4 of $\mathtt {TSS}$ is capped so that $\Vert u_j\Vert$ remains in the ball of radius 2b around the origin. Second, if $s_{j+1}$ leaves the ball of radius b (as checked in step 10) then we terminate this run of $\mathtt {TSS}$ by returning to the manifold. Lemma 4.1 guarantees that the iterates indeed remain in appropriate balls, that $\theta _j$ (19) in the capped momentum step is uniquely defined, and that if a momentum step is capped, then immediately after that $\mathtt {TSS}$ terminates.

The initial momentum $v_0$ is always set to zero. By default, the AGD sequence is initialized at the origin: $s_0 = 0$. However, for $\mathtt {PTAGD}$ we sometimes want to initialize at a different point (a perturbation away from the origin): this is only relevant for Sect. 6.

In the remainder of this section, we provide four general purpose lemmas about $\mathtt {TSS}$. Proofs are in Appendix D. We note that $\mathtt {TAGD}$ and $\mathtt {PTAGD}$ call $\mathtt {TSS}$ only at points x where $\Vert \mathrm {grad}f(x)\Vert \le \frac{1}{2} \ell b$. The first lemma below notably guarantees that, for such runs, all iterates $u_j, s_j$ generated by $\mathtt {TSS}$ remain (a fortiori) in balls of radius 3b, so that the strongest provisions of A2 always apply: we use this fact often without mention.

Lemma 4.1

($\mathtt {TSS}$ stays in balls) Fix parameters and assumptions as laid out in Sect. 3. Let $x \in {\mathcal {M}}$ satisfy $\Vert \mathrm {grad}f(x)\Vert \le \frac{1}{2}\ell b$. If $\mathtt {TSS}(x)$ or $\mathtt {TSS}(x, s_0)$ (with $\Vert s_0\Vert \le b$) defines vectors $u_0, \ldots , u_q$ (and possibly more), then it also defines vectors $s_0, \ldots , s_q$, and we have:

$$\begin{aligned} \Vert s_0\Vert , \ldots , \Vert s_q\Vert&\le b,&\Vert u_0\Vert , \ldots , \Vert u_q\Vert&\le 2b,&{\text { and }}&2\eta \gamma \le \theta \le \theta _j \le 1. \end{aligned}$$

If $s_{q+1}$ is defined, then $\Vert s_{q+1}\Vert \le 3b$ and, if $\Vert u_q\Vert = 2b$, then $\Vert s_{q+1}\Vert > b$ and $u_{q+1}$ is undefined.

Along the iterates of AGD, the value of the cost function ${{\hat{f}}}_x$ may not monotonically decrease. Fortunately, there is a useful quantity which monotonically decreases along iterates: Jin et al. [28] call it the Hamiltonian. In several ways, it serves the purpose of a Lyapunov function. Importantly, the Hamiltonian decreases regardless of any special events that occur while running $\mathtt {TSS}$. It is built as a combination of the cost function value and the momentum. The next lemma makes this precise: we use monotonic decrease of the Hamiltonian often without mention. This corresponds to [28, Lem. 9 and 20].

Lemma 4.2

(Hamiltonian decrease) Fix parameters and assumptions as laid out in Sect. 3. Let $x \in {\mathcal {M}}$ satisfy $\Vert \mathrm {grad}f(x)\Vert \le \frac{1}{2}\ell b$. For each pair $(s_j, v_j)$ defined by $\mathtt {TSS}(x)$ or $\mathtt {TSS}(x, s_0)$ (with $\Vert s_0\Vert \le b$), define the Hamiltonian

$$\begin{aligned} E_j&= {{\hat{f}}}_x(s_j) + \frac{1}{2\eta } \Vert v_j\Vert ^2. \end{aligned}$$

(20)

If $E_{j+1}$ is defined, then $E_j$, $\theta _j$ and $u_j$ are also defined and:

$$\begin{aligned} E_{j+1}&\le E_j - \frac{\theta _j}{2\eta } \Vert v_j\Vert ^2 - \frac{\eta }{4} \Vert \nabla {{\hat{f}}}_x(u_j)\Vert ^2 \le E_j. \end{aligned}$$

If moreover $\Vert v_j\Vert \ge {\mathscr {M}}$, then $E_j - E_{j+1} \ge \frac{4{\mathscr {E}}}{{\mathscr {T}}}$.

Jin et al. [28] formalize an important property of $\mathtt {TSS}$ sequences in the Euclidean case, namely, the fact that “either the algorithm makes significant progress or the iterates do not move much.” They call this the improve or localize phenomenon. The next lemma states this precisely in our context. This corresponds to [28, Cor. 11].

Lemma 4.3

(Improve or localize) Fix parameters and assumptions as laid out in Sect. 3. Let $x \in {\mathcal {M}}$ satisfy $\Vert \mathrm {grad}f(x)\Vert \le \frac{1}{2}\ell b$. If $\mathtt {TSS}(x)$ or $\mathtt {TSS}(x, s_0)$ (with $\Vert s_0\Vert \le b$) defines vectors $s_0, \ldots , s_q$ (and possibly more), then $E_0, \ldots , E_q$ are defined by (20) and, for all $0 \le q' \le q$,

$$\begin{aligned} \Vert s_q - s_{q'}\Vert ^2 \le (q-q') \sum _{j = q'}^{q-1} \Vert s_{j+1} - s_j\Vert ^2 \le 16 \sqrt{\kappa } \eta (q-q') (E_{q'} - E_q). \end{aligned}$$

For $q' = 0$ in particular, using $E_0 = {{\hat{f}}}_x(s_0)$ we can write $E_q \le {{\hat{f}}}_x(s_0) - \frac{\Vert s_q - s_0\Vert ^2}{16 \sqrt{\kappa } \eta q}$.

As outlined earlier, in case the $\mathtt {TSS}$ sequence witnesses non-convexity in ${{\hat{f}}}_x$ through the (NCC) check, we call upon the $\mathtt {NCE}$ algorithm to exploit this event. The final lemma of this section formalizes the fact that this yields appropriate cost improvement. (Indeed, if $\Vert s_j\Vert > {\mathscr {L}}$ one can argue that sufficient progress was already achieved; otherwise, the lemma applies and we get a result from $E_j \le E_0 = {{\hat{f}}}_x(s_0)$.) This corresponds to [28, Lem. 10 and 17].

Lemma 4.4

(Negative curvature exploitation) Fix parameters and assumptions as laid out in Sect. 3. Let $x \in {\mathcal {M}}$ satisfy $\Vert \mathrm {grad}f(x)\Vert \le \frac{1}{2}\ell b$. Assume $\mathtt {TSS}(x)$ or $\mathtt {TSS}(x, s_0)$ (with $\Vert s_0\Vert \le b$) defines $u_j$, so that $s_j, v_j$ are also defined, and $E_j$ is defined by (20). If (NCC) triggers with $(x, s_j, u_j)$ and $\Vert s_j\Vert \le {\mathscr {L}}$, then ${{\hat{f}}}_x(\mathtt {NCE}(x, s_j, v_j)) \le E_j - 2{\mathscr {E}}$.

5 First-Order Critical Points

Our algorithm to compute $\epsilon$-approximate first-order critical points on Riemannian manifolds is $\mathtt {TAGD}$: this is a deterministic algorithm which does not require access to the Hessian of the cost function. Our main result regarding $\mathtt {TAGD}$, namely, Theorem 5.1, states that it does so in a bounded number of iterations. As worked out in Theorem 1.3, this bound scales as $\epsilon ^{-7/4}$, up to polylogarithmic terms. The complexity is independent of the dimension of the manifold.

The proof of Theorem 5.1 rests on two propositions introduced hereafter in this section. Interestingly, it is only in the proof of Theorem 5.1 that we track the behavior of iterates of $\mathtt {TAGD}$ across multiple points on the manifold. This is done by tracking decrease of the value of the cost function f. All supporting results (lemmas and propositions) handle a single tangent space at a time. As a result, lemmas and propositions fully benefit from the linear structure of tangent spaces. This is why we can salvage most of the Euclidean proofs of Jin et al. [28], up to mostly minor (but numerous and necessary) changes.

Theorem 5.1

Fix parameters and assumptions as laid out in Sect. 3, with

$$\begin{aligned} \chi \ge \log _2(\theta ^{-1}) \ge 1. \end{aligned}$$

(21)

Given $x_0 \in {\mathcal {M}}$, $\mathtt {TAGD}(x_0)$ returns $x_t \in {\mathcal {M}}$ satisfying $f(x_t) \le f(x_0)$ and $\Vert \mathrm {grad}f(x_t)\Vert \le \epsilon$ with

$$\begin{aligned} t \le T_1 \triangleq \frac{f(x_0) - f_{\mathrm {low}}}{{\mathscr {E}}} {\mathscr {T}}. \end{aligned}$$

(22)

Running the algorithm requires at most $2T_1$ pullback gradient queries and $3T_1$ function queries (but no Hessian queries), and a similar number of calls to the retraction.

Proof of Theorem 5.1

The call to $\mathtt {TAGD}(x_0)$ generates a sequence of points $x_{t_0}, x_{t_1}, x_{t_2}, \ldots$ on ${\mathcal {M}}$, with $t_0 = 0$. A priori, this sequence may be finite or infinite. Considering two consecutive indices $t_i$ and $t_{i+1}$, we either have $t_{i+1} = t_i + 1$ (if the step from $x_{t_i}$ to $x_{t_{i+1}}$ is a single gradient step (Case 1)) or $t_{i+1} = t_i + {\mathscr {T}}$ (if that same step is obtained through a call to $\mathtt {TSS}$ (Case 2)). Moreover:

• In Case 1, Proposition 5.2 applies and guarantees

  $$\begin{aligned} f(x_{t_i}) - f(x_{t_{i+1}}) \ge \frac{{\mathscr {E}}}{{\mathscr {T}}} = \frac{{\mathscr {E}}}{{\mathscr {T}}}(t_{i+1} - t_i). \end{aligned}$$

• In Case 2, Proposition 5.3 applies and guarantees that if $\Vert \mathrm {grad}f(x_{t_{i+1}})\Vert > \epsilon$ then

  $$\begin{aligned} f(x_{t_i}) - f(x_{t_{i+1}}) \ge {\mathscr {E}} = \frac{{\mathscr {E}}}{{\mathscr {T}}}(t_{i+1} - t_i). \end{aligned}$$

It is now clear that $\mathtt {TAGD}(x_0)$ terminates after a finite number of steps. Indeed, if it does not, then the above reasoning shows that the algorithm produces an amortized decrease in the cost function f of $\frac{{\mathscr {E}}}{{\mathscr {T}}}$ per unit increment of the counter t, yet the value of f cannot decrease by more than $f(x_0) - f_{\mathrm {low}}$ because f is globally lower-bounded by $f_{\mathrm {low}}$.

Accordingly, assume $\mathtt {TAGD}(x_0)$ generates $x_{t_0}, \ldots , x_{t_k}$ and terminates there, returning $x_{t_k}$. We know that $f(x_{t_k}) \le f(x_0)$ and $\Vert \mathrm {grad}f(x_{t_k})\Vert \le \epsilon$. Moreover, from the discussion above and $t_0 = 0$, we know that

$$\begin{aligned} f(x_0) - f_{\mathrm {low}}&\ge f(x_0) - f(x_{t_k}) = \sum _{i = 0}^{k-1} f(x_{t_i}) - f(x_{t_{i+1}}) \\&\ge \frac{{\mathscr {E}}}{{\mathscr {T}}} \sum _{i = 0}^{k-1} t_{i+1} - t_i = \frac{{\mathscr {E}}}{{\mathscr {T}}} t_k. \end{aligned}$$

Thus, $t_k \le \frac{f(x_0) - f_{\mathrm {low}}}{{\mathscr {E}}} {\mathscr {T}} \triangleq T_1$.

How much work does it take to run the algorithm? Each (regular) gradient step requires one gradient query and increases the counter by one. Each run of $\mathtt {TSS}$ requires at most $2 {\mathscr {T}}$ gradient queries and $2{\mathscr {T}} + 3 \le 3{\mathscr {T}}$ function queries ($3 \le {\mathscr {T}}$ because ${\mathscr {T}}$ is a positive integer multiple of 4) and increases the counter by ${\mathscr {T}}$. Therefore, by the time $\mathtt {TAGD}$ produces $x_t$ it has used at most 2t gradient queries and 3t function queries. $\square$

The two following propositions form the backbone of the proof of Theorem 5.1. Each handles one of the two possible cases in one (outer) iteration of $\mathtt {TAGD}$, namely: Case 1 is a “vanilla” Riemannian gradient descent step, while Case 2 is a call to $\mathtt {TSS}$ to run (modified) AGD in the current tangent space. The former has a trivial and standard proof. The latter relies on all lemmas from Sect. 4 and on two additional lemmas introduced in Appendix F, all following Jin et al. [28].

Proposition 5.2

(Case 1) Fix parameters and assumptions as laid out in Sect. 3. Assume $x \in {\mathcal {M}}$ satisfies $\Vert \mathrm {grad}f(x)\Vert > 2\ell {\mathscr {M}}$. Then, $x_+ = \mathrm {R}_{x}(-\eta \mathrm {grad}f(x))$ satisfies $f(x) - f(x_+) \ge \frac{{\mathscr {E}}}{{\mathscr {T}}}$.

Proof of Proposition 5.2

This follows directly by property 4 in A2 with ${{\hat{f}}}_x = f \circ \mathrm {R}_x$ since ${{\hat{f}}}_x(0) = f(x)$ and $\nabla {{\hat{f}}}_x(0) = \mathrm {grad}f(x)$ by properties of retractions, and also using $\ell \eta = 1/4$:

$$\begin{aligned} f(x_+)&= {{\hat{f}}}_x(-\eta \mathrm {grad}f(x)) \le {{\hat{f}}}_x(0) - \eta \Vert \mathrm {grad}f(x)\Vert ^2 \\&\quad + \frac{\ell }{2} \Vert \eta \mathrm {grad}f(x)\Vert ^2 \le f(x) - (7/8) \ell {\mathscr {M}}^2. \end{aligned}$$

To conclude, it remains to use that $(7/8) \ell {\mathscr {M}}^2 \ge \frac{{\mathscr {E}}}{{\mathscr {T}}}$, as shown in Lemma C.1. $\square$

The next proposition corresponds mostly to [28, Lem. 12]. A proof is in Appendix F.

Proposition 5.3

(Case 2) Fix parameters and assumptions as laid out in Sect. 3, with

$$\begin{aligned} \chi \ge \log _2(\theta ^{-1}) \ge 1. \end{aligned}$$

(23)

If $x \in {\mathcal {M}}$ satisfies $\Vert \mathrm {grad}f(x)\Vert \le 2\ell {\mathscr {M}}$, then $x_{{\mathscr {T}}} = \mathtt {TSS}(x)$ falls in one of two cases:

• 1. Either $\Vert \mathrm {grad}f(x_{{\mathscr {T}}})\Vert \le \epsilon$ and $f(x) - f(x_{{\mathscr {T}}}) \ge 0$,

• 2. Or $\Vert \mathrm {grad}f(x_{{\mathscr {T}}})\Vert > \epsilon$ and $f(x) - f(x_{{\mathscr {T}}}) \ge {\mathscr {E}}$.

6 Second-Order Critical Points

As discussed in the previous section, $\mathtt {TAGD}$ produces $\epsilon$-approximate first-order critical points at an accelerated rate, deterministically. Such a point might happen to be an approximate second-order critical point, or it might not. In order to produce approximate second-order critical points, $\mathtt {PTAGD}$ builds on top of $\mathtt {TAGD}$ as follows.

Whenever $\mathtt {TAGD}$ produces a point with gradient smaller than $\epsilon$, $\mathtt {PTAGD}$ generates a random vector $\xi$ close to the origin in the current tangent space and runs $\mathtt {TSS}$ starting from that perturbation. The run of $\mathtt {TSS}$ itself is deterministic. However, the randomized initialization has the following effect: if the current point is not an approximate second-order critical point, then with high probability the sequence generated by $\mathtt {TSS}$ produces significant cost decrease. Intuitively, this is because the current point is a saddle point, and gradient descent-type methods slowly but likely escape saddles. If this happens, we simply proceed with the algorithm. Otherwise, we can be reasonably confident that the point from which we ran the perturbed $\mathtt {TSS}$ is an approximate second-order critical point, and we terminate there.

Our main result regarding $\mathtt {PTAGD}$, namely, Theorem 6.1, states that it computes approximate second-order critical points with high probability in a bounded number of iterations. As worked out in Theorem 1.6, this bound scales as $\epsilon ^{-7/4}$, up to polylogarithmic terms which include a dependency in the dimension of the manifold and the probability of success.

Mirroring Sect. 5, the proof of Theorem 6.1 rests on the two propositions of that section and on an additional proposition introduced hereafter in this section.

Theorem 6.1

Pick any $x_0 \in {\mathcal {M}}$. Fix parameters and assumptions as laid out in Sect. 3, with $d = \dim {\mathcal {M}}$, $\delta \in (0, 1)$, any $\Delta _f \ge \max \!\left( f(x_0) - f_{\mathrm {low}}, \sqrt{\frac{\epsilon ^3}{{\hat{\rho }}}}\right)$ and

$$\begin{aligned} \chi \ge \log _2\!\left( \frac{d^{1/2} \ell ^{3/2} \Delta _f}{({\hat{\rho }} \epsilon )^{1/4} \epsilon ^2 \delta } \right) \ge \log _2(\theta ^{-1}) \ge 1. \end{aligned}$$

The call to $\mathtt {PTAGD}(x_0)$ returns $x_t \in {\mathcal {M}}$ satisfying $f(x_t) \le f(x_0)$, $\Vert \mathrm {grad}f(x_t)\Vert \le \epsilon$ and (with probability at least $1-2\delta$) also $\lambda _{\mathrm {min}}(\nabla ^2 {{\hat{f}}}_{x_t}(0)) \ge -\sqrt{{{\hat{\rho }}} \epsilon }$ with

$$\begin{aligned} t + {\mathscr {T}} \le T_2 \triangleq \left( 2 + 4\frac{f(x_0) - f_{\mathrm {low}}}{{\mathscr {E}}} \right) {\mathscr {T}}. \end{aligned}$$

(24)

To reach termination, the algorithm requires at most $2T_2$ pullback gradient queries and $4T_2$ function queries (but no Hessian queries), and a similar number of calls to the retraction.

Notice how this result gives a (probabilistic) guarantee about the smallest eigenvalue of the Hessian of the pullback ${{\hat{f}}}_x$ at 0 rather than about the Hessian of f itself at x. Owing to Lemma 2.5, the two are equal in particular when we use the exponential retraction (more generally, when we use a second-order retraction): see also [13, §3.5].

Proof of Theorem 6.1

The proof starts the same way as that of Theorem 5.1. The call to $\mathtt {PTAGD}(x_0)$ generates a sequence of points $x_{t_0}, x_{t_1}, x_{t_2}, \ldots$ on ${\mathcal {M}}$, with $t_0 = 0$. A priori, this sequence may be finite or infinite. Considering two consecutive indices $t_i$ and $t_{i+1}$, we either have $t_{i+1} = t_i + 1$ (if the step from $x_{t_i}$ to $x_{t_{i+1}}$ is a single gradient step (Case 1)) or $t_{i+1} = t_i + {\mathscr {T}}$ (if that same step is obtained through a call to $\mathtt {TSS}$, with or without perturbation (Cases 3 and 2, respectively)). Moreover:

• In Case 1, Proposition 5.2 applies and guarantees

  $$\begin{aligned} f(x_{t_i}) - f(x_{t_{i+1}}) \ge \frac{{\mathscr {E}}}{{\mathscr {T}}} = \frac{{\mathscr {E}}}{{\mathscr {T}}}(t_{i+1} - t_i). \end{aligned}$$

  The algorithm does not terminate here.

• In Case 2, Proposition 5.3 applies and guarantees that if $\Vert \mathrm {grad}f(x_{t_{i+1}})\Vert > \epsilon$ then

  $$\begin{aligned} f(x_{t_i}) - f(x_{t_{i+1}}) \ge {\mathscr {E}} = \frac{{\mathscr {E}}}{{\mathscr {T}}}(t_{i+1} - t_i), \end{aligned}$$

  and the algorithm does not terminate here.

  If, however, $\Vert \mathrm {grad}f(x_{t_{i+1}})\Vert \le \epsilon$, then $f(x_{t_i}) - f(x_{t_{i+1}}) \ge 0$ and the step from $x_{t_{i+1}}$ to $x_{t_{i+2}}$ does not fall in Case 2: it must fall in Case 3. (Indeed, it cannot fall in Case 1 because the fact that a Case 2 step occurred tells us $\epsilon < 2\ell {\mathscr {M}}$.) The algorithm terminates with $x_{t_{i+1}}$ unless $f(x_{t_{i+1}}) - f(x_{t_{i+2}}) \ge \frac{1}{2}{\mathscr {E}}$. In other words, if the algorithm does not terminate with $x_{t_{i+1}}$, then

  $$\begin{aligned} f(x_{t_{i}}) - f(x_{t_{i+2}})&= f(x_{t_{i}}) - f(x_{t_{i+1}}) + f(x_{t_{i+1}}) \\&\quad - f(x_{t_{i+2}}) \ge \frac{1}{2}{\mathscr {E}} = \frac{{\mathscr {E}}}{4{\mathscr {T}}}(t_{i+2} - t_{i}). \end{aligned}$$

• In Case 3, the algorithm terminates with $x_{t_{i}}$ unless

  $$\begin{aligned} f(x_{t_{i}}) - f(x_{t_{i+1}}) \ge \frac{1}{2}{\mathscr {E}} = \frac{{\mathscr {E}}}{2{\mathscr {T}}}(t_{i+1} - t_{i}). \end{aligned}$$

Clearly, $\mathtt {PTAGD}(x_0)$ must terminate after a finite number of steps. Indeed, if it does not, then the above reasoning shows that the algorithm produces an amortized decrease in the cost function f of $\frac{{\mathscr {E}}}{4{\mathscr {T}}}$ per unit increment of the counter t, yet the value of f cannot decrease by more than $f(x_0) - f_{\mathrm {low}}$.

Accordingly, assume $\mathtt {PTAGD}(x_0)$ generates $x_{t_0}, \ldots , x_{t_{k+1}}$ and terminates there (returning $x_{t_k}$). The step from $x_{t_k}$ to $x_{t_{k+1}}$ necessarily falls in Case 3: $t_{k+1} - t_k = {\mathscr {T}}$. The step from $x_{t_{k-1}}$ to $x_{t_k}$ could be of any type. If it falls in Case 2, it could be that $f(x_{t_{k-1}}) - f(x_{t_k})$ is as small as zero and that $t_{k} - t_{k-1} = {\mathscr {T}}$. (All other scenarios are better, in that the cost function decreases more, and the counter increases as much or less.) Moreover, for all steps prior to that, each unit increment of t brings about an amortized decrease in f of $\frac{{\mathscr {E}}}{4{\mathscr {T}}}$. Thus, $t_{k+1} \le t_{k-1} + 2{\mathscr {T}}$ and

$$\begin{aligned} f(x_0) - f_{\mathrm {low}}\ge f(x_{0}) - f(x_{t_{k-1}}) \ge \frac{{\mathscr {E}}}{4{\mathscr {T}}} t_{k-1}. \end{aligned}$$

Combining, we find

$$\begin{aligned} t_k + {\mathscr {T}} = t_{k+1} \le \left( 2 + 4\frac{f(x_0) - f_{\mathrm {low}}}{{\mathscr {E}}} \right) {\mathscr {T}} \triangleq T_2. \end{aligned}$$

What can we say about the point that is returned, $x_{t_k}$? Deterministically, $f(x_{t_k}) \le f(x_0)$ and $\Vert \mathrm {grad}f(x_{t_k})\Vert \le \epsilon$ (notice that we cannot guarantee the same about $x_{t_{k+1}}$). Let us now discuss the role of randomness.

In any run of $\mathtt {PTAGD}(x_0)$, there are at most $T_2/{\mathscr {T}}$ perturbations, that is, “Case 3” steps. By Proposition 6.2, the probability of any single one of those steps failing to prevent termination at a point where the smallest eigenvalue of the Hessian of the pullback at the origin is strictly less than $-\sqrt{{{\hat{\rho }}} \epsilon }$ is at most $\frac{\delta {\mathscr {E}}}{3\Delta _f}$. Thus, by a union bound, the probability of failure in any given run of $\mathtt {PTAGD}(x_0)$ is at most (we use $\Delta _f \ge \max \!\left( f(x_0) - f_{\mathrm {low}}, \sqrt{\frac{\epsilon ^3}{{\hat{\rho }}}}\right) \ge \max \!\left( f(x_0) - f_{\mathrm {low}}, 2^7{\mathscr {E}} \right)$ because $\chi \ge 1$ and $c \ge 2$):

$$\begin{aligned} \frac{T_2}{{\mathscr {T}}} \cdot \frac{\delta {\mathscr {E}}}{3\Delta _f} = \left( 2 + 4\frac{f(x_0) - f_{\mathrm {low}}}{{\mathscr {E}}} \right) \frac{\delta {\mathscr {E}}}{3\Delta _f} \le \left( \frac{2{\mathscr {E}}}{3\Delta _f} + \frac{4}{3}\right) \delta \le 2\delta . \end{aligned}$$

In all other events, we have $\lambda _{\mathrm {min}}(\nabla ^2 {{\hat{f}}}_{x_{t_k}}(0)) \ge -\sqrt{{{\hat{\rho }}} \epsilon }$.

For accounting of the maximal amount of work needed to run $\mathtt {PTAGD}(x_0)$, use reasoning similar to that at the end of the proof of Theorem 5.1, adding the cost of checking the condition “$f(x_t) - f(x_{t+{\mathscr {T}}}) < \frac{1}{2}{\mathscr {E}}$” after each perturbed call to $\mathtt {TSS}$.

Note: the inequality $\frac{d^{1/2} \ell ^{3/2} \sqrt{\epsilon ^3 / {\hat{\rho }}}}{({{\hat{\rho }}} \epsilon )^{1/4} \epsilon ^2 \delta } \ge \theta ^{-1}$ holds for all $d \ge 1$ and $\delta \in (0, 1)$ with $c \ge 4$. $\square$

The next proposition corresponds mostly to [28, Lem. 13]. A proof is in Appendix G.

Proposition 6.2

(Case 3) Fix parameters and assumptions as laid out in Sect. 3, with $d = \dim {\mathcal {M}}$, $\delta \in (0, 1)$, any $\Delta _f > 0$ and

$$\begin{aligned} \chi \ge \max \!\left( \log _2(\theta ^{-1}), \log _2\!\left( \frac{d^{1/2} \ell ^{3/2} \Delta _f}{({{\hat{\rho }}} \epsilon )^{1/4} \epsilon ^2 \delta } \right) \right) \ge 1. \end{aligned}$$

If $x \in {\mathcal {M}}$ satisfies $\Vert \mathrm {grad}f(x)\Vert \le \min (\epsilon , 2\ell {\mathscr {M}})$ and $\lambda _{\mathrm {min}}(\nabla ^2 {{\hat{f}}}_x(0)) \le -\sqrt{{{\hat{\rho }}} \epsilon }$, and $\xi$ is sampled uniformly at random from the ball of radius r around the origin in $\mathrm {T}_x{\mathcal {M}}$, then $x_{{\mathscr {T}}} = \mathtt {TSS}(x, \xi )$ satisfies $f(x) - f(x_{{\mathscr {T}}}) \ge {\mathscr {E}}/2$ with probability at least $1 - \frac{\delta {\mathscr {E}}}{3\Delta _f}$ over the choice of $\xi$.

7 Conclusions and Perspectives

Our main complexity results for $\mathtt {TAGD}$ and $\mathtt {PTAGD}$ (Theorems 1.3 and 1.6) recover known Euclidean results when ${\mathcal {M}}$ is a Euclidean space. In particular, they retain the important properties of scaling essentially with $\epsilon ^{-7/4}$ and of being either dimension-free (for $\mathtt {TAGD}$) or almost dimension-free (for $\mathtt {PTAGD}$). Those properties extend as is to the Riemannian case.

However, our Riemannian results are negatively impacted by the Riemannian curvature of ${\mathcal {M}}$, and also by the covariant derivative of the Riemann curvature endomorphism. We do not know whether such a dependency on curvature is necessary to achieve acceleration. In particular, the non-accelerated rates for Riemannian gradient descent, Riemannian trust-regions and Riemannian adaptive regularization with cubics under Lipschitz assumptions do not suffer from curvature [2, 13].

Curvature enters our complexity bounds through our geometric results (Theorem 2.7). For the latter, we do believe that curvature must play a role. Thus, it is natural to ask:

Can we achieve acceleration for first-order methods on Riemannian manifolds with weaker (or without) dependency on the curvature of the manifold?

For the geodesically convex case, all algorithms we know of are affected by curvature [3,4,5, 48]. Additionally, Hamilton and Moitra [26] show that curvature can significantly slow down convergence rates in the geodesically convex case with noisy gradients.

Adaptive regularization with cubics (ARC) may offer insights in that regard. ARC is a cubically regularized approximate Newton method with optimal iteration complexity on the class of cost functions with Lipschitz continuous Hessian, assuming access to gradients and Hessians [19, 39]. Specifically, assuming f has $\rho$-Lipschitz continuous Hessian, ARC finds an $(\epsilon , \sqrt{\rho \epsilon })$-approximate second-order critical point in at most ${{\tilde{O}}}(\Delta _f \rho ^{1/2} / \epsilon ^{3/2})$ iterations, omitting logarithmic factors. This also holds on complete Riemannian manifolds [2, Cor. 3, eqs (16), (26)]. Note that this is dimension-free and curvature-free. Each iteration, however, requires solving a separate subproblem more costly than a gradient evaluation. Carmon and Duchi [18, §3] argue that it is possible to solve the subproblems accurately enough so as to find $\epsilon$-approximate first-order critical points with $\sim 1/\epsilon ^{7/4}$ Hessian-vector products overall, with randomization and a logarithmic dependency in dimension. Compared to $\mathtt {TAGD}$, this has the benefit of being curvature-free, at the cost of randomization, a logarithmic dimension dependency, and of requiring Hessian-vector products. The latter could conceivably be approximated with finite differences of the gradients. Perhaps that operation leads to losses tied to curvature? If not, as it is unclear why there ought to be a trade-off between curvature dependency and randomization, this may be the indication that the curvature dependency is not necessary for acceleration.

On a distinct note and as pointed out in the introduction, $\mathtt {TAGD}$ and $\mathtt {PTAGD}$ are theoretical constructs. Despite having the theoretical upper-hand in worst-case scenarios, we do not expect them to be competitive against time-tested algorithms such as Riemannian versions of nonlinear conjugate gradients or the trust-region methods. It remains an interesting open problem to devise a truly practical accelerated first-order method on manifolds.

In the Euclidean case, Carmon et al. [15] showed that if one assumes not only the gradient and the Hessian of f but also the third derivative of f are Lipschitz continuous, then it is possible to find $\epsilon$-approximate first-order critical points in just ${{\tilde{O}}}(\epsilon ^{-5/3})$ iterations. We suspect that our proof technique could be used to prove a similar result on manifolds, possibly at the cost of also assuming a bound on the second covariant derivative of the Riemann curvature endomorphism.

Appendices

Parallel Transport vs Differential of Exponential Map

In this section, we give a proof for Proposition 2.8 regarding the difference between parallel transport along a geodesic and the differential of the exponential map. We use these families of functions parameterized by ${K_{\mathrm {low}}}\in {{\mathbb {R}}}$:

$$\begin{aligned} h_{K_{\mathrm {low}}}(t)&= {\left\{ \begin{array}{ll} t &{} {\text { if }} {K_{\mathrm {low}}}= 0, \\ r \sin (t/r) &{} {\text { if }} {K_{\mathrm {low}}}= 1/r^2 > 0, \\ r \sinh (t/r) &{} {\text { if }} {K_{\mathrm {low}}}= -1/r^2 < 0. \end{array}\right. } \end{aligned}$$

(25)

$$\begin{aligned} g_{{K_{\mathrm {low}}}}(t)&= \int _{0}^{t} h_{{K_{\mathrm {low}}}}(\tau ) \mathrm {d}\tau = {\left\{ \begin{array}{ll} \frac{t^2}{2} &{} {\text { if }} {K_{\mathrm {low}}}= 0, \\ r^2\left( 1 - \cos (t/r) \right) &{} {\text { if }} {K_{\mathrm {low}}}= 1/r^2 > 0, \\ r^2\left( \cosh (t/r) - 1 \right) &{} {\text { if }} {K_{\mathrm {low}}}= -1/r^2 < 0. \end{array}\right. } \end{aligned}$$

(26)

$$\begin{aligned} f_{{K_{\mathrm {low}}}}(t)&= \frac{1}{t} \int _{0}^{t} g_{{K_{\mathrm {low}}}}(\tau ) \mathrm {d}\tau = {\left\{ \begin{array}{ll} \frac{t^2}{6} &{} {\text { if }} {K_{\mathrm {low}}}= 0, \\ r^2\left( 1 - \frac{\sin (t/r)}{t/r} \right) &{} {\text { if }} {K_{\mathrm {low}}}= 1/r^2 > 0, \\ r^2\left( \frac{\sinh (t/r)}{t/r} - 1 \right) &{} {\text { if }} {K_{\mathrm {low}}}= -1/r^2 < 0. \end{array}\right. } \end{aligned}$$

(27)

Under the assumptions we make below, these functions are only ever evaluated at points where they are nonnegative. In all cases, functions are dominated by the case ${K_{\mathrm {low}}}< 0$; formally, for all ${K_{\mathrm {low}}}\in {{\mathbb {R}}}$, all $K \ge |{K_{\mathrm {low}}}|$ and all $t \ge 0$:

$$\begin{aligned} h_{K_{\mathrm {low}}}(t)&\le h_{-K}(t),&g_{K_{\mathrm {low}}}(t)&\le g_{-K}(t),&f_{K_{\mathrm {low}}}(t)&\le f_{-K}(t). \end{aligned}$$

(28)

If ${K_{\mathrm {low}}}\ge 0$ and $t \ge 0$, then

$$\begin{aligned} h_{K_{\mathrm {low}}}(t)&\le t,&g_{K_{\mathrm {low}}}(t)&\le \frac{1}{2} t^2,&f_{K_{\mathrm {low}}}(t)&\le \frac{1}{6} t^2. \end{aligned}$$

(29)

Independently of the sign of ${K_{\mathrm {low}}}$, if $0 \le t \le \pi / \sqrt{|{K_{\mathrm {low}}}|}$, then

$$\begin{aligned} h_{K_{\mathrm {low}}}(t)&\le t + 0.2712 \cdot \quad {K_{\mathrm {low}}}t^3 \le 3.6761 \cdot t, \\ g_{K_{\mathrm {low}}}(t)&\le 1.0732 \cdot t^2, \quad f_{K_{\mathrm {low}}}(t) \le 0.2712 \cdot t^2. \end{aligned}$$

For t bounded as indicated, this last line shows that up to constants the sign of ${K_{\mathrm {low}}}$ does not substantially affect bounds.

To state our result, we need the notion of conjugate points along geodesics on Riemannian manifolds. The following definition is equivalent to the standard one [32, Prop. 10.20 and p. 303]. We are particularly interested in situations where there are no conjugate points on some interval: we discuss that event in a remark.

Definition A.1

Let ${\mathcal {M}}$ be a Riemannian manifold. Consider $(x, s) \in \mathrm {T}{\mathcal {M}}$ and the geodesic $\gamma (t) = \mathrm {Exp}_x(ts)$ defined on an open interval I around zero. For $t \in I$, we say $\gamma (t)$ is conjugate to x along $\gamma$ if $\mathrm {D}\mathrm {Exp}_x(ts)$ is rank deficient. We say $\gamma$ has an interior conjugate point on $[0, {{\bar{t}}}] \subset I$ if $\gamma (t)$ is conjugate to x along $\gamma$ for some $t \in (0, {{\bar{t}}})$.

Remark A.2

Let $\gamma$ be a geodesic on a Riemannian manifold ${\mathcal {M}}$. If $\gamma$ is minimizing on the interval $[0, {{\bar{t}}}]$, then it has no interior conjugate point on that interval [32, Thm. 10.26]. Assume the sectional curvatures of ${\mathcal {M}}$ are in the interval $[{K_{\mathrm {low}}}, {K_{\mathrm {up}}}]$. Then:

• 1. If ${K_{\mathrm {up}}}\le 0$, $\gamma$ has no conjugate points at all [32, Pb. 10-7];

• 2. If ${K_{\mathrm {up}}}> 0$, $\gamma$ has no interior conjugate points on $[0, \pi / \sqrt{{K_{\mathrm {up}}}}]$ [32, Thm. 11.9a]; and

• 3. If ${K_{\mathrm {low}}}> 0$ and $\gamma$ has no interior conjugate point on $[0, {{\bar{t}}}]$, then ${{\bar{t}}} \le \pi / \sqrt{{K_{\mathrm {low}}}}$ [32, p. 298 and Thm. 11.9b]. This will be why, under our assumptions, $h_{K_{\mathrm {low}}}$ (25) is only ever evaluated at points where it is nonnegative.

We now state and prove the main result of this section. A similar result appears in [45, Lem. 6] for general retractions. Constants there are not explicit (they are absorbed in $O(\cdot )$ notation). Their proof is based on Taylor expansions of the differential of the exponential map as they appear in [46, Thm. A.2.9], namely, for $s \mapsto \mathrm {D}\mathrm {Exp}_x(s)$ around $s = 0$. In the next section, we investigate a situation around $s \ne 0$. In appendices, we typically omit subscripts for inner products and norms.

Proposition A.3

Let ${\mathcal {M}}$ be a Riemannian manifold whose sectional curvatures are in the interval $[{K_{\mathrm {low}}}, {K_{\mathrm {up}}}]$, and let $K = \max (|{K_{\mathrm {low}}}|, |{K_{\mathrm {up}}}|)$. Consider $(x, s) \in \mathrm {T}{\mathcal {M}}$ and the geodesic $\gamma (t) = \mathrm {Exp}_x(ts)$. If $\gamma$ is defined and has no interior conjugate point on the interval [0, 1], then

$$\begin{aligned} \forall \dot{s} \in \mathrm {T}_x{\mathcal {M}},&\Vert (T_s - P_s)[\dot{s}]\Vert \le K \cdot f_{{K_{\mathrm {low}}}}(\Vert s\Vert ) \cdot \Vert \dot{s}_\perp \Vert , \end{aligned}$$

(30)

where $\dot{s}_\perp = \dot{s} - \frac{\left\langle {s},{\dot{s}}\right\rangle }{\left\langle {s},{s}\right\rangle }s$ is the component of $\dot{s}$ orthogonal to s, $T_s = \mathrm {D}\mathrm {Exp}_x(s)$ and $P_{ts}$ denotes parallel transport along $\gamma$ from $\gamma (0)$ to $\gamma (t)$. (The inequality holds with equality if ${K_{\mathrm {low}}}= {K_{\mathrm {up}}}$.)

If it also holds that $\Vert s\Vert \le \pi / \sqrt{|{K_{\mathrm {low}}}|}$, then

$$\begin{aligned} \forall \dot{s} \in \mathrm {T}_x{\mathcal {M}},&\Vert (T_s - P_s)[\dot{s}]\Vert \le \frac{1}{3} K \Vert s\Vert ^2 \Vert \dot{s}_\perp \Vert . \end{aligned}$$

(31)

Proof

For convenience, we consider $\Vert s\Vert = 1$: the result follows by a simple rescaling of t. Given any tangent vector $\dot{s} \in \mathrm {T}_x{\mathcal {M}}$, consider the following smooth vector field along $\gamma$:

$$\begin{aligned} J(t)&= \mathrm {D}\mathrm {Exp}_x(ts)[t \dot{s}]. \end{aligned}$$

(32)

By [32, Prop. 10.10], this is the unique Jacobi field satisfying the initial conditions

$$\begin{aligned} J(0)&= 0&{\text { and }}&\mathrm {D}_tJ(0)&= \dot{s}, \end{aligned}$$

(33)

where $\mathrm {D}_t$ is the covariant derivative along curves induced by the Riemannian connection. Thus, J is smooth and obeys the ordinary differential equation (ODE) known as the Jacobi equation:

$$\begin{aligned} \mathrm {D}_t^2J(t) + R(J(t), \gamma '(t))\gamma '(t) = 0, \end{aligned}$$

(34)

where R denotes Riemannian curvature. Fix $e_d = s$ and pick $e_1, \ldots , e_{d-1}$ so that $e_1, \ldots , e_d$ form an orthonormal basis for $\mathrm {T}_x{\mathcal {M}}$. Parallel transport this basis along $\gamma$ as

$$\begin{aligned} E_i(t)&= P_{ts}(e_i),&i&= 1, \ldots , d, \end{aligned}$$

(35)

so that $E_1(t), \ldots , E_d(t)$ form an orthonormal basis for $\mathrm {T}_{\gamma (t)}{\mathcal {M}}$. Expand J as

$$\begin{aligned} J(t)&= \sum _{i = 1}^{d} a_i(t) E_i(t) \end{aligned}$$

(36)

with uniquely defined smooth, real functions $a_1, \ldots , a_d$. Plugging this expansion into the Jacobi equation yields the ODE

$$\begin{aligned} \sum _{i = 1}^{d} a_i''(t) E_i(t) + \sum _{i = 1}^{d} a_i(t) R(E_i(t), E_d(t)) E_d(t) = 0, \end{aligned}$$

(37)

where we used the Leibniz rule on $\mathrm {D}_t$, the fact that $\mathrm {D}_tE_i = 0$, linearity of the Riemann curvature endomorphism in its inputs, and the fact that

$$\begin{aligned} \gamma '(t) = P_{ts}(\gamma '(0)) = E_d(t). \end{aligned}$$

Taking an inner product of this ODE against each one of the fields $E_j(t)$ yields d ODEs:

$$\begin{aligned} a_j''(t)&= - \sum _{i = 1}^{d} a_i(t) \left\langle {R(E_i(t), E_d(t)) E_d(t)},{E_j(t)}\right\rangle ,&j&= 1, \ldots , d. \end{aligned}$$

(38)

Furthermore, the initial conditions fix $a_i(0) = 0$ and $a_i'(0) = \left\langle {\dot{s}},{e_i}\right\rangle$ for $i = 1, \ldots , d$.

Owing to symmetries of Riemannian curvature, the summation above can be restricted to the range $1, \ldots , d-1$. For the same reason, $a_d''(t) = 0$, so that

$$\begin{aligned} a_d(t) = a_d(0) + t a_d'(0) = t \left\langle {\dot{s}},{s}\right\rangle . \end{aligned}$$

(39)

It remains to solve for the first $d-1$ coefficients (they are decoupled from $a_d$). This effectively splits the solution J into two fields: one tangent (aligned with $\gamma '$), and one normal (orthogonal to $\gamma '$):

$$\begin{aligned} J(t)&= t \left\langle {\dot{s}},{s}\right\rangle \gamma '(t) + J_\perp (t),&J_\perp (t)&= \sum _{i = 1}^{d-1} a_i(t) E_i(t). \end{aligned}$$

(40)

The normal part is the Jacobi field with initial conditions $J_\perp (0) = 0$ and $\mathrm {D}_tJ_\perp (0) = \dot{s}_\perp$, where $\dot{s}_\perp = \dot{s} - \left\langle {\dot{s}},{s}\right\rangle s$ is the component of $\dot{s}$ orthogonal to s.

Introducing vector notation for the first $d-1$ ODEs, let $a(t) \in {{\mathbb {R}}}^{d-1}$ have components $a_1(t), \ldots , a_{d-1}(t)$, and let $M(t) \in {{\mathbb {R}}}^{(d-1)\times (d-1)}$ have entries

$$\begin{aligned} M_{ji}(t) = \left\langle {R(E_i(t), E_d(t)) E_d(t)},{E_j(t)}\right\rangle . \end{aligned}$$

(41)

Then, equations in (38) for $j = 1, \ldots , d-1$ can be written succinctly as

$$\begin{aligned} a''(t)&= - M(t)a(t). \end{aligned}$$

(42)

Since a(t) is smooth, it holds that

$$\begin{aligned} a(t)&= a(0) + \int _{0}^{t} a'(\tau ) \mathrm {d}\tau = a(0) + t a'(0) + \int _{0}^{t} \int _{0}^{\tau } a''(\theta ) \mathrm {d}\theta \mathrm {d}\tau . \end{aligned}$$

(43)

Initial conditions specify $a(0) = 0$, so that (with $\Vert \cdot \Vert$ also denoting the standard Euclidean norm and associated operator norm in real space):

$$\begin{aligned} \Vert a(t) - t a'(0)\Vert&\le \int _{0}^{t} \int _{0}^{\tau } \Vert M(\theta )\Vert \Vert a(\theta )\Vert \mathrm {d}\theta \mathrm {d}\tau . \end{aligned}$$

(44)

The left-hand side is exactly what we seek to control. Indeed, initial conditions ensure $\dot{s} = a_1'(0) e_1 + \cdots + a_d'(0) e_d$, and:

$$\begin{aligned} \Vert (\mathrm {D}\mathrm {Exp}_x(ts) - P_{ts})[t\dot{s}]\Vert&= \Vert J(t) - P_{ts}(t\dot{s})\Vert \\&= \left\| \sum _{i = 1}^{d} \left[ a_i(t) E_i(t) - t a_i'(0) E_i(t) \right] \right\| \\&= \sqrt{\Vert a(t) - t a'(0)\Vert ^2 + |a_d(t) - t a_d'(0)|^2} \\&= \Vert a(t) - t a'(0)\Vert . \end{aligned}$$

For the right-hand side of (44), first note that M(t) is a symmetric matrix owing to the symmetries of R.

Additionally, for any unit-norm $z \in {{\mathbb {R}}}^{d-1}$,

$$\begin{aligned} z^\top \! M(t) z&= \sum _{i,j = 1}^{d-1} z_i z_j \left\langle {R(E_i(t), E_d(t)) E_d(t)},{E_j(t)}\right\rangle = \left\langle {R(v, \gamma '(t)) \gamma '(t)},{v}\right\rangle , \end{aligned}$$

(45)

where $v = z_1 E_1(t) + \cdots + z_{d-1} E_{d-1}(t)$ is a tangent vector at $\gamma (t)$: it is orthogonal to $\gamma '(t)$ and also has unit norm. By definition of sectional curvature $K(\cdot , \cdot )$ (10), it follows that

$$\begin{aligned} z ^\top \! M(t) z&= K(v, \gamma '(t)). \end{aligned}$$

(46)

By symmetry of M(t), we conclude that

$$\begin{aligned} \Vert M(t)\Vert&= \max _{z \in {{\mathbb {R}}}^{d-1}, \Vert z\Vert = 1} |z^\top \! M(t) z| \le K, \end{aligned}$$

(47)

where $K \ge 0$ is such that all sectional curvatures of ${\mathcal {M}}$ along $\gamma$ are in the interval $[-K, K]$. Going back to (44), we have so far shown that

$$\begin{aligned} \Vert (\mathrm {D}\mathrm {Exp}_x(ts) - P_{ts})[t\dot{s}]\Vert&\le K \int _{0}^{t} \int _{0}^{\tau } \Vert a(\theta )\Vert \mathrm {d}\theta \mathrm {d}\tau . \end{aligned}$$

(48)

It remains to bound $\Vert a(\theta )\Vert$. By (40), we see that $\Vert a(t)\Vert = \Vert J_\perp (t)\Vert$. By the Jacobi field comparison theorem [32, Thm. 11.9b] and our assumed lower-bound on sectional curvature, we can now claim that, for $t \ge 0$, with $h_{K_{\mathrm {low}}}(t)$ as defined by (25),

$$\begin{aligned} \Vert a(t)\Vert = \Vert J_\perp (t)\Vert&\le h_{K_{\mathrm {low}}}(t)\Vert \dot{s}_\perp \Vert , \end{aligned}$$

(49)

provided $\gamma$ has no interior conjugate point on [0, t]. Combining with (48) and with the definitions of $h_{K_{\mathrm {low}}}$ (25), $g_{K_{\mathrm {low}}}$ (26) and $f_{K_{\mathrm {low}}}$ (27), we find

$$\begin{aligned} \Vert (\mathrm {D}\mathrm {Exp}_x(ts) - P_{ts})[t\dot{s}]\Vert&\le K \Vert \dot{s}_\perp \Vert \int _{0}^{t} \int _{0}^{\tau } h_{K_{\mathrm {low}}}(\theta ) \mathrm {d}\theta \mathrm {d}\tau \nonumber \\&= K \Vert \dot{s}_\perp \Vert \int _{0}^{t} g_{K_{\mathrm {low}}}(\tau ) \mathrm {d}\tau \nonumber \\&= K \Vert \dot{s}_\perp \Vert \cdot t f_{K_{\mathrm {low}}}(t). \end{aligned}$$

(50)

It only remains to divide through by t, and to rescale s so that t plays the role of $\Vert s\Vert$.

For the special case where ${K_{\mathrm {up}}}= {K_{\mathrm {low}}}= \pm K$ (constant sectional curvature), one can show (for example by polarization) that $M(t) = \pm K I_{d-1}$, that is, M(t) is a multiple of the identity matrix. As a result, the ODEs separate and are easily solved (see also [32, Prop. 10.12]). Explicitly, with $\Vert s\Vert = 1$,

$$\begin{aligned} \mathrm {D}\mathrm {Exp}_x(ts)[t \dot{s}]&= J(t) = h_{\pm K}(t) P_{ts}(\dot{s}_\perp ) + t P_{ts}(\dot{s}_\parallel ), \end{aligned}$$

(51)

where $\dot{s}_\parallel = \left\langle {\dot{s}},{s}\right\rangle s$ is the component of $\dot{s}$ parallel to s. Hence,

$$\begin{aligned} \mathrm {D}\mathrm {Exp}_x(ts)[t \dot{s}] - P_{ts}(t \dot{s})&= (h_{\pm K}(t) - t) P_{ts}(\dot{s}_\perp ), \end{aligned}$$

(52)

and the claim follows easily after dividing through by t and rescaling. $\square$

As a continuation of the previous proof and in anticipation of our needs in Appendix B, we provide a lemma controlling the Jacobi field J and its covariant derivative, assessing both the full field and its normal component.

Lemma A.4

Let ${\mathcal {M}}$ be a Riemannian manifold whose sectional curvatures are in the interval $[{K_{\mathrm {low}}}, {K_{\mathrm {up}}}]$, and let $K = \max (|{K_{\mathrm {low}}}|, |{K_{\mathrm {up}}}|)$. Consider $(x, s) \in \mathrm {T}{\mathcal {M}}$ with $\Vert s\Vert = 1$ and the geodesic $\gamma (t) = \mathrm {Exp}_x(ts)$. Given a tangent vector $\dot{s} \in \mathrm {T}_x{\mathcal {M}}$, consider the Jacobi field J defined by (40):

$$\begin{aligned} J(t)&= t \left\langle {\dot{s}},{s}\right\rangle \gamma '(t) + J_\perp (t), \end{aligned}$$

where $J_\perp$ is the Jacobi field along $\gamma$ with initial conditions $J_\perp (0) = 0$ and $\mathrm {D}_tJ_\perp (0) = \dot{s}_\perp$, and $\dot{s}_\perp = \dot{s} - \left\langle {\dot{s}},{s}\right\rangle s$ is the component of $\dot{s}$ orthogonal to s. For $t \ge 0$ such that $\gamma$ is defined and has no interior conjugate point on the interval [0, t], the following inequalities hold:

$$\begin{aligned} \left\| J(t) \right\|&\le \max (t, h_{K_{\mathrm {low}}}(t)) \Vert \dot{s}\Vert ,&\left\| \mathrm {D}_tJ(t) \right\|&\le \left( 1 + K g_{{K_{\mathrm {low}}}}(t) \right) \Vert \dot{s}\Vert , \\ \left\| J_\perp (t) \right\|&\le h_{K_{\mathrm {low}}}(t)\Vert \dot{s}_\perp \Vert ,&\left\| \mathrm {D}_tJ_\perp (t) \right\|&\le \left( 1 + K g_{{K_{\mathrm {low}}}}(t) \right) \Vert \dot{s}_\perp \Vert , \end{aligned}$$

where $h_{K_{\mathrm {low}}}(t)$ and $g_{K_{\mathrm {low}}}(t)$ are defined by (25) and (26).

Proof

The proof is a continuation of that of Proposition A.3. Using notation as in there,

$$\begin{aligned} J_\perp (t)&= \sum _{i = 1}^{d-1} a_i(t) E_i(t). \end{aligned}$$

Since $J_\perp$ and $\mathrm {D}_tJ_\perp$ are orthogonal to $\gamma ' = E_d$, we know that

$$\begin{aligned} \Vert J\Vert ^2&= t^2 \left\langle {\dot{s}},{s}\right\rangle ^2 + \Vert J_\perp \Vert ^2&{\text { and }}&\left\| \mathrm {D}_tJ\right\| ^2&= \left\langle {\dot{s}},{s}\right\rangle ^2 + \left\| \mathrm {D}_tJ_\perp \right\| ^2. \end{aligned}$$

The bound $\Vert J_\perp (t)\Vert \le h_{K_{\mathrm {low}}}(t)\Vert \dot{s}_\perp \Vert$ appears explicitly as (49). With $\alpha$ denoting the angle between s and $\dot{s}$, we may write $\left\langle {\dot{s}},{s}\right\rangle ^2 = \cos (\alpha )^2\Vert \dot{s}\Vert ^2$ and $\Vert \dot{s}_\perp \Vert ^2 = \sin (\alpha )^2\Vert \dot{s}\Vert ^2$, so that

$$\begin{aligned} \Vert J\Vert ^2&\le t^2 \left( \cos (\alpha )^2 + \left( \frac{h_{K_{\mathrm {low}}}(t)}{t}\right) ^2 \sin (\alpha )^2 \right) \Vert \dot{s}\Vert ^2. \end{aligned}$$

Since the maximum of $\alpha \mapsto \cos (\alpha )^2 + q \sin (\alpha )^2$ with $q \in {{\mathbb {R}}}$ is $\max (1, q)$, we find for $t \ge 0$ that

$$\begin{aligned} \Vert J\Vert&\le \max (t, h_{K_{\mathrm {low}}}(t)) \Vert \dot{s}\Vert . \end{aligned}$$

With the same tools, we may also bound $\mathrm {D}_tJ = \left\langle {\dot{s}},{s}\right\rangle \gamma ' + \mathrm {D}_tJ_\perp$. Indeed, its coordinates in the frame $E_1, \ldots , E_d$ are given by $a_1', \ldots , a_d'$ with $a_d'(t) = \left\langle {\dot{s}},{s}\right\rangle$, so that

$$\begin{aligned} \left\| \mathrm {D}_tJ(t) \right\| ^2&= \left\langle {\dot{s}},{s}\right\rangle ^2 + \left\| \mathrm {D}_tJ_\perp (t) \right\| ^2 = \left\langle {\dot{s}},{s}\right\rangle ^2 + \Vert a'(t)\Vert ^2, \end{aligned}$$

where $a(t) \in {{\mathbb {R}}}^{d-1}$ collects the $d-1$ first coordinates. Moreover,

$$\begin{aligned} a'(t) = a'(0) + \int _{0}^{t} a''(\tau ) \mathrm {d}\tau = a'(0) - \int _{0}^{t} M(\tau ) a(\tau ) \mathrm {d}\tau . \end{aligned}$$

Note that

$$\begin{aligned} \left\| \int _{0}^{t} M(\tau ) a(\tau ) \mathrm {d}\tau \right\| \le K \Vert \dot{s}_\perp \Vert \int _{0}^{t} h_{{K_{\mathrm {low}}}}(\tau ) \mathrm {d}\tau = K \Vert \dot{s}_\perp \Vert g_{{K_{\mathrm {low}}}}(t). \end{aligned}$$

Combining with the fact that $\Vert a'(0)\Vert = \Vert \dot{s}_\perp \Vert$, we get

$$\begin{aligned} \left\| \mathrm {D}_tJ_\perp (t) \right\|&\le \left( 1 + K g_{{K_{\mathrm {low}}}}(t) \right) \Vert \dot{s}_\perp \Vert , \end{aligned}$$

as announced. We now conclude along the same lines as above with

$$\begin{aligned} \left\| \mathrm {D}_tJ(t) \right\| ^2&\le \left( \cos (\alpha )^2 + \left( 1 + K g_{{K_{\mathrm {low}}}}(t) \right) ^2 \sin (\alpha )^2 \right) \Vert \dot{s}\Vert ^2. \end{aligned}$$

Since $\max (1, 1 + K g_{{K_{\mathrm {low}}}}(t)) = 1 + K g_{{K_{\mathrm {low}}}}(t)$, we reach the desired conclusion. $\square$

Controlling the Initial Acceleration $c''(0)$

In this section, we build a proof for Proposition 2.10, whose aim is to control the initial intrinsic acceleration $c''(0)$ of the curve $c(t) = \mathrm {Exp}_x(s + t \dot{s})$. Since $c'(t) = \mathrm {D}\mathrm {Exp}_x(s + t \dot{s})[\dot{s}]$, we can think of this result as giving us access to a second derivative of the exponential map $\mathrm {Exp}_x$ away from the origin. As a first step, we build an ODE whose solution encodes $c''(0)$.

Proposition B.1

Let ${\mathcal {M}}$ be a Riemannian manifold with Riemannian connection $\nabla$ and Riemann curvature endomorphism R. Consider $(x, s) \in \mathrm {T}{\mathcal {M}}$ with $\Vert s\Vert = 1$ and the geodesic $\gamma (t) = \mathrm {Exp}_x(ts)$. Furthermore, consider a tangent vector $\dot{s} \in \mathrm {T}_x{\mathcal {M}}$ and the curve

$$\begin{aligned} c_{ts, \dot{s}}(q)&= \mathrm {Exp}_x(ts + q\dot{s}) \end{aligned}$$

defined for some fixed t. Let J be the Jacobi field along $\gamma$ with initial conditions $J(0) = 0$ and $\mathrm {D}_tJ(0) = \dot{s}$. We use it to define a new vector field H along $\gamma$:

$$\begin{aligned} H&= 4 R(\gamma ', J) \mathrm {D}_tJ + (\nabla _J R)(\gamma ', J) \gamma ' + \left( \nabla _{\gamma '} R\right) (\gamma ', J) J. \end{aligned}$$

The smooth vector field W along $\gamma$ defined by the linear ODE

$$\begin{aligned} \mathrm {D}_t^2W + R(W, \gamma ') \gamma '&= H \end{aligned}$$

with initial conditions $W(0) = 0$ and $\mathrm {D}_tW(0) = 0$ is also defined on the same domain as $\gamma$. This vector field is related to the initial intrinsic acceleration of the curve $c_{ts, \dot{s}}$ as follows:

$$\begin{aligned} W(t)&= t^2 c_{ts, \dot{s}}''(0). \end{aligned}$$

Furthermore, the vector field H is equivalently defined as

$$\begin{aligned} H&= 4 R(\gamma ', J_\perp ) \mathrm {D}_tJ + (\nabla _J R)(\gamma ', J_\perp ) \gamma ' + \left( \nabla _{\gamma '} R\right) (\gamma ', J_\perp ) J, \end{aligned}$$

where $J_\perp$ the Jacobi field along $\gamma$ with initial conditions $J_\perp (0) = 0$ and $\mathrm {D}_tJ_\perp (0) = \dot{s}_\perp = \dot{s} - \left\langle {\dot{s}},{s}\right\rangle s$.

Proof

Define

$$\begin{aligned} \Gamma (q, t)&= \mathrm {Exp}_x(t(s + q \dot{s})), \end{aligned}$$

a variation through geodesics of the geodesic

$$\begin{aligned} \gamma (t)&= \Gamma (0, t) = \mathrm {Exp}_x(ts). \end{aligned}$$

Then,

$$\begin{aligned} J(t)&= \partial _q \Gamma (0, t) = \left. \mathrm {D}\mathrm {Exp}_x(t(s + q\dot{s}))[t \dot{s}] \right| _{q = 0} = \mathrm {D}\mathrm {Exp}_x(ts)[t\dot{s}] \end{aligned}$$

is the Jacobi field along $\gamma$ with initial conditions $J(0) = 0$ and $\mathrm {D}_tJ(0) = \dot{s}$: the same field we considered in the proof of Proposition A.3. Further consider

$$\begin{aligned} W(t)&= \left( \mathrm {D}_q\partial _q \Gamma \right) (0, t), \end{aligned}$$

(53)

another smooth vector field along $\gamma$. This field is related to acceleration of curves of the form

$$\begin{aligned} c_{s, \dot{s}}(q)&= \mathrm {Exp}_x(s + q\dot{s}), \end{aligned}$$

because $c_{ts, t\dot{s}}(q) = \Gamma (q, t)$. Specifically,

$$\begin{aligned} W(t)&= \left( \mathrm {D}_q\partial _q \Gamma \right) (0, t) = c''_{ts, t\dot{s}}(0) = t^2 c''_{ts, \dot{s}}(0). \end{aligned}$$

(54)

To verify the last equality, differentiate the identity $c_{ts, t\dot{s}}(q) = c_{ts, \dot{s}}(tq)$ twice with respect to q, with the chain rule. This shows in particular that

$$\begin{aligned} W(0)&= 0&{\text { and }}&\mathrm {D}_tW(0)&= 0. \end{aligned}$$

(55)

Our goal is to derive a second-order ODE for W. In so doing, we repeatedly use the two following results from Riemannian geometry which allow us to commute certain derivatives:

$\bullet \quad$ [32, Prop. 7.5] For every smooth vector field V along $\Gamma$ (meaning V(q, t) is tangent to ${\mathcal {M}}$ at $\Gamma (q, t)$),

$$\begin{aligned} \mathrm {D}_t\mathrm {D}_qV - \mathrm {D}_q\mathrm {D}_tV = R(\partial _t \Gamma , \partial _q \Gamma ) V, \end{aligned}$$

(56)

where R is the Riemann curvature endomorphism.

$\bullet \quad$ [32, Lem. 6.2] The symmetry lemma states

$$\begin{aligned} \mathrm {D}_q\partial _t \Gamma = \mathrm {D}_t\partial _q \Gamma . \end{aligned}$$

(57)

With the link between W and $\mathrm {D}_q\partial _q \Gamma$ in mind, we compute a first derivative with respect to t:

$$\begin{aligned} \mathrm {D}_t\mathrm {D}_q\partial _q \Gamma = \mathrm {D}_q\mathrm {D}_t\partial _q \Gamma + R(\partial _t \Gamma , \partial _q \Gamma ) \partial _q \Gamma , \end{aligned}$$

then a second derivative:

$$\begin{aligned} \mathrm {D}_t\mathrm {D}_t\mathrm {D}_q\partial _q \Gamma&= \mathrm {D}_t\mathrm {D}_q\mathrm {D}_t\partial _q \Gamma + \mathrm {D}_t\left\{ R(\partial _t \Gamma , \partial _q \Gamma ) \partial _q \Gamma \right\} . \end{aligned}$$

Our goal is to evaluate this expression for $q = 0$, in which case the left-hand side yields $\mathrm {D}_t^2W$. However, it is unclear how to evaluate the first term on the right-hand side at $q = 0$. Focusing on that term for now, apply the commutation rule on the first two derivatives:

$$\begin{aligned} \mathrm {D}_t\mathrm {D}_q\mathrm {D}_t\partial _q \Gamma&= \mathrm {D}_q\mathrm {D}_t\mathrm {D}_t\partial _q \Gamma + R(\partial _t \Gamma , \partial _q \Gamma ) \mathrm {D}_t\partial _q \Gamma . \end{aligned}$$

Focusing on the first term once more, apply the symmetry lemma then the commutation rule:

$$\begin{aligned} \mathrm {D}_q\mathrm {D}_t\mathrm {D}_t\partial _q \Gamma&= \mathrm {D}_q\left\{ \mathrm {D}_t\mathrm {D}_q\partial _t \Gamma \right\} = \mathrm {D}_q\left\{ \mathrm {D}_q\mathrm {D}_t\partial _t \Gamma + R(\partial _t \Gamma , \partial _q \Gamma ) \partial _t \Gamma \right\} \\&= \mathrm {D}_q\left\{ R(\partial _t \Gamma , \partial _q \Gamma ) \partial _t \Gamma \right\} . \end{aligned}$$

To reach the last equality, we used that $\mathrm {D}_t\partial _t \Gamma$ vanishes identically since $t \mapsto \Gamma (q, t)$ is a geodesic for every fixed q. Combining, we find

$$\begin{aligned} \mathrm {D}_t\mathrm {D}_t\mathrm {D}_q\partial _q \Gamma&= R(\partial _t \Gamma , \partial _q \Gamma ) \mathrm {D}_t\partial _q \Gamma \nonumber \\&+ \mathrm {D}_t\left\{ R(\partial _t \Gamma , \partial _q \Gamma ) \partial _q \Gamma \right\} + \mathrm {D}_q\left\{ R(\partial _t \Gamma , \partial _q \Gamma ) \partial _t \Gamma \right\} . \end{aligned}$$

(58)

Using the chain rule for tensors as in (11) (see also [32, pp. 95–103] or [41, Def. 3.17]), we can further expand the right-most term:

$$\begin{aligned} \mathrm {D}_q\left\{ R(\partial _t \Gamma , \partial _q \Gamma ) \partial _t \Gamma \right\}&= \left( \nabla _{\partial _q \Gamma } R\right) (\partial _t \Gamma , \partial _q \Gamma ) \partial _t \Gamma + R\left( \mathrm {D}_q\partial _t \Gamma , \partial _q \Gamma \right) \partial _t \Gamma \\&\quad + R\left( \partial _t \Gamma , \mathrm {D}_q\partial _q \Gamma \right) \partial _t \Gamma + R\left( \partial _t \Gamma , \partial _q \Gamma \right) \mathrm {D}_q\partial _t \Gamma . \end{aligned}$$

It is now easier to evaluate the whole expression at $q = 0$: using

$$\begin{aligned} \partial _q \Gamma (0, t)&= J(t),&\partial _t \Gamma (0, t)&= \gamma '(t)&{\text { and }}&\left( \mathrm {D}_q\partial _q \Gamma \right) (0, t)&= W(t) \end{aligned}$$

repeatedly, and also $\mathrm {D}_q\partial _t \Gamma = \mathrm {D}_t\partial _q \Gamma$ twice so that it evaluates to $\mathrm {D}_tJ$ at $q = 0$, we find

$$\begin{aligned} \mathrm {D}_t^2W&= 2 R(\gamma ', J) \mathrm {D}_tJ + \mathrm {D}_t\left\{ R(\gamma ', J) J \right\} \\&\quad + (\nabla _J R)(\gamma ', J) \gamma ' + R\left( \mathrm {D}_tJ, J\right) \gamma ' + R(\gamma ', W) \gamma '. \end{aligned}$$

This is now an ODE in the single variable t, involving smooth vector fields J, W and $\gamma '$ along the geodesic $\gamma$. We may apply the chain rule for tensors again (we could just as well have done this earlier too):

$$\begin{aligned} \mathrm {D}_t\left\{ R(\gamma ', J) J \right\}&= \left( \nabla _{\gamma '} R\right) (\gamma ', J) J + R\left( \gamma ', \mathrm {D}_tJ\right) J + R(\gamma ', J) \mathrm {D}_tJ, \end{aligned}$$

here too simplifying one term since $\gamma ''$ vanishes. The algebraic Bianchi identity [32, p. 203] states $R(X, Y)Z + R(Y, Z)X + R(Z, X) Y = 0$, so that in particular

$$\begin{aligned} R\left( \mathrm {D}_tJ, J\right) \gamma ' + R\left( \gamma ', \mathrm {D}_tJ\right) J = - R(J, \gamma ') \mathrm {D}_tJ = R(\gamma ', J) \mathrm {D}_tJ. \end{aligned}$$

(We also used anti-symmetry of R). Overall, $\mathrm {D}_t^2W + R(W, \gamma ') \gamma ' = H$ with

$$\begin{aligned} H&= 4 R(\gamma ', J) \mathrm {D}_tJ + (\nabla _J R)(\gamma ', J) \gamma ' + \left( \nabla _{\gamma '} R\right) (\gamma ', J) J. \end{aligned}$$

The Jacobi field J splits into its tangent and normal parts (40):

$$\begin{aligned} J(t)&= t\left\langle {\dot{s}},{s}\right\rangle \gamma '(t) + J_\perp (t). \end{aligned}$$

Since $R(\gamma ', \gamma ') = 0$ by anti-symmetry of R, and since for the same reason $(\nabla _\cdot R)(\gamma ', \gamma ') = 0$ as well, by linearity, we may simplify H to:

$$\begin{aligned} H&= 4 R(\gamma ', J_\perp ) \mathrm {D}_tJ + (\nabla _J R)(\gamma ', J_\perp ) \gamma ' + \left( \nabla _{\gamma '} R\right) (\gamma ', J_\perp ) J. \end{aligned}$$

This concludes the proof. $\square$

To reach our main result, it remains to bound the solutions of the ODE in W. In order to do so, we notably need to bound the inhomogeneous term H. For that reason, we require a bound on the covariant derivative of Riemannian curvature.

Theorem B.2

Let ${\mathcal {M}}$ be a Riemannian manifold whose sectional curvatures are in the interval $[{K_{\mathrm {low}}}, {K_{\mathrm {up}}}]$, and let $K = \max (|{K_{\mathrm {low}}}|, |{K_{\mathrm {up}}}|)$. Also assume $\nabla R$—the covariant derivative of the Riemann curvature endomorphism—is bounded by F in operator norm. Pick any $(x, s) \in \mathrm {T}{\mathcal {M}}$ such that the geodesic $\gamma (t) = \mathrm {Exp}_x(ts)$ is defined for all $t \in [0, 1]$, and such that

$$\begin{aligned} \Vert s\Vert&\le \min \!\left( C \frac{1}{\sqrt{K}}, C' \frac{K}{F} \right) \end{aligned}$$

with some constants $C \le \pi$ and $C'$. For any $\dot{s} \in \mathrm {T}_x{\mathcal {M}}$, the curve

$$\begin{aligned} c(t) = \mathrm {Exp}_x(s + t \dot{s}) \end{aligned}$$

has initial acceleration bounded as

$$\begin{aligned} \Vert c''(0)\Vert&\le \bar{{{\bar{W}}}} K \Vert s\Vert \Vert \dot{s}\Vert \Vert \dot{s}_\perp \Vert , \end{aligned}$$

where $\dot{s}_\perp = \dot{s} - \frac{\left\langle {s},{\dot{s}}\right\rangle }{\left\langle {s},{s}\right\rangle } s$ is the component of $\dot{s}$ orthogonal to s and $\bar{{\bar{W}}} \in {{\mathbb {R}}}$ is only a function of C and $C'$. In particular, for $C, C' \le \frac{1}{4}$, we have $\bar{{{\bar{W}}}} \le \frac{3}{2}$.

Proof

By Remark A.2, since $C \le \pi$ we know that $\gamma$ has no interior conjugate point on [0, 1]. Since the claim is clear for either $s = 0$ or $\dot{s} = 0$, assume $\Vert s\Vert = 1$ for now—we rescale at the end—and $\dot{s} \ne 0$. We also assume $K > 0$: the case $K = 0$ follows easily by inspection of the proof below.

Following Proposition B.1, the goal is to bound W: the solution of an ODE with right-hand side given by the vector field H. As we did in earlier proofs, pick an orthonormal basis $e_1, \ldots , e_d$ for $\mathrm {T}_x{\mathcal {M}}$ with $e_d = s$ and transport it along $\gamma$ as $E_i(t) = P_{ts}(e_i)$. We expand W and H as

$$\begin{aligned} W(t)&= \sum _{i = 1}^{d} w_i(t) E_i(t),&H(t)&= \sum _{i = 1}^{d} h_i(t) E_i(t). \end{aligned}$$

(59)

This allows us to write the ODE in coordinates:

$$\begin{aligned} w''(t) + M(t)w(t)&= h(t), \end{aligned}$$

(60)

where M(t) is as in (41) but defined in ${{\mathbb {R}}^{d\times d}}$ (thus, it has an extra row and column of zeros), and $w(t), h(t) \in {{\mathbb {R}}^{d}}$ are vectors containing the coordinates of W(t) and H(t). Since $W(0) = \mathrm {D}_tW(0) = 0$, we have $w(0) = w'(0) = 0$ and we deduce

$$\begin{aligned} w(t)&= w(0) + t w'(0) + \int _{0}^{t} \int _{0}^{\tau } w''(\theta ) \mathrm {d}\theta \mathrm {d}\tau = \int _{0}^{t} \int _{0}^{\tau } -M(\theta )w(\theta ) + h(\theta ) \, \mathrm {d}\theta \mathrm {d}\tau . \end{aligned}$$

Thus,

$$\begin{aligned} \Vert W(t)\Vert = \Vert w(t)\Vert \le \int _{0}^{t} \int _{0}^{\tau } K \Vert w(\theta )\Vert + \Vert h(\theta )\Vert \, \mathrm {d}\theta \mathrm {d}\tau . \end{aligned}$$

(61)

To proceed, we need a bound on $\Vert H(t)\Vert = \Vert h(t)\Vert$ and a first bound on $\Vert W(t)\Vert$. We will then improve the latter by bootstrapping.

Let us first bound H.

Following [29, eq. (9)], we know that R is bounded (as an operator) as follows:

$$\begin{aligned} \Vert R(X, Y)Z\Vert&\le K_0 \Vert X\Vert \Vert Y\Vert \Vert Z\Vert \quad {\text { with }} \nonumber \\ K_0&= \sqrt{K^2 + (25/36)({K_{\mathrm {up}}}- {K_{\mathrm {low}}})^2} \le 2K, \end{aligned}$$

(62)

where X, Y, Z are arbitrary vector fields along $\gamma$. We further assume that

$$\begin{aligned} \Vert (\nabla _U R) (X, Y) Z\Vert&\le F \Vert U\Vert \Vert X\Vert \Vert Y\Vert \Vert Z\Vert \end{aligned}$$

(63)

for some finite $F \ge 0$. Then,

$$\begin{aligned} \Vert H\Vert&\le 4 K_0 \Vert \gamma '\Vert \left\| \mathrm {D}_tJ \right\| \Vert J_\perp \Vert + 2 F \Vert \gamma '\Vert ^2 \Vert J\Vert \Vert J_\perp \Vert . \end{aligned}$$

(64)

Since $\Vert \gamma '(t)\Vert = \Vert s\Vert = 1$ for all t, this expression simplifies somewhat. Using Lemma A.4, we can also bound all terms involving J and $J_\perp$, so that, also using $K_0 \le 2K$,

$$\begin{aligned} \Vert H(t)\Vert&\le h_{K_{\mathrm {low}}}(t) \Big ( 8K \left( 1 + K g_{{K_{\mathrm {low}}}}(t) \right) + 2F \max (t, h_{K_{\mathrm {low}}}(t)) \Big ) \Vert \dot{s}\Vert \Vert \dot{s}_\perp \Vert . \end{aligned}$$

(65)

Since $h_{K_{\mathrm {low}}}(t) \le h_{-K}(t) = t \frac{\sinh (\sqrt{K}t)}{\sqrt{K}t}$ and likewise $K g_{K_{\mathrm {low}}}(t) \le K g_{-K}(t) = \cosh (\sqrt{K}t) - 1$, and since $h_{-K}(t) \ge t$, we find

$$\begin{aligned} \Vert H(t)\Vert&\le t \frac{\sinh (\sqrt{K}t)}{\sqrt{K}t} \Big ( 8K \cosh (\sqrt{K}t) + 2F t \frac{\sinh (\sqrt{K}t)}{\sqrt{K}t} \Big ) \Vert \dot{s}\Vert \Vert \dot{s}_\perp \Vert \end{aligned}$$

(66)

for all $t \ge 0$. Assuming $0 \le \sqrt{K} t \le C$ for some $C > 0$, we find

$$\begin{aligned} \Vert H(t)\Vert&\le \left( aK + b F t \right) t \Vert \dot{s}\Vert \Vert \dot{s}_\perp \Vert \end{aligned}$$

(67)

with $a = 8\frac{\sinh (C)\cosh (C)}{C}$ and $b = 2 \frac{\sinh (C)^2}{C^2}$. Let us further assume that $0 \le t \le C' \frac{K}{F}$. Then, $Ft \le C' K$ and we write:

$$\begin{aligned} \frac{\Vert H(t)\Vert }{\Vert \dot{s}\Vert \Vert \dot{s}_\perp \Vert }&\le \left( a + b C' \right) K t \triangleq {{\bar{H}}} Kt. \end{aligned}$$

(68)

Let us now obtain a first crude bound on $\Vert W(t)\Vert$. To this end, introduce

$$\begin{aligned} u(t)&= w'(t) / \sqrt{K},&y(t)&= \Vert \dot{s}\Vert \Vert \dot{s}_\perp \Vert / \sqrt{K},&z(t)&= \begin{bmatrix} u(t) \\ w(t) \\ y(t) \end{bmatrix}. \end{aligned}$$

Then,

$$\begin{aligned} z'(t)&= A(t) z(t),&{\text { with }}&A(t)&= \begin{bmatrix} 0 &{} -M(t)/\sqrt{K} &{} h(t) / (\Vert \dot{s}\Vert \Vert \dot{s}_\perp \Vert ) \\ \sqrt{K} I &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 \end{bmatrix}. \end{aligned}$$

Let $g(t) = \Vert z(t)\Vert ^2$. Then, $g(0) = \Vert \dot{s}\Vert ^2 \Vert \dot{s}_\perp \Vert ^2 / K$ and

$$\begin{aligned} g'(t)&= 2\left\langle {z(t)},{z'(t)}\right\rangle = 2 \left\langle {z(t)},{A(t) z(t)}\right\rangle \le 2 \Vert A(t)\Vert \Vert z(t)\Vert ^2 = 2 \Vert A(t)\Vert g(t). \end{aligned}$$

Grönwall’s inequality states that

$$\begin{aligned} g(t)&\le g(0) \exp \!\left( 2 \int _{0}^{t} \Vert A(\tau )\Vert \mathrm {d}\tau \right) . \end{aligned}$$

By triangle inequality and using $\Vert M(t)\Vert \le K$, we have $\Vert A(t)\Vert \le 2\sqrt{K} + \Vert h(t)\Vert /(\Vert \dot{s}\Vert \Vert \dot{s}_\perp \Vert )$. Thus, $\Vert z(t)\Vert ^2$ can be bounded above and below:

$$\begin{aligned} \Vert w(t)\Vert ^2 + \frac{ \Vert \dot{s}\Vert ^2 \Vert \dot{s}_\perp \Vert ^2}{K}&\le \Vert z(t)\Vert ^2 \le \frac{ \Vert \dot{s}\Vert ^2 \Vert \dot{s}_\perp \Vert ^2}{K} \nonumber \\&\quad \times \exp \!\left( 4\sqrt{K}t + 2 \int _{0}^{t} \Vert h(\tau )\Vert / (\Vert \dot{s}\Vert \Vert \dot{s}_\perp \Vert ) \mathrm {d}\tau \right) . \end{aligned}$$

(69)

Using our bound on H(t) (68), we find

$$\begin{aligned} \exp \!\left( 4\sqrt{K}t + 2 \int _{0}^{t} \Vert h(\tau )\Vert / (\Vert \dot{s}\Vert \Vert \dot{s}_\perp \Vert ) \mathrm {d}\tau \right)&\le \exp \!\left( 4\sqrt{K}t + {{\bar{H}}} K t^2 \right) . \end{aligned}$$

Using $\sqrt{K}t \le C$ again we deduce this crude bound:

$$\begin{aligned} \frac{\Vert W(t)\Vert }{\Vert \dot{s}\Vert \Vert \dot{s}_\perp \Vert }&\le \frac{1}{\sqrt{K}} \sqrt{\exp \!\left( 4C + {{\bar{H}}} C^2 \right) - 1} \triangleq \frac{1}{\sqrt{K}} {{\bar{W}}}. \end{aligned}$$

(70)

We now return to (61) and plug in our bounds for H (68) and W (70) to get an improved bound on W: assuming t satisfies the stated conditions,

$$\begin{aligned} \frac{\Vert W(t)\Vert }{\Vert \dot{s}\Vert \Vert \dot{s}_\perp \Vert }&\le \int _{0}^{t} \int _{0}^{\tau } {{\bar{W}}} \sqrt{K} + {{\bar{H}}} K \theta \, \mathrm {d}\theta \mathrm {d}\tau = \frac{1}{2} {{\bar{W}}} \sqrt{K} t^2 + \frac{1}{6} {{\bar{H}}} K t^3. \end{aligned}$$

Plug this new and improved bound on W in (61) once again to get:

$$\begin{aligned} \frac{\Vert W(t)\Vert }{\Vert \dot{s}\Vert \Vert \dot{s}_\perp \Vert }&\le \int _{0}^{t} \int _{0}^{\tau } K \left( \frac{1}{2} {{\bar{W}}} \sqrt{K} \theta ^2 + \frac{1}{6} {{\bar{H}}} K \theta ^3\right) + {{\bar{H}}} K \theta \, \mathrm {d}\theta \mathrm {d}\tau \\&= \frac{1}{24} {{\bar{W}}} K^{3/2} t^4 + \frac{1}{120} {{\bar{H}}} K^2 t^5 + \frac{1}{6} {{\bar{H}}} K t^3 \\&= \left( \frac{1}{6} {{\bar{H}}} + \frac{1}{24} {{\bar{W}}} \sqrt{K}t + \frac{1}{120} {{\bar{H}}} Kt^2 \right) K t^3. \end{aligned}$$

We could now bound $\sqrt{K}t$ and $Kt^2$ by C and $C^2$, respectively, and stop here. However, this yields a constant which depends on ${{\bar{W}}}$: this can be quite large. Instead, we plug our new bound in (61) again, repeatedly. Doing so infinitely many times, we obtain a sequence of upper bounds, all of them valid. The limit of these bounds exists, and is hence also a valid bound. It is tedious but not difficult to check that this reasoning leads to the following:

$$\begin{aligned} \frac{\Vert W(t)\Vert }{\Vert \dot{s}\Vert \Vert \dot{s}_\perp \Vert }&\le \frac{1}{6} \bar{H} \left( 1 + \frac{C^2}{6 \cdot 7} + \frac{C^4}{6 \cdot 7 \cdot 8 \cdot 9} + \frac{C^6}{6 \cdots 11} + \cdots \right) Kt^3. \end{aligned}$$

It is clear that the series converges. Let z be the value it converges to; then:

$$\begin{aligned} z&= 1 + \frac{C^2}{6 \cdot 7} + \frac{C^4}{6 \cdot 7 \cdot 8 \cdot 9} + \frac{C^6}{6 \cdots 11} + \cdots \\&= 1 + \frac{C^2}{6 \cdot 7} \left( 1 + \frac{C^2}{8 \cdot 9} + \frac{C^4}{8 \cdots 11} + \cdots \right) \le 1 + \frac{C^2}{42}z. \end{aligned}$$

Thus, $z \le \frac{1}{1 - \frac{C^2}{42}}$. All in all, we conclude that

$$\begin{aligned} \frac{\Vert W(t)\Vert }{\Vert \dot{s}\Vert \Vert \dot{s}_\perp \Vert }&\le \bar{{{\bar{W}}}} Kt^3&{\text { with }}&\bar{{\bar{W}}}&= \frac{1}{6} {{\bar{H}}} \frac{1}{1 - \frac{C^2}{42}} {\text { and }}\\&&{{\bar{H}}}&= 8\frac{\sinh (C)\cosh (C)}{C} + 2 \frac{\sinh (C)^2}{C^2} C'. \end{aligned}$$

For example, with $C, C' \le \frac{1}{4}$, we have $\bar{{\bar{W}}} \le \frac{3}{2}$.

From Proposition B.1, we know that for the curve

$$\begin{aligned} c_{ts, \dot{s}}(q) = \mathrm {Exp}_x(ts + q\dot{s}) \end{aligned}$$

(recall that s has unit norm) it holds that $W(t) = t^2 c_{ts, \dot{s}}''(0)$. Thus,

$$\begin{aligned} \Vert c_{ts, \dot{s}}''(0)\Vert&\le \bar{{{\bar{W}}}} K \Vert \dot{s}\Vert \Vert \dot{s}_\perp \Vert t. \end{aligned}$$

Allowing s to have norm different from one and rescaling t, we conclude that for the curve

$$\begin{aligned} c(t)&= \mathrm {Exp}_x(s + t\dot{s}) \end{aligned}$$

we have

$$\begin{aligned} \Vert c''(0)\Vert&\le \bar{{{\bar{W}}}} K \Vert s\Vert \Vert \dot{s}\Vert \Vert \dot{s}_\perp \Vert , \end{aligned}$$

provided $\Vert s\Vert \le C \frac{1}{\sqrt{K}}$ with $C \le \pi$ and $\Vert s\Vert \le C' \frac{K}{F}$ and $\gamma (t) = \mathrm {Exp}_x(ts)$ is defined [0, 1]. $\square$

Lemma About Parameter Relations

As a general comments: here and throughout, constants are not optimized at all. In part, this is so that there is leeway in the precise definition of parameters. For example, the step-size $\eta$ does not need to be exactly equal to $1/4\ell$, but it is convenient to assume equality to simplify many tedious computations.

Lemma C.1

With parameters and assumptions as laid out in Sect. 3, the following hold:

$$\begin{aligned} \begin{array}{ll} 1. \,\kappa \ge 2 and \log _2(\theta ^{-1}) \ge \frac{5}{2}, &{} 5. \,\epsilon r + \frac{\ell }{2} r^2 \le \frac{1}{4} {\mathscr {E}},\\ 2.\, \epsilon \le \frac{1}{2} \ell b and 2\ell {\mathscr {M}} < \frac{1}{2} \ell b, &{} 6. \,\frac{{\mathscr {L}}^2}{16\sqrt{\kappa }\eta {\mathscr {T}}} = {\mathscr {E}},\\ 3.\, r \le \frac{1}{64} {\mathscr {L}} and {\mathscr {L}} \le s \le \frac{1}{32} b, &{} 7.\, \frac{s^2}{2\eta } \ge 2{\mathscr {E}} and \frac{(\gamma - 4{{\hat{\rho }}} s)s^2}{2} \ge 2{\mathscr {E}}, \\ 4.\, \ell {\mathscr {M}}^2 \ge \frac{64{\mathscr {E}}}{{\mathscr {T}}} and \theta \ell {\mathscr {M}}^2 \ge \frac{4{\mathscr {E}}}{{\mathscr {T}}}, &{} 8.\, {{\hat{\rho }}} ({\mathscr {L}} + {\mathscr {M}}) \le \sqrt{{{\hat{\rho }}} \epsilon }.\\ \end{array} \end{aligned}$$

Proofs from Sect. 4 About AGD in a Ball of a Tangent Space

We give a proof of the lemma which states that iterates generated by $\mathtt {TSS}$ remain in certain balls. Such a lemma is not necessary in the Euclidean case.

Proof of Lemma 4.1

Because of how $\mathtt {TSS}$ works, if it defines $u_j$ for some j, then $s_j$ must have already been defined. Moreover, if $\Vert s_{j+1}\Vert > b$, then the algorithm terminates before defining $u_{j+1}$. It follows that if $u_0, \ldots , u_q$ are defined then $\Vert s_0\Vert , \ldots , \Vert s_q\Vert$ are all at most b. Also, $\mathtt {TSS}$ ensures $\Vert u_0\Vert , \ldots , \Vert u_q\Vert$ are all at most 2b by construction.

Recall that $\theta = \frac{1}{4\sqrt{\kappa }}$. From Lemma C.1 we know $\kappa \ge 2$ so that $\theta \le 1$. Moreover, $2\eta \gamma = \frac{1}{8\kappa } = \frac{1}{2\sqrt{\kappa }} \theta \le \theta$. It follows that $\theta _j$ as presented in (19) is well defined in the interval $[\theta , 1]$. Indeed, either $\Vert s_j + (1-\theta ) v_j\Vert \le 2b$, in which case $\theta _j = \theta$; or the line segment connecting $s_j$ to $s_j + (1-\theta ) v_j$ intersects the boundary of the sphere of radius 2b at exactly one point. By definition, this happens at $s_j + (1-\theta _j) v_j$ with $1-\theta _j$ chosen in the interval $[0, 1-\theta ]$, that is, $\theta _j \in [\theta , 1]$.

Now assume that $\Vert \mathrm {grad}f(x)\Vert \le \frac{1}{2} \ell b$. Then, for all $0 \le j \le q$ we have

$$\begin{aligned} \Vert \eta \nabla {{\hat{f}}}_x(u_j)\Vert&\le \eta \left( \Vert \nabla {{\hat{f}}}_x(u_j) - \nabla {{\hat{f}}}_x(0)\Vert + \Vert \nabla {{\hat{f}}}_x(0)\Vert \right) \\&\le \eta \left( \ell \Vert u_j\Vert + \frac{1}{2}\ell b \right) \le \frac{5}{2}\eta \ell b = \frac{5}{8} b < b, \end{aligned}$$

where we used the fact that $\Vert u_j\Vert \le 2b$ and that $\nabla {{\hat{f}}}_x$ is $\ell$-Lipschitz continuous in the ball of radius 3b around the origin (by A2), the fact that $\mathrm {grad}f(x) = \nabla {{\hat{f}}}_x(0)$, and the fact that $\eta \ell = \frac{1}{4}$ by definition of $\eta$. Consequently, if $s_{q+1}$ is defined, then

$$\begin{aligned} \Vert s_{q+1}\Vert = \Vert u_q - \eta \nabla {{\hat{f}}}_x(u_q)\Vert \le \Vert u_q\Vert + \Vert \eta \nabla {{\hat{f}}}_x(u_q)\Vert \le 3b. \end{aligned}$$

If additionally it holds that $\Vert u_q\Vert = 2b$, then

$$\begin{aligned} \Vert s_{q+1}\Vert = \Vert u_q - \eta \nabla {{\hat{f}}}_x(u_q)\Vert \ge \Vert u_q\Vert - \Vert \eta \nabla {{\hat{f}}}_x(u_q)\Vert > b. \end{aligned}$$

(Mind the strict inequality: this one will matter.) $\square$

Lemma 4.1 applies under the assumptions of Lemmas 4.2, 4.3 and 4.4. This ensures all vectors $u_j, s_j$ remain in $B_x(3b)$, and hence the strongest provisions of A2 apply: we use this often in the proofs below.

We give a proof of the lemma which states that the Hamiltonian is monotonically decreasing along iterations.

Proof of Lemma 4.2

This follows almost exactly [28, Lem. 9 and 20], with one modification to allow $\theta _j$ (19) to be larger than 1/2: this is necessary in our setup because we need to cap $u_j$ to the ball of radius 2b, requiring values of $\theta _j$ which can be arbitrarily close to 1.

Since $\nabla {{\hat{f}}}_x$ is $\ell$-Lipschitz continuous in $B_x(3b)$ and $u_j, s_{j+1} \in B_x(3b)$, standard calculus and the identity $s_{j+1} = u_j - \eta \nabla {\hat{f}}_x(u_j)$ show that

$$\begin{aligned} {{\hat{f}}}_x(s_{j+1})&\le {{\hat{f}}}_x(u_j) + \langle {s_{j+1} - u_j},{\nabla {{\hat{f}}}_x(u_j)}\rangle + \frac{\ell }{2} \Vert s_{j+1} - u_j\Vert ^2 \\&= {{\hat{f}}}_x(u_j) - \eta \left( 1 - \frac{\ell \eta }{2} \right) \Vert \nabla {{\hat{f}}}_x(u_j)\Vert ^2. \end{aligned}$$

Since $\ell \eta = \frac{1}{4} \le \frac{1}{2}$, it follows that

$$\begin{aligned} {{\hat{f}}}_x(s_{j+1})&\le {{\hat{f}}}_x(u_j) - \frac{3 \eta }{4} \Vert \nabla {{\hat{f}}}_x(u_j)\Vert ^2. \end{aligned}$$

Turning to $E_{j+1}$ as defined by (20) and with the identity $v_{j+1} = s_{j+1} - s_j$, we compute:

$$\begin{aligned} E_{j+1} = {{\hat{f}}}_x(s_{j+1}) + \frac{1}{2\eta } \Vert v_{j+1}\Vert ^2 \le {{\hat{f}}}_x(u_j) - \frac{3 \eta }{4} \Vert \nabla {{\hat{f}}}_x(u_j)\Vert ^2 + \frac{1}{2\eta } \Vert s_{j+1} - s_j\Vert ^2. \end{aligned}$$

Notice that

$$\begin{aligned} \Vert s_{j+1} - s_j\Vert ^2&= \Vert u_j - \eta \nabla {\hat{f}}_x(u_j) - s_j\Vert ^2 \\&= \Vert u_j - s_j\Vert ^2 - 2\eta \langle {u_j - s_j},{\nabla {\hat{f}}_x(u_j)}\rangle + \eta ^2 \Vert \nabla {\hat{f}}_x(u_j)\Vert ^2. \end{aligned}$$

Moreover, the fact that $s_{j+1}$ is defined means that (NCC) does not trigger with $(x, s_j, u_j)$; in other words:

$$\begin{aligned} {\hat{f}}_x(s_j) \ge {\hat{f}}_x(u_j) - \langle {u_j - s_j},{\nabla {\hat{f}}_x(u_j)}\rangle - \frac{\gamma }{2}\left\| {u_j - s_j}\right\| ^2. \end{aligned}$$

Combining, we find that

$$\begin{aligned} E_{j+1}&\le {{\hat{f}}}_x(u_j) - \frac{3 \eta }{4} \Vert \nabla {{\hat{f}}}_x(u_j)\Vert ^2 - \langle {u_j - s_j},{\nabla {\hat{f}}_x(u_j)}\rangle \\&\quad + \frac{1}{2\eta } \Vert u_j - s_j\Vert ^2 + \frac{\eta }{2} \Vert \nabla {\hat{f}}_x(u_j)\Vert ^2 \\&\le {\hat{f}}_x(s_j) + \left( \frac{\gamma }{2} + \frac{1}{2\eta }\right) \left\| {u_j - s_j}\right\| ^2 - \frac{\eta }{4} \Vert \nabla {{\hat{f}}}_x(u_j)\Vert ^2. \end{aligned}$$

Using the identities $u_j - s_j = (1-\theta _j) v_j$ and $E_j = {{\hat{f}}}_x(s_j) + \frac{1}{2\eta } \Vert v_j\Vert ^2$, we can further write:

$$\begin{aligned} E_{j+1}&\le {\hat{f}}_x(s_j) + \left( \frac{\gamma }{2} + \frac{1}{2\eta }\right) (1-\theta _j)^2 \left\| {v_j}\right\| ^2 - \frac{\eta }{4} \Vert \nabla {{\hat{f}}}_x(u_j)\Vert ^2 \\&= E_j + \left( \frac{\gamma (1-\theta _j)^2}{2} + \frac{(1-\theta _j)^2 - 1}{2\eta } \right) \Vert v_j\Vert ^2 - \frac{\eta }{4} \Vert \nabla {{\hat{f}}}_x(u_j)\Vert ^2 \\&= E_j + \frac{1}{2\eta } \left( \eta \gamma (1-\theta _j)^2 + (1-\theta _j)^2 - 1 \right) \Vert v_j\Vert ^2 - \frac{\eta }{4} \Vert \nabla {{\hat{f}}}_x(u_j)\Vert ^2. \end{aligned}$$

From Lemma 4.1 we know that $\eta \gamma \le \frac{1}{2} \theta _j$ and that $\theta _j$ is in the interval [0, 1]. It is easy to check that the function $\theta _j \mapsto \frac{1}{2} \theta _j (1-\theta _j)^2 + (1-\theta _j)^2 - 1$ is upper-bounded by $-\theta _j$ over the interval [0, 1].

Thus,

$$\begin{aligned} E_{j+1}&\le E_j - \frac{\theta _j}{2\eta } \Vert v_j\Vert ^2 - \frac{\eta }{4} \Vert \nabla {{\hat{f}}}_x(u_j)\Vert ^2 \le E_j, \end{aligned}$$

as announced.

In closing, note that if $\Vert v_j\Vert \ge {\mathscr {M}}$ then Lemma C.1 shows

$$\begin{aligned} E_j - E_{j+1} \ge \frac{\theta _j}{2\eta } \Vert v_j\Vert ^2 \ge \frac{\theta }{2\eta } {\mathscr {M}}^2 = 2 \theta \ell {\mathscr {M}}^2 \ge \frac{4{\mathscr {E}}}{{\mathscr {T}}}, \end{aligned}$$

which concludes the proof. $\square$

We give a proof of the improve-or-localize lemma.

Proof of Lemma 4.3

This follows from [28, Cor. 11], with some modifications for variable $\theta _j$ and because we allow $\theta _j > \frac{1}{2}$. By triangular inequality then Cauchy–Schwarz, we have

$$\begin{aligned} \Vert s_q - s_{q'}\Vert ^2&= \left\| \sum _{j = q'}^{q-1} s_{j+1} - s_j \right\| ^2 \le \left( \sum _{j = q'}^{q-1} \Vert s_{j+1} - s_j\Vert \right) ^2 \\&\le (q - q') \sum _{j = q'}^{q-1} \Vert s_{j+1} - s_j\Vert ^2. \end{aligned}$$

Now use the inequality $\Vert a + b\Vert ^2 \le (1+C) \Vert a\Vert ^2 + \frac{1+C}{C} \Vert b\Vert ^2$ (valid for all vectors a, b and reals $C > 0$) with $C = 2\sqrt{\kappa } - 1$ (positive owing to $\kappa \ge 1$ by Lemma C.1) to see that

$$\begin{aligned} \Vert s_{j+1} - s_j\Vert ^2&= \Vert (s_{j+1} - u_j) + (u_j - s_j)\Vert ^2 \le 2\sqrt{\kappa } \Vert s_{j+1} - u_j\Vert ^2 \\&\quad + \frac{2\sqrt{\kappa }}{2\sqrt{\kappa } - 1} \Vert u_j - s_j\Vert ^2. \end{aligned}$$

By construction, we have $s_{j+1} = u_j - \eta \nabla {\hat{f}}_x(u_j)$ and $u_j = s_j + (1-\theta _j) v_j$. Thus:

$$\begin{aligned} \Vert s_{j+1} - s_j\Vert ^2&\le 2\sqrt{\kappa } \eta ^2 \Vert \nabla {\hat{f}}_x(u_j)\Vert ^2 + \frac{2\sqrt{\kappa }(1-\theta _j)^2}{2\sqrt{\kappa } - 1} \Vert v_j\Vert ^2 \\&= 16\sqrt{\kappa } \eta \left( \frac{\eta }{8} \Vert \nabla {\hat{f}}_x(u_j)\Vert ^2 + \frac{1}{2\eta }\frac{(1-\theta _j)^2}{4(2\sqrt{\kappa } - 1)} \Vert v_j\Vert ^2 \right) . \end{aligned}$$

We focus on the second term: recall from Lemma 4.1 that $\theta _j \in [\theta , 1]$ with $\theta = \frac{1}{4\sqrt{\kappa }}$, and notice that $(1-t)^2 \le 4(2\sqrt{\kappa } - 1)t$ for all t in the interval defined by $\frac{1-\theta \pm \sqrt{1-2\theta }}{\theta }$.

This holds a fortiori for all t in $[\theta , 1]$ because $\theta \le \frac{1}{4}$ owing to $\kappa \ge 1$.

It follows that

$$\begin{aligned} \Vert s_{j+1} - s_j\Vert ^2&\le 16\sqrt{\kappa } \eta \left( \frac{\eta }{8} \Vert \nabla {\hat{f}}_x(u_j)\Vert ^2 + \frac{\theta _j}{2\eta } \Vert v_j\Vert ^2 \right) . \end{aligned}$$

Apply Lemma 4.2 to the parenthesized expression to deduce that

$$\begin{aligned} \Vert s_{j+1} - s_j\Vert ^2&\le 16\sqrt{\kappa } \eta \left( E_j - E_{j+1} \right) . \end{aligned}$$

Plug this into the first inequality of this proof to conclude with a telescoping sum. $\square$

We give a proof of the lemma which states that, upon witnessing significant non-convexity, it is possible to exploit that observation to drive significant decrease in the cost function value.

Proof of Lemma 4.4

This follows almost exactly [28, Lem. 10 and 17]. We need a slight modification because the Hessian $\nabla ^2 {{\hat{f}}}_x$ may not be Lipschitz continuous in all of $B_x(3b)$: our assumptions only guarantee a type of Lipschitz continuity with respect to the origin of $\mathrm {T}_x{\mathcal {M}}$. Interestingly, even if the last momentum step was capped (that is, if $\theta _j \ne \theta$)—something which does not happen in the Euclidean case—the result goes through.

First, consider the case $\Vert v_j\Vert \ge s$, where s is a parameter set in Sect. 3. Then, $\mathtt {NCE}(x, s_j, v_j) = s_j$. It follows from the definition of $E_j$ (20) that

$$\begin{aligned} {{\hat{f}}}_x(\mathtt {NCE}(x, s_j, v_j))&= {{\hat{f}}}_x(s_j) = E_j - \frac{1}{2\eta } \Vert v_j\Vert ^2 \le E_j - \frac{s^2}{2\eta }. \end{aligned}$$

Second, consider the case $\Vert v_j\Vert < s$. We know that $v_j \ne 0$ as otherwise $u_j = s_j + (1-\theta _j) v_j = s_j$: this would contradict the assumption that (NCC) triggers with $(x, s_j, u_j)$. Expand ${{\hat{f}}}_x$ around $u_j$ in a truncated Taylor series with Lagrange remainder to see that

$$\begin{aligned} {{\hat{f}}}_x(s_j) = {{\hat{f}}}_x(u_j) + \langle {\nabla {{\hat{f}}}_x(u_j)},{s_j - u_j}\rangle + \frac{1}{2}\langle {\nabla ^2 {{\hat{f}}}_x(\zeta _j)[s_j - u_j]},{s_j - u_j}\rangle \end{aligned}$$

with $\zeta _j = ts_j + (1-t)u_j$ for some $t \in [0, 1]$. Since (NCC) triggers with $(x, s_j, u_j)$, we also know that

$$\begin{aligned} {\hat{f}}_x(s_j) < {\hat{f}}_x(u_j) + \langle {\nabla {\hat{f}}_x(u_j)},{s_j - u_j}\rangle - \frac{\gamma }{2}\left\| {s_j - u_j}\right\| ^2. \end{aligned}$$

The last two claims combined yield:

$$\begin{aligned} \langle {\nabla ^2 {{\hat{f}}}_x(\zeta _j)[s_j - u_j]},{s_j - u_j}\rangle < - \gamma \left\| {s_j - u_j}\right\| ^2. \end{aligned}$$

(71)

Consider ${\dot{v}} = s \frac{v_j}{\left\| {v_j}\right\| }$ as defined in the call to $\mathtt {NCE}$. Let ${{\tilde{v}}}$ be either $\dot{v}$ or $-\dot{v}$, chosen so that $\langle {\nabla {{\hat{f}}}_x(s_j)},{{{\tilde{v}}}}\rangle \le 0$ (at least one of the two choices satisfies this condition). By construction, $\mathtt {NCE}(x, s_j, v_j)$ is the element of the triplet $\{s_j, s_j+\dot{v}, s_j-\dot{v}\}$ where ${{\hat{f}}}_x$ is minimized. Since $s_j + \tilde{v}$ belongs to this triplet, it follows through another truncated Taylor series with Lagrange remainder (this time around $s_j$) that

$$\begin{aligned} {{\hat{f}}}_x(\mathtt {NCE}(x, s_j, v_j)) \le {{\hat{f}}}_x(s_j + {{\tilde{v}}})&= {{\hat{f}}}_x(s_j) + \langle {\nabla {{\hat{f}}}_x(s_j)},{{{\tilde{v}}}}\rangle + \frac{1}{2}\langle {\nabla ^2 {{\hat{f}}}_x(\zeta _j')[{{\tilde{v}}}]},{\tilde{v}}\rangle \nonumber \\&\le {{\hat{f}}}_x(s_j) + \frac{1}{2}\langle {\nabla ^2 {{\hat{f}}}_x(\zeta _j')[{{\tilde{v}}}]},{{{\tilde{v}}}}\rangle \end{aligned}$$

(72)

with $\zeta _j' = s_j + t'{{\tilde{v}}}$ for some $t' \in [0, 1]$. Since ${{\tilde{v}}}$ is parallel to $v_j$ which itself is parallel to $s_j - u_j$ (by definition of $u_j$), we deduce from (71) that

$$\begin{aligned} \langle {\nabla ^2 {{\hat{f}}}_x(\zeta _j)[{{\tilde{v}}}]},{{{\tilde{v}}}}\rangle < -\gamma \Vert {{\tilde{v}}}\Vert ^2 = -\gamma s^2. \end{aligned}$$

We aim to use this to work on (72), but notice that $\nabla ^2 {{\hat{f}}}_x$ is evaluated at two possibly distinct points, namely, $\zeta _j$ and $\zeta _j'$: we need to use the Lipschitz properties of the Hessian to relate them. To this end, notice that $\zeta _j$ and $\zeta _j'$ both live in $B_x(3b)$. Indeed, $\Vert {{\tilde{v}}}\Vert = \Vert \dot{v}\Vert = s \le b$ by Lemma C.1 and $\Vert s_j\Vert \le b, \Vert u_j\Vert \le 2b$ by Lemma 4.1. Thus, $\Vert \zeta _j\Vert \le \Vert s_j\Vert + \Vert u_j\Vert \le b + 2b = 3b$ and $\Vert \zeta _j'\Vert \le \Vert s_j\Vert + \Vert {{\tilde{v}}}\Vert \le b + b = 2b$. In contrast to the proof in [28], we have no Lipschitz guarantee for $\nabla ^2 {{\hat{f}}}_x$ along the line segment connecting $\zeta _j$ and $\zeta _j'$, but A2 still offers such guarantees along the line segments connecting the origin of $\mathrm {T}_x{\mathcal {M}}$ to each of $\zeta _j$ and $\zeta _j'$. Thus, we can write:

$$\begin{aligned} \langle {\nabla ^2 {{\hat{f}}}_x(\zeta _j')[{{\tilde{v}}}]},{{{\tilde{v}}}}\rangle&= \langle {\nabla ^2 {{\hat{f}}}_x(\zeta _j)[{{\tilde{v}}}]},{{{\tilde{v}}}}\rangle + \langle {(\nabla ^2 {{\hat{f}}}_x(\zeta _j') - \nabla ^2 {{\hat{f}}}_x(0))[{{\tilde{v}}}]},{{{\tilde{v}}}}\rangle \\&\quad - \langle {(\nabla ^2 {{\hat{f}}}_x(\zeta _j) - \nabla ^2 {{\hat{f}}}_x(0))[{{\tilde{v}}}]},{{{\tilde{v}}}}\rangle \\&\le -\gamma s^2 + \left( \Vert \nabla ^2 {{\hat{f}}}_x(\zeta _j') - \nabla ^2 {{\hat{f}}}_x(0)\Vert \right. \\&\quad \left. + \Vert \nabla ^2 {{\hat{f}}}_x(\zeta _j) - \nabla ^2 {{\hat{f}}}_x(0)\Vert \right) \Vert {{\tilde{v}}}\Vert ^2 \\&\le \left( -\gamma + {{\hat{\rho }}} (\Vert \zeta _j'\Vert + \Vert \zeta _j\Vert ) \right) s^2 \\&\le \left( -\gamma + 2{{\hat{\rho }}}(s + \Vert s_j\Vert ) \right) s^2, \end{aligned}$$

where on the last line we used $\zeta _j = ts_j + (1-t)u_j$, $u_j = s_j + (1-\theta _j) v_j$, $\theta _j \in [0, 1]$ and $\Vert v_j\Vert \le s$ to claim that $\Vert \zeta _j\Vert = \Vert s_j + (1-t)(1-\theta _j)v_j\Vert \le \Vert s_j\Vert + \Vert v_j\Vert \le \Vert s_j\Vert + s$, and also (more directly) that $\Vert \zeta _j'\Vert \le \Vert s_j\Vert + \Vert {{\tilde{v}}}\Vert = \Vert s_j\Vert + s$. Plugging our findings into (72), it follows that

$$\begin{aligned} {{\hat{f}}}_x(\mathtt {NCE}(x, s_j, v_j)) \le {{\hat{f}}}_x(s_j) - \frac{1}{2}\left( \gamma - 2{{\hat{\rho }}}(s + \Vert s_j\Vert ) \right) s^2. \end{aligned}$$

(73)

Since ${{\hat{f}}}_x(s_j) \le E_j$ by definition (20), the main part of the lemma’s claim is now proved.

We now turn to the last part of the lemma’s claim, for which we further assume $\Vert s_j\Vert \le {\mathscr {L}}$. Recall from Lemma C.1 that ${\mathscr {L}} \le s$. We deduce from the main claim that

$$\begin{aligned} {{\hat{f}}}_x(\mathtt {NCE}(x, s_j, v_j)) \le E_j - \min \!\left( \frac{s^2}{2\eta }, \frac{(\gamma - 4{{\hat{\rho }}} s)s^2}{2} \right) . \end{aligned}$$

To conclude, use Lemma C.1 anew to bound the right-most term. $\square$

Supporting Lemmas

In this section, we state and prove three additional lemmas about accelerated gradient descent in balls of tangent spaces that are useful for proofs in subsequent sections. The statements apply more broadly than the setup of parameters and assumptions in Sect. 3, but of course it is under those provisions that the conclusions are useful to us.

Throughout this section, we use the following notation. For some $x \in {\mathcal {M}}$, let ${\mathcal {H}} = \nabla ^2 {\hat{f}}_x(0)$. Given $s_0 \in \mathrm {T}_x{\mathcal {M}}$, set $v_0 = 0$ and define for $j = 0, 1, 2, \ldots$:

$$\begin{aligned} u_j&= s_j + (1-\theta )v_j,&s_{j+1}&= u_j - \eta \nabla {\hat{f}}_x(u_j)&{\text { and }}&v_{j+1}&= s_{j+1} - s_j \end{aligned}$$

(74)

with some arbitrary $\theta \in [0, 1]$ and $\eta > 0$. Also define $s_{-1} = s_0 - v_0$ for convenience and

$$\begin{aligned} \delta _k&= \nabla {\hat{f}}_x(u_k) - \nabla {\hat{f}}_x(0) - {\mathcal {H}}u_k, \nonumber \\ \delta _k'&= \nabla {\hat{f}}_x(u_k) - \nabla {\hat{f}}_x(s_\tau ) - {\mathcal {H}}(u_k-s_\tau ), \end{aligned}$$

(75)

where $\tau \ge 0$ is a fixed index. Notice that iterates generated by $\mathtt {TSS}(x, s_0)$ with parameters and assumptions as laid out in Sect. 3 conform to this notation so long as $\theta _j = \theta$. Owing to Lemma 4.1, the latter condition holds in particular if $\mathtt {TSS}$ runs all its iterations in full because if at any point $\theta _j \ne \theta$ then $\Vert s_{j+1}\Vert > b$ and $\mathtt {TSS}$ terminates early. This is the setting in which we call upon lemmas from this section.

The first lemma is a variation on [28, Lem. 18].

Lemma E.1

With notation as above, for all $j \ge 0$ we can write

$$\begin{aligned} \begin{pmatrix} s_{\tau +j} \\ s_{\tau +j-1} \end{pmatrix}&= A^j \begin{pmatrix} s_{\tau } \\ s_{\tau -1} \end{pmatrix} - \eta \sum _{k = 0}^{j-1} A^{j-1-k} \begin{pmatrix} \nabla {{\hat{f}}}_x(0) + \delta _{\tau + k} \\ 0 \end{pmatrix} \end{aligned}$$

(76)

and

$$\begin{aligned} \begin{pmatrix} s_{\tau +j} - s_{\tau } \\ s_{\tau +j-1} - s_{\tau } \end{pmatrix}&= A^j \begin{pmatrix} 0 \\ -v_{\tau } \end{pmatrix} - \eta \sum _{k=0}^{j-1} A^{j-1-k} \begin{pmatrix} \nabla {\hat{f}}_x(s_{\tau }) + \delta _{\tau +k}' \\ 0 \end{pmatrix} \end{aligned}$$

(77)

where

$$\begin{aligned} A&= \begin{pmatrix} (2-\theta )(I-\eta {\mathcal {H}}) &{} -(1-\theta )(I-\eta {\mathcal {H}}) \\ I &{} 0 \end{pmatrix}. \end{aligned}$$

(78)

Proof

By definition of $\delta _{\tau +j-1}$, we have $\nabla {\hat{f}}_x(u_{\tau +j-1}) = \nabla {\hat{f}}_x(0) + {\mathcal {H}}u_{\tau +j-1} + \delta _{\tau +j-1}$. Thus,

$$\begin{aligned} s_{\tau +j}&= u_{\tau +j-1} - \eta \nabla {\hat{f}}_x(u_{\tau +j-1}) \\&= u_{\tau +j-1} - \eta \nabla {\hat{f}}_x(0) -\eta {\mathcal {H}}u_{\tau +j-1} - \eta \delta _{\tau +j-1} \\&= (I -\eta {\mathcal {H}})u_{\tau +j-1} -\eta (\nabla {\hat{f}}_x(0) + \delta _{\tau +j-1}). \end{aligned}$$

Use the definitions of $u_{k}$ and $v_{k}$ to verify that $u_{k} = (2-\theta )s_{k} - (1-\theta )s_{k-1}$ (we use this several times in subsequent proofs). Plug this in the previous identity to see that

$$\begin{aligned} s_{\tau +j}&= (2-\theta ) (I -\eta {\mathcal {H}}) s_{\tau +j-1} - (1-\theta ) (I -\eta {\mathcal {H}}) s_{\tau +j-2} -\eta (\nabla {\hat{f}}_x(0) + \delta _{\tau +j-1}). \end{aligned}$$

Equivalently in matrix form, then reasoning by induction, it follows that

$$\begin{aligned} \begin{aligned} \left( {\begin{array}{c} s_{\tau +j}\\ s_{\tau +j-1} \\ \end{array} } \right)&= \left( {\begin{array}{cc} (2-\theta )(I-\eta {\mathcal {H}}) &{} -(1-\theta )(I-\eta {\mathcal {H}}) \\ I &{} 0 \\ \end{array} } \right) \left( {\begin{array}{c} s_{\tau +j-1 }\\ s_{\tau +j-2} \\ \end{array} } \right) \\ {}&\quad - \eta \left( {\begin{array}{c} \nabla {\hat{f}}_x(0) + \delta _{\tau +j-1}\\ 0 \\ \end{array} } \right) \\&= A^j \left( {\begin{array}{c} s_{\tau }\\ s_{\tau -1} \\ \end{array} } \right) - \eta \sum _{k=0}^{j-1} A^{j-1-k} \left( {\begin{array}{c} \nabla {\hat{f}}_x(0) + \delta _{\tau +k}\\ 0 \end{array} } \right) . \end{aligned} \end{aligned}$$

This verifies Eq. (76). To prove Eq. (77), observe that (76) together with

$$\begin{aligned} \delta _{\tau +k}&= \delta _{\tau +k}' + \nabla {{\hat{f}}}_x(s_\tau ) - \nabla {{\hat{f}}}_x(0) - {\mathcal {H}}s_\tau \end{aligned}$$

and $s_{\tau -1} = s_\tau - v_\tau$ imply

$$\begin{aligned} \begin{aligned} \left( {\begin{array}{c} s_{\tau +j}-s_{\tau }\\ s_{\tau +j-1} -s_{\tau } \end{array} } \right)&= A^j \left( {\begin{array}{c} 0\\ -v_{\tau } \\ \end{array} } \right) - \eta \sum _{k=0}^{j-1} A^{j-1-k} \left( {\begin{array}{c} \nabla {\hat{f}}_x(s_{\tau }) + \delta _{\tau +k}'\\ 0 \\ \end{array} } \right) \\&\quad + (A^j - I) \left( {\begin{array}{c} s_{\tau }\\ s_{\tau } \end{array} } \right) + \sum _{k=0}^{j-1} A^{j-1-k} \left( {\begin{array}{c} \eta {\mathcal {H}} s_{\tau }\\ 0 \\ \end{array} } \right) . \end{aligned} \end{aligned}$$

The last two terms cancel. Indeed, let $M \triangleq \sum _{k=0}^{j-1} A^{j-1-k} = A^0 + \cdots + A^{j-1}$. Notice that $M(A-I) = MA - M = A^j - I$. Thus,

$$\begin{aligned} \begin{aligned}&\sum _{k=0}^{j-1} A^{j-1-k} \left( {\begin{array}{c} \eta {\mathcal {H}} s_{\tau }\\ 0 \\ \end{array} } \right) + (A^j - I) \left( {\begin{array}{c} s_{\tau }\\ s_{\tau } \\ \end{array} } \right) \\&\quad = M\Bigg [ \left( {\begin{array}{cc} \eta {\mathcal {H}} &{} 0\\ 0 &{} \eta {\mathcal {H}} \\ \end{array} } \right) \left( {\begin{array}{c} s_{\tau }\\ 0 \\ \end{array} } \right) + (A - I)\left( {\begin{array}{c} s_{\tau }\\ s_{\tau } \\ \end{array} } \right) \Bigg ] \\&\quad = M\Bigg [ \left( {\begin{array}{cc} 0 &{} - \eta {\mathcal {H}}\\ 0 &{} \eta {\mathcal {H}} \\ \end{array} } \right) \left( {\begin{array}{c} s_{\tau }\\ 0 \\ \end{array} } \right) + (A-I)\left( {\begin{array}{cc} -I &{} -I\\ -I &{} -I \\ \end{array} } \right) \left( {\begin{array}{c} s_{\tau }\\ 0 \\ \end{array} } \right) + (A - I)\left( {\begin{array}{c} s_{\tau }\\ s_{\tau } \\ \end{array} } \right) \Bigg ]\\&\quad = M\Bigg [0\Bigg ] = 0. \end{aligned} \end{aligned}$$

To reach the second-to-last line, verify that $(A-I)\begin{pmatrix} -I &{} -I \\ -I &{} -I \end{pmatrix} = \begin{pmatrix} \eta {\mathcal {H}} &{} \eta {\mathcal {H}} \\ 0 &{} 0 \end{pmatrix}$ using (78). The last line follows by direct calculation. $\square$

The lemma below is a direct continuation from the lemma above. We use it only for the proof of Lemma G.1.

Lemma E.2

Use notation from Lemma E.1. Given $s_0, s_0' \in \mathrm {T}_x{\mathcal {M}}$, define two sequences $\{s_j, u_j, v_j\}$ and $\{s_j', u_j', v_j'\}$ by the update equations (74). Let $w_j = s_j - s_j'$. Then,

$$\begin{aligned} \begin{pmatrix} w_j \\ w_{j-1} \end{pmatrix}&= A^j \begin{pmatrix} w_0 \\ w_{-1} \end{pmatrix} - \eta \sum _{k = 0}^{j-1} A^{j-1-k} \begin{pmatrix} \delta _k'' \\ 0 \end{pmatrix} \end{aligned}$$

where $\delta _k'' = \nabla {\hat{f}}_x(u_k)-\nabla {\hat{f}}_x(u_k') - {\mathcal {H}} (u_k - u_k')$.

Proof

By Lemma E.1 with $\tau = 0$, both of these identities hold:

$$\begin{aligned} \begin{pmatrix} s_{j} \\ s_{j-1} \end{pmatrix}&= A^j \begin{pmatrix} s_{0} \\ s_{-1} \end{pmatrix} - \eta \sum _{k = 0}^{j-1} A^{j-1-k} \begin{pmatrix} \nabla {{\hat{f}}}_x(u_k) - {\mathcal {H}} u_{k} \\ 0 \end{pmatrix}, \\ \begin{pmatrix} s_{j}' \\ s_{j-1}' \end{pmatrix}&= A^j \begin{pmatrix} s_{0}' \\ s_{-1}' \end{pmatrix} - \eta \sum _{k = 0}^{j-1} A^{j-1-k} \begin{pmatrix} \nabla {{\hat{f}}}_x(u_k') - {\mathcal {H}} u_{k}' \\ 0 \end{pmatrix}. \end{aligned}$$

Taking the difference of these two equations reveals that

$$\begin{aligned} \begin{pmatrix} w_{j} \\ w_{j-1} \end{pmatrix}&= A^j \begin{pmatrix} w_{0} \\ w_{-1} \end{pmatrix} - \eta \sum _{k = 0}^{j-1} A^{j-1-k} \begin{pmatrix} \nabla {\hat{f}}_x(u_k)-\nabla {\hat{f}}_x(u_k') - {\mathcal {H}} (u_k - u_k') \\ 0 \end{pmatrix}. \end{aligned}$$

Conclude with the definition of $\delta _k''$. $\square$

The next lemma corresponds to [28, Prop. 19]. The claim applies in particular to iterates generated by $\mathtt {TSS}$ with parameters and assumptions as laid out in Sect. 3 and $R \le b$, so long as $\theta _j = \theta$ and the $s_j$ remain in the appropriate balls. There are a few changes related to indexing and to the fact that our Lipschitz assumptions are limited to balls.

Lemma E.3

Use notation from Lemma E.1. Assume $\Vert \nabla ^2{\hat{f}}_x(s) - \nabla ^2{\hat{f}}_x(0)\Vert \le {\hat{\rho }}\left\| {s}\right\|$ for all $s \in B_x(3R)$ with some $R > 0$, ${\hat{\rho }} > 0$. Also assume $\left\| {s_k}\right\| \le R$ for all $k = q'-1, \ldots , q$. Then for all $k = q', \ldots , q$ we have $\left\| {\delta _k}\right\| \le 5{\hat{\rho }} R^2$. Moreover, for all $k = q'+1, \ldots , q$ we have

$$\begin{aligned} \left\| {\delta _{k} - \delta _{k-1}}\right\|&\le 6{\hat{\rho }} R\big (\left\| {s_{k} - s_{k-1}}\right\| + \left\| {s_{k-1} - s_{k-2}}\right\| \big ). \end{aligned}$$

Additionally, we can bound their sum as:

$$\begin{aligned} \sum _{k=q'+1}^q \left\| {\delta _k - \delta _{k-1}}\right\| ^2&\le 144 {\hat{\rho }}^2R^2\sum _{k=q'}^q \left\| {s_{k} - s_{k-1}}\right\| ^2. \end{aligned}$$

(Mind the different ranges of summation.)

Proof

Recall that $u_k = (2-\theta ) s_k - (1-\theta )s_{k-1}$. In particular,

$$\begin{aligned} \Vert u_k\Vert&\le |2-\theta | \Vert s_k\Vert + |1-\theta | \Vert s_{k-1}\Vert \le 3R&{\text { for }}&k&= q', \ldots , q. \end{aligned}$$

We use this to establish each of the three inequalities.

First, by definition of ${\mathcal {H}} = \nabla ^2 {{\hat{f}}}_x(0)$ and of $\delta _k$, we know that

$$\begin{aligned} \delta _k = \nabla {\hat{f}}_x(u_k) - \nabla {\hat{f}}_x(0) - {\mathcal {H}} u_k = \int _0^1 \nabla ^2 {\hat{f}}_x(\phi u_k)[u_k] - \nabla ^2 {{\hat{f}}}_x(0)[u_k]\mathrm {d}\phi . \end{aligned}$$

Owing to $\Vert u_k\Vert \le 3R$, we can use the Lipschitz properties of $\nabla ^2 {{\hat{f}}}_x$ to find

$$\begin{aligned} \Vert \delta _k\Vert&\le \int _0^1\left\| {\nabla ^2 {\hat{f}}_x(\phi u_k)-\nabla ^2 {\hat{f}}_x(0)}\right\| \mathrm {d}\phi \left\| {u_k}\right\| \le \frac{1}{2} {\hat{\rho }}\left\| {u_k}\right\| ^2 \le \frac{9}{2} {{\hat{\rho }}} R^2. \end{aligned}$$

This shows the first inequality for $k = q', \ldots , q$.

For the second inequality, first verify that

$$\begin{aligned} \left\| {\delta _k - \delta _{k-1}}\right\|&= \left\| {\nabla {\hat{f}}_x(u_k) - \nabla {\hat{f}}_x(u_{k-1}) - \nabla ^2 {\hat{f}}_x(0) [u_k - u_{k-1}]}\right\| \\&= \left\| {\bigg (\int _0^1\nabla ^2 {\hat{f}}_x((1-\phi )u_{k-1} + \phi u_k) - \nabla ^2 {\hat{f}}_x(0)\mathrm {d}\phi \bigg )[u_k - u_{k-1}]}\right\| . \end{aligned}$$

Note that the distance between $(1-\phi )u_{k-1} + \phi u_k$ and the origin is at most $\max \{\left\| {u_k}\right\| ,\left\| {u_{k-1}}\right\| \}$ for all $\phi \in [0, 1]$. Since for $k = q'+1, \ldots q$ we have both $\Vert u_k\Vert \le 3R$ and $\Vert u_{k-1}\Vert \le 3R$, it follows that $\Vert (1-\phi )u_{k-1} + \phi u_k\Vert \le 3R$ for all $\phi \in [0, 1]$. As a result, we can use the Lipschitz-like properties of $\nabla ^2 {{\hat{f}}}_x$ and write:

$$\begin{aligned} \left\| {\delta _k - \delta _{k-1}}\right\|&\le 3{\hat{\rho }}R \left\| {u_k - u_{k-1}}\right\| . \end{aligned}$$

Combine $u_k = (2-\theta ) s_k - (1-\theta )s_{k-1}$ and $u_{k-1} = (2-\theta ) s_{k-1} - (1-\theta )s_{k-2}$ to find $u_{k} - u_{k-1} = (2-\theta )(s_k - s_{k-1}) - (1-\theta ) (s_{k-1} - s_{k-2})$. From there, it follows that

$$\begin{aligned} \left\| {\delta _k - \delta _{k-1}}\right\|&\le 3{\hat{\rho }} R \left\| {(2-\theta )(s_k - s_{k-1}) - (1-\theta ) (s_{k-1} - s_{k-2})}\right\| \\&\le 3{\hat{\rho }} R \left( 2 \Vert s_k - s_{k-1}\Vert + \Vert s_{k-1} - s_{k-2}\Vert \right) \\&\le 6{\hat{\rho }} R \left( \Vert s_k - s_{k-1}\Vert + \Vert s_{k-1} - s_{k-2}\Vert \right) . \end{aligned}$$

This establishes the second inequality for $k = q'+1, \ldots q$.

The third inequality follows from the second one through squaring and a sum, notably using $(a+b)^2 \le 2(a^2 + b^2)$ for $a, b \ge 0$:

$$\begin{aligned} \sum _{k=q'+1}^q \left\| {\delta _k - \delta _{k-1}}\right\| ^2&\le 36 {\hat{\rho }}^2 R^2 \sum _{k=q'+1}^q \left( \Vert s_k - s_{k-1}\Vert + \Vert s_{k-1} - s_{k-2}\Vert \right) ^2 \\&\le 72 {\hat{\rho }}^2 R^2 \sum _{k=q'+1}^q \left( \Vert s_k - s_{k-1}\Vert ^2 + \Vert s_{k-1} - s_{k-2}\Vert ^2 \right) \\&= 72 {\hat{\rho }}^2 R^2 \left( \sum _{k=q'+1}^q \Vert s_k - s_{k-1}\Vert ^2 + \sum _{k=q'}^{q-1} \Vert s_k - s_{k-1}\Vert ^2 \right) . \end{aligned}$$

To conclude, extend the ranges of both sums to $q', \ldots , q$. $\square$

We close this supporting section with important remarks about the matrix A (78), still following [28]. Recall the notation ${\mathcal {H}} = \nabla ^2 {{\hat{f}}}_x(0)$: this is an operator on $\mathrm {T}_x{\mathcal {M}}$, self-adjoint with respect to the Riemannian inner product on $\mathrm {T}_x{\mathcal {M}}$. Let $e_1, \ldots , e_d \in \mathrm {T}_x{\mathcal {M}}$ form an orthonormal basis of eigenvectors of ${\mathcal {H}}$ associated to ordered eigenvalues $\lambda _1 \le \cdots \le \lambda _d$. We think of A as a linear operator to and from $\mathrm {T}_x{\mathcal {M}}\times \mathrm {T}_x{\mathcal {M}}$. Conveniently, the eigenvectors of ${\mathcal {H}}$ reveal how to block-diagonalize A. Indeed, from

$$\begin{aligned} A \begin{pmatrix} e_m \\ 0 \end{pmatrix}&= \begin{pmatrix} (2-\theta )(I-\eta {\mathcal {H}}) &{} -(1-\theta )(I-\eta {\mathcal {H}}) \\ I &{} 0 \end{pmatrix} \begin{pmatrix} e_m \\ 0 \end{pmatrix}\\ {}&= \begin{pmatrix} (2-\theta )(1-\eta \lambda _m) e_m \\ e_m \end{pmatrix} \end{aligned}$$

and

$$\begin{aligned} A \begin{pmatrix} 0 \\ e_m \end{pmatrix}&= \begin{pmatrix} (2-\theta )(I-\eta {\mathcal {H}}) &{} -(1-\theta )(I-\eta {\mathcal {H}}) \\ I &{} 0 \end{pmatrix} \begin{pmatrix} 0 \\ e_m \end{pmatrix} \\ {}&= \begin{pmatrix} -(1-\theta )(1-\eta \lambda _m) e_m \\ 0 \end{pmatrix} \end{aligned}$$

it is a simple exercise to check that

$$\begin{aligned} J^* A J&= \mathrm {diag}\!\left( A_1, \ldots , A_d \right) \quad {\text { with }} J = \begin{pmatrix} e_1 &{} 0 &{} e_2 &{} 0 &{} \cdots &{} e_d &{} 0 \\ 0 &{} e_1 &{} 0 &{} e_2 &{} \cdots &{} 0 &{} e_d \end{pmatrix} \quad {\text { and }}\nonumber \\ A_m&= \begin{pmatrix} (2-\theta )(1-\eta \lambda _m) &{} -(1-\theta )(1-\eta \lambda _m) \\ 1 &{} 0 \end{pmatrix}. \end{aligned}$$

(79)

Here, J is a unitary operator from ${{\mathbb {R}}}^{2d}$ (equipped with the standard Euclidean metric) to $\mathrm {T}_x{\mathcal {M}}\times \mathrm {T}_x{\mathcal {M}}$, and $J^*$ denotes its adjoint (which is also its inverse). In particular, it becomes straightforward to investigate powers of A:

$$\begin{aligned} A^k&= \left( J \mathrm {diag}\!\left( A_1, \ldots , A_d \right) J^* \right) ^k = J \mathrm {diag}\!\left( A_1^k, \ldots , A_d^k \right) J^*. \end{aligned}$$

(80)

For $m, m'$ in $\{1, \ldots , d\}$ we have the useful identities

$$\begin{aligned} \left\langle {\begin{pmatrix} e_{m'} \\ 0 \end{pmatrix}},{A^k \begin{pmatrix} e_m \\ 0 \end{pmatrix}}\right\rangle&= {\left\{ \begin{array}{ll} (A_m^k)_{11} &{} {\text { if }} m = m', \\ 0 &{} {\text { if }} m \ne m', \end{array}\right. } \end{aligned}$$

(81)

where $(A_m^k)_{11}$ is the top-left entry of the $2 \times 2$ matrix $(A_m)^k$. Likewise,

$$\begin{aligned} \left\langle {\begin{pmatrix} e_{m'} \\ 0 \end{pmatrix}},{A^k \begin{pmatrix} 0 \\ e_m \end{pmatrix}}\right\rangle&= {\left\{ \begin{array}{ll} (A_m^k)_{12} &{} {\text { if }} m = m', \\ 0 &{} {\text { if }} m \ne m'. \end{array}\right. } \end{aligned}$$

(82)

Additionally, one can also check that [28, Lem. 24]:

$$\begin{aligned} \left\langle {\begin{pmatrix} 0 \\ e_{m'} \end{pmatrix}},{A^k \begin{pmatrix} e_m \\ 0 \end{pmatrix}}\right\rangle&= {\left\{ \begin{array}{ll} (A_m^{k-1})_{11} &{} {\text { if }} m = m', \\ 0 &{} {\text { if }} m \ne m'. \end{array}\right. } \end{aligned}$$

(83)

Proofs from Section 5 About $\mathtt {TAGD}$

1.1 Proof of Proposition 5.3

The next two lemmas support Proposition 5.3. Proofs are in Appendix F.2. They correspond to [28, Lem. 21 and  22]. Notice that it is in Lemma F.2 that the condition on $\chi$ originates, then finds its way into the conditions of Theorem 5.1 through Proposition 5.3. Ultimately, this causes the polylogarithmic factor in the complexity of Theorem 1.3.

Lemma F.1

Fix parameters and assumptions as laid out in Sect. 3. Let $x \in {\mathcal {M}}$ satisfy $\Vert \mathrm {grad}f(x)\Vert \le \frac{1}{2}\ell b$. Let ${\mathcal {S}}$ denote the linear subspace of $\mathrm {T}_x{\mathcal {M}}$ spanned by the eigenvectors of $\nabla ^2 {{\hat{f}}}_x(0)$ associated to eigenvalues strictly larger than $\frac{\theta ^2}{\eta (2-\theta )^2}$. Let $P_{\mathcal {S}}$ denote orthogonal projection to ${\mathcal {S}}$. Assume $\mathtt {TSS}(x)$ runs its course in full.

If there exists $\tau \in \{{\mathscr {T}}/4, \ldots , {\mathscr {T}}/2\}$ such that

$$\begin{aligned} \Vert s_\tau \Vert&\le {\mathscr {L}},&\Vert \nabla {{\hat{f}}}_x(s_\tau ) - P_{{\mathcal {S}}} \nabla {{\hat{f}}}_x(s_\tau )\Vert&\ge \epsilon / 6, \\ \Vert v_\tau \Vert&\le {\mathscr {M}}, {\text { and }}&\left\langle {P_{\mathcal {S}}v_\tau },{\nabla ^2 {{\hat{f}}}_x(0)[P_{\mathcal {S}}v_\tau ]}\right\rangle&\le \sqrt{{{\hat{\rho }}} \epsilon } {\mathscr {M}}^2, \end{aligned}$$

then $E_{\tau -1} - E_{\tau + {\mathscr {T}}/4} \ge {\mathscr {E}}$.

Lemma F.2

Fix parameters and assumptions as laid out in Sect. 3, with

$$\begin{aligned} \chi \ge \log _2(\theta ^{-1}) \ge 1. \end{aligned}$$

Let $x \in {\mathcal {M}}$ satisfy $\Vert \mathrm {grad}f(x)\Vert \le 2\ell {\mathscr {M}}$. Let ${\mathcal {S}}$ denote the linear subspace of $\mathrm {T}_x{\mathcal {M}}$ spanned by the eigenvectors of $\nabla ^2 {{\hat{f}}}_x(0)$ associated to eigenvalues strictly larger than $\frac{\theta ^2}{\eta (2-\theta )^2}$. Let $P_{\mathcal {S}}$ denote orthogonal projection to ${\mathcal {S}}$. Assume $\mathtt {TSS}(x)$ runs its course in full.

If $E_0 - E_{{\mathscr {T}}/2} \le {\mathscr {E}}$, then for each j in $\{ {\mathscr {T}}/4, \ldots , {\mathscr {T}}/2 \}$ we have

$$\begin{aligned} \Vert P_{\mathcal {S}}\nabla {{\hat{f}}}_x(s_j)\Vert&\le \epsilon / 6&{\text { and }}&\left\langle {P_{\mathcal {S}}v_j},{\nabla ^2 {{\hat{f}}}_x(0)[P_{\mathcal {S}}v_j]}\right\rangle&\le \sqrt{{{\hat{\rho }}} \epsilon } {\mathscr {M}}^2. \end{aligned}$$

In Lemmas F.1 and F.2, if ${\mathcal {S}}$ is empty then $P_{{\mathcal {S}}}$ maps all vectors to the zero vector, and the statements still hold.

Proof of Proposition 5.3

By Lemma C.1, $\Vert \mathrm {grad}f(x)\Vert \le 2\ell {\mathscr {M}} < \frac{1}{2} \ell b$. Thus, the strongest provisions of A2 apply at x, as do Lemmas 4.1, 4.2, 4.3 and 4.4. Let $u_j, s_j, v_j$ for $j = 0, 1, \ldots$ be the vectors generated by the computation of $x_{{\mathscr {T}}} = \mathtt {TSS}(x)$. Note that $s_0 = v_0 = 0$. There are several cases to consider, based on how $\mathtt {TSS}$ terminates:

• (Case 2a) The negative curvature condition (NCC) triggers with $(x, s_j, u_j)$. There are two cases to check. Either $\Vert s_j\Vert \le {\mathscr {L}}$, in which case Lemma 4.2 tells us $E_j \le E_0 = f(x)$ and Lemma 4.4 further tells us that

  $$\begin{aligned} f(x_{{\mathscr {T}}}) = {{\hat{f}}}_x(\mathtt {NCE}(x, s_j, v_j)) \le E_j - 2{\mathscr {E}} \le f(x) - 2{\mathscr {E}}. \end{aligned}$$

  Or $\Vert s_j\Vert > {\mathscr {L}}$, in which case Lemma 4.3 used with $q = j < {\mathscr {T}}$ and $s_0 = 0$ implies

  $$\begin{aligned} E_j \le f(x) - \frac{{\mathscr {L}}^2}{16 \sqrt{\kappa } \eta {\mathscr {T}}} = f(x) - {\mathscr {E}}. \end{aligned}$$

  (See Lemma C.1 for that last equality.) Owing to how $\mathtt {NCE}$ works, we always have $f(x_{{\mathscr {T}}}) = {{\hat{f}}}_x(\mathtt {NCE}(x, s_j, v_j)) \le {{\hat{f}}}_x(s_j) \le E_j$ (the last inequality is by definition of $E_j$ (20)). Thus, we conclude that $f(x_{{\mathscr {T}}}) \le f(x) - {\mathscr {E}}$.

• (Case 2b) The iterate $s_{j+1}$ leaves the ball of radius b, that is, $\Vert s_{j+1}\Vert > b$. In this case, apply Lemma 4.3 with $q = j + 1 \le {\mathscr {T}}$ and $s_0 = 0$ to claim

  $$\begin{aligned} f(x_{{\mathscr {T}}})&= {{\hat{f}}}_x(s_{j+1}) \le E_{j+1} \le f(x) - \frac{\Vert s_{j+1}\Vert ^2}{16 \sqrt{\kappa } \eta {\mathscr {T}}} \\&\le f(x) - \frac{{\mathscr {L}}^2}{16 \sqrt{\kappa } \eta {\mathscr {T}}} = f(x) - {\mathscr {E}}. \end{aligned}$$

  (The first inequality is by definition of $E_{j+1}$ (20); subsequently, we use $\Vert s_{j+1}\Vert> b > {\mathscr {L}}$ as in Lemma C.1.)

• (Case 2c) The iterate $s_{j+1}$ satisfies $\Vert \nabla {{\hat{f}}}_x(s_{j+1})\Vert \le \epsilon /2$. Recall the chain rule identity relating gradients of f and gradients of the pullback ${{\hat{f}}}_x = f \circ \mathrm {R}_x$ with $T_s = \mathrm {D}\mathrm {R}_x(s)$:

  $$\begin{aligned} \nabla {{\hat{f}}}_x(s) = T_s^* \mathrm {grad}f(\mathrm {R}_x(s)). \end{aligned}$$

  In our situation, $x_{{\mathscr {T}}} = \mathrm {R}_x(s_{j+1})$ and $\Vert s_{j+1}\Vert \le b$ (otherwise, Case 2b applies). Thus, A2 ensures $\sigma _{{\text {min}}}(T_{s_{j+1}}) \ge \frac{1}{2}$ and we deduce that

  $$\begin{aligned} \Vert \mathrm {grad}f(x_{{\mathscr {T}}})\Vert&= \Vert (T_{s_{j+1}}^*)^{-1} \nabla {{\hat{f}}}_x(s_{j+1})\Vert \\&\le \Vert (T_{s_{j+1}}^*)^{-1}\Vert \Vert \nabla {{\hat{f}}}_x(s_{j+1})\Vert \Vert \le 2 \cdot \frac{\epsilon }{2} = \epsilon . \end{aligned}$$

• (Case 2d) None of the other events occur: $\mathtt {TSS}(x)$ runs its ${\mathscr {T}}$ iterations in full. In this case, we apply the logic in the proof of [28, Lem. 12], as follows. We consider two cases. In the first case, $E_{0} - E_{{\mathscr {T}}/2} > {\mathscr {E}}$. Then, we apply Lemma 4.2 to claim that $E_{0} - E_{{\mathscr {T}}} \ge E_{0} - E_{{\mathscr {T}}/2} \ge {\mathscr {E}}$. Moreover, $E_0 = f(x)$ and $E_{{\mathscr {T}}} \ge {{\hat{f}}}_x(s_{\mathscr {T}}) = f(x_{{\mathscr {T}}})$. Thus, in this case, $f(x) - f(x_{{\mathscr {T}}}) \ge {\mathscr {E}}$. In the second case, $E_{0} - E_{{\mathscr {T}}/2} \le {\mathscr {E}}$. Then, Lemma F.2 applies and we learn the following: Let ${\mathcal {S}}$ denote the linear subspace of $\mathrm {T}_x{\mathcal {M}}$ spanned by the eigenvectors of $\nabla ^2 {{\hat{f}}}_x(0)$ associated to eigenvalues strictly larger than $\frac{\theta ^2}{\eta (2-\theta )^2}$. Let $P_{\mathcal {S}}$ denote orthogonal projection to ${\mathcal {S}}$. For each j in $\{ {\mathscr {T}}/4, \ldots , {\mathscr {T}}/2 \}$ we have

  $$\begin{aligned} \Vert P_{\mathcal {S}}\nabla {{\hat{f}}}_x(s_j)\Vert&\le \epsilon / 6&{\text { and }}&\left\langle {P_{\mathcal {S}}v_j},{\nabla ^2 {{\hat{f}}}_x(0)[P_{\mathcal {S}}v_j]}\right\rangle&\le \sqrt{{{\hat{\rho }}} \epsilon } {\mathscr {M}}^2. \end{aligned}$$

  Let $\tau$ be the first index in the range $\{{\mathscr {T}}/4, \ldots , {\mathscr {T}}\}$ for which $\Vert v_\tau \Vert \le {\mathscr {M}}$. Again, there are two possibilities. In the first case, $\tau > {\mathscr {T}}/2$. Then, $\Vert v_j\Vert > {\mathscr {M}}$ for all j in $\{{\mathscr {T}}/4, \ldots , {\mathscr {T}}/2\}$. The last part of Lemma 4.2 implies that, for each such j, $E_{j} - E_{j+1} \ge \frac{4{\mathscr {E}}}{{\mathscr {T}}}$. It follows that $E_{{\mathscr {T}}/4} - E_{{\mathscr {T}}/2} \ge {\mathscr {E}}$. Conclude this case with Lemma 4.2 which justifies these statements: $f(x) = E_0$, $f(x_{{\mathscr {T}}}) = {{\hat{f}}}_x(s_{{\mathscr {T}}}) \le E_{{\mathscr {T}}}$, and:

  $$\begin{aligned} f(x) - f(x_{{\mathscr {T}}}) \ge E_0 - E_{{\mathscr {T}}} \ge E_{{\mathscr {T}}/4} - E_{{\mathscr {T}}/2} \ge {\mathscr {E}}. \end{aligned}$$

  In the second case, $\tau \in \{{\mathscr {T}}/4, \ldots , {\mathscr {T}}/2\}$. We aim to apply Lemma F.1: there are a few preconditions to check. Here is what we already know:

  $$\begin{aligned} \Vert v_\tau \Vert&\le {\mathscr {M}},&\left\langle {P_{\mathcal {S}}v_\tau },{\nabla ^2 {{\hat{f}}}_x(0)[P_{\mathcal {S}}v_\tau ]}\right\rangle&\le \sqrt{{{\hat{\rho }}} \epsilon } {\mathscr {M}}^2,&{\text { and }}\\ \Vert P_{\mathcal {S}}\nabla {{\hat{f}}}_x(s_\tau )\Vert&\le \epsilon / 6. \end{aligned}$$

  Regarding the third one above: we know that $\Vert \nabla {\hat{f}}_x(s_{\tau })\Vert > \epsilon / 2$ because $\mathtt {TSS}(x)$ did not terminate with $s_\tau$. We deduce that

  $$\begin{aligned} \Vert \nabla {{\hat{f}}}_x(s_\tau ) - P_{{\mathcal {S}}} \nabla {{\hat{f}}}_x(s_\tau )\Vert&\ge \Vert \nabla {{\hat{f}}}_x(s_\tau )\Vert - \Vert P_{{\mathcal {S}}} \nabla {{\hat{f}}}_x(s_\tau )\Vert \ge \frac{\epsilon }{2} - \frac{\epsilon }{6} > \frac{\epsilon }{6}. \end{aligned}$$

  We now have a final pair of cases to check. Either $\Vert s_\tau \Vert \le {\mathscr {L}}$, in which case Lemma F.1 applies: it follows that $E_{\tau -1} - E_{\tau + {\mathscr {T}}/4} \ge {\mathscr {E}}$, and by arguments similar as above we conclude that $f(x) - f(x_{{\mathscr {T}}}) \ge {\mathscr {E}}$. Or $\Vert s_\tau \Vert > {\mathscr {L}}$, in which case Lemma 4.3 implies (using $s_0 = 0$):

  $$\begin{aligned} f(x_{{\mathscr {T}}}) \le E_{{\mathscr {T}}} \le E_\tau \le f(x) - \frac{{\mathscr {L}}^2}{16\sqrt{\kappa }\eta \tau } \le f(x) - {\mathscr {E}}. \end{aligned}$$

  (For the second and last inequalities, we use $\tau < {\mathscr {T}}$ and Lemmas 4.2 and C.1.)

This covers all possibilities. $\square$

1.2 Proofs of Lemmas F.1 and F.2

We include fulls proofs for the analogues of [28, Lem. 21 and 22] because we need small but important changes for our setting (as is the case for the other similar results we prove in full), and because of (ultimately inconsequential) small issues with some arguments pertaining to the subspace ${\mathcal {S}}$ in the original proofs. (Specifically, the subspace ${\mathcal {S}}$ is defined with respect to the Hessian of the cost function at a specific reference point, which for notational convenience in Jin et al. [28] is denoted by 0; however, this same convention is used in several lemmas, on at least one occasion referring to distinct reference points; the authors easily proposed a fix, and we use a different fix below; to avoid ambiguities, we keep all iterate references explicit.) Up to those minor changes, the proofs of the next two lemmas are due to Jin et al.

As a general heads-up for this and the next section: we call upon several lemmas from [28] which are purely algebraic facts about the entries of powers of the $2\times 2$ matrices $A_m$ (79): they do not change at all for our context, hence we do not include their proofs. We only note that Lemma 33 in [28] may not hold for all $x \in \left( \frac{\theta ^2}{(2-\theta )^2}, \frac{1}{4} \right]$ as stated (there are some issues surrounding their eq. (17)), but it is only used twice, both times with $x \in \left( \frac{2\theta ^2}{(2-\theta )^2}, \frac{1}{4} \right]$: in that interval the lemma does hold.

Proof of Lemma F.1

For contradiction, assume $E_{\tau -1} - E_{\tau + {\mathscr {T}}/4} < {\mathscr {E}}$. Then, Lemma 4.2 implies that $E_{\tau -1} - E_{\tau + j} < {\mathscr {E}}$ for all $-1 \le j \le {\mathscr {T}}/4$. Over that range, Lemmas 4.3 and C.1 tell us that

$$\begin{aligned} \Vert s_{\tau + j} - s_{\tau }\Vert ^2 \le 16 \sqrt{\kappa } \eta |j| |E_{\tau } - E_{\tau +j}| < 4 \sqrt{\kappa } \eta {\mathscr {T}} {\mathscr {E}} = \frac{1}{4}{\mathscr {L}}^2. \end{aligned}$$

(84)

The remainder of the proof consists in showing that $\Vert s_{\tau + {\mathscr {T}}/4} - s_{\tau }\Vert$ is in fact larger than $\frac{1}{2}{\mathscr {L}}$.

Starting now, consider $j = {\mathscr {T}}/4$. From (77) in Lemma E.1, we know that

$$\begin{aligned} \begin{pmatrix} s_{\tau +j} - s_{\tau } \\ s_{\tau +j-1} - s_{\tau } \end{pmatrix}&= A^j \begin{pmatrix} 0 \\ -v_{\tau } \end{pmatrix} - \eta \sum _{k=0}^{j-1} A^{j-1-k} \begin{pmatrix} \nabla {\hat{f}}_x(s_{\tau }) + \delta _{\tau +k}' \\ 0 \end{pmatrix}. \end{aligned}$$

Let $e_1, \ldots , e_d$ form an orthonormal basis of eigenvectors for ${\mathcal {H}} = \nabla ^2 {{\hat{f}}}_x(0)$ with eigenvalues $\lambda _1 \le \cdots \le \lambda _d$. Expand $v_\tau$, $\nabla {\hat{f}}_x(s_{\tau })$ and $\delta _{\tau +k}'$ in that basis as:

$$\begin{aligned} v_\tau&= \sum _{m = 1}^{d} v^{(m)} e_m,&\nabla {\hat{f}}_x(s_{\tau })&= \sum _{m = 1}^{d} g^{(m)} e_m,&\delta _{\tau +k}'&= \sum _{m = 1}^{d} (\delta _{\tau +k}')^{(m)} e_m. \end{aligned}$$

(85)

Then,

$$\begin{aligned} \begin{pmatrix} s_{\tau +j} - s_{\tau } \\ s_{\tau +j-1} - s_{\tau } \end{pmatrix}&= \sum _{m = 1}^{d} \left[ -v^{(m)} A^j \begin{pmatrix} 0 \\ e_m \end{pmatrix} - \eta \sum _{k=0}^{j-1} (g^{(m)} + (\delta _{\tau +k}')^{(m)}) A^{j-1-k} \begin{pmatrix} e_m \\ 0 \end{pmatrix} \right] . \end{aligned}$$

Owing to (81) and (82) which reveal how A block-diagonalizes in the basis e, we can further write

$$\begin{aligned} \left\langle {\begin{pmatrix} e_{m} \\ 0 \end{pmatrix}},{\begin{pmatrix} s_{\tau +j} - s_{\tau } \\ s_{\tau +j-1} - s_{\tau } \end{pmatrix}}\right\rangle&= -v^{(m)} (A_m^j)_{12} - \eta \sum _{k=0}^{j-1} \left( g^{(m)} + (\delta _{\tau +k}')^{(m)}\right) (A_m^{j-1-k})_{11}. \end{aligned}$$

This reveals the expansion coefficients of $s_{\tau +j} - s_{\tau }$ in the basis $e_1, \ldots , e_d$, which is enough to study the norm of $s_{\tau +j} - s_{\tau }$. Explicitly,

$$\begin{aligned} \Vert s_{\tau +j} - s_{\tau }\Vert ^2&= \sum _{m = 1}^d \left( v^{(m)} b_{m, j} - \eta \sum _{k=0}^{j-1} \left( g^{(m)} + (\delta _{\tau +k}')^{(m)}\right) a_{m, j-1-k} \right) ^2, \end{aligned}$$

(86)

where we introduce the notation

$$\begin{aligned} a_{m, t}&= (A_m^t)_{11},&b_{m, t}&= -(A_m^t)_{12}. \end{aligned}$$

(87)

To proceed, we need control over the coefficients $a_{m, t}$ and $b_{m, t}$, as provided by [28, Lem. 30]. We explore this for m in the set

$$\begin{aligned} S^c = \left\{ m : \eta \lambda _m \le \frac{\theta ^2}{(2-\theta )^2} \right\} , \end{aligned}$$

that is, for the eigenvectors orthogonal to ${\mathcal {S}}$. Under our general assumptions it holds that $\Vert \nabla ^2 {{\hat{f}}}_x(0)\Vert \le \ell$, so that $|\lambda _m| \le \ell$ for all m. This ensures $\eta \lambda _m \in [-1/4, \theta ^2/(2-\theta )^2]$ for $m \in S^c$. Recall that $A_m$ (79) is a $2 \times 2$ matrix which depends on $\theta$ and $\eta \lambda _m$. It is reasonably straightforward to diagonalize $A_m$ (or rather, to put it in Jordan normal form), and from there to get an explicit expression for any entry of $A_m^k$. The quantity $\sum _{k = 0}^{j-1} a_{m,k}$ is a sum of such entries over a range of powers: this can be controlled as one would a geometric series. In [28, Lem. 30], it is shown that, for $m \in S^c$, if $j \ge 1 + 2/\theta$ and $\theta \in (0, 1/4]$, then

$$\begin{aligned} \sum _{k = 0}^{j-1} a_{m,k}&\ge \frac{1}{c_4 \theta ^2}&{\text { and }}&\frac{b_{m,j}}{\sum _{k' = 0}^{j-1} a_{m,k'}}&\le c_5^{1/2} \max \!\left( \theta , \sqrt{|\eta \lambda _m|} \right) , \end{aligned}$$

(88)

with some universal constants $c_4, c_5$. The lemma applies because $\theta \in (0, 1/4]$ by Lemma C.1 and also $j = {\mathscr {T}}/4 = \chi (c/48) \cdot 3/ \theta \ge 3/\theta \ge 4\sqrt{\kappa } + 2/\theta \ge 1 + 2/\theta$, with $c \ge 48$.

Building on the latter comments, we can define the following scalars for $m \in S^c$:

$$\begin{aligned} p_{m,k,j}&= \frac{a_{m, j-1-k}}{\sum _{k' = 0}^{j-1} a_{m, k'}},&q_{m,j}&= -\frac{b_{m, j}}{\eta \sum _{k' = 0}^{j-1} a_{m, k'}}, \\ {{\tilde{\delta }}}_j'^{(m)}&= \sum _{k = 0}^{j-1} p_{m,k,j} (\delta _{\tau +k}')^{(m)}&{{\tilde{v}}}_j^{(m)}&= q_{m,j} v^{(m)}. \end{aligned}$$

In analogy with notation in (85), we also consider vectors ${{\tilde{\delta }}}_j'$ and ${{\tilde{v}}}_j$ with expansion coefficients as above. These definitions are crafted specifically so that (86) yields:

$$\begin{aligned} \Vert s_{\tau +j} - s_{\tau }\Vert ^2&\ge \sum _{m \in S^c} \left( \eta \left( \sum _{k = 0}^{j-1} a_{m,k} \right) \left( g^{(m)} + {{\tilde{\delta }}}_j'^{(m)} + {{\tilde{v}}}_j^{(m)} \right) \right) ^2. \end{aligned}$$

We deduce from (88) that

$$\begin{aligned} \Vert s_{\tau +j} - s_{\tau }\Vert&\ge \frac{\eta }{c_4 \theta ^2} \sqrt{\sum _{m \in S^c} \left( g^{(m)} + {{\tilde{\delta }}}_j'^{(m)} + {{\tilde{v}}}_j^{(m)} \right) ^2} \nonumber \\&= \frac{\eta }{c_4 \theta ^2} \left\| P_{{\mathcal {S}}^c}\!\left( \nabla {\hat{f}}_x(s_{\tau }) + {{\tilde{\delta }}}_j' + {{\tilde{v}}}_j \right) \right\| \nonumber \\&\ge \frac{\eta }{c_4 \theta ^2} \left( \frac{\epsilon }{6} - \Vert P_{{\mathcal {S}}^c}({{\tilde{\delta }}}_j')\Vert - \Vert P_{{\mathcal {S}}^c}({{\tilde{v}}}_j )\Vert \right) , \end{aligned}$$

(89)

where ${\mathcal {S}}^c$ is the orthogonal complement of ${\mathcal {S}}$, that is, it is the subspace of $\mathrm {T}_x{\mathcal {M}}$ spanned by eigenvectors $\{e_m\}_{m \in S^c}$, and $P_{{\mathcal {S}}^c}$ is the orthogonal projector to ${\mathcal {S}}^c$. In the last line, we used a triangular inequality and the assumption that $\Vert P_{{\mathcal {S}}^c}(\nabla {\hat{f}}_x(s_{\tau }))\Vert \ge \epsilon /6$. Our goal now is to show that $\Vert P_{{\mathcal {S}}^c}({{\tilde{\delta }}}_j')\Vert$ and $\Vert P_{{\mathcal {S}}^c}({{\tilde{v}}}_j )\Vert$ are suitably small.

Consider the following vector with notation as in (75):

$$\begin{aligned} \Delta =&\delta _{\tau + k} - \delta _{\tau + k}' = \nabla {{\hat{f}}}_x(s_\tau ) - \nabla {{\hat{f}}}_x(0) - \nabla ^2 {{\hat{f}}}_x(0)[s_\tau ] \\ =&\left( \int _{0}^{1} \nabla ^2 {{\hat{f}}}_x(\phi s_\tau ) - \nabla ^2 {{\hat{f}}}_x(0) \mathrm {d}\phi \right) \![s_\tau ]. \end{aligned}$$

By the Lipschitz-like properties of $\nabla ^2 {{\hat{f}}}_x$ and the assumption $\Vert s_\tau \Vert \le {\mathscr {L}} < b$, we deduce that

$$\begin{aligned} \Vert \Delta \Vert&\le \frac{1}{2} {{\hat{\rho }}} \Vert s_\tau \Vert ^2 \le \frac{1}{2} {{\hat{\rho }}} {\mathscr {L}}^2. \end{aligned}$$

Note that $\sum _{k = 0}^{j-1} p_{m, k, j} = 1$. This and the fact that $\Delta$ is independent of k justify that:

$$\begin{aligned} \Vert P_{{\mathcal {S}}^c}({{\tilde{\delta }}}_j')\Vert ^2 = \sum _{m \in S^c} \left( {{\tilde{\delta }}}_j'^{(m)} \right) ^2&= \sum _{m \in S^c} \left( \sum _{k = 0}^{j-1} p_{m,k,j} (\delta _{\tau +k}')^{(m)} \right) ^2 \\&= \sum _{m \in S^c} \left( \sum _{k = 0}^{j-1} p_{m,k,j} \left( (\delta _{\tau +k})^{(m)} - \Delta ^{(m)} \right) \right) ^2 \\&= \sum _{m \in S^c} \left( \sum _{k = 0}^{j-1} p_{m,k,j} (\delta _{\tau +k})^{(m)} - \Delta ^{(m)} \right) ^2, \end{aligned}$$

where $\Delta ^{(m)}$ denotes the expansion coefficients of $\Delta$ in the basis e. Define the vector ${{\tilde{\delta }}}_j$ (without “prime”) with expansion coefficients ${{\tilde{\delta }}}_j^{(m)} = \sum _{k = 0}^{j-1} p_{m,k,j} (\delta _{\tau +k})^{(m)}$. Then, by construction,

$$\begin{aligned} \Vert P_{{\mathcal {S}}^c}({{\tilde{\delta }}}_j')\Vert = \Vert P_{{\mathcal {S}}^c}( {{\tilde{\delta }}}_j - \Delta )\Vert \le \Vert P_{{\mathcal {S}}^c}( {{\tilde{\delta }}}_j )\Vert + \Vert \Delta \Vert \le \Vert P_{{\mathcal {S}}^c}( {{\tilde{\delta }}}_j )\Vert + {{\hat{\rho }}} {\mathscr {L}}^2. \end{aligned}$$

Through a simple reasoning using [28, Lem. 24, 26] one can conclude that, under our setting, both eigenvalues of $A_m$ (for $m \in S^c$) are positive, and as a result that the coefficients $a_{m,k}$ (hence also $p_{m, k, j}$) are positive.

Therefore,

$$\begin{aligned} \Vert P_{{\mathcal {S}}^c}({{\tilde{\delta }}}_j)\Vert ^2&= \sum _{m \in S^c} \left( \sum _{k = 0}^{j-1} p_{m,k,j} (\delta _{\tau +k})^{(m)} \right) ^2 \\&\le \sum _{m \in S^c} \left( \sum _{k = 0}^{j-1} p_{m,k,j} \left( |(\delta _{\tau })^{(m)}| + |(\delta _{\tau +k})^{(m)} - (\delta _{\tau })^{(m)}| \right) \right) ^2. \end{aligned}$$

Notice that for all $0 \le k \le j-1$ we have

$$\begin{aligned} |(\delta _{\tau +k})^{(m)} - (\delta _{\tau })^{(m)}|&\le \sum _{k' = 1}^{k} |(\delta _{\tau +k'})^{(m)} - (\delta _{\tau +k'-1})^{(m)}| \\&\le \sum _{k' = 1}^{j-1} |(\delta _{\tau +k'})^{(m)} - (\delta _{\tau +k'-1})^{(m)}|, \end{aligned}$$

and this right-hand side is independent of k. Thus, we can factor out $\sum _{k = 0}^{j-1} p_{m,k,j} = 1$ in the expression above to get:

$$\begin{aligned} \Vert P_{{\mathcal {S}}^c}({{\tilde{\delta }}}_j)\Vert ^2&\le \sum _{m \in S^c} \left( |(\delta _{\tau })^{(m)}| + \sum _{k = 1}^{j-1} |(\delta _{\tau +k})^{(m)} - (\delta _{\tau +k-1})^{(m)}| \right) ^2. \end{aligned}$$

Use first $(a + b)^2 \le 2a^2 + 2b^2$ then (another) Cauchy–Schwarz to deduce

$$\begin{aligned} \Vert P_{{\mathcal {S}}^c}({{\tilde{\delta }}}_j)\Vert ^2&\le 2 \sum _{m \in S^c} |(\delta _{\tau })^{(m)}|^2 + 2(j-1) \sum _{m \in S^c} \sum _{k = 1}^{j-1} |(\delta _{\tau +k})^{(m)} - (\delta _{\tau +k-1})^{(m)}|^2 \\&\le 2 \Vert \delta _\tau \Vert ^2 + 2j \sum _{k = 1}^{j-1} \Vert \delta _{\tau +k} - \delta _{\tau +k-1} \Vert ^2. \end{aligned}$$

To bound this further, we call upon Lemma E.3 with $R = \frac{3}{2} {\mathscr {L}} \le \frac{1}{3}b$, $q' = \tau$ and $q = \tau + \frac{{\mathscr {T}}}{4} - 1$. To this end, we must first verify that $\Vert s_{\tau + k}\Vert \le R$ for $k = -1, \ldots , \frac{{\mathscr {T}}}{4} - 1$. This is indeed the case owing to (84) and the assumption $\Vert s_\tau \Vert \le {\mathscr {L}}$:

$$\begin{aligned} \Vert s_{\tau +k}\Vert&\le \Vert s_{\tau +k} - s_\tau \Vert + \Vert s_\tau \Vert \le \frac{1}{2} {\mathscr {L}} + {\mathscr {L}} = R&{\text { for }}&k = -1, \ldots , {\mathscr {T}}/4. \end{aligned}$$

This confirms that we can use the conclusions of Lemma E.3, reaching:

$$\begin{aligned} \Vert P_{{\mathcal {S}}^c}({{\tilde{\delta }}}_j)\Vert ^2&\le 50 {{\hat{\rho }}}^2 R^4 + 288 {{\hat{\rho }}}^2 R^2 \cdot j\sum _{k = 0}^{j-1} \Vert s_{\tau +k} - s_{\tau +k-1} \Vert ^2 \\&= \frac{4050}{16} {{\hat{\rho }}}^2 {\mathscr {L}}^4 + 648 {{\hat{\rho }}}^2 {\mathscr {L}}^2 \cdot j \sum _{k = \tau -1}^{\tau +j-2} \Vert s_{k+1} - s_{k} \Vert ^2 \\&\le 256 {{\hat{\rho }}}^2 {\mathscr {L}}^4 + 648 {{\hat{\rho }}}^2 {\mathscr {L}}^2 \cdot 16 \sqrt{\kappa } \eta j (E_{\tau -1} - E_{\tau +j-2}), \end{aligned}$$

where the first and last lines follow from the definition of R and from Lemma 4.3, respectively. Recall that we assume $E_{\tau -1} - E_{\tau + {\mathscr {T}}/4} < {\mathscr {E}}$ for contradiction. Then, monotonic decrease of the Hamiltonian (Lemma 4.2) tells us that $E_{\tau -1} - E_{\tau +j-2} < {\mathscr {E}}$ for $0 \le j \le {\mathscr {T}}/4$. Combining with $16 \sqrt{\kappa } \eta {\mathscr {T}} {\mathscr {E}} = {\mathscr {L}}^2$ (Lemma C.1), we find:

$$\begin{aligned} \Vert P_{{\mathcal {S}}^c}({{\tilde{\delta }}}_j)\Vert ^2&\le 256 {{\hat{\rho }}}^2 {\mathscr {L}}^4 + 162 {{\hat{\rho }}}^2 {\mathscr {L}}^4 = 418 {{\hat{\rho }}}^2 {\mathscr {L}}^4. \end{aligned}$$

Thus, $\Vert P_{{\mathcal {S}}^c}({{\tilde{\delta }}}_j)\Vert \le 21 {{\hat{\rho }}} {\mathscr {L}}^2 = 84 \epsilon \chi ^{-4} c^{-6} \le \epsilon /24$ with $c \ge 4$ and $\chi \ge 1$, for $0 \le j \le {\mathscr {T}}/4$.

Recall that we aim to make progress from bound (89). The bound $\Vert P_{{\mathcal {S}}^c}({{\tilde{\delta }}}_j)\Vert \le \epsilon /24$ we just established is a first step. We now turn to bounding $\Vert P_{{\mathcal {S}}^c}({{\tilde{v}}}_j )\Vert$. Owing to (88), we have this first bound assuming $j = {\mathscr {T}}/4$:

$$\begin{aligned} \Vert P_{{\mathcal {S}}^c}({{\tilde{v}}}_j )\Vert ^2&= \sum _{m \in S^c} q_{m,j}^2 (v^{(m)})^2 \nonumber \\&= \sum _{m \in S^c} \left( \frac{b_{m, j}}{\eta \sum _{k' = 0}^{j-1} a_{m, k'}}\right) ^2 (v^{(m)})^2 \le \frac{c_5}{\eta ^2} \sum _{m \in S^c} (v^{(m)})^2 \max \!\left( \theta ^2, |\eta \lambda _m| \right) . \end{aligned}$$

(90)

(Recall from (85) that $v^{(m)}$ denotes the coefficients of $v_\tau$ in the basis $e_1, \ldots , e_d$.) We split the sum in order to resolve the max. To this end, note that $\theta \in [0, 1]$ implies $\theta ^2 \ge \frac{\theta ^2}{(2-\theta )^2}$, so that the $\max$ evaluates to $\theta ^2$ exactly when $-\theta ^2 \le \eta \lambda _m \le \frac{\theta ^2}{(2-\theta )^2}$ (remembering that $\eta \lambda _m \le \frac{\theta ^2}{(2-\theta )^2}$ because $m \in S^c$). Thus,

$$\begin{aligned}&\sum _{m \in S^c} (v^{(m)})^2 \max \!\left( \theta ^2, |\eta \lambda _m| \right) \\&\quad = \sum _{m : -\theta ^2 \le \eta \lambda _m \le \frac{\theta ^2}{(2-\theta )^2}} (v^{(m)})^2 \theta ^2 - \sum _{m : \eta \lambda _m < -\theta ^2} (v^{(m)})^2 \eta \lambda _m. \end{aligned}$$

Let us rework the last sum (we get a first bound by extending the summation range, exploiting that the summands are non-positive):

$$\begin{aligned} -\sum _{m : \eta \lambda _m< -\theta ^2} (v^{(m)})^2 \eta \lambda _m&\le -\sum _{m : \eta \lambda _m \le 0} (v^{(m)})^2 \eta \lambda _m \\&= \sum _{m : \eta \lambda _m> 0} (v^{(m)})^2 \eta \lambda _m - \sum _{m = 1}^d (v^{(m)})^2 \eta \lambda _m \\&= \sum _{m : \eta \lambda _m > 0} (v^{(m)})^2 \eta \lambda _m - \eta \left\langle {v_\tau },{{\mathcal {H}} v_\tau }\right\rangle \\&= \sum _{m : 0 < \eta \lambda _m \le \frac{\theta ^2}{(2-\theta )^2}} (v^{(m)})^2 \eta \lambda _m\\ {}&\quad + \eta \left\langle {P_{\mathcal {S}}v_\tau },{{\mathcal {H}}P_{\mathcal {S}}v_\tau }\right\rangle - \eta \left\langle {v_\tau },{{\mathcal {H}} v_\tau }\right\rangle \\&\le \theta ^2 \Vert v_\tau \Vert ^2 + \eta \left\langle {P_{\mathcal {S}}v_\tau },{{\mathcal {H}}P_{\mathcal {S}}v_\tau }\right\rangle - \eta \left\langle {v_\tau },{{\mathcal {H}} v_\tau }\right\rangle . \end{aligned}$$

(Recall that $P_{\mathcal {S}}$ projects to the subspace spanned by eigenvectors with eigenvalues strictly above $\frac{\theta ^2}{\eta (2-\theta )^2}$.) Combining all work done since (90), it follows that

$$\begin{aligned} \Vert P_{{\mathcal {S}}^c}({{\tilde{v}}}_j )\Vert ^2&\le \frac{c_5}{\eta ^2} \left( 2\theta ^2 \Vert v_\tau \Vert ^2 + \eta \left\langle {P_{\mathcal {S}}v_\tau },{{\mathcal {H}}P_{\mathcal {S}}v_\tau }\right\rangle - \eta \left\langle {v_\tau },{{\mathcal {H}} v_\tau }\right\rangle \right) . \end{aligned}$$

Use assumptions $\Vert v_\tau \Vert \le {\mathscr {M}}$ and $\left\langle {P_{\mathcal {S}}v_\tau },{{\mathcal {H}}P_{\mathcal {S}}v_\tau }\right\rangle \le \sqrt{{{\hat{\rho }}} \epsilon } {\mathscr {M}}^2$ to see that

$$\begin{aligned} \Vert P_{{\mathcal {S}}^c}({{\tilde{v}}}_j )\Vert ^2&\le \frac{c_5}{\eta ^2} \left( 2\theta ^2 {\mathscr {M}}^2 + \eta \sqrt{{{\hat{\rho }}} \epsilon } {\mathscr {M}}^2 - \eta \left\langle {v_\tau },{{\mathcal {H}} v_\tau }\right\rangle \right) \nonumber \\&= 4\ell c_5 \left( \frac{3}{2} \sqrt{{{\hat{\rho }}} \epsilon } {\mathscr {M}}^2 - \left\langle {v_\tau },{{\mathcal {H}} v_\tau }\right\rangle \right) . \end{aligned}$$

(91)

(For the last equality, use $2\theta ^2 = \frac{\sqrt{{{\hat{\rho }}} \epsilon }}{2} \eta$ and $\eta = 1/4\ell$.) To proceed, we must bound $\left\langle {v_\tau },{{\mathcal {H}} v_\tau }\right\rangle$. To this end, notice that by assumption the (NCC) condition did not trigger for $(x, s_\tau , u_\tau )$. Therefore, we know that

$$\begin{aligned} {\hat{f}}_x(s_\tau )&\ge {\hat{f}}_x(u_\tau ) + \langle {\nabla {\hat{f}}_x(u_\tau )},{s_\tau - u_\tau }\rangle - \frac{\gamma }{2}\left\| {s_\tau - u_\tau }\right\| ^2. \end{aligned}$$

Moreover, it always holds that

$$\begin{aligned} {\hat{f}}_x(s_\tau )&= {{\hat{f}}}_x(u_\tau ) + \langle {\nabla {\hat{f}}_x(u_\tau )},{s_\tau - u_\tau }\rangle \\&\quad + \frac{1}{2} \langle {s_\tau - u_\tau },{\nabla ^2 {{\hat{f}}}_x(\phi s_\tau + (1-\phi )u_\tau )[s_\tau - u_\tau ]}\rangle \end{aligned}$$

for some $\phi \in [0, 1]$. Also using $u_\tau = s_\tau + (1-\theta ) v_\tau$, we deduce that

$$\begin{aligned} \langle {v_\tau },{\nabla ^2 {{\hat{f}}}_x(\phi s_\tau + (1-\phi )u_\tau )[v_\tau ]}\rangle \ge -\gamma \Vert v_\tau \Vert ^2. \end{aligned}$$

With the help of Lemma C.1, note that

$$\begin{aligned} \Vert \phi s_\tau + (1-\phi )u_\tau \Vert&= \Vert s_\tau + (1-\phi )(1-\theta ) v_\tau \Vert \le \Vert s_\tau \Vert + \Vert v_\tau \Vert \le {\mathscr {L}} + {\mathscr {M}} \le b. \end{aligned}$$

Thus, the Lipschitz-type properties of $\nabla ^2 {{\hat{f}}}_x$ apply up to that point and we get

$$\begin{aligned} \Vert \nabla ^2 {{\hat{f}}}_x(\phi s_\tau + (1-\phi )u_\tau ) - {\mathcal {H}}\Vert \le {{\hat{\rho }}} ({\mathscr {L}} + {\mathscr {M}}) \le \sqrt{{{\hat{\rho }}} \epsilon }. \end{aligned}$$

Since $\gamma = \frac{\sqrt{{{\hat{\rho }}} \epsilon }}{4}$, it follows overall that

$$\begin{aligned} \langle {v_\tau },{{\mathcal {H}}v_\tau }\rangle \ge -\frac{5}{4} \sqrt{{{\hat{\rho }}} \epsilon } \Vert v_\tau \Vert ^2 \ge -\frac{5}{4}\sqrt{{{\hat{\rho }}} \epsilon } {\mathscr {M}}^2. \end{aligned}$$

Plugging this back into (91) with $c \ge 80\sqrt{c_5}$ reveals that

$$\begin{aligned} \Vert P_{{\mathcal {S}}^c}({{\tilde{v}}}_j )\Vert ^2&\le 11 \ell c_5 \sqrt{{{\hat{\rho }}} \epsilon } {\mathscr {M}}^2 = 11 c_5 \epsilon ^2 c^{-2} \le \epsilon ^2 / 24^2. \end{aligned}$$

This shows that $\Vert P_{{\mathcal {S}}^c}({{\tilde{v}}}_j )\Vert \le \epsilon / 24$ for $j = {\mathscr {T}}/4$.

We plug $\Vert P_{{\mathcal {S}}^c}({{\tilde{\delta }}}_j)\Vert \le \epsilon /24$ and $\Vert P_{{\mathcal {S}}^c}({{\tilde{v}}}_j )\Vert \le \epsilon / 24$ into (89) to state that, with $j = {\mathscr {T}} / 4$,

$$\begin{aligned} \Vert s_{\tau +j} - s_{\tau }\Vert&\ge \frac{\eta }{c_4 \theta ^2} \left( \frac{\epsilon }{6} - \frac{\epsilon }{24} - \frac{\epsilon }{24} \right) = \frac{\eta \epsilon }{12 c_4 \theta ^2}\\ {}&= \frac{1}{3c_4}\sqrt{\frac{\epsilon }{{{\hat{\rho }}}}} > \sqrt{\frac{\epsilon }{{{\hat{\rho }}}}} \chi ^{-2} c^{-3} = {\mathscr {L}} / 2. \end{aligned}$$

(We used $4\theta ^2 = \sqrt{{{\hat{\rho }}} \epsilon } \eta$, then we also set $c > (3c_4)^{1/3}$.) This last inequality contradicts (84). Thus, the proof by contradiction is complete and we conclude that $E_{\tau -1} - E_{\tau + {\mathscr {T}}/4} \ge {\mathscr {E}}$. $\square$

What follows is the equivalent of the proof of [28, Lem. 22], with the small changes needed for our purpose.

Proof of Lemma F.2

Since $E_0 - E_{{\mathscr {T}}/2} \le {\mathscr {E}}$ and $s_0 = 0$, Lemmas 4.2, 4.3 and C.1 yield:

$$\begin{aligned} \forall j \le {\mathscr {T}}/2,&\Vert s_j\Vert&= \Vert s_j - s_0\Vert \le \sqrt{8 \sqrt{\kappa } \eta {\mathscr {T}} {\mathscr {E}}} = \frac{{\mathscr {L}}}{\sqrt{2}} \le {\mathscr {L}} \le b. \end{aligned}$$

(92)

By Lemma E.1 with $\tau = 0$ and noting that $s_0 = 0$, $s_{-1} = s_0 - v_0 = 0$, we know that, for all j,

$$\begin{aligned} \begin{pmatrix} s_{j} \\ s_{j-1} \end{pmatrix}&= - \eta \sum _{k = 0}^{j-1} A^{j-1-k} \begin{pmatrix} \nabla {{\hat{f}}}_x(0) + \delta _{k} \\ 0 \end{pmatrix}. \end{aligned}$$

(93)

Define the operator $\Delta _j = \int _{0}^{1} \nabla ^2 {{\hat{f}}}_x(\phi s_j) - {\mathcal {H}} \mathrm {d}\phi$ with ${\mathcal {H}} = \nabla ^2 {{\hat{f}}}_x(0)$. We can write:

$$\begin{aligned} P_{\mathcal {S}}\nabla {{\hat{f}}}_x(s_j)&= P_{\mathcal {S}}\!\left( \nabla {{\hat{f}}}_x(0) + {\mathcal {H}}s_j + \Delta _js_j \right) . \end{aligned}$$

(94)

We shall bound this term by term.

The third term is straightforward, so let us start with this one. Owing to (92), the Lipschitz-like properties of the Hessian apply to claim $\Vert \Delta _j\Vert \le \frac{1}{2}{{\hat{\rho }}} \Vert s_j\Vert$. Therefore,

$$\begin{aligned} \Vert P_{\mathcal {S}}\Delta _js_j\Vert \le \Vert \Delta _j\Vert \Vert s_j\Vert \le \frac{1}{2}{{\hat{\rho }}} \Vert s_j\Vert ^2 \le \frac{1}{2}{{\hat{\rho }}} {\mathscr {L}}^2 = 2\epsilon \chi ^{-4} c^{-6} \le \epsilon /18 \end{aligned}$$

(95)

with $c \ge 2$ and $\chi \ge 1$. Below, we work toward bounding the other two terms.

As we did in the proof of Lemma F.1, let $e_1, \ldots , e_d$ form an orthonormal basis of eigenvectors for ${\mathcal {H}}$ with eigenvalues $\lambda _1 \le \cdots \le \lambda _d$. Expand $\nabla {{\hat{f}}}_x(0)$ and $\delta _{k}$ in that basis as

$$\begin{aligned} \nabla {{\hat{f}}}_x(0)&= \sum _{m = 1}^{d} g^{(m)} e_m,&\delta _{k}&= \sum _{m = 1}^{d} \delta _k^{(m)} e_m. \end{aligned}$$

From (93) and (81) it follows that

$$\begin{aligned} s_j&= \sum _{m' = 1}^{d} \left\langle {e_{m'}},{s_j}\right\rangle e_{m'} = -\eta \sum _{m' = 1}^{d} \sum _{k = 0}^{j-1} \sum _{m = 1}^d \left\langle {\begin{pmatrix} e_{m'} \\ 0 \end{pmatrix}},{A^{j-1-k} \begin{pmatrix} e_m \\ 0 \end{pmatrix}}\right\rangle (g^{(m)} + \delta _k^{(m)}) e_{m'} \\&= -\eta \sum _{k = 0}^{j-1} \sum _{m = 1}^d (A_m^{j-1-k})_{11} (g^{(m)} + \delta _k^{(m)}) e_{m}. \end{aligned}$$

Motivated by (94) and reusing notation $a_{m, j-1-k} = (A_m^{j-1-k})_{11}$ as in (87), we further write

$$\begin{aligned} P_{\mathcal {S}}\!\left( \nabla {{\hat{f}}}_x(0) + {\mathcal {H}}s_j\right)&= \sum _{m \in S} \left[ g^{(m)} - \eta \lambda _m \sum _{k = 0}^{j-1} a_{m, j-1-k} (g^{(m)} + \delta _k^{(m)}) \right] e_m \nonumber \\&= \sum _{m \in S} \left[ \left( 1 - \eta \lambda _m \sum _{k = 0}^{j-1} a_{m, k} \right) g^{(m)}\right. \nonumber \\ {}&\quad \left. - \eta \lambda _m \sum _{k = 0}^{j-1} a_{m, j-1-k} \delta _k^{(m)} \right] e_m, \end{aligned}$$

(96)

where $S = \big \{ m : \eta \lambda _m > \frac{\theta ^2}{(2-\theta )^2} \big \}$ indexes the eigenvalues of the eigenvectors which span ${\mathcal {S}}$. This identity splits in two parts, each of which we now aim to bound.

In the spirit of the comments surrounding (88), here too it is possible to control the coefficients $a_{m,k}$ and $b_{m,k}$ (both defined as in (87)), this time for $m \in S$. Specifically, combining [28, Lem. 25] with an identity in the proof of [28, Lem. 29], we see that

$$\begin{aligned} 1 - \eta \lambda _m \sum _{k = 0}^{j-1} a_{m, k}&= a_{m, j} - b_{m, j}. \end{aligned}$$

(97)

Moreover, owing to [28, Lem. 32] we know that

$$\begin{aligned} \forall j \ge 0, \forall m \in S,&\max (|a_{m, j}|, |b_{m, j}|) \le (j+1)(1-\theta )^{j/2}. \end{aligned}$$

(98)

Thus, the first part of (96) is bounded as:

$$\begin{aligned}&\left\| \sum _{m \in S} \left( 1 - \eta \lambda _m \sum _{k = 0}^{j-1} a_{m, k} \right) g^{(m)} e_m \right\| ^2 \\&\quad = \sum _{m \in S} (a_{m,j} - b_{m,j})^2 (g^{(m)})^2 \le 4 (j+1)^2 (1-\theta )^{j} \Vert \nabla {{\hat{f}}}_x(0)\Vert ^2. \end{aligned}$$

One can show using $\theta \in (0, 1/4]$, $\chi \ge \log _2(\theta ^{-1})$ and $c \ge 256$ (which we all assume) that

$$\begin{aligned} \forall j \ge {\mathscr {T}} / 4,&(j+1)^2&\le (1-\theta )^{-j/2}. \end{aligned}$$

(99)

Then use the assumption $\Vert \nabla {{\hat{f}}}_x(0)\Vert \le 2\ell {\mathscr {M}}$ and $j \ge {\mathscr {T}} / 4$ again to replace the power with $j / 2 \ge \sqrt{\kappa } \chi c / 8 \ge 4 \sqrt{\kappa } \cdot 2\chi$ (with $c \ge 64$) and see that

$$\begin{aligned} \left\| \sum _{m \in S} \left( 1 - \eta \lambda _m \sum _{k = 0}^{j-1} a_{m, k} \right) g^{(m)} e_m \right\| ^2&\le 16 \ell ^2 {\mathscr {M}}^2 (1-\theta )^{j/2}\\ {}&\le 16 \epsilon ^2 \kappa c^{-2} \left( 1 - \frac{1}{4\sqrt{\kappa }} \right) ^{4 \sqrt{\kappa } \cdot 2\chi }. \end{aligned}$$

Use the fact that $0< (1-t^{-1})^t < e^{-1} \le 2^{-1}$ for $t \ge 4$ together with $\kappa \ge 1$ to bound the right-hand side by $16 \epsilon ^2 \kappa c^{-2} 2^{-2\chi }$. This itself is bounded by $16 \epsilon ^2 \kappa c^{-2} \theta ^2 = \epsilon ^2 c^{-2}$ using $\chi \ge \log _2(\theta ^{-1})$. Overall, we have shown that

$$\begin{aligned} \left\| \sum _{m \in S} \left( 1 - \eta \lambda _m \sum _{k = 0}^{j-1} a_{m, k} \right) g^{(m)} e_m \right\|&\le \epsilon / 18, \end{aligned}$$

(100)

with $c \ge 18$. This covers the first term in (96).

We turn to bounding the second term in (96). For this one, we need [28, Lem. 34] which states that, for $m \in S$ and $j \ge {\mathscr {T}} / 4$, for any sequence $\{\epsilon _k\}$, we have

$$\begin{aligned} \sum _{k = 0}^{j-1} a_{m, k} \epsilon _k&\le \frac{\sqrt{c_2}}{\eta \lambda _m} \left( |\epsilon _0| + \sum _{k = 1}^{j-1} |\epsilon _{k} - \epsilon _{k-1}| \right) , {\text { and }} \end{aligned}$$

(101)

$$\begin{aligned} \sum _{k = 0}^{j-1} (a_{m, k} - a_{m, k-1}) \epsilon _k&\le \frac{\sqrt{c_3}}{\sqrt{\eta \lambda _m}} \left( |\epsilon _0| + \sum _{k = 1}^{j-1} |\epsilon _{k} - \epsilon _{k-1}| \right) , \end{aligned}$$

(102)

with some positive constants $c_1, c_2, c_3$ and $c \ge c_1$. Thus, to bound the remaining term in (96) we start with:

$$\begin{aligned}&\left\| \sum _{m \in S} \eta \lambda _m \sum _{k = 0}^{j-1} a_{m, j-1-k}^{} \delta _{k}^{(m)} e_m \right\| ^2 \le c_2 \sum _{m \in S} \left( |\delta _{j-1}^{(m)}| + \sum _{k = 1}^{j-1} | \delta _k^{(m)} - \delta _{k-1}^{(m)} | \right) ^2 \nonumber \\&\quad \le 2c_2 \sum _{m \in S} \left[ |\delta _{j-1}^{(m)}|^2 + \left( \sum _{k = 1}^{j-1} | \delta _k^{(m)} - \delta _{k-1}^{(m)} | \right) ^2 \right] \nonumber \\&\quad \le 2c_2 \sum _{m \in S} \left[ |\delta _{j-1}^{(m)}|^2 + (j-1) \sum _{k = 1}^{j-1} | \delta _k^{(m)} - \delta _{k-1}^{(m)} |^2 \right] \nonumber \\&\quad \le 2c_2 \Vert \delta _{j-1}\Vert ^2 + 2c_2 j \sum _{k = 1}^{j-1} \Vert \delta _k - \delta _{k-1}\Vert ^2. \end{aligned}$$

(103)

(We used $(a+b)^2 \le 2a^2 + 2b^2$ again, and another Cauchy–Schwarz on the remaining sum.) In order to proceed, we call upon Lemma E.3 with $R = {\mathscr {L}}$, $q' = 0$ and $q = j-1$, which is justified by (92) (recall that $s_{-1} = 0$). This yields the first inequality in:

$$\begin{aligned} \left\| \sum _{m \in S} \eta \lambda _m \sum _{k = 0}^{j-1} a_{m, j-1-k}^{} \delta _{k}^{(m)} e_m \right\| ^2&\le 50 c_2 {{\hat{\rho }}}^2 {\mathscr {L}}^4 + 2c_2 j \cdot 144 {{\hat{\rho }}}^2 {\mathscr {L}}^2 \sum _{k = 0}^{j-1} \Vert s_k - s_{k-1}\Vert ^2 \nonumber \\&\le 50 c_2 {{\hat{\rho }}}^2 {\mathscr {L}}^4 + 144 c_2 {{\hat{\rho }}}^2 {\mathscr {L}}^4. \end{aligned}$$

(104)

The second inequality above is supported by Lemmas 4.2, 4.3 and C.1 as well as $j \le {\mathscr {T}} / 2$ and the assumption $E_0 - E_{{\mathscr {T}}/2} \le {\mathscr {E}}$, through:

$$\begin{aligned} j \sum _{k = 0}^{j-1} \Vert s_k - s_{k-1}\Vert ^2 \le 16 \sqrt{\kappa } \eta j (E_{0} - E_{j}) \le 8 \sqrt{\kappa } \eta {\mathscr {T}} {\mathscr {E}} = {\mathscr {L}}^2 / 2. \end{aligned}$$

(105)

Continuing from (104), we see that the right- (hence also left-) hand side is upper-bounded by

$$\begin{aligned} 194 c_2 \cdot {{\hat{\rho }}}^2 {\mathscr {L}}^4&= 194 c_2 \cdot 16 \epsilon ^2 \chi ^{-8} c^{-12} \le \epsilon ^2 / 18^2, \end{aligned}$$

with $c \ge 4 c_2^{1/12}$ and $\chi \ge 1$. Combine this result with (94), (95), (96) and (100) to conclude that

$$\begin{aligned} \left\| P_{\mathcal {S}}\nabla {{\hat{f}}}_x(s_j) \right\|&\le \frac{\epsilon }{18} + \frac{\epsilon }{18} + \frac{\epsilon }{18} = \frac{\epsilon }{6} \end{aligned}$$

for all ${\mathscr {T}}/4 \le j \le {\mathscr {T}} / 2$. This proves the first part of the lemma.

For the second part of the result, consider (93) anew then (81) and (83) to see that:

$$\begin{aligned} v_j = s_j - s_{j-1}&= \sum _{m' = 1}^{d} \left\langle {\begin{pmatrix} s_{j} \\ s_{j-1} \end{pmatrix}},{\begin{pmatrix} e_{m'} \\ -e_{m' } \end{pmatrix}}\right\rangle e_{m'} \\&= - \eta \sum _{m' = 1}^{d} \sum _{k = 0}^{j-1} \sum _{m = 1}^d \left( g^{(m)} - \delta _k^{(m)} \right) \left\langle {A^{j-1-k} \begin{pmatrix} e_m \\ 0 \end{pmatrix}},{\begin{pmatrix} e_{m'} \\ -e_{m'} \end{pmatrix}}\right\rangle e_{m'} \\&= - \eta \sum _{k = 0}^{j-1} \sum _{m = 1}^d \left( g^{(m)} - \delta _k^{(m)} \right) \left( (A_m^{j-1-k})_{11} - (A_m^{j-2-k})_{11} \right) e_{m}. \end{aligned}$$

Using notation as in (87) for $a_{m, t}$, it follows that

$$\begin{aligned} P_{\mathcal {S}}v_j&= - \eta \sum _{m \in S} \sum _{k = 0}^{j-1} \left( g^{(m)} - \delta _k^{(m)} \right) \left( a_{m, j-1-k} - a_{m, j-2-k} \right) e_{m}. \end{aligned}$$

We aim to upper-bound $\left\langle {P_{\mathcal {S}}v_j},{{\mathcal {H}} P_{\mathcal {S}}v_j}\right\rangle$. Compute, then use (102) to bound the sum in k:

$$\begin{aligned} \left\langle {P_{\mathcal {S}}v_j},{{\mathcal {H}} P_{\mathcal {S}}v_j}\right\rangle&= \eta ^2 { \sum _{m \in S} \lambda _m \left( \sum _{k = 0}^{j-1} \left( g^{(m)} - \delta _k^{(m)} \right) \left( a_{m, j-1-k} - a_{m, j-2-k} \right) \right) ^2 } \nonumber \\&= \eta ^2 \sum _{m \in S} \lambda _m \left( g^{(m)} \sum _{k = 0}^{j-1} \left( a_{m, k} - a_{m, k-1} \right) \right. \nonumber \\ {}&\quad \left. - \sum _{k = 0}^{j-1} \delta _k^{(m)} \left( a_{m, j-1-k} - a_{m, j-2-k} \right) \right) ^2 \nonumber \\&\le 2 \eta ^2 \sum _{m \in S} \lambda _m \left( g^{(m)} \sum _{k = 0}^{j-1} \left( a_{m, k} - a_{m, k-1} \right) \right) ^2 \nonumber \\&\quad + 2 \eta ^2 \sum _{m \in S} \lambda _m \left( \sum _{k = 0}^{j-1} \delta _k^{(m)} \left( a_{m, j-1-k} - a_{m, j-2-k} \right) \right) ^2. \end{aligned}$$

(106)

(We used $(a + b)^2 \le 2a^2 + 2b^2$ again.)

Focusing on the first term of (106), use (97) twice to see that

$$\begin{aligned} \sum _{k = 0}^{j-1} \left( a_{m, k} - a_{m, k-1} \right)&= \frac{1}{\eta \lambda _m}(1 - a_{m, j} + b_{m, j}) \\&\quad - \frac{1}{\eta \lambda _m}(1 - a_{m, j-1} + b_{m, j-1}) - a_{m, -1} \\&= \frac{1}{\eta \lambda _m}(a_{m, j-1} - b_{m, j-1} - a_{m, j} + b_{m, j}). \end{aligned}$$

(Indeed, $a_{m, -1} = 0$ as it is the top-left entry of a matrix of the form $\left( {\begin{matrix} a &{} b \\ 1 &{} 0 \end{matrix}}\right) ^{-1}$: that is zero regardless of a and $b \ne 0$.)

Hence, the first term in (106) is equal to the right-hand side below; the first bound follows from $(a+b+c+d)^2 \le 4(a^2 + b^2 + c^2 + d^2)$ (Cauchy–Schwarz) and (98), while the second bound follows from (99) for $j \ge {\mathscr {T}} / 4$:

$$\begin{aligned}&\sum _{m \in S} \frac{2}{\lambda _m} \left| g^{(m)}\right| ^2 \left( a_{m, j-1} - b_{m, j-1} - a_{m, j} + b_{m, j}\right) ^2 \\&\quad \le \sum _{m \in S} \frac{16}{\lambda _m} \left| g^{(m)}\right| ^2 \left( (j+1)^2(1-\theta )^{j} + j^2(1-\theta )^{j-1} \right) \\&\quad \le \sum _{m \in S} \frac{16}{\lambda _m} \left| g^{(m)}\right| ^2 \left( (1-\theta )^{j/2} + (1-\theta )^{j/2-1} \right) \\&\quad \le \sum _{m \in S} \frac{128}{3\lambda _m} \left| g^{(m)}\right| ^2 (1-\theta )^{j/2}. \end{aligned}$$

(The last inequality uses $\theta \in (0, 1/4]$ so that $(1-\theta )^{-1} \le 4/3$.) Moreover, for $m \in S$ we have $\lambda _m > \frac{\theta ^2}{\eta (2-\theta )^2} \ge \frac{1}{4\eta } \theta ^2 = \frac{1}{4\eta } \frac{1}{16} \frac{\sqrt{{{\hat{\rho }}} \epsilon }}{\ell } = \frac{\sqrt{{{\hat{\rho }}} \epsilon }}{16}$. Therefore, in light of the latest considerations and using the assumption $\Vert \nabla {{\hat{f}}}_x(0)\Vert \le 2\ell {\mathscr {M}}$ and also $j / 2 \ge \sqrt{\kappa } \chi c / 8$ owing to $j \ge {\mathscr {T}} / 4$, the first term in (106) is upper-bounded by:

$$\begin{aligned} \sum _{m \in S} \frac{128}{3} \frac{16}{\sqrt{{{\hat{\rho }}} \epsilon }} \left| g^{(m)}\right| ^2 (1-\theta )^{j/2}&\le 3000 \frac{\ell ^2{\mathscr {M}}^2}{\sqrt{{{\hat{\rho }}} \epsilon }} (1-\theta )^{\sqrt{\kappa } \chi c / 8} \\&= 3000 {\mathscr {M}}^2 \sqrt{{{\hat{\rho }}} \epsilon } \kappa ^2 \left( 1-\frac{1}{4\sqrt{\kappa }}\right) ^{4\sqrt{\kappa } \cdot 4\chi \cdot c / 128} \\&\le 3000 {\mathscr {M}}^2 \sqrt{{{\hat{\rho }}} \epsilon } \kappa ^2 \cdot 2^{-4\chi } 2^{-c / 128} \le \frac{1}{4} {\mathscr {M}}^2 \sqrt{{{\hat{\rho }}} \epsilon }, \end{aligned}$$

where the second-to-last inequality uses again that $0< (1-t^{-1})^t < 2^{-1}$ for $t \ge 4$, as well as $4\chi \cdot c / 128 \ge 4\chi + c / 128$ with $c \ge 128$; and the last inequality uses $\chi \ge \log _2(\theta ^{-1}) = \log _2(4\sqrt{\kappa })$ to see that $\kappa ^2 2^{-4\chi } \le 4^{-4}$, and also $3000 \cdot 4^{-4} \cdot 2^{-c/128} \le 1/4$ with $c \ge 720$. (With care, one could improve the constant, here and in many other places.)

Now focusing on the second term of (106), we start with (102) to see that

$$\begin{aligned}&2 \eta ^2 \sum _{m \in S} \lambda _m \left( \sum _{k = 0}^{j-1} \delta _k^{(m)} \left( a_{m, j-1-k} - a_{m, j-2-k} \right) \right) ^2 \\&\quad \le 2 c_3 \eta \sum _{m \in S} \left( |\delta _{j-1}^{(m)}| + \sum _{k = 1}^{j-1} | \delta _k^{(m)} - \delta _{k-1}^{(m)} | \right) ^2 \\&\quad \le 4c_3\eta \Vert \delta _{j-1}\Vert ^2 + 4c_3\eta j \sum _{k = 1}^{j-1} \Vert \delta _k - \delta _{k-1} \Vert ^2 \\&\quad \le 388 c_3 \eta \cdot {{\hat{\rho }}}^2 {\mathscr {L}}^4. \end{aligned}$$

The last inequality follows through the same reasoning that was applied to go from (103) to (104). Through simple parameter manipulation we find

$$\begin{aligned} 388 c_3 \eta \cdot {{\hat{\rho }}}^2 {\mathscr {L}}^4&= \frac{97c_3}{\ell } \cdot 16\epsilon ^2 \chi ^{-8}c^{-12} \cdot \frac{\ell ^2}{\epsilon ^2 \kappa }c^{2} \cdot {\mathscr {M}}^2 \\&= 97c_3 \cdot 16 \chi ^{-8}c^{-10} \cdot \sqrt{{{\hat{\rho }}} \epsilon } {\mathscr {M}}^2 \le \frac{1}{4} {\mathscr {M}}^2 \sqrt{{{\hat{\rho }}} \epsilon }, \end{aligned}$$

with $c \ge 3 c_3^{1/10}$ and $\chi \ge 1$.

To conclude, we combine the two main results about (106) to confirm that $\left\langle {P_{\mathcal {S}}v_j},{{\mathcal {H}} P_{\mathcal {S}}v_j}\right\rangle \le \frac{1}{4} {\mathscr {M}}^2 \sqrt{{{\hat{\rho }}} \epsilon } + \frac{1}{4} {\mathscr {M}}^2 \sqrt{{\hat{\rho }} \epsilon } = \frac{1}{2} {\mathscr {M}}^2 \sqrt{{{\hat{\rho }}} \epsilon } \le {\mathscr {M}}^2 \sqrt{{{\hat{\rho }}} \epsilon }$ for all ${\mathscr {T}}/4 \le j \le {\mathscr {T}} / 2$. This proves the second part of the lemma. $\square$

Proofs from Sect. 6 About $\mathtt {PTAGD}$

1.1 Proof of Proposition 6.2

The following lemma supports Proposition 6.2. The proof is in Appendix G.2. It corresponds to [28, Lem. 23]. The condition on $\chi$ originates in this lemma, and from here appears in Theorem 6.1 through Proposition 6.2. It causes the occurrence of dimension in the polylogarithmic factor in the complexity of Theorem 1.6, but note that the real reason why d appears in the condition on $\chi$ here is so that dimension can be canceled out in the probabilistic argument in the proof of Proposition 6.2.

Lemma G.1

Fix parameters and assumptions as laid out in Sect. 3, with $d = \dim {\mathcal {M}}$, $\delta \in (0, 1)$, any $\Delta _f > 0$ and

$$\begin{aligned} \chi \ge \max \!\left( \log _2(\theta ^{-1}), \log _2\!\left( \frac{d^{1/2} \ell ^{3/2} \Delta _f}{({{\hat{\rho }}} \epsilon )^{1/4} \epsilon ^2 \delta } \right) \right) \ge 1. \end{aligned}$$

Let $s_0, s_0' \in B_x(r)$ be such that

• 1. $s_0 - s_0' = r_0 e_1$ where $e_1$ is an eigenvector of $\nabla ^2 {{\hat{f}}}_x(0)$ associated to the smallest eigenvalue and $r_0 \ge \frac{\delta {\mathscr {E}}}{2\Delta _f} \frac{r}{\sqrt{d}}$, and

• 2. $\mathtt {TSS}(x, s_0)$ and $\mathtt {TSS}(x, s_0')$ both run their ${\mathscr {T}}$ iterations in full, respectively, generating vectors $u_j, s_j, v_j$ and $u_j', s_j', v_j'$, with corresponding Hamiltonians $E_j, E_j'$.

If $\Vert \mathrm {grad}f(x)\Vert \le \frac{1}{2} \ell b$ and $\lambda _{\mathrm {min}}(\nabla ^2 {{\hat{f}}}_x(0)) \le -\sqrt{{{\hat{\rho }}} \epsilon }$, then $\max \!\left( E_0 - E_{{\mathscr {T}}}, E_0' - E_{{\mathscr {T}}}' \right) \ge 2{\mathscr {E}}$.

Proof of Proposition 6.2

By Lemma C.1, $\Vert \mathrm {grad}f(x)\Vert \le 2\ell {\mathscr {M}} < \frac{1}{2} \ell b$ and $\Vert \xi \Vert \le r < b$. Thus, the strongest provisions of A2 apply at x, as do Lemmas 4.1, 4.2, 4.3 and 4.4. Let $u_j, s_j, v_j$ for $j = 0, 1, \ldots$ be the vectors generated by the computation of $x_{{\mathscr {T}}} = \mathtt {TSS}(x, \xi )$. Note that $s_0 = \xi$ and $v_0 = 0$. Owing to how $\mathtt {TSS}$ works, there are several cases to consider, based on how it terminates. We remark that cases 3a and 3b are deterministic (they only use the fact that $\Vert s_0\Vert \le r$), that there is no case 3c, and that case 3d is the only place where probabilities are involved. Throughout, it is useful to observe that, since $f(x) = {{\hat{f}}}_x(0)$, $\Vert \mathrm {grad}f(x)\Vert \le \epsilon$ and $\mathrm {grad}f(x) = \nabla {{\hat{f}}}_x(0)$, the first property of A2 ensures:

$$\begin{aligned} {{\hat{f}}}_x(s_0) - f(x) \le \left\langle {\mathrm {grad}f(x)},{s_0}\right\rangle + \frac{\ell }{2} \Vert s_0\Vert ^2 \le \epsilon r + \frac{\ell }{2} r^2 \le \frac{1}{4} {\mathscr {E}}. \end{aligned}$$

(107)

(Use Lemma C.1 to relate parameters.) Compare details below with Proposition 5.3.

• (Case 3a) The negative curvature condition (NCC) triggers with $(x, s_j, u_j)$. Either $\Vert s_j\Vert \le {\mathscr {L}}$, in which case Lemma 4.2 tells us $E_j \le E_0 = {{\hat{f}}}_x(s_0)$ and, by Lemma 4.4,

  $$\begin{aligned} f(x_{{\mathscr {T}}}) = {{\hat{f}}}_x(\mathtt {NCE}(x, s_j, v_j)) \le E_j - 2{\mathscr {E}} \le f(x) - 2{\mathscr {E}} + {{\hat{f}}}_x(s_0) - f(x). \end{aligned}$$

  Or $\Vert s_j\Vert > {\mathscr {L}}$, in which case Lemma 4.3 used with $q = j < {\mathscr {T}}$ and $\Vert s_q - s_0\Vert \ge \Vert s_q\Vert - \Vert s_0\Vert \ge {\mathscr {L}} - r \ge \frac{63}{64}{\mathscr {L}}$ implies

  $$\begin{aligned} f(x_{{\mathscr {T}}}) \le E_j \le {{\hat{f}}}_x(s_0) - \frac{63^2}{64^2} \frac{{\mathscr {L}}^2}{16 \sqrt{\kappa } \eta {\mathscr {T}}} = f(x) - \frac{63^2}{64^2} {\mathscr {E}} + {{\hat{f}}}_x(s_0) - f(x). \end{aligned}$$

  (We used Lemma C.1 to relate parameters.) Either way, bound ${{\hat{f}}}_x(s_0) - f(x)$ with (107). Overall, we conclude that $f(x) - f(x_{{\mathscr {T}}}) \ge \frac{1}{2} {\mathscr {E}}$ (deterministically).

• (Case 3b) The iterate $s_{j+1}$ leaves the ball of radius b, that is, $\Vert s_{j+1}\Vert > b$. In this case, apply Lemma 4.3 with $q = j + 1 \le {\mathscr {T}}$ and

  $$\begin{aligned} \Vert s_{j+1} - s_0\Vert \ge \Vert s_{j+1}\Vert - \Vert s_0\Vert \ge b - r \ge 4{\mathscr {L}} - \frac{1}{64}{\mathscr {L}} \ge {\mathscr {L}} \end{aligned}$$

  to claim (as always, we use Lemma C.1 repeatedly to relate parameters)

  $$\begin{aligned} f(x_{{\mathscr {T}}}) =&{{\hat{f}}}_x(s_{j+1}) \le E_{j+1} \le {{\hat{f}}}_x(s_0) - \frac{\Vert s_{j+1} - s_0\Vert ^2}{16 \sqrt{\kappa } \eta {\mathscr {T}}} \\&\le {{\hat{f}}}_x(s_0) - \frac{{\mathscr {L}}^2}{16 \sqrt{\kappa } \eta {\mathscr {T}}} = {{\hat{f}}}_x(s_0) - {\mathscr {E}}. \end{aligned}$$

  By (107), it follows that $f(x) - f(x_{{\mathscr {T}}}) \ge \frac{3}{4} {\mathscr {E}}$ (deterministically).

• (Case 3d) None of the other events occur: $\mathtt {TSS}(x, s_0)$ runs its ${\mathscr {T}}$ iterations in full. In this case, we apply the logic in the proof of [28, Lem. 13], as follows. Define the set ${\mathcal {X}}^{(\mathrm {stuck})}_x$ as containing exactly all tangent vectors $s^* \in B_x(r)$ such that

• 1. $\mathtt {TSS}(x, s^*)$ runs its ${\mathscr {T}}$ iterations in full, and

• 2. $E_0^* - E_{{\mathscr {T}}}^* \le 2{\mathscr {E}}$, where $E_j^*$ denotes the Hamiltonians associated to $\mathtt {TSS}(x, s^*)$.

There are two cases. Either $s_0$ is not in ${\mathcal {X}}^{(\mathrm {stuck})}_x$, in which case $E_0 - E_{{\mathscr {T}}} > 2{\mathscr {E}}$: it is then easy to conclude (using (107)) that $f(x) - f(x_{{\mathscr {T}}}) > \frac{7}{4} {\mathscr {E}}$. Or $s_0$ is in ${\mathcal {X}}^{(\mathrm {stuck})}_x$, in which case we do not lower-bound $f(x) - f(x_{{\mathscr {T}}})$. The probability of this happening is

$$\begin{aligned} {\text {Prob}}\!\left\{ \xi \in {\mathcal {X}}^{(\mathrm {stuck})}_x\right\}&= \frac{{\text {Vol}}\!\left( {\mathcal {X}}^{(\mathrm {stuck})}_x\right) }{{\text {Vol}}\!\left( {\mathbb {B}}^d_r\right) }, \end{aligned}$$

where ${\text {Vol}}\!\left( \cdot \right)$ denotes the volume of a set, and ${\text {Vol}}\!\left( {\mathbb {B}}^d_r\right)$ is the volume of a Euclidean ball of radius r in a d-dimensional vector space. In order to upper-bound the volume of ${\mathcal {X}}^{(\mathrm {stuck})}_x$, we resort to Lemma G.1: this is where we use the assumption $\lambda _{\mathrm {min}}(\nabla ^2 {{\hat{f}}}_x(0)) \le -\sqrt{{{\hat{\rho }}} \epsilon }$.

Let $e_1$ denote an eigenvector of $\nabla ^2 {{\hat{f}}}_x(0)$ with minimal eigenvalue, and let $s_0, s_0'$ be two arbitrary vectors in ${\mathcal {X}}^{(\mathrm {stuck})}_x$ such that $s_0 - s_0'$ is parallel to $e_1$. Lemma G.1 implies that $\Vert s_0 - s_0'\Vert \le \frac{\delta {\mathscr {E}}}{2\Delta _f} \frac{r}{\sqrt{d}}$. Now consider a point $a \in B_x(r)$ orthogonal to $e_1$, and let $\ell _a$ denote the line parallel to $e_1$ passing through a. The previous reasoning tells us that the intersection of $\ell _a$ with ${\mathcal {X}}^{(\mathrm {stuck})}_x$ is contained in a segment of $\ell _a$ of length at most $\frac{\delta {\mathscr {E}}}{2\Delta _f} \frac{r}{\sqrt{d}}$. Thus, with ${\mathbf {1}}$ denoting the indicator function,

$$\begin{aligned} {\text {Vol}}\!\left( {\mathcal {X}}^{(\mathrm {stuck})}_x\right)&= \int _{B_x(r)} {\mathbf {1}}_{{\mathcal {X}}^{(\mathrm {stuck})}_x}(y) \mathrm {d}y\\&= \int _{a \in B_x(r) : a \perp e_1} \left[ \int _{\ell _a} {\mathbf {1}}_{{\mathcal {X}}^{(\mathrm {stuck})}_x}(z) \mathrm {d}z\right] \mathrm {d}a\\&\le \frac{\delta {\mathscr {E}}}{2\Delta _f} \frac{r}{\sqrt{d}} {\text {Vol}}\!\left( {\mathbb {B}}^{d-1}_r\right) . \end{aligned}$$

With $\Gamma$ denoting the Gamma function, it follows that

$$\begin{aligned} {\text {Prob}}\!\left\{ \xi \in {\mathcal {X}}^{(\mathrm {stuck})}_x\right\}&\le \frac{\delta {\mathscr {E}}}{2\Delta _f} \frac{r}{\sqrt{d}} \cdot \frac{{\text {Vol}}\!\left( {\mathbb {B}}^{d-1}_r\right) }{{\text {Vol}}\!\left( {\mathbb {B}}^d_r\right) } \\&= \frac{\delta {\mathscr {E}}}{2\Delta _f} \frac{r}{\sqrt{d}} \cdot \frac{1}{r\sqrt{\pi }} \frac{\Gamma (1 + d/2)}{\Gamma (1 + (d-1)/2)}. \end{aligned}$$

One can check (for example, using Gautschi’s inequality) that the last fraction is upper-bounded by $\sqrt{d}$ for all $d \ge 1$. Thus,

$$\begin{aligned} {\text {Prob}}\!\left\{ \xi \in {\mathcal {X}}^{(\mathrm {stuck})}_x\right\}&\le \frac{\delta {\mathscr {E}}}{2\sqrt{\pi }\Delta _f} \le \frac{\delta {\mathscr {E}}}{3\Delta _f}. \end{aligned}$$

This limits the probability of the only bad event.

This covers all possibilities. $\square$

1.2 Proof of Lemma G.1

Proof of Lemma G.1

For contradiction, assume $E_0 - E_{{\mathscr {T}}}$ and $E_0' - E_{{\mathscr {T}}}'$ are both strictly less than $2{\mathscr {E}}$. Then, by Lemmas 4.2, 4.3 and C.1 and the assumption $\Vert s_0\Vert , \Vert s_0'\Vert \le r$, we have

$$\begin{aligned} \forall j \le {\mathscr {T}}, \Vert s_j\Vert&\le r + \Vert s_j - s_0\Vert \le {\mathscr {L}}/64 + \sqrt{32 \sqrt{\kappa } \eta {\mathscr {T}} {\mathscr {E}}}\nonumber \\&= (1/64 + \sqrt{2}) {\mathscr {L}} \le 2{\mathscr {L}}, \Vert s_j'\Vert \le 2{\mathscr {L}}. \end{aligned}$$

(108)

The aim is to show that this cannot hold for $j = {\mathscr {T}}$.

Define $w_j = s_j - s_j'$ for all j. Observe $w_{-1} = s_{-1}^{} - s_{-1}' = (s_0 - v_0) - (s_0' - v_0') = s_0^{} - s_0' = w_0$ since $v_0 = v_0' = 0$. Then, Lemma E.2 provides that

$$\begin{aligned} \begin{pmatrix} w_j \\ w_{j-1} \end{pmatrix}&= A^j \begin{pmatrix} w_0 \\ w_{0} \end{pmatrix} - \eta \sum _{k = 0}^{j-1} A^{j-1-k} \begin{pmatrix} \delta _k'' \\ 0 \end{pmatrix}, \end{aligned}$$

(109)

where A is as defined and discussed in Appendix E, and

$$\begin{aligned} \delta _k''&\triangleq \nabla {\hat{f}}_x(u_k)-\nabla {\hat{f}}_x(u_k') - {\mathcal {H}} (u_k - u_k') \\&= \left( \int _{0}^{1} \left( \nabla ^2 {{\hat{f}}}_x(\phi u_k + (1-\phi )u_k') - \nabla ^2 {{\hat{f}}}_x(0) \right) \mathrm {d}\phi \right) \![u_k - u_k']. \end{aligned}$$

Recall that $u_k = (2-\theta ) s_k - (1-\theta ) s_{k-1}$. In particular, using (108) and Lemma C.1 we have:

$$\begin{aligned} \Vert u_k\Vert&\le |2-\theta | \Vert s_k\Vert + |1-\theta | \Vert s_{k-1}\Vert \le 6{\mathscr {L}} \le b. \end{aligned}$$

The same holds for $\Vert u_k'\Vert$, and $\Vert \phi u_k + (1-\phi )u_k'\Vert \le \max \!\left( \Vert u_k\Vert , \Vert u_k'\Vert \right) \le 6{\mathscr {L}} \le b$ for $\phi \in [0, 1]$. It follows that the Lipschitz-type properties of $\nabla ^2 {{\hat{f}}}_x$ apply along rays from the origin of $\mathrm {T}_x{\mathcal {M}}$ to any point of the form $\phi u_k + (1-\phi )u_k'$ for $\phi \in [0, 1]$. Therefore,

$$\begin{aligned} \Vert \delta _k''\Vert&\le 6 {{\hat{\rho }}} {\mathscr {L}} \Vert u_k - u_k' \Vert = 6 {{\hat{\rho }}} {\mathscr {L}} \Vert (2-\theta ) w_k - (1-\theta ) w_{k-1} \Vert \nonumber \\ {}&\le 12 {{\hat{\rho }}} {\mathscr {L}} \left( \Vert w_k\Vert + \Vert w_{k-1}\Vert \right) . \end{aligned}$$

(110)

This will come in handy momentarily.

As we did in previous proofs, let $e_1, \ldots , e_d$ form an orthonormal basis of eigenvectors for ${\mathcal {H}}$ with eigenvalues $\lambda _1 \le \cdots \le \lambda _d$. Expand the vectors $w_j$ and $\delta _k''$ in this basis as:

$$\begin{aligned} w_j&= \sum _{m = 1}^d w_j^{(m)} e_m ,&\delta _k''&= \sum _{m = 1}^{d} (\delta _k'')^{(m)} e_m. \end{aligned}$$

Going back to (109), we can write

$$\begin{aligned} w_j&= \sum _{m' = 1}^{d} \left\langle {\begin{pmatrix} e_{m'} \\ 0 \end{pmatrix}},{\begin{pmatrix} w_j \\ w_{j-1} \end{pmatrix}}\right\rangle e_{m'} \\&= \sum _{m' = 1}^{d} \sum _{m = 1}^{d} \left[ \left\langle {\begin{pmatrix} e_{m'} \\ 0 \end{pmatrix}},{A^j \begin{pmatrix} e_{m} \\ e_{m} \end{pmatrix}}\right\rangle w_0^{(m)}\right. \\ {}&\quad \left. - \eta \sum _{k = 0}^{j-1} \left\langle {\begin{pmatrix} e_{m'} \\ 0 \end{pmatrix}},{A^{j-1-k} \begin{pmatrix} e_m \\ 0 \end{pmatrix}}\right\rangle (\delta _k'')^{(m)} \right] e_{m'}. \end{aligned}$$

Owing to (81) and (82), only the terms with $m = m'$ survive. Also, recalling that $w_0 = r_0 e_1$ by assumption, we have

$$\begin{aligned} w_j&= \left( a_{1,j} - b_{1,j} \right) r_0 e_1 - \eta \sum _{m = 1}^{d} \sum _{k = 0}^{j-1} a_{m, j-1-k} (\delta _k'')^{(m)} e_{m}, \end{aligned}$$

(111)

where $a_{m,j}$, $b_{m,j}$ are defined by (87).

We aim to show that $w_{{\mathscr {T}}} = s_{\mathscr {T}}^{} - s_{\mathscr {T}}'$ is larger than $4{\mathscr {L}}$, as this will contradict the claim that both $\Vert s_{\mathscr {T}}\Vert$ and $\Vert s_{\mathscr {T}}'\Vert$ are smaller than $2{\mathscr {L}}$: in view of (108), this is sufficient to prove the lemma. To this end, we introduce two new sequences of vectors to split $w_j$ according to (111):

$$\begin{aligned} w_j&= y_j - z_j,&y_j&= \left( a_{1,j} - b_{1,j} \right) r_0 e_1,&z_j&= \eta \sum _{m = 1}^{d} \sum _{k = 0}^{j-1} a_{m, j-1-k} (\delta _k'')^{(m)} e_m. \end{aligned}$$

First, we show by induction that $\Vert z_j\Vert \le \frac{1}{2}\Vert y_j\Vert$ for all j. The base case holds since $z_0 = 0$. Now assuming the claim holds for $z_0, \ldots , z_j$, we must prove that $\Vert z_{j+1}\Vert \le \frac{1}{2} \Vert y_{j+1}\Vert$. Owing to the induction hypothesis, we know that

$$\begin{aligned} \forall j' \le j,&\Vert w_{j'}\Vert \le \Vert y_{j'}\Vert + \Vert z_{j'}\Vert \le \frac{3}{2} \Vert y_{j'}\Vert . \end{aligned}$$

(112)

By assumption, $\lambda _1$ (the smallest eigenvalue of $\nabla ^2 {{\hat{f}}}_x(0)$) is less than $-\sqrt{{{\hat{\rho }}} \epsilon }$. In particular, it is non-positive. Hence [28, Lem. 37] asserts that $\max _{m = 1, \ldots , d} |a_{m, j-k}| = |a_{1, j-k}|$, so that, also using (110) then (112):

$$\begin{aligned} \Vert z_{j+1}\Vert&\le \eta \sum _{k = 0}^{j} \left\| \sum _{m = 1}^{d} a_{m, j-k} (\delta _k'')^{(m)} e_m \right\| \le \eta \sum _{k = 0}^{j} |a_{1, j-k}| \Vert \delta _k''\Vert \\&\le 12 \eta {{\hat{\rho }}} {\mathscr {L}} \sum _{k = 0}^{j} |a_{1, j-k}| \left( \Vert w_k\Vert + \Vert w_{k-1}\Vert \right) \\&\le 18 \eta {{\hat{\rho }}} {\mathscr {L}} \sum _{k = 0}^{j} |a_{1, j-k}| \left( \Vert y_{k}\Vert + \Vert y_{k-1}\Vert \right) . \end{aligned}$$

Moreover, [28, Lem. 38] applies and tells us that

$$\begin{aligned} \forall j',&\Vert y_{j'+1}\Vert \ge \Vert y_{j'}\Vert&\ge \frac{\theta r_0}{2} \left( 1 + \frac{1}{2} \min \!\left( \frac{|\eta \lambda _1|}{\theta }, \sqrt{|\eta \lambda _1|} \right) \right) ^{j'}. \end{aligned}$$

(113)

In particular, $\Vert y_j\Vert$ is non-decreasing with j. Thus, continuing from above, we find that

$$\begin{aligned} \Vert z_{j+1}\Vert&\le 36 \eta {{\hat{\rho }}} {\mathscr {L}} \sum _{k = 0}^{j} |a_{1, j-k}| \Vert y_{k}\Vert = 36 \eta {{\hat{\rho }}} {\mathscr {L}} r_0 \sum _{k = 0}^{j} |a_{1, j-k}| |a_{1,k} - b_{1,k}|, \end{aligned}$$

where the last equality follows from the definition of $y_k$. Owing to [28, Lem. 36], the fact that $\lambda _1$ is non-positive implies that

$$\begin{aligned} \forall 0 \le k \le j,&|a_{1, j-k}| |a_{1,k} - b_{1,k}| \le \left( \frac{2}{\theta } + (j+1) \right) |a_{1,k+1} - b_{1,k+1}|. \end{aligned}$$

Moreover, $j+1 \le {\mathscr {T}}$ (as otherwise we are done with the proof by induction), and $\frac{2}{\theta } \le 2{\mathscr {T}}$ with $c \ge 4$. Hence,

$$\begin{aligned} \Vert z_{j+1}\Vert&\le 108 \eta {{\hat{\rho }}} {\mathscr {L}} {\mathscr {T}} r_0 \sum _{k = 0}^{j} |a_{1,k+1} - b_{1,k+1}| = 108 \eta {{\hat{\rho }}} {\mathscr {L}} {\mathscr {T}} \sum _{k = 0}^{j} \Vert y_{k+1}\Vert . \end{aligned}$$

Recall that $\Vert y_k\Vert$ is non-decreasing with k to see that, using $j+1 \le {\mathscr {T}}$ once more:

$$\begin{aligned} \Vert z_{j+1}\Vert&\le 108 \eta {{\hat{\rho }}} {\mathscr {L}} {\mathscr {T}}^2 \Vert y_{j+1}\Vert \le \frac{1}{2} \Vert y_{j+1}\Vert . \end{aligned}$$

(The last inequality holds with $c \ge 108$ because $108 \eta {{\hat{\rho }}} {\mathscr {L}} {\mathscr {T}}^2 = 54 c^{-1}$.) This concludes the induction, from which we learn that $\Vert w_j\Vert \ge \Vert y_j\Vert - \Vert z_j\Vert \ge \frac{1}{2} \Vert y_j\Vert$ for all $j \le {\mathscr {T}}$. In particular, it holds owing to (113) that

$$\begin{aligned} \Vert w_{\mathscr {T}}\Vert&\ge \frac{1}{2} \Vert y_{{\mathscr {T}}}\Vert \ge \frac{\theta r_0}{4} \left( 1 + \frac{1}{2} \min \!\left( \frac{|\eta \lambda _1|}{\theta }, \sqrt{|\eta \lambda _1|} \right) \right) ^{{\mathscr {T}}}. \end{aligned}$$

As per our assumptions, $\lambda _1 \le -\sqrt{{{\hat{\rho }}} \epsilon }$. Therefore, using the definitions of $\theta$, $\eta$ and $\kappa$,

$$\begin{aligned} \min \!\left( \frac{|\eta \lambda _1|}{\theta }, \sqrt{|\eta \lambda _1|} \right)&\ge \min \!\left( \frac{\sqrt{{{\hat{\rho }}}\epsilon } \sqrt{\kappa }}{\ell }, \sqrt{\frac{\sqrt{{{\hat{\rho }}} \epsilon }}{4\ell }} \right) = \min \!\left( \frac{1}{\sqrt{\kappa }}, \frac{1}{2} \frac{1}{\sqrt{\kappa }} \right) = \frac{1}{2} \frac{1}{\sqrt{\kappa }}. \end{aligned}$$

Moreover, ${\mathscr {T}} = \sqrt{\kappa } \chi c = 4 \sqrt{\kappa } \chi c/4$, so that, using $(1+1/t)^t \ge 2$ for $t \ge 4$ and $\kappa \ge 1$, $\chi c \ge 4$:

$$\begin{aligned} \Vert w_{\mathscr {T}}\Vert&\ge \frac{\theta r_0}{4} \left( 1 + \frac{1}{4\sqrt{\kappa }} \right) ^{4 \sqrt{\kappa } \cdot \chi c/4} \ge \frac{\theta r_0}{4} 2^{\chi c/4} \ge \frac{\theta }{4} \frac{\delta {\mathscr {E}}}{2\Delta _f} \frac{r}{\sqrt{d}} 2^{\chi (c/4-1)} 2^{\chi }. \end{aligned}$$

At this point, we finally use the assumption $\chi \ge \log _2\!\left( \frac{d^{1/2} \ell ^{3/2} \Delta _f}{({{\hat{\rho }}} \epsilon )^{1/4} \epsilon ^2 \delta } \right)$ on the $2^\chi$ factor:

$$\begin{aligned} \Vert w_{\mathscr {T}}\Vert&\ge \frac{\theta }{4} \frac{\delta {\mathscr {E}}}{2\Delta _f} \frac{r}{\sqrt{d}} 2^{\chi (c/4-1)} \frac{d^{1/2} \ell ^{3/2} \Delta _f}{({{\hat{\rho }}} \epsilon )^{1/4} \epsilon ^2 \delta } = \frac{1}{1024} \chi ^{-8} c^{-12} 2^{\chi (c/4-1)} \cdot 4{\mathscr {L}} > 4{\mathscr {L}}. \end{aligned}$$

(The last inequality holds with $c \ge 500$ and $\chi \ge 1$: this fact is straightforward to show by taking derivatives of $\frac{2^{\chi (c/4-1)}}{\chi ^{8} c^{12}}$ with respect to $\chi$ and c, and showing those derivatives are positive.) This concludes the proof by contradiction, from which we deduce that at least one of $E_0 - E_{{\mathscr {T}}}$ or $E_0' - E_{{\mathscr {T}}}'$ must be larger than or equal to $2{\mathscr {E}}$. $\square$