1 Introduction

Due to their importance in various fields of engineering and atmospheric sciences, impinging jets (IJs) have vastly been investigated over the last several decades [1,2,3,4,5,6,7]. This study focuses on the investigation of experimentally produced IJs with application to downburst outflows in nature. Downbursts develop from thunderstorm clouds when the falling rain and hail, associated with the evaporation and melting of hydrometeors inside and underneath the cloud, produces a strong downward current of negatively buoyant air. Once the downdraft hits the surface, the wind speeds in the radially expanding outflow can exceed 75 m s–1 [8] in the first 50–100 m from the surface. These high wind speeds can pose a serious hazard to people, structures and the environment. The complex characterization of downburst winds arises from their very limited temporal and spatial scales, respectively in the order of 10 min [9, 10] and few kilometers in diameter [9]. This makes downbursts small-scale, highly three dimensional (3D) and unsteady flows, and causes the full-scale recording of the complete phenomenon to be hardly practicable. Fujita [11] classified downbursts into microbursts (\(< 4{\text{ km}})\) and macrobursts (\(> 4{\text{ km}})\) based on the spatial extent of the outflow. Physical wind simulators need to be sufficiently large to replicate downburst outflows at reasonable geometric, velocity, and time scales. For example, an IJ of \({\mathcal{O}}\)(1 m) with a geometric scale of 1:1000 and a velocity scale of 1:1 results in a time scale of 1:1000. Therefore, an actual downburst that lasts for 10 min in the atmosphere needs to be shorter than 0.6 s in the laboratory setting to satisfy the prescribed time scale. Besides, the region of the maximum horizontal velocities in the actual outflow, \({\mathcal{O}}\)(100 m), reduces to the lowest ~ 1 cm from the wind tunnel floor given the above geometric scale. This small distance from the floor makes the punctual velocity measurements in this region technically challenging and unreliable.

The first field measuring campaigns [9, 11,12,13] used anemometers and Doppler radars to characterize downburst outflows. Full-scale measurements have become more and more frequent over the last several decades [14,15,16,17,18,19] and have employed the latest generation of downburst measuring techniques. These new datasets, such as the one presented in [10], facilitate more thorough analysis of both mean and turbulent characteristics of downburst flows and provided additional climatological descriptions of these wind events. In parallel with the field measurements, downbursts have also been investigated computationally using IJ models [20, 21], cloud and sub-cloud models [22,23,24] as well as mesoscale weather forecasting models [25]. While numerical models offer large diversity of results, flexibility and repeatability of the experiments under the same or different conditions, they often lack the proper representation of turbulence, instabilities, and coarse spatial and time resolutions to accurately represent all aspects of downburst outflows.

Physical simulations of downbursts in wind simulators mainly follow two experimental approaches: (1) buoyancy-driven currents; or (2) momentum-driven IJs. The former are typically called gravity currents [26,27,28,29,30], while the latter are simply referred to as IJs [31,32,33,34,35]. Our literature survey indicates that the number of experimental studies on downbursts is smaller than the number of either numerical or full-scale research on downburst winds. This discrepancy is partially due to the limitations of traditional atmospheric boundary layer (ABL) wind tunnels to replicate highly 3D and non-stationary wind systems, such as thunderstorm downburst winds. At the same time, the facilities that are capable of creating downburst-like IJs [33, 35, 36] are sometimes limited by small scales (discussed above) or, for instance, continuous impingement of the jet that creates a 3D, but steady-state outflow near the surface. In addition to being 3D and localized, downburst velocity records are also non-Gaussian [18, 37, 38].

A summary of several IJ studies with various applications to downburst outflows is presented in Table 1. The listed studies focused typically on the investigation of the flow field in downburst outflows and surface pressures on generic buildings. The prevalence of IJ over the gravity current methods in wind engineering is also noticeable in Table 1. Gravity current experiments provide a more realistic dynamical forcing of downbursts and replicability of some of their thermodynamically driven properties (e.g., baroclinically generated vorticity in the outflow). However, from a wind engineering point of view, the low outflow velocities involved in gravity current experiments due to Froude number mismatch between the experiments and the atmosphere lead to favor the IJ approach. IJ experiments are further subdivided into continuous and pulsed IJs, depending on the duration of the issued jet. Continuous experiments simulate a steady jet flow that is less realistic representation of transient downbursts in respect to the pulsed jet approach. Therefore, the current study adopted this latter approach by means of rapid release and closure of the jet nozzle. In Table 1, the terms translating and stationary refer to the cases when the nozzle that produces the jet is moving parallel to the impinging plate and the cases of a stationary nozzle, respectively. The translation of the impinging jet is adopted to simulate the movement of the cloud that is advected by the mean winds across the cloud depth (not applicable to supercell thunderstorms). Currently, the largest geometric scales of experimentally produced IJ downbursts are achieved in the Wind Engineering, Energy and Environment (WindEEE) Dome [39] at Western University (Canada). The reported geometric scales of downburst-like IJs in this facility are 1:200 and above [40, 41].

Table 1 Experimental studies on IJs with application to downburst outflows. While the list is not exhaustive, it indicates a wide range of experimental approaches and apparatuses used to reconstruct downburst-like IJs
Full size table

It is important to note that most of the studies presented in Table 1 used continuous IJs to replicate downburst outflows. However, this approach suffers from the stationarity of the outflow after the passage of the primary vortex.

On the other hand, several studies opted to simulate downburst-like IJs by introducing certain modifications of the traditional ABL wind tunnel apparatuses [22, 42, 43]. In many cases these approaches managed to accurately replicate downburst velocity records at a particular point in the flow, but they inherently lack the complete 3D flow structure of the starburst outflow that is observed in the real scenario [9, 16]. Also, recently Jubayer et al. [44] used a stationary IJ in the WindEEE Dome with the goal to simulate intermediate winds which are characterized as stationary, but non-Gaussian wind systems [37].

The experimental campaign discussed herein is composed of three separate contributions: (1) the measurements database that is published online in open-access mode [45]; (2) the description of the methodology, instrumentation and measurement grid setup that originate the database [46]; (3) the analysis and interpretation of the data, which is the focus of the current manuscript. The aim of these experiments is to produce and analyze a laboratory data set that generically reproduces full-scale downburst observations and at the same time serves as a calibration set for numerical simulations and analytical models of downburst-like flows. Here, the emphasize is on the vortex dynamics aspects and turbulent flow field characterization. The outcomes of this study, which fall under the umbrella of activities of the project THUNDERR [47], will allow to build a comprehensive, physically realistic, and simply applicable experimental model to adopt in the structural design stage.

The rest of this article is organized as follows. Section 2 briefly describes the WindEEE Dome facility and experimental setup as reported in Canepa et al. [46]. Canepa et al. [46] also discuss the data processing methodology and tools. In addition, Sect. 2 reports specifications of the flow visualization technology used to qualitatively inspect the generated flow field inside the chamber. Section 3 presents the results of this study together with their discussion. Here, the transient features of the generated downburst outflows, with focus to the primary vortex dynamics, are discussed in relation to the position in the flow field and jet intensity. Statistical analyses on the outflow radial and vertical profiles are provided with important insights into their rapid shift during the passage of the primary vortex. The space and time variation of turbulence characteristics is also investigated. Finally, Sect. 4 provides the main conclusions of this research and outlines the prospects for future work.

2 Experiment setup

All experiments analyzed in this study were carried out in the WindEEE Dome at Western University, Canada. The testing chamber of the facility is pictured in Fig. 1. Hangan et al. [39] describe in detail the laboratory and the generation of stationary and non-stationary flows. WindEEE Dome is a hexagonal chamber of 25 m in diameter surrounded by an outer return chamber of 40 m in diameter. Specifically, downburst flows at the WindEEE Dome are created as IJs using six large fans of diameter 2 m located in the upper chamber of the dome. The nozzle that connects upper and testing chamber is kept closed at first to allow the pressurization of the upper chamber. Opening of the nozzle issues an impinging jet towards the horizontal and flat surface of the testing chamber (Fig. 1). Upon hitting the surface, the flow travels radially outward replicating a downburst-like outflow.

Fig. 1
figure 1

Testing chamber of the WindEEE Dome with schematic of the downburst-like IJ. Cobra probes’ mast is drawn in yellow color at the 10 \(r/D\) positions. d is the size of the radial domain of measurements (radial increment \(\Delta\)r = 0.64 m)

Full size image

In our study, seven Cobra probes with sampling frequency \(f_{s} =\) 2500 Hz were mounted on a vertical stiff mast at heights \(z =\) 0.04, 0.10, 0.15, 0.20, 0.27, 0.42 and 0.50 m to measure the three flow velocity components. The displacement of the mast at 10 different radial positions \(r/D\) (0.2 to 2.0 with incremental step of 0.2), and the assumption of circular symmetry of the produced downburst outflow, allowed to accurately reconstruct the spatiotemporal dynamics of the phenomenon. Downward vertical velocities in the impinging jets produced in our experiments were \(W_{{{\text{jet}}}} =\) 8.9 and 16.4 m s−1 at the outlet section of the nozzle. Given their ratio of about 1.8, these two jet intensities are hereafter referred to as DB1.0 and DB1.8, respectively. Each experiment with same radial position of measurement and \(W_{{{\text{jet}}}}\) was repeated 20 times in order to increase the statistical value of the analyses.

The specification of the laboratory and of the downburst-like wind formation, along with a detailed description of the instrumentation and experimental setup, is provided in Canepa et al. [46].

The results throughout the paper will be referred to radial and height locations normalized to the position of maximum radial velocity \(\widehat{{\overline{V}}}\) over the entire flow, that in the following of this paper is found respectively at \(r_{{{\text{max}}}} = D = 3.2 {\text{m}}\) and \(z_{{{\text{max}}}} = 0.1{\text{ m}}\).

In addition to the Cobra probe velocity measurements, we also performed flow visualization experiments using theatrical fog fluid. These experiments facilitated an overall qualitative interpretation of the downburst outflow evolution in space and time. The visualization smoke is a water-based substance known under the name dipropylene glycol (http://www.ultratecfx.com). The percentage concentration of the composition was always between 60 and 100%. This odorless fluid creates a white cloud of fog with a medium to long hang time. The same seeding material was also used in several PIV measurements in the WindEEEE Dome [40, 62]. A fog machine (Power Fog Industrial 9D by Ultratec Special Effects) with a nozzle and a hose was used to release the fog particles with an average diameter of 1–5 μm into the WindEEE Dome testing chamber prior to the release of the downburst. Afterwards, the visualized outflow was captured using a full-frame digital single-lens reflex (DSLR) camera with the resolution of 1920 × 1080 pixels. The whole testing chamber was in dark with the exception of two light sheets that were used to illuminate one vertical cross section in the outflow. These two thin sheets of light were created using a couple of oppositely directed stroboscopic machines running in continuous mode. The images were taken at approximately 8 m away from the targeted cross section of downburst outflows and the height of the camera was about 1.6 m above the floor.

3 Results

Canepa et al. [46] showed that a typical downburst record, at least in controlled experimental conditions, consists of three main phases or segments: (1) PV segment, associated with the passage of the primary vortex (PV) over the instrument and this segment is further subdivided into: (1.1) ramp-up of the velocity signal, as PV approaches the instrument; (1.2) the first peak related to the PV and recorded slightly later with respect to its passage over the measuring instrument [9, 40]; (1.3) velocity slowdown as PV travels away from the instrument. (2) Plateau segment, related to the passage of smaller trailing vortices following the PV and characterized by a rather constant ensemble wind speed. The presence and length of the plateau segment in full-scale records depends on several factors, including the distance between the downdraft and the recording station, the velocity and direction of the downdraft translation (if any) with respect to the station. (3) Dissipation segment, related to the downburst depletion or to the transition of the phenomenon away from the measuring instrument. The analyses and results presented in the current manuscript will be often related to the individual segments of the downburst records. The reader is invited to refer to [46] for further details on the velocity signal phases, including the methodology adopted for their objective identification.

3.1 Primary and secondary vortices

Figure 2a shows the time series of the instantaneous radial velocity \(V\) from repetition #12 recorded at the position (\(r/r_{{{\text{max}}}} = 1.6\), \(z/z_{{{\text{max}}}} = 1.0\)) for DB1.0 and its moving average \(\overline{V}\) evaluated using a moving averaging window \(T = 0.1 {\text{s}}\) [40]. The “secondary” peak occurs at the beginning of the signal enclosed between two dashed black vertical lines. This occurrence is further analyzed using flow visualization of the radially advancing downburst in Fig. 2c,d. The secondary peak is associated with the passage of the secondary vortex (SV) that has an opposite rotation (and vorticity sign) in respect to the PV. The counter-rotating SV that precedes the PV is caused by the dynamic separation-reattachment (bubble) near the surface due to the passage of the PV [40]. The size of the SV and its associated velocities are smaller than those of the PV. The intensity of the secondary peak is proportional to the PV advection velocity, which according to Yao and Lundgren [49] is about four times smaller than the maximum wind speed in the PV. The peak velocity of about 12 m s–1 is the result of the superposition of advection velocity and PV circulation relative to the primary vortex center. The secondary peak velocity is about 4 m s–1 considering the instantaneous times series, and about 3 m s–1 considering its moving average. The sharp decrease of radial wind speed between the time occurrences of SV and PV (see the dashed black vertical line at about \(1.7 {\text{s}}\) in Fig. 2a) may be a consequence of the predominantly upward flow between the two vortices, as highlighted by positive values of the vertical velocity \(w\) in Fig. 2b. The analysis of the velocity signals shows that the SV is detected for \(r/r_{{{\text{max}}}} \ge 1.2\) and \(z/z_{{{\text{max}}}} > 0.4\). With increasing radial distance, the signature of the SV is more evident at the higher elevations. Indeed, the opposite vorticity in the PV and SV augments the vertical velocity between the vortex pair (see Fig. 2b), which consequently elevates the head of the PV and, in turn, the maximum velocities to higher elevations. Furthermore, the SV is overall less evident in the case DB1.8 where the higher outflow velocities may flatten the SV and therefore make it difficult to be captured.

Fig. 2
figure 2

The secondary vortex (SV) that forms in front of the primary vortex (PV): a time series (black line) of the radial wind speed from the repetition #12 at the position (\(r/r_{{{\text{max}}}} = 1.6\), \(z/z_{{{\text{max}}}} = 1.0\)) for the case DB1.0 and its moving average (orange line); b Zoom in on the time interval between SV and PV (red dashed rectangle in a) with reported radial wind speed (black line) and vertical wind speeds (colored lines) at all the instrumented heights and \(r/r_{{{\text{max}}}} = 1.6\); c flow visualization of a downburst outflow a few seconds after touchdown; and d a zoom in on the frontal zone (the red rectangle in c) with the indication of the PV and SV

Full size image

The SV was also observed in the gravity current experiments of microbursts in Lundgren et al. [48] and Yao and Lundgren [49] and other impinging jet studies [40, 63], as well as in the idealized numerical simulations of Mason et al. [64]. However, the presence of SV is not commonly observed in real downbursts. A weak SV is observed by Sherman [65] in his study of a weak downburst close to Brisbane, Australia, as well as by Romanic [66] in his study of severe microburst recorded on a 213-m tall tower in the Netherlands. The presence of the SV, preceding the passage of the PV, was also reported by Canepa et al. [19] in the downburst event recorded in Genoa on May 13, 2018 by means of a LiDAR vertical profiler. Due to the relative low elevation above the ground of the recorded profile in these real events, the top part of the SV can be hardly captured and, even more so, that of the PV.

The duration of ramp-up, plateau and dissipation segments are investigated in Fig. 3 based on the ensemble means of all repetitions. The advection velocity of the approaching PV is proportional to the maximum wind speed in the downburst outflow [48, 67], which, in turn, is proportional to the jet velocity. At the time of maximum outflow intensity, we found that this dependency is described by the relation \(\overline{V}_{{{\text{max}}}} \cong 1.5 \times W_{{{\text{jet}}}}\). For this reason, the ramp-up period lasts longer in the DB1.0 case compared to DB1.8. Furthermore, the duration of ramp-up can be considered almost constant throughout the radial domain. Assuming that the vorticity in the PV increases while expanding outwards because of vortex stretching, the translational speed has to initially decrease to keep the ramp-up duration constant. Afterwards, flow visualization shows that the size of PV tends to increase and the vorticity of the PV diminishes, in particular when \(r/r_{{{\text{max}}}}\) is larger than \(1.4 - 1.6\). Hence, the advection velocity of PV increases further from the touchdown position. From another point of view, the advection velocity of PV can be related to the potential flow model of a vortex ring in proximity to the ground (see, for instance, [68]), which explains the vortex evolution in space and time in terms of interaction between the real vortex and its virtual image placed symmetrically below the ground plane. As the vortex expands outwards, it stretches and increases its rotational speed, while at the same time it also slowly dissipates due to surface drag, entrainment of ambient air, and turbulent viscosity. While stretching increases the rotational speed and hence the PV advection velocity, dissipation terms reduce the rotation and decelerates the PV. The present experiments seem to show that the former term governs this process up to \(r/r_{{{\text{max}}}} = 1.4 - 1.6\), whereas the latter contributor becomes more relevant beyond this \(r/r_{{{\text{max}}}}\). This finding agrees with the experimental results of van Hout et al. [63].

Fig. 3
figure 3

Duration of ramp-up, plateau and dissipation segments

Full size image

The plateau segment, which is the longest segment of the signals, presents a decreasing trend and is roughly halved along the overall distance of \(r/r_{{{\text{max}}}} = 2\).

3.2 Radial and vertical velocity profiles

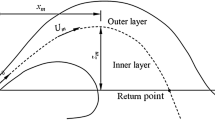
Figure 4 shows for each measurement height the radial profiles of the slowly-varying radial mean velocity, \(\overline{V}\), normalized by its maximum value over the entire flow \(\widehat{{\overline{V}}}\), at the peak (Fig. 4a,c) and averaged along the plateau segment (Fig. 4b,d). Differently from the absolute maximum of \(\overline{V}\) over the entire flow (\(\widehat{{\overline{V}}}\)), \(\overline{V}_{{{\text{max}}}}\) hereafter refers to the maximum \(\overline{V}\) in the time and/or space subdomain of the measurements. In both cases, the maximum velocities are observed at the lowest two measuring heights and show decreasing trend above. The highest velocities are observed at \(r/r_{{{\text{max}}}} = 1.0\), which is in accordance with many other experimental studies [e.g., 20, 33, 35]. The wind speed magnitude increases at first with radial distance under the influence of the favorable pressure gradient and, afterwards, decreases because of the viscous dissipation and adverse pressure gradient [69, 70]. Interestingly, the maximum wind speed at the higher heights, i.e. \(z/z_{{{\text{max}}}} \ge 4.2\), occurs radially closer to the jet touchdown position (around \(r/r_{{{\text{max}}}} = 0.8\)). Nevertheless, during the plateau segment \(\overline{V}_{{{\text{max}}}}\) occurs at \(r/r_{{{\text{max}}}} = 1.0\) only at the lower levels, i.e. \(z/z_{{{\text{max}}}} \le 1.5\); by increasing the height, \(\overline{V}_{{{\text{max}}}}\) occurs at smaller radial locations. Figure 5 provides an interpretation of this aspect. It shows the vertical profiles of the vertical wind speed \(\overline{w}\) for all \(r/r_{{{\text{max}}}}\) measurement positions, at the time of the horizontal velocity peak \(t\left( {\overline{V}_{{{\text{max}}}} } \right)\) (Fig. 5a,c) and averaged along the plateau segment (Fig. 5b,d). A quite strong downward flow component is observed along the vertical profiles for \(r/r_{{{\text{max}}}} \le 0.8\). In terms of magnitude, the sharp decrease of \(\overline{w}\) from \(z/z_{{{\text{max}}}} = 5.0\) to \(0.4\) clearly indicates that this area is still inside the downdraft. Upon exiting from the bell mouth, the jet widens in the radial direction beyond its geometric apex, defined by \(r/r_{{{\text{max}}}} = 0.5\), due to the entrainment of ambient air and tangential shear with the surrounding [4, 71]. As the jet approaches the ground, the vertical velocity decreases rapidly while the flow streamlines are forced to spread in the radial direction due to the pressure gradient [6, 69]. This region, where the jet’s momentum changes from vertical to horizontal, is named “deflection zone” after Bradshaw and Love [72]. Accordingly, the primary vortex forms at the edge of the downdraft as consequence of the high shear stress with the quiescent and overlying flow, and changes its propagation direction from vertical to horizontal upon the impingement [7]. The maximum radial velocities that are observed at the higher elevations for \(r/r_{{{\text{max}}}} \le 0.8\) (Fig. 4) are not produced by the passage of the primary vortex; significant horizontal velocities arise in the deflection zone and cause the maxima at these height and radial positions. In the wall-jet region after the impingement, the surface layer thickness is confined underneath the primary vortex [69] and the top measurement heights record a sharp decrease of the velocity magnitude that is clearly detected in Fig. 4a, c and corresponds to the flattening of the top part of the nose-shaped vertical profiles in this stage of the phenomenon. According to the experimental findings of Didden and Ho [70] and Landreth and Adrian [7], the vertical flow reversal highlighted by the positive values of the vertical velocity (upward flow component) for \(r/r_{{{\text{max}}}} \ge 1.0\), indicates the onset of surface layer separation near this point, which corresponds to the formation of the SV at the advancing front of the PV. The highest vertical wind speeds observed at the peak (Fig. 5a, c) at \(r/r_{{{\text{max}}}} = 1.6\) are the result of the strong interaction between the inner-region vortex (SV) formed as consequence of the separation-reattachment of the surface layer, and the outer-region vortex (PV). By moving downstream, the size of the SV increases in height and decreases in the streamwise direction. The coupling with the PV provides a strong upward induction on the SV [73] and high upward flow velocities develop at the boundary between the two vortex structures (see Fig. 2), which eventually induce the SV ejection from the surface. Furthermore, \(\overline{w}\) decreases and is very close to 0 for \(r/r_{{{\text{max}}}} = 1.8\) and 2.0. This is consistent with the increasing size of the PV as it spreads out from the touchdown position, while reducing the PV circulation and therefore both the \(\overline{V}\) and \(\overline{w}\) velocity components. In the plateau segment, \(\overline{w}\) is zero for all heights when \(r/r_{{{\text{max}}}} \ge 1.0\), because this region is dominated by smaller-scale random vortices and the mean flow is along horizontal streamlines.

Fig. 4
figure 4

Radial profiles of normalized radial wind speed: DB1.0 (a, b) and DB1.8 (c, d) at the peak (a, c) and plateau (b, d) segments. \(\widehat{{\overline{V}}}\) is the maximum value of the slowly-varying radial velocity \(\overline{V}\) over the entire flow

Full size image
Fig. 5
figure 5

Vertical profiles of normalized vertical wind speed: DB1.0 (a, b) and DB1.8 (c, d) at the peak (a, c) and plateau (b, d) segments of the radial wind speed. \(\widehat{{\overline{V}}}\) is the maximum value of the slowly-varying radial velocity \(\overline{V}\) over the entire flow

Full size image

Figure 6 shows the time history of the height of maximum radial slowly-varying mean wind speed \(z\left( {\overline{V}_{{{\text{max}}}} \left( t \right)} \right)\) along the profile, normalized by \(z_{{{\text{max}}}}\). \(z\left( {\overline{V}_{{{\text{max}}}} \left( t \right)} \right)\) is calculated as the ensemble over 20 repetitions at each radial location \(r/r_{{{\text{max}}}} > 0.8\). Since the main purpose here is to investigate the effect generated by the passage of PV on the height of maximum wind speed, the analysis covers the radial positions outside of the downdraft region (see Fig. 5). While the downburst outflow approaches the instrument (\(t < t\left( {\overline{V}_{{{\text{max}}}} } \right)\)), the ambient air pushed outwards by the vortex expansion is subjected to an unsteady adverse pressure gradient. Hence, strong viscous effects arise in the near-surface region and provoke the retardation of the flow at the lower levels. At the same time the flow accelerates in the inviscid region farther from the surface and shows rather high velocity gradients [70]. For this reason, the highest wind speeds at the beginning of the velocity ramp-up phase are usually experienced higher above the ground [3]. However, the ramp-up of the velocity time series (orange lines in Fig. 6) is dominated by the subsequent local minimum and maximum of \(z\left( {\overline{V}_{{{\text{max}}}} } \right)\) which relate to the formation of the SV in the inner layer of the outflow and to its interaction with the outer layer characterized by the presence of the PV. As a result the maximum velocities develop at the boundary between the two layers [4]. Accordingly, the minimum of \(z\left( {\overline{V}_{{{\text{max}}}} } \right)\) increases as the height of SV increases throughout the radial domain of measurements; this corroborates the observations above on the increase of the surface layer thickness by moving away from the jet touchdown. At \(r/r_{{{\text{max}}}} > 1.6\), the signature of the interaction between PV and SV is experienced almost at the top of the profile, suggesting that the SV is likely to be ejected from the surface. From here, the height of \(\overline{V}_{{{\text{max}}}}\) decays abruptly and reaches the minimum value of about \(z\left( {\overline{V}_{{{\text{max}}}} } \right)/z_{{{\text{max}}}} = 0.5\) few instants after \(t\left( {\overline{V}_{{{\text{max}}}} } \right)\). \(z\left( {\overline{V}_{{{\text{max}}}} } \right)\) appears higher on the ground at radial positions \(r/r_{{{\text{max}}}} \ge 1.6\) due to the increase of surface layer height. This behavior reflects the transient nature of the downburst outflow and particularly of the travelling vortex which, during its passage, constrains the flow in the area between the vortex lower end and the ground. Our findings demonstrate that the thickness, i.e., height, of the surface layer is both a function of the time and radial position. The theoretical models developed in the literature on this topic neglect the time-dependency of the surface layer thickness and assume the height at which the velocity equals half of the maximum radial velocity as the surface layer characteristic height, constant in time [2, 3, 74,75,76].

Fig. 6
figure 6

Ensemble average of 20 experiment repetitions of the height of maximum velocity \(z\left( {\overline{V}_{{{\text{max}}}} } \right)\), normalized by \(z_{{{\text{max}}}} = 0.1 {\text{m}}\), for \(r/r_{{{\text{max}}}} \ge 1.0\) and the cases DB1.0 (black line) and DB1.8 (red line). Orange lines show the ensemble average of the 20 mean wind speed time series at \(z/z_{{{\text{max}}}} = 1.0\) for the case DB1.0 (shown as reference signal). Vertical gray dotted lines show \(t\left( {\overline{V}_{{{\text{max}}}} } \right)\) for the case DB1.0

Full size image

Figures 7 and 8 provide a thorough characterization of the slowly-varying radial mean velocity field \(\overline{V} = \overline{V}\left( {r,z,t} \right)\), calculated as ensemble average across 20 repetitions, in the form \(\overline{V} = \overline{V}\left( {z,t} \right)\) and as function of radial positions \(0.6 \le r/r_{{{\text{max}}}} \le 1.6\). The remaining \(r/r_{{{\text{max}}}}\) locations are not shown here for sake of space but are available in the published database of measurements [45]. The maps of \(\overline{V}\left( {z,t} \right)\) show a clear maximum slightly before 2 s, that reaches the highest intensity at \(r/r_{{{\text{max}}}} = 1.0 - 1.2\). All these maxima correspond to vertical profiles with a clear nose shape. Moving radially outwards, the nose and maximum velocities are gradually constrained to the ground. This is mostly evident in the case DB1.0 for which the PV segment lasts longer because of the lower vortex advection velocity (see Fig. 3). In analogy to Fig. 3, the duration of the plateau segment is observed to decrease with radial distance due to flow dissipation. The transition to dissipation occurs faster in the case DB1.0 due to the lower flow speeds involved.

Fig. 7
figure 7

Profiles of \(\overline{V}\left( {z/z_{{{\text{max}}}} ,t} \right)\) for \(0.6 \le r/r_{{{\text{max}}}} \le 1.6\) and DB1.0

Full size image
Fig. 8
figure 8

Profiles of \(\overline{V}\left( {z/z_{{{\text{max}}}} ,t} \right)\) for \(0.6 \le r/r_{{{\text{max}}}} \le 1.6\) and DB1.8

Full size image

The spikes in the plateau segment of velocity profiles track the passage of trailing vortices. Underneath the bell mouth’s outlet section, Kelvin–Helmholtz instability in the shear layers leads to the formation of vortices with a natural frequency \(f\) that is characterized by a Strouhal number \(St\) defined in terms of jet velocity \(W_{{{\text{jet}}}}\) and diameter \(D\):

$$St = \frac{f\,D}{{W_{{{\text{jet}}}} }}$$
(1)

In an impinging jet, \(St\) also depends on Reynolds number \(Re\) and nozzle-to-plate height \(H/D\), other than on the initial velocity profile, turbulence state and other factors [77]. In the literature on impinging jets at low \(Re\) (\({\mathcal{O}}\)(104 – 105)) and scales, \(St\) is usually found between 0.35–0.65 depending on the parameters above [78,79,80]. To the authors’ knowledge, there are no impinging-jet studies in the literature assessing \(St\) for larger \(Re\) similar to those tested in the experiments here described (see Sect. 3.3). Considering this range of \(St\), \(D = 3.2 {\text{m}}\) and \(W_{{{\text{jet}}}} = 8.9 {\text{m s}}^{ - 1}\) and \(16.4 {\text{m s}}^{ - 1}\), we obtain a range of vortex shedding frequency \(f = 0.97 - 1.81 {\text{Hz}}\) and \(1.79 - 3.33 {\text{Hz}}\) for DB1.0 and DB1.8, respectively, which, despite being rather wide, qualitatively matches with the occurrence rate of velocity spikes observed in Fig. 7 and Fig. 8.

3.3 Turbulence intensity and statistical properties of downburst-like outflows

Several studies reported non-Gaussian properties of full-scale thunderstorm flow fields (see for instance [37]). Figure 9 shows the values of skewness and kurtosis as function of radial and height position for the plateau segment of the records. Because the plateau segment represents the steady-state phase of the outflow, the ensemble mean of multiple repetitions filters out fluctuations around the mean resulting in a nearly Gaussian statistics. The radial location \(r/r_{{{\text{max}}}} = 0.2\) is horizontally located in proximity of the geometrical downdraft center where the flow has a predominant vertical component; the very little radial velocities detected here cause the related distribution to deviate from the reference Gaussian properties. The same partly holds at the large radial and height locations of measurement, where the flow loses momentum and disperses in a three-dimensional-like pattern. Kurtosis shows a decreasing trend up to \(r/r_{{{\text{max}}}} = 2.0\), where \(\kappa = 2.5\).

Fig. 9
figure 9

Dependency of skewness (\(\gamma\)) and kurtosis (\(k\)) on height and radial position in the outflow

Full size image

The velocity histograms for the PV segment are depicted in Fig. 10. Here, the departure from the Gaussian distribution is more pronounced. As expected, velocity PDFs are asymmetric towards high values (\(\gamma < 0\)) in the area subjected to high radial wind speeds produced by the passage of PV, i.e. \(0.8 \le r/r_{{{\text{max}}}} \le 1.8\) and \(0.4 \le z/z_{{{\text{max}}}} \le 2.7\). Outside this region, the tail of the velocity distribution shifts to low values (\(\gamma > 0\)). The velocity distributions resemble the Gaussian distribution at radial locations close to the jet touchdown. However, no clear radial trend can be identified.

Fig. 10
figure 10

Velocity histograms of the PV segment (0.25 s on each side of the peak) of 20 downburst outflow repetitions at all heights (\(z/z_{{{\text{max}}}}\)) and radial positions (\(r/r_{{{\text{max}}}} )\), for the case DB1.0. The values of kurtosis (\(k\)) and skewness (\(\gamma\)) are included

Full size image

Table 2 shows the main turbulence properties, averaged along the vertical profile, at all radial locations in the outflow. The measured parameters are:

  • Temporal mean \(\overline{I}_{V} \left( {r,z} \right)\) of the slowly varying turbulence intensity \(I_{V} \left( {r,z,t} \right)\) given by:

    $$I_{V} \left( {r,z,t} \right) = \sigma_{V} \left( {r,z,t} \right)/\overline{V}\left( {r,z,t} \right)$$
    (2)
Table 2 Mean slowly-varying turbulence intensity \(\overline{I}_{V}\); skewness \(\gamma_{{\tilde{V}^{^{\prime}} }}\); kurtosis \(\kappa_{{\tilde{V}^{^{\prime}} }}\). The reported values are averaged over all heights
Full size table

\(\overline{V}\) is the slowly-varying radial mean velocity extracted applying a moving average period of \(T = 0.1 {\text{s}}\) [40], and \(\sigma_{V}\) is the slowly-varying standard deviation of the residual turbulent fluctuations, \(V^{\prime}\), given by \(V^{\prime}\left( {r,z,t} \right) = V\left( {r,z,t} \right) - \overline{V}\left( {r,z,t} \right)\). The temporal mean of \(I_{V} \left( {r,z,t} \right)\) was performed over the time interval included between the beginning of the velocity ramp-up period in the PV segment and the final part of the dissipation segment (for reference refer to the instances “1” to “5” in Fig. 4 and Fig. 5 of [46]).

  • Skewness \(\gamma_{{\tilde{V}^{^{\prime}} }}\) and kurtosis \(\kappa_{{\tilde{V}^{^{\prime}} }}\) of the reduced turbulent fluctuation \(\tilde{V}^{\prime}\left( {r,z,t} \right)\) given by:

    $$\tilde{V}^{\prime}\left( {r,z,t} \right) = V^{\prime}\left( {r,z,t} \right)/\sigma_{V} \left( {r,z,t} \right)$$
    (3)

Similar to Zhang et al. [81] and Canepa et al. [19], extremely large and unphysical values of the turbulence intensity (\(I_{V} > 0.2\)) corresponding to very low values of the slowly-varying mean velocity (\(\overline{V} < 5\) \({\text{m s}}^{ - 1}\)) are removed from the analysis.

The high flow mixing in the jet impingement area contributes to increasing turbulence levels. Outside the downdraft region, i.e., starting from \(r/r_{{{\text{max}}}} = 0.8\), \(\overline{I}_{V}\) increases almost linearly with radial location. At first, the primary vortex leads the downburst outflow and its downward induction has a stabilizing effect on the wall-jet flow [82]. In analogy to Fig. 9, from \(r/r_{{{\text{max}}}} = 1.0\) complex three-dimensional structures emerge and the turbulence intensity increases until the breakaway of the surface layer at large radial distances from the touchdown. \(\overline{I}_{V}\) appears overall greater in the case DB1.8. The ratio between DB1.8 and DB1.0 (not shown here) increases with a quasi-linear trend outside the impingement region up to \(r/r_{{{\text{max}}}} = 1.4\), where the ratio is equal to \(1.53\). Overall, the turbulence intensity values are in good agreement with those generally found in literature on full-scale downburst events. The recent findings by Canepa et al. [19] on downburst vertical profiles showed that the values of \(\overline{I}_{V}\), averaged along the height, are in the range 0.08–0.09. Solari et al. [83] and Zhang et al. [10, 81] reported \(\overline{I}_{V} = 0.12\) averaged over a large set of downburst outflows extracted from ultrasonic anemometer measurements. In our study, \(\overline{I}_{V}\) averaged along both the height and radial dimensions assumes values of 0.094 and 0.124, respectively for DB1.0 and DB1.8, which is in the range of values obtained from real events in the above studies.

Figure 11 shows the parameter \(\mu \left( {r,z,t} \right)\) evaluated as ensemble average of 20 experimental repetitions at each position \(r/r_{{{\text{max}}}} \ge 1.0\) and \(z/z_{{{\text{max}}}} = 0.4, 1.0, 2.0\) and \(4.2\).

$$\mu \left( {r,z,t} \right) = I_{V} \left( {r,z,t} \right)/\overline{I}_{V} \left( {r,z} \right)$$
(4)
Fig. 11
figure 11

Ensemble average of 20 experiment repetitions of \(\mu\) (Eq. 4), for \(r/r_{{{\text{max}}}} \ge 1.0\) and \(z/z_{{{\text{max}}}} = 0.4, 1.0, 2.0, 4.2\) and the cases DB1.0 (black line) and DB1.8 (red line). Orange dotted lines show the ensemble average of 20 mean wind speed time series for the case DB1.0 (shown as reference signal). Vertical gray dotted lines show \(t\left( {\overline{V}_{{{\text{max}}}} } \right)\)

Full size image

While it is usual practice to assume \(\overline{\mu } = 1\), Solari et al. [83] and Zhang et al. [10, 81] noticed asymmetry of \(\mu \left( t \right)\) around the primary velocity peak, namely in correspondence of the passage of the PV. This asymmetry is more pronounced in the present experiments due to lower Reynolds numbers involved which provide smoother surface compared to the fully turbulent environment in nature. \(Re\) is here defined as:

$$Re = \frac{{W_{jet} D}}{\nu }$$
(5)

where \(\nu = 1.48 \times 10^{ - 5} {\text{m}}^{2} {\text{s}}^{ - 1}\) is the kinematic viscosity of air at \(15 ^\circ C\), \(W_{{{\text{jet}}}}\) and \(D\) are the jet velocity and diameter, respectively, of either full-scale or experimentally produced downburst. The two cases here investigated, i.e. DB1.0 and DB1.8, provide Reynolds numbers \(Re = 1.92 \times 10^{6}\) and \(3.55 \times 10^{6}\), respectively, whereas full-scale downbursts typically present \({\text{Re}}\) in the order of \(10^{9}\). The same order of \(Re\) holds if \({\text{Re}}\) is evaluated as function of the maximum velocity over the entire flow and its height of occurrence, \(\widehat{{\overline{V}}}\) and \(z_{{{\text{max}}}}\), respectively.

Concurrently with the increase of velocity in the PV segment, \(\mu\) drastically increases and reaches the maximum shortly before the occurrence of \(\overline{V}_{{{\text{max}}}}\) (vertical gray dotted lines). The maximum value \(\mu = 3.28\) is detected at \(r/r_{{{\text{max}}}} = 1.2\) and \(z/z_{{{\text{max}}}} = 0.4\) for the case DB1.8, which shows overall greater values in respect to DB1.0, as expected. In general terms, \(\mu\) at the peak increases with the radial distance up to \(r/r_{{{\text{max}}}} = 1.4\) and decreases afterwards, while decreasing along the height. Furthermore, a prior spike of \(\mu\) sometimes higher than that related to \(\overline{V}_{{{\text{max}}}}\), is observed in the range of measurement positions \(1.4 \le r/r_{{{\text{max}}}} \le 1.8\) and \(0.4 \le z/z_{{{\text{max}}}} \le 2.0\). The domain of observation suggests the correlation with the high shear developed at the boundary between primary and secondary vortex. Upon reaching the maximum, \(\mu\) decreases to a local minimum below the unity which is recorded in correspondence of \(t\left( {\overline{V}_{{{\text{max}}}} } \right)\) or slightly later. The plateau segment is the longest segment in the velocity records and thus provides the main contribute to the evaluation of \(\overline{I}_{V}\). Accordingly, \(\mu\) is here close to the unity.

Therefore, in analogy to the full-scale measurements carried out by Zhang et al. [10] and Canepa et al. [19], a sharp peak of the turbulence intensity is observed slightly before the occurrence of the peak velocity. This behavior of \(\mu\), observed in both full-scale and controlled conditions, surely represents an important signature of the passage of the PV. The radial and height locations where the asymmetry of \(\mu\) is clearly recognizable corroborate this observation. As reported above, the maximum values of \(\mu\) are observed at the radial positions \(r/r_{{{\text{max}}}} = 1.2 - 1.4\), namely radially further from the location of the recorded maximum wind speed, i.e. \(r/r_{{{\text{max}}}} = 0.8 - 1.0\) (see Fig. 4). Hjelmfelt [9] first demonstrated that the maximum velocities underneath the vortex follow the vortex center in time and are thus recorded radially behind its location. The same findings are also found in experimentally produced downbursts [40, 67] and seem to be confirmed in our analysis by assuming that the maxima of \(\mu\) occur concurrently with the passage of PV. For \(z/z_{{{\text{max}}}} > 2.0\), where the trace of the travelling PV has nearly disappeared, the asymmetric trend of \(\mu\) is almost lost and the entire signal fluctuates around the mean value \(\mu = 1\).

In analogy to Fig. 6, Fig. 12 shows the time evolution of the height of maximum radial turbulence intensity in the wall-jet region, i.e., \(r/r_{{{\text{max}}}} > 0.8\). At the beginning of velocity ramp-up and for radial positions \(r/r_{{{\text{max}}}} \le 1.4\), turbulence is convected to higher levels in the free-shear layer due to the viscous-inviscid interaction [73]. From approximately \(r/r_{{{\text{max}}}} = 1.4 - 1.6\) the SV forms and turbulence mostly concentrates at the boundary with the PV. Concurrently with the passage of the PV, slightly before the occurrence of the peak velocity (vertical gray dotted lines), \(z\left( {I_{{V_{{{\text{max}}}} }} } \right)\) decreases rapidly to the height of occurrence of the maximum \(\mu\) observed in Fig. 11, i.e., \(z\left( {I_{{V_{{{\text{max}}}} }} } \right)/z_{{{\text{max}}}} < 2\). In correspondence of \(t(\overline{V}_{{{\text{max}}}} )\), as a result of the unsteady adverse pressure gradient induced by the passage of the PV [70], the maxima of turbulence intensity are recorded higher, around \(z\left( {I_{{V_{{{\text{max}}}} }} } \right)/z_{{{\text{max}}}} = 4\) throughout the plateau segment of the velocity due to the increase of the surface layer thickness. However, the same behavior is only partly detected at larger radial positions \(r/r_{{{\text{max}}}} > 1.6\), where the change of \(z\left( {I_{{V_{{{\text{max}}}} }} } \right)\) is less pronounced and the maximum turbulence intensity settles at lower heights.

Fig. 12
figure 12

Ensemble average of 20 experiment repetitions of the height of maximum turbulence intensity \(z\left( {I_{{V_{{{\text{max}}}} }} } \right)\), normalized by \(z_{{{\text{max}}}} = 0.1 {\text{m}}\), for \(r/r_{{{\text{max}}}} \ge 1.0\) and the cases DB1.0 (black line) and DB1.8 (red line). Orange lines show the ensemble average of 20 mean wind speed time series at \(z/z_{{{\text{max}}}} = 1.0\) for the case DB1.0 (shown as reference signal). Vertical gray dotted lines show \(t\left( {\overline{V}_{{{\text{max}}}} } \right)\)

Full size image

Overall, the height of maximum turbulence intensity shows a sudden switch in relation to the peak velocity, similarly to what was observed for \(z\left( {\overline{V}_{{{\text{max}}}} } \right)\) (Fig. 6). Contrary to \(z\left( {\overline{V}_{{{\text{max}}}} } \right)\), however, this change occurs from the lower to the upper heights.

Figures 13 and 14 show the profiles of slowly-varying standard deviation and turbulence intensity, \(\sigma_{V} \left( {r,z,t} \right)\) and \(I_{V} \left( {r,z,t} \right)\). The peak of turbulence intensity, mirrored in the standard deviation diagram, is again observed shortly prior to the occurrence of the radial velocity maxima, corroborating what was assumed above. These peaks gradually grow in magnitude for \(r/r_{{{\text{max}}}} > 1.0\) and the absolute maxima are detected radially further with respect to the position of maximum wind speed. The vertical profile of \(I_{V}\), at the time of maximum intensity, shows a nose shape that covers a gradually larger vertical extension by moving along the radial direction. The higher values of \(I_{V}\) at the top of the profile, that are clear for \(r/r_{{{\text{max}}}} > 1.0\), are caused by the decrease of the radial velocity at those elevations according to the nose-like vertical shape.

Fig. 13
figure 13

Profiles of \(\sigma_{V} \left( {z/z_{{{\text{max}}}} ,t} \right)\) for \(0.6 \le r/r_{{{\text{max}}}} \le 1.6\) and DB1.8

Full size image
Fig. 14
figure 14

Profiles of \(I_{V} \left( {z/z_{{{\text{max}}}} ,t} \right)\) for \(0.6 \le r/r_{{{\text{max}}}} \le 1.6\) and DB1.8

Full size image

Figure 15 shows the Reynolds stress \(\overline{u^{\prime}w^{\prime}} = \overline{{u^{\prime}w^{\prime}}} \left( {z,t} \right)\) as function of radial coordinate, in analogy to Fig. 7 and Fig. 8, for the case DB1.8. The aim here is to evaluate the momentum flux across the vertical section and provide insights into the flow direction at different elevations above the ground. The change of sign of this parameter eventually identifies the separation between inner and outer surface layer and hence the location of the nose tip of the velocity vertical profile.

Fig. 15
figure 15

Profiles of \(\overline{u^{\prime}w^{\prime}} \left( {z/z_{{{\text{max}}}} ,t} \right)\) for \(0.6 \le r/r_{{{\text{max}}}} \le 1.6\) and DB1.8

Full size image

The ambient air pushed outwards by the vortex expansion, before the PV segment of the velocity records, is slowed down at the lower elevations because of friction with the ground and assumes a logarithmic-type vertical profile, as shown in Fig. 6. Consequently, the momentum flux is directed downward along the whole vertical extension. With the passage of the PV and subsequent trailing vortices, the surface layer depth reduces and the tip of the nose-shaped profile moves gradually closer to the ground as the vortex advances radially outwards up to \(r/r_{{{\text{max}}}} = 1.6\). Beyond this location the lifting of the PV (not shown) produces a lift of the separation zone between the two layers. The red area defines the vertical range above the nose of the vertical profile where the velocity gradient is reversed with respect to a boundary layer flow.

The Gaussian and stationary properties of the reduced turbulent fluctuations, \(\tilde{V}^{\prime}\) [10, 83], are well retained in the flow generated during our experiments. \(\tilde{V}^{\prime}\) has always nearly zero mean and unit standard deviation; whereas the skewness and kurtosis are close to \(\gamma_{{\tilde{V}^{^{\prime}} }} = 0\) and \(\kappa_{{\tilde{V}^{^{\prime}} }} = 3\), respectively. The kurtosis is found to be higher in the case DB1.8, where it shows a quasi-periodic trend with maximum of \(\kappa_{{\tilde{V}^{^{\prime}} }} = 3.211\) at \(r/r_{{{\text{max}}}} = 0.6\), while it remains approximately constant around \(\kappa_{{\tilde{V}^{^{\prime}} }} = 2.9\) for DB1.0. The skewness assumes values \(\gamma_{{\tilde{V}^{^{\prime}} }} > 0\) within the impingement region while outside of that region fluctuates around zero.

The Kolmogorov’s similarity proves that the energy cascade in the inertial subrange is proportional to \(n^{{ - \frac{5}{3}}}\), where \(n\) is the frequency. In analogy to synoptic ABL winds, several studies in literature on full-scale downburst events demonstrate that the power spectral density (PSD) of \(\tilde{V}^{\prime}\) follows the law \(n^{{ - \frac{5}{3}}}\) [18, 83, 84]. Furthermore, Junayed et al. [40] investigated parametrically a set of experimentally produced downburst flows at the WindEEE Dome varying the Reynolds number \(Re\) and the ratio \(H/D\), where \(H\) is the height of the testing chamber and \(D\) the jet diameter. They found that the high frequency end of the spectra of the reduced turbulent fluctuation matches well with the full-scale observations. In particular, the slope \(n^{{ - \frac{5}{3}}}\) finds very good fit for large values of \(Re\) and \(H/D > 1\). The vortex forms fully and the larger range of scales allows a better match with the typical inertial subrange behavior. Figure 16 shows the PSD of \(\tilde{V}^{\prime}\) for DB1.8 which corroborates the observations above.

Fig. 16
figure 16

PSD of the reduced turbulent fluctuation \(\tilde{V}^{\prime}\) for DB1.8, matched with \(n^{{ - \frac{5}{3}}}\) profile (dashed lines). Note that the repetition #18 at the radial position \(r/D = 0.2\) was excluded from the analyses due to false readings in the measurement record

Full size image

4 Conclusions and prospects

This paper is an in-depth analysis of a large set of experimentally produced downburst winds at the WindEEE Dome, at Western University in Canada, as part of the project THUNDERR [47]. The aim of this experimental campaign is to produce and analyze a laboratory data set that generically reproduces full-scale observations and at the same time serves as a calibration set for numerical simulations of downburst-like flows. The dynamic characteristics of spatially-stationary, non-steady downburst winds are investigated by means of a refined spatial and temporal grid of Cobra probe measurements at 10 radial positions, 7 vertical positions repeated 20 times to achieve some statistical significance of the results. The database containing all the experimental measurements is published at the online repository PANGAEA [45] and described in detail by Canepa et al. [46]. This latter study shows a new procedure adopted to synchronize the velocity time series among the experimental repetitions.

In order to facilitate comparison with full-scale data collected under the THUNDERR Project, the wind speed records were decomposed into three main segments corresponding to three different time phases observed during full-scale downburst outflows and associated to: (1) passage of the primary vortex; (2) steady state condition, i.e. plateau stage, of the velocity signal; (3) dissipation stage of the downburst. (1) mainly presented asymmetric PDF velocity distributions concentrated towards high values, while (2) showed mostly gaussian properties with the exception of the downdraft region. Frequency peaks are identified as a result of the shear layer instability at the jet exit and can be expressed as a function of the Strouhal number \(St\). The high mixing and three-dimensionality of the flow in the downdraft region and at large radial locations due to surface layer separation, provide an increase of turbulence.

The primary vortex advection velocity depends on the jet intensity and the duration of the ramp-up period changes accordingly. Lower inflow wind speeds cause less energetic primary vortices that dissipate earlier. The secondary vortex often forms ahead of the outflow at large radii as consequence of the dynamic separation-reattachment of the surface layer due to the passage of the primary vortex. The relative large number of experiments allows to statistically address the time evolution of mean radial and vertical outflow profiles. At the beginning of the ramp-up phase of the signals, the maximum wind speed occurs at high heights due to the viscous-inviscid interaction. \(z\left( {\overline{V}_{{{\text{max}}}} } \right)\) is then found to increase with radial distance due to the lifting of the interface between primary and secondary vortices. During the primary vortex passage \(z\left( {\overline{V}_{{{\text{max}}}} } \right)/z_{{{\text{max}}}}\) decreases rapidly to values below \(1\) and fluctuates around it during the plateau segment. The rapid variation of \(z\left( {\overline{V}_{{{\text{max}}}} } \right)\) is thus a consequence of the time-dependency of the surface layer thickness which, at first, is driven by the interaction between primary and secondary vortex and, later, is constrained underneath the passing vortex. At large radii, the surface layer detaches from the surface due to the change of surface-pressure gradient upon the passage of the primary vortex. Previous theoretical models of downburst outflows neglect the time-dependency of the surface layer thickness. The implications of the rapid change of \(z\left( {\overline{V}_{{{\text{max}}}} } \right)\) on the structural dynamics deserve future studies.

The values of turbulence intensity match to a very good extent those found for large datasets of real thunderstorm events [10, 19, 81, 83]. The highest values are found shortly prior to the occurrence of the peak wind speed. The peak values of \(\mu \left( t \right) = I_{V} \left( t \right)/\overline{I}_{V}\) are observed at radial and vertical locations affected by the primary vortex passage, \(z\left( {I_{{V_{{{\text{max}}}} }} } \right)/z_{{{\text{max}}}} < 2\) and \(r/r_{{{\text{max}}}} > 1.0\), respectively. These maxima correspond to nose-like shape vertical profiles with tip covering a larger vertical extension by moving radially outwards. From here, the occurrence of \(I_{{V_{{{\text{max}}}} }}\) is observed at higher heights due to the unsteady pressure gradient upon the passage of the primary vortex. A first peak of turbulence intensity is sometimes observed at the beginning of the velocity ramp-up and is likely related to the primary-secondary vortex interaction. The rapid change in turbulence intensity reflects the recent findings of Zhang et al. [10, 81] and Canepa et al. [19] on full-scale events where a similar increase and decrease of \(I_{V}\) was observed immediately before and after the occurrence of \(V_{{{\text{max}}}}\), respectively. This puts into question the usual hypothesis \(I_{V} = \overline{I}_{V}\) adopted in literature, namely turbulence intensity invariant with time, and may have significant implications on the analysis of the dynamic response of structures to thunderstorm winds. Furthermore, the rapid change of vertical profiles of \(I_{V}\) in correspondence of the passage of the primary vortex emphasizes the transient behavior of downburst winds in terms of wind engineering applications. The asymmetric behavior of \(\mu\) is found both in controlled experimental conditions and in nature. This may have benefits on the procedures adopted for the systematic detection and extraction of thunderstorm records from large databases of wind measurements. We suggest, therefore, the implementation of \(\mu\) as well as \(z\left( {I_{{V_{{{\text{max}}}} }} } \right)\) in these techniques.

For the first time, a spatiotemporal \(\left( {r,z,t} \right)\) characterization of spatially-stationary non-steady downburst flow fields has been presented, with focus on the slowly-varying mean wind speed and turbulence intensity. The database of measurements published by Canepa et al. [45] and thoroughly described in [46] is here investigated and will form, in addition to parallel CFD and analytical solutions, the skeleton of a refined experimental model to reassess the design codes in terms of fluid–structure interaction.

Future work in the context of the experimental campaign carried out at the WindEEE Dome will address other important aspects of downburst winds. The present experiments are limited to a 2D axisymmetric flow field. In future studies we aim to expand the investigation to 3D by incorporating pointwise azimuthal detections as well as large scale Particle Image Velocimetry (PIV) measurements. A future goal is to reconstruct the complex mechanisms that take place during the occurrence of real downburst events, where the downburst does not develop as isolated system but rather interacts with the background ABL wind and thunderstorm cloud translation. This complex interaction is expected to have important effects on the near-surface outflow impacting on structures. Furthermore, future work will also quantify the effects produced by terrain roughness on downburst winds to achieve a refined and complete physical characterization of this phenomenon.