Introduction

Groundwater is the main source of freshwater across the world and the majority of people need it. But it is possible that groundwater is contaminated naturally or through human activities. Natural resources of the contaminants can include the sea water intrusion. Man-made resources also include leakages from the sewers and septic tank, improper disposal of waste, percolation of pesticides and chemical fertilizers used in agricultural activities, and many other human activities. In many cases, groundwater pollution can be dangerous and threaten human health. Therefore, continuous monitoring of groundwater quality is an important issue for groundwater, agriculture and the environment engineers.

In the last few decades, Groundwater pollution has got significant attention throughout the world (Fried 1975; Harter 2003; Mukherjee and Singh 2018). The governing equation for groundwater flow and contaminant transport are solved by numerical methods such as finite difference method (FDM), finite elements method (FEM) and meshfree (meshless) method which each one has possible benefits and drawbacks. For example, FDM and FEM involve with a computation in each grid/mesh, and constructing a grid/mesh requires several remeshing attempts (Pathania and Eldho 2020). FDM underperforms than FEM and meshless, besides the computational cost of the meshless method is much higher than the FEM. However, all three approaches can be identified as open source methods, which may be accounted for an advantage in groundwater flow and transport modeling. Therefore, FEM can be mentioned as a reasonable method in terms of appropriate accuracy and computational cost.

FEM has flexibility in dealing with irregular boundaries and complex boundary conditions by choosing elements (sharief and zakwan 2021). The finite element method is more commonly used among researchers (Karatzas 2017), so that, in the last few decades, this method has been employed to simulate groundwater flow and transport modeling. The salt water contamination assessment of the groundwater system (Bredehoeft and Pinder 1973), development of analytical solution for transport in porous media (Marino 1974), studying the dispersive phenomena of contaminants in porous media (Hunt 1978), using FEM for flow modelling in heterogeneous porous media (Smaoui et al. 2012), investigating the numerically simulated groundwater recharge using FDM and FEM (Kalkarni 2015), examining a three-dimensional finite element method program for analyzing two-phase flow in porous media (Yu and Lee 2019) are reported with FEM.

Javadi et al. (2007) presented a numerical model to simulate the flow of water, air and contaminant transport through unsaturated soils. Comparing the numerical model with the experimental results showed that the FEM model predicts the effects of chemical reactions precisely. In the element-free Galerkin method (EFGM), Praveen Kumar and Dodagoudar (2010) used the Lagrange multiplier method transport model for applying the Dirichlet boundaries. The Lagrange multiplier technique with increasing the size of the resultant global matrix in EFGM than FEM cause more computationally expensive. In order to better approximate the singularities, Březina and Exner (2021) studied the extended finite element methods (XFEM) with a proper enrichment to couple the flow between the wells and the bulk rock.

Since many numerical methods have been used in groundwater flow and contaminant transport modeling, Therefore, choosing a proper method that it can determine the amount of pollution with high accuracy and has a low computational cost is very important. The novelty of this study is groundwater flow and contaminant transport modeling using the finite element method to find the critical zone for right now or in the future. In this way, the concentration of contaminants in the location of pumping wells can be predicted. After that, preventive activities can be taken before the groundwater quality deteriorates in different parts of an aquifer. Also, this framework simply prepares continuous monitoring of contaminant concentration, therefore it is possible to adopt a suitable groundwater treatment strategy.

Methodology

Case study

Two real case and hypothetical aquifer have been performed to simply examine various processes that affect or are affected by groundwater flow.

Hypothetical aquifer

In this study, a hypothetical aquifer with length of the 1800 and its width equal to 1000 m is considered (Fig. 1). The hydrogeologic parameters for the aquifer are presented in Table 1. The entire aquifer has storativity of 0.0004. There is a pond with rate of seepage of 0.009 m/d in Zone A. Total dissolved solids (TDS) is assumed as contaminant with seepage at the rate 400 ppm/day. Also, Zones A and C are considered to be recharged at a rate of 0.00024 and 0.00012 m/d, respectively (Fig. 1).

Fig. 1
figure 1

Hypothetical aquifer configuration

Full size image
Table 1 Hydrogeologic data used for flow and transport model
Full size table

The flow model has constant head conditions on its left and right boundaries with 100 and 95 m, respectively. The bottom boundary is the no-flow boundary. For transport model, only the right boundary is kept open and other three boundaries are assumed to be impervious.

Real aquifer

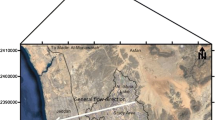
In this study, the Ghaen aquifer with 929.1 km2, in the eastern part of the Iran is also investigated. Ghaen aquifer is located in the west of Namakzar-e-Khaf – Daq-e-Petregan catchment between longitudes \(58^{^\circ } \,\,53^{\prime}\,\,39^{\prime\prime}\)–\(59^{^\circ } \,\,24^{\prime}\,\,40^{\prime\prime}\) east and \(33^{^\circ } \,\,32^{\prime}\,\,07^{\prime\prime}\)–\(33^{^\circ } \,\,51^{\prime}\,\,20^{\prime\prime}\) north.

The aquifer is recharged from the west and south by 8.28 and 3.61 Mm3/year, respectively. The length of recharging boundary on the west and south sides of the aquifer is 3000 and 9000 m, respectively. 0.5 Mm3 of groundwater is discharged annually from the east boundary of the aquifer. The length of the discharging boundary on the east side of the aquifer is equal to 2000 m. There are also six observation wells in this aquifer which are used to compare the results of groundwater flow modeling with observation data. Also, 11 observation wells in the aquifer are used for monitoring the sulfate concentration from 2010 to 2016. Figure 2 shows zones one, two, and three, that there are the boundaries with a constant flow of recharge and discharge and pumping wells in the aquifer. The transmissivity increases from the western and northwestern parts to the southeast of the aquifer. In order to enter hydraulic information for groundwater modeling, we make thiessen polygon for transmissivity using ArcGIS software with considering thickness of aquifer (Fig. 3).

Fig. 2
figure 2

Study area (Ghaen aquifer)

Full size image
Fig. 3
figure 3

Transmissivity thiessen in Ghaen aquifer

Full size image

Governing equations

Groundwater flow modeling

The governing groundwater flow equations for saturated porous media are derived based on mass balance approach and Darcy’s law. The equations describing the steady-state flow in a two-dimensional confined and unconfined aquifer are given as (Wang and Anderson 1995):

$$\frac{\partial }{\partial x}\left( {T_{x} \frac{\partial H}{{\partial x}}} \right) + \frac{\partial }{\partial y}\left( {T_{y} \frac{\partial H}{{\partial y}}} \right) + \frac{\partial }{\partial z}\left( {T_{z} \frac{\partial H}{{\partial z}}} \right) = R$$
(1)
$$\frac{\partial }{\partial x}\left( {K_{x} H\frac{\partial H}{{\partial x}}} \right) + \frac{\partial }{\partial y}\left( {K_{y} H\frac{\partial H}{{\partial y}}} \right) + \frac{\partial }{\partial z}\left( {K_{z} H\frac{\partial H}{{\partial z}}} \right) = R$$
(2)

The governing partial differential equations the transient flow in a two-dimensional confined and unconfined aquifer are given as (Wang and Anderson 1995):

$$\frac{\partial }{\partial x}\left( {T_{x} \frac{\partial h}{{\partial x}}} \right) + \frac{\partial }{\partial y}\left( {T_{y} \frac{\partial h}{{\partial y}}} \right) = S\frac{\partial h}{{\partial t}} + Q_{w} \delta \left( {x - x_{i} } \right)\left( {y - y_{i} } \right) - q$$
(3)
$$\frac{\partial }{\partial x}\left( {K_{x} h\frac{\partial h}{{\partial x}}} \right) + \frac{\partial }{\partial y}\left( {K_{y} h\frac{\partial h}{{\partial y}}} \right) = S_{y} \frac{\partial h}{{\partial t}} + Q_{w} \delta \left( {x - x_{i} } \right)\left( {y - y_{i} } \right) - q$$
(4)

where h(x, y, t) is groundwater head [L], Ki(x, y) is anisotropic hydraulic conductivity [LT−1], Ti(x, y) is anisotropic transmissivity [L2T−1], Sy(x, y) is specific yield, S(x, y) storage coefficient, Qw is source or sink function; (-Qw = source and Qw = sink) [LT−1]; δ is Dirac delta function; xi, yi = pumping or recharge well location; q(x, y, t) is vertical inflow rate [LT−1]; x, y is horizontal space variables [L]; and t is time [T].

The seepage velocity is computed using Darcy's law and can be written as: \(V_{i} = - \frac{{K_{i} }}{\theta }\frac{\partial h}{{\partial x_{i} }}\,\,,\,\,\,i = x,\,y\);

where Vi(x, y) = seepage velocity in i-direction [LT−1]; and θ = porosity [−].

FEM to solve governing equations for groundwater flow

The first step is to define a trial solution for the approximation of flow using FEM and two-dimensional element as following equation

$$\hat{h}(x,y,t) = \sum\limits_{L = 1}^{{{\text{NP}}}} {h_{L} (t)N_{L} (x,y)}$$
(5)

where NL is the basis function at node L, hL is the unknown head, NP is the total number of nodes. Equation (5) can be written as:

$$\iint\limits_{\Omega } {\left[ {\frac{\partial }{\partial x}\left( {T_{x} \frac{\partial h}{{\partial x}}} \right) + \frac{\partial }{\partial y}\left( {T_{y} \frac{\partial h}{{\partial y}}} \right) - Q_{w} + q - S\frac{\partial h}{{\partial t}}} \right]N_{L} (x,y){\text{d}}x{\text{d}}y = 0}$$
(6)

Equation 6, can be written as the summation of individual elements as:

$$\begin{gathered} \sum\limits_{e} {\iint {\left( {T_{x}^{e} \frac{{\partial \hat{h}^{e} }}{\partial x}\left\{ {\frac{{\partial N_{L}^{e} }}{\partial x}} \right\} + T_{y}^{e} \frac{{\partial \hat{h}^{e} }}{\partial y}\left\{ {\frac{{\partial N_{L}^{e} }}{\partial y}} \right\}} \right)}} {\text{d}}x{\text{d}}y + \sum\limits_{e} {\iint {\left( {S\frac{{\partial \hat{h}^{e} }}{\partial t}} \right)\left\{ {N_{L}^{e} } \right\}}} {\text{d}}x{\text{d}}y \hfill \\ = \sum\limits_{e} {\iint {\left( {Q_{w} } \right)\left\{ {N_{L}^{e} } \right\}}} {\text{d}}x{\text{d}}y - \sum\limits_{e} {\iint {\left( q \right)\left\{ {N_{L}^{e} } \right\}}} {\text{d}}x{\text{d}}y \hfill \\ \end{gathered}$$
(7)

For an element, Eq. 7 can be written in matrix form:

$$\left[ {G^{e} } \right]\left\{ {h_{I}^{e} } \right\} + \left[ {P^{e} } \right]\left\{ {\frac{{\partial h_{I}^{e} }}{\partial t}} \right\} = \left\{ {f^{e} } \right\}$$
(8)

where I = i, j, m, n are four nodes of rectangular element and G and P are the conductance matrix, storage matrix, respectively. f matrix is a column matrix which represents the boundary condition. Equation 8 for all the elements lying within the flow region gives the global matrix as:

$$\left[ G \right]\left\{ {h_{I} } \right\} + \left[ P \right]\left\{ {\frac{{\partial h_{I} }}{\partial t}} \right\} = \left\{ f \right\}$$
(9)

Applying the implicit finite difference scheme for the \(\frac{{\partial h_{t} }}{\partial t}\), term in time domain for Eq. 9 gives:

$$\left[ G \right]\left\{ {h_{I} } \right\}_{t + \Delta t} + \left[ P \right]\left\{ {\frac{{h_{t + \Delta t} - h_{t} }}{\Delta t}} \right\} = \{ f\}$$
(10)

Index t and \(t + \Delta t\) represent the groundwater head values at earlier and present time steps. By rearranging the terms of Eq. 10, the general form of the equation can be given as:

$$\left[ {\left[ P \right]} \right] + \omega \Delta t\left[ G \right]\left\{ h \right\}_{t + \Delta t} = \left[ {\left[ P \right] - \left( {1 - \omega } \right)\Delta t\left[ G \right]\left\{ h \right\}_{t} + \Delta t\left( {1 - \omega } \right)\left\{ f \right\}_{t} + \omega \left\{ f \right\}_{t + \Delta t} } \right]$$
(11)

where \(\Delta t\) is the length of time interval, \(\left\{ h \right\}_{t}\) and \(\left\{ h \right\}_{t + \Delta t}\) are groundwater head vectors at the time t and \(t + \Delta t\) respectively, ω is relaxation factor.

Contaminant transport modeling

The governing partial differential equation for contaminant transport in saturated porous media in three dimensions is given as:

$$\begin{aligned} R\frac{\partial C}{{\partial t}} & = \frac{\partial }{\partial x}\left( {D_{{\text{x}}} \frac{\partial C}{{\partial x}}} \right) + \frac{\partial }{\partial y}\left( {D_{{\text{y}}} \frac{\partial C}{{\partial y}}} \right) + \frac{\partial }{\partial z}\left( {D_{{\text{z}}} \frac{\partial C}{{\partial z}}} \right) \\ - v_{x} \frac{\partial C}{{\partial x}} - v_{y} \frac{\partial C}{{\partial y}} - v_{z} \frac{\partial C}{{\partial z}} - R\lambda C \\ \end{aligned}$$
(12)

where C(x,y,t) is solute concentration [ML−3], Dx, Dy represents components of dispersion coefficient tensor [L2T−1], λ is the reaction rate constant [T−1]; \(R = 1 + \frac{{\rho_{b} K_{d} }}{\theta }\) = retardation factor [−]; \(\rho_{b}\) and Kd are media bulk density [ML−3] and sorption coefficient [L3M−1], respectively.

FEM to solve the governing equation for transport

In the finite element method, using an imaginary computational grid, the solution domain is discretized into a number of elements, inter-connected at nodal points. The contaminant concentration (CL) is computed at nodal points. For any other given point, the concentration value is approximately as:

$$C(x,y,z,t) = \sum\limits_{L = 1}^{{{\text{NNODE}}}} {C_{L} (t).N_{L} (x,y,z)}$$
(13)

where NL(x, y, z) is shape function, of node L. Applying the FEM to the Eq. 12 leads to a set of simultaneous algebraic equations as follows:

$$[A]\left\{ C \right\}^{t + \Delta t} = [B]\left\{ C \right\}^{t} + \left\{ f \right\}$$
(14)

where:

$$[A] = [G] + [U] + [F] + \frac{1}{\Delta t}[P]$$
(15)
$$[B] = \frac{1}{\Delta t}[P]$$
(16)

\(\Delta t\) is the length of time interval, {C}t is the vector of known concentration at the beginning of any time step and \(\{ C\}^{t + \Delta t}\) is the vector of sought unknown concentration at the end of time step. [G], [U], [F] and [P] are square matrices. The elements of these matrices are computed as follows:

$$G_{(L,i)}^{e} = \iint\limits_{e} {\left( {D_{{\text{x}}} \frac{{\partial N_{i}^{e} }}{\partial x}\frac{{\partial N_{L}^{e} }}{\partial x} + D_{{\text{y}}} \frac{{\partial N_{i}^{e} }}{\partial y}\frac{{\partial N_{L}^{e} }}{\partial y} + D_{{\text{y}}} \frac{{\partial N_{i}^{e} }}{\partial y}\frac{{\partial N_{L}^{e} }}{\partial y}} \right){\text{d}}x{\text{d}}y{\text{d}}z}$$
(17)
$$P_{(L,i)}^{e} = \iint\limits_{e} {R.N_{i}^{e} N_{L}^{e} {\text{d}}x{\text{d}}y{\text{d}}z}$$
(18)
$$U_{(L,i)}^{e} = - \iint\limits_{e} {\left( {V_{x}^{e} \frac{{\partial N_{i}^{e} }}{\partial x}N_{L}^{e} + V_{y}^{e} \frac{{\partial N_{i}^{e} }}{\partial y}N_{L}^{e} + V_{z}^{e} \frac{{\partial N_{i}^{e} }}{\partial z}N_{L}^{e} } \right){\text{d}}x{\text{d}}y{\text{d}}z}$$
(19)
$$F_{(L,i)}^{e} = - \iint\limits_{e} {R.\lambda .N_{i}^{e} N_{L}^{e} {\text{d}}x{\text{d}}y{\text{d}}z}$$
(20)

{f} is the load vector calculated using the following boundary integral:

$$\left\{ f \right\} = \int\limits_{\Gamma } {\left( {D_{{\text{x}}} \frac{{\partial \hat{c}}}{\partial x}n_{x} + D_{{\text{y}}} \frac{{\partial \hat{c}}}{\partial y}n_{y} + D_{z} \frac{{\partial \hat{c}}}{\partial z}n_{z} } \right)} N_{L} {\text{d}}\Gamma$$
(21)

where \(\hat{c}\) denoted the given concentration values at boundary nodes, ni are directional cosines and \(\Gamma\) is the domain boundary.

Performance criteria

In this research, mean error and root mean squares error are used as performance criteria. These performance criteria are computed using following equations

$${\text{ME}} = \frac{{\sum\limits_{i = 1}^{n} {(O - S)} }}{n}$$
(22)
$${\text{RMSE}} = \sqrt {\frac{{\sum\limits_{i = 1}^{n} {(O - S)^{2} } }}{n}}$$
(23)

where O = observed head (ho) or observed contaminant concentration (Co) and S = simulated head (hs) or simulated contaminant concentration (CS), respectively. n = number of observation wells.

Validation of FEM model

Before applying FEM model for the hypothetical and the real aquifer, the FEM model must be validated. For this purpose, our FEM model is compared with the analytical solution Kulkarni (2015) research. In the Kulkarni’s research, he assumed a hypothetical aquifer 3200 m × 2800 m. Boundary conditions at the right and left sides of the aquifer boundary is considered no flow boundaries. Boundary conditions at the bottom and top sides of the aquifer boundary is considered to have constant value of 100 m. The location of two pumping wells are (1400 m, 1400 m) and (1800 m, 1400 m) from the origin, as shown in Fig. 4. The observation well is located at a (1000 m, 1000 m) from the origin and the water table drawdown caused by pumping are observed at this well.

Fig. 4
figure 4

Schematic of aquifer modeled for the validation of FEM model

Full size image

Results and discussion

Validation

Pumping by two wells for 210 days cause the groundwater head drawdown, which was calculated using the FEM model. Analytical solution and FEM model are compared as shown in Fig. 5. As can be seen from Fig. 5, the drawdown value is computed as 0.4283 m by finite element method which are comparable with the drawdown of 0.4359 m by analytical solution. The most difference between the modeling results and the analytical solution was about 0.0440 m in the 81 days of the pumping period.

Fig. 5
figure 5

Validation of FEM model

Full size image

The hypothetical aquifer modeling

In case of FEM model, we used Galerkin’s approach with Crank–Nicolson time scheme with regular distribution of nodes and 90 square element as shown in Fig. 6. The time step of 5 days is chosen for both groundwater flow and contaminant concentration transport models.

Fig. 6
figure 6

FEM mesh for the study area

Full size image

Seepage from the contaminant source is assumed to be continuous. Also, Zone A and Zone C are assumed to be recharged in nodes 12, 18 and 24 at the rate of 0.00024 m/day and nodes 42, 48 and 54 at the rate of 0.00012 m/day. Besides, nodes 15, 16, 21, 22, 27 and 28 are assumed to be monitoring nodes. These nodes are shown as squares in Fig. 6.

To solve the hypothetical aquifer modeling problem, first the aquifer geometry was created and then the model was run for five years. The groundwater head and TDS concentration at all nodes are shown in Figs. 7 and 8, respectively. TDS concentration values at six observation wells are also as given in Table 2.

Fig. 7
figure 7

Groundwater head distribution after 5 years

Full size image
Fig. 8
figure 8

TDS concentration distribution after 5 years

Full size image
Table 2 Contaminant concentration values in monitoring nodes
Full size table

The real aquifer modeling

After modeling the hypothetical aquifer, the real aquifer is modeled. We used Galerkin’s approach with Crank–Nicolson time scheme with regular distribution of nodes at a distance of 200 m and 3414 square element for FEM model. Initially, the sulfate concentration transport was modeled for 7 years due to sulfate concentration in 2009. The time step of 5 days. After transport modeling, the sulfate concentration compared to the observed values in the years 1389–1395. Also, the amount of recharge and discharging in zones one, two and three are equal to 0.047, 0.065 and 0.0104 m/day, respectively. These values have been calculated due to the transmissivity of 600 m/day in zones one and two and 100 m/day in zone three. The boundary line and the nodes with constant flow (gray rhombuses) as Neumann boundary are shown in Fig. 9. There are 167 pumping wells in the Ghaen aquifer, 33 of these wells are abandoned. Also due to the aquifer grid and distance between nodes (200 m), 17 number of pumping wells that were close to each other were placed in nearest nodes and their pumping rate were added together. There are also 6 observation wells to compare the groundwater head and 11 observation wells to compare the sulfate concentration, which are indicated by the symbols ( ×) and the blue squares in Fig. 9, respectively.

Fig. 9
figure 9

Neumann boundary, pumping wells, piezometers (observation wells) and monitoring wells

Full size image

In order to evaluate the effectiveness of the finite element model to solve governing equations for groundwater flow, the groundwater head from the model was compared to the observed values. The results of comparison of groundwater head from the model and observation values in 6 piezometers (observation wells) are given in Table 3. It should be noted that due to the aquifer grid and distance between nodes (200 m), the location of 6 observation wells were modified and placed on the nearest nodes, and then the groundwater head from the model was compared with the groundwater head in new location of observation wells. Also, the results of transport model and the values observed in 11 monitoring wells (observation wells) during 2010–2016 are given in Table 4.

Table 3 Groundwater head from the model and observed values (2016)
Full size table
Table 4 Sulfate concentration from the model and observed values (2010–2016)
Full size table

In this study, ME and RMSE performance criteria were also used and the results are given in Table 5. The results show that the RMSE is equal to 1.06 for 2016. In groundwater flow modeling, the results are acceptable when the RMSE was under + 1.9 (Anderson et al. 2015). Also, the RMSE in contaminant transport modeling for 2010–2016 are given in Table 6. As can be seen in this table, RMSE for 2010–2016 have different values. The lowest value is equal to 1.44 for 2011 and the maximum value is equal to 3.51 for 2012.

Table 5 The results of performance criteria for groundwater head
Full size table
Table 6 The results of performance criteria for sulfate concentration
Full size table

The groundwater head contour from the model and observed values interpolated by using ArcGIS software for 2016 are shown in Figs. 10 and 11, respectively. As can be seen in Figs. 10 and 11, the groundwater head decreases from west to east of the aquifer. So that in the northeast of the aquifer, the groundwater head reaches less than 1365 m. On the other hand, the density of pumping wells in this region is very high. Therefore, it is predicted that in the coming years we will see a sharp groundwater drawdown in the northeastern part of the aquifer. Also, the Sulfate concentration distribution from the model and observed values interpolated by using ArcGIS software for 2011 and 2012, which had the lowest values of RMSE and ME, are shown in Figs. 12 and 13, respectively. As can be seen in Figs. 12 and 13, some parts of the Ghaen aquifer have severe Sulfate pollution. The source of these contaminants can be human-made or natural. Due to the fact that the main wells drilled in the aquifer are for agricultural and industrial uses. The source of pollution can be considered the widely used of fertilizers, pesticides and wastewater in some industries.

Fig. 10
figure 10

Groundwater head contour lines from the model (2016)

Full size image
Fig. 11
figure 11

Groundwater head contour lines using spline (2016)

Full size image
Fig. 12
figure 12

Sulfate contamination contour lines (2011) a from the model b interpolated using kriging

Full size image
Fig. 13
figure 13

Sulfate contamination contour lines (2012) a from the model b interpolated using kriging

Full size image

Comparison of the results of FEM and interpolated groundwater head Sulfate concentration, indicates that the model has good performance. The main differences seen in the figures can be caused by modeling error, which includes grid and distance between nodes (200 m) and using different zoning methods such as kriging, spline and IDW. Because each of these zoning methods gives different results.

As mentioned, some of pumping wells for agricultural use, have been affected by Sulfate pollution. Sulfate pollution is higher in the northeast of the aquifer than in other region. Also, from 2011 to 2012, Sulfate pollution increases in this region. On the other hand, the density of pumping wells in this region is very high. The water quality standard for agricultural use in Iran and also recommended by the World Food and Agriculture Organization (FAO) is 10 me/lit. Therefore, it is recommended to use the pump-and-treatment method in the northeastern part of the aquifer and to use the treated water again.

Conclusion

In this study, the finite element method is used to solve the governing equation for groundwater flow and transport. The finite element code was validated before applying for modeling of hypothetical and real aquifers. Validation results indicated that finite element model had a good performance. The finite element model for the hypothetical aquifer was investigated in the transient flow for 5 years. The results indicated that the Sulfate concentration distribution is not completely symmetrical and small differences can be seen in the monitoring wells. The FEM model was also used for the real aquifer. For the real aquifer, the aquifer gridded by 200 m distance between nodes and square elements. For groundwater flow model, first the observation and pumping wells were moved to the nearest node and the pumping discharge of the pumping wells was added together. After that, the FEM model was used for groundwater flow and transfer for 5 years. The results of FEM model for groundwater flow indicated that the model with ME = 0.795 (m) and RMSE = 1.066 (m) had a good performance for groundwater flow in real aquifer. Also, the results of FEM model for transport indicated that the model with ME = 0.06 to ME = −3.31 (me/lit) and RMSE = 1.44–3.51 (me/lit) had a good performance for Sulfate transport in real aquifer. The FEM model also showed that in the northeast of the aquifer the groundwater head is low and the amount of Sulfate is high. This is also confirmed by real data.