Introduction

Cold Gas Dynamic Spray (CGDS), also known as cold spray, in which particles with high kinetic energy impact and adhere to the substrate, was first introduced in the mid-1980s by scientists from the Russian Academy of Sciences (Ref 1). In this process, fine powders (normally 1-80 microns) are accelerated by high pressure gas, typically nitrogen or helium, to a high velocity (in the range of 400-1200 m/s) and hit the substrate at a relatively low temperature (between 373 and 873 K). Its low temperature operation provides several potential benefits such as keeping original particle microstructure, providing good deposition efficiency and high bond strength, as well as avoiding particle/substrate oxidations (Ref 2,3,4). It has also been shown that with suitable conditions, CGDS can achieve good deposition rate and dense coatings (Ref 5). With the benefits it promises, the CGDS process has attracted good attention for applications in electronics, composites, nanostructured coatings, and recently in antimicrobial coatings for Sars-CoV-2 (COVID-19) inactivation (Ref 6,7,8). With the growth of additive manufacturing (AM), such attention has further intensified because of the CGDS’ AM abilities. It also brings possible solutions to challenges in typical AM approaches. For instance, the residual stress in additively manufactured layers using common AM techniques is generally high due to cooling from elevated temperature, but is much lower in layers produced by cold spray (Ref 9). It is widely accepted that cold spray is a solid-state coating process, during) which the bonding is formed due to plastic deformation rather than heat. To date, numerous studies have been carried out to investigate the cold spray process and several bonding mechanisms were proposed, including adiabatic shear instability at the interface during deposition (Ref 2, 10, 11), development of interfacial instability which induces physical anchoring effect Ref 12, 13), and fracture and removal of the surface oxide layer due to high-velocity impact and subsequent metal jet formation (Ref 14, 15). Nonetheless, there remains contention on the exact bonding mechanism during cold spray (Ref 3, 16,17,18,19,20).

It is difficult to perform accurate in situ observations of the whole deposition process of particles, due to the dynamic nature of the deposition process within a noticeably short duration. Only the deformed particles post bonding can be observed by microscopy. As a result, numerical simulations have been employed as alternatives to investigate the bonding mechanism during cold spray (Ref 2, 10, 11, 21,22,23,24,25,26,27). Modeling cold spray deposition is a challenging problem as in a full scale it would involve modeling of multiple particle contacts, bonding and de-bonding with plastic deformation of individual particles. The traditional finite element method (FEM) has been successfully applied in simulating the high-velocity impact problems. However, due to the high computational cost and complicated modeling to obtain accurate results, much research has focused on a single spherical particle impact model (Ref 2, 3, 20, 23, 28, 29). Few FEM studies focused on the impact of multiple particles (Ref 30,31,32,33), but the number of particles was limited so that only the first a few layers of deposited particles could be simulated.

Despite the success of FEM in modeling cold spray, the large deformations induced by high-velocity impacts, on the other hand, pose challenges to the traditional mesh-based Lagrangian approach. The elements can get severely distorted leading to degradation in numerical accuracy (Ref 34,35,36). Furthermore, in many classical FEM studies the proper modeling of bonding or de-bonding of cold spray particles was not considered. The typical treatment is that the particle will either bounce off or be enforced bonded after impacting the substrate. This contradicts the reality where only particles fulfilling certain velocity/deformation conditions would bounce off or be bonded to the surface. Recently, Rahmati and Jodoin (Ref 35) proposed a numerical method based on Arbitrary Lagrangian–Eulerian (ALE) to model the metallurgical bonds forming in cold spray. Later, Rahmati et al. (Ref 37) further improved this model by explicitly taking into account of the effects of the oxide film removal process. These studies provide great advances toward numerical modeling and prediction of bonding during particle deposition. However, the implementation is quite complex, and it is not clear whether this method can be easily applicable to model particle-particle collision and dissimilar material bonding behaviors.

Besides FEM, the discrete element method (DEM) is another popular method often applied to investigate microparticles impact and/or deposition behaviors (Ref 38,39,40,41,42,43,44,45,46). The adhesive contact interactions among particles and those between particles and surface can be specified in the DEM framework (Ref 39). The DEM-based approach assumed that particles and substrates were rigid bodies (Ref 47). Under the high-velocity impact, however, the deformation of the particles and substrate becomes a significant factor in the deposition process, thus making it necessary to describe them as deformable bodies using appropriate constitutive laws (Ref 48). Consequently, it is challenging for DEM-based modeling to correctly predict global system behaviors or to properly capture relevant physics or mechanics of deposition during cold spray.

Motivated by the challenges described above, the present study aims to conduct preliminary numerical development of a computational model that can simultaneously handle the deformation, bonding and rebounding of impacting particles during cold spray deposition in one unified theoretical framework. For this purpose, on the base of the peridynamics (PD), interfacial contact models were implemented to simulate the bonding between the impacting particle and the substrate. Due to the meshless discretization and nonlocal nature of PD, it is straightforward to add bond forces at the particle/substrate interface. These forces are highly tunable, making our method more flexible for modeling general cold spray depositions, regardless of the material types and bonding mechanisms. This more realistic model can also reproduce the adhesion strength of particle to the substrate that is consistent with experimental observations and can be naturally extended to include interaction and bonding between the same or dissimilar particles, thus making it possible to simulate multi-particle impacts and their effects on the first bonded particle adhesion. It is noted that the native oxide films covering the particle and substrate are not considered in our model, the focus of this study is to accurately describe particle-substrate (and potentially particle-particle) bonding behavior thus to pave the way for correctly simulating the coating build-up process. The modeling of oxide layer based on PD is under investigation and will be presented in another publication.

The peridynamic theory reformulates continuum mechanics in which material points interact with each other over a finite distance, and the physical interaction is called a peridynamic bond (Ref 49). This gives peridynamics the capability of modeling discontinuities using the concept of bond failure (Ref 50). Ever since its first introduction, peridynamics has been successfully applied in modeling various fracture problems (Ref 49, 51,52,53) as well as impact simulations (Ref 52,53,54).

In this paper, instead of modeling of discontinuities, we propose an original approach in the framework of peridynamics to simulate physical processes of bonding formation in cold spray. This expands the scope of peridynamics to incorporate a variety of physics in which deformation and adhesion play an important role in system behavior. It is worth noting that the previous study by Jin et al. (Ref 55) has proposed a model that utilizes peridynamics for impact bonding. However, the bonding in that work was realized through enforcing material points across the interface to have the same velocities. Different from the work of Jin et al., here in our study bonding formation is treated differently in that it explicitly accounts for the repulsion and adhesion forces between material points, and the bond can be broken and re-form under certain criteria. Motivated from the interatomic potential in molecular dynamics (MD), we use a Lennard-Jones type potential as the representative to handle the bonding process due to impact. A force-stretch approach to simulate interface interaction that is directly derived from bulk material fracture response is also proposed. The contact model can be calibrated to achieve bonding, de-bonding, and the desired adhesion strength resulted from particles impacting. In the numerical implementation, the interaction of contacting bodies is realized by integrating contact forces on the pairs of nodes of meshless discretization of these two bodies. This kind of interaction is activated only when the nodes of opposing bodies are within a certain distance. It is noted that recently another particle-based method, i.e., the smoothed-particle hydrodynamics (SPH) has also been proposed as a means to model CS deposition (Ref 15), in which metal-to-metal interface treatment was considered in a 2D SPH model. Our approach, however, differs from the SPH method in two main aspects. Theoretically, the PD approach solves integral equations and treats discontinuity (material interface) in a consistent way to the continuum (bulk material), while classical theory like SPH is based on partial differential equations (PDEs) (Ref 49, 56). Second, the bond forces between material points across the interface in the PD model is explicitly specified to give a desired adhesive effect, distinct from the artificial energy dissipation and velocity averaging technique used in SPH (Ref 55, 57).

This paper is organized as follows. First, the peridynamic modeling approach and state-based peridynamic theory were introduced. Then the numerical discretization and implementation were described. Next, the contact models we developed to simulate impact bonding of particle and substrate were presented, followed by a section detailing the simulation details as well as the Johnson-Cook (JC) plasticity model used to describe the deformation of the particles and substrate are introduced. In the end, our results are summarized and the implication to modeling of cold spray was discussed.

Model Development

In this section, the theoretical basis of peridynamics is briefly introduced. In the peridynamics framework, the material of interest is discretized as the sets of multiple points called material points, and these points in the discrete system interact with each other within a certain distance range δ. Two types of interactions are considered: (1) intra-solid interaction acting between material points within the solid that is subjected to the external boundary conditions, and (2) the inter-solid interaction governing the particle-particle and particle-substrate contacts that explicitly account for the compression and adhesion forces between distinct bodies. State-based peridynamics is used to model intra-solid interaction, that is, single solid deformation. For contacts, an MD interatomic-like potential and a force-stretch relation are proposed. The advantage of this contact model is its ability for describing irregular-shaped interfaces because the contact is applied between the material points rather than between the whole solids (Ref 48), and the flexibility of complex contact via a potential function.

Here we review key features and equations of the peridynamic theory for the completeness of the paper, and readers can refer to Ref. 58, 59 for detailed formulations. In the peridynamic theory, a material point interacts with other neighboring points within a region called the horizon. The peridynamic equation of motion is (Ref 60):

$$ \rho {{\ddot{\mathbf u}}}\left( {{\mathbf{x}},~t} \right) = \mathop \smallint \limits_{{H_{{\left( x \right)}} }} {\mathbf{~f}}\left( {{\mathbf{u}}\left( \user2{x} \right),~{\mathbf{u}}({\mathbf{x}}^{\prime } ),~t~} \right)~dV_{{x'}} + {\mathbf{b}}\left( {x,t} \right) $$
(1)

where x is the position vector for a material point \({\text{X}}\) in the reference configuration. H(x) is the horizon of the material point \({\text{X}}\), which is typically a sphere with radius δ. Material point \(\user2{ }{\text{X}}^{{\prime }}\) with a position vector \( x^{\prime }\) is inside the horizon of the material point \({\text{X}}\). The points beyond the horizon will not interact with \({\text{X}}\). \(V_{{{\mathbf{x}}^{{\prime }} }}\) is the volume element associated with \({\text{X}}^{{\prime }}\). The vector \({\mathbf{u}}\) is the displacement vector field, b(x, t) is a prescribed body force density field at \({\text{X}}\) and at time t\( \rho\) is the mass density in the reference configuration. \({\mathbf{f}}\) is the force density per unit reference volume that material point \({\text{X}}^{{\prime }}\) exerts on material point \({\text{X}}\), and has the unit of force per unit volume squared. The first term on the right-hand side of Eq 1 denotes the total force exerted on \({\text{X}}\) by all the material point \({\text{X}}^{{\prime }}\) in its horizon.

In contrast to classical solid mechanics, the peridynamic theory of solid mechanics is based on integral equations, so the divergence of the stress term in the classical equations is replaced by an integral over the horizon of the current point of forces acting in the peridynamic bonds (Ref 51). This horizon size was set to be three times the average node spacing in the current study. As a multiscale material model, peridynamics has been demonstrated to be an upscaling of molecular dynamics and it has been implemented within a massively parallel open-source code, Peridigm (Ref 61).

Interfacial forces can be incorporated easily as part of the constitutive model (Ref62). This is because the model treats all forces between material points through bonds that extend over a finite distance, in contrast with the classical theory, which is based on the idea that all forces internal to a body result from direct contact. Analogous to MD, PD bond could be used to produce forces between material points in particle, substrate and at interface during cold spray deposition.

State-Based Peridynamic Theory

In the original bond-based peridynamic theory, the deformation of each bond is independent of all other bonds, which leads to an effective Poisson ratio of \(0.25\) in 3D models. It also has difficulties in modeling ductile response such as metal plasticity. As an extension of the bond-based formulation, in the state-based theory, the behavior of a material point is dependent on the collective deformation of all bonds within its horizon.

Silling proposed the non-ordinary state-based peridynamic theory (SB-PD), in which conventional models that are able to describe various nonlinear mechanical behavior of materials can be incorporated (Ref 52, 53, 59). The equation of motion in the non-ordinary state-based peridynamics can be formulated as (Ref 59):

$$ \rho \left( {\mathbf{x}} \right){{\ddot{\mathbf u}}}\left( {\mathbf{x},t} \right) = \mathop \smallint \limits_{{{\varvec{H}}\left( x \right)}} \left\{ {{\mathbf{\underline {T} }}\left[ {{\mathbf{x}}, t} \right]\left\langle {{\mathbf{x}}^{\prime } - {\mathbf{x}}} \right\rangle - {\mathbf{\underline {T} }}\left[ {{\mathbf{x}}^{\prime } , t} \right]{\mathbf{x}} - {\mathbf{x}}^{\prime } } \right\}dV_{{\mathbf{x^{\prime}}}} + {\mathbf{b}}\left( {{\mathbf{x}}, t} \right) $$
(2)

where b is an external body force density vector, \(x^{\prime } - x\) is the relative position vector between two material points and is named a peridynamic bond ξ. \({\mathbf{\underline {T} }}\left[ {{\mathbf{x}}, t} \right]\left\langle {{\mathbf{x}}^{{{\prime }}} - {\mathbf{x}}} \right\rangle \) and \({\mathbf{\underline {T} }}\left[ {{\mathbf{x}}, t} \right]\left\langle {{\mathbf{x}} - {\mathbf{x}}^{\prime } } \right\rangle\) are the force-vector states act on the peridynamic bonds, which can be nonlinear and discontinuous. \({\mathbf{\underline {T} }} \) is a function of the deformation vector state \({\mathbf{Y}}\)

$$ {\mathbf{\underline {T} }} = {\mathbf{\underline {T} }}\left( {\underline{{\mathbf{Y}}} } \right) $$
(3)

and the deformation vector state field \(Y\) is defined as

$$ \user2{\underline {Y} } = y^{\prime } - y, $$
(4)

where \({\mathbf{y}}\) and \({\mathbf{y}}^{{\prime }}\) are the positions of material points \({\text{X}}\) and \({\text{X}}^{{\prime }}\) at time t (the current configuration).

Non-ordinary state-based peridynamic material models use the nonlocal deformation gradient tensor to connect the traditional continua mechanics to the nonlocal peridynamic framework (Ref 59). A nonlocal version of the deformation gradient tensor is defined as (Ref 59)

$$ {\mathbf{F}} = [\mathop \smallint \limits_{{{\varvec{H}}\left( {\mathbf{x}} \right)}} \underline {\omega } \left\langle \xi \right\rangle {\text{Y}} \otimes \xi dV_{{{\mathbf{x^{\prime}}}}} ]{\mathbf{K}}^{ - 1} $$
(5)

where K is the nonlocal second-order shape tensor given by

$$ K = \mathop \smallint \limits_{H\left( x \right)} \underline {\omega } \left\langle \xi \right\rangle \xi \otimes \xi dV_{{x^{\prime}}} $$
(6)

ω \({\varvec{\xi}}\) is a scalar state called the influence function used to describe the relative degree of interactions between the material points. By using the first Piola-Kirchhoff stress tensor \({\mathbf{P}} = {\mathbf{P}}\left( {\mathbf{F}} \right)\) as an intermediate step, a classical constitutive model can be incorporated, and the following force vector state is obtained

$$ {\mathbf{\underline {T} }} = \omega .\xi {\mathbf{PK}}^{ - 1} \xi $$
(7)

Numerical Implementation

We use the meshfree approach proposed by Ref. Ref49, which has been widely utilized by many researchers (Ref 49,50,51,52,53,54,55, 62,63,64), to discretize peridynamics model discussed above. It has proven to be reliable and efficient and particularly suitable for large deformation simulations because there are no geometrical connections between the nodes. In the meshfree discretization, the physical system is discretized into a set of nodes (with initial coordinates), and a nodal volume \({\Delta }V\) associated with it. Here, the nodes are used to track and store the positions of the particles associated with a discretization, and also as material points for evaluating constitutive models (Ref 65). As a result, the integral in Eq 2 is replaced by a finite summation over the horizon for material point x, leading to the following semidiscrete equation of motion over time,

$$ \rho \left( {\mathbf{x}} \right){{\ddot{\mathbf u}}}\left( {{\text{x}},t} \right) = \mathop \sum \limits_{{{\mathbf{H}}\left( {\text{x}} \right)}} \left\{ {{\mathbf{\underline {T} }}\left[ {{\mathbf{x}}, t} \right]x^{\prime } - x - {\mathbf{\underline {T} }}\left[ {{\mathbf{x}}^{\prime } , t} \right]\left\langle {{\text{x - x}}^{\prime } } \right\rangle } \right\}\Delta V_{{{\text{x}}\prime }} + {\mathbf{b}}\left( {{\text{x}}, t} \right) $$
(8)

Let \({\mathbf{x}} \in \Omega_{1}\), \({\mathbf{y}} \in \Omega_{2} \) be the discretized nodes of two distinct bodies \(\Omega_{1}\), \(\Omega_{2}\). Define the current positions \({\varvec{q}}\left( {{\mathbf{x}}, t} \right) = {\mathbf{x}} + {\mathbf{u}}\left( {{\mathbf{x}}, t} \right) \) and \({\mathbf{q}}^{\prime } \left( {{\varvec{y}}, t} \right) = {\mathbf{y + u}}\left( {{\varvec{y}}, t} \right)\).\({\mathbf{y}} \in \Omega_{2}\) generates an external contact force on \({\mathbf{x}} \in \Omega_{1}\) which is given by

$$ {\mathbf{F}}_{c} = \left\{ \begin{gathered} f_{c} \Delta V_{x} \Delta V_{y} \user2{\hat{r}}\,\,\,\,\,\,\,if~\left| {\user2{q}\left( x \right) - \user2{q}'\left( y \right)} \right| \le R_{c} \hfill \\ 0\qquad\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,otherwise \hfill \\ \end{gathered} \right. $$
(9)

where \(f_{c}\) is the magnitude of the contact force density vector has the unit of force per volume squared, \({\Delta }V_{{\mathbf{x}}}\) and \({\Delta }V_{y}\) are the nodal volume associated with x and y, respectively (Ref48). The unit direction vector \({\hat{\mathbf{r}}}\) between points x and \({\mathbf{y}}\) is defined by

$$ {\hat{\mathbf{r}}} = \frac{{\mathbf{r}}}{r} $$
(10)

in which

$$ {\mathbf{r}} = {\mathbf{q}}\left( x \right) - {\mathbf{q}}^{\prime } \left( {\mathbf{y}} \right), r = \left| {{\mathbf{q}}\left({x} \right) - {\mathbf{q}}^{{{\prime }}} \left( {\mathbf{y}} \right)} \right| $$
(11)

Let

$$ {\text{B}}\left( {\text{x}} \right) = \left\{ {y:\left| {{\mathbf{q}}^{{{\prime }}} \left( y \right) - {\mathbf{q}}\left( x \right)} \right| \le R_{c} } \right\} $$
(12)

denote the family of material points within a critical contact radius of material point x in the current configuration. The total contact force on a material point \(x \in \Omega_{1}\) by all material points \(y \in \Omega_{2}\) that are in the action range of this force is now given by an integral of \(f_{c}\) over a different horizon than that used in the intra-solid interaction

$$ \mathop \smallint \limits_{B\left( x \right)} f_{c} \hat{\user2{r}}dV_{y} $$
(13)

Contact interactions are taken into consideration by adding an additional nodal force density into Eq 8. Thus, the motion of material points near a bonding interface is collectively determined by internal force density (determined by the constitutive models) and contact force density (determined by the contact models). Neglecting all other external body force densities, the equation of motion becomes:

$$ \rho \left( {\text{x}} \right){{\ddot{\mathbf u}}}\left( {{\text{x}},t} \right) = \mathop \sum \limits_{{x^{\prime } \in H\left( x \right)}} \left\{ {{\mathbf{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{T} }}\left[ {{\text{x}},~t} \right]\left( {{\text{x}}^{\prime } - {\text{x}}} \right) - {\mathbf{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{T} }}\left[ {{\mathbf{x}}^{\prime } ,~t} \right]\left\langle {{\text{x}} - {\text{x}}^{\prime } } \right\rangle } \right\}\Delta V_{{x^{\prime}}} + ~\mathop \sum \limits_{{y \in B\left( x \right)}} f_{c} {\mathbf{\hat{r}}}\Delta V_{y} $$
(14)

Contact Models

The main difficulties in developing numerical simulation of the coating build-up process result from the multiscale nature of the process. Build-up involves phenomena which occur at the particle scale and the coating scale. Adhesion between particles and that between particle and substrate play an important role in structure and strength of the deposited coating. The distinguishing feature of peridynamics that makes it potentially suitable to model interfacial bonding in cold spray is that it uses bond forces which act between material points separated from each other by finite distances.

In this study, we use a model that employs discretized material points to represent the average response of a large group of atoms. It is assumed that when intimate metal-to-metal contact is within the range of interatomic attractive forces, metallurgical bonding will be formed. However, the atomistic contact is not directly applicable to model contact between two macroscale bodies. Hence, we propose a contact model that employs the concept of interatomic potential but can be applied to increasing scales in which interaction between separate continuum solids is taken into account by considering forces between material points within distinct bodies. To determine the contact between two bodies, a proximity search in the current configuration is performed by the detection algorithm to check the distance between the opposing nodes. When the distance between two material points is below a threshold contact radius \(R_{c}\) defined in Eq 12, which is an adjustable numerical parameter in the current study, the bonds are considered to be formed.

As the bodies (particle and substrate) contact and deform, the configuration of the contacting surfaces changes, and the bonds generating the surface interactions change according to the deformation. New bonds may be formed, and old bonds could be broken due to the evolution of the system. Here, we propose two contact models that can add interface interactions to the modeling of particle deposition in cold spray. Contact model 1 uses a long-range Lenard-Johns type potential, and contact model 2 employs a force-stretch relation of the interface directly derived from fracture properties of the bulk material. Below the two models were described in detail.

Contact Model 1

As a particle-based method, discretizing peridynamics results in force interactions that are similar to interatomic forces used in MD (Ref 66). On the other hand, interaction potentials have been used in cohesive zone models to simulate bonding between macroscopic bodies (Ref 67, 68). In this proposed model, we assume that the interaction potential \(\phi\) between two PD points located at \({\mathbf{q}}\) and \({\mathbf{q}}^{\prime}\) (\({\mathbf{q}}\) and \({\mathbf{q}}^{\prime}\) belongs to different bodies) can be described as a function of their distance \(r\). The function was taken to assume a Lennard-Jones (Ref 69, 70) like form

$$ \phi = \alpha \left[ {\left( {\frac{{r_{0} }}{r}} \right)^{m} - 2\beta \left( {\frac{{r_{0} }}{r}} \right)^{n} } \right]^{{}} $$
(15)

In the equation, the first and second terms on the right-hand side represent the repulsion and attraction terms, respectively. The two parameters \(\alpha\) and β denote tunable parameters that characterize the strength of repulsion and attraction forces, respectively, the parameter \(r_{0}\) denotes a length scale that determines the equilibrium distance and is set a little larger than the node spacing in the current study, and the parameters m and n are set as 12 and 6, respectively, in accordance with the classical Lennard-Jones for simplicity. It is worth noting that here we choose Lennard-Jones as a representative for its simple form, easy implementation, yet ability to consider both tensile and compressive forces. The contact force \({\mathbf{F}}_{c}\) a material point \({\mathbf{q}}^{\prime}\) on \({\mathbf{q}}\) is then given by the gradient

$$ {\mathbf{F}}_{c} = - \frac{d\phi }{{dr}}\hat{\user2{r}} = \left[ {\frac{12\alpha }{{r_{0} }}\left( {\frac{{r_{0} }}{r}} \right)^{13} - \frac{12\alpha \beta }{{r_{0} }}\left( {\frac{{r_{0} }}{r}} \right)^{7} } \right]\hat{\user2{r}} = \frac{12\alpha }{{r_{0} }}\left[ {\left( {\frac{{r_{0} }}{r}} \right)^{13} - \beta \left( {\frac{{r_{0} }}{r}} \right)^{7} } \right]\hat{\user2{r}} $$
(16)

where \({\hat{\mathbf{r}}}\) is defined by Eq 10. The potential \(\phi\) and force would decay close to zero for large r values, and thus may be neglected beyond a cut-off distance, similar to the horizon in peridynamic theory. In the proposed model, the cut-off radius \(R_{c}\) is set to be \(2.75r_{0}\). It should be noted that other function forms with different parameterization can been readily adopted if necessary.

The equilibrium distance where the contact force is zero

$$ r_{e} = r_{0} \beta^{{ - \frac{1}{6}}} $$
(17)

To give a first approximation of \(\alpha\), a liner spring system is used to approximate the Lennard-Jones potential for small deformations (Ref 71). Assuming that the force magnitude between points \({\mathbf{x}}\) and \({\mathbf{y}}\) with distance \(r\) can be modeled as a linear spring with the spring constant \(c\) (Ref 48)

$$ F_{s} = - c\left( {r - r_{e} } \right){\Delta }V_{{\mathbf{x}}} {\Delta }V_{{\mathbf{y}}} $$
(18)

Taking the derivative of \(F_{c}\) at \(r = r_{e}\)

$$ \left. {\frac{{dF_{c} }}{dr}} \right|_{{r_{e} }} = \left. {\frac{12\alpha }{{r_{0}^{2} }}\left[ { - 13\left( {\frac{{r_{0} }}{r}} \right)^{14} + 7\beta \left( {\frac{{r_{0} }}{r}} \right)^{8} } \right]} \right|_{{r_{e} }} = - \frac{72\alpha }{{r_{0}^{2} }}\beta^{\frac{7}{3}} $$
(19)

This provides the slope of \(F_{c}\) at \(r_{e}\) which is approximately equaled to \(- c{\Delta }V_{{\mathbf{x}}} {\Delta }V_{{\mathbf{y}}}\), thus

$$ c \cong \frac{{72\alpha \beta^{\frac{7}{3}} }}{{r_{0}^{2} {\Delta }V_{{\mathbf{x}}} {\Delta }V_{{\mathbf{y}}} }} $$
(20)

The spring constant \(c\) can be related to the bulk modulus \(k\) as follows (Ref 48, 49)

$$ c = \frac{18k}{{\pi \delta^{5} }} $$
(21)

therefore

$$ \alpha \cong \frac{{18kr_{0}^{2} {\Delta }V_{{\mathbf{x}}} {\Delta }V_{{\mathbf{y}}} }}{{72\beta^{\frac{7}{3}} \pi \delta^{5} }} $$
(22)

Considering that the adhesion energy is the work done to move two surfaces from equilibrium separation to infinity, the parameters involved in this potential model determine the strength of the force interactions that lead to the adhesion energy. In this model, \(\beta\) can be tuned to provide desired adhesion which affects the particle deposition. A parametric study on \(\beta\) is presented in “Results” section.

Contact Model 2

Based on the critical stretch model in peridynamics, the second constitutive contact model used in PD simulations is proposed and shown in Fig 1. With the critical stretch model, the bond between material points is broken irreversibly when the elongation ratio of the bond exceeds the critical bond stretch, \(s_{c}\). When all bonds crossing a surface are broken, the separation of material (crack) forms. Thus, \(s_{c}\) can be related to the critical energy release rate \(G_{c}\) in classical fracture

$$ G_{c} = \frac{{\pi cs_{c}^{2} \delta^{5} }}{10} $$
(23)
Fig. 1
figure 1

The proposed constitutive model 2 for characterizing interfacial properties

Full size image

Here, we use the PD bond that is within the bulk metal material to calibrate the bond formed at the interface. To extract information of the bulk bonds, we conducted a numerical simulation in which a bulk material was stretched until fracture occurs. The force exerted on the separated parts were recorded and plotted in Fig. 1, with the curve denoted as “Bulk.” Then, an interfacial constitutive model is fitted based on the bulk material behavior and is named “Exponential” in Fig. 1. The force-stretch model is set in form of a two-segment relation with a linear elastic behavior, and a damage evolution characterized by an exponential degradation. Based on this model, the attractive force between two material points which have been connected through an interface bond increases linearly by increasing the interfacial separation. Then, the force starts to reduce when the displacement across the interface reaches a threshold value, due to the bond breakage along the interface. This leads to the strength reduction or the “softening” of the bonding interface. Finally, when all bonds connecting the separated material are broken, the force becomes zero indicating complete de-bonding. The force‐stretch relation of the interface is given by (Ref 72)

$$ f_{c} = f_{c} \left( s \right) = cs_{y} exp\left( { - m\left( {s - s_{y} } \right)} \right) $$
(24)

where \(f_{c}\) is the magnitude of the contact force density vector, \(s\) is the unitless bond stretch, and sy is the yield bond stretch .

During contact, the contact model is activated by the creation of neighbor lists to calculate pairwise forces. At this stage, both the normal pressure and the contact surface area increase between the two bodies. The contact compression force in the normal direction is defined in the same manner as Eq 24, except that the “stretch” of the bond is negative

$$ f_{c} = f_{c} \left( s \right) = c\left| s \right| $$
(25)

where \(f_{c}\) is the magnitude of the compressive force density vector, \(\left| s \right|\) is the magnitude of the bond stretch. Finally, during separation the two bodies are subjected to tensile forces determined by Eq 24.

One of the advantages of this model is that it is possible to employ a different “force-stretch” law for modeling dissimilar materials contacts. However, one thing worth mentioning is that though contact model 2 enables the interface to reproduce the bulk material fracture behavior, it does not have the flexibility of varying adhesion (unlike contact model 1) once the parameters are fitted.

It should be noted that the critical stretch damage model in peridynamics is used extensively for modeling brittle material fracture. Here we are focusing on establishing a relationship between “interface material” and bulk material, to mimic the formation of the metallic bond in the cold spray process.

Simulation Setup

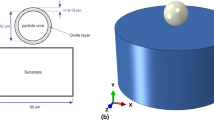
The impacts of single spherical copper particles on the copper substrate were investigated in the following sections using the open-source code Peridigm (Ref 61). A research code written in C++ was developed within the framework of Peridigm in order to take advantage of the massive parallel computing abilities of this package. The simulation setup is shown in Fig. 2, where a spherical particle of 30 μm in diameter impacts onto a flat cylindrical substrate. The substrate is much larger in dimensions than the impacting particle, with its radius and height being four times as the particle radius. It should be noted that the substrate dimensions have been confirmed to sufficient to ensure that our results remain unchanged with further increase in the substrate dimensions.

Fig. 2
figure 2

The 2D sketch and 3D peridynamics model of single-particle deposition in cold spray

Full size image

Our peridynamic modeling efforts were also accompanied by FEM modeling, conducted using the commercially available software ABAQUS/Explicit (Ref 73). The FEM results were used as a benchmark to confirm the validity and accuracy of the peridynamic numerical method. The element size for the particle and the substrate in FEM simulations was set to 1/50 of particle’s diameter. Accordingly, the average node spacing in the peridynamic discretization was kept about the same as the mesh size in the FEM model to give a direct comparison of the results provided by these two numerical methods. In all simulations, the side surface is restricted in the \(X\) and \(Y\) directions and the fixed boundary conditions are enforced to the bottom.

The aforementioned contact algorithms and a pure repulsion contact model are used for the contact between the particle and the substrate in peridynamic simulations. The gravity force is ignored in all the simulations because it is much smaller compared to the contact forces. The surface-to-surface penalty contact algorithm is used in FEM simulations.

Material Model and Implementation

In a high-speed impact application such as cold spray, the induced high strain rate plastic deformation leading to softening of the material due to the heat generated by plastic work. As a result, the effects of isotropic strain hardening, thermal softening and strain rate hardening are important in dynamic problems. The JC constitutive model accounts for all of these effects. The Von-Mises equivalent stress calculated by the JC model is given by (Ref 74):

$$ \sigma = \left[ {A + B\varepsilon^{n} } \right]\left[ {1 + C\ln \dot{\smallint }^{*} } \right]\left[ {1 - (T^{*} )^{m} } \right] $$
(26)
$$ T^{*} = \frac{{T - T_{{{\text{ref}}}} }}{{T_{m} - T_{{{\text{ref}}}} }} $$
(27)

where σ is the flow stress, ε is the equivalent plastic strain (PEEQ), and \( \dot{\varepsilon }* \) is the equivalent plastic strain rate normalized by a reference strain rate, Tref is the threshold temperature above which thermal softening is allowed for the particle, and Tm denotes the melting temperature of the metal. A, B C, n and m are experimentally derived constants. T refers to the initial temperature for the particle which is usually set to room temperature. The JC model takes account of strain hardening, strain rate hardening, and thermal softening effects, thus is suitable to describe the material behavior in cold spray. The material properties are listed in Table 1.

Table 1 Material properties of copper (Ref 74)
Full size table

As presented in subsection “State-based peridynamic theory,” the approximate deformation gradient \({\mathbf{F}}\) is used to adapt classical constitutive models for state-based peridynamics. The velocity gradient tensor is obtained by

$$ {\mathbf{L}} = \frac{\partial v}{{\partial x}} = {\dot{\mathbf{F}}\mathbf{F}}^{ - 1} $$
(28)

The deformation rate of tensor \({\mathbf{D}}\) and spin tensor \({\mathbf{W}}\)

$$ {\mathbf{D}} = {\text{sym}}\left( {\mathbf{L}} \right) = \frac{1}{2}\left[ {{\mathbf{L}}{ + }{\mathbf{L}}^{{\mathbf{T}}} } \right], {\mathbf{W}}{\text{ = skew}}\left( {\mathbf{L}} \right){ = }\frac{{1}}{{2}}\left[ {{\mathbf{L - L}}^{{\text{T}}} } \right] $$
(29)

The unrotated deformation rate of tensor \({\mathbf{d}}\) is decomposed as (Ref 53)

$$ {\mathbf{d}} = {\mathbf{d}}^{e} + {\mathbf{d}}^{p} + {\varvec{d}}^{T} = {\mathbf{R}}^{T} {\varvec{DR}} $$
(30)

where \({\mathbf{d}}^{{\text{e}}}\), \({\mathbf{d}}^{{\text{p}}}\) and \({\mathbf{d}}^{{\text{T}}}\) denote elastic, plastic and thermal parts of \({\mathbf{d}}\), respectively. \({\mathbf{R}}\) is an orthogonal tensor describing a rigid-body rotation. To calculate the unrotated Cauchy stress τ, the radial return mapping algorithm is used. And interested readers can refer to Ref (Ref 75) for more detailed implementing information. After that, the von-Mises stress is updated using the JC model and then the equivalent plastic strain is incremented.

The temperature rise can be assumed adiabatic in CS deposition due to the extremely short time period of the high strain rate deformation, which is calculated according to:

$$ T = \mathop \smallint \limits_{0}^{\varepsilon } \chi \frac{\sigma d\varepsilon }{{\rho C_{p} }} $$
(31)

where \(C_{{\text{p}}}\) is the specific heat of the material and \(\rho\) is its density. \(\chi\) is the Taylor–Quinney coefficient characterizing the percentage of the plastic work that converts into adiabatic heating and is set as 0.9.

Results

Single-Particle Impact

An axisymmetric particle/substrate model is used in the FEM simulations, with both the substrate and the particle material being copper. On the other hand, the whole 3D peridynamics models were employed in this study. Figure 3 shows the resulted shapes as copper particles impact on copper substrates at the velocity of 400 m/s, 500 m/s, and 600 m/s, respectively, obtained from both the peridynamics method and FEM. We can see from the FEM results that the particle underwent significant deformation, resulting in a crater in the flat substrate and an obvious metal jetting at the rim. The peridynamics results compare fairly well with the simulation results from the FEM method, the de-facto standard method for single-particle impact in cold spray. This confirms validity and accuracy of the peridynamics method for simulating the impacting behaviors of particles during cold spray.

Fig. 3
figure 3

The resulted deformation configurations of single copper particle impacts modeled by the peridynamics method (a-c) and FEM (d-f) at the velocity of 400, 500, and 600 m/s, respectively. The configuration snapshots were taken at 105 ns

Full size image

Besides the deformation configurations, we also examined the equivalent plastic strain (PEEQ) distribution resulted from the impact. Figure 4 shows the equivalent plastic strain (PEEQ) distribution of a 30μm copper particle after impacting the substrate at a velocity of 400 m/s. The particle’s periphery around the particle-substrate interface deforms most intensively (i.e., highest PEEQ) within a narrow band. The extreme and highly localized deformation causes jetting of material, and a significant temperature rise in the interface region (Fig. 5). The increase in temperature leads to the loss of shear strength or thermal softening behavior described by the JC model. We see from Figs 4-5 that the peridynamic results match well with FEM, in terms of both the strain (i.e., PEEQ) and temperature profiles. One thing worth noting is that in FEM the outmost periphery of the deformed particle exhibits unphysically large PEEQ due to the highly distorted local elements, which has been reported in previous research (Ref 76). In contrast, in peridymamics the domain is discretized into a set of nodes rather than elements so that the artificially large plastic strains observed in FEM result can be alleviated to some extent. However, owing to the total-Lagrangian nature of the traditional peridynamic theory, in which the interaction between material points is determined by a mapping between the current (deformed) and reference (undeformed) configurations, such unphysical phenomenon is not completely avoided under extremely large deformations.

Fig. 4
figure 4

Simulated contours of PEEQ for a 30 μm Cu particle with impact velocity of 400m/s, obtained from (a) FEM (b) peridynamics simulations, at 105 ns

Full size image
Fig. 5
figure 5

Simulated temperature contours for a 30 μm Cu particle with impact velocity of 400m/s, obtained from (a) FEM (b) peridynamics simulations at 105 ns

Full size image

Contact with Tunable Adhesion

During the impact, the initial kinetic energy of the in-flight particle is largely dissipated in the form of plastic deformation in the particle and substrate. The remaining kinetic energy is then stored as elastic strain energy in the contacting bodies. Part of the recovered strain energy becomes energy toward rebounding, namely the rebounding energy. When the rebounding energy is strong, the particle will be able to overcome the adhesion and particle rebounding then occurs. To demonstrate the competition between the rebounding energy and adhesion, we consider a Cu particle of 30 μm in diameter impacting onto a flat Cu substrate at 500 m/s with varying levels of adhesion strength at the interface, shown in Fig. 6. Specifically, the three scenarios presented in Fig. 6. The scenario in Fig. 6(a) corresponds to impact using a repulsive only contact algorithm without adhesion force, which resembles the common case in FEM simulations. On the other hand, Fig. 6(b) shows the numerical simulations with contact model 1 and Fig. 6(c) shows the numerical simulations with contact model 2. These configurations were taken at the simulation time of 190 ns at which either rebounding or bonding has occurred, thus being effectively “pseudo-final configurations.” Clearly when there is no adhesion, rebounding occurs to result in particle-substrate separation as shown in the inset in Fig. 6(a). While for the other two with contact models, the power particle remains adhered to the substrate after impact.

Fig. 6
figure 6

The sample pseudo-final configurations obtained (at 190 ns) from impact simulations of a 30 μm Cu particle impacting onto a Cu substrate at 500 m/s, under conditions of (a) no adhesion, (b) contact model 1 with the parameter \(\beta = 0.005\) and (c) contact model 2, at the interface

Full size image

Figure 6 clearly illustrated the critical role of adhesion. Below a more detailed, quantitative analysis of such role is presented. In the contact model 1, we know that the adhesion may be adjusted by the parameter β. A series of different initial velocity single-particle impact tests were performed with varying β. As stated previously, the particle deposition behavior depends on the competition between the rebounding energy (\(E_{r}\)) and adhesion energy (\(E_{a}\)). We define the final kinetic energy (\(E_{f}\)) of the particle after the impact

$$ E_{f} = \left\{ \begin{gathered} E_{r} - E_{a} \,\,\,\,\,if~E_{a} \le ~E_{r} \hfill \\ 0\qquad\,\,\,\,\,\,\,\,\,\,\,\,otherwise \hfill \\ \end{gathered} \right. $$
(32)

For a given initial velocity, e.g., \(v_{i} = 500 m/s\), and material combination of the particle and substrate (Cu), \(E_{r}\) is a constant (Ref 77). As a result, to quantitatively describe the role of adhesion, one can use the coefficient of restitution (CoR) as a parameter to represent \(E_{f}\) during the elastic rebound phase (Ref 78). The CoR is given by:

$$ R = \frac{{v_{f} }}{{v_{i} }} = \sqrt {\frac{{E_{f} }}{{E_{i} }}} $$
(33)

where \(v_{i}\) is the initial velocity of the particle and \(v_{f}\) is the final velocity after the impact. \(E_{i}\) represents the initial kinetic energy. R = 0 implies bonding after the collision, otherwise, the particle is bouncing off due to the remaining rebound energy. Figure 7 shows the variation of CoR as a function of β for different initial velocities. Again, for simplicity, we use the case of a 30 μm Cu particle impacting a Cu substrate at the velocity of \(v_{i} = 500 ,m/s\) as the representative case. We can see that the CoR is declining as β increases and drops to zero when β exceeds a threshold value of \(4.5 \times 10^{ - 3}\). This plot illustrates the competition between the adhesion energy and the rebounding energy. The adhesion energy is able to offset the rebounding energy when \(\beta > 0.0045\), but it is not sufficient to stop the particle detachment when β is less. Similar observations of CoR vs. β curves can be found for cases with different powder particle impact velocities, though the threshold β beyond which CoR becomes zero differ.

Fig. 7
figure 7

Coefficient of restitution as a function of adhesion parameter for 30 μm copper particle with the impact velocity of \(400 \), \(500 \), and \(600\;{\text{m}}/{\text{s}}\), respectively

Full size image

Meanwhile, we also examined the effect of the parameter β on the velocity history. The results are shown in Fig. 8, where negative velocities mean that the particle is approaching or deforming into the substrate, while positive velocities indicate that the particle is moving away from the substrate. As shown in this figure, the velocity magnitude of the particle is first dropping to zero at the beginning of the simulation. This means the particle is impacting the substrate and the kinetic energy is gradually dissipated as deformation progresses. Afterward, the velocity turns positive which indicates the elastic energy remained is driving the particle to bounce off.

Fig. 8
figure 8

Effect of adhesion parameter β on history of velocity of a 30 μm copper particle with the impact velocity of 500 m/s

Full size image

It can be seen that the velocity is increasing and reaches a maximum at 135 ns. After this, the velocity of the particle is plateaued for \(\beta = 0\) and decreasing again in the cases of \(\beta > 0\) due to the lost energy to break the bonds between bonded material points. With the increase in the adhesion parameter β, the velocity drop after 135 ns becomes larger indicates larger adhesion force exerts on the particle by the substrate to slow down the bouncing particle. In the cases with high value of β, i.e., \(\beta = 4.5 \times 10^{ - 3}\) and \(\beta = 5.0 \times 10^{ - 3}\), the velocity turns to negative which means the adhesion force is so strong that it pulls the particle backwards to substrate. This prevents the particle from de-bonding.

Figure 9 shows the evolutions of contact force of the entire particle with respect to time in the simulations that employ contact model 1. This is calculated by integrating all contact forces of each material point within the particle that has an interaction with the material point inside the substrate. Again, the effect of adhesion parameter β is examined. Positive force represents repulsion, and negative force represents adhesive force. It can be seen that in all cases the contact force first increases drastically to avoid interpenetration during compression. The force drops quickly due to the deformation of the substrate and particle while they store their elastic energies. When the particle tries to bounce off, that is, during interface separation, the particle is subjected to tensile force. It also can be seen that larger β results in larger adhesion force as mentioned previously. For cases with relatively small β (up to \(4.3 \times 10^{ - 3}\)), the contact force almost drops to zero after 304 ns while the velocity keeps positive and unchanged. This indicates the particle bounces off and is out of the action range of interface interaction. In the case of \(\beta = 5.0 \times 10^{ - 3}\), the force becomes positive again at the end of the simulation because the particle is moving toward the substrate, and the contact force turns repulsive when they are getting too close. As can be seen in Fig. 8, for \(\beta = 5.0 \times 10^{ - 3}\) the velocity of the particle is-18.7 m/s at 270 ns where the contact force is 0.02 N (Fig. 9). This repulsion force slows down the particle to-0.98 m/s after 34 ns during which the force increases to 0.09 N. In the next few nanoseconds, the particle will be pushed back to equilibrium distance where the net contact force is zero.

Fig. 9
figure 9

Effect of adhesion parameter β on the history of contact force of a 30 μm copper particle with the impact velocity of 500 m/s

Full size image

In Table 2, we list the values of maximum adhesion force (MAF) the substrate exerts on a 30 μm copper particle with the impact velocity of 500 m/s for various β. As clearly indicated in Table 2, a larger β leads to a larger MAF value, namely stronger adhesion.

Table 2 Maximum adhesion force for the single-particle impact test at an impact velocity of 500 m/s
Full size table

Figure 10 shows the evolution of the contact force of the entire particle with respect to time in the simulation that employs contact model 2. Compared to Fig. 9, it can be found that the evolution of the contact force exhibits more oscillation, compared to those obtained using contact model 1. Such difference is attributed to the interface force in contact model 2 being much shorter ranged than that in contact model 1 which employed a long-range Lennard-Jones type potential.

Fig. 10
figure 10

Evolutions of contact force for a 30 μm Cu powder impact onto a Cu substrate at 500 m/s with contact model 2. Positive force represents repulsion, and negative force represents adhesive force.

Full size image

Discussion

The afore-described numerical approach takes advantage of the nonlocal nature and meshless discretization of peridynamics is proposed for more realistic simulations of the CS process. With this new approach, the CS particle deposition, using copper as the sample material, was successfully modeled with the particle/substrate adhesion accounted. The explicit formulation of adhesion in our approach enables us to calibrate the model parameters to reproduce the actual bonding strength, e.g., particle on substrate, when experimental measurements are available. To further illustrate this, below we demonstrate one possible means to achieve this. Starting with a single-particle impact simulation, we can produce the after-impact configurations. The configuration prior to particle rebounding can then be recreated by duplicating the coordinates and volumes of all the material points, but with velocities zeroed. Subsequently, a numerical tensile test, illustrated in Fig. 11a can be performed in which the particle is rigidly displaced away from the substrate. The force required in this process is recorded. Fig. 11b illustrates a typical force-displacement response expected for the adhesion force, where the force would first increase, reach a peak value, and then gradually drop to zero. This numerical test resembles the tensile pull-off test typically seen in experiments for bond strength measurement of the coating to the substrate, except that we did this numerical test on one single particle. In experiments, the coating is bonded to a high-strength epoxy resin to be pulled off the substrate. The ratio of the maximum load to the sample’s cross-section area is considered as the adhesion strength (Ref 79, 80). In the numerical test, the single bonded particle is pulled off the substrate and the force needed to break all the bonds between material points adjacent to the interface is recorded. To compare the adhesion stress obtained from simulation to the macroscopic experimental data, the simulated peak force of a single particle can be multiplied by the number density of particles in a certain area of an experiment sample to calculate the averaged adhesion strength (Ref 81). The above is more of a proof-of-concept type demo. The numerical test can certainly be made more sophisticated to better resemble the experimental test if necessary.

Fig. 11
figure 11

Illustration of a numerical tensile test performed on an after-impact particle-substrate configuration (inset figure), and the typical force-displacement relation expected from such test.

Full size image

Besides the tensile pull-off test, there are, of course, other types of experiments to measure the bond strength. One of them is the shear test, in which a stylus is used to apply tangential force on a single particle to shear the splat along the substrate. Then the difference between the baseline tangential force and the peak tangential force, divided by projected area of the particle is obtained as the adhesion strength (Ref 82, 83). One can also design the corresponding numerical test, depending on the shear experiments, for the calibration of the proposed model parameters.

Conclusion

In conclusion, the numerical approach introduced in this study is expected to provide a new numerical tool for more realistic simulations of CS, as well as other engineering processes involving complicated bonding and de-bonding like dynamic interactions. The model describes particle adhesion based on the interaction of individual material points, with the intra-solid interaction for material deformation and the inter-solid interaction to describe material (e.g., particle-substrate) bonding through the adhesive contact models. The simulated deformation behaviors were shown to compare well with the conventional FEM results, while meanwhile the formation and breakage of material bonding can be properly considered.

This new approach allows the realization of different deposition scenarios by modulating the adhesion strength and contact stiffness. For deposited particles, the bond strength can be calibrated with experimental measurements. It can readily be extended for simulations of multiple-particle impacts, with customized particle-particle and particle-substrate bonding depending on the types of particles and/or substrate materials, and can be easily deployed in large parallel computing facilities for simulations of larger scale and longer timespan.

Starting from this base numerical framework, we expect to work on further developments to consider defects and damage, so as to take full advantage of PD’s ability to handle discontinuity. Other future possibilities include bridging with smaller-scale simulations, such as molecular dynamics (MD) (Ref 84), or even the development of a PD-MD concurrent multiscale method (Ref 63), for a more precise investigation of the metallurgical bonding mechanism.