Abstract
The number of free trade agreements (FTAs) has increased in the past few decades, and the cross-country variation of the most-favored-nation (MFN) tariffs has decreased. Motivated by these two facts, we study whether the reduced variance in cross-country MFN tariffs can help explain the expansion of FTAs. Using an oligopolistic trade model with the equilibrium concept of pairwise stable networks, we reveal the existence of a set of pairwise stable network equilibria, where the number of FTAs rises as tariffs become increasingly symmetrical. This finding contributes to theoretical FTA literature by showing that an incomplete FTA network can be supported as a pairwise stable network equilibrium.







Similar content being viewed by others
Notes
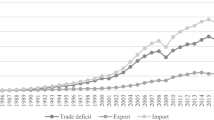
World Integrated Trade Solution (WITS) of the World Bank provides a database of the applied MFN tariff rates of countries. The lists of reporting countries in WITS may vary over time because it is not mandatory for countries to report their tariffs rates every year. In Fig. 1 Panel A, the solid line depicts the annual means of the applied MFN tariffs for each year. We also calculate the standard deviations of applied MFN rates for each year and draw the two dotted lines above and below the solid line by adding and subtracting them from each annual means. For this reason, we have the lower dotted line drawn below zero point.
The details of all regional trade agreements (RTAs) are available on the WTO website (www.wto.org). In calculating a bilateral FTA relationship based on RTA data, we count the following types of bilateral links from 1958 to 2012. First, we count the agreements that involve both the rules of General Agreement on Tariffs and Trade (GATT) XXIV and the Enabling Clause concerning the formation of free trade areas and customs unions for trade in goods. We exclude the cases of FTAs that pertain solely to services and several partial scope agreements. Second, we count the agreements among GATT/WTO member countries only; doing so enables us to effectively exclude agreements among small-sized countries, colonial territories, small island nations, and nations at wars. As a result, we are able to capture 177 RTAs from the 247 RTAs concluded between 1958 and 2012. Lastly, we calculate each bilateral FTA’s links over the period and derive the cumulative numbers of bilateral FTA relationships (Fig. 1 Panel B).
Conversely, earlier studies by Kennan and Riezman (1990), Richardson (1993), Bagwell and Staiger (1999) and Bond and Syropoulos (2004) theoretically showed that the multilaterally negotiated tariff level can be lowered after the formation of an FTA. The reported empirical evidence for this is somewhat mixed. Positive evidence includes Bohara and Sanguinetti (2004), and negative evidence includes Limao (2006) and Karacaovali and Limao (2008).
In Sect. 5, we discuss and analyze the case of endogenous tariffs.
When every pair of tariffs has a large (resp., small) gap, the standalone network (H) (resp., the complete network (A)) emerges as a pairwise stable network; when only a strict subset of countries has comparable tariff levels, an intermediate FTA network, such as (B), (E), or (F), arises as a pairwise stable network. As previously mentioned, the intuition behind these observations is that a high-tariff country incurs a high cost by forming an FTA link with a low-tariff country when their tariff levels are asymmetric.
For the case with three countries, we obtain an unexpected result: if \(n=3\), then \(\lambda _1\ge \lambda _2\ge \lambda _3\implies \tau _1^*=\tau _2^*=\tau _3^*\). The reason is as follows. When a country increases its tariff, the benefits of producer surplus and tariff revenues are exactly offset by the loss of consumer surplus. This results in identical optimal tariffs and the absence of a tariff gap between countries, which does not affect the incentive of forming FTA links among countries. This finding is a by-product of the current simple linear demand model.
References
Aghion, P., Antras, P., & Helpman, E. (2007). Negotiating free trade. Journal of International Economics, 73(1), 1–30.
Bagwell, K., & Staiger, R. (1999). Regionalism and multilateralism tariff co-operation. In: J. Piggott & A. Woodland (Eds.), International Trade Policy and The Pacifi Rim. Proceedings of the IEA Conference held in Sydney, Australia. MacMillan, Palgrave.
Baier, B. (2004). The economic determinants of free trade agreements. Journal of Internat, 64, 29–63.
Bohara, K. G., & Sanguinetti, P. (2004). Trade diversion and declining tariffs: Evidence from mercosur. Journal of International Economics, 64, 65–88.
Bond, R. R., & Syropoulos, C. (2004). A strategic and welfare theoretica analysis of free trade areas. Journal of International Economics, 64, 1–27.
Chen, M. X., & Joshi, S. (2010). Third-country effects on the formation of free trade agreements. Journal of International Economics, 82(2), 238–248.
Ethier, W. (1998). Regionalism in a multilateral world. Journal of Political Economy, 106, 1214–1245.
Facchini, G., Silva, P., & Willmann, G. (2013). The customs union issue: Why do we observe so few of them? Journal of International Economics, 90(1), 136–147.
Freund, C. (2000). Multiltaralism and the endogenous formation of preferential trade agreements. Journal of International Economics, 52, 359–379.
Furusawa, T., & Konishi, H. (2005). Free trade networks with transfers. Japanese Economic Review, 56(2), 144–164.
Furusawa, T., & Konishi, H. (2007). Free trade networks. Journal of International Economics, 72(2), 310–335.
Goyal, S., & Joshi, S. (2006). Bilateralism and free trade. International Economic Review, 47(3), 749–778.
Hur, J., & Qiu, L. D. (2020). Tariffs and formation of free trade agreements networks. World Economy, 43(1), 33–59.
Jackson, M. O., & Wolinsky, A. (1996). A strategic model of social and economic networks. Journal of Economic Theory, 71, 44–74.
Karacaovali, B., & Limao, N. (2008). The clash of liberalizations: Preferential vs. multilateral trade liberalization in the European Union. Journal of International Economics, 74(2), 299–327.
Kennan, J., & Riezman, R. (1990). Optimal tariff equilibrium with customs unions. Canadian Journal of Economics, 23, 70–83.
Lake, J. (2017). Free trade agreements as dynamic farsighted networks. Economic Inquiry, 55(1), 31–50.
Lake, J., Nken, M., & Yildiz, H. M. (2020). Tariff bindings and the dynamic formation of preferential trade agreements. Journal of International Economics, 122, 103279.
Lake, J., & Roy, S. (2017). Are global trade negotiations behind a fragmented world of gated globalization? Journal of International Economics, 108, 117–136.
Lake, J., & Yildiz, H. M. (2016). On the different geographic characteristics of free trade agreements and customs unions. Journal of International Economics, 103, 213–233.
Limao, N. (2006). Preferential trade agreements as stumbling blocks for multilateral trade liberalization: Evidence for the united stages. American Economic Review, 96(3), 896–914.
Mauleon, A., Song, H., & Vannetelbosch, V. (2010). Networks of free trade agreements among heterogeneous countries. Journal of Public Economic Theory, 12(3), 471–500.
Nken, M., & Yildiz, H. M. (2021). Implications of multilateral tariff bindings on the extent of preferential trade agreement formation. Economic Theory, 1–47.
Ornelas, E. (2008). Feasible multilateralism and the effects of regionalism. Journal of International Economics, 74(1), 202–224.
Richardson, M. (1993). Endogenous protection and trade diversion. Journal of International Economics, 34, 309–324.
Saggi, K., & Yildiz, H. (2010). Bilateralism, multilateralism and the quest for global free trade. Journal of International Economics, 81, 26–37.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
We appreciate the comments of two anonymous referees. This project is financially supported by RGC Competitive Earmarked Research Grant 2012–2014 (No. HKU751812B) of the HKSAR Government.
Appendix A: Characterization of pairwise stability
Appendix A: Characterization of pairwise stability
Proof of Lemma 1
We show that \(\beta _{E}(m,\tau )-c(m,\tau )>0\). Note that \(\beta _{E}(m,0)-c(m,0)=0\). From direct computation, we find
for a sufficiently large a. Next, we show that \(c(m,\tau )>0.\) Again, we observe that \(c(m,0)=0.\) In addition,
for a sufficiently large a. \(\square \)
Proof of Lemma 2
The derivative with respect to m follows from direct computation by treating m as a real number. That is,
Similarly, we obtain
via the assumption \(a>(n+1)\tau .\) \(\square \)
Proof of Lemma 3
From the proof of Lemma 1, we have \(\frac{\partial c}{\partial \tau }(m,\tau )>0\) when a is sufficiently large. The second part can be easily expressed by direct computation as follows:
\(\square \)
Proof of Proposition 2
Let a linearly hierarchical network g be given. Note that it is sufficient to consider interior links, \(\{23,\,34,\,\ldots ,\,(n-2,n-1)\}.\) In addition, we can restrict our attention to the incentive of the high-tariff country against the low-tariff country (Lemma (4)). First, consider links, \((i,i-1)\) for \(i=3,\,4,\,\ldots ,\,n-1.\) Given that \({\underline{\tau }}(2,\tau _{i+1})\le \tau _{i}\text { for }i=2,\,3,\,\ldots ,n-2\), we obtain
for \(i=2,\,3\,,\ldots ,\,n-2.\) This shows that no link in \(\{23,\,34,\,\ldots ,\,(n-2,n-1)\}\) is severed, that is, \(u_{i}(g)\ge u_{i}(g-(i,i-1))\) for \(i=3,\,4,\,\ldots ,\,n-1.\) Second, consider links \((i-1,i+1)\) for \(i=3,\,4,\,\ldots ,\,n-2.\) Similarly, because \(\tau _{i-1}<{\underline{\tau }}(3,\tau _{i+1})\) for \(i=3,\,4,\,\ldots ,\,n-2\), we obtain
for \(i=3,\,4,\,\ldots ,\,n-2.\) This shows that any link between countries i and j, such as \(|i-j|=2\), will not be formed because the net marginal cost of the link is larger than the benefit to the high-tariff country, that is, \(u_{i+1}(g)>u_{i+1}(g+(i-1,i+1))\) for \(i=3,\,4,\,\ldots ,\,n-2.\) Moreover, increasing the marginal benefit and net marginal cost functions with respect to \(\tau \) implies that any link between countries i and j, such as \(|i-j|\ge 2\), cannot be formed. Thus, \(u_{i}(g)>u_{i}(g+(i-l,i))\) for any i and \(l>2\). \(\square \)
Proof of Proposition 3
Consider network g to be \(g_{ij}=P(g)_{ij}P(g)_{ji}\) for all \(i,\,j\). Consider two countries i and j. First, assume that \(g_{ij}=1\). Then, \(P(g)_{ij}=P(g)_{ji}=1\), so \(u_{i}(g)\ge u_{i}(g-ij)\) and \(u_{j}(g)\ge u_{j}(g-ij)\). On the contrary, assume that \(g_{ij}=0\). Then, either \(P(g)_{ij}=0\) or \(P(g)_{ji}=0\). We may assume that \(P(g)_{ij}=0\). We obtain \(u_{i}(g+ij)<u_{i}(g)\). Therefore, network g is pairwise stable.
Conversely, suppose that network g is pairwise stable. Note that it is impossible for \(u_{i}(g+ij)-u_{i}(g)\) and \(u_{j}(g+ij)-u(g)\) to be zero at the same time when a is sufficiently large because
where f is a function that is constant in a. Therefore, for \(i,\,j\) such that \(i<j\) and \(g_{ij}=0\), we may assume that \(u_{j}(g)>u_{j}(g+ij)\). We obtain \(P(g)_{ji}=0\), implying \(P(g)_{ij}P(g)_{ji}=0\). Similarly, for \(i,\,j\) such that \(g_{ij}=1\), it should be \(u_{i}(g)\ge u_{i}(g-ij)\) and \(u_{j}(g)\ge u_{j}(g-ij)\). Therefore, we obtain \(P(g)_{ij}=P(g)_{ji}=1\), implying \(P(g)_{ij}P(g)_{ji}=1\). This completes the proof. \(\square \)
Proof of Lemma 6
Note that \(\beta _{E}(n-1,0)-c(1,0)=0\). From direct computation, we find that
which is strictly positive if a is sufficiently large. The result follows because \(\beta _{E}(m_{j},\tau )-c(m_{i},\tau )\ge \beta _{E}(n-1,\tau )-c(1,\tau )\) for any \(m_{i}\) and \(m_{j}\). \(\square \)
Proof of Proposition 4
Consider two countries i and j with \(i<j\). Assume that \(\tau _{j}/\tau _{i}<2n/3\) to prove the case of (i). We can check that
for any \(m_i\) and \(m_j\), where f is a function that is constant in a. Therefore, \(\beta _{E}(m_{i},\tau _{i})-c(m_{j},\tau _{j})>0\) for a sufficiently large a, which implies that \(P(g)_{ji}=1\) in any network g. Given that \(\beta _{E}\) and c are increasing functions with respect to \(\tau \), \(P(g)_{lk}=1\) for any countries \(i\le k<l\le j\). We can apply a similar argument to prove (ii). \(\square \)
Proof of Proposition 5
The uniqueness is guaranteed by the necessary part of Proposition 4.
(ii) Let g be a complete network. Given that \(r<(2n/3)^{1/(n-1)}\), \(\tau _{n}/\tau _{1}<2n/3\). Thus, we obtain \(P(g)_{ji}=1\) for any \(i,\,j\) by Proposition 4. By combining this with Lemma 6, we obtain \(g_{ij}=P(g)_{ij}P(g)_{ji}=1\) for all \(i,\,j\). Therefore, g is a pairwise stable network due to Proposition 3.
(ii) Let g be a standalone network. Given that \(r>2n/3\), we have \(P(g)_{i+1,i}=0\) for all \(i=1,\,2,\,\dotsc ,\,n-1\), which implies that \(P(g)_{ji}=0\) for all \(i,\,j\) with \(i<j\) by Proposition 4. Combining this with Lemma 6, we have \(g_{ij}=P(g)_{ij}P(g)_{ji}=0\) for all \(i,\,j\). By Proposition 3, g is pairwise stable.
(iii) Let g be a hierarchical network of size 2m. Given that \(\tau _{i+m}/\tau _{i}=r^{m}<2n/3\) for any \(i=1,\,2,\,\dotsc ,\,n-m\), we obtain \(P(g)_{ji}=1\) for all \(i,\,j\) where \(i<j\le i+m\). By adopting a similar argument, we can easily verify that \(P(g)_{ji}=0\) for all \(i,\,j\), where \(j>i+m\). Combining this with Lemma 6 provides \(g_{ij}=P(g)_{ij}P(g)_{ji}\) for all \(i,\,j\). Therefore, g is pairwise stable by Proposition 3. \(\square \)
Proof of Proposition 6
Given that a is sufficiently large, it suffices to check the incentives of high-tariff countries against those of low-tariff countries. Consider any two countries i and j with \(\tau _{i}\le \tau _{j}.\) If the variation of tariffs, \(\sigma \), increases to \(\sigma '\), the tariff system \(\tau \) should be either \(\tau _{i}'\ge \tau _{i}\) or \(\tau _{i}'\le \tau _{i}.\) In the former case, we can easily verify that \(t\le \tau _{i},\tau _{i}',\tau _{j},\tau _{j}'\le 2t\) to ensure \(\tau _{1}(t,\sigma ,1)\ge 0\) for any \(\sigma \in [0,1].\) We claim that any link between countries \(i\le j\) with \(\tau _{j}\le 2\tau _{i}\) will be always connected in a pairwise stable network, implying that the number of links included in the former case will not be changed by the increase in \(\sigma .\) Here, we write \(ij\in g\) if \(g_{ij}=1\) and \(ij\not \in g\) if \(g_{ij}=0\). \(\square \)
Claim 1
For any \(i\le j\) such that \(\tau _{j}\le 2\tau _{i}\), \(ij\in g( {\tau }).\)
Consider i, j such that \(\tau _{i}\le \tau _{j}\le 2\tau _{i}\). Note that
for any \(m_{i}\) and \(m_{j}\). Given that \(\beta (n-1,\tau _{i})-c(1,2\tau _{i})>0\) for a sufficiently large a, we obtain \(\beta (m_{i}-1,\tau _{i})-c(m_{j}-1,\tau _{j})>0\) as desired.
Next, we claim that the number of links included in the latter case, \(\tau _{i}'\le \tau _{i},\) is decreasing (or not increasing) with respect to a variation in tariff levels. Combining this with the first claim will complete the proof.
Claim 2
Consider a link \(ij\,(i\le j)\) such that \(\tau _{i}'\le \tau _{i}\). If \(ij\notin g(\tau ),\) then \(ij\notin g(\tau ').\)
Note that we are assuming two adjacent pairwise stable networks, \(g(T)\,\text{ and } g(T')\). Suppose that \(ij\notin g\) but \(ij\in g'\). Then \(m_{i}'=m_{i}+1\) and \(m_{j}'=m_{j}+1\) because the two networks are adjacent. Hence, we obtain
To obtain a contradiction, we need to show that
Since it is trivial when \(\tau _{j}'\ge \tau _{j}\), consider the case of \(\tau _{j}>\tau _{j}'.\) Note that \(\tau _{i}-\tau _{i}'>\tau _{j}-\tau _{j}'\), \(\frac{\partial ^{2}}{\partial m\partial \tau }\beta _{E}(m,\tau )=-\frac{4n\tau }{(n+1)^{2}}<0,\) and \(\frac{\partial ^{2}}{\partial m\partial \tau }c(m,\tau )=-\frac{2(2n+5)\tau }{(n+1)^{2}}<0.\) Given that two functions, \(\beta _{E}\) and c, are differentiable in \(\tau \), the mean value theorem implies that there are two points \(\hat{\tau _{i}}\in [\tau _{i}',\,\tau _{i}]\) and \(\hat{\tau _{j}}\in [\tau _{j}',\,\tau _{j}]\), such that
and
Thus, we obtain
and
Given that
it is positive when a is sufficiently large. Hence,
, which is equivalent to
About this article
Cite this article
Do, J., Hur, J., Hwang, SH. et al. Tariff diversity and FTA network. Rev World Econ 159, 333–360 (2023). https://doi.org/10.1007/s10290-022-00469-y
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10290-022-00469-y