Although philosophers enacted thought experiments about how many objects the mind can hold simultaneously (Hamilton, 1859, p. 253), it was Stanley Jevons who designed a disarmingly simple experiment using a round paper box and randomly selected handfuls of black beans (Jevons, 1871). He established that during a single glance he was able to identify the correct number of beans only if there were less than five of them. This ability to evaluate the number of elements in a set—numerosity—without symbolic representation is a form of primitive perceptual intelligence, which emerged relatively early in evolution (Gatto et al., 2021; Nieder, 2021). Because the approximate number of objects can be registered without precise counting, psychologists usually prefer simple tasks in which the observer is instructed to decide which of the two distinctive sets of objects appears more numerous. These two sets can occupy two spatially or temporally distinct observational areas (Allik et al., 1991; Allik & Tuulmets, 1991, 1993; Anobile et al., 2015; Burgess & Barlow, 1983; Durgin, 1995; Libertus et al., 2011; Newman, 1974), or they can be spatially intermixed but distinguished by a certain visual attribute, such as color, orientation, or motion direction (Dakin et al., 2011; Halberda et al., 2008; Honig & Matheson, 1995; Morgan et al., 2014; Raidvee et al., 2011; Raidvee et al., 2017; Ratcliff & McKoon, 2018; Tokita & Ishiguchi, 2010; Varey et al., 1990; Viviani, 1979).

Usually, participants are not given instructions regarding the response speed in these numerosity discrimination tasks. It is believed that the response time (RT) that is needed to discriminate two numerosities depends mainly on the number of response alternatives (e.g., Seibel, 1962), not the number of elements that participants were asked to discriminate. Thus, there was no incentive to analyze RTs in experiments with a fixed number of response alternatives even if they were registered. Not surprisingly, we are aware of only a few studies in which RTs were analyzed in addition to the correctness of answers. As an exception, Viviani observed that the response latencies were longest when discriminated numerosities were very similar, and they shortened when the disparity between numbers increased (Viviani, 1979). Because discrimination probabilities alone cannot identify the exact form of the internal representation of numerosities, the use of RTs has been proposed for both correct and wrong responses, to reconstruct the exact form of internal representations (Ratcliff & McKoon, 2018). These two studies are examples of using RTs as a relevant source of additional information for specification of the psychological architecture underlying numerosity discrimination.

As is well documented, experimental psychology started from the analysis of RTs (Boring, 1957/1929; Grice et al., 1982; Niemi & Näätänen, 1981; Robinson, 2001). Because RTs are believed to measure the amount of information processing that is needed to reach a decision, it can potentially be used as an indicator of these psychological processes that precede overt responses. There is a common language to describe how the nervous system reaches decisions, which assumes that some unobservable processes are developing in time and result in overt responses when these processes meet certain termination criteria. It was noticed that there are two principally different ways to describe this preparatory process (Grice, 1968; McGill, 1963). First, the process developing in time is stochastic achieving a fixed termination criterion. Second, the growth process is deterministic, but the threshold to reach is variable. However, these two modeling schemes turned out to be formally identical ways of expressing mathematically identical models (Dzhafarov, 1993). As an inevitable consequence, these two models are not falsifiable models but rather equivalent statements in two different formal languages (cf. Jones & Dzhafarov, 2014).

One of the main reasons, however, to propose the decision process that develops in time is a frequent observation that the strength of the stimulus determines the length of the RT. One of the first noticed regularities was RT shortening with the intensity of the stimulus (Piéron, 1913). This regularity was observed on numerous occasions (cf. Murray, 1970). In the numerosity discrimination task studied here, intensity can be defined as the absolute difference |ΔN| between numbers in the two sets. It is expected that RTs will be longer for two sets with approximately the same number of elements and RTs will shorten as the difference in numbers becomes larger (cf. Ratcliff & McKoon, 2018; Viviani, 1979).

Another consequence of describing RT as a process evolving in time, is speed–accuracy trade-off (SAT), which arises due to the inherent contradiction between response speed and decision accuracy (Grice & Spiker, 1979; Heitz, 2014; Niemi & Näätänen, 1981; Wickelgren, 1977). The SAT characterizes flexibility of responding, allowing to choose strategically between time that is needed to accumulate evidence and a sufficient amount of information that is needed for an informed decision (Heitz, 2014). There are several methods for manipulating SAT, such as verbal instructions, payoff matrices rewarding correct decisions and penalizing errors, and imposing response deadlines (Wickelgren, 1977). Numerous studies have shown that these manipulations can effectively change SAT within a given set of experimental conditions (Grice & Spiker, 1979). However, if different experimental conditions are compared then SAT cannot be observed unless response criteria are systematically manipulated. For example, replacing an easy task with a more challenging one does not imply that it necessarily takes more time to answer. It was observed that discriminating numerosities of two sets of elements distinguished by color (red and green dots) can be more accurate than that of two sets that differ by element symmetry (parallel lines versus converging lines; Tokita & Ishiguchi, 2009, 2010). However, there is no evidence that a more difficult task takes necessarily more time to execute. It is possible that a more complicated perceptual task is answered more quickly in spite of a higher error rate (cf. Raidvee et al., 2017). Thus, without manipulating instruction, payoff, or response deadline, it is not expected to observe SAT between tasks of various difficulties.

Like any other discrimination task, Thurstonian psychophysics (Thurstone, 1927) is a convenient tool for describing numerosity discriminations. It is assumed that the number of elements in each set creates a noisy internal representation of these numbers based on which discrimination decisions can be made. The standard deviation of the best fitting cumulative normal distribution provides an estimate of the magnitude of these summary noises (cf. Burgess & Barlow, 1983; Dakin et al., 2011; Halberda et al., 2008; Van Oeffelen & Vos, 1982). Like many perceptual attributes, the precision with which an absolute difference |ΔN| between two numerosities can be discriminated depends on the total number N. The difference |ΔN| that can be discriminated with a fixed threshold probability is called the just noticeable difference (JND). It was observed that the JND tends to be approximately proportional to the number N from which deviations are discriminated: JND/N ≈ constant (e.g., Ditz & Nieder, 2016; Emmerton & Renner, 2006; Newman, 1974; Testolin & McClelland, 2021). This constant fraction is also known as Weber’s law, which is believed to have a special meaning for the approximate number system (Dehaene, 2003; Testolin & McClelland, 2020). However, the relationship between JND and N for numerosity discrimination can be more generally described by a power function JND = kNp where p is closer to .7 or .8 (Allik & Tuulmets, 1991; Anobile et al., 2014; Burgess & Barlow, 1983; Krueger, 1984), which appears to suggest that the constant ratio between JND and N is not a necessary outcome. Although it is obvious that increasing N also increases JND, there is no reason why their ratio should remain the same (p = 1).

Beside deviations from the strict Weber’s law there are some other problems that make the Thurstonian approach problematic when applied to discrimination of numerosities. One of these hitches was previously indicated as an infinite size of internal representations (Raidvee et al., 2017). The assumption that the number of elements in each set is represented on a continuum of perceptual states resembling the axis of real numbers may be debatable. Although the choice of Gaussian distribution for internal representations seems to have no realistic alternatives, it is obviously not true. For example, it was possible to demonstrate that the binomial probability β, with which each element can be noticed and registered by the perceptual system, can provide an equally accurate explanation for numerosity discriminations (Raidvee et al., 2017).

This idea that the number of elements that observers are instructed to discriminate cannot be detected with absolute certainty is well known in another context. The assumption that each element can be detected with a probability β less than 1 (Raidvee et al., 2017) leads inevitably to the conclusion that numerosity discriminations are based on a fraction of all displayed elements. Ronald Fisher (1925) proposed that statistical efficiency can be estimated by measuring the ratio of information that is used in decisions to the amount of available information. Applying this idea to discriminations between the numbers of dots in a pair of irregular arrays, it was indeed shown that the observed precision can be characterized by the size of an incomplete sample which was used for discrimination (Burgess & Barlow, 1983). Thus, the detection probability β can be regarded also as a measure of statistical efficiency.

In the abovementioned study (Raidvee et al., 2017), the observers were instructed to discriminate numerical proportions of two sets of spatially intermingled elements (N = 9, 13, 33, and 65) that differed either by their color or orientation. Because the precision of numerosity discrimination was the main interest, only the choice probabilities when one of these two sets appeared more numerous were analyzed. However, all RTs were recorded and can be analyzed as indicators of the preparatory processes. Because no instructions were given about response speed, participants were free to choose the response pace most convenient for them. Nevertheless, it is possible that their RTs reflect the psychological processes that are required for them to choose one of two response alternatives. If the decision process needs more time to reach a termination criterion, then it could be reflected in prolongation of the RT. In this follow-up study we focus solely on the previously ignored RTs and their relations to the numerosity discrimination accuracy.

Method

The methods are described briefly since a more detailed description was given in the previous paper (Raidvee et al., 2017).

Participants

Four 20-year-old female observers with normal or corrected-to-normal vision were asked to decide which of the two distinctive sets of objects was more numerous.

Stimuli

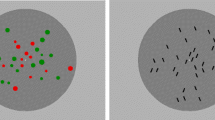
In two separate series, the two sets of objects were distinguished either by color or by orientation. A schematic view of the two types of stimulus configurations is depicted in Figure 1. In the first series, a randomly distributed collection of red and green circles was presented. In the second series of experiments, a collection of short black line segments with a 20° tilt either to the left or to the right was presented.

Fig. 1
figure 1

Schematic view of two types of stimuli used for the study of discrimination of numeric proportions. This figure is reproduced from Raidvee et al. (2017). (Color figure online)

Full size image

The total number of objects N presented on the display was kept constant through each experimental session and was equal to N = 9, 13, 33, or 65 elements. During experimental sessions, the relative proportion of type A and type B elements was varied in random order. The total number of elements N was constant throughout each session while the number of elements in each subset varied around the mean value N/2.

The choice probabilities of category A (red circles or leftward-tilt) was plotted as a function of the proportion of red or leftward tilt elements NA of the total number of elements on the display N = NA + NB. All these probabilities were shown in our previous publication (Raidvee et al., 2017, Fig. 2), and are thus not reproduced here. We were interested in the RTs, which were measured as time intervals from the beginning of the stimulus prresentation until pressing one of the response buttons.

Fig. 2
figure 2

(A) Response times as a function of the absolute difference |ΔN| in the number of elements in two sets distinguished by the elements’ color. (B) Response times as a function of the absolute difference |ΔN| in the number of elements in two sets distinguished by the elements’ tilt. (Color figure online)

Full size image

Results

For each number of elements (N = 9, 13, 33, and 65) and stimulus attribute (color or tilt) an empirical discrimination function dependent on the differences in the number of elements ΔN was constructed. It is important to remember that N is the sum of numbers of elements in two sets and the average number of elements in each set was N/2. Because data of the four observers were similar both qualitatively and quantitatively it would be more economic to analyze their average data. For these averaged empirical discrimination functions (Raidvee et al., 2017, Fig. 2e) the best fitting cumulative normal distribution was determined, the standard deviation (reverse to the slope) of which characterizes the imprecision with which numerosity differences ΔN between two sets of elements can be noticed. The JND that is required to tell the difference between two sets apart in 84.1% of the trials is equal to the standard deviation of the cumulative normal discrimination function. In Table 1, JND values for two discrimination tasks (color and orientation) and different number of elements N = 9, 13, 33, and 65 are presented. We also determined the best fitting parameter β in the binomial model that provided optimal description for the collected data (see Table 1). An alternative method for finding β is based on a simple formula transforming the standard deviation of normal distribution into the corresponding binomial parameter β (Raidvee et al., 2017, Appendix 2).

Table 1 The best fitting binomial model parameter β and the respective JND for two discrimination tasks (color and orientation) and different total number of elements, N = 9, 13, 33, and 65
Full size table

Both β and JND reveal that numerosity discriminations based on the elements’ color were easier than discrimination based on the elements’ orientation. For example, for the smallest set of  N = 9 each element was noticed with probability .83 when color was the distinctive attribute and only with probability .51 when elements were distinguished by their tilt. In terms of JND, the average difference noticed was .5 elements for color and 1.0 for orientation. As the total number of elements N increases the binomial parameter β decreases and JND increases. For example, two sets of elements N = 9 distinct in orientation were discriminated with a JND = 1. However, to notice a difference in numbers in a set N = 65, more than JND = 6.2 extra elements were required in one of these two sets.

Four participants made altogether over 27,200 discrimination decisions for the variety of numerical proportions of the two sets of elements that differed either by color or orientation. Although no demands were presented on response speed, to eliminate responses that were not related to the stimulus, we analyzed RTs that were in the range from RT >300 ms to RT <2,000 ms. According to this criterion, about 1.2% and 1.5% of trials were eliminated from the analyses for color and orientation discrimination series, respectively. For each series of experiments with a constant total number of elements N we computed the mean RT for the correct answers and plotted them as a function of the absolute difference |ΔN| between numbers of elements in these two sets of elements. Figure 2 demonstrates the mean RT as a function of the absolute difference |ΔN| for sets of elements distinguished by the elements’ color (Fig. 2a) and tilt (Fig. 2b). We also computed linear regression between RT and |ΔN| for each block of data for a fixed total number of elements N. The relationship between the mean RT and the absolute difference in numbers |ΔN| between two sets can be described by linear regressions. Because correlations were in the range from .92 to .99, the linear component was in all cases ubiquitous. The slopes of these regressions flatten as the total number of elements N grows. In proportion discrimination by color (Fig. 2a) the regression coefficients were 39.5, 23.8, 17.9, and 7.22 for N = 65, 33, 13, and 9, respectively. Similar sequence of regression coefficients for the tilt discrimination (Fig. 2b) was 31.3, 18.1, 5.1, and 1.7. For example, the increase of difference |ΔN| by one more element decreased the mean RT by about 39 and 32 ms for N = 9 red–green dots and left–right lines, respectively. However, the slope of regression was flatter when there were N = 65 elements in total: the mean RT decreased by 7 and by 2 ms for color and tilt respectively with each unit increase in |ΔN|.

It is possible to see the slope of the regression function become flatter or smaller as the number of elements increases. Together with the decrease of the regression slope the residual RT (|ΔN| = 0) became shorter with the increase of N, which was particularly unmistakable with the largest number of elements N = 65. Figure 3 demonstrates the dependence on these regression coefficients of the parameter β of the binomial model, which can be interpreted as the probability with which each element in these two sets of objects is noticed. There is a sufficiently strict linear relationship between efficiency with which two sets of elements can be distinguished and the rate with which the mean RT becomes shorter as the absolute difference |ΔN| increases. For both attributes, color and tilt, as the discrimination precision β decreases with increasing total number of elements N, the rate with which the mean RT diminishes becomes slower as well. However, the relationship between the regression coefficients and JNDs (Table 1) was less straightforward than with the binomial probabilities β, suggesting that the binomial model provides slightly better explanation than the more traditional Gaussian noise model.

Fig. 3
figure 3

The mean probability β with which each element can be noticed as a function of the regression coefficients shown in Fig. 2a–b. (Color figure online)

Full size image

Although discrimination of two sets based on elements’ tilt was a more demanding task than discrimination based on color, the observed drop in β values was not accompanied by an increase in RTs as would have been expected by a speed-accuracy tradeoff. For example, the residual time (intercept or |ΔN| = 0) to discriminate two sets with total number of elements N = 65 was 819 ms (Fig. 2a), which was considerably longer than 633 ms (Fig. 2b) that was residually needed to discriminate sets by the tilt of their elements even though colored elements were registered (β = .36) about two times more accurately than tilted elements (β = .18).

Discussion

The ability to discriminate two sets by their numbers of elements, without invoking symbolic representations, is a form of primitive perceptual intelligence (cf. Näätänen et al., 2001) which appeared in evolution long before the emergence of semiotic and symbolic competences (Gatto et al., 2021; Nieder, 2021). Although assessing which of two distinct sets includes more elements is a popular task in the study of numerosity perception (e.g., Allik & Tuulmets, 1991; Burgess & Barlow, 1983; Halberda et al., 2008; Tokita & Ishiguchi, 2010), researchers have seldom asked the question of how much time does it take to make these discriminations (for exceptions, see Ratcliff & McKoon, 2018, 2020; Viviani, 1979). However, time and again a question arises how numerosity is perceived. A traditional view established in Thurstonian psychophysics is that the number of elements is projected onto a continuum of psychological states which can be described by a cumulative normal or Gaussian distribution (e.g., Van Oeffelen & Vos, 1982). Recently, we proposed an alternative explanation that instead of an infinite continuous representation numerosity can be represented equally well by a discrete binomial distribution (Raidvee et al., 2017; Raidvee, Põlder, et al., 2012), which is based on another basic idea that only a fraction of available information is used. However, if the correctness of answers is analyzed, then the predictions of these two models have only subtle differences. One additional but rarely used resource is the analysis of response times (cf. Ratcliff & McKoon, 2018, 2020; Viviani, 1979).

In this study, two principal results deserve to be mentioned. The first is that RTs precisely follow stimulus strength (cf. Grice, 1968) which in the present case is the absolute difference in the number of elements |ΔN| in the two presented sets. As the disparity between two sets |ΔN| increased, the choice probability became more accurate and RTs became shorter. The relationship between the mean RT and the absolute difference in the number of elements was described by a linear function: an increase of  |ΔN| by each additional element reduced the mean RT by approximately the same amount of time. However, the slope of the linear relationship was not constant across different conditions. The regression coefficient decreased (or the slope was flattened) as the total number of elements N increased. This means, as expected, that the perceptual strength of the same extra number of elements |ΔN| is more salient among small sets of elements, let’s say N = 9, becoming more restrained among larger sets such as N = 65. This is another way of saying that the speed of discrimination is a function of the total number of elements N. The slopes of regression between RT and |ΔN| were different for different perceptual attributes -- color vs tilt. Judging by the discrimination precisions, color—red vs green—was a stronger perceptual attribute than tilt—rightward vs leftward. Thus, parallel to the discrimination precision, mean RT may also be used as an indicator of the perceptual strength of the stimulus.

The second result to mention is the slope of regression between RT and |ΔN| that was more directly related to the binomial probability β than to the standard deviation of the best fitting psychometric function (Raidvee et al., 2017). A traditional approach assumes, as we mentioned above, that the number of elements in each set is transformed into a noisy representation with supposedly normal or Gaussian distribution (e.g., Burgess & Barlow, 1983; Ratcliff & McKoon, 2018; Van Oeffelen & Vos, 1982). As an alternative approach, it was assumed that each element has a probability β with which it can be noticed and registered (Raidvee et al., 2017). Despite obvious differences, these two explanations are formally identical in the large n approximation because for every binomial probability β there is a corresponding standard deviation of the normal distribution characterizing the precision with which numerosities can be discriminated (Raidvee et al., 2017, Appendix 2). Thus, the representational Gaussian noise is directly related to the binomial probability β which characterizes the observer’s failure to see salient objects because of a lack of attention, i.e., inattentional blindness (Mack & Rock, 1998; Simons, 2000). Nonetheless, the binomial model has an advantage due to the smaller number of the model’s free parameters. While Gaussian distribution has two parameters— mean and standard deviation—then binomial distribution has only one—the probability β of noticing each element. Usually, the goodness of fit of a candidate model is assessed by estimators such as the Akaike information criterion, which includes penalties for an increasing number of the estimated model’s free parameters. For that reason, the binomial model had an advantage over Gaussian model although the goodness of fit in absolute terms was very similar (Raidvee et al., 2017). Since there were no numerosity illusions which would have made, for example, red dots appear more numerous than the same number of green dots, the normal cumulative function was always centered around zero |ΔN| value which means that one of the model’s free parameters can be fixed without losing much in the goodness of fit. Not least, the distinction between Gaussian and binomial distributions is elusive because binomial distribution becomes practically inseparable from the normal distribution with the increase of the number of binomial trials n. Only for a sufficiently small number of elements it is possible to distinguish between the Gaussian vs binomial models. The same holds true for numerical proportion discrimination models based on binomial vs hypergeometric distributions. The distinction between these two distributions, binomial and hypergeometric, is relevant if we suspect that proportion discrimination has a serial component and some of the elements may be processed more than once (cf. Raidvee, Põlder, et al., 2012a). Unfortunately, the question of whether the already-processed elements can be separated from the to-be-processed elements in forming impressions about numerosities is seldom considered.

As a consequence, based on formal criteria alone, it would be difficult to decide which of the two models—Gaussian or binomial—is a more adequate description of the discrimination of numerical proportions. There seems to be a tacit assumption that the central limit theorem also applies in visual perception, and independent neural processes that underlie numerosity perception are summed up to form a normal distribution even if they themselves are not normally distributed. However, this  assumption has very limited empirical support. In most cases, the choice of the Gaussian distribution is a mathematical convenience, not a conclusion derived from evidence. For instance, if the exact form of underlying noise distribution was tested it was clearly not Gaussian but better described by the double-exponential Laplacian distribution (cf. Neri, 2013). Nevertheless, while normal distribution implements the fundamental principle that all perceived attributes have a noisy internal representation, the binomial model represents another basic idea that observer’s performance is degraded by inattention with only a subsample of actually available information being processed (Burgess & Barlow, 1983). Please notice that the product of the binomial parameter and number of elements, ßN, specifies the size of a subsample presumably used in discrimination decisions. Unfortunately, these two principles—representational noise and inattentional feature blindness—are difficult to separate in tasks assuming forming statistical summaries of some visual attributes such as size or orientation. In distinguishing the Gaussian model from the binomial one, it is necessary to demonstrate whether all displayed elements are taken into account for making decisions. An assumption of the binomial model is that not all of the elements are necessarily used for making decisions. Recently, a method was proposed for detection of inattentional feature blindness -- the idea was to use only a single informative element which when neglected is reflected in the lapse rate deforming the shape of the psychometric function (Raidvee et al., 2021). Another possibility is to use different instructions with regard to the same stimulus patterns to separate visibility from accountability (Raidvee, Averin, et al., 2012b). However, this second task, demonstrating that all elements in the set were indeed noticed and processed, needs yet to be invented.

Previous studies have suggested, however, that if there is not enough information to decide how numerosities are perceptually represented, it may be necessary to analyze response times as an additional source of information about representations (cf. Ratcliff & McKoon, 2018; Viviani, 1979). Following these recommendations, it was stimulating to see how the discovered regularity—the rate with which RTs become shorter as the numerical difference |ΔN| increases—is related to the binomial probability β (Fig. 3) and to the standard deviation of the best fitting cumulative normal distribution from which we can compute JND or the smallest detectable numerical difference |ΔN|. As demonstrated in Fig. 3, the mean RT decrease rate measured by the coefficient of linear regression was quite straightforwardly related to the binomial probability β. Because the binomial probability β is inversely related to the standard deviation of the corresponding Gaussian fit of the discrimination function (Raidvee et al., 2017, Appendix 2), if the regression coefficients between RTs and |ΔN| are linearly related to the binomial β, then a linear relationship with the standard deviation of the normal distribution function or JND is unlikely. If the binomial probability β and the standard deviation values are not selected from a narrow section of the inverse function where the relationship is more or less linear then we can decide which of these two parameters is more simply related to the rate of the RT reduction. Avoiding categorical conclusions, it seems that the reduction rate of RTs is more directly related to the estimated binomial probability ß than to the standard deviation of the best fitting Gaussian function and the JND derived from it. Thus, in addition to the analyses of correct and wrong answers (Raidvee et al., 2017), this result supports the idea that the binomial model is a realistic alternative to a more traditional Gaussian representation.