Abstract
Jacobi’s results on the computation of the order and of the normal forms of a differential system are translated in the formalism of differential algebra. In the quasi-regular case, we give complete proofs according to Jacobi’s arguments. The main result is Jacobi’s bound, still conjectural in the general case: the order of a differential system \(P_{1}, \ldots , P_{n}\) is not greater than the maximum \({{\mathcal {O}}}\) of the sums \(\sum _{i=1}^{n} a_{i,\sigma (i)}\), for all permutations \(\sigma \) of the indices, where \(a_{i,j}:=\mathrm{ord}_{x_{j}}P_{i}\), viz. the tropical determinant of the matrix \((a_{i,j})\). The order is precisely equal to \({{\mathcal {O}}}\) iff Jacobi’s truncated determinant does not vanish. Jacobi also gave a polynomial time algorithm to compute \({{\mathcal {O}}}\), similar to Kuhn’s “Hungarian method” and some variants of shortest path algorithms, related to the computation of integers \(\ell _{i}\) such that a normal form may be obtained, in the generic case, by differentiating \(\ell _{i}\) times equation \(P_{i}\). Fundamental results about changes of orderings and the various normal forms a system may have, including differential resolvents, are also provided.





Similar content being viewed by others
Notes
References to manuscripts and first editions are given page 92.
From some optimistic standpoint, it could have been a way to escape ethical issues raised by the use of psychology in management.
Jacobi defined also the maximal elements in right columns as “starred”; we prefer to reserve this denomination to left transversal maxima to underline the specific roles played by these two sets of maxima in the algorithm.
Determinans mancum, or Determinans mutilatum.
Ritt [86, chap. II Sect. 17 p. 32] defines singular components only in the case of an ideal generated by a single polynomial.
The meaning of this classical notion of regularity is of a different nature and will be investigated in Sect. 7.4
Jacobi used many different notations for his bound. In our translation [40], we used H for consistency, following Borchardt’s posthumous edition [Crelle 64]. The bound is actually denoted by \(\mu \) in the manuscript [II/13 b)]. See [40, fig. p. 32]. We prefer here the notation \({{\mathcal {O}}}\), used in [II/23 b)], as H is now a standard notation in differential algebra for the product of initials and separants.
We allow ourselves to write
 instead of \(a_{{{\mathcal {P}}}\!,\,i,\,j}\) for more readability.
instead of \(a_{{{\mathcal {P}}}\!,\,i,\,j}\) for more readability.In the linear case, the result has been proved by Ritt [85].
Looking for the order of the system, as one only considers the highest derivatives in the linear equations to which the proposed ones are reduced, one may assume [their] coefficients to be constants. Because, differentiating the equations 3) iterated times in order to obtain new equations [...]
The orders \(a_{i}\) or \(b_{i}\) correspond to \(\alpha _{i}\) or \(\beta _{i}\) in Jacobi’s notations, in order to reserve these Greek letters to covers. This writing can coexist with the order matrix notation \(a_{i,j}=\mathrm {ord}_{x_{j}}A_{i}\), so that \(a_{i}\) is a convenient shorthand for \(a_{i,i}\).
These orders are already in Riquier [83, p. 195].
As we are only concerned here with the differential case, we omit “differential” in the sequel.
The word resolvent was not used by Jacobi, but he evokes the notion as something well known in the the mathematical folklore of his time: “It is usual that this type of normal forms be considered before others by mathematicians”.
Nanson [76] and Jordan [54] proposed independently heuristic methods for proving Jacobi’s bound, that rely on resolvent computations. The first considers the case \(n=3\) and the second the case \(n=4\), recursively using formula \({{\mathcal {O}}}=\max _{i} a_{i,j_{0}}+{\bar{{{\mathcal {O}}}}}_{i,j_{0}}\) and the bound \({\bar{{{\mathcal {O}}}}}_{i,j_{0}}\) on the order of differentiation of each equation \(P_{i}\), which is guessed using informal considerations on the number of derivatives of the equation \(P_{i}\), and the number of derivatives of the \(x_{j}\), \(j\ne j_{0}\) that the computation of a resolvent requests. Their relation is expressed by the formula
$$\begin{aligned} \sum _{i=1}^{n}\left( {\bar{{{\mathcal {O}}}}}_{i,j_{0}}+1\right) =1+\sum _{j\ne j_{0}}\left( \max _{i=1}^{n}({\bar{{{\mathcal {O}}}}}_{i,j_{0}}+a_{i,j})+1\right) , \end{aligned}$$so that there are exactly one more algebraic equations than derivatives of the \(x_{j}\), \(j\ne j_{0}\), involved in them, making their potential elimination possible. The last formula is proved in Corollary 173.
It may be computed as in Sect. 3.6. By Proposition 54, the path relation does not depend on the choice of the permutation \(\sigma \). The canon itself is also independent of this choice: if \(a_{j_{0},j_{0}}+\ell _{j_{0}}\) is maximal, then for any permutation \(\sigma \) such that \({{\mathcal {O}}}=\sum _{i=1}^{n}a_{i,\sigma (i)}\), the quantity \(a_{\sigma ^{-1}(j_{0}),j_{0}}+\ell _{\sigma ^{-1}(j_{0})}\) must be maximal too.
One may look at formula (3) p. 14 for an illustration of the situation. The notion of increasing path is used here in the reverse way: one deduces a maximal transversal sum for \({{\bar{A}}}_{i_{0},j_{0}}\) from a maximal transversal sum for \(A_{P}\).
Reference established from Bull. Amer. Math. Soc. 12 (1906), p. 212. In the copy I could consult, there is no publisher indication, and the handwritten date 1852.
References
Adelson-Velsky, G., Landis, E.: An algorithm for the organization of information. Doklady Akademiya Nauk SSSR 146, 263–266, 1962; English translation, Soviet Math. 3, 1259–1263, (1962)
Aroca, F., Garay, C., Toghani, Z.: The fundamental theorem of tropical differential algebraic geometry. Pac. J. Math. 283(2), 257–270 (2016)
Bass, H., Connell, E.H., Wright, D.: The Jacobian conjecture: reduction of degree and formal expansion of the inverse. Bull. Am. Math. Soc. (New Ser.) 7(2), 287–330 (1982)
Bellman, R.: On a routing problem. Q. Appl. Math. 16, 87–90 (1958)
Boulier, F., Lemaire, F., Moreno Maza, M.: “PARDI !”, ISSAC 2001, ACM Press, 38–47, (2001)
Boulier, F., Lazard, D., Ollivier, F., Petitot, M.: Computing representations for radicals of finitely generated differential ideals. Spec. Issue Jacobi’s Legacy AAECC 20(1), 73–121 (2009)
Burkard, R., Dell’Amico, M., Martello, S.: Assignment Problems. SIAM, Philadelphia (2012)
Briefwechsel Zwischen, C.G.J., Jacobi und, M.H. Jacobi, Herausgegeben von W. Ahrens, Abhandlungen zur Geschichte der Mathematischen Wissenschaften, XXII. Heft, Leipzig, Druck und Verlag von B.G. Teubner (1907)
Ferro, C.: Giuseppa: a resultant theory for ordinary algebraic differential equations. In: Mora, T., Mattson, H. (eds.) Applied Algebra, Algebraic Algorithms and Error-Correcting Codes, LNCS vol 1255, 55–65. Springer, Berlin (1997)
Castro-Jiménez, F.-J.: Calculs effectifs pour les idéaux d’opérateurs différentiels, Actas de la II Conferencia Internacional de Geometría Algebraica, La Rábida, Travaux en Cours 24. Hermann, Paris (1987)
Castro-Jiménez, F-J., Granger, M.: Explicit calculations in rings of differential operators. Séminaires & Congrès, 8, 89–128, SMF (2004)
Chrystal, G.: A fundamental theorem regarding the equivalence of systems of differential equations, and its application to the determination of the order and the systematic solution of a determinate system of such equations. Trans. R. Soc. Edinb. 38(1), 163–178 (1897)
Cluzeau, T., Hubert, É.: Resolvent representation for regular differential ideals. AAECC 13(5), 395–425 (2003)
Cohn, R.M.: Order and dimension. Proc. Am. Math. Soc. 87(1), 1–6 (1983)
D’Alfonso, L., Jeronimo, G., Solernó, P.: On the complexity of the resolvent representation of some prime differential ideals. J. Complex. 22(3), 396–430 (2006)
D’Alfonso, L., Jeronimo, G., Solernó, P.: A linear algebra approach to the differentiation index of generic DAE systems. AAECC 19(6), 441–473 (2008)
D’Alfonso, L., Jeronimo, G.G., Ollivier, F., Sedoglavic, A., Solernó, P.: A geometric index reduction method for implicit systems of differential algebraic equations. J. Symb. Comput. 46(10), 1114–1138 (2011)
D’Alfonso, M.E.: Métodos simbólicos para sistemas de ecuaciones álgebro-diferenciales. PhD thesis, University of Buenos Aires (2006)
Dora, D., Jean, D., Claire, D.: Dominique: about a new method for computing in algebraic number fields. Eurocal’85. Springer, LNCS 204, 289–290 (1985)
Dijkstra, E.W.: A note on two problems in connexion with graphs. Numerische Mathematik, 1, 269–271, Springer (1959)
Dinic, E.A., [Dinic (Yefim)], Kronrod, M.A.: An algorithm for the solution of the assignment problem. Soviet Math. Dokl. 69(6), 1324–1326 (1969)
Duan, R., Pettie, S.: Approximating maximum weight matching in near-linear time. Proceedings of the \(51^{rst}\) Annual IEEE Symposium on Foundations of Computer Science (FOCS), 673–682 (2010)
Edmonds, J., Karp, R.M.: Theoretical improvements in algorithmic efficiency for network flow problems. J. ACM 19, 248–264 (1972)
Egerváry, J.: Matrixok kombinatorius tulajdonságairól. In: Hungarian: On combinatorial properties of matrices, Matematikai és Fizikai Lapok, vol. 38, 1931, 16–28; translated by H.W. Kuhn as Paper 4, Issue 11 of Logistik Papers, Georges Washington University Research Project (1955)
Faugère, J.-C., Gianni, P., Lazard, D., Mora, T.: Efficient computation of zero-dimensional Gröbner bases by change of ordering. J. Symb. Comput. 16(4), 329–344 (1993)
Ford, L.R., Jr.: Network flow theory, Paper P-923. RAND Corporation, Santa Monica, California (1956)
Fredman, M.L., Tarjan, R.E.: Fibonacci heaps and their uses in improved network optimization algorithms. J. ACM 34(3), 596–615 (1987)
Frobenius, F.G.: Über Matrizen aus nicht negativen Elementen. Sitzungsberichte der Königlich Preußischen Akademie der Wissenschaften zu Berlin, 456–477 (1912)
Frobenius, F.G.: Über zerlegbare Determinanten. Sitzungsberichte der Königlich Preußischen Akademie der Wissenschaften zu Berlin, 274–277 (1917)
Gabow, H.N., Tarjan, R.E.: Faster scaling algorithms for network problems. SIAM J. Comput. 18, 1013–1036 (1989)
Giusti, M., Lecerf, G., Salvy, B.: A Gröbner free alternative for polynomial system solving. J. Complex. 17(1), 154–211 (2001)
Golubitsky, O., Kondratieva, M., Moreno Maza, M., Ovchinnikov, A.: Bounds and algebraic algorithms in differential algebra: the ordinary case. In: Decker, W., Dewar, M., Kaltofen, E., Watt, S.M. (eds.) Challenges in Symbolic Computation Software, N\(^{{\rm o}}\) 06271 in Dagstuhl Seminar Proceedings, Internationales Begegnungs und Forschungszentrum für Informatik (IBFI). Schloss Dagstuhl, Germany (2007)
Grier, D.A.: When Computers were Human. Princeton University Press, Princeton (2005)
Hopcroft, J.E., Karp, R.M., et al.: An \(n^{5/2}\) algorithm for maximum matchings in bipartite graphs. SIAM J. Comput. 2(4), 225–231 (1973)
Houtain, L.: Des solutions singulières des équations différentielles. Ann. des Universités de Belgique Années 1851–1854, 973–1323
Hrushovski, E.: The elementary theory of Frobenius automorphisms, preprint, 1996, revised 2004, (2014) arXiv:math/0406514
Hubert, É.: Essential components of an algebraic differential equation. J. Symb. Comput. 21, 1–24 (1999)
Ibarra, O.H., Moran, S.: Deterministic and probabilistic algorithms for maximum bipartite matching via fast matrix multiplication. Inform. Process. Lett. 13(1), 12–15 (1981)
Jacobi, C.G., Jacob: De eliminatione variabilis e duabus aequationibus algebraicis. J. für die Reine und Angew. Mathematik 15, 101–124 (1836)
Jacobi, C.G., Jacob: De investigando ordine systematis aequationum differentialum vulgarium cujuscunque, [Crelle 65], 297–320, [GW V], 193–216. English translation, AAECC 20(1), 7–32 (2009)
Jacobi, C.G., Jacob: De aequationum differentialum systemate non normali ad formam normalem revocando, [VD], 550–578 and [GW V], 485–513. English translation, AAECC 20(1), 33–64 (2009)
Jacobi, C.G.J.: “Theoria novi multiplicatoris systemati aequationum differentialium vulgarium applicandi”, first published in [Crelle 27] Heft III 199–268 (part I) and [Crelle 29] Heft III 213–279 and Heft IV 333–376 (part II), reproduced in [GW IV], 317–509
Jacobi, C.G.J.: Lettre adressée à M. le président de l’Académie des sciences. J. de Math. Pures et Appl., V, 1840, 350–351
Jacobi, C.G.J.: Sur un nouveau principe de la mécanique analytique. C. R. Acad. Sci. Paris, XV, 1842, 202–205; [GW IV], 289–294
Jacobi, C.G.J.: Sul principo dell’ultimo multiplicatore e suo uso como nuovo principio generale di meccanica. Giornale arcadico, XCIX, 129–146, (1844); [GW IV] 511–522
Jacobi, C.G.J.: Sur un théorème de Poisson. C. R. Acad. Sci. Paris, XI, (1840), p. 529; [GW IV], 143–146
Jacobi, C.G.J.: Canon arithmeticus, sive talulæ quibus exhibentur pro singulis numeris primis. Berolini, typis academicis (1839)
Janet, M.: Sur les systèmes d’équations aux dérivées partielles. J. de MathéMat. Pures et Appl., 8e série, tome 3, 65–152. Gauthier-Villars, Paris (1920)
Johnson, D.B.: Efficient algorithms for shortest paths in sparse networks. J. ACM 24(1), 1–13 (1977)
Johnson, J.: Differential dimension polynomials and a fundamental theorem on differential modules. Am. J. Math. 91, 251–257 (1969)
Johnson, J.: Kähler differentials and differential algebra. Ann. Math. 89(1), 92–98 (1969)
Johnson, J.: A notion of regularity for differential local algebras. Contributions to algebra, A Collection of Papers Dedicated to Ellis Kolchin, Edited by Hyman Bass, Phyllis J. Cassidy and Jerald Kovacic, Elsevier, 211–232 (1977)
Johnson, J.: Systems of \(n\) partial differential equations in \(n\) unknown functions: the conjecture of M. Janet. Trans. AMS 242, 329–334 (1978)
Jordan, C.: Sur l’ordre d’un système d’équations différentielles. Ann. de la société Sci. de Bruxelles, 7, B., 127–130 (1883)
Jüttner, A: On the efficiency of Egerváry’s perfect matching algorithm. TR-2004-13, Egerváry Research Group, Budapest, (2004). ISSN 1587–4451
Keller, O.-H.: Ganze Cremona-transformationen. Monatsh. Math. Phys. 47, 299–306 (1939)
Knuth, D.E.: The art of computer programming III. Sorting and searching. Addison-Wesley, Reading (1973)
Koenigsberger, L.: Carl Gustav Jacob Jacobi. Festschrift zur Feier der hundertsten Wiederkehr seines Geburstages, B.G. Teubner, Leipzig (1904), xviii, 554 p
Kolchin, E.R.: Differential Algebra and Algebraic Groups. Academic Press, New York (1973)
Kondratieva, M.V., Mikhalev, A.V., Pankratiev, E.V.: Jacobi’s bound for systems of differential polynomials. Algebra. M.: MGU, s. 79-85 (1982) (in Russian)
Kondratieva, M.V., Mikhalev, A.V., Pankratiev, E.V.: Jacobi’s bound for independent systems of algebraic partial differential equations. AAECC 20(1), 65–71 (2009)
Kőnig, D.: Gráfok és mátrixok. Matematikai és Fizikai Lapok 38, 116–119 (1931)
Kőnig, D.: Theorie der endlichen und unendlichen Graphen, Math. in Monogr. und Lehrb. XVI., Akad. Verlagsges., Leipzig, (1936); AMS Chelsey Publishing, Rhode Island (2001)
Kuhn, H.W.: The Hungarian method for the assignment problem. Naval Res. Logist. Quart. 2, 83–97 (1955)
Kuhn, H.W.: A tale of three eras: the discovery and rediscovery of the Hungarian Method. Eur. J. Oper. Res. 219, 641–651 (2012)
Munkres, J.: Algorithms for the assignment and transportation problems. J. Soc. Industr. Appl. Math. 5, 32–38 (1957)
Landau, L.D., Lifshitz, E.M: Theoretical physics, vol. 1, Mechanics, 3\(^{rd}\) ed., Pergamon Press, Oxford (1976)
Lando, B.A.: Jacobi’s bound for the order of systems of first order differential equations. Trans. Am. Math. Soc. 152, 119–135 (1970)
Le Gall, F.: Powers of tensors and fast matrix multiplication. In: Proceedings of ISSAC’2014, ACM Press, 296–303 (2014)
Li, W., Yuan, C.-M., Gao, X.-S.: Sparse differential resultant for laurent differential polynomials. Found. Comput. Math. 15(2), 451–517 (2015)
Maclagan, D., Sturmfels, B.: Introduction to Tropical Geometry, Graduate Studies in Mathematics 161, AMS, Providence, 363 p., (2015)
Martello, S.: Jenő Egerváry: from the origins of the Hungarian algorithm to satellite communication. Cent. Eur. J. Oper. Res. 18(1), 47–58 (2010)
Matera, G., Sedoglavic, A.: Fast computation of discrete invariants associated to a differential rational mapping. J. Symb. Comput. 36(3–4), 473–499 (2003)
Morrison, S.: The differential ideal \([P]:M^{\infty }\). J. Symb. Comput. 28, 631–656 (1999)
Monge, G.: “Mémoire sur la théorie des déblais et des remblais”, Histoire de l’Académie royale des Sciences, [année 1781. Avec les Mémoires de Mathématique & de Physique pour la même Année] (2e partie) (1784) [Histoire: 34–38, Mémoires :] 666–704
Nanson, E.J.: On the number of arbitrary constants in the complete solution of ordinary simultaneous differential equations. Messenger Math. 6, 77–81 (1876)
Nucci, M.C., Leach, P.G.L.: Jacobi’s last multiplier and symmetries for the Kepler problem plus a lineal story. J. Phys. A Math. Gen. 37, 7743–7753 (2004)
Nucci, M.C., Leach, P.G.L.: The Jacobi last multiplier and its applications in mechanics. Phys. Scr. 78(6), 065011 (2008)
Ollivier, F., Sadik, B.: La borne de Jacobi pour une diffiété définie par un système quasi régulier (Jacobi’s bound for a diffiety defined by a quasi-regular system). C. R. Math. 345(3), 139–144 (2007)
Ollivier, F.: Jacobi’s bound and normal forms computations. A historical survey. World Scientific Publishing Company, Differential Algebra And Related Topics (2008)978-981-283-371-6
Pryce, J.D.: A simple structural analysis method for DAEs. BIT: Numerical Mathematics, vol. 41, no. 2, 364–394, Swets & Zeitlinger (2001)
Rabinowitsch, J.L.: [Rainich (George Yuri)], Zum Hilbertschen Nullstellensatz. Math. Ann. 102, 520 (1929)
Riquier, C.: Les systèmes d’équations aux dérivées partielles. Gauthier-Villars, Paris (1910)
Ritt, J.F.: Differential equations from the algebraic standpoint. Am. Math. Soc. Colloq. Publ., vol. xiv. A.M.S., New-York (1932)
Ritt, J.F.: Jacobi’s problem on the order of a system of differential equations. Ann. Math. 36, 303–312 (1935)
Ritt, J.F.: Differential Algebra. Am. Math. Soc. Colloq. Publ., vol. xxxiii. A.M.S., New-York (1950)
Saltykow, N.N.: L’Œuvre de Jacobi dans le domaine des équations différentielles du premier ordre. Bull. des Sci. Mathématiques, Gauthier-Villars, Paris, 213–228 (1939)
Saltykow, N.N.: Ordre d’un système d’équations différentielles ordinaires de la forme générale. Bulletin (Académie serbe des sciences et des arts. Classe des sciences mathématiques et naturelles. Sciences mathématiques), n\(^{\rm o}\) 1, 141–148 (1952)
Sankowski, P.: Maximum weight bipartite matching in matrix multiplication time. Theoret. Comput. Sci. 410, 4480–4488 (2009)
Sedoglavic, A.: A probabilistic algorithm to test local algebraic observability in polynomial time. J. Symb. Comput. 33(5), 735–755 (2002)
Shaleninov, A.A.: Removal of topological degeneracy in systems of differential evolution equations. Automation and Remote Control, 51, 1599–1605, 1991 (English version). Translation from Avtomatika i Telemekhanika, Issue 11, 163–170 (1990)
Schrijver, A.: Combinatorial Optimization. Springer, Polyhedra and Efficiency (2003)
Schrijver, A.: On the history of combinatorial optimization (till 1960). In: Aardal, K., Nemhauser, G.L., Weismantel, R. (eds.) Handbook of Discrete Optimization, pp. 1–68. Elsevier, Amsterdam (2005)
Schrijver, A.: On the history of the shortest path problem. Documenta Math. Extra Vol. Optim. Stories 155–167 (2012)
Tomizawa, N.: On some techniques useful for solution of transportation network problems. Networks 1, 173–194 (1971)
Volevich, L.R.: On general systems of differential equations. Dokl. Akad. Nauk SSSR, 132(1) 20–23, (1960). English translation Soviet. Math., 1, 458–465 (1960)
Acknowledgements
With the support of Agence Nationale de la Recherche, project ANR-10-BLAN 0109 LÉDA (Logistic of Differential Algebraic Equations) and Maths AM-Sud, project 13MATH-06 SIMCA (Implicit Systems, Modeling and Automatic Control).
Author information
Authors and Affiliations
Corresponding author
Additional information
Dedicated to the memory of Harold W. Kuhn (1925–2014).
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Ollivier, F. Jacobi’s Bound: Jacobi’s results translated in Kőnig’s, Egerváry’s and Ritt’s mathematical languages. AAECC 34, 793–885 (2023). https://doi.org/10.1007/s00200-022-00547-6
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00200-022-00547-6
Keywords
- Differential algebra
- Order of a differential system
- Jacobi’s bound
- Assignment problem
- Differential resolvent
- Shortest reduction in normal form
- tropical determinant



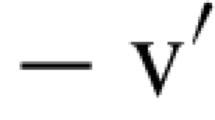
 instead of
instead of