Abstract
Quantum circuit theory has become a powerful and indispensable tool to predict the dynamics of superconducting circuits. Surprisingly however, the question of how to properly account for a time-dependent driving via external magnetic fields has hardly been addressed so far. Here, we derive a general recipe to construct a low-energy Hamiltonian, taking as input only the circuit geometry and the solution of the external magnetic fields. We find that the interplay of geometry and field distribution leads to a much richer circuit dynamics than commonly anticipated, already in devices as simple as the superconducting quantum interference device (SQUID). These dynamics can be captured by assigning negative, time-dependent or even momentarily singular capacitances to the Josephson junctions. Negative capacitances give rise to a strong enhancement of the qubit relaxation rates, while time-dependent capacitances lead to a finite Berry phase.
Similar content being viewed by others
Introduction
Superconducting circuits have proved to be a successful design kit for the creation of new quantum systems, especially for quantum information processing. Artificial atoms, and crafted light-matter couplings, have emulated and extended nature, using the new paradigm of circuit quantum electrodynamics (cQED)1. This paradigm has now produced quantum-computing devices of unrivalled complexity (See https://www.ibm.com/blogs/research/2020/09/ibm-quantum-roadmap/). cQED has been underpinned by a very handy scheme for turning the description of an electric circuit into a quantum Hamiltonian2,3,4,5,6; taking a lumped-element point of view, one identifies capacitors, inductors, and Josephson junctions, each of which contributes its own piece to this Hamiltonian. It has always been understood that, as successors of the superconducting quantum interference device (SQUID), these circuits have a very effective means for in-place control of their quantum characteristics, via the setting of threading magnetic fields.
However, it was very recently remarked by You, Sauls, and Koch7 that some important aspects of the Hamiltonian description of cQED have not yet been appropriately discussed, when including time-dependent (electro)magnetic fields. Inspired by their work, which was based on a purely effective lumped-element approach for the circuit, we rederive the problem of time-dependently driven quantum circuits from scratch, explicitly considering the electromagnetic field problem in continuous space. Our work is therefore, in spirit, reminiscent of efforts to extend the single-mode description of the circuit environment8,9,10,11,12 to more realistic models with continuous degrees of freedom13,14. Importantly, we find that while the results from ref. 7 represent an important first step in the right direction, their treatment is still incomplete, and conclude that already circuits as simple as a SQUID exhibit a much richer dynamics than commonly anticipated.
The issue at hand can be discussed by beginning with the gauge transformations of standard electrodynamics, where the electric and magnetic force fields are expressed by the scalar and vector potentials
As is well-known, a transformation of the potentials, \(V,{{{\bf{A}}}}\to V^{\prime} ,{{{\bf{A}}}}^{\prime}\), is a gauge transformation, if it leaves E, B invariant.
Ultimately, in any Hamiltonian description of a quantum system, it is the gauge-dependent scalar and vector potentials which enter. Thus, there is an entire class of Hamiltonians describing one and the same physical system. In this context, gauge transformations of the potentials can be equivalently expressed as unitary transformations applied to the Hamiltonian. Crucially, for a time-dependent system, the unitary is likewise time-dependent in general, such that it has to show up as an additional term in the Schrödinger equation, H → UHU† − iU∂tU† 15.
Surprisingly, for time-dependent (electro)magnetic fields, this connection between gauge transformations and time-dependent changes of basis, has not yet been correctly taken into account in the existing cQED literature. In fact, prior to ref. 7, the community seems to have disregarded the problem altogether, ignoring the importance of the − iU∂tU† term. You et al.7 first noticed this mistake, and mended it in the limited setting of a lumped element point of view of the circuit, wherein a well-defined, constant, capacitance is assigned to each Josephson junction. We on the other hand find that, while a mapping from the continuous circuit model onto a lumped-element circuit is not per se problematic, it comes in general at the expense of having to assign negative or even time-dependent capacitances to each Josephson junction, depending on the circuit geometry and magnetic field distribution.
We note that the negative-capacitance effect is of purely dynamical origin, and has nothing to do with any material properties such as, e.g., negative capacitances in ferroelectric materials16,17,18,19,20,21. In particular, the total capacitance of an island (sum of junction and other capacitances) remains constant and positive. Nonetheless, the picture of negative and time-dependent capacitances is useful to understand a variety of important consequences. When applying our results to the example of a 1D SQUID-circuit geometry, we find that negative capacitances result in a strong enhancement of qubit relaxation rates, compared to what the standard, lumped-element cQED approach predicts. What is more, time-dependent capacitances lead to a completely new understanding of the dynamics of the SQUID in the presence of a time-dependent flux. Contrary to popular opinion, it is actually not a system with a single time-dependent parameter, but with two. Consequently, a time-dependent flux control of a SQUID can yield a finite Berry phase in the adiabatic regime, the measurement of which is experimentally achievable22,23.
Moreover, we take up an interesting notion of a particular gauge choice proposed by ref. 7: the “irrotational” gauge. In the case of7, this gauge had the property, that terms linear in the circuit charges disappear in the Hamiltonian. In our treatment, we are able to show that the notion of such a gauge can be strongly generalized, and corresponds to the gauge choice, wherein the entirety of the electric field \({{{{\bf{E}}}}}_{\dot{B}}\) induced by the time-varying magnetic field B is represented by the vector potential, \({{{{\bf{E}}}}}_{\dot{B}}=-{\dot{{{{\bf{A}}}}}}_{{{\rm{irr}}}}\). In particular, we find that this irrotational gauge for Airr is the Coulomb gauge, supplemented with an additional boundary condition at the (super)conductor surfaces. The part of Airr parallel to the surfaces connects to the London gauge (and thus to the Meissner screening currents), whereas a generally dominant perpendicular part relates to surface charges generated by the time-varying magnetic field. With this gauge we are able to formulate a precise set of steps in order to arrive at the correct time-dependent Hamiltonian, starting from a general device geometry and a given time dependent magnetic field as the input.
In addition, our proposed gauge allows for a considerable reduction of the computational effort in experimentally relevant device geometries. Namely, due to the widespread use of the Niemeyer-Dolan technique24,25, Josephson junctions are often incorporated in thin, long filamentary structures. The conditions of the irrotational gauge allow us to show that if such junction filaments are sufficiently thin, they can be eliminated from the device geometry altogether when we solve for Airr.
For a general circuit model, finding Airr in practice requires finding the low-frequency solution of \({{{{\bf{E}}}}}_{\dot{B}}({{{\bf{r}}}},t)\) as a response to B(r, t). This is essentially equivalent to a first order expansion in the finite-frequency circuit impedance calculation Feynman presented in his 23rd lecture26, and is also known as the quasi-magnetostatic approximation27. As a result, we expect that state-of-the-art numerical field solvers for capacitances and inductances (such as FastCapTM and FastHenryTM, built on the fundamental methodological insights of Ruehli28,29), often deployed for realistic circuit geometries, would require an extension with corrections due to finite driving frequencies.
To summarize, we expect that a significant portion of existing theory work on circuits driven via time-dependent magnetic fields may have to be reevaluated. In particular, we expect that our results are relevant for the time-dependent control of topological circuits. Namely, to guarantee for a certain topological system in a given symmetry class30,31 to remain in said class under the influence of an external drive imposes in general the same symmetry restrictions onto the extra term − iU∂tU†. In this regard, we believe that our work could for instance be of importance to reevaluate the topological protection of time-dependent flux-driving of Majorana-based circuits32 for realistic device geometries.
Results
The state of the art
For visualization purposes, we refer to the example of a SQUID circuit with a generic geometry (Fig. 1(a)), driven with a time-dependent magnetic field \({{{\bf{B}}}}\left({{{\bf{r}}}},t\right)\). We comment at the end of the “Results” section, how to generalize to arbitrary circuits. We assume that the lumps making up the circuit are perfect (super)conductors, expelling both electric and magnetic fields from their interior. In the SQUID, we refer to one of the lumps as the island i and the other one as the ground g (setting its voltage to zero). They have surfaces \({{{{\mathcal{S}}}}}_{l}\), with vector nl normal to the surface. The index l = i, g enumerates the lumps. Only the surface of the island has to form a closed manifold, the ground surface can be (and usually is) extended. Two Josephson junctions connecting the two lumps enclose a finite area \({{{\mathcal{A}}}}\), which is pierced by the flux
where \({{{\mathcal{A}}}}\) will lie in the \(\left(x,y\right)\)-plane in our examples later.
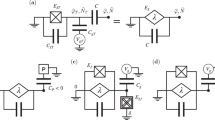
a We develop a recipe to derive the correct time-dependent Hamiltonian for circuits with a general geometry, taking as input the time-dependent magnetic field \({{{\bf{B}}}}\left(t\right)\) (red), from which the time-dependent electric field \({{{\bf{E}}}}\left(t\right)\) (blue) is derived. b We find that in this general case, it is not always possible to assign well-behaved capacitances to the two Josephson junction of a SQUID. While the total capacitance \({C}_{{{\rm{tot}}}}={C}_{{{\rm{eff,}}}1}\left(t\right)+{C}_{{{\rm{eff}}},2}\left(t\right)\) is guaranteed to be constant in time and positive definite, if we force a mapping to a model with effective junction capacitances \({C}_{{{\rm{eff}}},j}\left(t\right)\), these may be negative, time-dependent or even momentarily singular.
Circuits as in Fig. 1(a) are usually right away transformed into a lumped element circuit as shown in Fig. 1(b), where to each junction with Josephson energy EJk one assigns a capacitance Ck.
Any external flux Φ(t) enters the Hamiltonian as a phase \(\phi \left(t\right)=2\pi {{\Phi }}\left(t\right)/{{{\Phi }}}_{0}\) where \({{{\Phi }}}_{0}=h/\left(2e\right)\) is the flux quantum. For a time-independent flux, \(\dot{\phi }=0\), the dynamics of the SQUID circuit is described by a Hamiltonian of the form
where the island charge and phase operators satisfy the commutation relations \(\left[\widehat{\varphi },\widehat{n}\right]=i\), and the total capacitance of the island is Ctot = ∑k=1,2Ck. The capacitive energy term, related to \(\widehat{n}\), can be understood as the kinetic energy of the circuit, while the Josephson energy term, depending on φ, can be regarded as the potential energy. Importantly, in the absence of time-dependent driving, the constant, real parameter α can be chosen arbitrarily: all Hamiltonians Hα will give rise to the same predictions irrespective of α, making α a gauge degree of freedom, expressed by the unitary transformation \({\widehat{H}}_{\alpha }={\widehat{U}}_{\alpha }{\widehat{H}}_{0}{\widehat{U}}_{\alpha }^{{\dagger} }\), with \({\widehat{U}}_{\alpha }={e}^{i\alpha \phi \widehat{n}}\).
When including a time-dependent driving of B, resulting in a time-dependent flux ϕ, it seems tempting to simply take the Hamiltonian (4) for a given α, and insert a time-dependent flux \(\phi \to \phi \left(t\right)\). However, as discussed in ref. 7, this is generally not correct. For a time-dependent \(\phi \left(t\right)\), Hamiltonians (4) with different α give rise to a physically distinct time evolution, simply because the unitary transformation \({\widehat{U}}_{\alpha }\) is now time dependent, and therefore needs to show up in the Schrödinger equation through the extra term \(-i{\widehat{U}}_{\alpha }{\partial }_{t}{\widehat{U}}_{\alpha }^{{\dagger} }=-\alpha \dot{\phi }\widehat{n}\). Hence, to correctly predict the dynamics of the time-dependent problem, when replacing ϕ → ϕ(t), α has to be fixed. The authors of ref. 7 deploy the Lagrangian method including time-dependent contraints, and show that for the SQUID, the time-dependent version of the Hamiltonian Eq. (4) is correct when
The authors refer to this as the irrotational gauge. Thus,7 argues that a Hamiltonian of the form of Eq. (4) can only be found for the time-dependent problem when fixing α through the knowledge of the capacitances of the Josephson junctions Ck. Let us insist, that fixing α does by no means represent a breaking of gauge invariance. Within the above described framework, one may still choose to have any arbitrary α in the potential energy term in the Hamiltonian, Eq. (4). However, for any α other than the one given in Eq. (5), the work of You et al. shows that there will appear linear terms \(\sim \dot{\phi }\widehat{n}\) in the Hamiltonian, due to the time-dependent basis transformation.
Crucially, while we deem the procedure proposed in ref. 7 to be correct when based on the assumptions stated therein, it comes with one particular assumption which we want to put under further scrutiny: the hypothesis that one can assign a definite, constant, positive capacitance Ck to each junction.
In the following, we will consider the problem from a pure electrodynamic point of view, with general, realistic device geometries living in continuous 3D space. Importantly, we will show that indeed, in general this critical hypothesis must be relaxed. In particular, we find that a mapping of the realistic circuit Fig. 1(a) to the lumped element circuit in Fig. 1(b) is only possible if one accepts potentially negative, time-dependent, or even momentarily singular capacitances \({C}_{k}\left(t\right)\), which depend not only on the circuit geometry, but also on the spatial distribution of the magnetic field. It is only guaranteed that the total capacitance \({C}_{{{\mbox{tot}}}}={\sum }_{k}{C}_{k}\left(t\right)\) remains constant and positive. Instead of negative or time-dependent capacitances, one may characterize the Hamiltonian for realistic circuits alternatively via a generalized definition of α (Eqs. (4), and (5)), without explicitly referring to any junction capacitances. According to the treatment by You et al., we see that α has the following properties. It is constant in time, and bounded from above and below, as 0 ≤ α ≤ 1. In our general treatment, both of these traits can be broken. α being either < 0 or > 1 can be interpreted as negative capacitances, whereas a time-dependent α expresses time-dependent capacitances. Crucially, in the second case, the Hamiltonian is in general no longer an operator depending on one time-dependent parameter, but on two. This gives rise to a completely new understanding of the dynamics of a SQUID driven by a time-dependent flux, cf. the “Discussion” section.
The demonstration of the above facts will involve the following two steps. We first lay out the precise conditions under which the induced electric field \({{{\bf{E}}}}\left({{{\bf{r}}}},t\right)\) can be uniquely determined based on a certain circuit geometry as well as a given magnetic field \({{{\bf{B}}}}\left({{{\bf{r}}}},t\right)\). Then, we discuss how we can, given E(r, t), arrive at the scalar and vector potentials with the gauge fixed according to a generalization of the irrotational condition of7.
Solutions of time-dependent electromagnetic fields
Let us assume that a specific magnetic field texture \({{{\bf{B}}}}\left({{{\bf{r}}}},t\right)\) is provided by some external source. Because of the Meissner effect, the magnetic field is expelled from the inside of the conductors, on the length scale given by the London penetration depth λ. In order to figure out the resulting electric field E, it is useful to separate the discussion for the field inside the conductors and outside.
First, let us discuss the interior of the conductors. The Meissner effect involves a screening supercurrent, given by Ampère’s law j = ∇ × B/μ0. For a time-varying magnetic field, there immediately emerges the resulting electric field due to the first London equation, E = μ0λ2∂tj.
Let us say a couple of words about the nature of this electric field. Due to current conservation ∇ ⋅ j = 0, so the current, and therefore the electric field inside, must be fully tangential to the surface, nl ⋅ E = 0. Just like the magnetic field, this tangential electric field penetrates the superconductor to a distance λ inside the surface, as determined by the ac Meissner screening currents. This insight is of importance for the now following discussion of the exterior electric fields.
Namely, for said exterior, the resulting electric field \({{{\bf{E}}}}\left({{{\bf{r}}}},t\right)\) is determined by
As mentioned in the introduction, this is equivalent to a first order expansion of the field solutions discussed by Feynman26. Moreover, the electric field at the conductor surfaces has to satisfy the general boundary condition33, nl × (E1 − E2) = 0, where E1,2 are the electric fields at the interface, when approaching it from the outside or from the inside, respectively. Here, this amounts to
where E on the left-hand side is the solution, when approaching the surface \({{{{\mathcal{S}}}}}_{l}\) from the exterior. The above condition essentially requires the part of the electric field tangential to the conductor surfaces to be continuous, whereas in the exterior, there is an additional component of the electric field, which is allowed to be normal to the surface (henceforth referred to as longitudinal), which abruptly (discontinuously) goes to zero in the interior. Thus, while the tangential part is associated to screening currents, the longitudinal part gives rise to surface charges, localized on the Thomas-Fermi screening length scale, which can be essentially taken to be zero. This approximation, valid for driving frequencies below the plasma frequency, is standard in the literature34,35,36. The solution for E is then fixed and unique if we take the island to have a well-defined total charge,
which is determined through the integral over the above mentioned surface charge
From the uniqueness of E, it follows that one can uniquely decompose the electric field into two components
where EQ satisfies Eqs. (6)–(9) for \(\dot{{{{\bf{B}}}}}=0\), and \({{{{\bf{E}}}}}_{\dot{B}}\) satisfies Eqs. (6)–(9) for Q = 0. Due to linearity, the total electric field is just the sum of these two contributions. Note that even for Q = 0, the time-varying magnetic field in general induces a nonzero surface charge density, captured by the longitudinal part of \({{{{\bf{E}}}}}_{\dot{B}}\). However, in order to comply with Q = 0, the integral of the surface charges associated to \({{{{\bf{E}}}}}_{\dot{B}}\) has to vanish for each individual island.
The two fields EQ and \({{{{\bf{E}}}}}_{\dot{B}}\) have the following properties. Due to a simple scaling argument, we know immediately that EQ must be linear in Q,
where the vector field e, with units of Newtons per Coulomb squared, solves the above equations for \(\dot{{{{\bf{B}}}}}=0\) and Q = 1.
As for \({{{{\bf{E}}}}}_{\dot{B}}\), it can in the most general case only be formally represented as a functional
However, the functional has certain general properties. Firstly, it only contains integrals over spatial compontents, whereas the time-dependence is parametrical (because the problem is time local). Therefore, as long as the circuit geometry stays stationary, \({\partial }_{t}\left({{{\bf{F}}}}\left[{{{\bf{B}}}}\right]\right)={{{\bf{F}}}}\left[\dot{{{{\bf{B}}}}}\right]\). Secondly, due to the linearity of the differential equations, the functional is likewise linear, \({{{\bf{F}}}}\left[a{{{\bf{B}}}}\right]=a{{{\bf{F}}}}\left[{{{\bf{B}}}}\right]\).
Finally, we note that it is possible to considerably simplify the boundary condition, Eq. (8), if one considers geometries, where the dominant length scales are much larger than the London penetration depth. Then, one is entitled to set λ → 0, leading to,
In some sense, this corresponds to rescaling the device geometry to length scales where the London penetration depth is negligibly small. We note that there are model systems with an artificially high degree of radial symmetry (such as, e.g., spherical conductors in a uniform magnetic field, see ref. 37) where the longitudinal electric fields must vanish, such that the simplification in Eq. (14) may fail, even if λ is small. For generic device geometries however, the above approximation can be expected to work.
Importantly, there is another highly relevant limit for superconducting circuits made of thin films, with a film thickness comparable to λ (for measurements of λ for various materials, as a function of film thickness, disorder, and other parameters, see38,39,40,41,42). Here, the tangential E field may in general have to be considered. However, it is worth noting that there is a complementary limit of a very large λ compared to the island dimensions, which allows likewise for a discarding of the tangential electric field. Now, the small cut-off length scale is the island size instead of λ. Later, in the “Discussion” section, we will show in particular the example of a parallel plate capacitor, where the validity of Eq. (14) can be explicitly shown, when the capacitor dimensions (in particular the plate separation) are larger than λ, or conversely when the island thickness is much smaller than λ.
Irrotational gauge
In order to formulate a suitable Lagrangian, and then a Hamiltonian, we have to find the scalar and vector potentials, V and A, which generate the force fields. Starting from the electric field determined along the lines above, we have to find a solution for
To this equation, there is of course no unique solution - a suitable gauge has to be chosen. In the same spirit as ref. 7, we here want to formulate an irrotational gauge for this generic problem based on B and E.
As stated above (when summarizing the state of the art) the unique trait of the irrotational gauge is that there occur no linear terms \(\sim \widehat{n}\) in the Hamiltonian, but rather only quadratic terms \(\sim {\widehat{n}}^{2}\). This means that on the level of the Lagrangian, the kinetic energy associated with the voltage difference between ground and island should likewise be purely quadratic in V. This will be guaranteed by defining the voltage in our irrotational gauge as
where \({{{{\mathcal{L}}}}}_{g\to i}\) denotes an arbitrary path from a point inside g to a point inside i. Since EQ is curl-free, the voltage is thus single-valued as it should be. Moreover, due to EQ = 0 inside the conductors (the ac field penetrating the superconductors on the length scale λ is fully included in \({{{{\bf{E}}}}}_{\dot{B}}\)), for this gauge choice the voltage assumes a single, constant value within each conductor volume, such that the voltage difference between ground and island is well defined, independent of the starting and end points of \({{{{\mathcal{L}}}}}_{g\to i}\). In principle, we would be free to choose a gauge where V is not constant within a single bulk of superconductor. This would however artificially and unnecessarily complicate the problem, as the corresponding superconductor could no longer be described by a single phase. Because of the linear dependence of EQ on Q, see Eq. (12), the irrotational voltage is related to the island charge Q as
where the total capacitance between island and ground is defined as
Importantly, we see now that for this gauge choice, the kinetic energy (defined as the time integral of the electric power43, see also the “Methods” section) results in a purely quadratic term in V,
With this choice, the remaining electric field \({{{{\bf{E}}}}}_{\dot{B}}\) must be captured by the vector potential, which we can now uniquely define as
cf. Eq. (13) and subsequent discussion. When applied to the interior, Eq. (20) states that the vector potential in the interior corresponds to the London gauge, A = − μ0λ2j, whereas in the exterior, it has to satisfy ∇ × Airr = B, with the additional constraints ∇ ⋅ Airr = 0 (Coulomb gauge), and
In addition, Eq. (20) implies that the integral of \({\left.{{{{\bf{n}}}}}_{i}\cdot {{{{\bf{A}}}}}_{{{\mbox{irr}}}}\right|}_{{{{\bf{x}}}}\in {{{{\mathcal{S}}}}}_{i}}\) over the island surface must vanish, in analogy to the surface charge discussion for \({{{{\bf{E}}}}}_{\dot{B}}\). All of these properties are obviously inherited from \({{{{\bf{E}}}}}_{\dot{B}}\), and therefore render the solution for Airr unique. Crucially, Eq. (21) implies that the tangential component of the vector potential in the exterior must equal the interior vector potential at the surface, when the latter is computed in the London gauge. The longitudinal part on the other hand is discontinuous, just like \({{{{\bf{E}}}}}_{\dot{B}}\). In essence, one might consider our result as a prescription to continue the London gauge to the exterior of the superconductor.
Let us point out that in analogy to the discussion of E, we may likewise simplify the computation of A by setting λ → 0, under the assumption that the relevant length scales of the device geometry are larger than the London penetration depth. This leads to the simplified condition
following directly from Eq. (14). Consequently, when the approximation λ → 0 is justified, the irrotational gauge loses its connection to the standard London gauge because the interior vector potential becomes irrelevant.
At this point, we are able to fully appreciate how the generalized irrotational gauge Airr as defined above, can be related to the connection between electromagnetic force fields, and the corresponding potentials, Eqs. (1) and (2), as described in the introduction. Namely, the generalized irrotational gauge corresponds to the gauge, where the part of the electric field induced by the time-dependent magnetic field, \({{{{\bf{E}}}}}_{\dot{B}}\), is entirely encoded as \(-{\dot{{{{\bf{A}}}}}}_{{{\rm{irr}}}}\). Consequently, the absence of linear terms in \(\widehat{n}\) in the Hamiltonian translates to ∇ V = 0 in Eq. (1).
The phases that appear inside the potential energy in this irrotational gauge at the Josephson junction k are then given through the line integrals
where we take \({{{{\mathcal{L}}}}}_{Jk}\) to be the shortest path across junction k. Note that since Airr is by construction not curl-free, the resulting phase would in principle depend on the path, such that this choice needs to be justified. Large deviations from this shortest path are not considered because they are extremely unlikely, as can be seen, e.g., by means of standard path integral considerations. Small deviations from the shortest path (where the Cooper pairs still take quantum paths within the vicinity of the junction) leave the integral in Eq. (23) approximately invariant provided that the magnetic flux penetrating the junction is much smaller than the flux quantum. If fashioned for quantum hardware purposes, Josephson junctions are likely to satisfy this constraint (to avoid, e.g., Fraunhofer diffraction effects44).
For a SQUID with two Josephson junctions we thus find the Lagrangian in the irrotational gauge, with \({V}_{{{\rm{irr}}}}=2e\dot{\varphi }\),
which represents the main result of this work. Indeed, from Eq. (24), we find the charge as the canonically conjugate momentum \(Q=2en=2e{\partial }_{\dot{\varphi }}{L}_{{{\mbox{irr}}}}={C}_{{{\mbox{tot}}}}\dot{\varphi }/2e\) as defined in Eq. (17). By means of a standard Legendre transformation, and the quantization of charge and phase, \(\varphi ,n\to \widehat{\varphi },\widehat{n}\) with \([\widehat{\varphi },\widehat{n}]=i\), we arrive at the sought-after Hamiltonian \({\widehat{H}}_{{{\mbox{irr}}}}(t)\) in the irrotational gauge:
Let us make two important remarks. First, here we propose a procedure to obtain the correct Lagrangian which strongly generalizes the work of ref. 7. Reference7 invokes initially separate degrees of freedom for each junction, taking separate capacitances for each junction as the input. These degrees of freedom are then reduced by means of appropriate constraints in the Lagrangian. While this is a valid strategy under the hypothesis that the capacitances of the individual junctions are known and well-defined, our approach generalizes their effort beyond such simple geometries, and actually provides a procedure which not only gives the correct Lagrangian for specified junction capacitances, but in fact can be taken to provide also the correct junction capacitances themselves, by matching the solutions for \({\phi }_{k,{{\mbox{irr}}}}\left(t\right)\) with the relations involving Ck, see Eqs. (4) and (5). As a matter of fact, this general approach will lead to anomalous capacitances (negative or even time-dependent) already for quite standard circuit and magnetic field models, as we will discuss in the following.
Second, we note that the procedure is readily generalizable to arbitrary circuits. Considering a single charge island instead of two islands simply results in the kinetic (charging) energy term becoming redundant, while Eq. (23) remains applicable. Furthermore, one may also include many islands carrying island charges Qi by expressing the electric field EQ in Eq. (12) as a linear superposition, EQ = ∑iQiei. With this extension, the formulation of the irrotational gauge for the scalar and vector potentials remains the same; in particular, for the latter, that would be the Coulomb gauge plus the boundary condition, Eq. (21). For an arbitrary number of Josephson junctions, each junction k adds a contribution \(-{E}_{Jk}\cos ({\varphi }_{k}+{\phi }_{k,{{\mbox{irr}}}})\) to the potential energy, with \({\dot{\varphi }}_{k}=2e{V}_{k}\) where Vk is the voltage difference between the islands connected by junction k, and ϕk,irr still defined as in Eq. (23).
We note one nontrivial extension: in general, there could be an additional capacitively coupled gate with a voltage Vg, inducing offset gate charges ng = CgVg, \(\widehat{n}\to \widehat{n}+{n}_{g}\). In this case, the Hamiltonian would of course no longer be purely quadratic in \(\widehat{n}\). This however necessitates only a minor extension of the above prescription for finding the irrotational gauge for A. Namely, any gate gives rise to an additional source term in the electromagnetic problem, \({{{\bf{E}}}}={{{{\bf{E}}}}}_{Q}+{{{{\bf{E}}}}}_{\dot{B}}+{{{{\bf{E}}}}}_{{V}_{g}}\), where the new field \({{{{\bf{E}}}}}_{{V}_{g}}\) is linearly independent of the others. Hence, in order to determine Airr we simply have to set all gate voltages to zero, Vg = 0 (that is, all gate voltages equal to a common ground), resulting again in \({{{{\bf{E}}}}}_{\dot{B}}=-{{{\bf{F}}}}\left[\dot{{{{\bf{B}}}}}\right]\), allowing us to proceed as above.
Finally, let us point out that there is a straightforward generalization of our gauge constraints, which eventually allow for terms linear in \(\widehat{n}\) in the Hamiltonian. The physical charge Q in Eq. (9) may be supplemented with an auxiliary (and in general time-dependent) shift Q → Q − Q0(t), leading to a new solution \({{{\bf{E}}}}_{Q}^{\prime} =\left(Q-{Q}_{0}\right){{\,{\bf{e}}}}\). Since this shifted charge is not physical (unlike an offset charge induced by a physical gate, as discussed above), it has to be subtracted again as an extra term in a new \({{{\bf{E}}}}_{\dot{B}}^{\prime}\), such that \({{{\bf{E}}}}_{Q}^{\prime} +{{{\bf{E}}}}_{\dot{B}}^{\prime} ={{{{\bf{E}}}}}_{Q}+{{{{\bf{E}}}}}_{\dot{B}}\). Continuing the subsequent steps of the above recipe with these new fields will give rise to a new Hamiltonian \(\widehat{H}_{{{\mbox{irr}}}}^{\prime} =\widehat{U}{\widehat{H}}_{{{\mbox{irr}}}}{\widehat{U}}^{{\dagger} }-i\widehat{U}{\partial }_{t}{\widehat{U}}^{{\dagger} }\), where the time-dependent unitary \(\widehat{U}\) depends on the integral of the shifted charge, \({\int}^{t}dt^{\prime} {Q}_{0}\). For further details, see the “Methods” section. At any rate, such a variably-shifted irrotational gauge connects a more general choice of decomposing the electric field (and thus finding a different gauge for the resulting scalar and vector potentials) with a more general class of Hamiltonians describing the same driven circuit, see also Eqs. (13-14) of7.
Flux felt by the SQUID and neglecting junction filaments
Before moving on to applying the above procedure for concrete models, we have two remaining general items to discuss, which actually turn out to be related. First, our procedure provides an answer to the long-standing question of what flux the SQUID actually couples to when λ is large. The necessary insight to answer this question then allows for a second important realization: that small filaments can be neglected in obtaining field solutions.
Let us return to the result from Eqs. (23) and (25), where we see that the flux felt by the SQUID is encoded in the highly local quantities ϕ1,irr and ϕ2,irr. Note that for a time-independent field, we may simply rearrange these phase contributions by a unitary transformation, such that the only relevant phase appearing in the Hamiltonian is the phase difference ϕ = ϕ2,irr − ϕ1,irr. For a strong Meissner effect (i.e., λ → 0) it is obvious that ϕ indeed corresponds to the flux enclosed by the entire SQUID, see Eq. (3), taking the area \({{{\mathcal{A}}}}\) to be the one enclosed by the two junctions, exluding the superconductors. In fact, for λ → 0, all electric fields tangential to the superconducting surfaces are zero at the surfaces, as we already discussed [see paragraph containing Eq. (14)]. Therefore, for the irrotational gauge Airr we find that we can connect any two points 1 and 2 on the same surface by any arbitrary path on the surface \({{{{\mathcal{L}}}}}_{12}\), such that the integral \({\int}_{{{{{\mathcal{L}}}}}_{12}}d{{{\bf{l}}}}\cdot {{{{\bf{A}}}}}_{{{\rm{irr}}}}\) vanishes independent of the path. Thus, the local phases ϕk,irr are guaranteed to contain full information of the flux enclosed by the two Josephson junctions (which is a nonlocal property).
Matters are much subtler when considering circuits with dimensions comparable to λ38,39,40,41,42. Here, Meissner screening currents play an essential role, and tangential electric fields on the surfaces cannot be discarded. In particular, since the magnetic field penetrates the superconductor, it is per se not at all obvious what area \({{{\mathcal{A}}}}\) has to be inserted into Eq. (3). However, even in this general regime, one can show that there still exist paths \({{{{\mathcal{L}}}}}_{12}\) connecting two arbitrary points on the surface for which \({\int_{{{{{\mathcal{L}}}}}_{12}}}d{{{\bf{l}}}}\cdot {{{{\bf{A}}}}}_{{{\rm{irr}}}}=0\). Let us refer to them as ‘zero phase paths’. The difference from the previous case is simply that here, there are not infinitely many arbitrary paths. All that can be guaranteed, in general, is that at least two such paths exist, provided that the superconducting lump has genus 0.
The existence of such paths hinges on the 2-dimensional version45 of the Poincaré-Hopf theorem (for an instructive proof in 2 dimensions, see ref. 46). This theorem guarantees that a continuous tangential vector field on a 2-dimensional sphere (in our case the tangential component of Airr) must vanish somewhere. Since a closed 2D manifold with genus 0 has Euler characteristic 2, the theorem guarantees at least two zero points. Importantly, as long as the 2D curl of Airr on the surface is nonzero, a zero point z can be reached from any other point on the surface (e.g., points 1 and 2), by choosing paths which are perpendicular to the tangential Airr, thus yielding \({\int}_{{{{{\mathcal{L}}}}}_{1z}}d{{{\bf{l}}}}\cdot {{{{\bf{A}}}}}_{{{\rm{irr}}}}=0\) and \({\int}_{{{{{\mathcal{L}}}}}_{z2}}d{{{\bf{l}}}}\cdot {{{{\bf{A}}}}}_{{{\rm{irr}}}}=0\), see Fig. 2. These two paths can then be easily stitched together to yield \({\int}_{{{{{\mathcal{L}}}}}_{12}}d{{{\bf{l}}}}\cdot {{{{\bf{A}}}}}_{{{\rm{irr}}}}=0\). We provide more details on these zero phase paths, and some practical examples, in the Supplementary Material (see in particular Supplementary Fig. 1). Consequently, the relevant area \({{{\mathcal{A}}}}\) for the total flux felt by the SQUID is given by the sum of the area for λ → 0 (i.e., the area excluding the superconductors), plus an additional area \({{\Delta }}{{{\mathcal{A}}}}\) including parts of the superconductor, carved out by such paths (see Fig. 2).
Take two arbitrary points 1 and 2 on the surface of the superconductor. One can then always find a path \({{{{\mathcal{L}}}}}_{12}\) with the property \({\int}_{{{{{\mathcal{L}}}}}_{12}}d{{{\bf{l}}}}\cdot {{{{\bf{A}}}}}_{{{\rm{irr}}}}=0\). Such paths must go through a zero point z in the vector field on the surface, where Airr = 0. In the inset, a generic vector field (gray) in the neighborhood of a zero z is drawn. The paths \({{{{\mathcal{L}}}}}_{1z}\) and \({{{{\mathcal{L}}}}}_{z2}\) are always perpendicular to Airr. When projected onto 2D, the zero phase path carves out an area \(\Delta {{{\mathcal{A}}}}\) of the superconductor.
The existence of such special paths on the superconducting surfaces enables a further important conclusion. As mentioned in the introduction, Josephson junctions connecting individual bulk conductors often have a filamentary structure [as indicated in Figs. 1(a) and 3(a)], because the Josephson junctions are fabricated using the Niemeyer-Dolan technique24,25. We now show why these filaments can be neglected, a simplification which we expect to be very useful for reducing computational effort. The argument requires two main assumptions. (i) The filaments’ contribution to the capacitance is negligible. Thus, their presence will distort the solutions of the electric fields \({{{{\bf{E}}}}}_{\dot{B}}({{{\bf{r}}}},t)\) and EQ(r) only locally, whereas far away from the junctions, these fields will be the same as if the filaments were not present. We can therefore always expect to find a path \({{{{\mathcal{L}}}}}_{{{\rm{far}}}}\) connecting ground and island, where the field solutions are the same as when the junction filaments are absent, see Fig. 3(a) and (b), respectively. (ii) The filaments likewise do not distort the tangential field lines on the surfaces by much, such that zero phase paths remain the same away from the filaments.
Equipped with these two assumptions, let us consider a closed path for the circuit with the filament [Fig. 3(a)] and without it [Fig. 3(b)]. In general, the two circuits will have different field solutions, \({{{{\bf{E}}}}}_{\dot{B}}\) and \({\widetilde{{{{\bf{E}}}}}}_{\dot{B}}\) as well as Airr and \({\widetilde{{{{\bf{A}}}}}}_{{{\rm{irr}}}}\) [as per the irrotational gauge defined in Eq. (21)]. Due to (ii), it is possible to choose a path \({{{{\mathcal{L}}}}}_{{{\rm{filament}}}}\) in Fig. 3(b), such that the closed path covers the exact same area as the one in Fig. 3(a), resulting in the same enclosed flux Φ. Hence,
Because of the special zero phase property of the paths \({{{{\mathcal{L}}}}}_{i,g}\), their contribution has to vanish, leaving us with
Finally, in accordance with assumption (i), sufficiently far from the junction the vector field solution is the same for both circuits, such that the first term on either side of the equation cancels, resulting in
which thus shows that one may neglect the actual junction filaments for the computation of the field solutions, as long as an equivalent path, \({{{{\mathcal{L}}}}}_{{{\rm{filament}}}}\), is chosen. We note that the above proof can be extended to an arbitrary number of junctions, as long as (i) and (ii) remain valid. The observation described in Eq. (28) can in some sense be interpreted as a ‘lightning rod effect’ of the filament. Namely, if it holds, it means that the vector potential at the junction is increased by a factor Lfilament/d ≫ 1 compared to the solution in the absence of the filament (where d is the junction thickness and Lfilament is the length of the filament path \({{{{\mathcal{L}}}}}_{{{\rm{filament}}}}\)).
Explicit solution for irrotational vector potential
We now apply the above general scheme to a concrete SQUID geometry that allows for simple analytic solutions of the Maxwell equations. We will show that for this concrete case, a mapping from the general circuit to a lumped element model, see Fig. 1, cannot be accomplished unless negative or even time-dependent capacitances are assigned to the individual junctions.
We assume that the ground and island form a parallel plate capacitor with width W and separation D (x- and y-directions, respectively), see Fig. 4. In z-direction the plates extend to height H. Both H, W ≫ D, such that fringe effects can be neglected. The total capacitance is therefore the standard expression for the parallel plate capacitor Ctot = ϵHW/D. As shown in Fig. 4, the junctions are incorporated in the form of filaments. In accordance with the “Results” section, we here neglect the influence of the junction filaments for the field solutions in what follows.
The setup as shown in this figure leads to all the predicted effects in the main text, such as negative capacitances, or time-dependent capacitances. a Top view of the SQUID circuit. The ground and island form a parallel plate capacitor with distance D (y-direction) and width W ≫ D (x-direction). Two current wire sources I1 (red) and I2 (blue) produce magnetic fields. We indicate the spatial distribution of the field for the first source (red curve). The Josephson junctions are placed at positions x1 and x2, 0 < x1,2 < W while the sources are placed at \({x}_{{I}_{1}} \,<\, 0\) and \({x}_{{I}_{2}} \,>\, W\). Note that for illustration purposes, the y-axis is exaggerated; in the actual model both the plate distance D and the plate thicknesses should be much smaller than any of the length scales in x direction. b In z-direction the planes are of a height H which is large with respect to the distance, H ≫ D, but small with respect to the width H ≪ W.
In order to derive the Hamiltonian, we need to know the vector potential Airr within the thin volume separating the two plates. As for the magnetic field, we assume for simplicity that it is created by two wires carrying a time-dependent current \({I}_{1,2}\left(t\right)\), oriented in y-direction, at positions \(x={x}_{{I}_{1,2}}\) and z = zI, which we set to be zI = H/2 (see Fig. 4). It is therefore of the form
with the components given as per Ampère’s law,
with the distance from the current source I1,2, \({r}_{1,2}^{2}={\left(x-{x}_{{I}_{1,2}}\right)}^{2}+{\left(z-{z}_{I}\right)}^{2}\).
The solution for the electric field, \({{{{\bf{E}}}}}_{\dot{B}}\), fulfilling the conditions detailed in the “Results” section, is given as follows [see Supplementary Eqs. (3)–(26) for the derivation]. In the interior of the conductor plates, the magnetic field decays exponentially on the length scale λ. The Meissner screening currents give rise to an ac electric field via the first London equation, E = μλ2∂tj, which can be given for the two capacitor plates as
respectively
where ny = (0, 1, 0)T. The condition \(\nabla \cdot {{{{\bf{E}}}}}_{\dot{B}}=0\) for the interior is a consequence of the likewise source-free screening currrent ∇ ⋅ j = 0, which in turn follows from ∇ × B = 0 for the magnetic field in the exterior (away from the wires).
The above solutions for \({{{{\bf{E}}}}}_{\dot{B}}\), evaluated at the plate surfaces y = 0 and y = D, respectively, provide the right-hand side of the boundary conditions in Eq. (8), such that we can now solve for the volume in between the plates, 0 < y < D and 0 < z < H. For this particular geometry, it turns out to be helpful to explicitly decompose the field into a longitudinal (oriented along y) and tangential (parallel to the plate surfaces) component, \({{{{\bf{E}}}}}_{\dot{B}}(0 \,<\, y \,<\, D)={{{{\bf{E}}}}}_{L}+{{{{\bf{E}}}}}_{T}\). We find for the longitudinal field EL = EL,yny with,
where \(2{b}_{x}\left(x,x^{\prime\prime} ,z^{\prime} \right)={B}_{x}\left(x,z^{\prime} \right)+{B}_{x}\left(x^{\prime\prime} ,z^{\prime} \right)\) as well as \(2{b}_{z}\left(x^{\prime} ,z,z^{\prime\prime} \right)={B}_{z}\left(x^{\prime} ,z\right)+{B}_{z}\left(x^{\prime} ,z^{\prime\prime} \right)\). The tangential field reads
Here, the tangential field continuously matches the solution for the interior of the conductors, given in Eqs. (32) and (33). The longitudinal field abruptly goes to zero at y = 0, D, thus giving rise to a surface charge, as defined in Eq. (10), induced by \(\dot{{{{\bf{B}}}}}\,\ne\, 0\). This surface charge must integrate to zero. This can be verified when integrating EL over x and z. In the first line, there will be the total integral \(\int\nolimits_{0}^{W}dx\int\nolimits_{0}^{W}dx^{\prime\prime}\) applied to a function of the form \(\int\nolimits_{x}^{x^{\prime\prime} }dx^{\prime} \ldots\), which is obviously antisymmetric upon exchanging x ↔ x″. The argument applies similarly for z in the second line.
Following the lines of the “Results” section, the vector potential is obtained in a straightforward fashion by taking the solutions for the E-field in Eqs. (32)–(35), and replacing \(\dot{{{{\bf{B}}}}}\to -{{{\bf{B}}}}\). We are now able to make some crucial simplifications. First of all, we notice that if the capacitor plate separation D ≫ λ, we may simplify λ/D ≈ 0 in Eq. (34), and ET ≈ 0. The remaining terms of the longitudinal field then correspond to the field solutions with the simplified boundary condition, Eq. (14). We thus explicitly show at the example of the parallel plate capacitor, that λ → 0 is justified if the relevant length scales of the device geometry exceed λ. Note another interesting limit. If we assume the thickness of the capacitor plates, tC, to be comparable to λ, then, the exponentially decaying field inside the capacitor plates, Eqs. (32) and (33), has to be replaced by \(\cosh\)-functions. In the limit where the capacitors are much thinner than λ there only remains a very weak screening current inside the plates, and the length scale λ in Eqs. (34) and (35) has to be replaced by tC. If we then assume tC ≪ D, we actually get yet again that the tangential field can be neglected, and only the longitudinal part survives. It is thus interesting to note that we get the exact same field solutions as if we set λ → 0, in spite of λ being finite.
To proceed, we assume in addition a quasi one-dimensional parallel plate capacitor, W ≫ H ≫ D, such that we may simplify Bx ≈ 0 and Bz(x, z) ≈ Bz(x), that is, the magnetic field is mainly oriented in z-direction, and depends only on x. For this approximation to remain valid, we always need to consider distances between the wires and the capacitor larger than H. Hence, whenever we refer to the wires being close to the capacitor, we always mean distances smaller than W, but larger than H. As a consequence, bx ≈ 0 and \({b}_{z}(x^{\prime} ,z,z^{\prime\prime} )\approx {B}_{z}(x)\). For the resulting irrotational gauge, as defined in Eq. (21), we find,
The phases at the two Josephson junctions return as a result,
Based on this solution, we now may examine the extent to which a mapping onto a lumped element circuit Fig. 1(b) can be achieved. The mapping must give rise to junctions with the effective capacitances [see Eqs. (4), (5)]
In what follows, we will derive explicit expressions for Ceff,k starting from above Eqs. (38) and (39). As we will see, the spatial inhomogeneity of the magnetic fields is at the heart of the nontrivial behavior for Ceff,k. We will argue, in particular, that for a single source, negative effective capacitances Ceff,k emerge. Two independent sources lead to time-dependent capacitances.
Negative junction capacitances and qubit relaxation rates
Let us first consider the case of only one source, I ≡ I1 and set I2 = 0. In this case, the vector potential in the irrotational gauge is, according to Eq. (36), in the limit \(\left|{x}_{{I}_{1}}\right|\ll W\) (while still \(| {x}_{{I}_{1}}| \gg H\))
The resulting phases ϕirr,k depend on time only through a global prefactor, \({\phi }_{{{\rm{irr}}},k} \sim I\left(t\right)\) which cancels in Eqs. (38) and (39). The resulting capacitances are therefore time-independent,
However, they can be negative. Notably, already for a completely symmetric junction placement x1,2 = W/2 ∓ δx, we find Ceff,2 < 0 and Ceff,1 > Ctot if
where e here denotes Euler’s number (not to be confused with the elementary charge). Note that this corresponds to a very strong asymmetry in the junction capacitances, even though the circuit geometry itself is perfectly symmetric. The effect stems solely from the spatial asymmetry of the time-dependent magnetic field.
Crucially, the presence of negative capacitances strongly affects the accurate prediction of the transition rates between the ground and excited states of the Hamiltonian. Along the same lines as in ref. 7, let us consider fluctuations of the flux ϕ = ϕ0 + δϕ around an equilibrium value ϕ0 (which could in this concrete case correspond to current fluctuations). These give rise to the relaxation rate (for simplicity, for symmetric junctions, EJ1 = EJ2 = EJ)
where m is the index that counts the eigenstates of H, and the phase noise power spectrum \({S}_{\delta \phi }\left(\omega \right)\) is taken at the frequency corresponding to the transition energy \({\omega }_{mm^{\prime} }={\epsilon }_{m}-{\epsilon }_{m^{\prime} }\). We see now that ignoring the possibility of anomalous capacitances leads to a potential massive underestimation of the transition rates. While for regular capacitances, we find
for anomalous capacitances, it may happen that
Note though, that negative capacitances do not lead to a breakdown of the perturbation theory. For concreteness, consider the above model of a single wire source, in the limit where the separation of the two junctions is small, δx ≪ W. Then,
On the one hand, the prefactor \({\left(W/\delta x\right)}^{2}\) (due to negative capacitances) is large. On the other hand, for δx → 0 (where the two junctions essentially merge to one), the total flux enclosed by the two junctions approaches zero, too, δϕ → 0, linearly with δx. Hence, the phase noise power spectrum Sδϕ goes to zero at the same rate the prefactor \({\left(W/\delta x\right)}^{2}\) diverges, such that the product \({\left(W/\delta x\right)}^{2}{S}_{\delta \phi }\) remains finite.
To summarize, without appropriately taking into account the spatial distribution of the magnetic field, one might have naively expected that with the total phase ϕ, respectively, its fluctuations δϕ going to zero, the circuit may loose its sensitivity to the noise emitted by the magnetic field source. We here show that this is not so; depending on the spatial details of the magnetic field the qubit relaxation rate due to magnetic noise remains relevant even if the area enclosed by the SQUID is small.
By means of the above expressions, we may easily quantify the mistake that is made, if the spatial distribution of the magnetic field, and the resulting negative capacitances are disregarded. Based on current understanding, a completely symmetric SQUID geometry would probably have been modeled by symmetric junction capacitances, C1,eff ≈ C2,eff, such that the capacitance prefactor in Eq. (44), actually approaches zero, up to small corrections ≪ 1 due to a residual asymmetry in the device geometry. The correct treatment as presented here however, would predict even for a perfectly symmetric SQUID geometry, a prefactor of order 1 or above, if the separation of the two junctions δx is smaller than the critical value given in Eq. (43). Therefore, the estimate for the relaxation rate would potentially have been off by several orders of magnitude.
Geometric phase generated by time-dependent capacitances
Now we consider a driving of the device by means of two wires, as shown in Fig. 4, such that in the expression for Bz in Eq. (31), we keep both I1 and I2 nonzero. Crucially, in a standard description of the circuit by means of regular, constant capacitances, such a SQUID would have been described by only one time-dependent parameter, the total flux enclosed by the junctions ϕ(t), irrespective of the number of current sources. Here we show that such a treatment is fundamentally wrong.
For simplicity, we consider again a fully symmetric geometry for both the circuit, x1,2 = W/2 ∓ δx, and the current sources approach the edges of the capacitor from both sides, \({x}_{{I}_{1}}\to 0\) and \({x}_{{I}_{2}}\to W\) (again, provided that \(| {x}_{{I}_{1}}| ,| W-{x}_{{I}_{2}}| \gg H\)). We find for the vector potential
For the resulting phases, we compactify the expressions by introducing the decomposition \({\phi }_{1,2}=\frac{1}{2}(\overline{\phi }\mp \phi )\), where
When driving I1 and I2 independently, the Hamiltonian is driven by two genuinely independent parameters, ϕ1 and ϕ2, instead of just the single total phase enclosed by the SQUID, ϕ2 − ϕ1, as would be the case with a naive lumped-element approach. In fact, as predicted, the result here can only be mapped to a lumped element circuit of the form in Fig. 1(b) if the effective junction capacitances are allowed to be time dependent, \({C}_{{{\rm{eff}}},1,2}\left(t\right)=\frac{1}{2}\left(1\pm \overline{\phi }/\phi \right){C}_{{{\mbox{tot}}}}\), since the time-dependent prefactor for \(\overline{\phi }/\phi \sim \left[{I}_{1}\left(t\right)+{I}_{2}\left(t\right)\right]/\left[{I}_{1}\left(t\right)-{I}_{2}\left(t\right)\right]\) does not cancel.
What is more, for independent currents I1 and I2 it can very easily occur that I1 − I2 = 0 while I1 + I2 ≠ 0 at certain moments in time, leading to singular capacitances. We stress though, that this singularity is not a sign of a failure of the theory: all system parameters in the Hamiltonian stay regular. Instead, such singularities merely represent the failure to capture the dynamics of the realistic system by means of the lumped element approach in Fig. 1(b), when trying to decompose the total capacitance into partial capacitances for each junction.
The presence of two explicit time-dependent parameters can be experimentally accessed as follows. Consider a periodic ac driving of the two currents. The two parameters ϕ1, ϕ2, or equivalently \(\phi ,\overline{\phi }\), enclose a finite area in the 2D parameter space. In the adiabatic driving regime (when the ac frequency is low with respect to the qubit frequency) a nontrivial Berry phase may emerge as a consequence. When preparing the system in a certain eigenstate \(\left|m\right\rangle\), this Berry phase may be expressed as
In order to simplify further, let us focus on EJ1 = EJ2 ≡ EJ. As will become clear in a moment, we should include a stationary gate voltage in our system inducing a charge ng (see end of the “Results” section), such that the Hamiltonian reads
with \({E}_{C}={\left(2e\right)}^{2}/{C}_{{{\mbox{tot}}}}\) and \({E}_{J}\left(\phi \right)=2\cos \left(\phi /2\right){E}_{J}\). For further evaluation, it is helpful to reexpress the Berry curvature as
where \({\partial }_{\phi }\widehat{H} \sim \cos \left(\widehat{\varphi }-\overline{\phi }/2\right)\) and \({\partial }_{\overline{\phi }}\widehat{H} \sim \sin \left(\widehat{\varphi }-\overline{\phi }/2\right)\). Now, the importance of a finite gate voltage shift becomes obvious. Observe that if ng = 0, the wave functions can be separated into two subsets, one containing all wave functions which are symmetric, respectively antisymmetric, in φ-space (with respect to \(\overline{\phi }/2\)), resulting in a vanishing \({{{{\mathcal{B}}}}}_{m}\). But for finite (non-integer) ng we can expect a finite Berry phase.
In fact, the Berry phase should have its largest value close to ϕ ≈ ± π (up to multiples of 2π), where the interference of Josephson tunnelings across the two junctions is destructive, \({E}_{J}\cos \left(\phi /2\right)\ll {E}_{C}\), while at the same time, keeping ng close to a charge degeneracy point, ng ≈ 1/2 (up to integer multiples), making sure that Cooper pair transport is not fully suppressed. This corresponds to the Cooper pair box regime47, where it is easy to find a good analytic approximation for the Berry curvature of the even parity ground state m = 0 (see “Methods” section),
where δng = ng − 1/2 is the distance of ng away from the charge degeneracy point. This result represents a measurable effect of the highly nontrivial interaction of spatially asymmetric time-dependent magnetic fields with a SQUID. Berry curvatures have been successfully measured in superconducting qubits, see ref. 22,23, which is why we expect this effect to be readily observable.
Refined lumped-element approach
We have shown above that the naive lumped element approach from Fig. 1 does not succeed in predicting the correct system dynamics of a realistic SQUID geometry, unless one allows for the possibility of anomalous (negative or time-dependent) capacitances. This raises the question, if there even exists a limit, where the ordinary lumped-element approach, with constant positive capacitances, can be salvaged.
In this final section, we show that a description of the circuit with regular, constant capacitances may indeed still work to describe realistic geometries, provided that the circuit is greatly refined. That is, one needs to introduce a finely-meshed network of lumped elements which can capture the spatial details of the externally applied field. In addition, capacitances need to be introduced at all nodes, even (or especially) the ones which are not connected via Josephson junctions. By means of such a network, we show, for the above example of a 1D SQUID, that our irrotational gauge procedure is equivalent to the one developed by You et al.7, when going to the continuum limit. In addition, through this procedure we also include the internal dynamics of the island (by describing it as a transmission line), and thus provide an upper bound for the driving frequency, below which the description of the island by means of a single independent degree of freedom, \(\left(\varphi ,\dot{\varphi }\right)\), is justified.
To begin, we model the simple 1D version of the SQUID from Fig. 1(a) by means of a finite element approach, see Fig. 5(a), where the island is described by a transmission line. In terms of the branch variables [see Fig. 5(b)], we find the Lagrangian
with a part describing the transmission line (i.e., the island)
and the capacitive coupling to ground
Finally, the Josephson junctions are included in
where the first junction is at position j = j1, and the second one at position j = j2 > j1. The spatial dependence of the magnetic field, \(B\left(x\right)\) is here taken into account by the flux distribution \({\phi }_{j}\left(t\right)\) (for j = 1… J) [see Fig. 5(b)]. Thus, the branch variables are subject to the constraints
This gives rise to J constraints. Given that there are J + 1 branch variables for the capacitances, φj, all but one of these variables can be eliminated. The transmission line variables φTL,j remain free at this stage. This is equivalent to the prescription advocated by7 to uniquely determine the Hamiltonian.
a Finite element model to describe the SQUID geometry in Fig. 4(a). The upper arm of the SQUID is described through a transmission line, whereas the lower arm is simply a ground. The Josephson junctions (red) are at positions j = j1 and j = j2. b The same finite element model, now showing the temporally and spatially varying flux \({\phi }_{j}\left(t\right)\), as well as the branch phase variables for the transmission line, φTL,j, and the ones describing the capacitive and Josephson coupling between ground and transmission line, φj.
Importantly, it can now be shown [for details, see Supplementary Eqs. (27)–(67)] that there is a low-frequency regime for the time-dependent driving of the ϕj for which the transmission line dynamics are irrelevant, such that φTL,j ≈ 0. This corresponds to the situation where the driving is sufficiently slow that the transmission line can quasi-instantaneously follow the perturbation (the exact condition will be discussed below). The resulting low-frequency Hamiltonian can be obtained by means of a Schrieffer-Wolff transformation,
with
for the junction index k = 1, 2, and having defined the (discrete) flux integral \({f}_{j}\left(t\right)=\mathop{\sum }\nolimits_{k = 1}^{j}{\phi }_{k}\left(t\right).\) The total capacitance is simply \({C}_{{{\mbox{tot}}}}=\left(J+1\right)C\). Crucially, when approaching the continuum limit for the network (i.e., the distance between the lumps dx → 0)
where D is also here the distance between the transmission line and the ground and \(W=\left(J+1\right)dx\) is the width. Thus, we recover the result from the continuous field calculation, Eq. (37). This demonstrates the equivalence of the approach of You et al.7 and our gauge prescription for the vector potential, Airr, as outlined in the “Results” section. Note in addition, that if we changed the capacitance profile, such that instead of equivalent capacitances C on each node (see Fig. 5) we would only have capacitances C1 and C2 at the junction nodes j1 and j2 (capacitance dominated by the junctions), we would indeed obtain the simplified result Eq. (5).
Finally, let us comment on the regime of validity of Hlow in Eq. (60). As we detail in the Supplementary Materials, neglecting the internal dynamics of the island is justified for driving frequencies ω satisfying
where l is the inductance density of the transmission line, such that L = l dx. The frequency ω0 corresponds to the lowest mode of the internal transmission line dynamics. Assuming that the kinetic part of the inductance is dominant, we estimate \(l \sim {m}_{{{\mbox{e}}}}/\left({n}_{{{\rm{s}}}}{e}^{2}{{{\mathcal{S}}}}\right)\)48,49, with me as the electron mass and the Cooper pair density ns ~ 4 × 106 μm−350, and assuming a transmission line cross section of \({{{\mathcal{S}}}} \sim 10\,{{\rm{nm}}}\,\times 20\,\mu m\) as well as W ~ 200 μm, we find ω0 ~ 20 GHz. For a typical qubit frequency between 5 and 10 GHz, it seems plausible that neglecting the internal island dynamics is justified even when an ac magnetic field would be used to drive bit flips.
Discussion
We develop a general recipe to construct a Hamiltonian for realistic quantum circuits driven by external electomagnetic fields which vary in time. This construction invokes the notion of an irrotational gauge for the time-dependent vector field, which corresponds to the Coulomb gauge, with additional boundary conditions. The part of the vector potential parallel to the superconductor surfaces is continuous, and thus relates to Meissner screening currents. A second part, perpendicular to the surfaces, is in general dominant, and relates to the surface charges induced by the time-varying magnetic field. Based on this result, we show, in the example of a simple SQUID geometry, that assigning individual capacitances to each Josephson junction results in negative and potentially time-dependent capacitances. These realizations lead to a highly revised understanding of the dynamics of a driven SQUID. We discuss measurable effects of such anomalous capacitances, such as a strongly enhanced qubit relaxation rate, and a nonzero Berry phase. Finally, we establish a connection between the here proposed vector potential gauge for continuous circuit geometries and irrotational gauge developed in ref. 7 for discrete circuits. In doing so, we also provide an estimate for the validity of the lumped-element approach, given a certain driving frequency.
Methods
More general Hamiltonians from continuum electrodynamics
In the “Results” secion, we showed the choice of gauge that leads to a Lagrangian and Hamiltonian satisfying the irrotational condition of You et al.7. Here we show another choice that leads to forms that resemble the more general Lagrangians/Hamiltonians that arise in the previous discrete circuit analysis. For this purpose however, we first need the correct definition for the kinetic energy term which enters the Lagrangian.
We start with the definition for the energy stored in a capacitor via the electric power43,
where the lower integration limit is not specified as it merely provides an irrelevant constant shift (which we disregard here). Through I = ∂tQ, we may immediately substitute the time integral for an integral over charge,
or, through partial integration, for an integral over voltage
Identifying Q as the canonically conjugate momentum, we see that EQ and EV are related through a Legendre transformation. We thus conclude that the kinetic energy in the Lagrangian is given by T = EV [see also Eq. (19) in the main text], whereas EQ corresponds to the kinetic energy of the Hamiltonian. Importantly, for the irrotational gauge, where the energies are quadratic in both V and Q, EQ = EV, and the above distinction is moot. However, for the gauges considered in this appendix, there will appear linear terms where this distinction is important, and the definition of the Lagrangian kinetic energy via the voltage integral is imperative.
To continue, we introduce a variably shifted irrotational gauge. This is a simple variant on the irrotational gauge introduced in the main text. We now divide the electric field into two parts as in Eq. (11),
Here \({{{\bf{E}}}}^{\prime}\) satisfies the same conditions as EQ, except that Eq. (9) is replaced by an shifted island charge:
Note that this island charge function Q0(t) should not be confused with the offset gate charge ng. ng is a real physical quantity, while Q0(t), merely parametrizing a new set of gauges, cannot appear in any physical observable. Equation (68) emphasizes that the shifted charge function can be taken to be time dependent, and we will assume that this time dependence is expressed as the time derivative of a fixed function f0(t). The solution for the electric field is thus of the form
The other contribution to the field, \({\epsilon\oint\oint_{{{{{\mathcal{S}}}}}_{i}}}{d}^{2}x\left({{{{\bf{n}}}}}_{i}\cdot {{{\bf{E}}}}_{Q}^{\prime} \right)=Q-{Q}_{0}(t)=Q-{\dot{f}}_{0}(t)\,.\), must likewise be changed; instead of corresponding to zero island charge, it will require the island charge
resulting in
and the resulting new vector potential
In this gauge the constitutive equation (17) is replaced by
defining the island potential \(V^{\prime}\) in the new gauge (it is again uniform in space across the island). The new kinetic energy in the Lagrangian is
This introduces the superconducting phase variable in the variably-shifted irrotational gauge, \(\dot{\varphi }^{\prime}\). After Legendre transformation, this leads to the full Hamiltonian
where the shift 2ef0/Ctot of the phase in the Josephson term follows from the line integral of the new \(A^{\prime}\) in Eq. (72). Indeed, \({\widehat{H}}_{{{\mbox{irr}}}}=\widehat{U}\widehat{H}^{\prime} {\widehat{U}}^{{\dagger} }-i\widehat{U}{\partial }_{t}{\widehat{U}}^{{\dagger} }\), with \(\widehat{U}={e}^{-i2e{f}_{0}\widehat{n}/{C}_{{{\mbox{tot}}}}}\). Here we see the more general form for the kinetic energy, with both quadratic and linear number operators, as it occurs in Eqs. (13-14) of7.
Berry curvature
Here, we show how to arrive at the approximate expression for the Berry curvature in Eq. (54). Assuming in particular that ng is close to 1/2, we write the Hamiltonian given in Eq. (52) in the sub-basis of either one or zero extra Cooper pair on the island, \(\left|1\right\rangle ,\left|0\right\rangle\)
with δng = ng − 1/2. This Hamiltonian has the eigenvalues \(\pm \frac{1}{2}\sqrt{{E}_{C}^{2}\delta {n}_{g}^{2}+{E}_{J}^{2}\left(\phi \right)}\) and the corresponding eigenvectors
Denoting \(\left|-\right\rangle\) as the even parity ground state m = 0, the above eigenvector can be plugged into Eq. (54).
Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.
References
Blais, A., Grimsmo, A. L., Girvin, S. M. & Wallraff, A. Circuit quantum electrodynamics. Rev. Mod. Phys. 93, 025005 (2021).
Yurke, B. & Denker, J. S. Quantum network theory. Phys. Rev. A 29, 1419–1437 (1984).
Devoret, M. H. Quantum fluctuations in electrical circuits, in quantum fluctuations (Les Houches Session LXIII, Elsevier Science, 1997), pp. 351–386.
Burkard, G., Koch, R. H. & DiVincenzo, D. P. Multilevel quantum description of decoherence in superconducting qubits. Phys. Rev. B 69, 064503 (2004).
Ulrich, J. & Hassler, F. Dual approach to circuit quantization using loop charges. Phys. Rev. B 94, 094505 (2016).
Vool, U. & Devoret, M. Introduction to quantum electromagnetic circuits. Int. J. Circuit Theory Appl. 45, 897–934 (2017).
You, X., Sauls, J. A. & Koch, J. Circuit quantization in the presence of time-dependent external flux. Phys. Rev. B 99, 174512 (2019).
Houck, A. A. et al. Controlling the spontaneous emission of a superconducting transmon qubit. Phys. Rev. Lett. 101, 080502 (2008).
Bourassa, J. et al. Ultrastrong coupling regime of cavity qed with phase-biased flux qubits. Phys. Rev. A 80, 032109 (2009).
Niemczyk, T. et al. Circuit quantum electrodynamics in the ultrastrong-coupling regime. Nat. Phys. 6, 772–776 (2010).
Filipp, S. et al. Multimode mediated qubit-qubit coupling and dark-state symmetries in circuit quantum electrodynamics. Phys. Rev. A 83, 063827 (2011).
Viehmann, O., von Delft, J. & Marquardt, F. Superradiant phase transitions and the standard description of circuit qed. Phys. Rev. Lett. 107, 113602 (2011).
Nigg, S. E. et al. Black-box superconducting circuit quantization. Phys. Rev. Lett. 108, 240502 (2012).
Solgun, F., Abraham, D. W. & DiVincenzo, D. P. Blackbox quantization of superconducting circuits using exact impedance synthesis. Phys. Rev. B 90, 134504 (2014).
Messiah, A. Quantum Mechanics, Vol. 1 (North Holland, 1961). [Eq. VIII.49].
Landauer, R. Can capacitance be negative? Collect. Phenom. 2, 167–170 (1976).
Catalan, G., Jiménez, D. & Gruverman, A. Negative capacitance detected. Nat. Mater. 14, 137–139 (2015).
Ng, K., Hillenius, S. J. & Gruverman, A. Transient nature of negative capacitance in ferroelectric field-effect transistors. Solid State Commun. 265, 12 – 14 (2017).
Hoffmann, M. et al. Ferroelectric negative capacitance domain dynamics. J. Appl. Phys. 123, 184101 (2018).
Luk’yanchuk, I., Tikhonov, Y., Sené, A., Razumnaya, A. & Vinokur, V. M. Harnessing ferroelectric domains for negative capacitance. Commun. Phys. 2, 22 (2019).
Hoffmann, M., Slesazeck, S., Schroeder, U. & Mikolajick, T. What’s next for negative capacitance electronics? Nat. Electron. 3, 504–506 (2020).
Abdumalikov, A. A.Jr. Experimental realization of non-abelian non-adiabatic geometric gates. Nature 496, 482–485 (2013).
Roushan, P. et al. Observation of topological transitions in interacting quantum circuits. Nature 515, 241–244 (2014).
Niemeyer, J. & Kose, V. Observation of large dc supercurrents at nonzero voltages in josephson tunnel junctions. Appl. Phys. Lett. 29, 380–382 (1976).
Dolan, G. J. Offset masks for lift off photoprocessing. Appl. Phys. Lett. 31, 337–339 (1977).
Feynman, R. P. The Feynman lectures on physics (Reading, Mass. : Addison-Wesley Pub. Co., 1963-1965).
Zangwill, A. Modern electrodynamics (Cambridge Univ. Press, Cambridge, 2013). Chap. 14.9.
Ruehli, A. E. Inductance calculations in a complex integrated circuit environment. IBM J. Res. Dev. 16, 470–481 (1972).
Ruehli, A. E. & Brennan, P. A. Efficient capacitance calculations for three-dimensional multiconductor systems. IEEE Trans. Microw. Theory Techn. 21, 76–82 (1973).
Altland, A. & Zirnbauer, M. R. Nonstandard symmetry classes in mesoscopic normal-superconducting hybrid structures. Phys. Rev. B 55, 1142–1161 (1997).
Chiu, C.-K., Teo, J. C. Y., Schnyder, A. P. & Ryu, S. Classification of topological quantum matter with symmetries. Rev. Mod. Phys. 88, 035005 (2016).
van Heck, B., Akhmerov, A. R., Hassler, F., Burrello, M. & Beenakker, C. W. J. Coulomb-assisted braiding of majorana fermions in a josephson junction array. New J. Phys. 14, 035019 (2012).
Jackson, J. D. Classical electrodynamics 2nd edn. (Wiley, New York, NY, 1975).
London, F. Macroscopic theory of superconductivity, Vol. 1. (Wiley, New York, NY, 1950).
Bardeen, J. & Pines, D. Electron-phonon interaction in metals. Phys. Rev. 99, 1140–1150 (1955).
Bardeen, J., Cooper, L. N. & Schrieffer, J. R. Theory of superconductivity. Phys. Rev. 108, 1175–1204 (1957).
Matute, E. A. On the superconducting sphere in an external magnetic field. Am. J. Phys. 67, 786–788 (1999).
Reagor, M. et al. Reaching 10ms single photon lifetimes for superconducting aluminum cavities. Appl. Phys. Lett. 102, 192604 (2013).
Deutscher, G. New Superconductors: From Granular to High TC (WORLD SCIENTIFIC, 2006).
Gubin, A. I., Il’in, K. S., Vitusevich, S. A., Siegel, M. & Klein, N. Dependence of magnetic penetration depth on the thickness of superconducting nb thin films. Phys. Rev. B 72, 064503 (2005).
Kubo, S., Asahi, M., Hikita, M. & Igarashi, M. Magnetic penetration depths in superconducting nbn films prepared by reactive dc magnetron sputtering. Appl. Phys. Lett. 44, 258–260 (1984).
Ogasawara, T., Kubota, Y. & Yasukochi, K. Magnetic properties of superconducting niobium-tantalum alloys. J. Phys. Soc. Jpn. 25, 1307–1323 (1968).
Peikari, B. Fundamentals of Network Analysis and Synthesis. (Prentice-Hall, Englewood Cliffs, New Jersey, 1974).
Tinkham, M.Introduction to Superconductivity 2nd edn (Dover Publications, 2004).
Poincaré, H. Sur les courbes définies par les équations différentielles (III). J. Math. Pures Appl. 1, 167–244 (1885).
Eisenberg, M. & Guy, R. A proof of the hairy ball theorem. Am. Math. Mon. 86, 571–574 (1979).
Cottet, A. Implementation of a quantum bit in a superconducting circuit. Ph.D. thesis, Université Paris VI (2002).
Little, W. A. Device application for super-inductors, in Proc. of the Symposium on the Physics of Superconducting Devices, Charlottesville, VA (1967), pp. S-1.
Meservey, R. & Tedrow, P. M. Measurements of the kinetic inductance of superconducting linear structures. J. Appl. Phys. 40, 2028–2034 (1969).
Wang, C. et al. Measurement and control of quasiparticle dynamics in a superconducting qubit. Nat. Commun. 5, 5836 (2014).
Acknowledgements
We thank F. Hassler, I. Pop, and G. Catelani for stimulating discussions. We gratefully acknowledge funding by the German Federal Ministry of Education and Research within the funding program “Photonic Research Germany” under contract number 13N14891, and within the funding program “Quantum Technologies - From Basic Research to the Market” (project GeQCoS), contract number 13N15685. D. P. D. thanks the OpenSuperQ project (820363) of the EU Flagship on Quantum Technology, H2020-FETFLAG-2018-03, for support.
Author information
Authors and Affiliations
Contributions
Overall, both authors were equally involved in the conceiving of the project, as well as the discussion and interpretation of the results. Explicit calculations were mostly conducted by R.-P.R. Both authors contributed to the writing of the text and reviewed the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Riwar, RP., DiVincenzo, D.P. Circuit quantization with time-dependent magnetic fields for realistic geometries. npj Quantum Inf 8, 36 (2022). https://doi.org/10.1038/s41534-022-00539-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41534-022-00539-x
This article is cited by
-
Observation of Josephson harmonics in tunnel junctions
Nature Physics (2024)
-
Compact description of quantum phase slip junctions
npj Quantum Information (2023)
-
Quasiperiodic circuit quantum electrodynamics
npj Quantum Information (2023)